Работа магнитных сил – Магнитное поле и его свойства. Магнитная индукция. Сила Ампера. Работа при перемещении проводника в магнитном поле. Намагничивание веществ, страница 23
- Комментариев к записи Работа магнитных сил – Магнитное поле и его свойства. Магнитная индукция. Сила Ампера. Работа при перемещении проводника в магнитном поле. Намагничивание веществ, страница 23 нет
- Работа для всех
Силы магнитного поля. Работа сил магнитного поля — Мегаобучалка
Основные формулы
1. Сила Ампера, действующая на элемент тока d в магнитном поле с индукцией В:
dFA = I d B sin ,
где I-сила тока, – угол между направлением вектора и силы тока.
2. Сила Ампера, действующая на все элементы тока сложной формы проводника:
3. Сила Лоренца, действующая на заряд q, движущийся со скоростью V в магнитном поле с индукцией B:
Л = q V B sin ,
где – угол между направлениями векторов и .
4. Сила взаимодействия параллельных проводников с токами I1 и I2
F = ,
где – длина проводников, d – расстояние между ними, = 4 Н/А2 – магнитная постоянная вакуума.
5. Сила, действующая на рамку с током в неоднородном магнитном поле:
= ,
где Рm – магнитный момент рамки с током, d /d – градиент индукции магнитного поля.
6. Работа магнитных сил по перемещению проводника с током
A = I .
7. Работа магнитных сил по перемещению замкнутого контура c током
A = I (Ф2 –Ф1),
где Ф1 и Ф2 – магнитный поток через площадь, ограниченную контуром с током в начальном и конечном состояниях.
Примеры решения задач
Задача 1. Квадратная рамка с током 2 А расположена в одной плоскости с длинным прямым проводником, по которому течёт ток 10 А. Сторона рамки 15 см. Ближайшая сторона рамки отстоит от проводника на расстоянии 10 см. Найти силу, действующую на рамку.
| Дано: I1 = 2 A I2 = 10 A a = 5 см = 0,15 м в = 10 см = 0,1 м F-? | Решение Прямой проводник с током I1 создаёт вокруг себя неоднородное магнитное поле, индукция которого уменьшается с увеличением расстояния r согласно формуле В 1 = . (1) |
В таком магнитном поле на каждую сторону квадратной рамки с током I2 будет действовать сила Ампера, направление которой определяется по правилу левой руки (рис. 6.1).
Силы F1 и F3 можно найти, используя закон взаимодействия параллельных токов:
F1 = ,
F3 = .
Для нахождения силы F2 разобьём проводник на элементы тока I2d (рис. 6.2). Пусть некоторый элемент расположен на расстоянии r от тока I1. В месте расположения элемента тока I2d индукция поля направлена к нам и определяется формулой (1). Сила Ампера, действующая на элемент тока I2d (d = dr):
Поскольку все силы d A направлены в одну сторону, то вся сила
.Заметим, что сила F4 = F2 , но противоположно направлена.
Результирующая сила, действующая на рамку с током I2 :
F = F1 – F3 + F2 – F4 = F1 – F3 .
F = = .
Подставим числовые значения:
F = = 0,36 .
Задача 2. Проводник в виде тонкого полукольца радиусом 0,1 м находится в однородном магнитном поле с индукцией 0,05 Тл. По проводнику течёт ток 10 А. Найти силу, действующую на проводник, если плоскость полукольца перпендикулярна линиям индукции.
| Дано: R = 0,1 м В = 5×102 Тл I = 10 А F – ? | Решение Разобьем проводник на элементы тока Id , причем d = R×da (рис. 6.3). Рис. 6.3 |
Положение элемента на окружности будем углом . Со стороны магнитного поля на элемент тока будет действовать сила Ампера dF:
, (1)
где угол между элементом тока и магнитной индукцией .
Разложим силу dF на две составляющие силы dFY и dFX.
, .
Заметим, что ввиду симметрии силы dFXi от всех элементов проводника уничтожат друг друга, а результирующая сила по оси Y будет отлична от нуля.
. (2)
Подставим в выражение (2) формулу (1) и после интегрирования получим
= .
Подставим числовые значения:
Н.
Задача 3. Небольшая катушка с током, имеющая магнитный момент 2 А/м2, находится на оси кругового витка радиусом 20 см, по которому идёт ток 10 А. Найти модуль силы, действующей на катушку, если её расстояние от центра витка равно 10 см. Вектор магнитного момента совпадает по направлению с осью витка.
| Дано: Рм = 2 А/ м2 R = 20 см=0,2 м I = 10 А А=10 см=0,1 м F – ? | Решение Магнитное поле кругового витка является неоднородным. В таком поле на магнитный момент катушки будет действовать сила (1)Градиент индукции направлен в сторону возрастания индукции (рис 6.4), направление магнитной индукции В определяется по правилу буравчика. |
Выберем ось X вдоль оси витка и спроецируем выражение (1) на эту ось.
. (2)
Индукция магнитного поля от кругового тока
. (3)
Возьмём производную от выражения (3) по переменной X:
.
Окончательно для силы FX имеем при X = а
.
Знак минус означает, что катушка будет втягиваться в область сильного поля.
Подставим числовые значения:
= Н = мН.
Задача 4. Квадратная рамка со стороной 2 см, содержащая 100 витков, подвешена на упругой нити с постоянной кручения 10 мкН/град. Плоскость рамки совпадает с направлением линий индукции внешнего магнитного поля. Определить индукцию магнитного поля, если при пропускании по рамке тока 1 А она повернулась на угол 60 0, а также определить работу сил, действующих со стороны магнитного поля (рис. 6.5).
Дано: Решение
а = 2 см = 2 м
N = 100 витков
C = 10-5 Н/град
= 900
I = 1 А= 600
B-? А-?
Рис. 6.5
Рамка с током находится в равновесии при выполнении условия: , где -момент сил, действующих на рамку с током, – момент упругих сил, действующих на рамку.
Известно, что
M1 = ,
M2 = , .
Магнитный момент рамки .
Учитывая, что , получим .
Теперь можно найти величину индукции магнитного поля:
.
Подставим числовые значения:.
Найдём работу сил магнитного поля по повороту рамки на угол :
,
.
Знак минус в выражении для означает, что под действием момента сил М происходит убыль угла α.
Работу сил магнитного поля можно вычислить и другим способом:
,
где – приращение потока вектора через поверхность контура с током I.
.
Задача 5. Протон движется в магнитном поле с индукцией Тл по винтовой линии радиусом 2 см и шагом 5 см. Определить скорость протона и угол её наклона к линиям индукции.
| Дано: R = 2×10-2 м В = 10-2 Тл qп = 1,.6×10-19 Кл mп = 1,67×10-27 кг h = 5 см = 5×10-2 м V – ? a – ? |
Решение
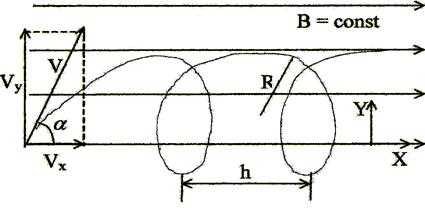 Заряженная частица движется в магнитном поле по винтовой линии, если она в него влетает под углом a к линиям индукции (рис 6.6).
|
Движение по винтовой линии считается двумерным. Введём оси координат X и Y . Поскольку магнитное поле однородное, то движение вдоль общих осей будет равномерным. Скорость частицы раскладываем на две проекции VX и VY, причём
, (1)
. (2)
Шаг винтовой линии (расстояние между витками) определяется как
, (3)
где Т – период обращения по окружности, которая расположена в плоскости Y. Движение по окружности происходит со скоростью . Период обращения
. (4)
Выражение (4) подставим в формулу (3):
.
Из последнего выражения определим угол наклона скорости V к оси X:
.
, .
Радиус винтовой линии определяется выражением
,
из которого определим скорость VY:
.
м/с.
Искомую скорость V определим по формуле (2):
м/с.
Задача 6
|
I1 = 5 A
I2 = 15 A
a = 50 см = 0,5 м
в = 10 см = 0,1 м
Так как магнитное поле проводника с током I2 неоднородное, сначала определим элементарный поток dФ через площадку dS = , в пределах которой индукцию магнитного поля можно считать постоянной величиной (рис. 6.7):
,
где – угол между нормалью к элементу dS и вектором индукции = .
Полный магнитный поток через площадь всей рамки найдём суммированием всех dФ:
.
Соответственно после поворота магнитный поток .
Так как = 0, , то Ф2 = 0. Окончательно работа по повороту рамки
.
Подставим числовые значения:
.
megaobuchalka.ru
3.15. Работа сил магнитного поля
На движущиеся
заряды в магнитном поле действует сила
Лоренца, которая всегда перпендикулярна
скорости движения заряженной частицы
и, следовательно, ее перемещению
.
На проводник с
током в магнитном поле действует сила
Ампера. Совершает ли работу эта сила?
Рассмотрим прямолинейный проводник
длиной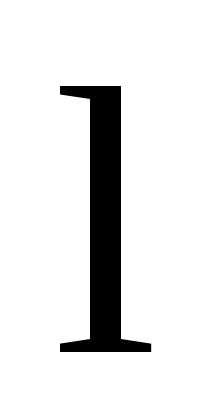 
и током I
в однородном магнитном поле (рис. 3.22а).
Работа силы Ампера при перемещении
проводника на расстояние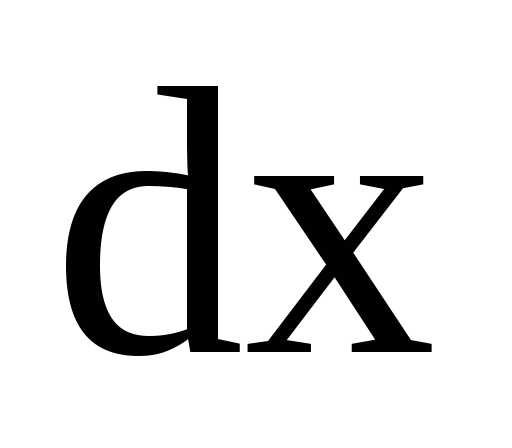 
вдоль
направления силы
где – площадь, которую очерчивает проводник при движении, ВdS=dФ – магнитный поток пронизывающий эту площадь.
dА=IdФ, (3.32)
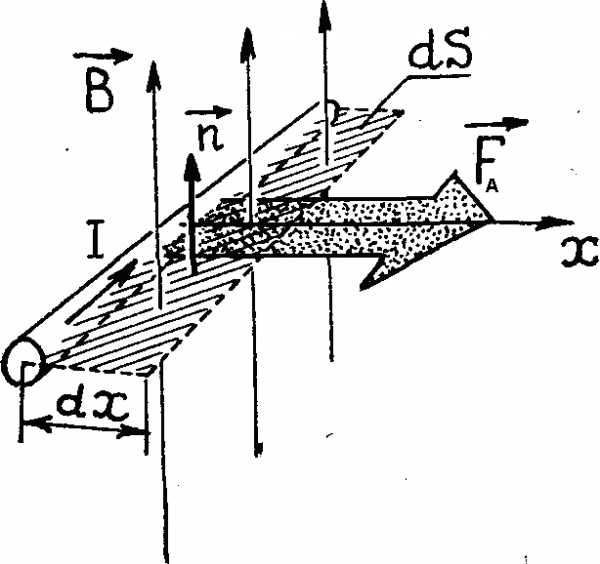
а) б)
Рис.3.22
Следовательно,
элементарная работа, совершаемая силой
Ампера, равна произведению тока в
проводнике I на магнитный поток dФ,
пронизывающий площадь, которую очерчивает
проводник при своем движении. При перемещении проводника на конечное
расстояние x,
получаем: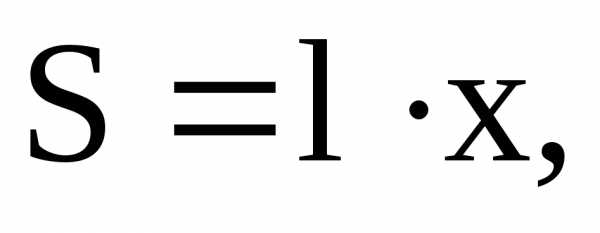 
и
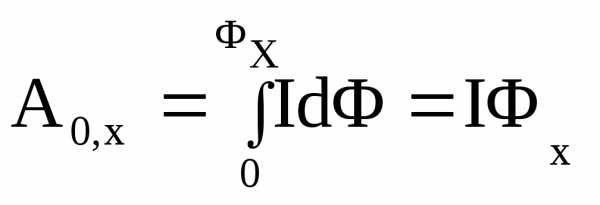(3.33)
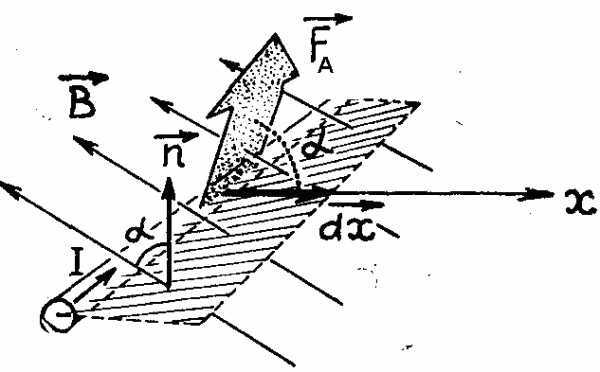
Если перемещение проводника происходит в произвольном направлении (рис. 3.22б), то
где 
– угол между
и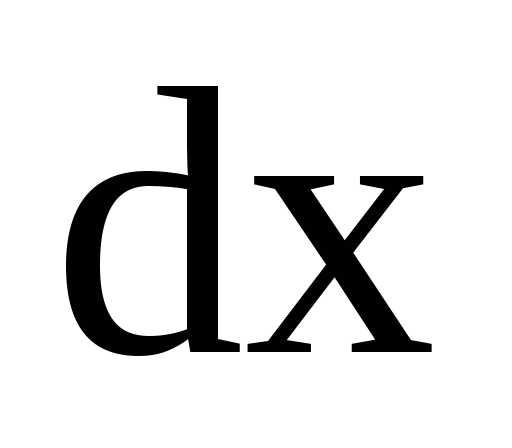
или, что то жеРис.
3.23.
самое,
между 
и
,
так как
,
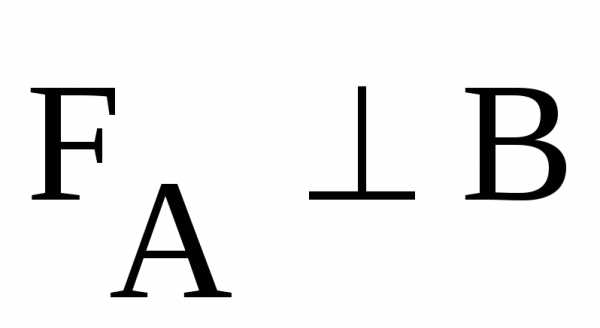а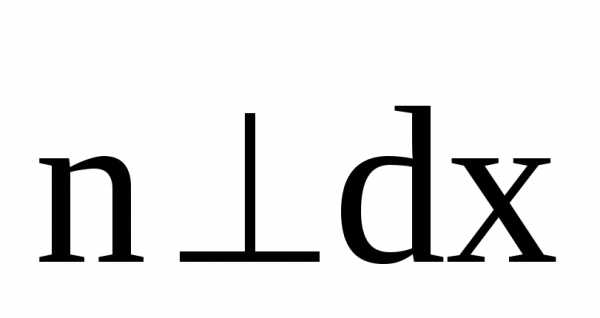
.
Ноldх=dS,
BdSсоs
=dФ,
так что по-прежнему dA=IdФ.
На
контур с током в магнитном поле действует
сила Ампера 
,
которая вращает его вокруг оси (рис.
3.23). Чтобы найти работу, совершаемую
при конечном вращением контура,
необходимо проинтегрировать соотношение
(3.32).
,
где 
и
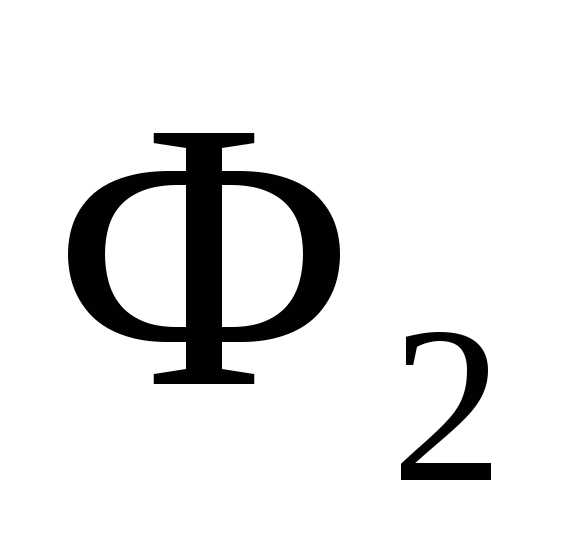потоки, пронизывающие контур в его
начальном и конечном положении.
Вопросы и задания для самопроверки.
Дайте определение магнитного потока и назовите случаи когда он максимальный и минимальный.
Чему равен поток в однородном и неоднородном магнитных полях?
Чему равен поток через замкнутую и незамкнутую поверхности?
В каких единицах в системе СИ измеряется магнитный поток?
Выведите формулу для работы сил по перемещению проводника в магнитном поле.
Какая сила совершает работу в магнитном поле?
Будет ли совершаться работа при движении заряженной частицы в магнитном поле?
3.16. Магнитное поле в веществе
Вещество состоит
из атомов, а атомы из электронов и ядер.
Электрон, вращаясь по замкнутой орбите
вокруг ядра, образует орбитальный
(дипольный) магнитный момент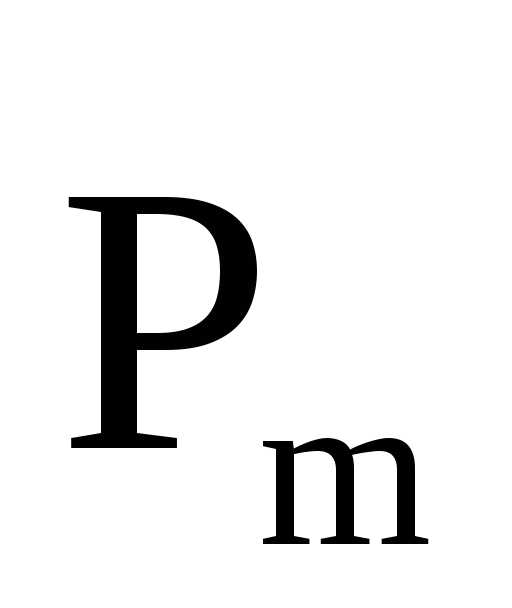 
.
Кроме того, электрон обладает собственным
механическим моментом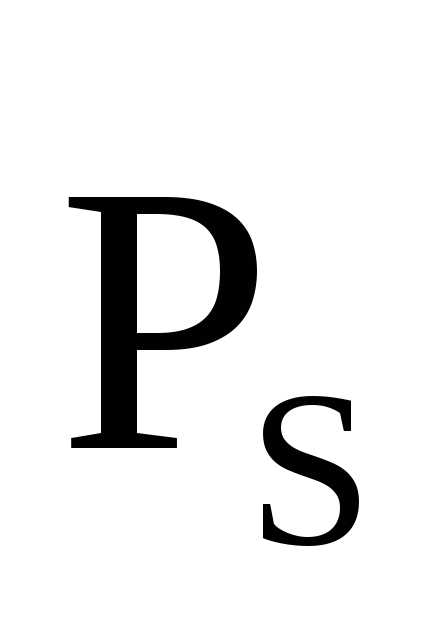
,
называемымспином. Спину
электрона соответствует спиновой
магнитный момент 
.
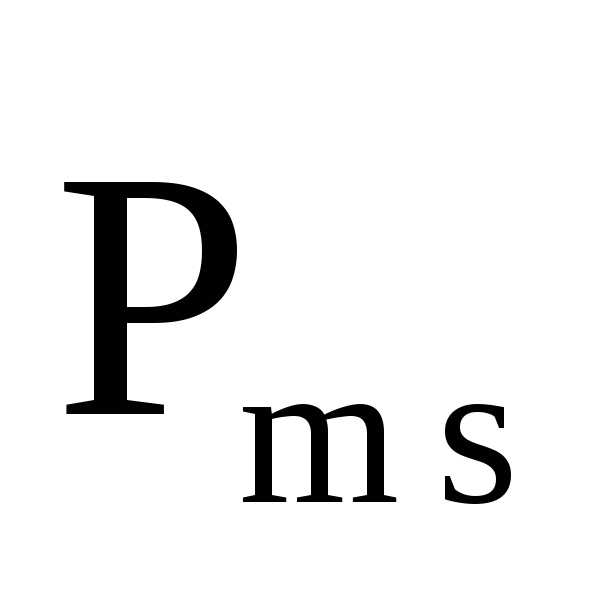Магнитный момент атома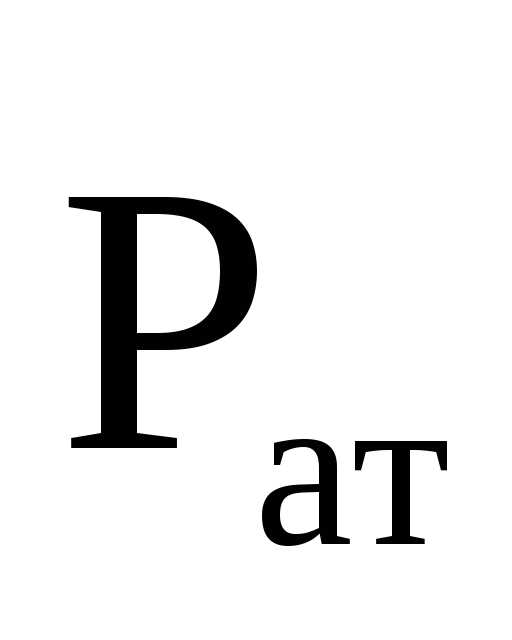 
геометрически складывается из орбитальных
магнитных моментов его электронов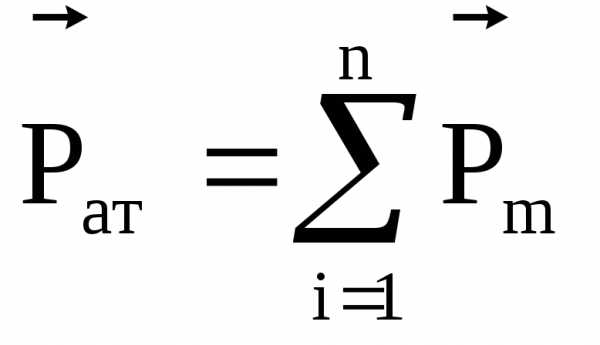
,
где
число
электронов в атоме.
Внешнее магнитное
поле с индукцией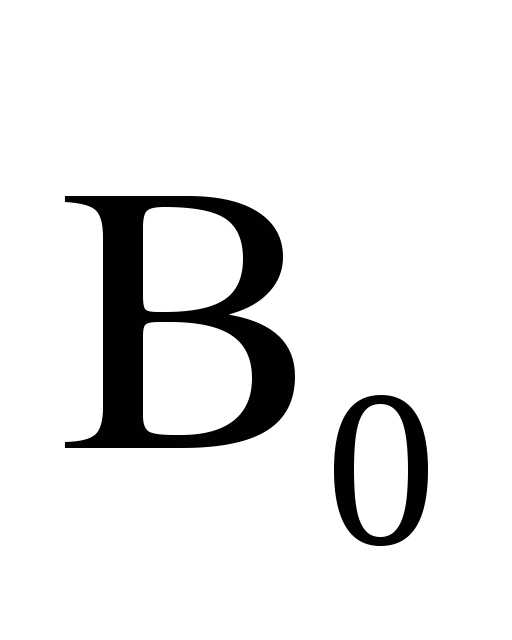 
влияет на магнитные моменты атомов
вещества и создает в нем дополнительное
магнитное поле. Это явление называется
намагничиванием. Индукция магнитного
поля в веществе
, (3.34)
где 
–
индукция магнитного поля, образованного
в результатенамагничивания.
Отличие магнитного
поля в веществе 
от индукции внешнего магнитного поля
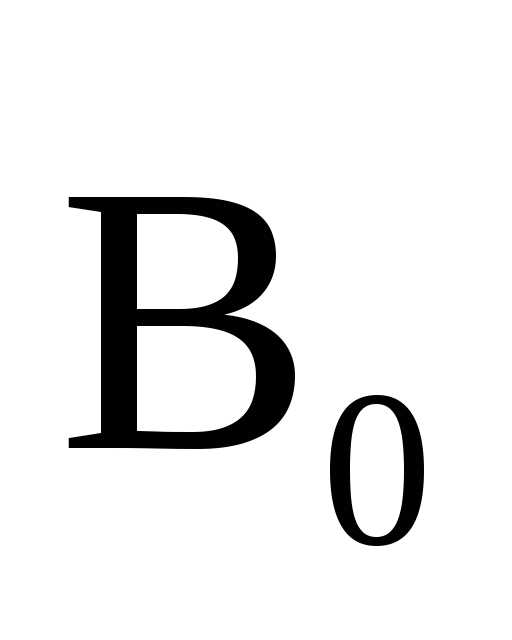определяется относительной магнитной
проницаемостью среды
.Магнитная
проницаемость показывает, во сколько
раз изменяется магнитное поле в веществе
по сравнению с внешним магнитным полем. Величина 
находится из соотношения
.
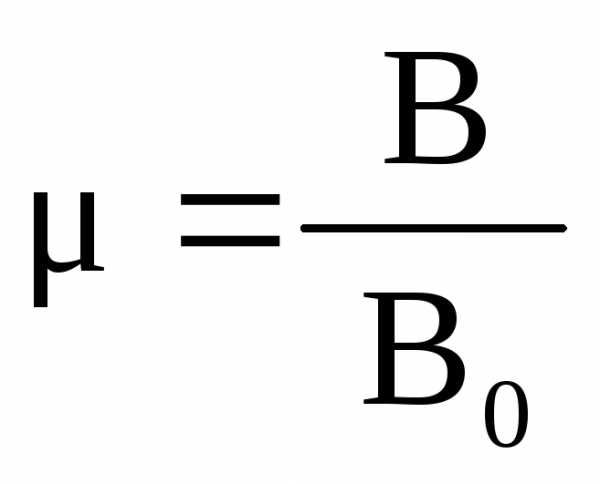Намагничивание
вещества определяется вектором
намагниченности 
:
,
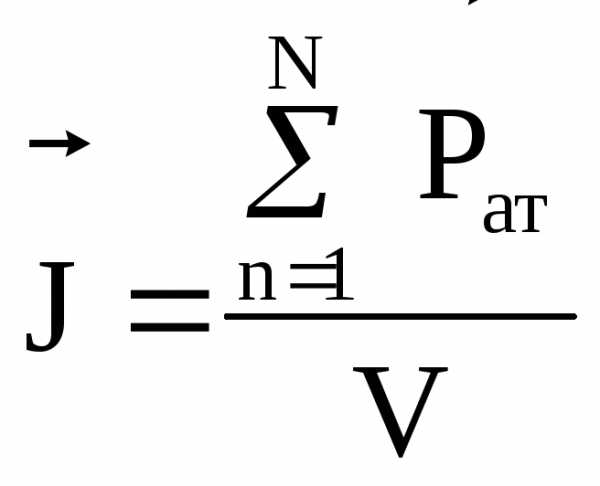где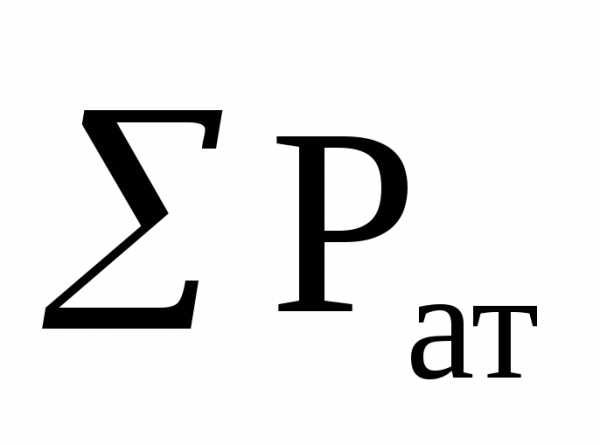 
– суммарный магнитный моментN
атомов в веществе объёмом V.
Как показывает
опыт, для большинства веществ и слабых
полей, магнитное поле 
пропорционально вектору намагниченности
и определяется как
.
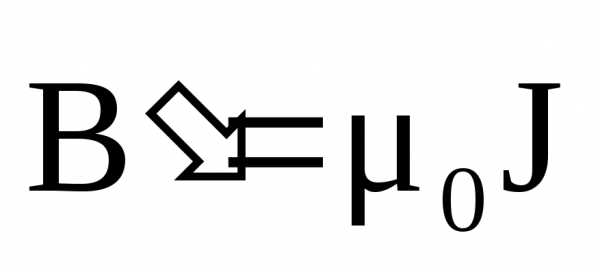Учитывая, что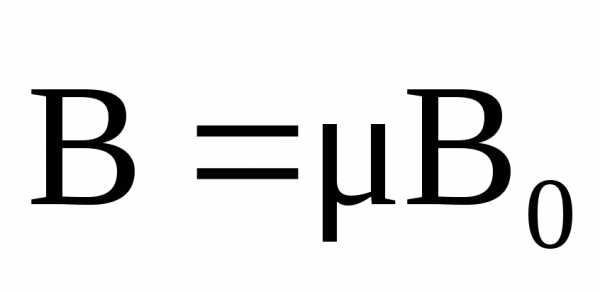 
равенство (3.34) можно записать в виде:
,
, (3.35)
а вектор намагниченности
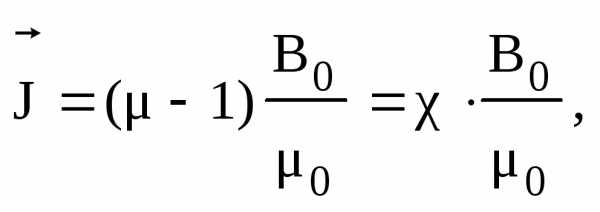(3.36)
где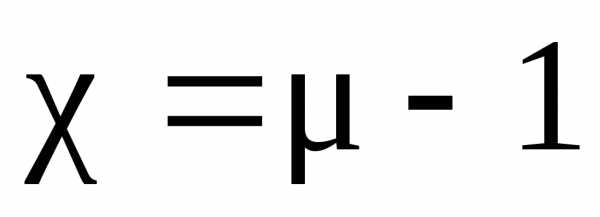 
– магнитная восприимчивость вещества.
studfiles.net
48. Работа магнитного поля по перемещению проводника и контура с током
Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис.). Этот контур находится во внешнем однородном магнитном поле , перпендикулярном к плоскости контура. При показанном на рисунке направлении токаI, вектор сонаправлен с.
На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо:
Пусть проводник l переместится параллельно самому себе на расстояние dx. При этом совершится работа:
Итак,
| , |
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.
Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис.). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток , пронизывающий контур, направлен по нормалик контуру, поэтому.
Переместим этот контур параллельно самому себе в новое положение 1′-2′-3′-4′-1′. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком .
Площадка 4-3-2′-1′-4, расположенная между старым и новым контуром, пронизывается потоком .
Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
где , равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).
.
Провод 1–2 перерезает поток ( ), но движется против сил действия магнитного поля.
.
Тогда общая работа по перемещению контура
или
| , |
|
|
здесь – это изменение магнитного потока, сцепленного с контуром.
Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.
Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле
| , |
Это соотношение остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется , то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу
49. Энергия магнитного поля. Объемная плотность энергии магнитного и электромагнитного полей
Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля. Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна Значит, энергия магнитного поля, которое связано с контуром, (1) Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем Так как I=Bl/(μ0μN) и В=μ0μH , то (2) где Sl = V — объем соленоида. Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью (3) Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам.
studfiles.net
действие магнитного поля, вращающий момент магнитного поля, работа сил магнитного поля
Магнитное поле воздействует с определенной силой на любой перемещающийся в нем электрический заряд.
Сила, действующая на движущийся в магнитном поле электрический заряд, направлена перпендикулярно к магнитным силовым линиям.
Аналогично одиночному электрическому заряду проводник с током, помещенный в магнитном поле, также испытывает действие сил магнитного поля.
Величина механической силы, действующей на прямолинейный проводник с током, помещенный в однородное магнитное поле, определяется по формуле
где I – ток в амперах;
B – магнитная индукция в теслах;
l – активная длина провода с током в метрах;
α – угол, под которым расположен проводник по отношению к магнитным силовым линиям.
Направление механической силы, действующей на помещенный в магнитное поле проводник с током, определяет правило левой руки: если расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее, а вытянутые пальцы указывали направление тока, то отставленный большой палец укажет направление силы, действующей на проводник.
Если в однородном магнитном поле помещен плоский контур прямоугольной формы с током, то на него действует пара сил, стремящихся повернуть контур вокруг оси (рисунок в начале статьи).
Вращающий момент этой пары сил равен произведению величины одной из сил на расстояние (плечо) между токами приложения этих сил:
Вращающий момент, действующий на контур с током, можно определить по формуле
где В – магнитная индукция внешнего поля в теслах;
I – ток контура в амперах;
S – площадь проекции рамки на плоскость, перпендикулярную магнитным силовым линиям в квадратных метрах;
Мвр – вращающий момент в ньютон-метрах;
α – угол между перпендикуляром к плоскости контура и направлением магнитных силовых линий.
Контур с током стремится установиться во внешнем магнитном поле так, чтобы внутри контура внешнее магнитное поле и собственное магнитное поле контура совпали по своему направлению. При этом, α = 0 и Мвр = BIsin0 = 0.
Вращающий момент плоской катушки с числом витков ω определяется по формуле
Направление пары сил, действующих на контур с током и на плоскую катушку, определяется по правилу левой руки.
Два достаточно длинных прямолинейных и параллельно расположенных проводника одинаковой длины с токами I1 и I2 взаимодействуют друг с другом, причем сила взаимодействия равна
где µ – магнитная проницаемость среды;
d – расстояние между проводниками в метрах
l – длина проводника в метрах;
I1,I2 – сила тока в проводниках в амперах;
F – сила взаимодействия в ньютонах.
Два параллельных проводника с токами одинакового направления взаимно притягиваются, а проводники с токами противоположного направления взаимно отталкиваются.
Механические силы, действующие на проводник, совершают некоторую работу.
Работа сил магнитного поля определяется по формуле
где В – магнитная индукция внешнего магнитного поля в теслах;
I – сила тока в проводнике в амперах;
l – активная длина проводника в метрах;
d – расстояние, на которое переместился проводник с током под действием сил магнитного поля, в метрах;
А – работа сил магнитного поля в джоулях.
Поделитесь этой статьей с друзьями в социальных сетях:
Свяжитесь с автором статьи в социальных сетях:
lightelectronics.ru
Механическая работа в магнитном поле — Мегаобучалка
 |
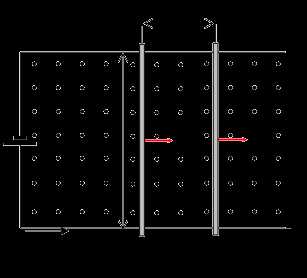Так как на проводник с током в магнитном поле действуют силы Ампера, то при перемещении проводника эти силы совершают работу. Пусть в однородном магнитном поле проводник длиной совершает поступательное движение в направлении, перпендикулярном направлению вектора (рис. 4.14). Для простоты будем считать, что этот проводник скользит по двум параллельным шинам и замыкает электрическую цепь. Вектор индукции магнитного поля направлен к нам. Тогда сила Ампера направлена вправо, и при перемещении проводника с током на расстояние совершается работа
.
Произведение равно площади контура S между двумя положениями подвижного проводника, а – изменение магнитного потока, пронизывающего контур при движении проводника . Следовательно, работа силы Ампера может быть выражена через силу тока I и изменение магнитного потока :
| (4.3) |
Полученный результат можно применить для подсчета работы в случае неоднородного поля. Для этого, используя выражение (4.3), можно посчитать работу силы Ампера на тех участках, на которых поле можно считать однородным, а затем просуммировать работы на отдельных участках. В результате можно получить, что результирующая работа сил Ампера равна
,
где разность равна изменению магнитного потока через поверхность контура, то есть разности потоков вектора магнитной индукции в конечном и начальном положениях контура.
Это интересно!
Магнитное поле Земли
Туристам и путешественникам, живущим на Земле, крупно повезло, так как Земля обладает достаточно сильным магнитным полем, полюса которого к тому же расположены близко к географическим полюсам. Далеко не все планеты Солнечной системы обладают такими свойствами. Кроме Земли, лишь у Юпитера, Сатурна, Урана и Нептуна имеются магнитные поля.
По сравнению с магнитными полями, с которыми мы сталкиваемся в повседневной жизни (сердечники акустических колонок, магнитные импульсы переменного тока в бытовых приборах, лампы, линии электропередач и др.), магнитное поле Земли относится к разряду очень слабых полей. Так, к примеру, магнитный элемент защелки книжного шкафа создает магнитное поле, магнитная индукция которого в 10 раз превосходит индукцию магнитного поля Земли. Тем не менее, это так называемое главное геомагнитное поле, имеющее планетарную природу, существует на 3емле повсеместно.
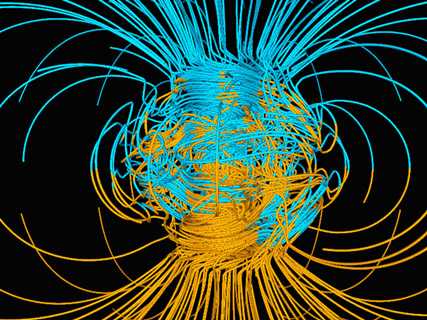
Компьютерная модель магнитного поля Земли.
Голубым цветом показаны линии, направленные внутрь, желтым – наружу.
Почему у Земли есть магнитное поле? На вопрос о том, чем это вызвано, до настоящего времени нет точного ответа. Более того, достоверно известно, что так было не всегда. За счет проводимости расплавленной плазмы в земном ядре магнитное поле Земли должно было исчезнуть за несколько тысяч лет. Однако у нашей Земли, возраст которой пять миллиардов лет, все еще существует сильное магнитное поле. Эта загадка до сих пор не раскрыта, но в последнее время считают, что магнитное поле объясняется движениями во внешней жидкой оболочке ядра Земли: по мере того как внешняя оболочка ядра охлаждается, и части ее падают внутрь, океаны магмы, богатой железом, поднимаются вверх под действием вращения Земли. Геологи полагают, что именно это движение поддерживает земной магнетизм.
| Современное местонахождение Северного и Южного магнитных полюсов |
Точки Земли, в которых индукция магнитного поля имеет вертикальное направление, называют магнитными полюсами. Таких точек на Земле две: северный магнитный полюс (в южном полушарии) и южный магнитный полюс (в северном полушарии). Магнитные полюса Земли не остаются на месте. Они перемещаются, а иногда меняются местами. В настоящее время Северный магнитный полюс находится в точке с координатами 79°19′ северной широты и 105°26′ западной долготы у полуострова Исаксен острова Эллеф-Рингнес на севере Канады, Южный – на 67°2′ южной широты и 142° восточной долготы. В районе полюсов силовые линии магнитного поля практически вертикально входят в землю, вследствие чего не могут повернуть магнитную стрелку компаса, и ориентирование становится невозможным. Индукция магнитного поля в точках магнитного экватора имеет горизонтальное направление. Линии магнитной индукции, идущие от одного магнитного полюса до другого, образуют так называемые магнитные меридианы. Магнитная стрелка устанавливается вдоль этих линий.
Средняя индукция поля на поверхности Земли составляет около 50 мкТл и сильно зависит от географического положения. Индукция магнитного поля на магнитном экваторе примерно в 2 раза меньше, чем у магнитных полюсов. В некоторых районах (в так называемых районах магнитных аномалий, например, Курская магнитная аномалия) индукция магнитного поля резко возрастает.
Знакомство человека с удивительными свойствами земного магнетизма состоялось еще на заре исторического времени. Уже в античную эпоху людям был известен магнитный железняк – магнетит. А вот кто и когда определил, что природные магниты всегда ориентируются одинаково в пространстве по отношению к географическим полюсам Земли, точно неизвестно. В китайских трактатах, датированных XII в. до н.э., встречаются фрагменты, которые можно истолковать как свидетельства применения компаса для целей навигации. Первые из известных описаний компаса появились в Китае лишь спустя 23 столетия – в XI, а в Европе еще позже – в XII в. Первым же достоверным сообщением о магнитном компасе, появившемся в Европе, мы обязаны английскому монаху Александру Некэму. Он около 1187 г. описал устройство, состоящее из стрелки, указывающей направление, причем в его компасе стрелка плавала, а не была подвешена на нити. Еще одной важной вехой в истории геомагнетизма является письмо, написанное в 1269 г. Пьером де Мерикуром. В этом послании, в частности, говорилось, что природный магнит имеет два полюса, и что полюсы эти стремятся установиться вдоль географического меридиана, указывая на полюса 3емли – северный и южный.
Магнитные бури
Еще в средние века мореплаватели обратили внимание, что бывают дни, когда стрелка компаса вдруг начинает беспорядочно колебаться в продолжение нескольких часов и даже нескольких суток, делая компас совершенно непригодным для навигационных расчетов. Это явление моряки и окрестили магнитной бурей. Но только в XVIII в. французский астроном Лемонт заметил, что интенсивность и частота магнитных бурь тем больше, чем больше на Солнце пятен. Это стало первым открытием связи земных явлений с солнечной активностью.
Магнитное поле Земли захватывает из космического пространства заряженные частицы (протоны и электроны), которые движутся вдоль силовых линий магнитного поля и образуют так называемый радиационный пояс Земли. Для погоды в космосе, как и для погоды в обычном понимании этого слова, характерно чередование спокойных периодов (например, минимум цикла солнечной активности) с периодами резкой смены обстановки с мощными колебаниями радиационного пояса, которые вызывают магнитные бури. Оценка, состояние и протяженность магнитной бури зависят не от нашей планеты, а от ближайшей звезды, то есть Солнца.
Солнце представляет собой кипящий атомный котел. Это термоядерный шар гигантских размеров. Поскольку температура верхних слоев атмосферы Солнца (корона) около миллиона градусов, атомы водорода и гелия приобретают такие громадные скорости, что при столкновениях выбивают друг у друга электроны. В результате многочисленных столкновений некоторые частицы развивают такие большие скорости, что им удается преодолеть притяжение Солнца и навсегда уйти в окружающее космическое пространство. Эти потоки плазмы, берущие свое начало в короне Солнца и двигающиеся в обычных условиях со скоростью около 200 км/с, получили название «солнечный ветер». В моменты солнечной активности солнечный ветер от 200 км/с (привычной скорости) достигает скорости 1000 км/с и летит к Земле, через сутки-двое достигает Земли и приводит к нарушению равновесия геомагнитной обстановки Земли. Она становится неспокойной, величина индукции магнитного поля увеличивается, и образуется магнитная буря.
Землю можно рассматривать как большой магнит, южный полюс которого располагается вблизи северного географического полюса, а северный – вблизи южного. Силовые линии магнитного поля Земли выходят из области северного магнитного полюса Земли, охватывают нашу планету и входят в нее в области южного магнитного полюса Земли. Когда плазма солнечного ветра встречает на своем пути магнитное поле Земли, она, согласно законам физики, сначала сжимает магнитные силовые линии, а затем начинает обтекать Землю. На обращенной к Солнцу стороне Земли граница обтекания устанавливается на расстоянии 10–12 радиусов Земли. На ночной стороне магнитное поле вытягивается в виде шлейфа, похожего на хвост кометы, до расстояний около 1000 радиусов Земли. Вся эта область, в которой заключено магнитное поле и околоземная плазма, называется магнитосферой Земли. Магнитосфера Земли надежно ограждает нашу планету от мощного потока космических частиц.
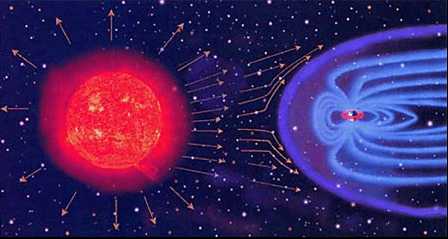Взаимодействие солнечного ветра с магнитосферой Земли
|
Какое же воздействие оказывают магнитные бури на земные процессы? Было замечено, что частота инфарктов миокарда и инсультов у пожилых людей резко возрастала в дни, когда наблюдались магнитные бури. Во время солнечных вспышек резко возрастает количество несчастных случаев и травматизма на транспорте и в производстве
Существует немало свидетельств воздействия магнитных бурь на технические системы и сооружения, особенно на линии электропередач и металлические нефте- и газопроводы. Хорошо известна магнитная буря 13 марта 1989 г., которая привела к короткому замыканию в главном трансформаторе Квебекского гидроузла. В результате более 6 млн канадцев и американцев на 9 часов остались без электричества. Уже стали привычными сообщения о потере спутников во время сильных магнитных бурь из-за сбоев в работе электронных систем управления и связи, а также о преждевременном сходе их с орбит и гибели в плотных слоях атмосферы.
Сегодня уже понятны некоторые физические механизмы, лежащие в основе воздействия магнитных бурь на технические, биологические и природные объекты. Так, лабораторные эксперименты показали, что во время магнитных бурь на поверхности металлических конструкций возникают наведенные электрические токи. Они-то и становятся причиной пожаров и взрывов на нефте- и газопроводах и повреждений в линиях электропередач. Наведенные токи на поверхности искусственных спутников Земли иногда вызывают сбои в работе гироскопов стабилизации, что приводит к их сходу с орбит и гибели в плотных слоях атмосферы. Сильные вариации магнитного поля Земли во время магнитных бурь создают наведенные токи не только в металлических проводниках, но также и на поверхности Земли. Именно это стало причиной аварии трансформатора в Квебеке.
Полярное сияние
Особенно интересным и зрелищным эффектом, сопровождающим магнитную бурю, является полярное сияние. Полярные сияния разной формы и окраски возникают на высоте 80–1000 км. Долгое время полярные сияния рассматривали как предвестников катастроф – эпидемий, голода и войн. Например, это явление связали с падением Иерусалима и смертью Юлия Цезаря. В этом видели проявление гнева богов или других сверхъестественных сил.
Сегодня известно, что полярные сияния сигнализируют о месте и времени воздействия Космоса на земные процессы. Мы знаем, что это свечение верхней атмосферы в высоких широтах северного и южного полушарий Земли, которое вызывается энергичными заряженными частицами, вторгающимися в земную магнитосферу на своем пути от Солнца.
Если заряженная частица движется вдоль силовых линий магнитного поля, то оно никак не влияет на ее движение. В высоких широтах Земли силовые линии магнитного поля почти вертикальны, что создает благоприятные условия для проникновения частиц в атмосферу Земли.
Если заряженная частица движется перпендикулярно к силовым линиям магнитного поля, на нее действует сила Лоренца, которая закручивает ее вокруг силовой линии магнитного поля. В результате при отсутствии столкновений с другими частицами рассматриваемые частицы будут просто вращаться вокруг силовых линий. Столкновения могут приводить к перескоку частиц с одних круговых орбит на другие. Но скорость такого движения существенно меньше, чем скорость направленного движения потока частиц при отсутствии магнитного поля. В низких широтах силовые линии почти параллельны поверхности Земли. Поэтому, чтобы частицы, вызывающие полярное сияние, могли здесь проникнуть в атмосферу, они должны прорваться поперек силовых линий Земли, а это для них практически невозможно.
Если частица движется под определенным углом к направлению магнитного поля, то такое движение можно разложить на два независимых движения: перпендикулярно к силовым линиям магнитного поля и параллельно им. Траектория частицы в этом случае будет спиралью, накручивающейся на силовую линию магнитного поля. Шаг спирали зависит от величины продольной скорости, а радиус – от поперечной скорости. Таким образом, заряженная частица, попадая в магнитное поле Земли, может достигнуть ее атмосферы только в полярных областях, независимо от того, где она оказалась вначале.
Электроны и протоны, попавшие из солнечного ветра в магнитное поле Земли, стекают в область полюсов, где достигают плотных слоев атмосферы и возбуждают атомы и молекулы газов. Для этого они имеют достаточно энергии. Возбужденные атомы испускают энергию в виде света. Анализ спектров излучения в полярных сияниях показывает, что зеленое и красное свечение испускается возбужденными атомами кислорода, а инфракрасное и фиолетовое – ионизованными молекулами азота.
megaobuchalka.ru
Тема № 2. Силы магнитного поля. Работа сил магнитного поля Краткие теоретические сведения для решения задач
2.1. Действие магнитного поля на токи, магнитные моменты
На проводники с током, находящиеся в магнитном поле, действуют силы, называемые силами Ампера. Сила Ампера, приложенная к малому элементу проводника с токомI(рис. 2.1),равна арифметической сумме сил Лоренца, которые действуют на движущиеся в проводнике носители заряда.
,dFA=IdlBsina, (2.1)
где
dn – количество носителей заряда в элементе
проводника длиной dl и сечением S,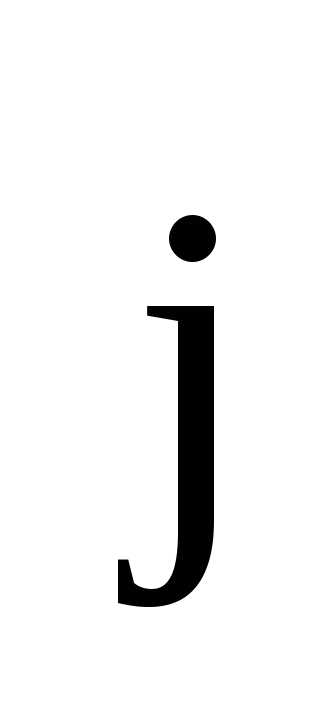 
– плотность тока в проводнике, I – сила тока в проводнике, 
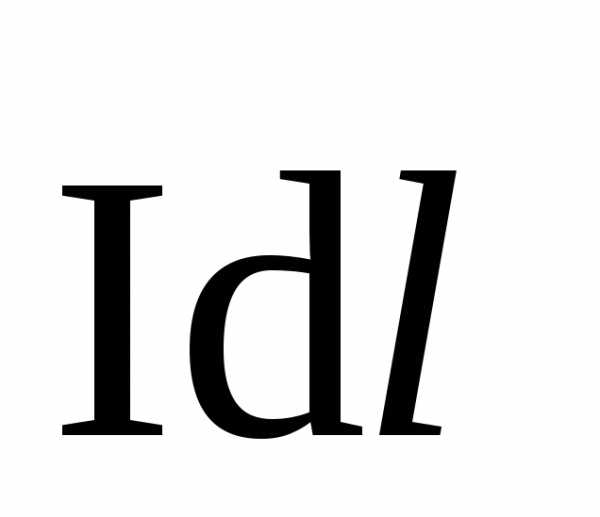– линейный элемент тока, α
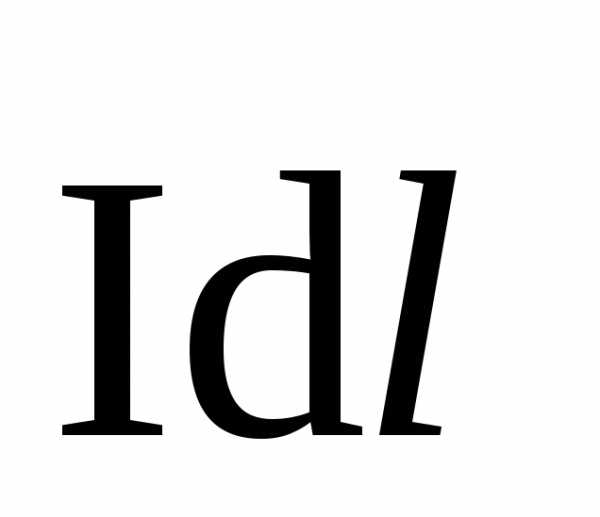угол между векторами 
и
.
Сила Ампера, действующая в магнитном поле на проводник конечной длины,
, . (2.2)
В частности, если поле однородно, а проводник прямолинейный, то
F = IBl sin (2.3)
Расчет силы Ампера, действующей на участок длиной l бесконечно длинного проводника с током I2 со стороны длинного прямолинейного проводника с током I1, расположенного параллельно данному проводнику, дает величину:
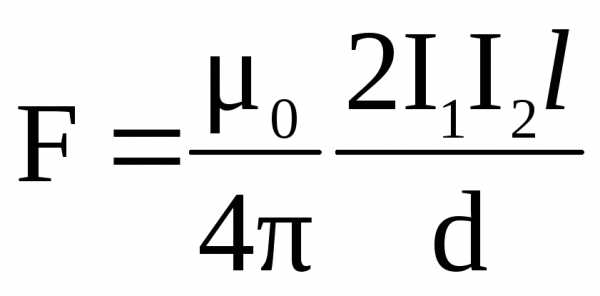,(2.4)
где
d
расстояние между проводниками, о=4
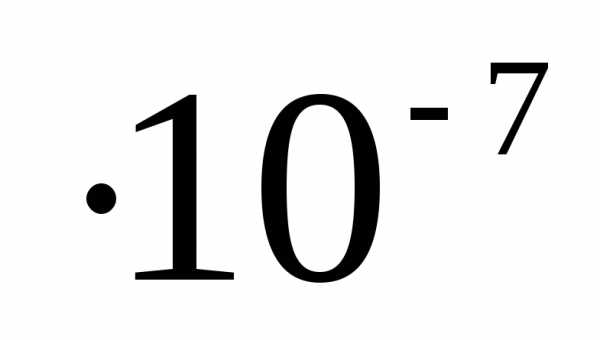Гн/м
магнитная постоянная.
На
малый замкнутый контур с током (магнитный
момент) в однородном магнитном поле
действует вращающий момент сил
(рис. 2.2)
,
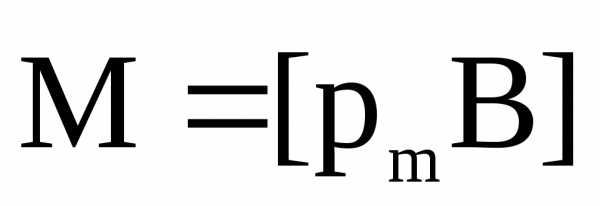М = рmВsin
, (2.5)
где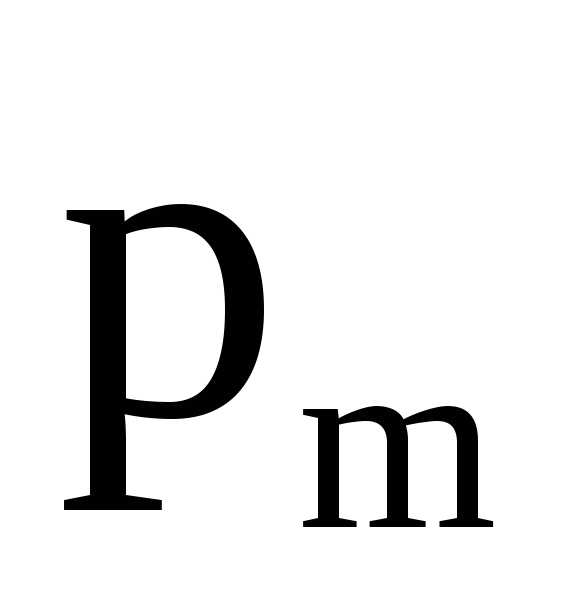 
магнитный момент контура с током, а
угол между векторами магнитного момента
и магнитной индукции.
М
омент сил стремится установить
магнитный момент по направлению магнитной
индукции
в положение устойчивого равновесия.
Если внешние силы увеличивают угол,
то они совершают работу против сил
магнитного поля и тем самым увеличивают
энергию контура, которую можно вычислить
следующим способом
,. (2.6)
В неоднородном магнитном поле на магнитный момент дополнительно действует отличная от нуля сила, сообщающая ему поступательное движение
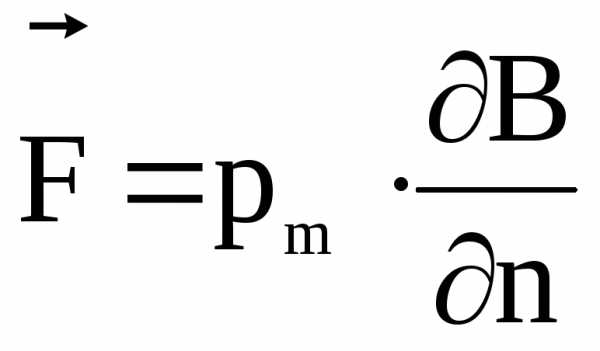, (2.7)
где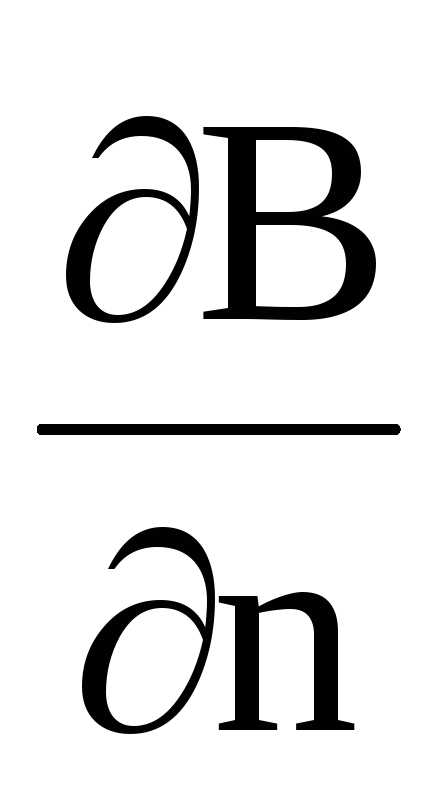 
производная вектора магнитной индукции
по направлению магнитного момента.
2.2. Действие магнитного поля на заряженные частицы
На
частицу с электрическим зарядом q,
движущуюся в магнитном поле со скоростью 
,
направленной произвольным образом по
отношению к вектору магнитной индукции
,
действуетсила
Лоренца
=q[
,
].
В скалярном виде величина силы Лоренца может быть представлена формулой:
F Л = qBsin , (2.8)
где
– угол между векторами 
и 
(рис.
1.1).
Сила Лоренца влияет на направление вектора скорости и сообщает частице нормальное ускорение.
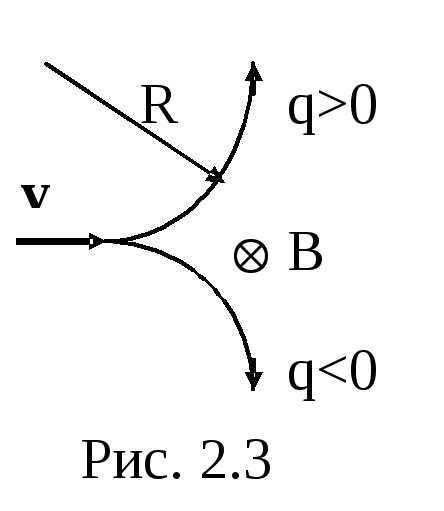Радиус
окружности R
(рис. 2.3), по которой движется частица,
можно найти из соотношения:
,
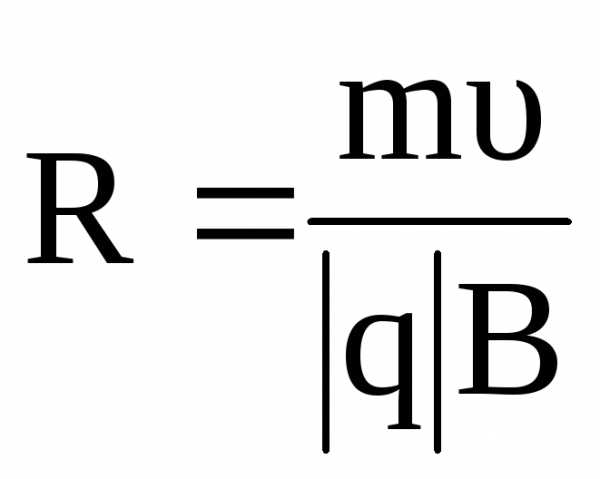если 
. (2.9)
Период обращения частицы
.
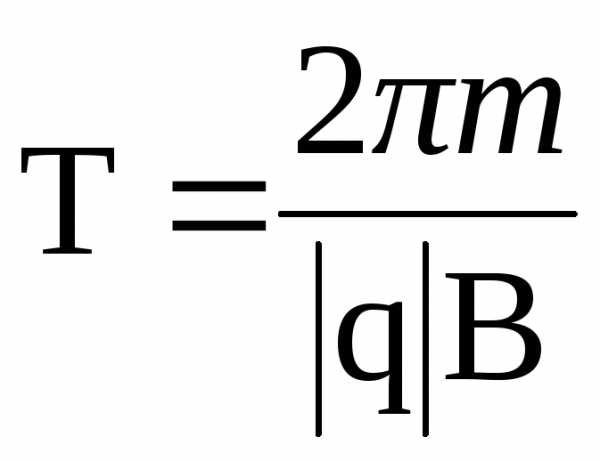(2.10)
Если
вектор скорости 
заряженной
частицы составляет угол
с направлением вектора 
однородного
магнитного поля, то частица движется
по винтовой линии, навивающейся на линию
магнитной индукции поля. РадиусR и
шаг h
винтовой линии (при <<c):
R=msin /(|q|B), (2.11)
h=2mcos/(B|q|). (2.12)
2.3. Работа сил магнитного поля
Элементарная
работа А,
совершаемая силой Ампера d
А при малом перемещении d
в магнитном поле элемента токаId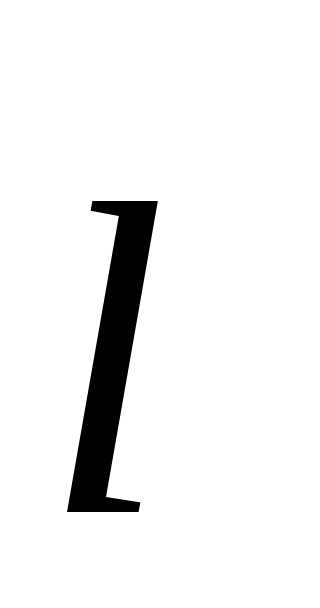
A
= 
= = 
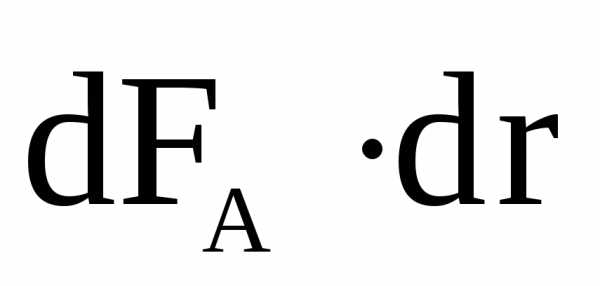= I
dm,
(2.13)
где dm магнитный поток сквозь поверхность, которую прочерчивает элемент проводника при его перемещении.
Работа перемещения проводника с током в постоянном магнитном поле
A = I∙m, (2.14)
где Fm – магнитный поток сквозь поверхность, которую прочерчивает весь проводник при его полном перемещении.
Работа при перемещении в магнитном поле замкнутого контура с постоянным током I из положения 1 в положение 2
A12 = I (Фm2 –Фm1) =Im, (2.15)
где Фm1 и Фm2 – магнитные потоки через поверхность контура с током в начальном и конечном положениях.
Если в магнитном поле перемещается катушка, имеющая N витков, то работа может быть определена
A12 = I 12 = INФm12,
где – изменение потокосцепления контура при его перемещении.
Все приведенные соотношения справедливы, если значения сил токов в проводниках поддерживаются неизменными при любых перемещениях.
studfiles.net
2.5. Механические силы и работа тока в магнитном поле
На проводник с током, помещенный в магнитное поле, действует механическая сила F, стремящаяся сместить проводник (рис. 17). Направление этой силы удобно определять, пользуясь правилом левой руки: нужно поставить ладонь навстречу направлению поля (чтобы магнитные линии входили в ладонь) и вытянуть четыре пальца вдоль проводника по направлению тока, тогда отставленный большой палец покажет направление механической силы, действующей на проводник и стремящейся сместить этот проводник. Так как эта сила есть следствие взаимодействия тока и магнитного поля, то она часто именуется электромагнитной силой.
Эта сила F пропорциональна произведению силы тока I на магнитную индукцию В поля, в котором находится проводник. Она пропорциональна также активной длине проводника l (т. е. длине той части проводника, которая находится в магнитном поле) и зависит от направления проводника по отношению F. Если прямолинейный проводник образует с направлением магнитных линий угол α, а магнитная индукция вдоль всей длины l одинакова (т. е. магнитное поле равномерно), то электромагнитная сила
F=B·I·l sin α, (2.1)
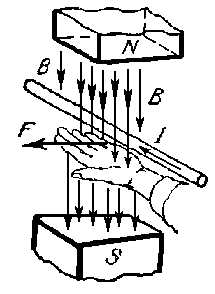
Рис. 17
Если проводник расположен практически перпендикулярно к направлению магнитного поля sin α = 1, что имеет место в большом числе электрических машин и аппаратов, тоF=B·I·l (2.2)
В системе СИ электромеханическое действие магнитного поля можно использовать для определения единицы магнитной индукции. Тесла (Тл) — это индукция в таком равномерном магнитном поле, в котором на прямолинейный проводник длиной в 1 м, когда по нему проходит ток силой в 1 А, действует сила в 1 Н; при этом направление проводника образует с нап-равлением поля угол 90°. Следовательно, 1 Тл = (Н/А)·м. Напомним, что Н•м = Дж = В•А•сек, на основании чего тесла Тл = (Дж/А) •м2 = В •А •(сек/А) •м2 = сек/м2 = Вб/м2,
1 Тл=104 Гс.
Рис. 18
Если длина измерена в сантиметрах, что делается в большинстве случаев при практических электротехнических расчетах, тоF = 0,01B I l sin, Н
или, если же индукция измерена в гауссах и длина в сантиметрах, а желательно определить силу в килограммах,
F= 10,2B I l sin10-8, кГ. (2.3)
Электромагнитные силы используются во всех электродвигателях для получения вращающего момента, а в генераторах они создают тормозящий момент, который должен преодолевать первичный двигатель.
В обоих случаях проводники на вращающейся части машины расположены практически перпендикулярно к направлению магнитного поля, следовательно, = 90°, sin = 1, а электромагнитная сила в этих условиях будет:
F=B·I·l.
2.6. Электромагнитная индукция
Закон электромагнитной индукции можно рассматривать как прямое следствие закона электромагнитной силы, хотя он был выведен на основании экспериментов.
В проводнике, движущемся в магнитном поле, возбуждается электрическое поле, пропорциональное магнитной индукции и скорости движения проводника. В проводнике происходит смещение зарядов против направления сил электрического поля, как это имеет место внутри всякого источника электроэнергии. Следовательно, здесь действует э.д.с., называемая индуктированной э.д.с. Если проводник движется под углом α к направлению магнитного поля, то э.д.с. будет:
E = –υBl sinα (2.4)
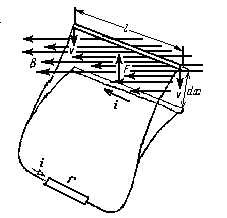
Рис. 19
Направление смещения зарядов в проводнике можно определить при помощи правила левой руки. Но проще определять непосредственно направление э. д. с. по правилу правой руки (рис. 18): если поставить правую руку ладонью навстречу магнитным линиям и направить отставленный большой палец по направлению движения проводника, то вытянутые пальцы покажут направление индуктированной э.д.с.Знак минус в уравнении э.д.с. выражает собой принцип Ленца — то обстоятельство, что индуктированная э.д.с. стремится противодействовать причине, ее вызывающей. Например, если замкнуть проводник на некоторое сопротивление (рис.19), то э. д. с. вызовет в созданном таким образом контуре ток i. Взаимодействие этого тока с магнитным полем создаст электромагнитную силу, противодействующую движению проводника, т. е. причине, возбуждающей э. д. с. в контуре.
Закон электромагнитной индукции может быть выражен и другой формулой, имеющей более общее значение. Скорость движения проводника может быть выражена через путь dx, проходимый им за время dt, т, е. υ = dх / dt. На основании этого
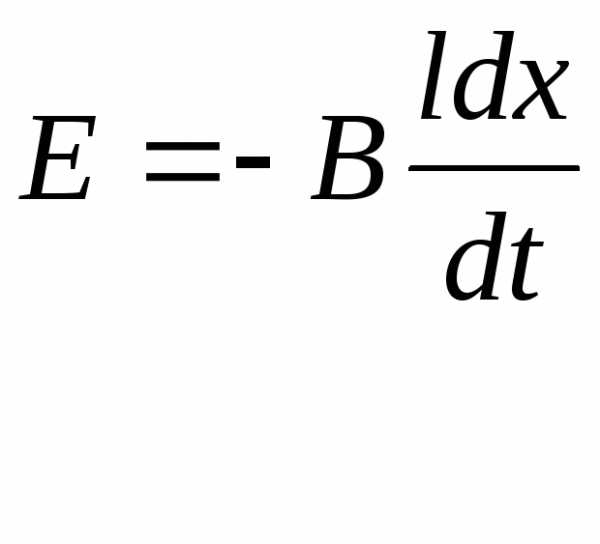
Произведение индукции В на площадь ldx есть магнитный поток dФ = Вldх, пересеченный проводником за время dt; следовательно,
.
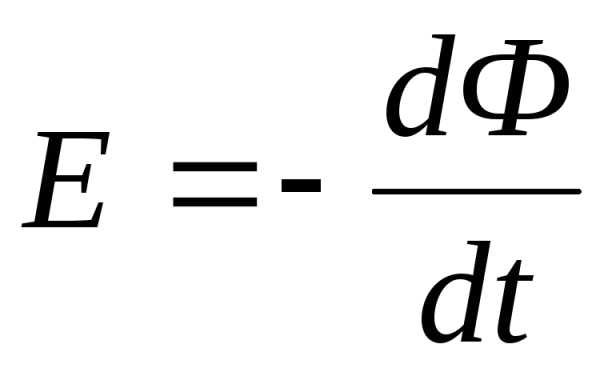(2.5)
Вэтом уравненииdФ — поток, который проводник пересек за время dt, но вместе с тем dФ есть изменение потока Ф, сцепленного с контуром, в котором индуктируется э. д. с. Следовательно, индуктированная э. д. с. равна скорости изменения потока, сцепленного с контуром. На основании закона электромагнитной индукции определяется единица магнитного потока. Один вебер есть магнитный поток, при убывании которого до нуля за 1 сек в контуре, сцепленном с этим потоком, индуктируется э. д. с., равная 1 В.
Электрические токи индуктируются не только в проводах обмоток электрических машин, аппаратов и приборов, но они возникают в любых проводящих телах, находящихся в переменном магнитном поле. Они называются вихревыми токами. В электрических цепях токи направлены вдоль проводников и замыкаются по точно определенным путям. Вихревые токи замыкаются непосредственно в проводящей массе образуя в ней вихреобразные контуры, сцепляющиеся с индуктирующим эти токи магнитным потоком.
Согласно принципу Ленца магнитное поле вихревых токов стремится противодействовать изменениям магнитного потока, их индуктирующего, вследствие чего при переменном намагничивающем токе вихревые токи обладают сильным размагничивающим действием, в частности в массивном железном сердечнике они почти полностью уничтожают переменный магнитный поток. Кроме того, они вызывают значительные потери энергии на нагревание сердечника.
studfiles.net
