Что такое интеграл на понятном языке – как понять и решать неопределенные и определенные интегралы, правила и примеры - Центр социальной реабилитации инвалидов и детей-инвалидов Фрунзенского района Санкт-Петербурга

30.04.202016.08.2019

Что такое интеграл на понятном языке – как понять и решать неопределенные и определенные интегралы, правила и примеры

Содержание

Объясните, пожалуйста, что такое интеграл и как его расчитывать (подробно).

интеграл это противоположное производной, брать его по таблице

Интеграл показывает площадь функции. Разбивает на бесконечное количество маленьких кусочков и суммирует. А рассчитывать – это зависит от того какой интеграл – определенный или нет.

Тут в вопросе речь об ОПРЕДЕЛЁННОМ интеграле. Определённый интеграл есть обощение понятия “сумма” на случай непрерывного изменения “слагаемых”. Поэтому проще всего его представлять себе как площадь под кривой. Вот если задана какая-то функция, то её интеграл “в пределах от t до t+Δt” – это берётся кривая, описываемая функцией, берутся две точки на оси х (t и t+Δt), и ищется площадь “кривого прямоугольника”, у которого нижнее основание – кусок оси х между этими точками, верхнее основание – кусок кривой между этими же точками, ну а высота оказывается переменной. (Если часть кривой – или даже она вся – лежит ниже оси Х, то высота считается отрицательной, так что и значение интеграла может оказаться отрицательным. ) КАК СЧИТАТЬ интеграл – это уже отдельный вопрос. Да, для вычисления определённого интеграла надо уметь считать неопределённые интегралы, которые представляют собой функцию. Вычисление неопределённого интегграла есть операция, обратная нахождению производной. То есть если f(x) = F'(x), то по определению F(x) есть неопределённый интеграл от f(x). Функция F(x) называется первообразной от f(x) – аналогично тому, как f(x) называется производной от F(x). И тогда определённый интеграл от f(x) в пределах от а до b – при некоторых условиях – равен разности значений первообразной на пределах интегрирования, т. е. F(b) – F(a), или, как для примера в вопросе, F(t+Δt) – F(t).

В девятом классе это объясняют примерно так: определённый интеграл – это площадь криволинейной трапеции, ограниченной сверху графиком функции. Пусть у нас есть какая-то величина, которая меняется со временем – например, скорость при неравномерном движении. А нам необходимо найти путь, пройденный телом. Вот это и делается с помощью интеграла. Формально для этого составляется интегральная сумма – мы разбиваем процесс движения тела на маленькие промежутки по времени – по миллисекунде, например – Δt = 0,001 мс. Измеряем во время этой миллисекунды скорость, получаем какое-то её значение V1. Считаем, что за такое время скорость почти не изменяется, то есть движение на каждом промежутке равномерное. Тогда путь на этом небольшом отрезочке Δt будет Δs1 = V1 Δt. Потом переходим к следующей точке, там скорость уже меняется и Δs2 = V2 Δt и так далее по всему пути. Весь путь будет приближённо равен сумме этих маленьких отрезков s = Σ (VΔt). На графике это означает, что плавная кривая заменяется набором чёрточек, а площадь под кривой покрывается узенькими “столбиками”. Понятно, что скорость никогда не остаётся постоянной, а непрерывно изменяется, поэтому чем чаще мы будем измерять её очередное значение, тем точнее вычислим путь. Поэтому интеграл – это предельный случай, когда мы берём значение в каждой точке, то есть когда Δt -> 0. Это и записывается как интеграл: s ≈ Σ (VΔt) -> ∫ V dt При этом V = ds/dt – скорость есть производная пути по времени. Получается, что мы, вычисляя площадь, в каждой точке графика заменяем какую-то криволинейную функцию прямой (её производной) . Фактически с этого и начинают вычисление интеграла. Интегрирование – это действие, обратное дифференцированию. Чтобы вычислить интеграл, нужно найти первообразную подынтегральной функции в двух точках – на границах, указанных при интеграле (время начала движения – время окончания движения) . Пусть, например, тело свободно падает из состояния покоя. Тогда его скорость будет зависеть от времени как V = gt. Чтобы найти путь тела, нам нужно найти такую функцию, производная которой равна gt – это функция gt²/2 (что легко проверяется дифференцированием) . Получаем известную формулу пути s = gt²/2. Здесь и возникает связь с Δt. Если скорость от времени не изменяется, то (её можно вынести за знак интеграла) путь будет равен s = VΔt = V(t2-t1). Общих правил интегрирования нет. Есть даже интегралы, которые невозможно записать в элементарных функциях, но в школе такие не встретятся. Для распространённых функций существуют таблицы интегралов (легко гуглится).

Интеграл это первообразная.

touch.otvet.mail.ru

Что такое интеграл и зачем мне знать это — T&P

IMAGE 1287 NOT FOUND

Иллюстрация: Максим Чатский

Представьте, что у нас есть какая-то функция зависимости чего-то от чего-то.

Например, вот так примерно можно на графике представить скорость моей работы в зависимости от времени суток:

Скорость я измеряю в строках кода в минуту, в реальной жизни я программист.

Объем работы — это скорость работы умножить на время. То есть если я пишу 3 строки в минуту, то в час получается 180. Если у нас есть такой график, можно узнать, сколько работы я сделал за день: это площадь под графиком. Но как это посчитать?

Разделим график на столбики равной ширины величиной в час. А высоту этих столбиков сделаем равной скорости работы в середине этого часа.

Площадь каждого столбика по отдельности легко посчитать, надо умножить его ширину на высоту. Получается, что площадь каждого столбика — это сколько примерно я работы сделал за каждый час. А если просуммировать все столбики, то получится примерная моя работа за день.

Проблема в том, что результат получится примерный, а нам нужно точное число. Разобьем график на столбики по полчаса:

На картинке видно, что это уже гораздо ближе к тому, что мы ищем.

Так уменьшать отрезки на графике можно до бесконечности, и каждый раз мы все ближе и ближе будем подходить к площади под графиком. А когда ширина столбиков будет стремиться к нулю, тогда сумма их площадей будет стремиться к площади под графиком. Это и называется интегралом и обозначается вот так:

В этой формуле f(x) означает функцию, которая зависит от величины x, а буквы a и b — это отрезок на котором мы хотим найти интеграл.

Зачем это нужно?

Ученые стараются все физические явления выразить в виде математической формулы. Как только у нас есть формула, дальше уже можно при помощи нее посчитать что угодно. А интеграл — это один из основных инструментов работы с функциями.

Например, если у нас есть формула круга, мы можем при помощи интеграла посчитать его площадь. Если у нас есть формула шара, то мы можем посчитать его объем. При помощи интегрирования находят энергию, работу, давление, массу, электрический заряд и многие другие величины.

Нет, зачем мне это нужно?

Да низачем — просто так, из любопытства. На самом деле интегралы входят даже в школьную программу, но не так много людей вокруг помнят, что это такое.

theoryandpractice.ru

Неопределённый интеграл — Википедия

Неопределённый интегра́л для функции f(x){\displaystyle f(x)} — это совокупность всех первообразных данной функции^[1].

Если функция f(x){\displaystyle f(x)} определена и непрерывна на промежутке (a,b){\displaystyle (a,b)} и F(x){\displaystyle F(x)} — её первообразная, то есть F′(x)=f(x){\displaystyle F'(x)=f(x)} при a<x<b{\displaystyle a<x<b}, то

∫f(x)dx=F(x)+C,{\displaystyle \int f(x)dx=F(x)+C,} a<x<b{\displaystyle a<x<b},

где С — произвольная постоянная.

Основные свойства неопределённого интеграла приведены ниже.

d(∫f(x)dx)=f(x)dx{\displaystyle d\left(\int f(x)dx\right)=f(x)dx}

∫d(F(x))=F(x)+C{\displaystyle \int d(F(x))=F(x)+C}

ru.wikipedia.org

Что такое интеграл, и каков его физический смысл

Возникновение понятия интеграла было обусловлено необходимостью нахождения первообразной функции по ее производной, а также определения величины работы, площади сложных фигур, расстояния пройденного пути, при параметрах, очерченных кривыми, описываемыми нелинейными формулами.

Из курс

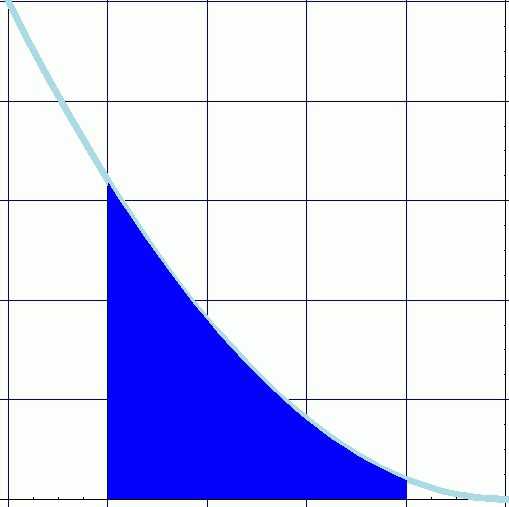а физики известно, что работа равна произведению силы на расстояние. Если все движение происходит с постоянной скоростью или расстояние преодолевается с приложением одной и той же силы, то все понятно, нужно их просто перемножить. Что такое интеграл от константы? Это линейная функция вида y=kx+c.

Но сила на протяжении работы может меняться, причем в какой-то закономерной зависимости. Такая же ситуация возникает и с вычислением пройденного расстояния, если скорость непостоянна.

Итак, понятно, для чего нужен интеграл. Определение его как суммы произведений значений функции на бесконечно малое приращение аргумента вполне описывает главный смысл этого понятия как площадь фигуры, ограниченной сверху линией функции, а по краям – границами определения.

Жан Гастон Дарбу, французский математик, во второй половине XIX века очень наглядно объяснил, что такое интеграл. Он сделал это настолько понятно, что в целом разобраться в этом вопросе не составит труда даже школьнику младших классов средней школы.

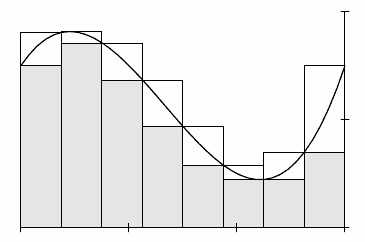
Допустим, есть функция любой сложной формы. Ось ординат, на которой откладываются значения аргумента, разбивается на небольшие интервалы, в идеале они бесконечно малы, но так как понятие бесконечности довольно абстрактно, то достаточно представить себе просто небольшие отрезки, величину которых обычно обозначают греческой буквой Δ (дельта).

Функция оказалась «нарезанной» на маленькие кирпичики.

Каждому значению аргумента соответствует точка на оси ординат, на которой откладываются соответствующие значения функции. Но так как границ у выделенного участка две, то и значений функции тоже будет два, большее и меньшее.

Сумма произведений бо́льших значений на приращение Δ называется большой суммой Дарбу, и обозначается как S. Соответственно, меньшие на ограниченном участке значения, умноженные на Δ, все вместе образуют малую сумму Дарбу s. Сам участок напоминает прямоугольную трапецию, так как кривизной линии функции при бесконечно малом ее приращении можно пренебречь. Самый простой способ найти площадь такой геометрической фигуры – это сложить произведения большего и меньшего значения функции на Δ-приращение и поделить на два, то есть определить как среднее арифметическое.

Вот что такое интеграл по Дарбу:

s=Σf(x) Δ – малая сумма;

S= Σf(x+Δ)Δ – большая сумма.

Итак, что такое интеграл? Площадь, ограниченная линией функции и границами определения будет равна:

∫f(x)dx = {(S+s)/2} +c

То есть среднее арифметическое большой и малой сумм Дарбу.с – величина постоянная, обнуляемая при дифференцировании.

Исходя из геометрического выражения этого понятия, становится понятен и физический смысл интеграла. Площадь фигуры, очерченная функцией скорости, и ограниченная временным интервалом по оси абсцисс, будет составлять длину пройденного пути.

L = ∫f(x)dx на промежутке от t1 до t2,

Где

f(x) – функция скорости, то есть формула, по которой она меняется во времени;

L – длина пути;

t1 – время начала пути;

t2 – время окончания пути.

Точно по такому же принципу определяется величина работы, только по абсциссе будет откладываться расстояние, а по ординате – величина силы, прилагаемая в каждой конкретной точке.

fb.ru

Объясните пожалуйста нормальныи понятным языком что такое производная и интеграл?

Не совсем строгие определения. Производная, это функция, полученная от другой функции следующим способом: 1. Независимому переменному в исходной функции дается некоторое приращение. (все в буквенных обозначениях) . 2. Вычисляется новое значение функции при новом значении независимой переменной. 3. Находится разница между новым значением функции и ее значением при старом значении независимого переменного. 4. Полученная разница (приращение функции) делится на приращении независимого переменного и находится предел этого сотношения при условии, что приращение стремится к нулю. Этот предел и называется производной от первоначальной функции. Конечно, существуют и свои правила нахождения предела. Что касается интеграла, нужно различать неопределенный интеграл от определенного. Если коротко и немножко утрированно, неопределенный интеграл это нахождение первоначальной функции (их бесконечное множество) при условии, что известна ее производная, а определенный интеграл – число полученному по вполне определенным правилам по которым сперва находится неопределенный интеграл, а затем находится соответтсвующее число. Думаю, что касается определенного интеграла, полезно вникнуть в само слово “интеграл”, которое можно перевести на русский язык как “сумма”. Совет: прочитайте хорошо несколько раз об этих понятиях в каком нибудь хорошем учебнике по высшей математике, где приведены несколько примеров и убедитесь в простоте самых понятиях. Ну а дальше, может быть, убедитесь, что математика не скучная наука и почувствуете ее прелесть

жопа полнейшая

Что такое интеграл и зачем он вообще нужен. Площадь ромба, площадь прамоугольника, площадь круга, площадь поверхности куба и т. д. ты знаешь как определять. Есть конкретные формулы. А как определить площадь с зигзагообразным периметром, т. е. какая- то площадь ограниченная какой-то невообразимой ломонной кривой. Например, как определить площадь поверхности озера или моря с их кривыми берегами? Эти расчеты можно сделать намного проще с помощью интеграла.

понятное и простое объеснение не даст точного понятия для применения этих понятий. ну если говорить проще, то интеграл-это сумма, сумма бесконечно малых или дифференциалов. дифференциал это в свою очередь -абстрактная вещь означающая, что то очень маленькое, настолько маленькое насколько можно представить

Кто такой интеграл, кто такая производная… Кто ты, кто я… -Вечная тема, мучащая диванных пи3даболов всех времен.

touch.otvet.mail.ru

ИНТЕГРАЛ – это… Что такое ИНТЕГРАЛ?

ИНТЕГРАЛ — (обозначение т ). Математический символ, используемый в ИСЧИСЛЕНИИ, представляющий операцию суммирования. Интеграл функции f(x), записанный как т f(x)dx, может представлять площадь фигуры, ограниченной кривой y=f(x) и осью абсцисс. ИНТЕГРИРОВАНИЕ … Научно-технический энциклопедический словарь

ИНТЕГРАЛ — (integral) Функция, первая производная (first derivative) которой равна другой функции. Если f(х) является первой производной от g(x), то, следовательно, g(x) является интегралом f(х) и, таким образом, h(x)=g(x)+k, где k – произвольно выбранная… … Экономический словарь

интеграл — а, м. intégrale f. &LT;лат. integer целый. Математическое понятие о целой величине как сумме своих бесконечно малых частей. Нахождение интеграла. БАС 1. Найти интеграл уравнения. 1766. Котельников Геодет 175. // Сл. 18. Алферинька недурно… … Исторический словарь галлицизмов русского языка

ИНТЕГРАЛ — муж., мат., лат. конечная, измеримая величина, в отношении к бесконечно малой части ее, к дифференциалу. Интегральное вычисление, искусство отыскивать интеграл по дифференциалу. Интегрировать, вычислять, находить интеграл; интеграция жен.… … Толковый словарь Даля

ИНТЕГРАЛ — (вово лат., от лат. integer ценный). В математике количество, дифференциал которого равен данной величине. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. интеграл (лат. integer целый) лет. 1) неопределенный и. от… … Словарь иностранных слов русского языка

интеграл — первообразная, термин Словарь русских синонимов. интеграл сущ., кол во синонимов: 2 • первообразная (1) • … Словарь синонимов

интеграл — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] интеграл Есть два различных понятия — неопределенный И. и определенный И. Говорят, что функция f(x) имеет … Справочник технического переводчика

ИНТЕГРАЛ — (от латинского integer целый), одно из основных понятий интегрального исчисления … Современная энциклопедия

ИНТЕГРАЛ — (от лат. integer целый) см. Интегральное исчисление … Большой Энциклопедический словарь

ИНТЕГРАЛ — [тэ ], а, муж. В математике: величина, получающаяся в результате действия, обратного дифференцированию. | прил. интегральный, ая, ое. Интегральное исчисление. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

dic.academic.ru

интеграл – это… Что такое интеграл?