Что такое матрицы: Матрицы в математике: определения и применение
- Матрицы: определение и основные понятия.
- Основные сведения о матрицах
- Матрицы. Виды матриц
- Матрица строка
- Матрица столбец
- Нулевая матрица
- Квадратная матрица
- Главная диагональ матрицы
- Побочная диагональ матрицы
- Диагональная матрица
- Единичная матрица
- След матрицы
- Верхняя треугольная матрица
- Нижняя треугольная матрица
- Ядро или нуль пространство матрицы
- Противоположная матрица
- Кососимметричная (Кососимметрическая) матрица
- Разность матриц
- Степень матрицы
- Симметричная (Симметрическая) матрица
- Основы высшей математики – Матрицы – Высшая математика – Теория, тесты, формулы и задачи
- Что такое матрица? Понятие матрицы
- что это такое в математике, операции и действия, как составить, примеры
- Знакомство с матрицами
- Матрицы
- 2.1: Введение в матрицы – математика LibreTexts
- | математика | Britannica
- Что такое матрица?
- Матрицы и матричная алгебра – Статистика How To
- : Обозначение
- Матричная алгебра: сложение и вычитание
- Дополнение матрицы для неравных размеров
- Умножение матриц: две матрицы
- Аддитивная идентификационная матрица
- Проверка ответа
- Пример собственного значения
- Расчет
- Написание системы уравнений
- Определитель матрицы 2 × 2
- Определитель матрицы 3 × 3
- Определитель матрицы 4 × 4
- Обозначение
- Верхняя и нижняя треугольные матрицы
- Прямоугольные диагональные матрицы
- Символы для транспонированной матрицы
- Свойства матриц транспонирования
- Альтернативное определение
- Максимальное количество номеров
- Диагональные матрицы
- Что такое асимметричная матрица?
- Косоэрмитский
- Построение матрицы дисперсии-ковариации
- Определение и примеры матрицы, ее записей, строк, столбцов, обозначений матрицы. Матрица – это просто …
- Операции с матрицами
Матрицы: определение и основные понятия.
Навигация по странице:
Определение матрицы
Определение.
Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами.Количество строк и столбцов задают размеры матрицы.
Обозначение
Матрица – это таблица данных, которая берется в круглые скобки:
| A = | 4 | 1 | -7 | ||
| -1 | 0 | 2 |
Матрица обычно обозначаются заглавными буквами латинского алфавитв. Матрица содержащая n строк и m столбцов, называется матрицей размера n×m. При необходимости размер матрицы записывается следующим образом: An×m.
Элементы матрицы
Элементы матрицы A обозначаются aij, где i – номер строки, в которой находится элемент, j – номер столбца.
Пример.
Элементы матрицы A4×4:| A = | 4 | 1 | -7 | 2 | ||
| -1 | 0 | 2 | 44 | |||
| 4 | 6 | 7 | 9 | |||
| 11 | 3 | 1 | 5 |
a11 = 4
Определение.
Строка матрицы называется нулевой, если все ее элементы равны нулю.Определение.
Если хотя бы один из элементов строки матрицы не равен нулю, то строка называется ненулевой.Пример.
Демонстрация нулевых и ненулевых строк матрицы:| 4 | 1 | -7 | < не нулевая строка | ||
| 0 | 0 | 0 | < нулевая строка | ||
| 0 | 1 | 0 | < не нулевая строка |
Определение.
не не нулевой столбец
Диагонали матрицы
Определение.
Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний угол.Определение.
Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний угол.Пример.
Демонстрация главной и побочной диагонали матрицы:| 0 | 1 | -7 | – главнаяпобочная диагональ | ||
| 0 | 0 | 2 |
| 0 | 1 | -7 | – главнаяпобочная диагональ | ||
| 0 | 0 | 2 | |||
| 8 | 2 | 9 |
Определение.
Следом матрицы называется сумма диагональных элементов матрицы.
Обозначение.
След матрицы обозначается trA = a11 + a22 + … + ann.Основные сведения о матрицах
В этом разделе мы даем основные сведения о матрицах, необходимые для понимания статистики и анализа данных.
Матрицей размера m x n (читается m на n) называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,….
Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: aij, где i – номер строки, j – номер столбца.
Например, матрица:
В сокращенной записи обозначаем A=(aij); i=1,2,…m; j=1,2,…,n
Приведем пример матрицы 2 на 2:
Вы видите, что a11 = 1, a12 = 0, a21 = 2, a22=5
Наряду с круглыми скобками используются и другие обозначения матрицы:
Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, aij = bij для любых i=1,2,…m; j=1,2,…n
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором) – строкой, а из одного столбца – матрицей (вектором)- столбцом:
A=(a11,a12,…,a1n) – матрица – строка
B=
Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.
Например,
Элементы матрицы aij, у которых номер столбца равен номеру строки образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a11, a22,…,ann.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые – специфические.
1. Умножение матрицы на число. Произведение матрицы А на число называется матрица B=A, элементы которой bij=aij для i=1,2,…m; j=1,2,…n
Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.
В частности, произведение матрицы А на число 0 есть нулевая матрица.
2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой cij=aij+bijдля i=1,2,…m; j=1,2,…n (т. е. матрицы складываются поэлементно).
е. матрицы складываются поэлементно).
3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B.
4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц Am∙B kназывается такая матрица Cm, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:
i=1,2,…,m; j=1,2,…,n
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):
A+B=B+A
(A+B)+C=A+(B+C)
λ (A+B)= λA+ λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ (AB)=( λA)B=A(λB)
A(BC)=(AB)C
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
a) Если АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.
b) Если АВ и ВА существуют, то они могут быть матрицами разных размеров.
5. Транспонирование матрицы – переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А’ называется транспонированной относительно матрицы А:
Из определения следует, что если матрица А имеет размер m, то транспонированная матрица А’ имеет размер n
В литературе встречаются и другие обозначения транспонированной матрицы, например, АТ
Связанные определения:
Вырожденная матрица
Обобщенная обратная матрица
Обратная матрица
Плохо обусловленная матрица
Псевдообратная матрица
Эрмитова матрица
Эрмитово-сопряженная матрица
В начало
Содержание портала
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами
Числа m и n называются порядками или размерами
Матрица порядка m × n записывается в форме:
или (i=1,2,…m; j=1,2,…n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j– номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей .
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Элементы расположенные на местах a11, a22 ,…, ann образуют главную диагональ матрицы. Например:
В случае m×n -матриц элементы aii ( i=1,2,…,min(m,n)) также образуют главную диагональ. Например:
Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .
Побочная диагональ матрицы
Элементы расположенные на местах a1n, a2n-1 ,.
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n, где n – порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
Верхняя треугольная матрица
Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т. е. aij=0, при всех i>j . Например:
е. aij=0, при всех i>j . Например:
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i<j. Например:
Cтроки матрицы A образуют пространство строк матрицы и обозначаются через R(AT).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x– вектор длины n – образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
AT=−A.
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
C=A+(-1)B.
Для обозначения разности двух матриц используется запись:
C=A-B.
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
A0=E,
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q– произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=AT называется симметричной матрицей.
Для симметричных матриц имеет место равенство:
aij=aji ; i=1,2,…n, j=1,2,…n
Основы высшей математики – Матрицы – Высшая математика – Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Матрицы
К оглавлению…
Матрицей называют прямоугольную таблицу, заполненную числами. Важнейшие характеристики матрицы – число строк и число столбцов. Если у матрицы одинаковое число строк и столбцов, ее называют квадратной. Обозначают матрицы большими латинскими буквами.
Важнейшие характеристики матрицы – число строк и число столбцов. Если у матрицы одинаковое число строк и столбцов, ее называют квадратной. Обозначают матрицы большими латинскими буквами.
Сами числа называют элементами матрицы и характеризуют их положением в матрице, задавая номер строки и номер столбца и записывая их в виде двойного индекса, причем вначале записывают номер строки, а затем столбца. Например, a14 есть элемент матрицы, стоящий в первой строке и четвертом столбце, a32 стоит в третьей строке и втором столбце.
Главной диагональю квадратной матрицы называют элементы, имеющие одинаковые индексы, то есть те элементы, у которых номер строки совпадает с номером столбца. Побочная диагональ идет «перпендикулярно» главной диагонали.
Особую важность представляют собой так называемые единичные матрицы. Это квадратные матрицы, у которых на главной диагонали стоят 1, а все остальные числа равны 0. Обозначают единичные матрицы E. Матрицы называют равными, если у них равны число строк, число столбцов, и все элементы, имеющие одинаковые индексы, равны. Матрица называется нулевой, если все ее элементы равны 0. Обозначается нулевая матрица О.
Обозначают единичные матрицы E. Матрицы называют равными, если у них равны число строк, число столбцов, и все элементы, имеющие одинаковые индексы, равны. Матрица называется нулевой, если все ее элементы равны 0. Обозначается нулевая матрица О.
Простейшие действия с матрицами
1. Умножение матрицы на число. Для этого необходимо умножить каждый элемент матрицы на данное число.
2. Сложение матриц. Складывать можно только матрицы одинакового размера, то есть имеющие одинаковое число строк и одинаковое число столбцов. При сложении матриц соответствующие их элементы складываются.
3. Транспонирование матрицы. При транспонировании у матрицы строки становятся столбцами и наоборот. Полученная матрица называется транспонированной и обозначается AT. Для транспонирования матриц справедливы следующие свойства:
4. Умножение матриц. Для произведения матриц существуют следующие свойства:
- Умножать можно матрицы, если число столбцов первой матрицы равно числу строк второй матрицы.

- В результате получится матрица, число строк которой равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.
- Умножение матриц некоммутативно. Это значит, что от перестановки местами матриц в произведении результат меняется. Более того, если можно посчитать произведение A∙B, это совсем не означает, что можно посчитать произведение B∙A.
- Пусть C = A∙B. Для определения элемента матрицы С, стоящего в i-той строке и k-том столбце необходимо взять i-тую строку первой умножаемой матрицы и k-тый столбец второй. Далее поочередно брать элементы этих строки и столбца и умножать их. Берем первый элемент из строки первой матрицы и умножаем на первый элемент столбца второй матрицы. Далее берем второй элемент строки первой матрицы и умножаем на второй элемент столбца второй матрицы и так далее. А потом все эти произведения надо сложить.
Свойства произведения матриц:
Определитель матрицы
Определителем (детерминантом) квадратной матрицы А называется число, которое обозначается detA, реже |A| или просто Δ, и вычисляется определённым образом. Для матрицы размера 1х1 определителем является сам единственный элемент матрицы. Для матрицы размера 2х2 определитель находят по следующей формуле:
Для матрицы размера 1х1 определителем является сам единственный элемент матрицы. Для матрицы размера 2х2 определитель находят по следующей формуле:
Миноры и алгебраические дополнения
Рассмотрим матрицу А. Выберем в ней s строк и s столбцов. Составим квадратную матрицу из элементов, стоящих на пересечении полученных строк и столбцов. Минором матрицы А порядка s называют определитель полученной матрицы.
Рассмотрим квадратную матрицу А. Выберем в ней s строк и s столбцов. Дополнительным минором к минору порядка s называют определитель, составленный из элементов, оставшихся после вычеркивания данных строк и столбцов.
Алгебраическим дополнением к элементу aik квадратной матрицы А называют дополнительный минор к этому элементу, умноженный на (–1)i+k, где i+k есть сумма номеров строки и столбца элемента aik. Обозначают алгебраическое дополнение Aik.
Обозначают алгебраическое дополнение Aik.
Вычисление определителя матрицы через алгебраические дополнения
Рассмотрим квадратную матрицу А. Для вычисления ее определителя необходимо выбрать любую ее строку или столбец и найти произведения каждого элемента этой строки или столбца на алгебраическое дополнение к нему. А дальше надо просуммировать все эти произведения.
Когда будете считать алгебраические дополнения, не забывайте про множитель (–1)i+k. Чтобы счет был более простым, выбирайте ту строку или столбец матрицы, который содержит наибольшее число нулей.
Расчет алгебраического дополнения может сводиться к расчету определителя размером более чем 2х2. В этом случае такой расчет также нужно проводить через алгебраические дополнения, и так далее до тех пор, пока алгебраические дополнения, которые нужно будет считать, не станут размером 2х2, после чего воспользоваться формулой выше.
Обратная матрица
К оглавлению. ..
..
Рассмотрим квадратную матрицу А. Матрица A–1 называется обратной к матрице А, если их произведения равны единичной матрице. Обратная матрица существует только для квадратных матриц. Обратная матрица существует, только если матрица А невырождена, то есть ее определитель не равен нулю. В противном случае обратную матрицу посчитать невозможно. Для построения обратной матрицы необходимо:
- Найти определитель матрицы.
- Найти алгебраическое дополнение для каждого элемента матрицы.
- Построить матрицу из алгебраических дополнений и обязательно транспонировать ее. Часто про транспонирование забывают.
- Разделить полученную матрицу на определитель исходной матрицы.
Таким образом, в случае, если матрица А имеет размер 3х3, обратная к ней матрица имеет вид:
Матрицы. Вся теория и задачи с решениями или ответами
К оглавлению…
Что такое матрица? Понятие матрицы
Матрицы — традиционная головная боль для очень многих студентов. Я бы даже сказал, подавляющего большинства. Ну вот не любят студенты матрицы, хоть ты убей!
Я бы даже сказал, подавляющего большинства. Ну вот не любят студенты матрицы, хоть ты убей!
Но высшая математика на то и высшая, что работает с более сложными объектами, чем привычная школьная. От этого никуда не деться.) И матрица — один из первых таких объектов, с которым студенты знакомятся уже на первом курсе ВУЗа. И мы тоже познакомимся.)
Итак, ключевые причины, почему же студенты не любят матрицы и всячески стараются избегать работы с ними. Перечислю их.
Причина первая — визуальное восприятие. Оно… непривычно, да.) С формулами, уравнениями, графиками у народа обычно всё более-менее ясно и прозрачно: в школе всё худо-бедно решалось, строилось, ощущалось. Всё знакомо. А тут… Какая-то табличка, какие-то малопонятные буковки с индексами (аж двумя!), которые так и норовят путаться перед глазами. Всё это поначалу очень смущает и даже пугает, да…
Причина вторая — это действия с матрицами. Их очень и очень много. Сложение матриц, умножение матриц, транспонирование матриц, поиск обратной матрицы, вычисление определителя, вычисление миноров матрицы, ранга матрицы… Причём все эти операции тоже весьма специфичны и имеют очень мало общего с действиями над обычными числами и алгебраическими выражениями из школьной математики. Эти фишки тоже очень здорово выбивают из колеи.
Их очень и очень много. Сложение матриц, умножение матриц, транспонирование матриц, поиск обратной матрицы, вычисление определителя, вычисление миноров матрицы, ранга матрицы… Причём все эти операции тоже весьма специфичны и имеют очень мало общего с действиями над обычными числами и алгебраическими выражениями из школьной математики. Эти фишки тоже очень здорово выбивают из колеи.
Причина третья — это рутина. Спору нет, работа с матрицами порой бывает весьма занудной. И скучной. А вместе с рутиной неизбежно возрастает и вероятность глупых арифметических ошибок, да… Особенно при работе с матрицами больших размерностей и/или в процессе элементарных преобразований. Где-то минус теряется, где-то вместо нуля единица пишется, где-то 3+4 двенадцать получается… Эти ляпы на общем фоне рутинной работы просто-напросто не замечаются. И лечатся только лишь предельным вниманием. К сожалению.
И даже после прочтения всех этих ужасов отчаиваться и впадать в панику рано.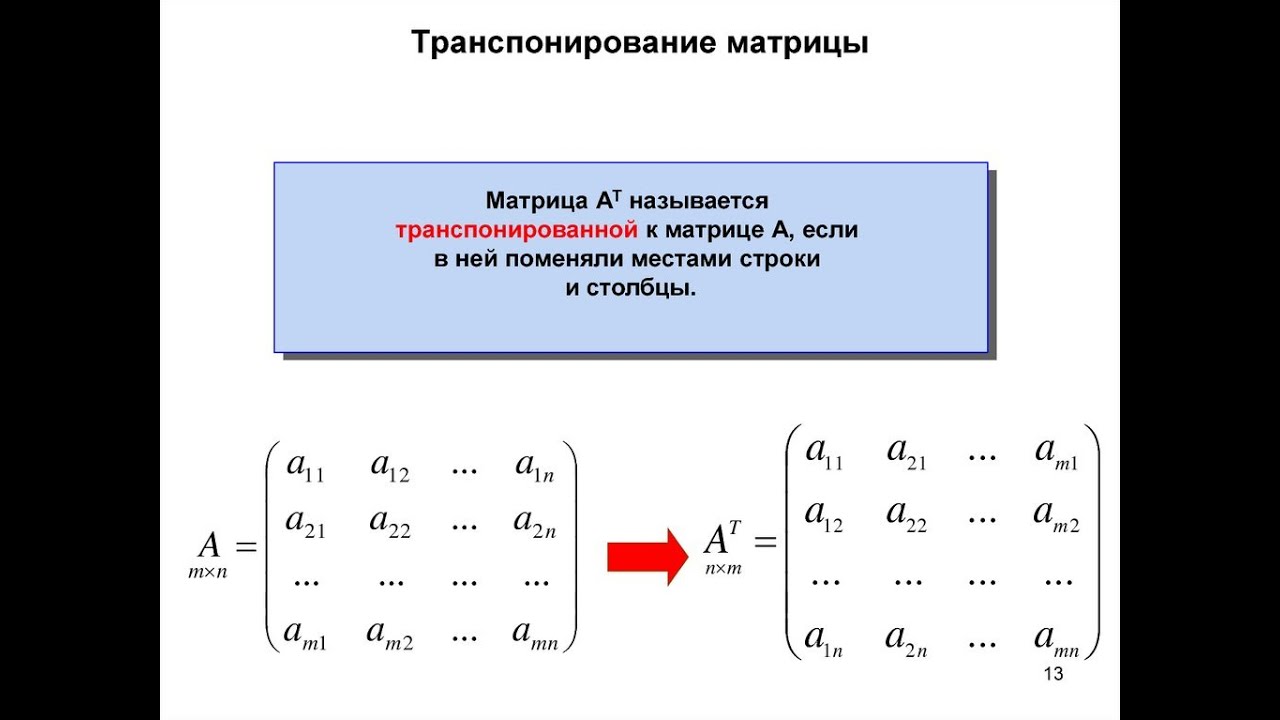 Прорвёмся!) Для начала успокою: матрица сама по себе — понятие очень простое. Да-да! И главное — полезное и очень мощное в высшей математике. Такое же полезное и мощное, как, скажем, формулы сокращённого умножения в школьной алгебре.) Сомневаетесь? Не надо.) Всё сами дальше увидите. Нужно лишь собраться с духом, рискнуть и… почитать.)
Прорвёмся!) Для начала успокою: матрица сама по себе — понятие очень простое. Да-да! И главное — полезное и очень мощное в высшей математике. Такое же полезное и мощное, как, скажем, формулы сокращённого умножения в школьной алгебре.) Сомневаетесь? Не надо.) Всё сами дальше увидите. Нужно лишь собраться с духом, рискнуть и… почитать.)
Итак, начнём с первой проблемы — с визуального восприятия.)
Что такое матрица? Устройство матрицы.
Так что же такое матрица? Нет, ничего общего с известным американским научно-фантастическим боевиком данное понятие не имеет. Ну… очень-очень отдалённое сходство всё же есть.)
Итак, удивляемся, но запоминаем:
Матрица — это просто прямоугольная таблица каких-либо элементов.
И всё! Ничего хитрого за этим страшным понятием больше не кроется.) Разумеется, каждое слово в определении несёт свой собственный смысл, да. Разберёмся?)
Слова “прямоугольная таблица” вопросов ни у кого не вызывают (надеюсь).
Например, можно сочинить что-нибудь типа такого:
Чем не прямоугольная табличка?) Но матрицы в высшей математике изображаются и выглядят немножко по-другому, нежели то что мы называем таблицей в привычном восприятии.
Чаще всего матрица в математике записывается вот так:
Всё очень просто и компактно, правда? Никаких рамок, никаких ячеек — ничего чертить и рисовать не нужно. Любая матрица записывается просто набором каких-то чисел в скобочках. Скобочки, кстати, могут быть не только круглыми. Могут быть и квадратными:
Или даже в виде вот таких двойных прямых палочек:
Это всё одно и то же. В большинстве учебников обычно используются круглые скобки. Квадратные скобки чаще встречаются в технических дисциплинах — в сопромате, строительной механике, теории упругости и т.п. Двойные — почти нигде не встречал. Я всё-таки буду следовать традициям и рисовать круглые скобки. Надеюсь, возражений нет.)
Итак, с таблицей разобрались. Что же такое “элемент”? Тоже элементарно (сорри за тавтологию). Любое число, стоящее в матрице на определённом месте, и будет её элементом! Для нашей матрицы число 1 — элемент, 5 — тоже элемент, и 10 — тоже элемент. В общем, вы поняли…
Кстати, слова “на определённом месте” я выделил не зря. И вот почему. Дело всё в том, что любую матрицу следует воспринимать именно как таблицу! А вовсе не как простое множество или набор чисел. Поясняю в чём суть. Рассматривая простое множество чисел, скажем, {1; 2; 3}, мы имеем полное право переставлять элементы множества как попало.
Например, мы можем переставить единичку и двойку. Получим:
{2; 1; 3}
Или переставить двойку и тройку:
{1; 3; 2}
И так далее. Перестановки элементов множества на его сути никак не сказываются. А вот матрицы более чувствительны к перестановкам. И переставлять элементы матрицы просто так нельзя! Каждый элемент строго на своём месте, в своей ячейке. И если переставить местами хотя бы два элемента, то получится, вообще говоря, уже другая матрица. С другими свойствами, да.
Элементами матрицы, кстати, могут быть не только числа. Могут быть и буквенные выражения, и даже функции. Всякое может быть.) Матрицы с функциями в качестве элементов так и называются — функциональными. Это — довольно сложная штука. И встречается уже в серьёзных разделах высшей математики — в дифференциальных уравнениях, в теории функций нескольких переменных и т.п. Этих ужасов пока не будет.)
Мы же пока будем работать только с матрицами, элементами которых являются числа. Или с числовыми матрицами. Намёк понятен?)
Откуда взялись матрицы, зачем они нужны и в чём их смысл?
Итак, мы выяснили, что матрица — это какая-то табличка. Чаще всего с какими-то числами. Ну и что из этого — спросите вы? Табличка и табличка… Что с ней делать-то? Просто пучить глазки? А делать можно очень много полезного! В соответствующих уроках сами увидите.)
На самом деле с матрицами вы постоянно сталкивались ещё в школе. Сами того не подозревая. Не верите? Сейчас удивитесь.)
Слова “система уравнений” вам знакомы?
Например, такая простенькая системка из двух линейных уравнений:
Решив её (например, подстановкой), получим ответ:
х=1; у=2.
Или, кратенько: (1; 2).
Можно изменить коэффициенты при икс и игрек и получить какую-то новую систему. Например, такую:
Решив её, получим новый ответ: (1; 3).
А можно, например, коэффициенты при переменных не трогать, зато как-то поменять свободные члены. Вместо 8 и 3 записать, скажем, 1 и 2. Получим снова какую-то систему и какое-то решение…
Короче говоря, меняя в системе уравнений коэффициенты при неизвестных и/или свободные члены, можно получать какие-то решения для конкретной системы. Для каждого набора чисел — свои. Кстати, можно и такое наподбирать, что система вообще не будет иметь решений или будет иметь бесконечно много решений.)
Например:
Эта система имеет бесконечно много решений. И (1; 1) — решение, и (0; 2) — решение, и (0,5; 1,5) — тоже решение. Можно перечислять до посинения…)
А теперь я изменю в этой системе всего одно число и получу систему, которая вообще не имеет решений:
Кому интересно, можете решить подстановкой. Получите забавный результат 6=5. Попробуйте.)
Итак, что мы видим? Мы видим, что решение системы колоссальным образом зависит от этого самого набора чисел. Причём только от него! Этот факт настолько важен, что математики даже придумали этот самый набор чисел (коэффициентов и свободных членов системы) оформлять в виде таблички. Или, говоря математическим языком, в виде матрицы.
Вот так:
Меняя содержимое табличек (матриц) коэффициентов и свободных членов, мы будем получать различные системы линейных уравнений. С различными решениями, да.)
Кстати, вот вам и ответ на вопрос, почему мы не можем просто так переставлять элементы в матрице. Не догадались? Да! Переставив местами хотя бы два элемента, мы получим уже другую матрицу, соответствующую другой системе уравнений. И с другими решениями…
Ну ладно, системы из двух уравнений — это ещё легко. При их решении про матрицы можно особо не вспоминать: выражай себе по-школьному икс через игрек (или наоборот), делай подстановку, решай — и дело с концом. А вот система из трёх линейных уравнений с тремя неизвестными уже гораздо злее.) Заниматься явным выражением одной переменной через другую, подстановкой и прочим школьным занудством уже неохота, да… А если уравнений и/или неизвестных ещё больше? Скажем, четыре или пять…)
И вот тут возникает вполне закономерный вопрос: а можно ли, как-то работая напрямую только с матрицами (коэффициентов и свободных членов), попробовать выяснить:
1) Есть у системы решение или нет его? Или решений вообще бесконечно много?
2) Если решение есть и единственно, то отыскать его быстро и легко.
Новость хорошая: да, можно! Добро пожаловать в новый раздел высшей математики! Под названием линейная алгебра.)
Именно этот раздел и занимается решением систем линейных алгебраических уравнений. Сокращённо — СЛАУ.) Эта страшная аббревиатура будет мозолить вам глаза на протяжении почти всех уроков этого раздела. Привыкаем.)
Причём прошу обратить особое внимание на слово “линейных”. Это слово означает, что все неизвестные (x, y, z, …) входят во все уравнения максимум в первой степени и нигде не должно быть деления на неизвестное.
Например:
Это система двух линейных алгебраических уравнений (СЛАУ) с тремя неизвестными. Все неизвестные (x, y, z) в только первой степени, деления на неизвестное ни в одном из уравнений нету. То что число неизвестных больше числа уравнений — вопрос другой. В соответствующем уроке мы научимся с такими злыми системами расправляться.) Главное, что оба уравнения — линейные. Это важно.)
А теперь я изменю в этой системе всего одно слагаемое. Нарисую, например, квадратик над иксом во втором уравнении:
А вот такая система уравнений будет уже нелинейна, да… Именно из-за этого самого квадратика, нарушающего базовый принцип “все неизвестные только в первой степени”. К нелинейным системам имеется свой индивидуальный подход, и линейная алгебра перед ними бессильна… С такими системами мы в этом разделе работать не будем. На радость студентам.)
Итак, запоминаем:
Матрицы — очень мощный инструмент для решения систем линейных алгебраических уравнений (СЛАУ).
Намёк понятен?)
Но не одними лишь системами уравнений ограничивается применение матриц! Матрица — это ещё и своего рода математический оператор. Или преобразователь. Который что-то куда-то преобразует. Или отображает. Как фотоаппарат.) Скажем, один вектор через матрицу можно отобразить в другой. Мощная штука.) Об этом в более серьёзных темах линейной алгебры будет. А системы — так, частный случай. Для начального знакомства.
Как обозначать матрицу и её элементы?
Очень просто. Любые матрицы в математике обозначаются большими буквами латинского алфавита: A, B, C и так далее.
Например, нашу матрицу, приведённую в начале урока, можно обозначить вот так:
И все дела. Слева от знака равенства — название матрицы, справа — её содержимое. В скобочках.)
Но это ещё не все обозначения. Есть и другие, более специфические. Разберём и их.
Любая матрица — это ведь табличка, не так ли? А из чего у нас состоит любая табличка? Правильно, из строчек и колонок! Только это в обиходе.) А в математике те же самые названия звучат более научно — строки и столбцы! Зацените.)
Количество этих самых строк и столбцов коротко записывают в виде произведения m x n и называют размерностью матрицы. Которая дополнительно может указывается в виде подстрочного знака.
Вот так:
Am x n
Читается эта запись очень просто: “матрица A размерности m на n”. И вот тут студентов могут подстерегать первые проблемы. Какое число (буква) за что отвечает?
Запоминаем:
В размерности матрицы m x n первое число (m) — это (всегда!) количество СТРОК в матрице. Второе число (n) — количество СТОЛБЦОВ.
Именно в таком порядке. Сначала строки, а потом — столбцы. А не наоборот. Например, наша матрица — это матрица размера “два на три”:
У неё две строки (m=2) и три столбца (n=3).
Размерность — ключевая характеристика любой матрицы. Почему? А потому, что на некоторые операции с матрицами (например, на сложение, умножение, взятие определителя и обратной матрицы) существуют очень жёсткие ограничения по размерности! Сами увидите. В соответствующих уроках.)
А как кратко в общем виде обозначать элементы матрицы? Тоже просто. Маленькими латинскими буквами с двойным индексом.
Например, вот так:
aij
И всё. Читается эта закорючка так: “а и-жи”. Или: “а итое-житое”. Забавно, да? Тем не менее вполне себе научно.)
И снова могут быть проблемы с расшифровкой индексов. В школе ведь мы привыкли работать с одиночными индексами. В прогрессиях, например. А тут — двойной! Какой индекс что означает? Не беда! Принцип расшифровки индексов тот же самый — сначала строка, а потом столбец. Первый индекс “i” (“и”)– это номер строки, где находится интересующий нас элемент. Второй индекс “j“ (“жи”) – номер столбца.
Например, нам дана такая матрица A:
Размерности какой, кстати? Правильно, “три на три”. Или A3x3. Пусть нам надо обратиться, скажем, к элементу матрицы a23.
Здесь первый индекс “и” равен двойке (i=2), а второй индекс “жи” – тройке (j=3). Вот и пересекаем (мысленно!) вторую строку и третий столбец. На пересечении получаем нужный нам элемент a23 = 3.
Вот так:
Точно так же на пересечении первой строки и первого столбца мы получим элемент матрицы a11 = 0, на пересечении третьей строки и второго столбца — элемент a32 = 7 и так далее. Чем-то похоже на игру в кораблики или морской бой, не находите?) Вроде бы, всё элементарно. И что, думаете не ошибаются люди? Ошибаются, ещё как! Ещё один источник дурацких ошибок при работе с элементами матриц — это неправильная нумерация строк и столбцов. Со столбцами обычно всё ясно — нумеруем и читаем привычно, слева направо. Не арабы, чай…) А вот со строками могут случаться и непонятки — сверху вниз их нумеровать или снизу вверх…
Запоминаем:
В элементе матрицы aij первый индекс (i) — номер строки, второй индекс (j) — номер столбца. Нумерация строк (всегда!) — сверху вниз. Нумерация столбцов (всегда!) — слева направо.
А теперь, разобравшись с загадочными индексами i и j, мы подходим к самому научному способу задания матрицы — через элемент матрицы в общем виде и диапазон изменения индексов.
Вот она, эта запись:
Расшифровываются эти страшные иероглифы так:
Задана матрица А с элементами aij, где индекс “i” принимает все натуральные значения от единицы до “эм” включительно, а индекс “j” — все натуральные значения от единицы до “эн” включительно.
Солидно, да… Куда проще не заморачиваться и написать кратко и точно Amxn, правда? Но будьте готовы и к такой супернаучной форме записи. Особенно в каких-нибудь продвинутых учебниках.)
Внимание! Запись элемента a23 читается и произносится как “а два три“. Именно так, вы не ослышались.) Ни в коем случае не “a двадцать три“! Или b11 — это элемент “бэ один один“ (а не “бэ одиннадцать“)! Такое чтение — это… гм… серьёзный вызов преподавателю.) И говорит о полном отсутствии хоть какого-то понимания. О “зачёте” (или “удовл”) даже и не мечтайте после этого. Вот так.
что это такое в математике, операции и действия, как составить, примеры
При решении алгебраических или дифференциальных уравнений студенты сталкиваются с понятием матрицы. Этот термин используется в программировании, электронике, фотоискусстве, но основная область применения — математика. Рассмотрим, что это такое, как применяется и какие операции позволяет осуществить.
Что такое матрицы в математике
Матрица в математике — это абстрактный объект, имеющий вид таблицы чисел или других математических величин. Чаще таблица прямоугольная, но встречаются и другие виды (квадратные, треугольные).
Обычно матрица называется заглавной буквой латинского алфавита: матрица A, матрица B. В таблице есть строки (их количество называется m) и столбцы (их количество называется n). Количество строк и столбцов определяет размер матрицы и может называться порядком. Матрицы такого типа называются матрицами строения m×n, или размера m×n, или порядка m×n.
Элементы матрицы, т.е. числа или остальные величины, называются строчной буквой. Они имеют 2 нижних индекса, необходимых для определения их положения в матрице. Например, элемент a13 располагается на пересечении 2 строки и 3 столбца. Значения элемента а13 читаются по-отдельности, не как целое число: «а один-три».
Откуда они взялись и чем полезны
Первые упоминания матрицы появились в Древнем Китае. Это была квадратная таблица, получившая название магического или волшебного квадрата. Самым древним и известным считается квадрат 3×3, датируемый около 2200 г до н.э. Он был высечен на панцире черепахи. В Китае его называют квадрат Ло Шу, а в Западной Европе — «Печать Сатурна».
Таким же древним является квадрат, найденный в Кхаджурахо, столице средневекового государства Чандела (IX–XIII вв.) в Центральной Индии. Это первый из «дьявольских квадратов». Также он называется пандиагональным.
В древности матрицы были необходимы преимущественно для решения линейных уравнений. Когда матрицы появились в арабских странах, стали разрабатываться принципы работы с ними, в том числе, принцип сложения. В XVIII веке швейцарский математик, «отец линейной алгебры» Габриэль Крамер опубликовал правило Крамера. Это способ решения систем линейных уравнений с помощью матрицы.
Источник: ruspekh.ruСпособ Крамера не подходит для решения тех систем линейных уравнений, в которых может быть бесконечное множество решений.
В следующем веке появляется метод немецкого математика Карла Фридриха Гаусса. Этот способ решения алгебраических уравнений не является открытием ученого. Впервые о методе Гаусса написали в китайском трактате «Математика в девяти книгах», а сам он только привел способ в удобную форму.
Для решения уравнений таким способом необходимо записать расширенную матрицу системы.
Источник: ruspekh.ruВ отличие от метода Крамера, правило Гаусса можно использовать для решения любых систем линейных уравнений.
Детальная разработка теории матриц активно продолжилась с середины XIX века. Наиболее значимые ученые: Уильям Гамильтон, Артур Кэли, Карл Вейерштрасс, Мари Энмон Камиль Жордан, Фердинанд Георг Фробениус.
Сам термин «матрица» предложил английский математик Джеймс Сильвестр в 1850 г.
В наше время матрицы используются не только для записи и решения систем линейных уравнений. Списки, статистические данные, табеля с информацией — все это в какой-то степени матрица. Их применяют для упрощения подачи и работы с информацией в любой сфере. Например, таблица продаж, где указан год (первый столбец), вид продукции (первая строка), а остальные значения — количество проданных единиц.
Обозначения матриц
Помимо самого термина «матрицы», при их решении нужно знать и другие обозначения.
Элементы матрицы — любые математические объекты: числа, переменные, другие матрицы. Элемент обозначается как aab, где a — номер строки расположения элемента, b — номер столбца.
Главная диагональ матрицы — диагональ, пересекающая квадратную матрицу из верхнего левого угла в нижний правый угол (квадратные матрицы имеют одинаковое количество строк и столбцов). Прямоугольные матрицы также могут иметь диагонали: они пересекают элементы с одинаковыми индексами.
Побочная диагональ матрицы — диагональ, пересекающая верхний правый и нижний левый углы. Для прямоугольного вида матриц понятие «побочные диагонали» не используется.
Диагональные элементы — числа и другие математические величины матрицы, расположенные на главной диагонали.
Размер (порядок) матрицы — произведение количества строк на количество столбцов: m×n. Например, если матрица содержит 2 строки и 3 столбца, то ее обозначают матрицей 2×3.
След матрицы — сумма элементов матрицы, расположенных на главной диагонали. Обозначается как Sp (А) или Tr (A), где A — название матрицы.
Равные матрицы — матрицы, у которых соответствующие элементы равны.
Виды матриц, какие бывают
В математике существует несколько видов матриц в зависимости от их размера.
- Матрица–строка. Имеет размер 1×n, т.е. состоит из одной строки и нескольких столбцов.
\(\begin{vmatrix}54&2&-7&0&4\end{vmatrix}\) - Матрица–столбец. Имеет размер m×1, т.е. состоит из одного столбца и нескольких строк.
\(\begin{vmatrix}3\\-6\\64.5\end{vmatrix}\)
Также различают матрицы по значениям их элементов.
- Нулевая матрица. Все элементы матрицы равны 0.
\(\begin{vmatrix}0&0&0\\0&0&0\end{vmatrix}\) - Квадратная матрица. Количество строк и столбцов одинаковое: m=n.
\(\begin{vmatrix}4&5&1\\5&0&0\\-2&2&-8\end{vmatrix}\) - Диагональная матрица — разновидность квадратной матрицы, у которой все элементы равны 0, за исключением диагональных элементов.
\(\begin{vmatrix}3&0&0\\0&-8&0\\0&0&1.5\end{vmatrix}\) - Единичная матрица — разновидность диагональной матрицы. На главной диагонали расположены 1, а все остальные элементы равны 0. Обозначается латинской буквой E.
\(\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}\) - Треугольная матрица. Имеет 2 разновидности: верхняя и нижняя. У верхней треугольной матрицы равны 0 элементы под главной диагональю, а у нижней треугольной матрицы — над главной диагональю.
\(A=\begin{vmatrix}4&1.5&-2\\0&1&7\\0&0&4\end{vmatrix}\)
Треугольная матрица всегда квадратная: m=n.
- Противоположная матрица. Обозначается -A и всегда рассматривается в отношении матрицы A. Ее элементы имеют обратный знак от элементов матрицы A.
- Кососимметрическая (антисимметричная) матрица. Отличается множителем -1. Т.е. все элементы матрицы A были умножены на -1 и получилась матрица AT, или транспонированная матрица.
\(A=\begin{vmatrix}0&5&217\\-5&0&-43\\-217&43&0\end{vmatrix},\;A^T=\begin{vmatrix}0&-5&-217\\5&0&43\\217&-43&0\end{vmatrix}\)
Кососимметрическая матрица всегда квадратная.
- Симметрическая матрица. Элементы лежат симметрично по отношению к главной диагонали. Матрица всегда квадратная.
\(A=\begin{vmatrix}1&3&0\\3&2&6\\0&6&5\end{vmatrix}\) - Трапециевидная матрица. Есть ряд условий, при которых матрица становится такого вида. Например, она должна быть квадратной или прямоугольной, при этом количество столбцов обязательно больше числа строк. Также элементы, расположенные над главной диагональю, не равны 0, а элементы под главной диагональю равны 0.
\(A=\begin{vmatrix}1&2&3&4&5&6\\0&-1&0&7&-3&2\\0&0&4&1&-1&-2\end{vmatrix}\)
Применение матриц в математико-экономическом моделировании
С древности и по настоящее время матрицы используются для решения и удобной записи системы линейных алгебраических или дифференциальных уравнений. Но их также применяют в математико-экономическом моделировании для структурирования данных и комфортной работы с ними.
Наиболее популярной является матричная модель экономики «затраты–выпуск». Ее внедрил Василий Леонтьев — американский экономист. За развитие этого метода он получил нобелевскую премию: матричная модель упростила решение некоторых экономических проблем. В последствии Леонтьева стали называть «апостолом планирования».
Суть модели «затраты–выпуск» в том, что экономист разделил производственный сектор экономики на отрасли, число которых обозначается n. 1 отрасль — 1 вид продукции. Значит, n количество отраслей выпускает n количество продуктов. Это приводит к появлению межотраслевых связей: одна отрасль заимствует у другой продукт и использует в процессе производства своей продукции. Данная балансовая модель представлена в виде системы линейных уравнений, решаемых с помощью матрицы.
Какие операции можно производить с матрицами
С матрицами можно проводить несколько операций.
- Сложение и вычитание. Это действие можно проводить только с теми матрицами, у которых одинаковый размер. Например, матрица размера 3×2. Ответом будет матрица такого же размера. Чтобы получить ответ нужно вычесть или сложить соответствующие элементы двух матриц. Т.е. при сложении элемент a11 складывается с элементом b11.
- Умножение матрицы на число. Каждый элемент матрицы нужно умножить на число. Получится матрица такого же размера.
- Умножение матриц. Не все матрицы можно умножить между собой. Обязательное свойство: число столбцов первой матрицы должно равняться числу строк второй матрицы. Например, можно умножить матрицу A размером 3×2 и матрицу B размером 2×3. Как осуществляется умножение: чтобы получить элемент a11 новой матрицы, нужно поочередно умножить элементы строки матрицы A на соответствующие элементы столбца матрицы B, а затем суммировать эти произведения.
При умножении матрицы нельзя менять местами.
- Транспонирование матрицы. Смена мест строк и столбцов матрицы. Первая строка матрицы становится первым столбцом. Дальше по аналогии.
Примеры решения задач на матрицы
Пример решения задачи на умножение.
Дано: \( A=\begin{vmatrix}1&-1\\2&0\\3&0\end{vmatrix},\;B=\begin{vmatrix}1&1\\2&0\end{vmatrix}\)
Найти: \(A*B\)
Решение:
Назовем искомую матрицу \(C\). Она будет иметь следующий вид:
\(C=\begin{vmatrix}c_{11}&c_{12}\\c_{21}&c_{22}\\c_{31}&c_{32}\end{vmatrix}\)
Найдем значение каждого элемента:
\(с_{11}=a_{11}*b_{11}+a_{12}*b_{21}=1*1+(-1)*2=-1\)
\(c_{12}=a_{11}*b_{12}+a_{12}*b_{22}=1*1+(-1)*0=1\)
\(c_{21}=a_{21}*b_{11}+a_{22}*b_{21}=2*1+0*2=2\)
\(c_{22}=a_{21}*b_{12}+a_{22}*b_{22}=2*1+0*0=2\)
\(c_{31}=a_{31}*b_{11}+a_{32}*b_{21}=3*1+0*2=3\)
\(c_{32}=a_{31}*b_{12}+a_{32}*b_{22}=3*1+0*0=3\)
Ответ: \(C=\begin{vmatrix}-1&1\\2&2\\3&3\end{vmatrix}\)
Пример решения задачи на умножение матрицы на число 5.
Дано: \(A=\begin{vmatrix}12&-1\\7&0\end{vmatrix}\)
Найти: \(A*5\)
Решение: \(5\ast\begin{vmatrix}12&-1\\7&0\end{vmatrix}=\begin{vmatrix}5\ast12&5\ast(-1)\\5\ast7&5\ast0\end{vmatrix}=\begin{vmatrix}60&-5\\35&0\end{vmatrix}\)
Ответ: \(\begin{vmatrix}60&-5\\35&0\end{vmatrix}\)
Учитесь работать с матрицами и продолжайте осваивать математику, а если задач накопилось слишком много и «горят» сроки, вам поможет сервис Феникс.Хелп. Обращайтесь!
Знакомство с матрицами
Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
- Вектор — это просто группа из нескольких чисел, выстроенных в определённой последовательности. Например, рост и вес человека можно представить как вектор (172, 80). Ничего сложного.
- У вектора может быть внутри сколько угодно чисел. Главное — чтобы мы договорились, что для нас значат эти числа, и не меняли их местами просто так, произвольно.
- Векторы можно складывать, вычитать, умножать. Это чуть сложнее, чем с обычными числами.
- У вектора есть понятие линейной зависимости. Грубо говоря — параллельны друг другу векторы или нет. От этого зависит, какие операции можно делать с этими векторами.
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.
Что такое матрица
Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.
Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.
Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.
В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.
Общая схема матрицы Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число триПростые операции с матрицами
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.
И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.
Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычисленийУмножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.
Пример умножения матрицы на числоТранспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.
⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.
Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правилСложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.
Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами Пример вычитания двух матрицУмножение матриц
Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
- У нас есть две матрицы A и B. Их нужно перемножить, чтобы получить новую матрицу C.
- Размер матрицы A два на два: есть две строки и два столбца. Первая строка состоит из элементов А₁₁ и А₁₂; вторая — А₂₁ и А₂₂.
- У матрицы B такая же размерность: есть две строки и два столбца. Первая строка состоит из элементов B₁₁ и B₁₂; вторая — B₂₁ и B₂₂.
- У нас две одинаковые по размеру матрицы с двумя строками и столбцами. Это значит, что и матрица C будет размером два на два. Первая строка будет состоять из элементов C₁₁ и C₁₂; вторая — C₂₁ и C₂₂.
- Считаем элемент C₁₁. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть, после которой ставим знак плюс. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем обе части и получаем первый элемент первой строки матрицы С (C₁₁).
- Считаем элемент C₁₂. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент первой строки матрицы С (C₁₂).
- Считаем элемент C₂₁. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем части и получаем первый элемент второй строки матрицы С (C₂₁).
- Считаем элемент C₂₂. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент второй строки матрицы С (C₂₂).
Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.
Формула умножения матриц Пример умножения квадратных матриц размерностью 2×2Что дальше
В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽
Текст:
Александр Бабаскин
Редактура:
Максим Ильяхов
Художник:
Даня Берковский
Корректор:
Ирина Михеева
Вёрстка:
Мария Дронова
Соцсети:
Олег Вешкурцев
Матрицы
Матрица – это массив чисел:
Матрица
(в ней 2 строки и 3 столбца)
Речь идет об одной матрице , или нескольких матрицах .
Мы можем многое с ними сделать …
Добавление
Чтобы сложить две матрицы: сложите числа в соответствующих позициях:
Это расчеты:
| 3 + 4 = 7 | 8 + 0 = 8 |
| 4 + 1 = 5 | 6−9 = −3 |
Две матрицы должны быть одинакового размера, т.е.е. строки должны совпадать по размеру, а столбцы должны совпадать по размеру.
Пример: матрица с 3 строками и 5 столбцами может быть добавлена к другой матрице из 3 строк и 5 столбцов .
Но не удалось добавить в матрицу с 3 строки и 4 столбца (столбцы не совпадают по размеру)
отрицательный
Негатив матрицы тоже прост:
Это расчеты:
| – (2) = – 2 | – (- 4) = + 4 |
| – (7) = – 7 | – (10) = – 10 |
Вычитание
Чтобы вычесть две матрицы: вычтите числа в совпадающих позициях:
Это расчеты:
| 3-4 = -1 | 8−0 = 8 |
| 4−1 = 3 | 6 – (- 9) = 15 |
Примечание: вычитание фактически определяется как сложение отрицательной матрицы: A + (−B)
Умножить на константу
Мы можем умножить матрицу на константу (в данном случае значение 2) :
Это расчеты:
| 2 × 4 = 8 | 2 × 0 = 0 |
| 2 × 1 = 2 | 2 × −9 = −18 |
Мы называем константу скаляром , поэтому официально это называется «скалярное умножение».
Умножение на другую матрицу
Чтобы перемножить две матрицы вместе немного сложнее … прочтите Умножение матриц, чтобы узнать, как.
Разделение
А что с делением? Ну, мы не делим матрицы на , мы делаем это так:
A / B = A × (1 / B) = A × B -1
, где B -1 означает «инверсию» B.
Таким образом, мы не делим, вместо этого мы умножаем на обратное значение .
Есть особые способы найти обратное, подробнее см. Обратный к матрице.
Транспонирование
Чтобы «транспонировать» матрицу, поменяйте местами строки и столбцы.
Мы ставим букву “Т” в верхнем правом углу, чтобы обозначить транспонирование:
Обозначение
Матрица обычно обозначается заглавной буквой (например, A или B)
Каждая запись (или «элемент») обозначается строчной буквой с «нижним индексом» строки , столбец :
Строки и столбцыИтак, что это за строка, а какая за столбец?
Чтобы помнить, что строки идут перед столбцами, используйте слово «дуга» : а р, в |
Пример:
| B = |
Вот несколько примеров записей:
b 1,1 = 6 (запись в строке 1, столбце 1 – 6)
b 1,3 = 24 (запись в строке 1, столбце 3 – 24)
b 2,3 = 8 (запись в строке 2, столбце 3 – 8)
2.1: Введение в матрицы – математика LibreTexts
Цели обучения
В этом разделе вы узнаете:
- Сложить и вычесть матрицы.
- Умножить матрицу на скаляр.
- Умножьте две матрицы.
Матрица – это двумерный массив чисел, упорядоченный по строкам и столбцам. Матрицы обеспечивают метод организации, хранения и работы с математической информацией. Матрицы имеют множество приложений и используются в реальном мире.Матрицы представляют собой полезный инструмент для работы с моделями, основанными на системах линейных уравнений. Мы будем использовать матрицы в разделах 2.2, 2.3 и 2.4 для решения систем линейных уравнений с несколькими переменными в этой главе.
Матрицыиспользуются в шифровании, которое мы рассмотрим в разделе 2.5, и в экономическом моделировании, которое рассматривается в разделе 2.6. Мы снова используем матрицы в главе 4 при решении таких задач оптимизации, как максимизация прибыли или дохода или минимизация затрат. Матрицы используются в бизнесе для планирования, маршрутизации транспортировки и отгрузки, а также для управления запасами.
Практически любое приложение, которое собирает данные и управляет ими, может применять матрицы. Использование матриц расширилось по мере увеличения доступности данных во многих сферах жизни и бизнеса. Они являются важными инструментами для организации данных и решения проблем во всех областях науки, от физики и химии до биологии и генетики, до метеорологии и экономики. В информатике матричная математика лежит в основе анимации изображений в фильмах и видеоиграх.
Информатика анализирует диаграммы сетей, чтобы понять, как вещи связаны друг с другом, например, отношения между людьми на социальном веб-сайте, отношения между результатами в линейном поиске и то, как люди переходят с одного веб-сайта на другой.Математика для работы с сетевыми диаграммами составляет область «теории графов»; он полагается на матрицы для организации информации в графах, которые схематически отображают соединения и ассоциации в сети. Например, если вы используете Facebook, Linked-In или другие сайты социальных сетей, эти сайты используют сетевые графики и матрицы для организации ваших отношений с другими пользователями.
Введение в матрицы
Матрица – это прямоугольный массив чисел. Матрицы полезны при организации и управлении большими объемами данных.Чтобы понять, что такое матрицы, мы рассмотрим следующий пример.
Пример \ (\ PageIndex {1} \)
Fine Furniture Company производит стулья и столы на своих фабриках в Сан-Хосе, Хейворде и Окленде. Общий объем производства в сотнях сотен на трех заводах за 2014 и 2015 годы приведен в таблице ниже.
| 2014 | 2015 | |||
| СТУЛЬЯ | ТАБЛИЦЫ | СТУЛЬЯ | ТАБЛИЦЫ | |
| САН-ХОСЕ | 30 | 18 | 36 | 20 |
| HAYWARD | 20 | 12 | 24 | 18 |
| OAKLAND | 16 | 10 | 20 | 12 |
- Представьте производство за 2014 и 2015 годы в виде матриц A и B.
- Найдите разницу в продажах между 2014 и 2015 годами.
- Компания прогнозирует, что в 2020 году производство на этих заводах вырастет вдвое по сравнению с 2014 годом. Каким будет производство в 2020 году?
Решение
а) Матрицы следующие:
\ [A = \ left [\ begin {array} {ll}
30 & 18 \\
20 & 12 \\
16 & 10
\ end {array} \ right] \ nonumber \]
\ [\ mathrm {B} = \ left [\ begin {array} {ll}
36 & 20 \\
24 & 18 \\
20 & 12
\ end {array} \ right] \ nonumber \]
б) Ищем матрицу \ (B – A \).Когда две матрицы имеют одинаковое количество строк и столбцов, матрицы могут быть добавлены или вычтены запись за записью. Следовательно, получаем
\ [\ mathrm {B} – \ mathrm {A} = \ left [\ begin {array} {ll}
36-30 & 20-18 \\
24-20 & 18-12 \\
20-16 & 12-10
\ end {array} \ right] = \ left [\ begin {array} {ll}
6 & 2 \\
4 & 6 \\
4 & 2
\ end {array} \ right] \ nonumber \]
c) Нам нужна матрица, которая в два раза больше матрицы 2014 года, то есть \ (2A \).
Каждый раз, когда матрица умножается на число, каждая запись умножается на число.
\ [2 \ mathrm {A} = 2 \ left [\ begin {array} {ll}
30 & 18 \\
20 & 12 \\
16 & 10
\ end {array} \ right] = \ left [\ begin {array} {ll}
60 & 36 \\
40 & 24 \\
32 & 20
\ end {array} \ right] \ nonumber \]
Прежде чем мы продолжим, нам необходимо ознакомиться с некоторыми терминами, связанными с матрицами. Числа в матрице называются элементами или элементами матрицы.
Когда мы говорим о матрице, нам нужно знать размер или размер матрицы. Размерность матрицы – это количество содержащихся в ней строк и столбцов. Когда мы говорим, что матрица – это «матрица 3 на 4», мы говорим, что она имеет 3 строки и 4 столбца. Строки всегда упоминаются первыми, а столбцы – вторыми. Это означает, что матрица \ (3 \ times 4 \) не имеет той же размерности, что и матрица \ (4 \ times 3 \).
\ [A = \ left [\ begin {array} {cccc}
1 & 4 & -2 & 0 \\
3 & -1 & 7 & 9 \\
6 & 2 & 0 & 5
\ end { массив} \ right] \]
\ [B = \ left [\ begin {array} {ccc}
2 & 9 & 8 \\
-3 & 0 & 1 \\
6 & 5 & -2 \\
-4 & 7 & 8
\ end {array} \ right] \]
Матрица \ (A \) имеет размеры \ (3 \ times 4 \), а матрица \ (B \) имеет размеры \ (4 \ times 3 \).
Матрица, которая имеет такое же количество строк, как и столбцов, называется квадратной матрицей . Матрица со всеми нулевыми элементами называется нулевой матрицей . Квадратная матрица с единицами по главной диагонали и нулями везде, называется единичной матрицей . Когда квадратная матрица умножается на единичную матрицу того же размера, матрица остается той же.
\ [I = \ left [\ begin {array} {lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\ end {array} \ right] \]
Матрица \ (I \) – это единичная матрица \ (3 \ times 3 \)
Матрица только с одной строкой называется матрицей-строкой или вектором-строкой , , а матрица только с одним столбцом называется матрицей-столбцом или вектором-столбцом .Две матрицы равны равным , если они имеют одинаковый размер и соответствующие записи равны.
Мы умеем выполнять арифметические операции с матрицами. Далее мы определим и приведем примеры, иллюстрирующие операции сложения и вычитания матриц, скалярного умножения и умножения матриц. Обратите внимание, что умножение матриц сильно отличается от того, что вы интуитивно ожидаете, поэтому обратите особое внимание на объяснение. Также обратите внимание, что возможность выполнения матричных операций зависит от того, насколько соответствующие матрицы совместимы по размеру или размерам для этой операции.Определение совместимых размеров различается для разных операций, поэтому внимательно обратите внимание на требования для каждой из них.
Сложение и вычитание матриц
Если две матрицы имеют одинаковый размер, их можно складывать или вычитать. Операции выполняются над соответствующими записями.
Пример \ (\ PageIndex {2} \)
Учитывая матрицы \ (A \), \ (B \), \ (C \) и \ (D \), ниже
\ [A = \ left [\ begin {array} {lll}
1 & 2 & 4 \\
2 & 3 & 1 \\
5 & 0 & 3
\ end {array} \ right] \ quad B = \ left [\ begin {array} {lll}
2 & -1 & 3 \\
2 & 4 & 2 \\
3 & 6 & 1
\ end {array} \ right] \ quad C = \ left [\ begin {array} {l}
4 \\
2 \\
3
\ end {array} \ right] \ quad D = \ left [\ begin {array} {r}
-2 \\
– 3 \\
4
\ end {array} \ right] \ nonumber \]
Найдите, если возможно.
- \ (А + В \)
- \ (C – D \)
- \ (A + D. \)
Решение
Как мы упоминали ранее, сложение и вычитание матриц включает выполнение этих операций ввод за вводом.
a) Мы добавляем каждый элемент \ (A \) к соответствующей записи \ (B \).
\ [A + B = \ left [\ begin {array} {lll}
3 & 1 & 7 \\
4 & 7 & 3 \\
8 & 6 & 4
\ end {array} \ right] \ nonumber \]
б) Как и в описанной выше задаче, мы выполняем вычитание по каждой записи.
\ [\ mathrm {C} – \ mathrm {D} = \ left [\ begin {array} {c}
6 \\
5 \\
-1
\ end {array} \ right] \ nonumber \]
c) Сумма \ (A + D \) не может быть найдена, потому что две матрицы имеют разные размеры.
Примечание. Две матрицы можно складывать или вычитать только , если они имеют одинаковую размерность.
Умножение матрицы на скаляр
Если матрица умножается на скаляр, каждая запись умножается на этот скаляр. Мы можем рассматривать скалярное умножение как умножение числа и матрицы для получения новой матрицы как произведения.
Пример \ (\ PageIndex {3} \)
Учитывая матрицу \ (A \) и \ (C \) в приведенном выше примере, найдите \ (2A \) и \ (- 3C \).
Решение
Чтобы найти \ (2A \), мы умножаем каждый элемент матрицы \ (A \) на 2, а чтобы найти \ (- 3C \), мы умножаем каждый элемент матрицы C на -3. Результаты представлены ниже.
a) Мы умножаем каждую запись A на 2.
\ [2 \ mathrm {A} = \ left [\ begin {array} {ccc}
2 & 4 & 8 \\
4 & 6 & 2 \\
10 & 0 & 6
\ end {array} \ справа] \ nonumber \]
б) Мы умножаем каждую запись C на -3.
\ [- 3 C = \ left [\ begin {array} {c}
-12 \\
-6 \\
-9
\ end {array} \ right] \ nonumber \]
Умножение двух матриц
Умножить одну матрицу на другую не так просто, как сложение, вычитание или скалярное умножение матриц. Поскольку он широко используется в прикладных задачах, важно, чтобы мы хорошо его усвоили. Поэтому мы постараемся изучить процесс пошагово. Сначала мы начнем с поиска произведения матрицы-строки и матрицы-столбца.
Пример \ (\ PageIndex {4} \)
Найдите продукт \ (AB \), учитывая
\ [A = \ left [\ begin {array} {lll}
2 & 3 & 4
\ end {array} \ right] \ nonumber \]
и
\ [B = \ left [\ begin {array} {l}
a \\
b \\
c
\ end {array} \ right]. \ nonumber \]
Решение
Произведение представляет собой матрицу \ (1 \ times 1 \), элемент которой получается путем умножения соответствующих элементов и последующего формирования суммы.
\ [\ begin {align *}
\ mathrm {AB} & = \ left [\ begin {array} {lll}
2 & 3 & 4
\ end {array} \ right] \ left [\ begin {array } {l}
\ mathrm {a} \\
\ mathrm {b} \\
\ mathrm {c}
\ end {array} \ right] \\ [4pt] & = [2 (\ mathrm {a} +3 \ mathrm {b} +4 \ mathrm {c})]
\ end {align *} \]
Обратите внимание, что \ (AB \) – это матрица \ (1 \ times 1 \), и ее единственный элемент – \ (2a + 3b + 4c \).
Пример \ (\ PageIndex {5} \)
Найдите продукт \ (AB \), учитывая
\ [A = \ left [\ begin {array} {lll}
2 & 3 & 4
\ end {array} \ right] \ nonumber \]
и
\ [B = \ left [\ begin {array} {l}
5 \\
6 \\
7
\ end {array} \ right] \ nonumber \]
Решение
Опять умножаем соответствующие записи и складываем.
\ [\ begin {align *} \ mathrm {AB} & = \ left [\ begin {array} {lll}
2 & 3 & 4
\ end {array} \ right] \ left [\ begin {array} {l}
5 \\
6 \\
7
\ end {array} \ right] \\ [4pt] & = [2 \ cdot 5 + 3 \ cdot 6 + 4 \ cdot 7] \\ [4pt] & = [10 + 18 + 28] \\ [4pt] & = [56] \ end {align *} \]
Примечание. Для существования произведения матрицы строк и матрицы столбцов количество записей в матрице строк должно быть таким же, как количество записей в матрице столбцов.
Пример \ (\ PageIndex {6} \)
Найдите продукт AB, учитывая
\ [A = \ left [\ begin {array} {lll}
2 & 3 & 4
\ end {array} \ right] \ nonumber \]
и
\ [B = \ left [\ begin {array} {ll}
5 & 3 \\
6 & 4 \\
7 & 5
\ end {array} \ right].\ nonumber \]
Решение
Мы знаем, как умножить матрицу-строку на матрицу-столбец. Чтобы найти произведение \ (AB \), в этом примере мы умножим матрицу-строку \ (A \) на первый и второй столбцы матрицы \ (B \), в результате получим \ (1 \ times 2 \ ) матрица.
\ [\ mathrm {AB} = \ left [\ begin {array} {lll}
2 \ cdot 5 + 3 \ cdot 6 + 4 \ cdot 7 & 2 \ cdot 3 + 3 \ cdot 4 + 4 \ cdot 5
\ end {array} \ right] = \ left [\ begin {array} {ll}
56 & 38
\ end {array} \ right] \ nonumber \]
Мы умножили матрицу \ (1 \ times 3 \) на матрицу размером \ (3 \ times 2 \).Таким образом, в отличие от сложения и вычитания, можно умножить две матрицы с разными размерами, если количество записей в строках первой матрицы такое же, как количество записей в столбцах второй матрицы.
Пример \ (\ PageIndex {7} \)
Найдите продукт \ (AB \), учитывая:
\ [A = \ left [\ begin {array} {lll}
2 & 3 & 4 \\
1 & 2 & 3
\ end {array} \ right] \]
и
\ [\ mathrm {B} = \ left [\ begin {array} {ll}
5 & 3 \\
6 & 4 \\
7 & 5
\ end {array} \ right] \]
Решение
На этот раз мы умножаем две строки матрицы \ (A \) на два столбца матрицы \ (B \).Поскольку количество записей в каждой строке \ (A \) такое же, как количество записей в каждом столбце \ (B \), произведение возможно. Делаем именно то, что делали в последнем примере. Единственное отличие состоит в том, что в матрице \ (A \) есть еще одна строка.
Умножаем первую строку матрицы \ (A \) на два столбца \ (B \) по одному, а затем повторяем процесс со второй строкой A. Получаем
\ [\ mathrm {AB} = \ left [\ begin {array} {lll}
2 & 3 & 4 \\
1 & 2 & 3
\ end {array} \ right] \ left [\ begin {array } {ll}
5 & 3 \\
6 & 4 \\
7 & 5
\ end {array} \ right] = \ left [\ begin {array} {ll}
2 \ cdot 5 + 3 \ cdot 6 + 4 \ cdot 7 и 2 \ cdot 3 + 3 \ cdot 4 + 4 \ cdot 5 \\
1 \ cdot 5 + 2 \ cdot 6 + 3 \ cdot 7 & 1 \ cdot 3 + 2 \ cdot 4 + 3 \ cdot 5
\ end {array} \ right] \]
\ [\ mathrm {AB} = \ left [\ begin {array} {ll}
56 & 38 \\
38 & 26
\ end {array} \ right] \]
Пример \ (\ PageIndex {8} \)
Найдите, если возможно:
- \ (EF \)
- \ (FE \)
- \ (FH \)
- \ (GH \)
- \ (HG \)
\ [\ mathrm {E} = \ left [\ begin {array} {ll}
1 & 2 \\
4 & 2 \\
3 & 1
\ end {array} \ right] \ quad \ mathrm {F} = \ left [\ begin {array} {ll}
2 & -1 \\
3 & 2
\ end {array} \ right] \ quad \ mathrm {G} = \ left [\ begin {array } {lll}
4 & 1
\ end {array} \ right] \ quad \ mathrm {H} = \ left [\ begin {array} {l}
-3 \\
-1
\ end {array} \ right] \ nonumber \]
Решение
a) Чтобы найти \ (EF \), мы умножаем первую строку \ (\ left [\ begin {array} {ll}
1 & 2
\ end {array} \ right] \)
из E со столбцами \ (\ left [\ begin {array} {l}
2 \\
3
\ end {array} \ right] \ text {и} \ left [\ begin {array} {l}
1 \\
-2
\ end {array} \ right] \) матрицы F, а затем повторите процесс, умножив две другие строки E на эти столбцы F.Результат выглядит следующим образом:
\ [\ mathrm {EF} = \ left [\ begin {array} {ll}
1 & 2 \\
4 & 2 \\
3 & 1
\ end {array} \ right] \ left [\ begin {массив} {cc}
2 & -1 \\
3 & 2
\ end {array} \ right] = \ left [\ begin {array} {cc}
1 \ cdot 2 + 2 \ cdot 3 & 1 \ cdot-1 + 2 \ cdot 2 \\
4 \ cdot 2 + 2 \ cdot 3 и 4 \ cdot-1 + 2 \ cdot 2 \\
3 \ cdot 2 + 1 \ cdot 3 и 3 \ cdot-1 +1 \ cdot 2
\ end {array} \ right] = \ left [\ begin {array} {cc}
8 & 3 \\
14 & 0 \\
9 & -1
\ end {array} \ справа] \]
b) Произведение \ (FE \) невозможно, потому что матрица F имеет два элемента в каждой строке, а матрица E имеет три элемента в каждом столбце.Другими словами, матрица F имеет два столбца, а матрица E – три строки.
c) \ [\ mathrm {FH} = \ left [\ begin {array} {cc}
2 & -1 \\
3 & 2
\ end {array} \ right] \ left [\ begin {array} {c}
-3 \\
-1
\ end {array} \ right] = \ left [\ begin {array} {c}
2 \ cdot-3 + -1 \ cdot-1 \\
3 \ cdot-3 + 2 \ cdot-1
\ end {array} \ right] = \ left [\ begin {array} {c}
-5 \\
-11
\ end {array} \ right] \]
d) \ [\ mathrm {GH} = \ left [\ begin {array} {ll}
4 & 1
\ end {array} \ right] \ left [\ begin {array} {l}
-3 \ \
-1
\ end {array} \ right] = \ left [\ begin {array} {l}
4 \ cdot-3 + 1 \ cdot-1 \\
-1
\ end {array} \ right ] = [- 13] \]
e) \ [\ mathrm {HG} = \ left [\ begin {array} {l}
-3 \\
-1
\ end {array} \ right] \ left [\ begin {array} {ll}
4 & 1
\ end {array} \ right] = \ left [\ begin {array} {ll}
-3 \ cdot 4 & -3 \ cdot 1 \\
-1 \ cdot 4 & -1 \ cdot 1
\ end {array} \ right] = \ left [\ begin {array} {cc}
-12 & -3 \\
-4 & -1
\ end {array} \ right] \]
Мы суммируем некоторые важные свойства умножения матриц, которые мы наблюдали в предыдущих примерах.
Для существования продукта \ (\ bf {AB} \) :
- количество столбцов \ (\ bf {A} \) должно равняться количеству строк \ (\ bf {B} \)
- , если матрица \ (\ bf {A} \) имеет размерность \ (\ bf {m \ times n} \) , а матрица \ (\ bf {B} \) имеет размерность \ (\ bf {n \ times p} \) , то произведение \ (\ bf {AB} \) будет матрицей с размерностью \ (\ bf {m \ times p} \) .
Умножение матриц не коммутативно: если существуют оба произведения матриц \ (\ bf {AB} \) и \ (\ bf {BA} \) , большую часть времени \ (\ bf {AB} \) не будет равно \ (\ bf {BA} \) .
Пример \ (\ PageIndex {9} \)
Для заданных ниже матриц \ (R \), \ (S \) и \ (T \) найдите \ (2RS – 3ST \).
\ [R = \ left [\ begin {array} {lll}
1 & 0 & 2 \\
2 & 1 & 5 \\
2 & 3 & 1
\ end {array} \ right] \ quad S = \ left [\ begin {array} {lll}
0 & -1 & 2 \\
3 & 1 & 0 \\
4 & 2 & 1
\ end {array} \ right] \ quad T = \ left [\ begin {array} {lll}
-2 & 3 & 0 \\
-3 & 2 & 2 \\
-1 & 1 & 0
\ end {array} \ right] \]
Решение
Умножаем матрицы R и S.
\ begin {align}
& \ mathrm {RS} = \ left [\ begin {array} {ccc}
8 & 3 & 4 \\
23 & 9 & 9 \\
13 & 3 & 5
\ end {array} \ right] \\
& \ begin {array} {l}
2 \ mathrm {RS} = 2 \ left [\ begin {array} {ccc}
8 & 3 & 4 \\
23 & 9 & 9 \\
13 & 3 & 5
\ end {array} \ right] = \ left [\ begin {array} {ccc}
16 & 6 & 8 \\
46 & 18 & 18 \\
26 & 6 и 10
\ end {array} \ right] \\
\ mathrm {ST} = \ left [\ begin {array} {ccc}
1 & 0 & -2 \\
-9 & 11 & 2 \\
-15 и 17 и 4
\ end {array} \ right] \\
3 \ mathrm {ST} = 3 \ left [\ begin {array} {ccc}
1 & 0 & -2 \\
-9 & 11 & 2 \\
-15 & 17 & 4
\ end {array} \ right] = \ left [\ begin {array} {ccc}
3 & 0 & -6 \\
-27 & 33 & 6 \\
-45 & 51 & 12
\ end {array} \ right]
\ end {array}
\ end {align}
Таким образом,
\ [2 \ mathrm {RS} -3 \ mathrm {ST} = \ left [\ begin {array} {ccc}
16 & 6 & 8 \\
46 & 18 & 18 \\
26 & 6 & 10
\ end {array} \ right] – \ left [\ begin {array} {ccc}
3 & 0 & -6 \\
-27 & 33 & 6 \\
-45 & 51 & 12
\ end { массив} \ right] = \ left [\ begin {array} {ccc}
13 & 6 & 14 \\
73 & -15 & 12 \\
71 & -45 & -2
\ end {array} \ right ] \]
Пример \ (\ PageIndex {10} \)
Найти \ (F ^ 2 \) заданную матрицу
\ [\ mathrm {F} = \ left [\ begin {array} {ll}
2 & -1 \\
3 & 2
\ end {array} \ right] \]
Решение
\ (F ^ 2 \) находится путем умножения матрицы \ (F \) на себя, используя умножение матриц.2 \), возможно, только если матрица является квадратной матрицей.
ИСПОЛЬЗОВАНИЕ МАТРИЦ ДЛЯ ПРЕДСТАВЛЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
В этой главе мы будем использовать матрицы для решения линейных систем. В разделе 2.4 нас попросят выразить линейные системы как матричное уравнение \ (\ bf {AX = B} \), где \ (A \), \ (X \) и \ (B \) – матрицы.
- Матрица \ (A \) называется матрицей коэффициентов .
- Матрица \ (X \) – это матрица с 1 столбцом, содержащая переменные.
- Матрица \ (B \) – это матрица с 1 столбцом, содержащая константы.
Пример \ (\ PageIndex {11} \)
Проверить, что система двух линейных уравнений с двумя неизвестными:
\ begin {array} {l}
a x + b y = h \\
c x + d y = k
\ end {array}
можно записать как \ (AX = B \), где
\ [A = \ left [\ begin {array} {ll}
a & b \\
c & d
\ end {array} \ right] \ quad X = \ left [\ begin {array} {l}
x \\
y
\ end {array} \ right] \ text {and} B = \ left [\ begin {array} {l}
h \\
k
\ end {array} \ right] \ nonumber \]
Решение
Если мы умножим матрицы \ (A \) и \ (X \), мы получим
\ [AX = \ left [\ begin {array} {ll}
a & b \\
c & d
\ end {array} \ right] \ left [\ begin {array} {l}
x \\
y
\ end {array} \ right] = \ left [\ begin {array} {c}
a x + by \\
c x + dy
\ end {array} \ right] \ nonumber \]
Если \ (AX = B \), то
\ [\ left [\ begin {array} {l}
a x + by \\
c x + dy
\ end {array} \ right] = \ left [\ begin {array} {l}
h \ \
k
\ end {array} \ right] \ nonumber \]
Если две матрицы равны, то их соответствующие элементы равны.Отсюда следует, что
\ begin {array} {l}
a x + b y = h \\
c x + d y = k
\ end {array}
Пример \ (\ PageIndex {12} \)
Выразите следующую систему в виде матричного уравнения в форме \ (AX = B \).
\ begin {array} {l}
2 x + 3 y-4 z = 5 \\
3 x + 4 y-5 z = 6 \\
5 x \ quad-6 z = 7
\ end {array }
Решение
Эта система уравнений может быть выражена в форме \ (AX = B \), как показано ниже.
\ [\ left [\ begin {array} {ccc}
2 & 3 & -4 \\
3 & 4 & -5 \\
5 & 0 & -6
\ end {array} \ right] \ left [\ begin {array} {l}
x \\
y \\
z
\ end {array} \ right] = \ left [\ begin {array} {l}
5 \\
6 \\
7
\ end {array} \ right] \]
| математика | Britannica
matrix , набор чисел, расположенных в строках и столбцах, чтобы сформировать прямоугольный массив.Числа называются элементами или элементами матрицы. Матрицы находят широкое применение в технике, физике, экономике и статистике, а также в различных областях математики. Исторически первым распознаванием была не матрица, а определенное число, связанное с квадратным массивом чисел, называемое определителем. Лишь постепенно возникла идея матрицы как алгебраической сущности. Термин матрица был введен английским математиком 19-го века Джеймсом Сильвестром, но именно его друг математик Артур Кэли развил алгебраический аспект матриц в двух статьях 1850-х годов.Кэли впервые применил их к изучению систем линейных уравнений, где они до сих пор очень полезны. Они также важны, потому что, как признал Кэли, определенные наборы матриц образуют алгебраические системы, в которых действуют многие обычные законы арифметики (например, ассоциативные и распределительные законы), но в которых действуют другие законы (например, закон коммутативности). недействительно. Матрицы также нашли важное применение в компьютерной графике, где они использовались для представления поворотов и других преобразований изображений.
Если имеется m строк и n столбцов, матрица называется матрицей « m на n », записанной « m × n ». Например,
– это матрица 2 × 3. Матрица с n строками и n столбцами называется квадратной матрицей порядка n . Обычное число можно рассматривать как матрицу 1 × 1; таким образом, 3 можно рассматривать как матрицу [3].
В общепринятых обозначениях заглавная буква обозначает матрицу, а соответствующая строчная буква с двойным нижним индексом описывает элемент матрицы.Таким образом, a ij – это элемент в строке i и j -м столбце матрицы A . Если A – это матрица 2 × 3, показанная выше, то a 11 = 1, a 12 = 3, a 13 = 8, a 21 = 2, a 22 = −4 и a 23 = 5. При определенных условиях матрицы можно складывать и умножать как отдельные объекты, что дает начало важным математическим системам, известным как матричные алгебры.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасМатрицы естественным образом встречаются в системах одновременных уравнений. В следующей системе для неизвестных x и y массив чисел представляет собой матрицу, элементы которой являются коэффициентами неизвестных. Решение уравнений полностью зависит от этих чисел и от их конкретного расположения. Если бы 3 и 4 поменяли местами, решение было бы другим.
Две матрицы A и B равны друг другу, если они имеют одинаковое количество строк и одинаковое количество столбцов и если a ij = b ij для каждый i и каждый j .Если A и B – две матрицы m × n , их сумма S = A + B представляет собой матрицу m × n , элементы которой s ij = a ij + b ij . То есть каждый элемент S равен сумме элементов в соответствующих позициях A и B .
Матрица Матрица может быть умножена на обычное число c , которое называется скаляром. Продукт обозначается cA или Ac и представляет собой матрицу, элементы которой равны ca ij .
Умножение матрицы A на матрицу B для получения матрицы C определяется только тогда, когда количество столбцов первой матрицы A равно количеству строк второй матрицы B .Чтобы определить элемент c ij , который находится в строке i и столбце j продукта, первый элемент в строке i строки A умножается на первый элемент в столбце j -й столбца B , второй элемент в строке – второй элемент в столбце и так далее, пока последний элемент в строке не умножится на последний элемент столбца; сумма всех этих произведений дает элемент c ij .В символах для случая, когда A имеет m столбцов и B имеет m строк, матрица C имеет столько же строк, сколько A и столько же столбцов, сколько B .
В отличие от умножения обычных чисел a и b , в котором ab всегда равно ba , умножение матриц A и B не является коммутативным. Однако оно ассоциативно и распределительно по сравнению с сложением.То есть, когда операции возможны, всегда выполняются следующие уравнения: A ( BC ) = ( AB ) C , A ( B + C ) = AB + AC и ( B + C ) A = BA + CA . Если матрица 2 × 2 A со строками (2, 3) и (4, 5) умножается сама на себя, то произведение, обычно записываемое как A 2 , имеет строки (16, 21) и ( 28, 37).
Матрица O со всеми ее элементами 0 называется нулевой матрицей. Квадратная матрица A с единицами на главной диагонали (вверху слева направо вниз) и нулями во всех остальных местах называется единичной матрицей. Он обозначается I или I n , чтобы показать, что его порядок равен n . Если B – любая квадратная матрица, а I и O – единичная и нулевая матрицы одного порядка, всегда верно, что B + O = O + B = B и BI = IB = B .Следовательно, O и I ведут себя как 0 и 1 в обычной арифметике. Фактически, обычная арифметика является частным случаем матричной арифметики, в которой все матрицы имеют размер 1 × 1.
Связано с каждой квадратной матрицей A – это число, известное как определитель A , обозначаемое det A . Например, для матрицы 2 × 2det A = ad – bc . Квадратная матрица B называется невырожденной, если det B ≠ 0.Если B неособое, существует матрица, обратная B , обозначенная B -1 , так что BB -1 = B -1 B = Я . Уравнение AX = B , в котором A и B – известные матрицы, а X – неизвестная матрица, может быть решено однозначно, если A – невырожденная матрица, тогда A −1 существует, и обе части уравнения можно умножить слева на него: A −1 ( AX ) = A −1 B .Теперь A −1 ( AX ) = ( A −1 A ) X = IX = X ; следовательно, решение будет X = A -1 B . Система из m линейных уравнений в n неизвестных всегда может быть выражена как матричное уравнение AX = B , в котором A – это матрица коэффициентов неизвестных m × n , X – это матрица неизвестных n × 1, а B – это матрица n × 1, содержащая числа в правой части уравнения.
Проблема, имеющая большое значение во многих областях науки, заключается в следующем: по квадратной матрице A порядка n, найти матрицу n × 1 X, , называемую n -мерным вектором, таким образом, что AX = cX . Здесь c – число, называемое собственным значением, а X – собственным вектором. Существование собственного вектора X с собственным значением c означает, что определенное преобразование пространства, связанное с матрицей A , растягивает пространство в направлении вектора X на коэффициент c .
Что такое матрица?
Этот урок знакомит с матрицей – прямоугольным массивом, лежащим в основе матричная алгебра. Матричная алгебра довольно часто используется в расширенной статистике, в основном потому что он дает два преимущества.
- Эффективные методы манипулирования наборами данных и решения наборов уравнения.
Определение матрицы
Матрица представляет собой прямоугольный массив чисел, расположенных в строки и столбцы. Приведенный ниже массив чисел является примером матрицы.
Количество строк и столбцов матрицы называется ее размер или его заказ . Условно, строки указываются первыми; и столбцы, вторые. Таким образом, можно сказать, что размер (или порядок) вышеуказанной матрицы составляет 3 x 4, что означает, что она имеет 3 ряда и 4 столбика.
Числа, которые появляются в строках и столбцах матрицы, называются элементов матрицы. В приведенной выше матрице элемент в первом столбце первой строки 21; элемент во втором столбец первой строки – 62; и так далее.
Матричная нотация
Статистики используют символы для обозначения матричных элементов и матриц.
Матричные элементы. Рассмотрим матрицу ниже, в котором элементы матрицы полностью представлены символами.
По соглашению первый нижний индекс относится к номер строки; а второй индекс – к номеру столбца. Таким образом, первый элемент в первой строке представлен А 1 1 . Второй элемент в первой строке – представлен A 1 2 .И так далее, пока мы не дойдем до четвертого элемента во второй строке, которая представлена А 2 4 .Матрицы. Есть несколько способов изобразить матрица символически. Простейший – использовать жирный шрифт, например A , B , или C . Таким образом, A может представлять собой Матрица 2 x 4, как показано ниже.
Другой подход для представления матрицы A :
A = [ A i j ], где i = 1, 2 и j = 1, 2, 3, 4
Это обозначение означает, что A – это матрица с 2 строками и 4 колонки.Фактические элементы массива не отображаются; они есть представлен символом A i j .
При необходимости будут введены другие матричные обозначения. Для описания всех матричных обозначений, используемых в этом руководстве, увидеть Матричные обозначения Приложение.
Равенство матриц
Чтобы понять алгебру матриц, нам нужно понять матрицу равенство. Две матрицы равны, если все три из следующих условий выполнены:
- Каждая матрица имеет одинаковое количество строк.
- Каждая матрица имеет одинаковое количество столбцов.
- Соответствующие элементы в каждой матрице равны.
Рассмотрим три матрицы, показанные ниже.
Если A = B , мы знаем, что x = 222 и у = 333; поскольку соответствующие элементы равных матриц также равны. А мы знаем, что матрица C не равно A или B , потому что C имеет больше столбцов, чем A или В .
Проверьте свое понимание
Задача 1
Приведенные ниже обозначения описывают две матрицы – матрицу A, и матрица B .
A = [ A i j ]
, где i = 1, 2, 3 и j = 1, 2
Какие из следующих утверждений о A и B верны?
I. Матрица A состоит из 5 элементов.
II. Размер матрицы B составляет 4 x 2.
III. В матрице B элемент B 2 1 равно 222.
(A) Только I
(B) Только II
(C) Только III
(D) Все вышеперечисленное
(E) Ничего из вышеперечисленного
Решение
Правильный ответ (E).
- Матрица A имеет 3 строки и 2 столбца; это, 3 ряда по 2 элемента в каждом. Это в сумме составляет 6 элементов, всего – нет 5.
- Размер матрицы B равно 2 х 4, а не 4 х 2.То есть матрица B имеет 2 строки и 4 столбца, а не 4 строки и 2 столбца.
- И, наконец, элемент B 2 1 относится к первый элемент в вторая строка матрицы B , которая равна 555, а не 222.
Матрицы и матричная алгебра – Статистика How To
Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):
- Матричная алгебра: введение
- Добавление матрицы: дополнительные примеры
- Умножение матриц
- Определение сингулярной матрицы
- Матрица идентичности
- Что такое обратная матрица?
- Собственные значения и собственные векторы
- Расширенные матрицы
- Определитель матрицы
- Диагональная матрица
- Что такое симметричная и кососимметричная матрицы?
- Что такое матрица транспонирования?
- Что такое матрица дисперсии-ковариации?
- Корреляционные матрицы
- Идемпотентная матрица.
Матрица – это прямоугольный массив чисел, упорядоченный по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:
Преобразование в матричную алгебру в основном просто включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, которые появляются в матрице, называются элементами матрицы .
: Обозначение
Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список вроде этого: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы соблюсти соглашение.
Некоторые из наиболее распространенных терминов, с которыми вы столкнетесь при работе с матрицами:
- Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, у которой есть единицы.
- Скаляр : любое действительное число.
- Матрица Функция: скаляр, умноженный на матрицу, чтобы получить другую матрицу.
Матрицы идентичности. Изображение: Википедия.com.
Матричная алгебра: сложение и вычитание
Размер матрицы (т. Е. 2 x 2) также называется размером матрицы , размером или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размеры должны быть точно так же, как . Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одном и том же месте (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Примечание к обозначениям: рабочий лист (например, в Excel) использует буквы столбцов (ABCD) и номера строк (123), чтобы указать местоположение ячейки, например A1 или D2. Для матриц типично использовать обозначение типа g ij , что означает i-ю строку и j-й столбец матрицы G.
Матричное вычитание работает точно так же.
В начало
Матричное дополнение – это всего лишь серия дополнений. Для матрицы 2 × 2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом положении.
- Сложите верхние правые числа и запишите сумму в верхнем правом углу.
- Сложите нижние левые числа вместе и запишите сумму в нижнем левом углу.
- Сложите числа справа внизу и запишите сумму справа внизу:
Используйте ту же процедуру для матрицы 2 × 3:
Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Вышеупомянутый метод иногда называют «начальным суммированием», поскольку вы просто складываете элементы и фиксируете результат.
Другой способ подумать об этом…
Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z. И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.
Дополнение матрицы для неравных размеров
Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод.Один из таких приемов – прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q является матрицей размера (m + p) × (n + q):
Например:
В начало
Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14
Результат четырех умножений дает числа в новой матрице справа.
Умножение матриц: две матрицы
Когда вы хотите перемножить две матрицы, процесс становится немного сложнее. Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:
Не можете посмотреть видео? Кликните сюда.
Вы можете выполнить матричное умножение двух матриц, только если количество столбцов в первой матрице равно количеству строк во второй матрице. Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете умножить несколько матриц вместе.
Microsoft Excel также может выполнять матричное умножение с использованием функций «массива». Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
В начало
Быстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):
Существуют и другие типы сингулярных матриц, некоторые из которых не так-то легко обнаружить.Следовательно, необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет обратного.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов. Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Сингулярная матрица – это квадратная матрица, но не все квадратные матрицы сингулярны.
Необратимые матрицы
Если квадратная матрица не имеет обратной, то это особая матрица.
Обратная матрица – это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, получится единичная матрица , , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.
Матрицы идентичности. Изображение: Wikipedia.com.
Определитель нуля
Определитель – это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы. Например, матрица 2 × 2, формула ad-bc.
Эта простая матрица 2 × 2 сингулярна, потому что ее определитель равен нулю:
К началу
Единичная матрица – это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева направо снизу и нулями в остальных местах.Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным. Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т. Е. 10 * 1 = 10 ). В более формальных терминах, если x – действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x.По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n .На главной диагонали всегда будут единицы, а оставшиеся пробелы – нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Аддитивная идентификационная матрица
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности. Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах – нули.Поэтому их иногда называют нулевой матрицей .
Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началу
Обзор поиска инверсий смотрите в этом коротком видео:
Не можете посмотреть видео? Кликните сюда.
Обратные матрицы – это то же самое, что и обратные. В элементарной алгебре (и, возможно, даже раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.
Изображение любезно предоставлено LTU
Если вы умножите одну матрицу на ее обратную, вы получите матричный эквивалент 1: Identity Matrix , которая в основном представляет собой матрицу с единицами и нулями.
Шаг 1: Найдите адъюгат матрицы. Сопряжение матрицы можно найти, переставив одну диагональ и взяв отрицания другой:
Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) – (b * c).
Шаг 3: Умножить 1 / определитель * адъюгат. .
Проверка ответа
Вы можете проверить свой ответ умножением матриц.Умножьте свою матрицу ответов на исходную матрицу, и вы получите единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
В начало
Собственное значение (λ) – это специальный скаляр, используемый при матричном умножении и имеющий особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем. Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением . Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его по вектору x .
Пример собственного значения
В следующем примере 5 – собственное значение A, а (1,2) – собственный вектор:
Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу размера n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что если бы вместо новой матрицы nx 1 можно было получить ответ с тем же вектором, который вы умножили на вместе с новым скаляром?
Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр – собственным значением.Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в так называемом разложении по собственным значениям . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:
Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:
Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) – (3) (3)
Упрощая, получаем:
-5 – 5λ + λ + λ 2 – 9
= λ 2 – 4λ – 14
Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ 2 – 4λ – 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором.Находя корни (нули), получаем x = 2 + 3√2, 2 – 3√2
Ответ : 2 + 3√2 и 2-3√2
Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.
В начало
На изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений, и именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11
Может быть помещено в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.
У вас нет , у вас нет , чтобы использовать вертикальную полосу в расширенной матрице. Обычно матрицы вообще не содержат линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.
Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно запишите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, а затем укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, а затем укажите «z.«Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y – 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце, поставив перед знаком равенства.
-1x + 7y + 3 = 0
2x + 4y – 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом шаге стоит отрицательный знак, просто сделайте константу отрицательным числом.
В начало
Определитель матрицы – это просто специальное число, которое используется для описания матриц для поиска решений систем линейных уравнений, поиска обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:
- Это действительное число. Сюда входят отрицательные числа.
- Определители существуют только для квадратных матриц.
- Обратная матрица существует только для матриц с ненулевыми определителями.
Символ для определителя матрицы A – | A |, который также является тем же самым символом, который используется для абсолютного значения, хотя эти два не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2 × 2
Формула определителя матрицы 2 × 2 – ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3 × 3
Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei – fh) – b (di – fg) + c (dh – eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:
= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
По сути, здесь происходит умножение a, b и d на детерминанты меньших 2×2 в матрице 3×3. Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Определитель матрицы 4 × 4
Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые находятся в матрице 4 × 4.В виде формулы:
Вернуться к началу
Диагональная матрица – это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.
Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.
Единичная матрица, которая содержит все 1s по диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е.2,2,2 или 9,9,9), является скалярным кратным единичной матрицы и также может быть классифицировано как диагональное.
Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n – порядок матрицы. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Обозначение
Для описания диагональной матрицы обычно используется обозначение diag (a, b, c) , где abc представляет собой числа в первой диагонали.Для приведенной выше матрицы это обозначение будет diag (3,2,4). .
Верхняя и нижняя треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. В нижнетреугольной матрице числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.
Диагональная матрица – это матрица с нижней диагональю и с нижней диагональю.
Прямоугольные диагональные матрицы
Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n . Существуют и другие формы, которые обычно не используются, например, прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
В начало
Транспонирование матрицы (или транспонирование матрицы) – это как раз то место, где вы переключаете все строки матрицы в столбцы.Матрицы транспонирования полезны при комплексном умножении.
Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r». Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица – это частный случай транспонированной матрицы; он равен своей транспонированной матрице.
Выражаясь более формально, A = A T .
Символы для транспонированной матрицы
Обычный символ для транспонированной матрицы – A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и.
Свойства матриц транспонирования
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным). Основные свойства матриц:
- (A T ) T = A: транспонированная матрица транспонирования является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.
- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент – это величина, которая может умножать матрицу).
- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, совпадает с произведением их матриц транспонирования в обратном порядке.
- (A -1 ) T = (A T ) -1 : транспонирование и инверсия матрицы могут выполняться в любом порядке.
В начало
Симметричная матрица – это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо. Представьте себе складку в матрице по диагонали (не включайте числа в действительную диагональ). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом по линии симметрии ( всегда – ведущая диагональ), как в примере справа , у вас симметричная матрица.
Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной. При транспонировании матрицы первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию.С математической точки зрения, M = M T , где M T – матрица транспонирования.
Максимальное количество номеров
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ – это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.
Диагональные матрицы
Диагональная матрица – это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.
Что такое асимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:
Математически асимметричная матрица удовлетворяет условию a ij = -a ji .Например, возьмите запись в строке 3, столбце 2, которая равна 4. Его симметричный аналог – -4 в строке 2, столбце 3. Это условие также можно записать в терминах его транспонированной матрицы: A T = – А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T – это транспонированная матрица.
Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми. Это потому, что a i, i = −a i, i подразумевает i, i = 0.
Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:
Добавление двух кососимметричных матриц все вместе.
Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг – убедиться, что все элементы на главной диагонали равны нулю (что невозможно «доказать» математически!).Второй шаг – сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a ij = – a ji .
Косоэрмитский
Косоэрмитова матрица по сути такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.
Косоэрмитова матрица, показывающая комплексные числа.
Фактически, кососимметричный и косоэрмитовый эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началу
Матрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) – это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Разница – это мера того, насколько разбросаны данные. Ковариация – это мера того, насколько две случайные величины перемещаются вместе в одном направлении.
Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариативной матрицы, потому что, по сути, эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках.Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете смотреть в столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Построение матрицы дисперсии-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1).Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Если вы хотите сделать один вручную:
Шаг 1: Вставьте отклонения для ваших данных в диагонали матрицы.
Шаг 2: Рассчитайте ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A). На следующей диаграмме показано, где появляются ковариация и дисперсия для каждого варианта.
В начало
См. Также:
Что такое матрица неточностей?
Следующий : Форма эшелона строк / Форма сокращенного эшелона строк
————————————————– —————————-Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Определение и примеры матрицы, ее записей, строк, столбцов, обозначений матрицы. Матрица – это просто …
Матрица – это способ организации данных в столбцы и строки. В скобках [] пишется матрица. Посмотрите на картинку ниже, чтобы увидеть пример.
Каждый элемент в матрице называется записью.
Матрица, изображенная ниже, состоит из двух строк и трех столбцов.
- Его размеры 2 × 3
- Элементы матрицы ниже: 2, -5, 10, -4, 19, 4.
Размер матрицы
Размеры матрицы относятся к количеству строк и столбцов данной матрицы. По соглашению размер матрицы определяется числом строк • числом столбцов
Один из способов, которым некоторые люди запомнили, что обозначение размеров матрицы – это строки за столбцами (а не столбцы за строками), – это вспомнить некогда популярную газировку:
RC Cola - строки перед столбцами!
Ниже вы можете увидеть два изображения одной и той же матрицы с выделенными строками и столбцами.
Размеры этой матрицы
- размеры: 2 × 3
- 2 строки × 3 столбца
Матричная запись
Чтобы идентифицировать запись в матрице, мы просто пишем нижний индекс строки соответствующей записи, за которой следует столбец.
В матрице A слева мы пишем 23 для обозначения записи во второй строке и третьем столбце.
Один из способов запомнить, что в этой нотации на первом месте строки, а на втором – столбцы, – это думать об этом как о чтении книги. Вы всегда сначала читаете сбоку, так же как всегда сначала пишете строки. Продолжая аналогию, когда вы заканчиваете читать строку в книге, ваши глаза опускаются, как столбцы после строк. A 23 указывает сначала номер строки, затем 2, затем номер столбца 3.
Практика определения записей
Практика 1
Шаг 1 Габаритные размеры
Размеры матрицы 3 × 3 (3 строки × 3 столбца)
Шаг 2Найдите запись G 23 в матрице G слева.
ВходG 23 – запись во второй строке и третьем столбце: 55.
Шаг 3 Габаритные размерыРазмеры 3 × 5 (3 строки × 5 столбцов)
Практика 2
Шаг 1 Отвечать
Запись j 34 – это запись в третьей строке и четвертом столбце.
Шаг 2 ОтвечатьJ 12 – это число в первой строке и втором столбце: -5
Практика 3
Шаг 1 Отвечать
Размеры матрицы 4 × 5 (4 строки × 5 столбцов)
Шаг 2 ОтвечатьЗапись 31 (строка 1 и столбец 4)
Шаг 3 Отвечатьv 45 обозначает запись в четвертой строке и пятом столбце, число 15 в правом нижнем углу.
Сложение и вычитание матриц
Вы можете складывать или вычитать матрицы, если каждая матрица имеет одинаковые размеры (другими словами, каждая из них должна иметь одинаковое количество столбцов и строк).
Чтобы сложить или вычесть матрицы, вы просто добавляете или вычитаете соответствующие записи (записи или числа, которые находятся в одном месте).
Почему для сложения и вычитания требуются одинаковые размеры?
Подумайте об этом: Поскольку добавление / вычитание матриц включает добавление / вычитание соответствующих записей. Что бы вы сделали с записями в одной матрице, которым нет соответствующей записи в другой?)
Рассмотрим пример, изображенный выше.. Матрица №1 имеет на один столбец больше, чем Матрица №2. Как бы вы сопоставили, не говоря уже о добавлении, записи в столбце 3 №1 с соответствующими записями в столбце №2. Что ж, ответ – вы не можете, поскольку вы не можете добавлять матрицы, если они не имеют одинакового количества строк и столбцов.
Операции с матрицами
Что касается линейной алгебры, две наиболее важные операции с векторами – это сложение векторов [сложение двух (или более) векторов] и скалярное умножение (умножение вектора на скаляр).Аналогичные операции определены для матриц.
Матрица сложения . Если A и B – это матрицы одного размера , то их можно складывать. (Это похоже на ограничение на добавление векторов, а именно, только векторы из того же пространства R n ; вы не можете добавить, например, 2-вектор к 3-вектору.) Если A = [ a ij ] и B = [ b ij ] – обе матрицы m x n , затем их сумма, C = A + B , также является матрицей m x n , и ее элементы задаются формулой
Таким образом, чтобы найти записи A + B , просто добавьте соответствующие записи A и B .
Пример 1 : Рассмотрим следующие матрицы:
Какие два можно добавить? Какова их сумма?
Поскольку можно складывать только матрицы одного размера, определяется только сумма F + H ( G не может быть добавлен ни к F , ни к H ). Сумма F и H составляет
Поскольку сложение действительных чисел коммутативно, отсюда следует, что сложение матриц (если оно определено) также коммутативно; то есть для любых матриц A и B одного размера, A + B всегда будет равно B + A .
Пример 2 : Если какая-либо матрица A добавляется к нулевой матрице того же размера, результат явно будет равен A :
Это матричный аналог утверждения a + 0 = 0 + a = a , который выражает тот факт, что число 0 является аддитивным тождеством в наборе действительных чисел.
Пример 3 : Найдите матрицу B такую, что A + B = C , где
Если
, тогда матричное уравнение A + B = C становится
Поскольку две матрицы равны тогда и только тогда, когда они имеют одинаковый размер и их соответствующие элементы равны, из этого последнего уравнения следует
Следовательно,
Этот пример мотивирует определение вычитания матрицы : Если A и B являются матрицами одинакового размера, то элементы A – B находятся простым вычитанием элементов B из соответствующие записи A .Поскольку уравнение A + B = C эквивалентно B = C – A , использование вычитания матрицы выше даст тот же результат:
Скалярное умножение . Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] – матрица, а k – скаляр, то
То есть матрица kA получается путем умножения каждой записи A на k .
Пример 4 : Если
, то скалярное кратное 2 A получается путем умножения каждой записи A на 2:
Пример 5 : Если A и B – это матрицы одного размера, то A – B = A + (- B ), где – B – скалярное кратное (-1) В . Если
, затем
Это определение вычитания матрицы согласуется с определением, проиллюстрированным в Примере 8.
Пример 6 : Если
, затем
Матричное умножение . Безусловно, самая важная операция с матрицами – это умножение матриц , процесс умножения одной матрицы на другую. Первый шаг в определении умножения матриц – вспомнить определение скалярного произведения двух векторов. Пусть r и c будут двумя векторами n ‐. Записывая r как матрицу-строку 1 x n и c как матрицу столбца n x 1, скалярное произведение r и c равно
Обратите внимание, что для определения скалярного произведения r и c оба должны содержать одинаковое количество записей.Кроме того, здесь важен порядок, в котором эти матрицы записаны в этом продукте: вектор-строка идет первым, вектор-столбец – вторым.
Теперь последний шаг: как умножаются две общие матрицы? Во-первых, чтобы сформировать продукт AB, количество столбцов A должно соответствовать количеству строк B ; если это условие не выполняется, то продукт AB не определен. Этот критерий следует из указанного выше ограничения для умножения матрицы строк r на матрицу столбцов c , а именно, что количество записей в r должно соответствовать количеству записей в c .Если A равен m x n и B равен n x p , то продукт AB определен, и размер матрицы продукта AB будет m x с. . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размеры продукта:
Представление матрицы m x n A как составной из векторов-строк r 1 , r 2 ,…, r m из 6 R n и n x p матрица B , составленная из векторов-столбцов c 1 , c 2 ,…, c p от p n ,
и
правило вычисления элементов матричного произведения AB : r i · c j = ( AB ) ij , то есть
Пример 7 : Учитывая две матрицы
определяет, какой матричный продукт, AB или BA , определен, и оценивает его.
Поскольку A – 2 x 3, а B – 3 x 4, продукт AB в таком порядке определяется, и размер матрицы продукта AB будет 2 x 4. Продукт BA – это , а не , поскольку первый фактор ( B ) имеет 4 столбца, а второй фактор ( A ) имеет только 2 строки. Количество столбцов первой матрицы должно соответствовать количеству строк второй матрицы, чтобы их произведение было определено.
Взяв скалярное произведение строки 1 в строке A и столбца 1 в строке B , получаем запись (1, 1) в строке AB . С
запись (1, 1) в AB – это 1:
Скалярное произведение строки 1 в строке A и столбца 2 в строке B дает запись (1, 2) в строке AB ,
и скалярное произведение строки 1 в строке A и столбца 3 в строке B дает запись (1, 3) в строке AB :
Первая строка произведения завершается скалярным произведением строки 1 в A и столбца 4 в B , что дает запись (1, 4) в AB :
Теперь для второй строки AB : скалярное произведение строки 2 в A и столбца 1 в B дает запись (2, 1) в AB ,
и скалярное произведение строки 2 в строке A и столбца 2 в строке B дает запись (2, 2) в строке AB :
Наконец, взяв скалярное произведение строки 2 в A со столбцами 3 и 4 в B , получаем (соответственно) записи (2, 3) и (2, 4) в AB :
Следовательно,
Пример 8 : Если
и
вычисляет (3, 5) запись продукта CD .
Во-первых, обратите внимание, что, поскольку C равен 4 x 5, а D равен 5 x 6, продукт CD действительно определен, и его размер равен 4 x 6. Однако нет необходимости вычислять все двадцать‐ четыре записи CD , если требуется только одна конкретная запись. Запись (3, 5) в CD является скалярным произведением строки 3 в C и столбца 5 в D :
Пример 9 : Если
убедитесь, что
но
В частности, обратите внимание, что хотя оба продукта AB и BA определены, AB не равно BA ; действительно, они даже не одного размера!
Предыдущий пример иллюстрирует, возможно, самое важное различие между умножением скаляров и умножением матриц.Для действительных чисел a и b всегда выполняется уравнение ab = ba , то есть умножение действительных чисел коммутативно; порядок, в котором написаны коэффициенты, не имеет значения. Однако категорически неверно, что умножение матриц коммутативно. Для матриц A и B , приведенных в Примере 9, были определены оба продукта AB и BA , но они определенно не были идентичными. Фактически, матрица AB была 2 x 2, а матрица BA была 3 x 3.Вот еще одна иллюстрация некоммутативности умножения матриц: Рассмотрим матрицы
Поскольку C – 3 x 2, а D – 2 x 2, продукт CD определен, его размер 3 x 2 и
Продукт DC , однако, не определен, поскольку количество столбцов D (которое равно 2) не равно количеству строк C (которое равно 3). Следовательно, CD ≠ DC , поскольку DC даже не существует.
Из-за чувствительности к порядку записи коэффициентов обычно не говорят просто: «Умножьте матрицы A и B ». Обычно важно указать, какая матрица идет первой, а какая – второй в продукте. По этой причине выражение «Умножить A справа на B » означает образовать произведение AB , а «Умножить A слева на B » означает образовать произведение BA . .
Пример 10 : Если
и x – это вектор (−2, 3), покажите, как A можно умножить справа на x , и вычислите произведение.
Поскольку A равно 2 x 2, чтобы умножить A справа на матрицу, эта матрица должна иметь 2 строки. Следовательно, если x записано как 2 x 1 столбец , матрица
, то можно вычислить произведение A x , и в результате получится еще одна матрица столбца 2 x 1:
Пример 11 : Рассмотрим матрицы
Если A умножить справа на B , получится
, но если A умножить слева на B , то получится
Обратите внимание, что оба продукта определены и имеют одинаковый размер, но не равны.
Пример 12 : Если A и B – квадратные матрицы, такие что AB = BA , то A и B говорят, что коммутируют . Покажите, что любые две квадратные диагональные матрицы порядка 2 коммутируют.
Пусть
– две произвольные диагональные матрицы 2 x 2. Тогда
и
Начиная с a 11 b 11 = b 11 a 11 и a 22 b 22 10 =
9 22 = 22 , AB действительно равно BA , как и нужно.Хотя матричное умножение обычно не коммутативно, оно , иногда , коммутативно; например, если
, затем
Несмотря на такие примеры, как эти, необходимо указать, что в целом умножение матриц не является коммутативным .
Есть еще одно различие между умножением скаляров и умножением матриц. Если a и b – действительные числа, тогда уравнение ab = 0 означает, что a = 0 или b = 0.То есть, единственный способ, при котором произведение действительных чисел может быть равным 0, – это если хотя бы один из множителей сам равен 0. Аналогичное утверждение для матриц, однако, неверно. Например, если
, затем
Обратите внимание, что даже если ни G , ни H не являются нулевой матрицей, произведение GH будет.
Еще одним отличием умножения скаляров от умножения матриц является отсутствие общего закона сокращения для умножения матриц.Если a, b и c – действительные числа с a ≠ 0, то, отбрасывая множитель a , уравнение ab = ac подразумевает b = c . Для умножения матриц такого закона не существует; то есть утверждение AB = AC означает , а не , подразумевает B = C , даже если A не равно нулю. Например, если
, затем оба
и
Таким образом, даже если AB = AC и A не является нулевой матрицей, B не равно C .
Пример 13 : Хотя матричное умножение не всегда коммутативно, оно всегда ассоциативно . То есть, если A, B и C – это любые три матрицы, такие, что продукт (AB) C определен, то продукт A (BC) также определен, и
То есть, пока порядок факторов не меняется, то, как они сгруппированы не имеет значения.
Проверить ассоциативный закон для матриц
Первый, с
продукт (AB) C это
Сейчас, с
продукт A (BC) это
Следовательно, (AB) C = A (BC) , как и ожидалось.Обратите внимание, что ассоциативный закон подразумевает, что произведение A, B и C (в таком порядке) может быть записано просто как ABC ; круглые скобки не нужны, чтобы разрешить двусмысленность, потому что нет двусмысленности.
Пример 14 : Для матриц
проверьте уравнение ( AB ) T = B T A T .
Первая,
означает
Сейчас, с
B T A T действительно равно ( AB ) T .Фактически, уравнение
справедливо для любых двух матриц, для которых определено произведение AB . Это говорит о том, что если продукт AB определен, то транспонирование продукта равно произведению перемещений в обратном порядке .
Матрицы идентичности . Нулевая матрица 0 m x n играет роль аддитивной идентичности в наборе матриц m x n точно так же, как число 0 в наборе действительных чисел (вспомните пример 7).То есть, если A является матрицей m x n и 0 = 0 m x n , то
Это матричный аналог утверждения, что для любого действительного числа a ,
Имея в руках аддитивную идентичность, вы можете спросить: «А как насчет мультипликативной идентичности ?» В наборе действительных чисел мультипликативным тождеством является число 1, так как
Есть матрица, которая играет эту роль ? Рассмотрим матрицы
и убедитесь, что
и
Таким образом, AI = IA = A .Фактически, легко показать, что для этой матрицы I оба продукта AI и IA будут равны A для любой 2 x 2 матрицы A . Следовательно,
– мультипликативная единица в наборе матриц 2 x 2. Аналогично матрица
– мультипликативная единица в наборе матриц 3 x 3 и так далее. (Обратите внимание, что I 3 – это матрица [δ ij ] 3 x 3 .В общем случае матрица I n – диагональная матрица nxn с каждым диагональным элементом, равным 1 – называется единичной матрицей порядка n и служит мультипликативной единицей в наборе всех Матрицы nxn .
Есть ли мультипликативная идентичность в наборе всех матриц m x n , если m ≠ n ? Для любой матрицы A в M mxn ( R ), матрица I m является левой идентичностью ( I m A = A ) и I n – это правый идентификатор ( AI n = A ).Таким образом, в отличие от набора матриц n x n , набор неквадратных матриц m x n не обладает двухсторонней идентичностью qunique , потому что I m ≠ I n , если m ≠ n .
Пример 15 : Если A – квадратная матрица, то A 2 обозначает продукт AA, A 3 обозначает продукт AAA и т. Д. Если A – это матрица
показывают, что A 3 = – A .
Расчет
показывает, что A 2 = – I . Умножение обеих частей этого уравнения на A дает A 3 = – A , если требуется. [Техническое примечание: можно показать, что в определенном точном смысле набор матриц вида
, где a и b – действительные числа, структурно идентичен набору комплексных чисел a + bi .Поскольку матрица A в этом примере имеет такую форму (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i и аналогу матричное уравнение A 2 = – I , полученное выше, равно i 2 = −1, уравнение, которое определяет мнимую единицу, i .]
Пример 16 : Найдите недиагональную матрицу, которая коммутирует с
Проблема заключается в запросе недиагональной матрицы B такой, что AB = BA .Как и A , матрица B должна быть 2 x 2. Один из способов создать такую матрицу B – сформировать A 2 , поскольку, если B = A 2 , ассоциативность подразумевает
(Это уравнение доказывает, что A 2 будет коммутировать с A для с любой квадратной матрицей A ; кроме того, оно предлагает, как можно доказать, что каждые интегральной степени квадратной матрицы A будет добираться до A .)
В данном случае
, который недиагонален. Эта матрица B действительно коммутирует с A , что подтверждается расчетами
.и
Пример 17 : Если
доказывают, что
для каждого целого положительного числа n .
Несколько предварительных расчетов показывают, что данная формула действительно верна:
Однако, чтобы установить, что формула выполняется для всех натуральных чисел n , необходимо общее доказательство.Здесь это будет сделано с использованием принципа математической индукции , который читается следующим образом. Пусть P (n) обозначает предложение относительно положительного целого числа n . Если можно показать, что
и
, то оператор P (n) действителен для всех целых положительных чисел n . В данном случае утверждение P (n) является утверждением
Поскольку A 1 = A , утверждение P (1) определенно верно, поскольку
Теперь, предполагая, что P (n) истинно, то есть предполагая, что
теперь необходимо установить срок действия выписки P ( n + 1), что составляет
Но это утверждение действительно верно, потому что
По принципу математической индукции доказательство завершено.
Инверсия матрицы . Пусть a будет заданным действительным числом. Поскольку 1 является мультипликативным тождеством в наборе действительных чисел, если существует число b такое, что
, затем b называется , обратным или мультипликативным обратным для a и обозначается a -1 (или 1/ a ). Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет заданной матрицей n x n .Поскольку I = I n является мультипликативным тождеством в наборе матриц n x n , если существует матрица B , такая что
, затем B называется (мультипликативным) , обратным A и обозначается A -1 (читается « A inverse»).
Пример 18 : Если
, затем
с
и
Еще одно различие между умножением скаляров и умножением матриц заключается в существовании инверсий.Хотя каждое ненулевое действительное число имеет обратное, существуют ненулевые матрицы, у которых нет обратного .
Пример 19 : Показать, что ненулевая матрица
не имеет обратного.
Если бы эта матрица имела инверсию, то
для некоторых значений a, b, c и d . Однако, поскольку вторая строка A является нулевой строкой, вы можете видеть, что вторая строка продукта также должна быть нулевой строкой:
(Когда звездочка, * появляется как запись в матрице, это означает, что фактическое значение этой записи не имеет отношения к настоящему обсуждению.) Поскольку (2, 2) элемент произведения не может равняться 1, произведение не может быть равным единичной матрице. Следовательно, невозможно построить матрицу, которая могла бы служить обратной для A .
Если матрица имеет инверсию, она называется обратимой . Матрица в примере 23 обратима, а матрица в примере 24 – нет. Позже вы узнаете различные критерии для определения обратимости данной квадратной матрицы.
Пример 20 : Пример 18 показал, что
Учитывая, что
проверьте уравнение ( AB ) −1 = B −1 A −1 .
Сначала вычислим AB :
Затем вычислим B −1 A −1 :
Теперь, поскольку произведение AB и B −1 A −1 составляет I ,
B −1 A −1 действительно является инверсией AB . Фактически, уравнение
справедливо для любых обратимых квадратных матриц того же размера.Это говорит о том, что если A и B являются обратимыми матрицами одинакового размера, то их произведение AB также обратимо, и обратное произведение равно произведению обратных чисел в обратном порядке . (Сравните это уравнение с уравнением с транспонированием в примере 14 выше.) Этот результат можно в общем доказать, применяя ассоциативный закон для матричного умножения. С
и
следует, что ( AB ) -1 = B -1 A -1 , как и нужно.
Пример 21 : Обратная матрица
это
Покажите, что обратное значение B T равно ( B −1 ) T .
Форма B T и ( B −1 ) T и умножьте:
Этот расчет показывает, что ( B −1 ) T является обратным для B T .[Строго говоря, это показывает только то, что ( B −1 ) T – это правый обратный B T , то есть когда он умножает B T справа, продукт – это личность. Также верно, что ( B −1 ) T B T = I , что означает ( B −1 ) T – левый обратный из В Т .Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратное, нет различия между левым обратным и правым обратным.] Таким образом,
уравнение, которое на самом деле справедливо для любой обратимой квадратной матрицы B . Это уравнение говорит, что если матрица обратима, то ее транспонирование также является обратимым, а обратное транспонирование – это транспонирование обратного.
Пример 22 : Используйте свойство распределения для матричного умножения, A ( B ± C ) = AB ± AC , чтобы ответить на этот вопрос: если матрица 2 x 2 D удовлетворяет уравнение D 2 – D -6 I = 0 , какое выражение для D −1 ?
По указанному выше распределительному свойству D 2 – D = D 2 – DI = D (D – I) .Следовательно, уравнение D 2 – D -6 I = 0 подразумевает D (D – I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает
, что означает
В качестве иллюстрации этого результата матрица
удовлетворяет уравнению D 2 – D – 6 I = 0 , как вы можете убедиться.С
и
матрица 1/6 ( D − I ) действительно равна D −1 , как заявлено.
Пример 23 : Уравнение ( a + b ) 2 = a 2 + 2 ab + b 2 является тождеством, если a и b настоящие числа. Однако покажите, что ( A + B ) 2 = A 2 + 2 AB + B 2 – это , а не , если A и B – это матрицы 2 x 2.[Примечание: законы распределения для матричного умножения: A ( B ± C ) = AB ± AC , приведенные в примере 22, и сопутствующий закон ( A ± B ). C = AC ± BC .]
Из законов распределения для умножения матриц следует
Поскольку матричное умножение не коммутативно, BA обычно не равно AB , поэтому сумма BA + AB не может быть записана как 2 AB .В общем, тогда ( A + B ) 2 ≠ A 2 + 2 AB + B 2 . [Любые матрицы A и B , которые не коммутируются (например, матрицы в Примере 16 выше), предоставят конкретный контрпример к утверждению ( A + B ) 2 = A 2 + 2 AB + B 2 , что также установит, что это не идентичность.]
Пример 24 : Предположим, что B обратимый. Если A коммутирует с B , покажите, что A также коммутирует с B −1 .
Доказательство . Сказать « A коммутирует с B » означает AB = BA . Умножьте это уравнение на B −1 слева и справа и используйте ассоциативность:
Пример 25 : Число 0 имеет только один квадратный корень: 0.Покажите, однако, что нулевая матрица (2 на 2) имеет бесконечно много квадратных корней, найдя все матрицы 2 x 2 A , такие, что A 2 = 0 .
Точно так же, как число a называется квадратным корнем из b , если a 2 = b , матрица A называется квадратным корнем из B , если A 2 = B . Пусть
– произвольная матрица 2 x 2.Возводя его в квадрат и устанавливая результат равным 0 , получаем
Записи (1, 2) в последнем уравнении означают, что b ( a + d ) = 0, что выполняется, если (Случай 1) b = 0 или (Случай 2) d = – а .
Случай 1. Если b = 0, то диагональные записи означают, что a = 0 и d = 0, а записи (2, 1) означают, что c является произвольным. Таким образом, для любого значения c каждая матрица вида
– это квадратный корень из 0 2×2 .
Случай 2. Если d = – a , то оба недиагональных входа будут равны 0, а диагональные записи будут равны a 2 + bc . Таким образом, если выбраны b и c , то bc = – a 2 , A 2 будет равно 0 .
Аналогичная цепочка рассуждений, начинающаяся с записей (2, 1), приводит либо к a = c = d = 0 (и b произвольно), либо к такому же выводу, что и раньше: до тех пор, пока b и c выбираются так, что bc = – a 2 , матрица A 2 будет равна 0 .
Все эти случаи можно резюмировать следующим образом. Любая матрица следующей формы будет иметь свойство, состоящее в том, что ее квадрат представляет собой нулевую матрицу 2 на 2:
Поскольку существует бесконечно много значений a, b и c , таких что bc = – a 2 , нулевая матрица 0 2×2 имеет бесконечно много квадратных корней. Например, выбор a = 4, b = 2 и c = −8 дает ненулевую матрицу
площадью
.

