Движение с ускорением это – Ускорение — Википедия
Понятие об ускорении. Движение с постоянным ускорением по прямой линии. Формулы и решение задачи
Изучением классического механического движения в физике занимается кинематика. В отличие от динамики, наука изучает, почему движутся тела. Она отвечает на вопрос, как они это делают. В данной статье рассмотрим, что такое ускорение и движение с постоянным ускорением.
Понятие об ускорении
Когда тело движется в пространстве, за некоторое время оно преодолевает определенный путь, который является длиной траектории. Чтобы рассчитать этот путь, пользуются понятиями скорости и ускорения.
Скорость как физическая величина характеризует быстроту во времени изменения пройденного пути. Скорость направлена по касательной к траектории в сторону перемещения тела.
Ускорение — это несколько более сложная величина. Говоря кратко, она описывает изменение скорости в рассматриваемый момент времени. Математическое определение ускорения выглядит так:
a¯ = dv¯/dt.
Чтобы яснее понять эту формулу, приведем простой пример: предположим, что за 1 секунду движения скорость тела увеличилась на 1 м/с. Эти цифры, подставленные в выражение выше, приводят к результату: ускорение тела в течение этой секунды было равно 1 м/с2.
Направление ускорения совершенно не зависит от направления скорости. Его вектор совпадает с вектором результирующей силы, которая вызывает это ускорение.
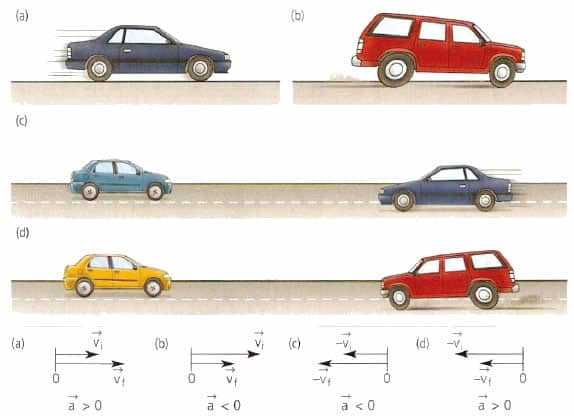
Следует отметить важный момент в приведенном определении ускорения. Эта величина характеризует не только изменение скорости по модулю, но и по направлению. Последний факт следует учитывать в случае криволинейного движения. Далее в статье будет рассматриваться только прямолинейное движение.
Скорость при движении с постоянным ускорением
Ускорение является постоянным, если оно в процессе движения сохраняет свой модуль и направление. Такое движение называют равноускоренным или равнозамедленным — все зависит от того, приводит ли ускорение к увеличению скорости или к ее уменьшению.
В случае движения тела с постоянным ускорением определить скорость можно по одной из следующих формул:
v = a*t;
v = v0 + a*t;
v = v0 – a*t.
Первые два уравнения характеризуют равноускоренное перемещение. Отличие между ними заключается в том, что второе выражение применимо для случая ненулевой начальной скорости.
Третье уравнение — это выражение для скорости при равнозамедленном движении с постоянным ускорением. Ускорение при этом направлено против скорости.
Графиками всех трех функций v(t) являются прямые. В первых двух случаях прямые имеют положительный наклон относительно оси абсцисс, в третьем случае этот наклон является отрицательным.
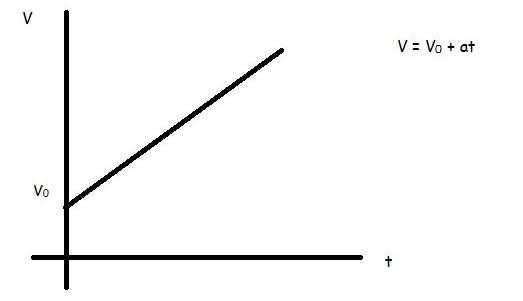
Формулы пройденного пути
Для пути в случае движения с ускорением постоянным (ускорение a = const) получить формулы несложно, если вычислить интеграл от скорости по времени. Проделав эту математическую операцию для записанных выше трех уравнений, мы получим следующие выражения для пути L:
L = a*t2/2;
L = v0*t + a*t2/2;
L = v0*t – a*t2/2.
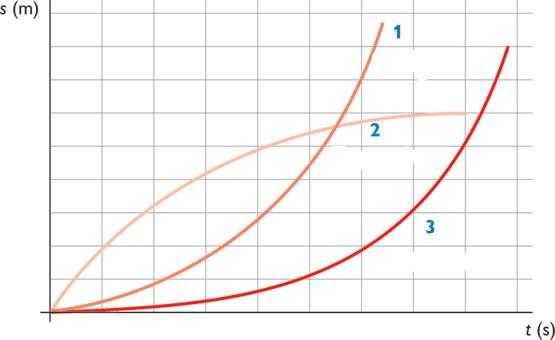
Графиками всех трех функций пути от времени являются параболы. В первых двух случаях правая ветвь параболы возрастает, а для третьей функции она постепенно выходит на некоторую константу, которая соответствует пройденному пути до полной остановки тела.
Решение задачи
Двигаясь со скоростью 30 км/ч, автомобиль начал ускоряться. За 30 секунд он прошел расстояние 600 метров. Чему было равно ускорение автомобиля?
В первую очередь переведем начальную скорость из км/ч в м/с:
v0 = 30 км/ч = 30000/3600 = 8,333 м/с.
Теперь запишем уравнение движения:
L = v0*t + a*t2/2.
Из этого равенства выразим ускорение, получим:
a = 2*(L – v0*t)/t2.
Все физические величины в этом уравнении известны из условия задачи. Подставляем их в формулу и получаем ответ: a ≈ 0,78 м/с2. Таким образом, двигаясь с ускорением постоянным, автомобиль за каждую секунду увеличивал свою скорость на 0,78 м/с.
Рассчитаем также (для интереса), какую скорость он приобрел через 30 секунд ускоренного движения, получаем:
v = v0 + a*t = 8,333 + 0,78*30 = 31,733 м/с.
Полученная скорость равна 114,2 км/ч.
fb.ru
Движение с постоянным ускорением
Физика > Движение с постоянным ускорением
Движение с ускорением в физике. Изучите, как происходит ускорение движения тела, как определить ускорение, как выглядит движение с постоянным ускорением.
Постоянное ускорение наступает в том случае, если скорость объекта меняется на равную величину через каждый одинаковый временной промежуток.
Задача обучения
- Разобраться в том, как постоянное ускорение воздействует на движение.
Основные пункты
- Если мы полагаем, что ускорение будет постоянным, то это не ограничивает ситуацию и не ухудшает результат.
- Из-за алгебраических свойств постоянного ускорения есть кинематические уравнения, которые можно применить для расчета скорости, смещения, ускорения и времени.
- Расчеты с постоянным ускорением можно использовать для одномерного и двумерного движений.
Термины
- Кинематический – обладает связью с движением или кинематикой.
- Ускорение – количество, с которым увеличивается скалярная и векторная скорости.
Скорость тела при движении с ускорением изменяется на одинаковую величину через каждые равные временные промежутка. Ускорение выводится из главных принципов кинематики. Это первая производная по времени от скорости:
а = ∂v/dt = ∂2x/dt2.
Если предположить, что ускорение будет постоянным, то это не несет серьезных ограничений и не влияет в худшую сторону на точность. Если же оно не постоянно, то можно рассмотреть в различных частях формулы или же использовать среднее значение для определенного временного промежутка.
Наиболее простой пример движения с постоянным ускорением – падающие предметы. Они одномерные и лишены горизонтального движения.

Когда вы бросаете объект, он падает вертикально земному центру из-за постоянного ускорения силы тяжести
Метательное движение – перемещение объекта, выброшенного или проецированного в воздух и подверженного ускорению силой тяжести. Сам объект именуют снарядом, а путь – траекторией. В двумерном движении присутствует вертикальный и горизонтальный компоненты.
Есть кинематическая формула, связывающая смещение, начальную и конечную скорости, а также время и ускорение:
X = x0 + vt
v = (v0 + v)/2
v = v0 + at
x = x0 + v0 t + ½ at2
v2 = v20 + 2a(x – x0).
Теперь вы знаете, как выглядит движение с ускорением в физике и как определить ускорение движения для тела.
v-kosmose.com
Понятие ускорения. Движение с постоянным ускорением. Формулы и пример задачи
Понятие ускорения. Движение с постоянным ускорением. Формулы и пример задачи
От DA
12.12.2018 17:31Кинематика – это раздел механики движения в физике, который занимается исследованием и описанием перемещения тел. В данной статье приведены основные величины, что описывают механическое движение. Рассмотрим, что такое ускорение и движение с постоянным ускорением, приведем соответствующие формулы.
Три величины кинематики
Этими величинами являются путь L, скорость v¯ и ускорение a¯. Первая из них является скаляром и измеряется в метрах, вторая и третья – это величины векторные, которые выражаются в метрах в секунду и в метрах в квадратную секунду, соответственно. Все единицы соответствуют системе СИ.
Согласно определению, скорость – это быстрота перемещения тела в пространстве, то есть:
v¯ = dL/dt
В свою очередь, ускорение – это быстрота изменения скорости, что математически записывается так:
a¯ = dv¯/dt
Кинематические характеристики имеет смысл рассматривать применительно к данной траектории движения. Последняя может быть прямолинейной или криволинейной. От типа траектории зависит направление полного ускорения. Скорость же направлена к траектории всегда по касательной.
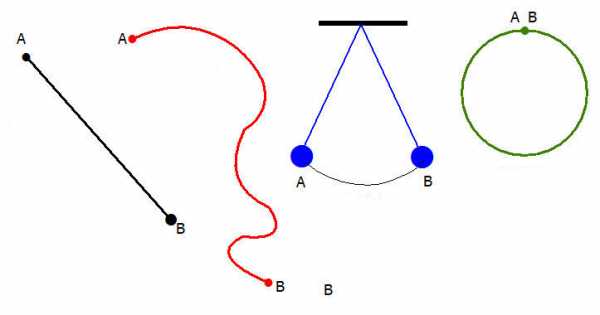
Особенности ускорения во время движения по кривой
Поскольку ускорение – это численная характеристика изменения скорости, то она однозначно описывает все аспекты этого изменения. Речь идет не только об абсолютной величине, но также и о векторе направления v¯. Изменение абсолютной величины скорости описывает тангенциальное, или касательное ускорение. Оно направлено или по вектору скорости, либо против него. Формула для его расчета имеет вид:
at = dv/dt
Поскольку тело перемещается по кривой, например по окружности, то величина v¯ постоянно меняет свое направление. Какова причина этого изменения? Она заключается в действии на тело нормального или центростремительного ускорения. Эта величина направлена перпендикулярно линии траектории и вычисляется по формуле:
an = v2/r
Где v – абсолютное значение скорости, r – кривизна траектории (радиус окружности).
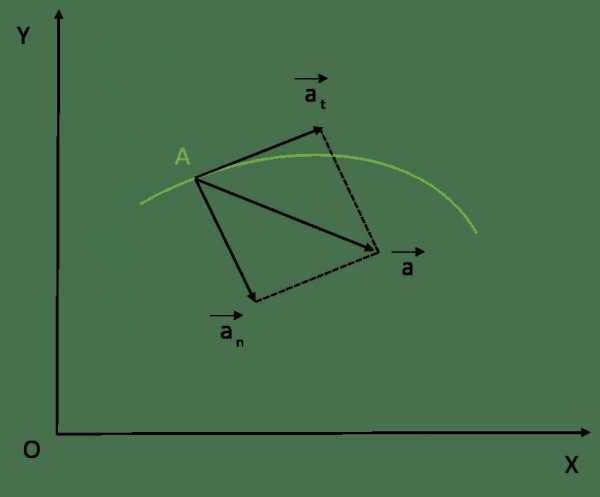
Обе составляющие полного ускорения a позволяют определить его с помощью такого равенства:
a = √(at2 + an2)
Отметим, что движение по криволинейной траектории всегда предполагает наличие у тела двух компонентов ускорения.
Движение с постоянным ускорением по прямой
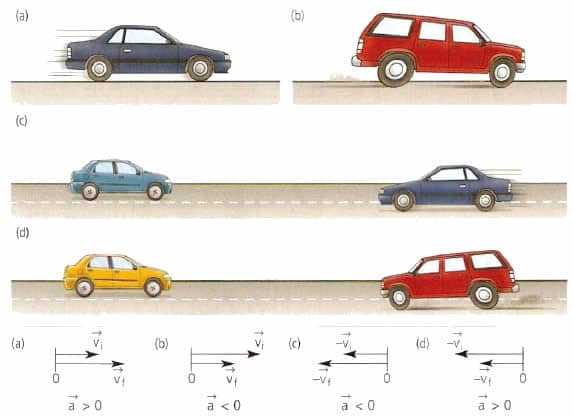
Если траектория является прямой линией, то изучение процесса движения значительно облегчается. Дело в том, что при таком движении скорость направлена всегда в одном направлении, а это означает, что нормальная компонента ускорения отсутствует. Полное ускорение при прямолинейном движении однозначно определяется его тангенциальной компонентой. Далее в статье будем рассматривать только движение по прямой, поэтому величину a будем называть просто ускорением.
Особое внимание заслуживает рассмотрение процесса перемещения тела по прямой, которое осуществляется с постоянным ускорением. Для такого перемещения просто записать математические уравнения движения. Они будут рассмотрены ниже.
Примерами движения тел с постоянным ускорением являются разгон автомобиля со старта, свободное падение тел в однородном поле гравитации, торможение транспортных средств.
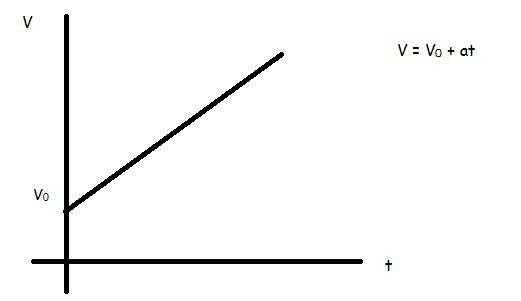
Формулы для скорости
Рассматривая ускорение и движение с постоянным ускорением в 10 классе общеобразовательных школ, учащиеся знакомятся с формулами для определения скорости и пройденного пути. Начнем с формул для скорости.
Предположим, что тело находилось в состоянии покоя, затем оно начало движение с постоянным ускорением. Как при этом будет меняться его скорость? Ответ на этот вопрос содержит следующее равенство:
v = a*t
То есть скорость линейно будет возрастать. Коэффициентом пропорциональности между величинами v и t является ускорение a.
Теперь представим ситуацию, что тело двигалось с постоянной скоростью v0, а затем начало ускоряться. Как изменится при этом предыдущая формула для скорости? Она примет вид:
v = v0 + a*t.
Отметим, что отсчет времени в этой формуле начинается с момента появления у тела ускорения.
Теперь предположим третий вариант: вместо ускорения движения в предыдущем примере тело начало замедляться. В такой ситуации следует использовать выражение:
v = v0 – a*t.
Во всех трех случаях графиками скорости от времени являются прямые линии.
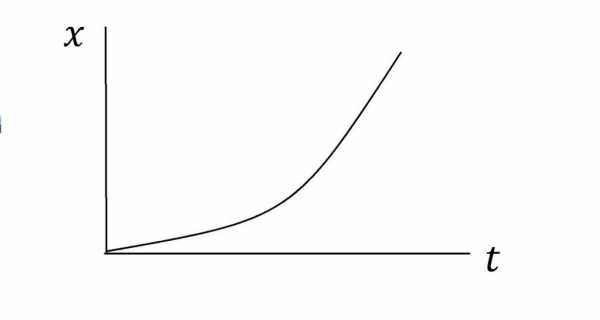
Формулы для пути
Рассматривая тему ускорения и движения с постоянным ускорением прямолинейное, необходимо также привести формулы для пройденного телом пути. В конечном счете на практике именно эта кинематическая величина имеет смысл.
Соответствующие формулы для L можно получить, если взять интеграл по времени для приведенных выше выражений для скоростей. Три формулы записаны ниже:
L = a*t2/2;L = v0*t + a*t2/2;L = v0*t – a*t2/2
Первое выражение определяет путь для чистого движения с неизменным ускорением, второе равенство описывает ускоренное движение с ненулевой начальной скоростью, третья формула используется для вычисления пути торможения при равнозамедленном движении.
Задача с подъемом тела в гравитационном поле
Как выше было отмечено, свободное падение происходит с постоянным ускорением. Движение с ускорением постоянным характеризуется величиной g, которая вблизи поверхности нашей планеты равна 9,81 м/с2.
Известно, что тело было брошено вверх вертикально. Начальная скорость равна 30 м/с. Необходимо вычислить высоту, на которую тело поднимется.
Данная задача является типичной проблемой на равнозамедленное перемещение по прямой линии. Обозначим высоту подъема буквой h. Она будет равна пути, который тело пролетит до момента его полной остановки в высоте. Эта высота равна:
h = v0*t – g*t2/2
Время полета можно определить из условия равенства величины v нулю в точке максимальной высоты, то есть:
v = v0 – g*t = 0 =>t = v0/g
Подставляя равенство для t в формулу для h, получаем:
h = v02/g – g*(v0/g)2/2 = v02/(2*g)
Подставляя значение начальной скорости, приходим к ответу: h = 45,9 метра.
www.navolne.life
Ускоренное движение — synset
Понятно, что в релятивистской теории равноускоренное движение, аналогичное классической механике, невозможно. Если скорость тела всё время увеличивается , то она рано или поздно превысит фундаментальную скорость . Это невозможно в силу энергетических ограничений, которые будут изучены в следующей главе. Сейчас же мы рассмотрим один из вариантов ускоренного движения, при котором скорость постоянно увеличивается, оставаясь, тем не менее, все время меньше единицы ().
Пусть для наглядности мимо неподвижного наблюдателя пролетает космический корабль, имеющий в данный момент времени скорость . Этот корабль плавно увеличивает свою скорость. Перейдём в систему отсчёта, связанную с ним (правый рисунок):
Так как за малое время скорость корабля увеличивается незначительно, мы можем считать, что относительно своего предыдущего состояния она увеличилась на , где — некоторая константа. По правилу сложения скоростей (2.2) новая скорость с точки зрения неподвижного наблюдателя равна:
Так как мал, разложим знаменатель в ряд [], и, сохраняя порядок малости, перемножим его с числителем:
где . Учитывая, что время по часам корабля идёт медленнее, и вводя производную скорости , получим:
(2.19) |
Это дифференциальное уравнение описывает, как изменяется скорость некоторого объекта для неподвижного наблюдателя, если с “точки зрения” объекта, он пытается двигаться равноускоренно.
Выбрав начальное условие в виде и проинтегрировав это дифференциальное уравнение, получим:
(2.20) |
Динамика величины совпадает с классической зависимостью увеличения скорости и она может быть сколь угодно большой. Однако релятивистская скорость всегда остаётся меньше единицы:
(2.21) |
Учитывая, что , после ещё одного интегрирования ( H) с начальным условием можно получить траекторию движения:
(2.22) |
Напомним, что мы работаем в системе единиц, в которой . Чтобы восстановить в формулах , необходимо сделать замены , и , так как ускорение имеет размерность []. В этом случае и , и будут делиться на . В пределе , раскладывая в ряд по малым и , мы получим хорошо известные классические выражения для движения равноускоренного объекта:
Ниже приведены графики изменения скорости и координаты объекта, который ускоряется в течение единичного времени с единичным ускорением, а затем сразу начинает тормозить:
Верхние тонкие линии на каждом графике соответствуют классической равноускоренной динамике.
Как в равномерно двигающемся, так и в ускоренном корабле время замедляется. Рассмотрим этот эффект с позиции земного наблюдателя. Пусть корабль разгоняется в течении времени , затем равномерно летит, и через время начинает тормозить в течении времени :
Вычислим собственное время путешествия, прошедшее на корабле. За малый интервал времени скорость корабля изменяется незначительно, и её можно рассматривать, как локально инерциальную систему отсчета. Поэтому время, прошедшее на двигающихся часах, связано со временем неподвижного наблюдателя следующим образом:
В результате этого интегрирования мы суммируем малые интервалы времени на Земле и на корабле. При этом предполагаем, что ускорение не влияет на ход времени. В следующем разделе мы подробнее остановимся на этом допущении.
Будем помечать, как и раньше, интервал времени у космонавта нулевым индексом. На первом этапе разгона корабля имеем:
(2.23) |
где — гиперболический арксинус, являющийся обратным к гиперболическому синусу ( C):
За время разгона корабль достигает скорости [см. (2.21)]:
и дальше двигается равномерно. Поэтому на втором этапе:
время замедляется наиболее сильно, так как скорость максимальна.
Финальный интервал времени при торможении равен
Из соображений симметрии можно сразу взять результат разгона корабля. Складывая интервалы времени каждого этапа, окончательно получаем:
Первое слагаемое меньше, чем , а второе меньше, чем . Их можно ( H) разложить в ряд Тейлора:
Время, прошедшее в неподвижной системе отсчета, равно . Время путешествия по часам корабля меньше, причём на ускоренных этапах оно замедлялось медленнее, чем на этапе равномерного движения.
Сделаем оценки времени полёта к звёздной системе Альфа-Центавра, удалённой от Земли на расстояние 4.3 световых лет. Световой год — это расстояние, которое свет проходит в течении года:
Измеряя расстояние в световых годах, а время — в обычных годах, мы по-прежнему работаем в системе . В этой системе единичное ускорение близко к ускорению свободного падения на поверхности Земли. Пусть из соображений комфорта (искусственная гравитация) космический корабль двигается с ускорением половину пути, а затем сразу начинает тормозить С точки зрения Земли [см.(2.22)] половина пути к звезде св. лет занимает время:
Соответственно, общее время полёта туда и обратно составит 12 лет. Собственное же время космонавта в момент возвращения будет равно года, т.е. на 40% меньше. За 64 года собственного времени космонавт может “слетать” (вернувшись) к галактике Андромеды, удалённой на 2.5 млн. св. лет. На Земле пройдёт около 5 млн. лет. К сожалению, всё не так просто, и технологическая реалистичность подобных перелётов будет проанализирована в следующей главе.
Релятивистский мир – лекции по теории относительности, гравитации и космологии
Движение с постоянным ускорением
При равноускоренном движении справедливы следующие уравнения, которые мы приводим без вывода:
| = o t + ½ t² | ⇒ | sx = υox t + ½ ax t² | ||
| sy = υoy t + ½ ay t² |
Как вы понимаете, векторная формула слева и две скалярные формулы справа равноправны. С точки зрения алгебры, скалярные формулы означают, что при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Сравните это с характером проекций мгновенной скорости (см. § 12-з).
Зная, что sx = x – xo и sy = y – yo (см. § 12-е), из двух скалярных формул из правой верхней колонки получим уравнения для координат:
| x = xo + υox t + ½ ax t² | и | y = yo + υoy t + ½ ay t² |
Поскольку ускорение при равноускоренном движении тела постоянно, то координатные оси всегда можно расположить так, чтобы вектор ускорения был направлен параллельно одной оси, например оси Y. Следовательно, уравнение движения вдоль оси X заметно упростится:
x = xo + υox t + ( 0 ) и y = yo + υoy t + ½ ay t²
Обратите внимание, что левое уравнение совпадает с уравнением равномерного прямолинейного движения (см. § 12-ж). Это означает, что равноускоренное движение может «складываться» из равномерного движения вдоль одной оси и равноускоренного движения вдоль другой. Подтверждением этому служит опыт с ядром на яхте (см. § 12-б).
Задача. Вытянув руки, девочка подбросила шар. Он поднялся на 80 cм и вскоре упал к ногам девочки, пролетев 180 cм. С какой скоростью шар был подброшен и какую скорость шар имел при ударе о землю?
Рекомендация. Для решения задач, в которых не дано время и не просят его найти, очень удобно применять не содержащую время формулу для квадрата проекции мгновенной скорости. Выведем эту формулу.
Возведём в квадрат обе части уравнения для проекции на ось Y мгновенной скорости: υy = υoy + ay t (см. § 12-и). Получим равенство:
υy² = ( υoy + ay t )² = υoy² + 2 υoy ay t + ay² t²
Вынесем за скобки множитель 2 ay только для двух правых слагаемых:
υy² = υoy² + 2 ay ( υoy t + ½ ay t² )
Заметим, что в скобках получилась формула для вычисления проекции перемещения: sy = υoy t + ½ ay t². Заменяя её на sy , получим:
| υy² = υoy² + 2 ay sy |
Решение. Сделаем чертёж: ось Y направим вверх, а начало координат поместим на земле у ног девочки. Применим выведенную нами формулу для квадрата проекции скорости сначала в верхней точке подъёма шара:
0 = υoy² + 2·(–g)·(+h) ⇒ υoy = ±√¯2gh = +4 м/с
Затем при начале движения из верхней точки вниз:
υy² = 0 + 2·(–g)·(–H) ⇒ υy = ±√¯2gh = –6 м/с
Ответ: шар был брошен вверх со скоростью 4 м/с, а в момент приземления имел скорость 6 м/с, направленную против оси Y.
Примечание. Надеемся, вы понимаете, что формула для квадрата проекции мгновенной скорости будет верна по аналогии и для оси X:
| υx² = υox² + 2 ax sx |
Если движение одномерное, то есть происходит только вдоль одной оси, можно пользоваться любой из двух формул в рамках.
questions-physics.ru
