Эдс источника тока формула – Электродвижущая сила — Википедия
Формула ЭДС в физике
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал (учтем, что носители тока предполагаются положительными зарядами) постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения. Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи или на отдельных участках цепи.
Определение и формула ЭДС
ОпределениеСкалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС), действующей в цепи или на участке цепи. ЭДС обозначается . Математически определение ЭДС запишем как:
где A – работа сторонних сил, q – заряд, над которым производится работа.
Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению.
ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:
где – напряженность поля сторонних сил. Если напряженность поля сторонних сил не равна нулю только в части цепи, например, на отрезке 1-2, тогда интегрирование в выражении (2) можно вести только по данному участку. Соответственно, ЭДС, действующая на участке цепи 1-2 определяется как:
Формула (2) дает самое общее определение ЭДС, которое можно использовать для любых случаев.
Закон Ома для произвольного участка цепи
Участок цепи, на котором действуют сторонние силы,
www.webmath.ru
определение и формула, в чём измеряется, работа источника электродвижущей силы
Электрический ток не протекает в медном проводе по той же причине, по которой остаётся неподвижной вода в горизонтальной трубе. Если один конец трубы соединить с резервуаром таким образом, чтобы образовалась разность давлений, жидкость будет вытекать из одного конца. Аналогичным образом, для поддержания постоянного тока необходимо внешнее воздействие, перемещающее заряды. Это воздействие называется электродвижущая сила или ЭДС.От электростатики к электрокинетике
Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.
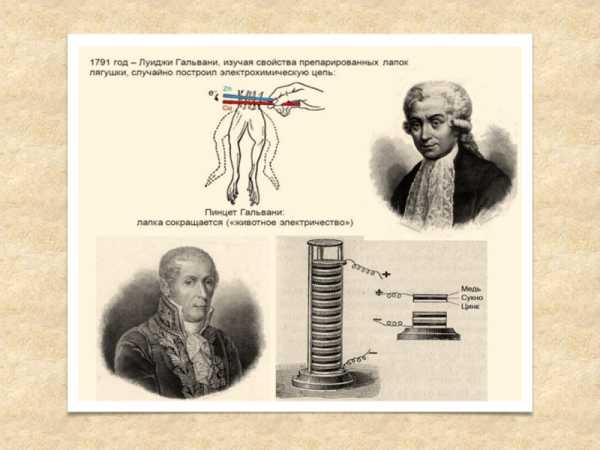
Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.
Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.
Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.
Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:
- 1800 г. — создание Вольтой гальванической батареи;
- 1826 г. — Ом формулирует свой закон для полной цепи;
- 1831 г. — обнаружение электромагнитной индукции Фарадеем.
Определение и физический смысл
Приложение некоторой разности потенциалов между двумя концами проводника создаст перетекание электронов от одного конца к другому. Но этого недостаточно для поддержания потока зарядов в проводнике. Дрейф электронов приводит к уменьшению потенциала до момента его уравновешивания (прекращение тока). Таким образом, для создания постоянного тока необходимы механизмы, непрерывно возвращающие описанную систему в первоначальную конфигурацию, то есть, препятствующие агрегации зарядов в результате их движения. Для этой цели используются специальные устройства, называемые источники питания.
В качестве иллюстрации их работы удобно рассматривать замкнутый контур из сопротивления и гальванического источника питания (батареи). Если предположить, что внутри батареи тока нет, то описанная проблема объединения зарядов остаётся неразрешённой. Но в цепи с реальным источником питания электроны перемещаются постоянно. Это происходит благодаря тому, что поток ионов протекает и внутри батареи от отрицательного электрода к положительному. Источник энергии, перемещающий эти заряды в батарее — химические реакции. Такая энергия называется электродвижущей силой.
ЭДС является характеристикой любого источника энергии, способного управлять движением электрических зарядов в цепи. В аналогии с замкнутым гидравлическим контуром работа источника э. д. с. соответствует работе насоса для создания давления воды. Поэтому значок, обозначающий эти устройства, неотличим на гидравлических и электрических схемах.
Несмотря на название, электродвижущая сила на самом деле не является силой и измеряется в вольтах. Её численное значение равно работе по перемещению заряда по замкнутой цепи. ЭДС источника выражается формулой E=A/q, в которой:
- E — электродвижущая сила в вольтах;
- A — работа сторонних сил по перемещению заряда в джоулях;
- q — перемещённый заряд в кулонах.
Из этой формулы ЭДС следует, что электродвижущая сила не является свойством цепи или нагрузки, а есть способность генератора электроэнергии к разделению зарядов.
Сравнение с разностью потенциалов
Электродвижущая сила и разность потенциалов в цепи очень похожие физические величины, так как оба измеряются в вольтах и определяются работой по перемещению заряда. Одно из основных смысловых различий заключается в том, что э. д. с. (E) вызывается путём преобразования какой-либо энергии в электрическую, тогда как разность потенциалов (U) реализует электрическую энергию в другие виды. Другие различия выглядят так:
- E передаёт энергию всей цепи. U является мерой энергии между двумя точками на схеме.
- Е является причиной U, но не наоборот.
- Е индуцируется в электрическом, магнитном и гравитационном поле.
- Концепция э. д. с. применима только к электрическому полю, в то время как разность потенциалов применима к магнитным, гравитационным и электрическим полям.
Напряжение на клеммах источника питания, как правило, отличается от ЭДС источника. Это происходит из-за наличия внутреннего сопротивления источника (электролита и электродов, обмоток генератора). Связывающая разность потенциалов и ЭДС источника тока формула выглядит как U=E-Ir. В этом выражении:
- U — напряжение на клеммах источника;
- r — внутреннее сопротивление источника;
- I — ток в цепи.
Из этой формулы электродвижущей силы следует, что э. д. с. равна напряжению когда ток в цепи не течёт. Идеальный источник ЭДС создаёт разность потенциалов независимо от нагрузки (протекающего тока) и не обладает внутренним сопротивлением.
В природе не может существовать источника с бесконечной мощностью при замыкании на клеммах, как и материала с бесконечной проводимостью. Идеальный источник используется как абстрактная математическая модель.
Источники электродвижущей силы
Суть источника ЭДС заключается в преобразовании других видов энергии в электрическую с помощью сторонних сил. С точки зрения физики обеспечения э. д. с различают следующие два основных вида источников:
- гальванические;
- электромагнитные.

Первые представляют собой электрохимические источники, основанные на вовлечение в химическую реакцию процесса переноса электронов. В обычных условиях химические взаимодействия сопровождаются выделением или поглощением тепла, но существует немало реакций, в результате которых генерируется электрическая энергия.
Электрохимические процессы в большинстве случаев обратимы, поскольку энергия электрического тока может быть использована, чтобы заставить реагировать вещества между собой. Эта возможность позволяет создавать возобновляемые гальванические источники — аккумуляторы.
В генераторах тока э. д. с. создаётся другим способом. Разделение зарядов происходит с помощью явления электромагнитной индукции, которое заключается в том, что изменение величины или направления магнитного поля создаёт ЭДС. Согласно закону Фарадея, нахождение э. д. с. индукции возможно из выражения E=—dФ/dt. В этой формуле:
- Ф — магнитный поток;
- t — время.
ЭДС индукции измеряется также в вольтах. В зависимости от того, каким способом вызываются изменения магнитного потока, различают:
- Динамически индуцированную. Когда в стационарном магнитном поле перемещается проводник. Характерен для генераторов.
- Статически индуцированную. Когда изменения потока возникают из-за изменений магнитного поля вокруг неподвижного проводника. Так работают трансформаторы.
Существуют также источники э. д. с, не основанные на электрохимии или магнитной индукции. К таким устройствам можно отнести полупроводниковые фотоэлементы, контактные потенциалы и пьезокристаллы. Понятие ЭДС имеет практическое применение прежде всего как параметр выбора источников питания для тех или иных целей. Чтобы получить максимальный эффект от работы устройств в цепи, нужно согласовывать их возможности и характеристики. Прежде всего внутреннее сопротивление источника ЭДС силы с характеристиками подключаемой нагрузки.
rusenergetics.ru
2.2. Электродвижущая сила источника тока
Циркуляция
вектора напряженности электростатического
поля равна нулю, поэтому в замкнутой
цепи наряду с участками, на которых
положительные носители движутся в
сторону убывания потенциала  ,
должны иметься участки, на которых
перенос положительных зарядов происходит
в направлении возрастания
,
должны иметься участки, на которых
перенос положительных зарядов происходит
в направлении возрастания

 ,
т.е. против сил электростатического
поля. Перемещение носителей на этих
участках возможно лишь с помощью сил
неэлектрического происхождения,
называемых сторонними силами. Таким
образом, для поддержания тока необходимы
сторонние силы, действующие либо на
всем протяжении цепи, либо на отдельных
ее участках. Эти силы могут быть
обусловлены химическими процессами,
диффузией носителей тока в неоднородной
среде и т.д. Сторонние силы действуют
на носители тока, вызывая их упорядоченное
движение, и поддерживают ток в цепи
(рис.2.2).
,
т.е. против сил электростатического
поля. Перемещение носителей на этих
участках возможно лишь с помощью сил
неэлектрического происхождения,
называемых сторонними силами. Таким
образом, для поддержания тока необходимы
сторонние силы, действующие либо на
всем протяжении цепи, либо на отдельных
ее участках. Эти силы могут быть
обусловлены химическими процессами,
диффузией носителей тока в неоднородной
среде и т.д. Сторонние силы действуют
на носители тока, вызывая их упорядоченное
движение, и поддерживают ток в цепи
(рис.2.2).
Величина,
равная работе сторонних сил по перемещению
единичного положительного заряда по
цепи, называется электродвижущей силой
(ЭДС)  :
:
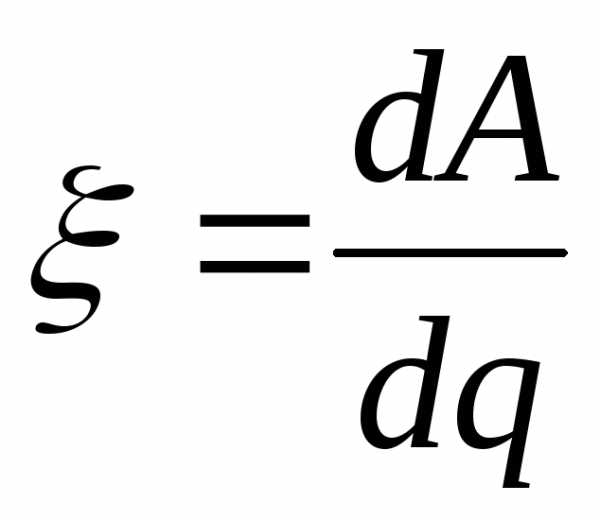 .
.
Если
на заряд q действует сторонняя сила 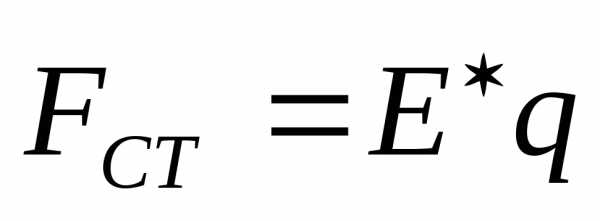 ,
где
,
где – напряженность поля сторонних сил, то
работа сторонних сил над зарядомq на участке цепи 1-2 равна:
– напряженность поля сторонних сил, то
работа сторонних сил над зарядомq на участке цепи 1-2 равна:
.
Для
ЭДС на участке цепи имеем: 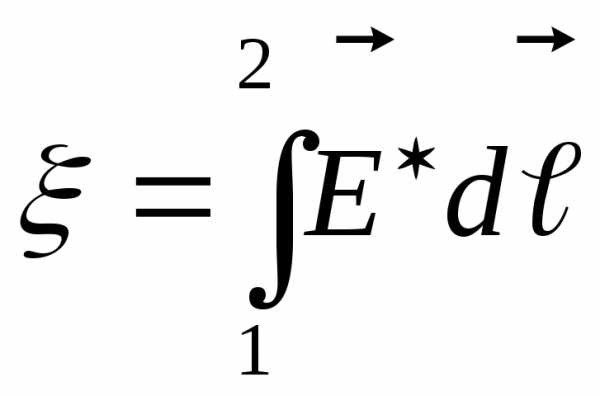 .
Если цепь замкнута
.
Если цепь замкнута 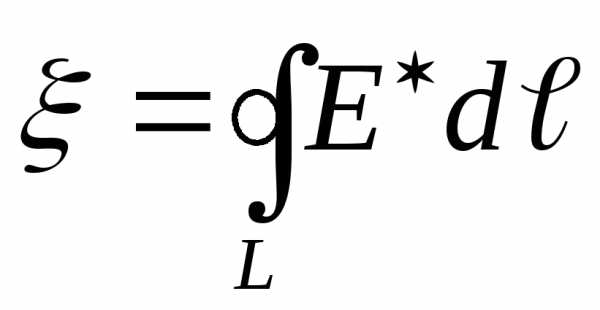 –
–
ЭДС равна циркуляции вектора напряженности поля сторонних сил.
Кроме
сторонних сил, на заряд действуют силы
электростатического поля: 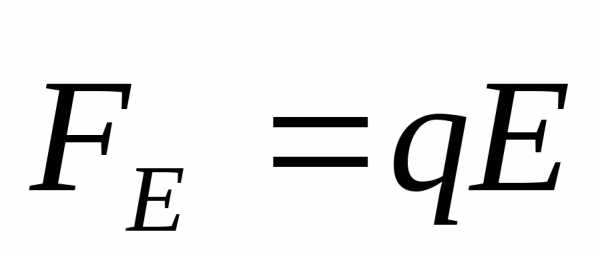 .
Результирующая всех сил:
.
Работа этой силы под зарядом q на участке 1-2 равна
.
.
Результирующая всех сил:
.
Работа этой силы под зарядом q на участке 1-2 равна
.
Для
единичного положительного заряда – мы получили выражение для падения
напряжения на данном участке. Падением
напряжения 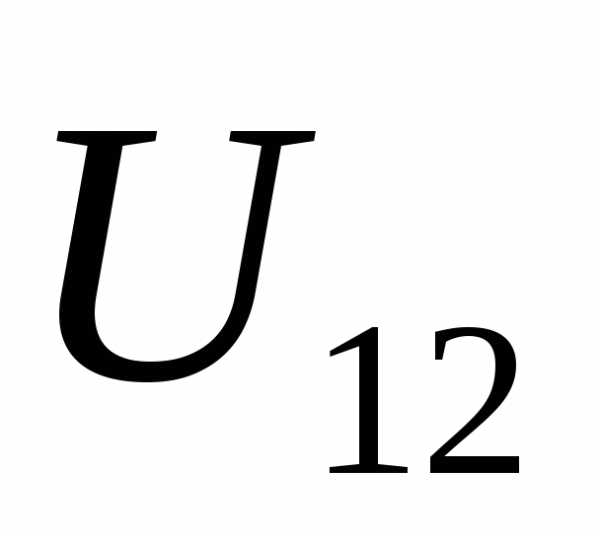 (или просто напряжением) на участке цепи1-2 называется физическая величина, численно
равная работе, совершаемой суммарным
полем кулоновских и сторонних сил при
перемещении вдоль цепи единичного
положительного заряда из точки 1 в точку 2.
(или просто напряжением) на участке цепи1-2 называется физическая величина, численно
равная работе, совершаемой суммарным
полем кулоновских и сторонних сил при
перемещении вдоль цепи единичного
положительного заряда из точки 1 в точку 2.
Если 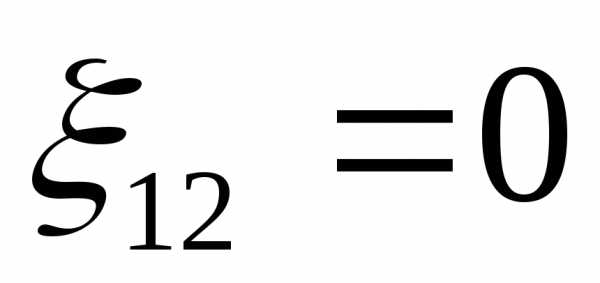 (сторонние силы не действуют) участок
называется однородным:
.
(сторонние силы не действуют) участок
называется однородным:
.
2.3. ЗАКОН ОМА В ИНТЕГРАЛЬНОЙ И ДИФФЕРЕНЦИАЛЬНОЙ ФОРМАХ. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОЛНОСТИ МЕТАЛЛОВ (ТЕОРИЯ ДРУДЕ-ЛОРЕНЦА). УСЛОВИЯ ЕЕ ПРИМЕНИМОСТИ И ПРОТИВОРЕЧИЯ С ЭКСПЕРИМЕНТАЛЬНЫМИ РЕЗУЛЬТАТАМИ. МАКСВЕЛЛОВСКАЯ РЕЛАКСАЦИЯ ОДНОРОДНОСТИ ЗАРЯДА В ПРОВОДНИКЕ
Закон Ома был экспериментально открыт в 1826 году в следующей форме:
Сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
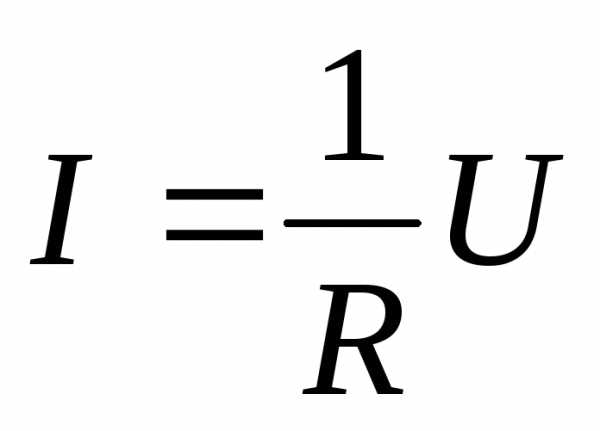 ,
(2.1)
,
(2.1)
где R электрическое сопротивление проводника, 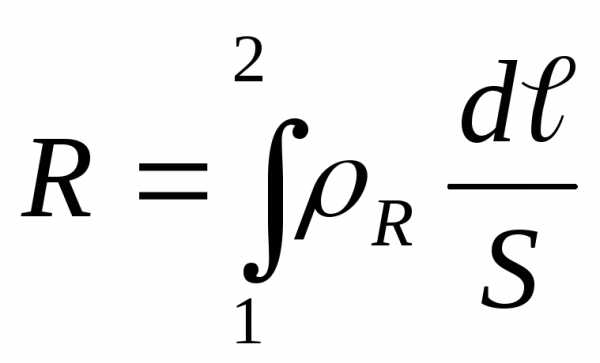 ,
, -удельное
сопротивление (
-удельное
сопротивление (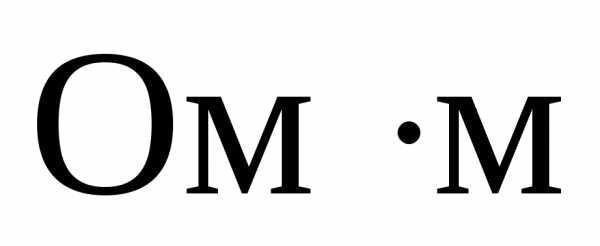 ),
),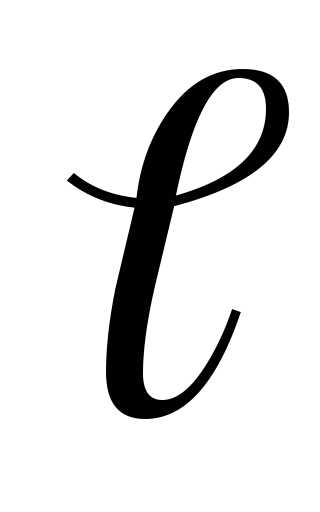 -длина,S –площадь сечения проводника.
-длина,S –площадь сечения проводника.
Однородным называется такой участок цепи, на котором действуют только электростатические силы. Выражение (2.1) определяет соотношение между током и напряжением для однородного участка цепи и называется законом Ома в интегральной форме.
Единица
сопротивления – Ом, 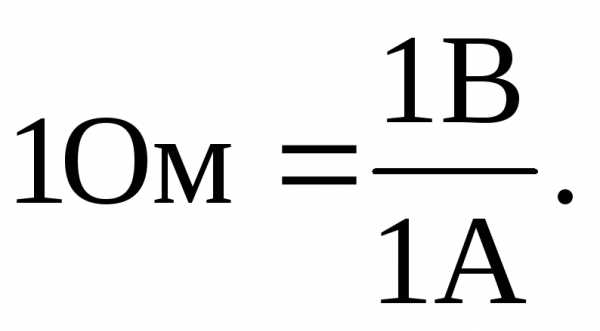
Сопротивление
проводника определяется его геометрическими
размерами (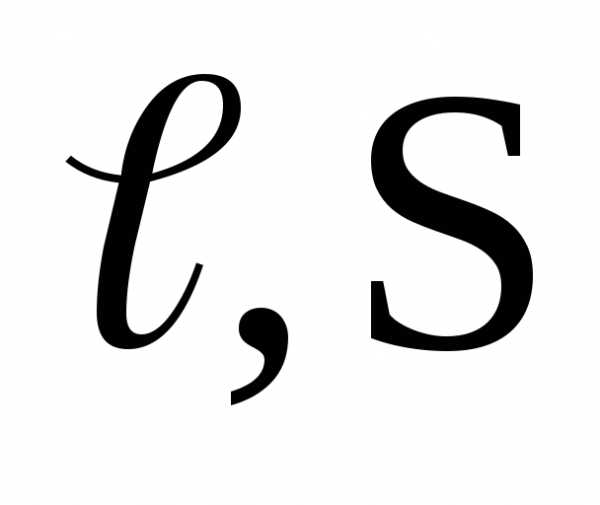 )
и материалом, их которого этот проводник
изготовлен. Наименьшими удельными
сопротивлениями обладают серебро, медь,
золото, алюминий. Величина
)
и материалом, их которого этот проводник
изготовлен. Наименьшими удельными
сопротивлениями обладают серебро, медь,
золото, алюминий. Величина , обратная удельному сопротивлению,
называется удельной электропроводимостью
или электропроводностью вещества. В
дифференциальной форме закон Ома
принимает вид:
, обратная удельному сопротивлению,
называется удельной электропроводимостью
или электропроводностью вещества. В
дифференциальной форме закон Ома
принимает вид:
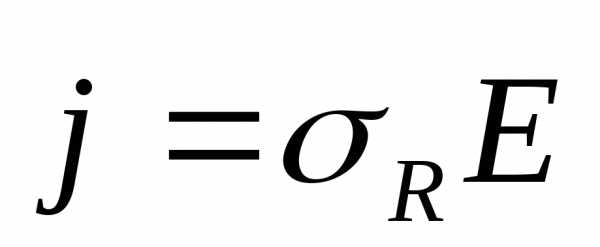
вектор плотности тока равен произведению электропроводности и вектора напряженности электростатического поля.
Действительно, рассмотрим однородный участок проводника, в пределах которого площадь сечения остается постоянной (рис. 2.3). Тогда сила тока равна
 ,
связь напряженности и потенциала дает
значение напряжения
,
связь напряженности и потенциала дает
значение напряжения ,
сопротивление участка определяется
формулой
,
сопротивление участка определяется
формулой .
Подставив в формулу (2.1), имеем:
.
Подставив в формулу (2.1), имеем:
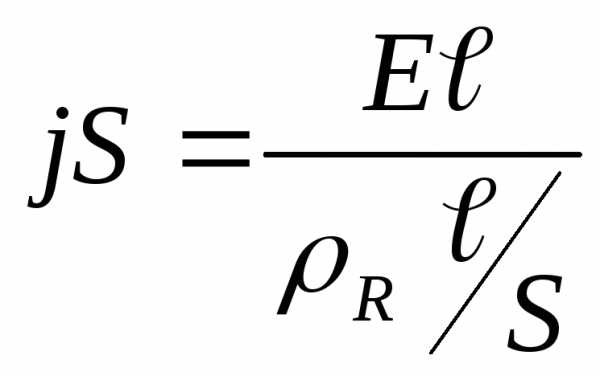 ;
отсюда
;
отсюда 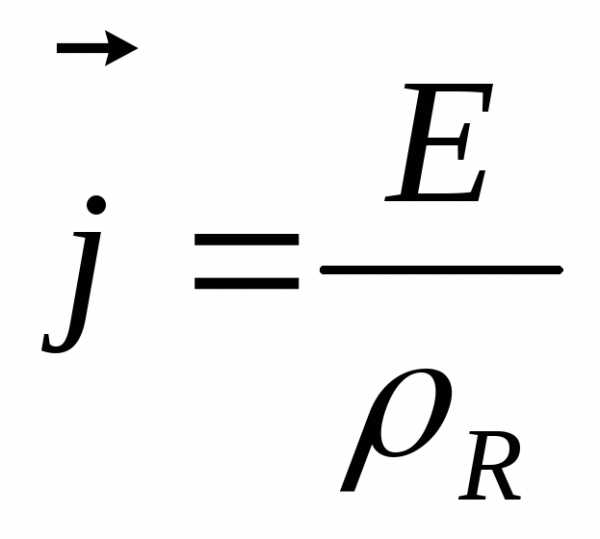 или
или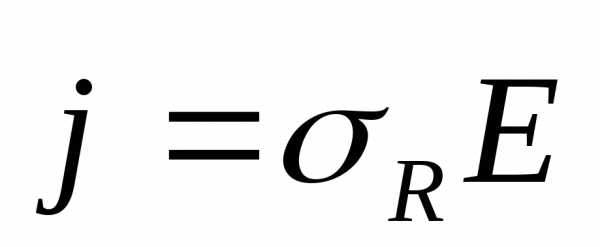 .
.
В
равновесном состоянии в проводнике
отсутствуют объемные заряды, так как
при появлении объемного заряда в
проводнике появляется ток и идет до тех
пор, пока заряд в объеме не исчезнет. В
уединенном проводнике весь сообщенный
заряд располагается на поверхности
проводника . Равновесное состояние
возникает тогда, когда электрическое
поле и объемный заряд внутри проводника
равны нулю. Установление нейтральности
в проводнике происходит очень быстро.
Рассмотрим изменение объемного заряда
во времени. Пусть в начальный момент
времени 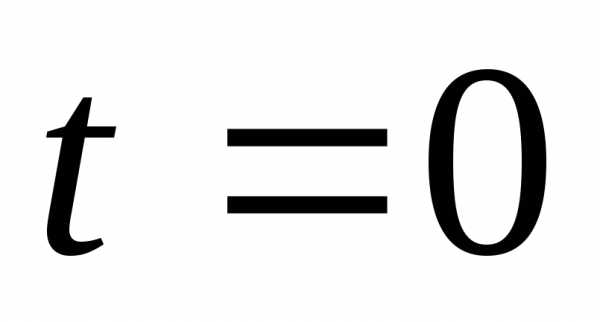 создана некоторая плотность объемного
заряда
создана некоторая плотность объемного
заряда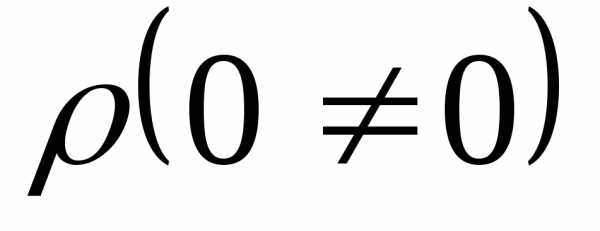 .
Воспользуемся законом сохранения заряда
и законом Ома в дифференциальной форме:
.
Воспользуемся законом сохранения заряда
и законом Ома в дифференциальной форме:
.
Здесь
проводимость проводника  =const.Согласно теореме Гаусса
=const.Согласно теореме Гаусса 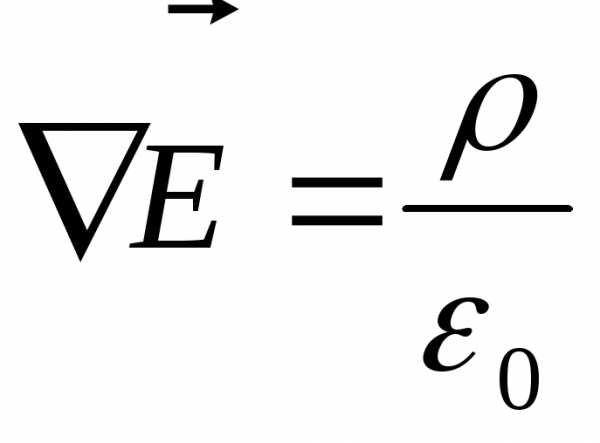 ,
тогда
,
тогда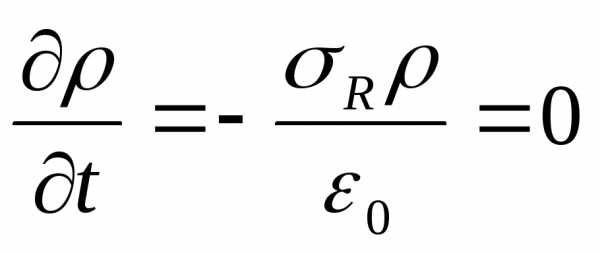 .
Решение этого дифференциального
уравнения дает закон уменьшения плотности
объемного заряда:
.
Решение этого дифференциального
уравнения дает закон уменьшения плотности
объемного заряда: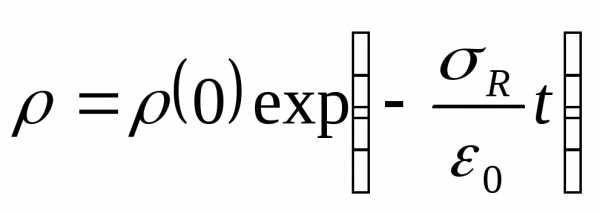 .
Характерное время – Максвелловское
время релаксации – определяется
моментом, когда плотность заряда падает
вераз:
.
Характерное время – Максвелловское
время релаксации – определяется
моментом, когда плотность заряда падает
вераз: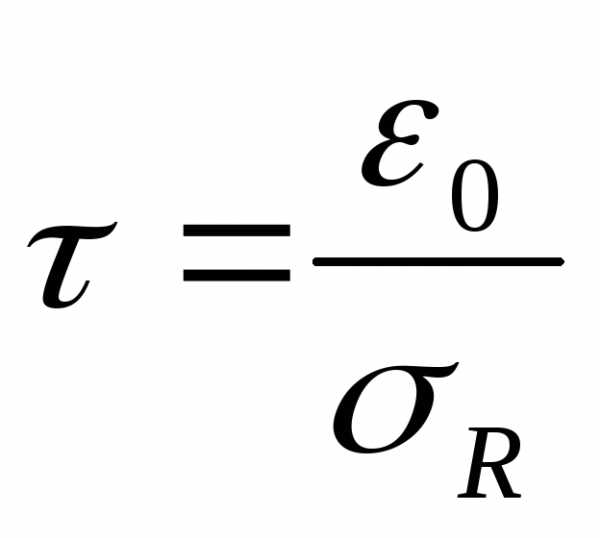 .
.
Закон
Ома объясняет классическая теория
металлов, созданная физиками Друде и
Лоренцем. Согласно этой теории валентные
электроны в металле являются общими
для всех атомов и движутся в пространстве
между положительными ионами, которые
находятся в узлах кристаллических
решеток. Электроны проводимости образуют
электронный газ, подчиняющийся законам
идеального газа. Однако, в отличие от
молекул идеального газа, которые при
движении сталкиваются друг с другом,
электроны в металле сталкиваются с
узлами кристаллической решетки, и
расстояние, которое проходит электрон
между двумя такими соударениями, есть
длина свободного пробега электрона λ. В результате таких
столкновений устанавливается тепловое
равновесие между электронным газом и
кристаллической решеткой. Друде
распространил на электронный газ
результаты кинетической теории газов.
В этой теории средняя скорость теплового
движения электронов равна
,
при комнатной температуреПри внесении проводника в поле, на
хаотическое тепловое движение электронов
накладывается упорядоченное движение
электронов некоторой средней скоростью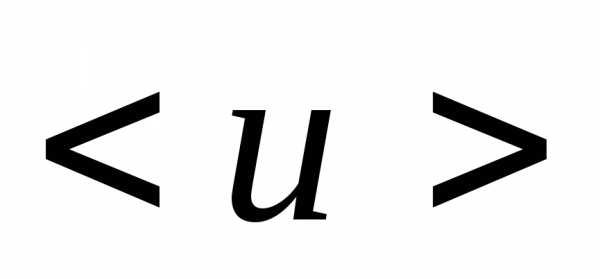 ,
при этом плотность тока:.
Максимально возможное значение,
т.е. в
,
при этом плотность тока:.
Максимально возможное значение,
т.е. в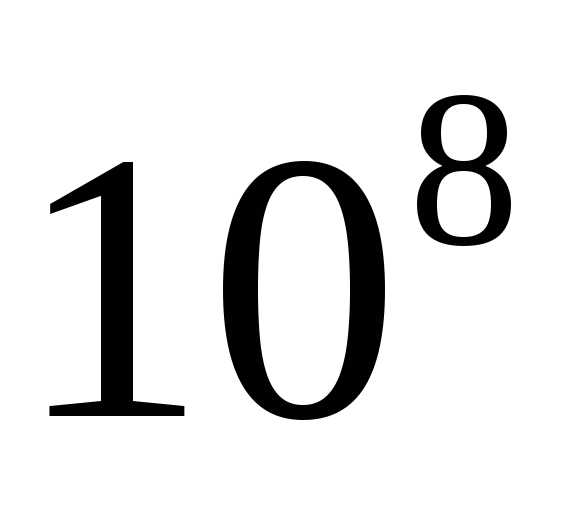 раз меньше средней скорости теплового
движения
раз меньше средней скорости теплового
движения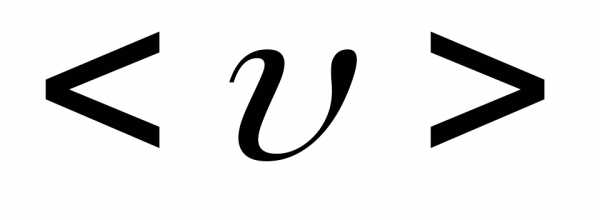 .
.
Найдем изменение кинетической энергии электронов, вызываемое полем. Для этого определим средний квадрат результирующей скорости:
Величины  и
и независимы,
поэтому,(среднее значение вектора скорости
теплового движении электронов равно
нулю, т.к. ее направление меняется
хаотично) , следовательно,
независимы,
поэтому,(среднее значение вектора скорости
теплового движении электронов равно
нулю, т.к. ее направление меняется
хаотично) , следовательно,
.
Таким
образом, упорядоченное движение
увеличивает кинетическую энергию
электронов на
.
Двигаясь в кристалле, электроны
испытывают соударение с узлами
кристаллической решетки. Время между
двумя соударениями:, где -длина
свободного пробега электрона в металле.Благодаря
столкновениям электрон приходит в
состояние теплового равновесия со своим
окружением, средняя кинетическая энергия
электрона равна
-длина
свободного пробега электрона в металле.Благодаря
столкновениям электрон приходит в
состояние теплового равновесия со своим
окружением, средняя кинетическая энергия
электрона равна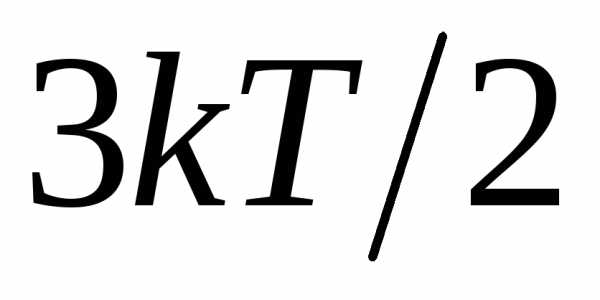 , гдеТ – локальная температура в месте
нахождения электрона. В состоянии
теплового равновесия распределение
электронов по энергиям соответствует
распределению Максвелла- Больцмана.
, гдеТ – локальная температура в месте
нахождения электрона. В состоянии
теплового равновесия распределение
электронов по энергиям соответствует
распределению Максвелла- Больцмана.
Друде
предположил, что при соударении электронов
с узлом кристаллической решетки вся
дополнительная энергия передается
иону, в результате соударения u=0.
Если поле, ускоряющее электроны,
однородно, электрон получает постоянное
ускорение 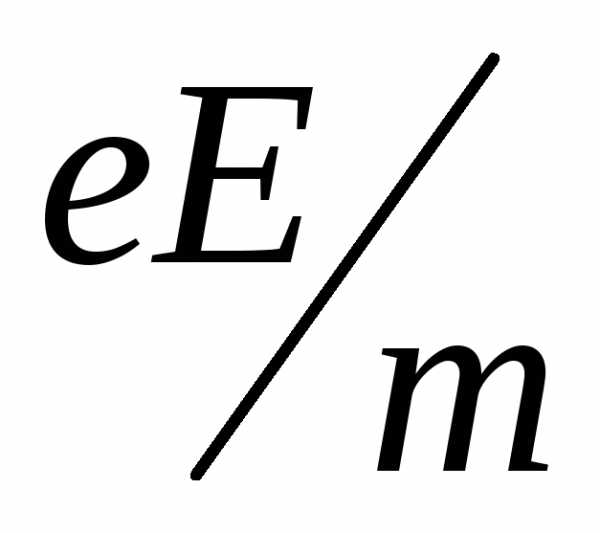 ,
и к концу пробега скорость упорядоченного
движения достигает максимума (рис.2.4).
,
и к концу пробега скорость упорядоченного
движения достигает максимума (рис.2.4).
Скоростьu изменяется во времени линейно, поэтому
Для плотности токаj получим: 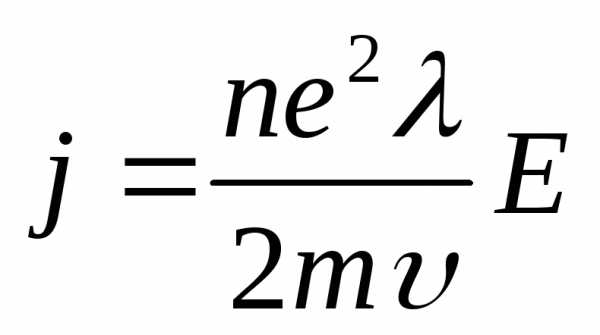 ,
т.е. j ~ E – это закон Ома.
Коэффициент пропорциональности
,
т.е. j ~ E – это закон Ома.
Коэффициент пропорциональности 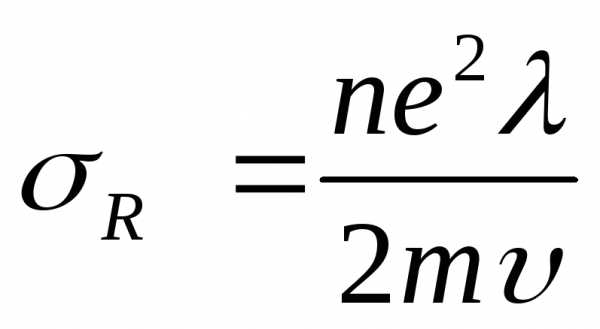 есть проводимость. Если бы электроны
не сталкивались с ионами кристаллической
решетки, их скорости росли бы
беспрепятственно, и проводимость была
бы неограниченно большой
есть проводимость. Если бы электроны
не сталкивались с ионами кристаллической
решетки, их скорости росли бы
беспрепятственно, и проводимость была
бы неограниченно большой 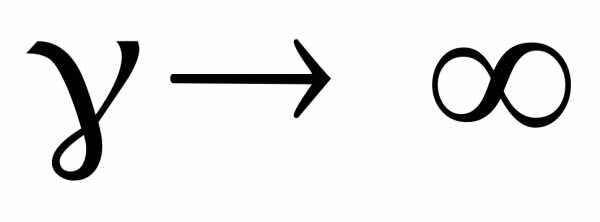 ,
т.к. неограниченно росла бы при этом
длина свободного пробега.
,
т.к. неограниченно росла бы при этом
длина свободного пробега.
Сопротивление проводника зависит от температуры и давления. Сопротивление металлических проводников зависит от температуры по закону (рис.2.5)
,
где  –
температурный коэффициент сопротивления.
Для некоторых металлов и сплавов вблизи
абсолютного нуля температуры наблюдается
скачкообразное падение сопротивления
практически до нуля. Это явление называют
сверхпроводимостью. Температура перехода
в сверхпроводящее состояние для разных
металлов лежит в интервале от 2 до 10 К.
–
температурный коэффициент сопротивления.
Для некоторых металлов и сплавов вблизи
абсолютного нуля температуры наблюдается
скачкообразное падение сопротивления
практически до нуля. Это явление называют
сверхпроводимостью. Температура перехода
в сверхпроводящее состояние для разных
металлов лежит в интервале от 2 до 10 К.
Согласно
закону Видемана-Франца для всех металлов
отношение коэффициента теплопроводности  к удельной электрической проводимости
к удельной электрической проводимости прямо пропорционально абсолютной
температуреТ:
,
где
прямо пропорционально абсолютной
температуреТ:
,
где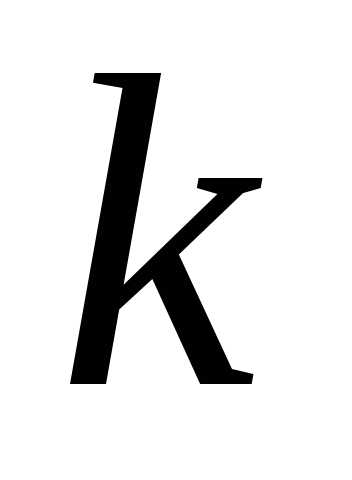 –
постоянная Больцмана,е – заряд электрона.
–
постоянная Больцмана,е – заряд электрона.
Теория Друде качественно объясняет ряд кинетических явлений: электропроводность металлов, эффект Холла, закон Ома. Поскольку скорость электрона после каждого столкновения соответствует локальной температуре в месте столкновения, то при наличии градиента температуры возникает поток энергии, направленный в сторону области с более низкой температурой и пропорциональный градиенту температуры. Коэффициент пропорциональности в условиях, когда средняя скорость направленного движения равна нулю ( разомкнутая внешняя цепь), представляет собой коэффициент теплопроводности. Отсутствие электрического тока при наличии градиента температуры обеспечивается возникновением электрического поля, пропорционального градиенту температуры (эффект Зеебека). Это поле создает электрический ток, компенсирующий ток, создаваемый потоком «горячих» электронов (максвелловская релаксация однородности заряда в проводнике). Таким образом, теория Друде качественно объясняет электронную теплопроводность и некоторые термоэлектрические явления.
Наиболее впечатляющим, хотя и ошибочным, результатом теории Друде явилось объяснение закона Видемана-Франца. Оно было связано с взаимной компенсацией двух ошибок при вычислении электронной теплоемкости ( в теории Друде она была в 100 раз больше истинной) и среднего квадрата скорости электрона ( он во столько же раз меньше истинного). Кроме того, Друде ошибся в два раза при вычислении электропроводности.
Теория металлов Друде, будучи классической, не могла принципиально объяснить ряд экспериментальных фактов: а) отсутствие электронного вклада в теплоемкость; б) величину свободного пробега электронов, превосходящую в сотни раз расстояние между ионами; в) знак постоянной Холла, который может быть как положительным, так и отрицательным; г) зависимость сопротивления всех металлов от внешнего магнитного поля; д) наблюдаемые значения термоэдс, которые примерно на два порядка меньше, чем следует из теории Друде.
Развитие квантовой статистики и квантовой механики привело к появлению квантовостатистической теории электронного газа в металлах.
studfiles.net
ОПРЕДЕЛЕНИЕ ЭДС И МОЩНОСТИ ИСТОЧНИКА ТОКА — МегаЛекции
Цель работы: определить ЭДС источника постоянного тока методом компенсации, определить полезную мощность и КПД в зависимости от сопротивления нагрузки.
Оборудование: исследуемый источник тока, источник стабилизированного напряжения, магазин сопротивления Р32, миллиамперметр М45, гальванометр М122.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Источники тока – это устройства, в которых происходит преобразование различных видов энергии (механической, химической, тепловой) в электрическую энергию. В источниках тока происходит разделение электрических зарядов разного знака. Поэтому если полюса источника замкнуть на проводник, то по проводнику потечет электрический ток, вызванный движением зарядов под действием электростатического поля. За направление тока принято направление движения положительных зарядов. Ток потечет от положительного полюса источника через проводник к отрицательному полюсу. Но через источник тока заряды движутся наоборот, против сил электростатического поля. Это может происходить только под действием сил не электростатической природы, так называемых сторонних сил. Например, магнитной силы Лоренца в генераторах электростанций, сил диффузии в химических источниках тока.
Характеристикой источника тока является электродвижущая сила – ЭДС. Она равна отношению работы сторонних сил к величине заряда, перенесенного через источник:
. (1)
Рассмотрим электрическую цепь из источника тока с внутренним сопротивлением r, замкнутого на нагрузку сопротивлением R. Работа сторонних сил по закону сохранения энергии при неподвижных проводниках превращается в теплоту, выделяемую на нагрузке и внутреннем сопротивлении источника. Согласно закону Джоуля – Ленца теплота, выделяемая в проводнике, равна произведению квадрата силы тока на сопротивление и время протекания тока. Тогда . После сокращения на Jt получим, что сила тока в цепи равна отношению ЭДС к полному сопротивлению электрической цепи:
. (2)
Это закон Ома для полной цепи.
| Измерение мощности |
| Измерение ЭДС |
| Милли- амперметр |
При отсутствии тока через источник, при R→∞ J→0, падение напряжения на внутреннем сопротивлении отсутствует и ЭДС равна напряжению между полюсами источника . Единицей измерения ЭДС является вольт (В).
ЭДС можно измерить различными методами. Если, в простейшем случае, вольтметр c сопротивлением R подсоединить к полюсам источника с внутренним сопротивлением r, то, по закону Ома, показания вольтметра будут . Это меньше, чем ЭДС. Погрешность измерения тем меньше, чем больше сопротивление вольтметра: .
В компенсационном методе измерения ЭДС ток через источник не течет (рис. 1). Если с помощью регулятора блока питания БП подобрать напряжения на магазине сопротивлений R точно равным ЭДС источника, то ток через источник и через гальванометр Г не потечет. Тогда ЭДС источника будет равна падению напряжения на магазине сопротивлений:
. (3)
Полезная мощность источника тока при неподвижных проводниках – это тепловая мощность, выделяемая на нагрузке. По закону Джоуля – Ленца Р = J 2R. Подставив силу тока, согласно закону Ома (2), получим формулу зависимости полезной мощности от сопротивления нагрузки:
. (4)
В режиме короткого замыкания при отсутствии нагрузки, R = 0, вся теплота выделяется на внутреннем сопротивлении и полезная мощность равна нулю (рис. 2). С увеличением сопротивления нагрузки, пока R<<r, полезная мощность возрастает почти прямо пропорционально сопротивлению R. С дальнейшим возрастанием сопротивления нагрузки наступает ограничение силы тока, и мощность, достигнув максимума, начинает спадать. При больших значениях сопротивления нагрузки (R>>r), мощность уменьшается обратно пропорционально сопротивлению, стремясь к нулю при разрыве цепи.
Максимум мощности соответствует условию равенства нулю первой производной от тепловой мощности по сопротивлению. Продифференцировав (4), получим . Отсюда следует, что полезная мощность максимальна, если R = r. Подставив в (4), получим .
Работа источника тока характеризуется коэффициентом полезного действия. Это, по определению, отношение полезной работы к полной работе источника тока: . После сокращения формула КПД примет вид
.(5)
В режиме короткого замыкания при R = 0, КПД равен нулю, так как равна нулю полезная мощность (рис. 3). В режиме максимальной мощности КПД источника тока равен 50%. С ростом сопротивления нагрузки КПД растет и стремится к 100% при больших значениях сопротивлениях(R>>r).
ВЫПОЛНЕНИЕ РАБОТЫ
1. Измерение ЭДС. Установить переключатель режима работы в положение «ЭДС». Установить на магазине сопротивление 500 Ом, предел измерения миллиамперметра 3 мА. На короткое время нажать на кнопку К и заметить, как отклоняется стрелка гальванометра при протекании тока от исследуемого источника.
Включить блок питания в сеть 220 В.
2. Нажать на кнопку К включения тока через гальванометр. Если стрелка гальванометра отклоняется так же, как при включении только источника тока, то увеличивайте силу компенсирующего тока от блока питания, контролируя его по миллиамперметру. Если стрелка отклоняется в обратном направлении, то уменьшайте силу тока, пока не добьетесь компенсации напряжений.
Повторить измерения не менее пяти раз, изменяя сопротивление в пределах 500 – 3000 Ом. Результаты записать в табл. 1
Таблица 1
| Сопротивление R, Ом | |||||||
| Сила тока J, мА | |||||||
| ЭДС Е, В | < Е>, В |
3. Измерение мощности.
Установить и удерживать пружинный переключатель режима измерений в положение «Мощность». Выключить сопротивление магазина, R=0. Измерить при коротком замыкании силу тока по миллиамперметру. Цена деления миллиамперметра . Результат записать в табл. 2.
Повторить измерения, изменяя сопротивление с интервалом 100 Ом в диапазоне 0 – 1000 Ом. Результаты записать в табл. 2.
Выключить приборы.
4. Произвести расчеты.
Рассчитать ЭДС исследуемого источника по формуле Е = JR в каждом опыте. Определить среднее значение ЭДС <Е>.
| Сопротивление магазина R, Ом | ||||||||
| Сила тока J, мА | ||||||||
| Полезная мощность Рпол, мВт | ||||||||
| Полная мощность Рзатр, мВт | ||||||||
| КПД |
Таблица 2
5. Оценить случайную погрешность измерения ЭДС по формуле прямых погрешностей
, (6)
где n – число измерений.
6. Рассчитать полезную Рпол =J 2R и полную Рзатр = <Е>J мощности источника тока.
Рассчитать КПД источника по формуле h = Рпол/Рзатр .
7. Построить графики зависимости полезной мощности от сопротивления нагрузки. Построить график КПД от сопротивления нагрузки. Размер графиков не менее половины страницы. На осях координат указать равномерный масштаб. Около точек провести плавные кривые линии так, чтобы отклонения точек от линий были минимальны.
8. Записать результат Е =<E> ±d E, Р = 90%.
Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Объясните роль источника тока в электрической цепи. Дайте определение электродвижущей силы источника тока (ЭДС).
2. Выведите, используя закон сохранения энергии, и сформулируйте закон Ома для полной цепи.
3. Объясните суть компенсационного метода измерения ЭДС. Можно ли измерить ЭДС источника тока вольтметром?
4. Выведите формулу для полезной мощности источника тока. Изобразите график зависимости полезной мощности от величины сопротивления нагрузки, объясните эту зависимость.
5. Выведите условие максимальной мощности источника тока.
6. Выведите формулу КПД источника тока. Изобразите график зависимости КПД от сопротивления нагрузки источника тока. Объясните эту зависимость.
Работа 22
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Что такое ЭДС источника тока?
Если замкнуть между собой полюса заряженного конденсатора, то под влиянием электростатического поля, накопленного между его обкладками, во внешней цепи конденсатора в направлении от положительного полюса к отрицательному начинается движение носителей заряда – электронов.
Однако в процессе разряда конденсатора электрическое поле, действующее на движущиеся заряженные частицы, быстро ослабевает до полного исчезновения. Поэтому возникшее в цепи разряда протекание электрического тока имеет кратковременный характер и процесс быстро затухает.
Для длительного поддержания тока в проводящей цепи используются устройства, неточно называемые в быту источниками тока (в строго физическом смысле это не так). Чаще всего такими источниками служат химические батареи.
Вследствие происходящих в них электрохимических процессов на их клеммах происходит накопление разноименных электрических зарядов. Силы не электростатической природы, под действием которых осуществляется подобное распределение зарядов, называют сторонними силами.
Уяснить природу понятия ЭДС источника тока поможет рассмотрение следующего примера.
Представим себе проводник, находящийся в электрическом поле, как показано ниже на рисунке, то есть таким образом, что внутри него также существует электрическое поле.
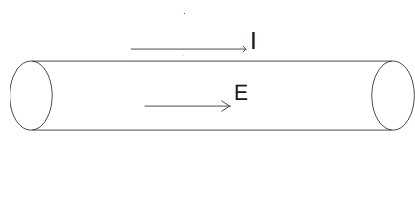
Известно, что под воздействием этого поля в проводнике начинает протекать электрический ток. Теперь возникает вопрос о том, что происходит с носителями заряда, когда они достигают конца проводника, и будет ли этот ток оставаться неизменным с течением времени.
Мы можем легко сделать вывод, что при разомкной цепи в результате влияния электрического поля заряды будут накапливаться на концах проводника. В связи с этим электрический ток не будет оставаться постоянным и движение электронов в проводнике будет очень кратковременным, как показано ниже на рисунке.
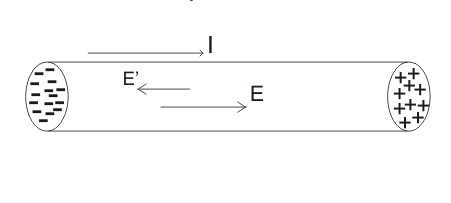 Таким образом, для того, чтобы поддерживать в проводящей цепи постоянное протекание тока, эта цепь должна быть замкнута, т.е. иметь форму петли. Однако для поддержания тока даже это условие не является достаточным, так как заряд всегда движется в сторону меньшего потенциала, а электрическое поле всегда делает положительную работу над зарядом.
Таким образом, для того, чтобы поддерживать в проводящей цепи постоянное протекание тока, эта цепь должна быть замкнута, т.е. иметь форму петли. Однако для поддержания тока даже это условие не является достаточным, так как заряд всегда движется в сторону меньшего потенциала, а электрическое поле всегда делает положительную работу над зарядом.Теперь после путешествия по замкнутой цепи, когда заряд возвращается к исходной точке, где он начал свой путь, потенциал в этой точке должен быть таким же, каким он был в начале движения. Однако протекание тока всегда связано с потерей потенциальной энергии.
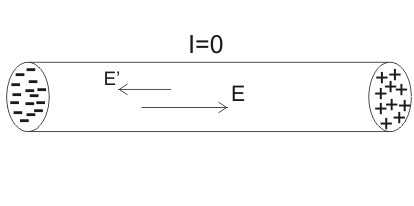
Следовательно, нам необходим некий внешний источник в цепи, на клеммах которого поддерживается разность потенциалов, увеличивающая энергию движения электрических зарядов.
Такой источник позволяет осуществить путешествие заряда от более низкого потенциала к более высокому в направлении, противоположном движению электронов под действием электростатической силы, пытающейся протолкнуть заряд от более высокого потенциала к более низкому.
Эту силу, заставляющую заряд двигаться от более низкого к более высокому потенциалу, принято называть электродвижущей силой. ЭДС источника тока – это физический параметр, который характеризует работу, затраченную на перемещение зарядов внутри источника сторонними силами.
В качестве устройств, обеспечивающих ЭДС источника тока, как уже упоминалось, используются аккумуляторы, а также генераторы, термоэлементы и т.д.
Теперь мы знаем, что элемент питания за счет своей внутренней ЭДС обеспечивает разность потенциалов между выводами источника, способствуя непрерывному перемещению электронов в направлении, противоположном действию электростатической силы.
ЭДС источника тока, формула которой приведена ниже, как и разность потенциалов выражается в вольтах :
E = Aст/Δq,
где Аст – работа сторонних сил, Δq – заряд, перемещенный внутри источника.
fb.ru
ОПРЕДЕЛЕНИЕ ЭДС И МОЩНОСТИ ИСТОЧНИКА ТОКА — Мегаобучалка
ЧИПС, филиал УрГУПС
Кафедра ЕНД
Работа 20
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Студенты
Группа
Преподаватель
Дата
Челябинск
Цель работы: определить положение эквипотенциальных поверхностей и силовых линий электростатического поля методом моделирования, рассчитать напряженность поля.
Оборудование: лист металлической фольги с координатной сеткой и электродами, источник питания ВСП-33, мультиметр, зонд.
РАСЧЕТНЫЕ ФОРМУЛЫ
Электростатическое поле – это форма материи, проявляющая себя в воздействии на электрические заряды. Электростатическое поле создается:
Силовой характеристикой поля является напряженность. Это вектор, определяемый …
Энергетической характеристикой электростатического поля является потенциал. По определению он равен …
Между двумя характеристиками поля, напряженностью и потенциалом существует связь:
Электростатическое поле для наглядности изображают графически с помощью силовых и эквипотенциальных линий. Это линии, …
Приближенно по расположению эквипотенциальных линий напряженность можно рассчитать по формуле:
Е=
ВЫПОЛНЕНИЕ РАБОТЫ
Расчет напряженности Е=…………………..
Оценка погрешности измерения напряженности δЕ=
ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
ЧИПС, филиал УрГУПС
Кафедра ЕНД
Работа 21
ОПРЕДЕЛЕНИЕ ЭДС И МОЩНОСТИ ИСТОЧНИКА ТОКА
Студенты
Группа
Преподаватель
Дата
Челябинск
Цель работы: определить ЭДС источника постоянного тока методом компенсации, определить полезную мощность и КПД в зависимости от сопротивления нагрузки.
Оборудование: исследуемый источник тока, источник стабилизированного напряжения, магазин сопротивления, миллиамперметр, гальванометр.
РАСЧЕТНЫЕ ФОРМУЛЫ
Источники тока – это устройства, в которых происходит преобразование различных видов энергии в………
Характеристикой источника тока является ………… По определению она равна отношению ………………..
Рассмотрим электрическую цепь из источника тока с внутренним сопротивлением r, замкнутого на нагрузку сопротивлением R. По закону сохранения энергии работа сторонних силпревращается ……… согласно уравнению ……………………… Откуда получим закон Ома для замкнутой цепи в виде:
В компенсационном методе измерения ЭДС с помощью регулятора блока питания БП напряжение на магазине сопротивлений R подбирают точно равным …………….. Тогда ЭДС источника будет равна ………..
Полезная мощность источника тока – это тепловая мощность, выделяемая на нагрузке. По закону Джоуля – Ленца ……………………………
Подставив силу тока согласно закону Ома, получим формулу полезной мощности:
Работа источника тока характеризуется коэффициентом полезного действия. Это, по определению ……
Формула для КПД источника тока имеет вид:
ВЫПОЛНЕНИЕ РАБОТЫ
ЭДС
| Сопротивление R, Ом | |||||||
| Сила тока J, мА | |||||||
| ЭДС Е, В | < Е>, В |
Примеррасчета ЭДС Е = JR =
Среднее значение ЭДС <Е> =
Оценка случайной погрешности измерения ЭДС источника =
| Сопротивление магазина R, Ом | ||||||
| Сила тока J, мА | ||||||
| Полезная мощность Рпол, мВт | ||||||
| Полная мощность Рзатр, мВт | ||||||
| КПД |
Результат измерения ЭДС Е =………±……….В Р = 90%.
Пример расчета: полезной мощности: Рпол =J 2R =
полной мощности Рзатр = <Е>J= КПД η
= Мощность
| |||||||||||||||||||
Выводы.
ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
ЧИПС, филиал УрГУПС
Кафедра ЕНД
Работа 22
megaobuchalka.ru

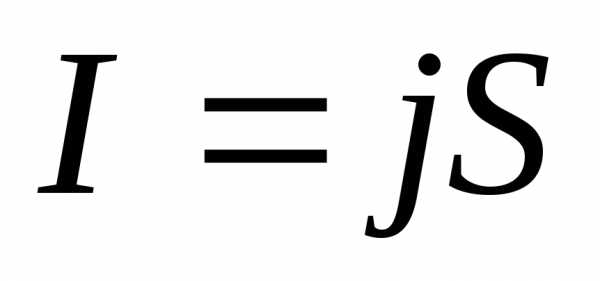 ,
связь напряженности и потенциала дает
значение напряжения
,
связь напряженности и потенциала дает
значение напряжения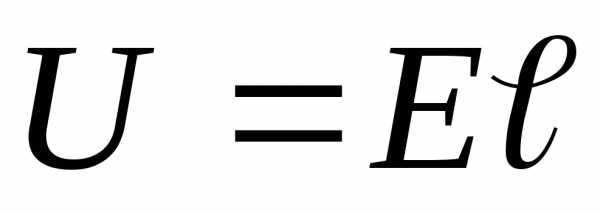 ,
сопротивление участка определяется
формулой
,
сопротивление участка определяется
формулой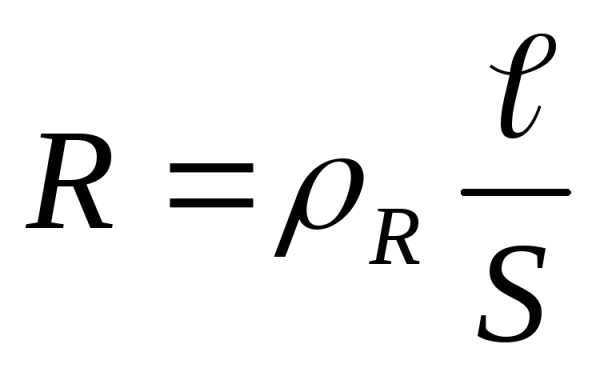 .
Подставив в формулу (2.1), имеем:
.
Подставив в формулу (2.1), имеем: