Эффект спин: эффект – это… Что такое спин-эффект?
- Физики объяснили влияние закрученного света на спин электронов
- Эффект спин-холла – Spin Hall effect
- Спин-эффект аномальный – Справочник химика 21
- Найден новый квантовый эффект: спин-вращательная связь – 11 March 2020
- СПИН-ОРБИТАЛЬНОЕ ВЗАИМОДЕЙСТВИЕ • Большая российская энциклопедия
- Эффект спин-селективной адсорбции водяного пара
- SPIN MUSIC SERVICE
- Произошла ошибка при настройке пользовательского файла cookie
- Селективное управление спиновым угловым моментом фотона с помощью электронно-индуцированного оптического спинового эффекта Холла
- Акустический спиновый эффект Холла в металлах с сильной спин-орбитой
- Физика тенниса | Вращение мяча в полете
- Наблюдение антиферромагнитного спинового эффекта Холла
- Спиновый фотогальванический эффект в двумерных коллинеарных антиферромагнетиках
- Эффекты фазы отжима? – Вопросы и ответы в МРТ
Физики объяснили влияние закрученного света на спин электронов
Формула Дирака
Международная группа физиков-теоретиков показала, что предсказанная недавно возможность влиять на спины электронов закрученным светом может быть выведена на основе одного из фундаментальных уравнений современной физики — уравнения Дирака. Соответствующий математический вывод приведен в статье, опубликованной в журнале Physical Review B.
Два
года назад в ведущем научном физическом
журнале Physical Review Letters вышла
удивительная статья сотрудников
университета Арканзаса (США), в которой
предсказывалось наличие взаимодействия
между орбитальным моментом света,
распространяющегося в среде, и магнитным
моментом этой среды.
Магнитным моментом среды называется величина, характеризующая магнитные свойства вещества. Возникновение магнитного момента в веществе может быть вызвано или вращением заряженных частиц (обычно электронов) в нем, или собственным магнитным моментом этих частиц — так называемым спином.
Известно также, что если в веществе распространяется свет, имеющий ненулевой орбитальный момент (такая световая волна имеет необычную закрученную структуру, подробнее о которой можно почитать, например, здесь), то он может передать этот момент среде, придав вращение ей и составляющим ее частицам. На этом явлении основана работа, например, оптических «гаечных ключей» (спаннеров), позволяющих при помощи лазерных импульсов закручивать микрообъекты.
Но
если свет может закрутить среду, то он
может закрутить и электроны в этой
среде, создав тем самым магнитный момент. Именно это и было показано в опубликованной
работе. Однако, в ней делалось и более
сильно утверждение: с помощью закрученного
света можно управлять и собственными
магнитными моментами электронов, спинами, которые не связаны ни с какими
механическими вращениями.
Именно это и было показано в опубликованной
работе. Однако, в ней делалось и более
сильно утверждение: с помощью закрученного
света можно управлять и собственными
магнитными моментами электронов, спинами, которые не связаны ни с какими
механическими вращениями.
Это утверждение, однако, было сделано на основе исключительно соображений симметрии и неких общих формул электродинамики. Физическая же природа этого взаимодействия была ясна не до конца. Чтобы решить эту проблему, два автора статьи в Physical Review Letters совместно с группой теоретиков из университета Уппсалы (Швеция) и университета Париж-Сакле (Франция) рассмотрели вывод предсказанного взаимодействия из уравнения Дирака — фундаментального уравнения квантовой физики, описывающего движение электрона с учетом наличия у него спина, а также релятивистских эффектов. Этот вывод и был опубликован в новой статье.
Оказалось,
что связь между орбитальным моментом
света и спином электрона, которое авторы
называют орбитальным магнитоэлектрическим,
во многом аналогична хорошо известному
в атомной физике спин-орбитальному
взаимодействию между спином электрона
и его вращательным движением. Так же как и спин-орбитальное, орбитальное
магнитоэлектрическое взаимодействие
является чисто релятивистским эффектом,
не требующим, однако, чтобы скорость
частицы была близка к скорости света.
Так же как и спин-орбитальное, орбитальное
магнитоэлектрическое взаимодействие
является чисто релятивистским эффектом,
не требующим, однако, чтобы скорость
частицы была близка к скорости света.
Орбитальное магнитоэлектрическое взаимодействие, по утверждению авторов работы, может объяснить многие уже известные магнитооптические эффекты, в том числе и те, которые до этого оставались не понятыми детально. Например, она объясняет существование так называемой спин-токовой модели в мультиферроиках, позволяющей управлять магнитными свойствами вещества при помощи электрических полей или наоборот, диэлектрическими свойствами при помощи магнитных полей.
То же взаимодействие дает вклад и в еще один важный эффект — возникновение магнитного поля при прохождении через вещество закрученного света. Это явление, известное как обратный эффект Фарадея, вызывает в последние годы повышенный интерес в связи с перспективностью его использования для сверхбыстрой магнитной памяти.
Пользуясь
предсказанным новым типом магнито-оптического
взаимодействия, авторы объясняют также
и более традиционные эффекты, такие как
плоский и аномальный эффекты Холла, а
также анизотропное магнетосопротивление
в ферромагнетиках.
Артем Коржиманов
Эффект спин-холла – Spin Hall effect
Спиновый эффект Холла (ОНА) представляет собой явление переноса предсказывается Российские физики М.И. Дьяконов и Владимира I. Переля в 1971 г. Он состоит из появления спинового накопления на боковых поверхностях электрического тока образца -проведение, признаки На противоположных границах направления вращения противоположны. В цилиндрическом проводе индуцированные током поверхностные вращения будут наматываться на провод.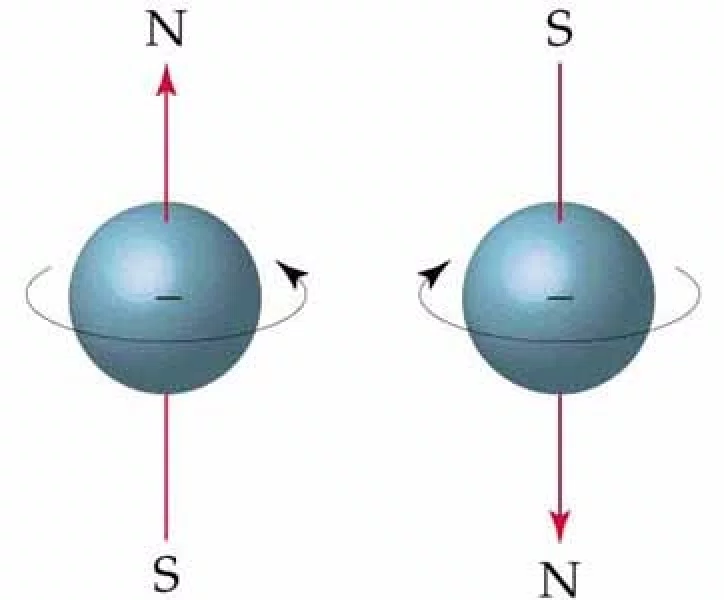
Определение
Спиновый эффект Холла – это явление переноса, состоящее в появлении накопления спинов на боковых поверхностях образца, по которому проходит электрический ток. Противоположные границы поверхности будут иметь спины противоположного знака. Он аналогичен классическому эффекту Холла , когда заряды противоположного знака появляются на противоположных боковых поверхностях в электрическом токопроводящем образце в магнитном поле . В случае классического эффекта Холла накопление заряда на границах является компенсацией силы Лоренца, действующей на носители заряда в образце из-за магнитного поля. Для спинового эффекта Холла, который является чисто спиновым явлением, магнитное поле не требуется . Спиновый эффект Холла принадлежит к тому же семейству, что и давно известный в ферромагнетиках аномальный эффект Холла , также возникающий в результате спин-орбитального взаимодействия .
История
Спиновый эффект Холла (прямой и обратный) был предсказан российскими физиками Михаилом Дьяконовым и Владимиром Перелем в 1971 году. Они также впервые ввели понятие спинового тока .
В 1983 году Аверкиев и Дьяконов предложили способ измерения обратного спинового эффекта Холла при оптической ориентации спина в полупроводниках. Первая экспериментальная демонстрация обратного спинового эффекта Холла, основанная на этой идее, была выполнена Бакун и др. в 1984 г.
Термин «спиновой эффект Холла» был введен Хиршем, который повторно предсказал этот эффект в 1999 году.
Экспериментально (прямой) спиновый эффект Холла наблюдался в полупроводниках более чем через 30 лет после первоначального предсказания.
Физическое происхождение
Два возможных механизма приводят к возникновению спинового эффекта Холла, при котором электрический ток (состоящий из движущихся зарядов) преобразуется в спиновый ток (ток движущихся спинов без потока заряда). Первоначальный (внешний) механизм, разработанный Дьяконовым и Перелем, состоял из спин-зависимого моттовского рассеяния , когда носители с противоположным спином диффундируют в противоположных направлениях при столкновении с примесями в материале. Второй механизм обусловлен внутренними свойствами материала, когда траектории носителей искажаются из-за спин-орбитального взаимодействия как следствие асимметрии в материале.
Первоначальный (внешний) механизм, разработанный Дьяконовым и Перелем, состоял из спин-зависимого моттовского рассеяния , когда носители с противоположным спином диффундируют в противоположных направлениях при столкновении с примесями в материале. Второй механизм обусловлен внутренними свойствами материала, когда траектории носителей искажаются из-за спин-орбитального взаимодействия как следствие асимметрии в материале.
Можно интуитивно представить себе внутренний эффект, используя классическую аналогию между электроном и вращающимся теннисным мячом. Теннисный мяч отклоняется от своей прямой траектории в воздухе в направлении, зависящем от направления вращения, что также известно как эффект Магнуса . В твердом теле воздух заменяется эффективным электрическим полем из-за асимметрии материала, относительное движение между магнитным моментом (связанным со спином) и электрическим полем создает связь, которая искажает движение электронов.
Подобно стандартному эффекту Холла, как внешний, так и внутренний механизмы приводят к накоплению спинов противоположных знаков на противоположных боковых границах.
Математическое описание
Спиновый ток описывается тензором второго ранга q ij , где первый индекс относится к направлению потока, а второй – к текущему компоненту спина. Таким образом, q xy обозначает плотность потока y -компоненты спина в x- направлении. Введем также вектор q i плотности потока заряда (который связан с нормальной плотностью тока j = e q ), где e – элементарный заряд. Связь между спиновым и зарядовым токами обусловлена спин-орбитальным взаимодействием. Это может быть описано в очень простым способом путем введения одного безразмерного параметра сочетания ʏ .
Магнитосопротивление спинового холла
Нет магнитное поле не требуется для спинового эффекта Холла. Однако, если достаточно сильное магнитное поле приложено в направлении, перпендикулярном ориентации спинов на поверхности, спины будут прецессировать вокруг направления магнитного поля, и спиновый эффект Холла исчезнет. Таким образом, в присутствии магнитного поля совместное действие прямого и обратного спинового эффекта Холла приводит к изменению сопротивления образца – эффекту второго порядка по спин-орбитальному взаимодействию. Это было отмечено Дьяконовым и Перелем еще в 1971 г., а затем более подробно разработано Дьяконовым. В последние годы спин-холловское магнитосопротивление интенсивно исследовалось экспериментально как в магнитных, так и в немагнитных материалах (тяжелых металлах, таких как Pt, Ta, Pd, где спин-орбитальное взаимодействие является сильным).
Таким образом, в присутствии магнитного поля совместное действие прямого и обратного спинового эффекта Холла приводит к изменению сопротивления образца – эффекту второго порядка по спин-орбитальному взаимодействию. Это было отмечено Дьяконовым и Перелем еще в 1971 г., а затем более подробно разработано Дьяконовым. В последние годы спин-холловское магнитосопротивление интенсивно исследовалось экспериментально как в магнитных, так и в немагнитных материалах (тяжелых металлах, таких как Pt, Ta, Pd, где спин-орбитальное взаимодействие является сильным).
Обмен спиновых токов
Преобразование спиновых токов , состоящих в перестановке ( замены ) спина и направления потока ( д IJ → д джи ) было предсказано Лифшиц и Дьяконов. Таким образом, поток в направлении x спинов, поляризованных вдоль y , преобразуется в поток в направлении y спинов, поляризованных вдоль x . Это предсказание пока не подтверждено экспериментально.
Это предсказание пока не подтверждено экспериментально.
Оптический мониторинг
Прямой и обратный спиновый эффект Холла можно отслеживать оптическими средствами. Накопление спинов вызывает круговую поляризацию излучаемого света , а также фарадеевское (или керровское ) вращение поляризации прошедшего (или отраженного) света. Наблюдение за поляризацией излучаемого света позволяет наблюдать спиновый эффект Холла.
Совсем недавно существование как прямых, так и обратных эффектов было продемонстрировано не только в полупроводниках , но и в металлах .
Приложения
Спиновый эффект Холла можно использовать для электрического управления спинами электронов. Например, в сочетании с эффектом электрического перемешивания спиновой эффект Холла приводит к спиновой поляризации в локализованной проводящей области.
дальнейшее чтение
Для обзора спинового эффекта Холла см., Например:
Смотрите также
Рекомендации
Спин-эффект аномальный – Справочник химика 21
Отметим, что, как показано в [124, 125], даже в немагнитных неполяризованных кристаллах, помещенных во внешнее магнитное поле, можно наблюдать. многочастотную прецессию спина нейтрона и зависящий от Н эффект подавления ядерных реакций, а при воздействии на монокристалл переменного внешнего поля (магнитного, звукового) возникают зависящие от частоты поля эффекты аномального подавления ядерных реакций (аналогичный рассмотренному выше) и многочастотной прецессии спина нейтрона. [c.144]
многочастотную прецессию спина нейтрона и зависящий от Н эффект подавления ядерных реакций, а при воздействии на монокристалл переменного внешнего поля (магнитного, звукового) возникают зависящие от частоты поля эффекты аномального подавления ядерных реакций (аналогичный рассмотренному выше) и многочастотной прецессии спина нейтрона. [c.144] Эффект Зеемана для нескольких электронов с учетом спина электрона имеет более сложный характер ( аномальный или сложный эффект Зеемана). Его рассмотрение следует проводить на основе квантовой механики. [c.254]
Происхождение названий аномальный и нормальный эффекты Зеемана относится к периоду, когда представления об электронном спине еще не были введены в квантовую механику. Поскольку зеемановский триплет, как это легко показать, может быть объяснен и в рамках описания с набором обычных квантовых чисел п, [c.83]
Неравновесная заселенность ядерных спиновых состояний в продуктах радикальных реакций проявляется в ЯМР-спектрах двояким образом в виде интегрального и мультиплетного эффектов. Интегральный эффект заключается в том, что в продуктах реакции наблюдается преимущественная ориентация ядерных спинов в направлении внешнего поля или против него, вследствие чего в ЯМР-спектре продукта наблюдается или аномально высокое поглощение (А) или вынужденное излучение ( ). [c.200]
Интегральный эффект заключается в том, что в продуктах реакции наблюдается преимущественная ориентация ядерных спинов в направлении внешнего поля или против него, вследствие чего в ЯМР-спектре продукта наблюдается или аномально высокое поглощение (А) или вынужденное излучение ( ). [c.200]
Тем не менее аномальный эффект оставался большой загадкой вплоть до введения гипотезы о спине электрона это произошло лишь спустя двадцать пять лет. [c.364]
Интегральный эффект. Интегральный эффект ХПЯ или ХПЭ — это преимущественная ориентация ядерных спинов в продуктах реакции (или спинов неспаренных электронов в радикалах) в направлении внешнего поля или против него. Мерой интегрального эффекта химической поляризации может служить зеемановская энергия спинов, которая в термодинамическом равновесии отрицательна. Если в ходе химической реакции зеемановская энергия спина становится положительной, это означает, что в дальнейшем спиновая система может отдать накопленную в ней энергию. В этом случае на частоте магнитного резонанса спинов будет наблюдаться вынужденное излучение. Если же в ходе реакции зеемановская энергия спинов уменьшается, т. е. резервуар зеемановского взаимодействия спинов охлаждается, то для нагрева спиновой системы до температуры термостата нужно подвести дополнительно энергию. В этом случае в спектрах магнитного резонанса будут наблюдаться линии, отвечающие аномально большому поглощению. [c.89]
В этом случае на частоте магнитного резонанса спинов будет наблюдаться вынужденное излучение. Если же в ходе реакции зеемановская энергия спинов уменьшается, т. е. резервуар зеемановского взаимодействия спинов охлаждается, то для нагрева спиновой системы до температуры термостата нужно подвести дополнительно энергию. В этом случае в спектрах магнитного резонанса будут наблюдаться линии, отвечающие аномально большому поглощению. [c.89]
Контактное сверхтонкое Л/5-взаимодействие в ближайшем окружении парамагнитного иона. Времена корреляции. Справедливость неравенства (1.17) была неоднократно подтверждена [22, 35, 50, 61, 62] при исследовании растворов ряда парамагнитных солей элементов 3 -группы. Однако в ряде случаев было установлено, что для измеряемых на опыте времен релаксации данное соотношение не выполняется. Так, в водных растворах солей марганца 38], хрома и ванадила [35] времена спин-решеточной релаксации протонов оказались много больше времен спин-спиновой релаксации протонов Т]в >Т2в- Первая попытка объяснить этот эффект была сделана [35]. Замечено, что для ионов, которые дают аномальное отношение Т в/Т в протонов, всегда наблюдается спектр ЭПР в растворах при комнатной температуре, т. е. они имеют длинные времена электронной релаксации Тз. На основании этого сделано предположение, что Те может быть корреляционным временем не только тогда, когда оно короче времени броуновской диффузии [см. уравнение (1.14)], но также и в том случае, когда имеет место обратная зависимость. [c.21]
Замечено, что для ионов, которые дают аномальное отношение Т в/Т в протонов, всегда наблюдается спектр ЭПР в растворах при комнатной температуре, т. е. они имеют длинные времена электронной релаксации Тз. На основании этого сделано предположение, что Те может быть корреляционным временем не только тогда, когда оно короче времени броуновской диффузии [см. уравнение (1.14)], но также и в том случае, когда имеет место обратная зависимость. [c.21]
Предположение о спине электрона объясняет также аномальный эффект Зеемана и так называемую тонкую структуру многих спектральных линий, как, нанример, О-дублета натрия. Эти вопросы будут рассмотрены в дальнейшем. Приписывание электрону дополнительной степени свободы увеличивает кратность вырождения атомных уровней мы увидим, что это позволяет устранить расхождение, отмеченное в табл. 13, где указано, что некоторые из наблюдаемых уровней гелия имеют более высокую кратность вырождения, чем это предсказывается теорией. [c. 233]
233]
Теперь на.м понятно происхождение аномального эффекта Зеемана. Когда атом и.меет спин, мы рассматриваем его в тер.мннах квантовых чисел S, I я j (для одного электрона) полный угловой момент получается путе.м комбинанни спинового и орбитального моментов (рис. 14.17). Если магнитные моменты имеют ту же самую связь с угловым моментом независимо от того, являются опи орбитальными пли спиновыми, то результирующий магнитный момент должен совпадать по направлению с результирующим полным угловым моментом. Поскольку, однако.спиновый магнитный момент аномален, результирующий магнитный. момент не сов- [c.502]
Внеш. магн. поле влияет на выход продуктов р-ции, скорость элементарных процессов взаимод. парамагнитных частиц (рекомбинации радикалов, аннигиляции триплетно-возбужденных молекул, тушения триплетных молекул радикалами и т.п.), интенсивность флуоресценции и хеми-люминесценции, темновую и фотопроводимость мол. кристаллов и орг. полупроводников.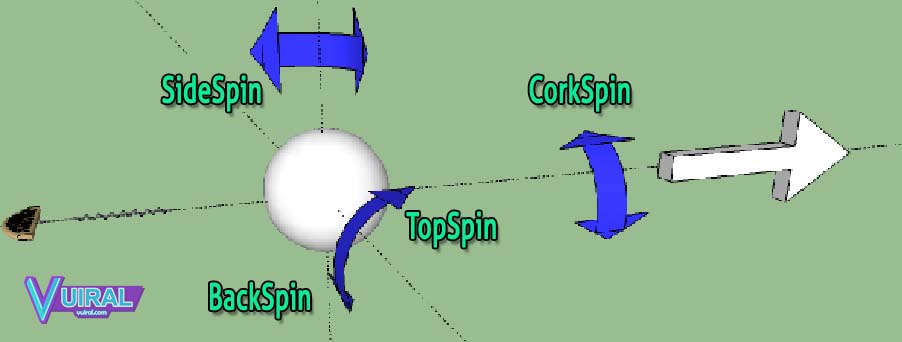 Магн. изотопный эффект сопровождается разделением магн. и немагн. изотопов (напр., С и С, о и О). Хим. поляризация электронов и ядер проявляется в спектрах ЭПР и ЯМР продуктов р-ций (радикалов и молекул), при этом положит, поляризация приводит к аномально сильным линиям поглощения, а отрицательная-к линиям эмиссии. В последнем случае создается инверсная населенность зеемановских уровней электронов или ядер (см. Зеемана эффект. Лазер). Когда химически индуцированная отрицат. поляризация ядер достигает значит, величины, превосходящей порог генерации, происходит самовозбуждение радиочастотного излучения и хим. система становится мол. квантовым генератором-хим. радиочастотным мазером. Внеш. высокочастотное резонансное поле стимулирует изменение спина и, следовательно, выхода продукта р-ции или интенсивности люминесценции. Это позволяет регистрировать спектры ЭПР короткоживущих пар парамагнитных частиц по изменению выхода электронов, дырок, возбужденных молекул. На этом принципе основан новый метод магн.
Магн. изотопный эффект сопровождается разделением магн. и немагн. изотопов (напр., С и С, о и О). Хим. поляризация электронов и ядер проявляется в спектрах ЭПР и ЯМР продуктов р-ций (радикалов и молекул), при этом положит, поляризация приводит к аномально сильным линиям поглощения, а отрицательная-к линиям эмиссии. В последнем случае создается инверсная населенность зеемановских уровней электронов или ядер (см. Зеемана эффект. Лазер). Когда химически индуцированная отрицат. поляризация ядер достигает значит, величины, превосходящей порог генерации, происходит самовозбуждение радиочастотного излучения и хим. система становится мол. квантовым генератором-хим. радиочастотным мазером. Внеш. высокочастотное резонансное поле стимулирует изменение спина и, следовательно, выхода продукта р-ции или интенсивности люминесценции. Это позволяет регистрировать спектры ЭПР короткоживущих пар парамагнитных частиц по изменению выхода электронов, дырок, возбужденных молекул. На этом принципе основан новый метод магн. резонанса-двойной магн. резонанс (ДМР). [c.624]
резонанса-двойной магн. резонанс (ДМР). [c.624]
Другим следствием Г-конверсии в радикальных парах в результате передачи электронного спинового момента ядерным спинам является поляризация последних. Синхронный переворот электронных и ядерных спинов при обмене энергией способствует аномальной заселенности даерных зеемановских уровней. Это проявляется либо в эмиссии радиоизлучения в случае избыточной заселенности верхних уровней (отрицательная поляризация), либо в дополнительном поглощении радиоизлучения (положительная поляризация). Эффекты химической поляризации ядер отчетливо проявляются в ЯМР. Они являются причиной радиочастотной генерации, зарегистрированной недавно в реакциях фотопереноса электрона с порфи-рина на хинон (АЛ.Бучаченко, ВЛ.Бердинский). [c.485]
Методом лазерной масс-спектрометрии исследован изотопный состав легких элементов в речной раковине Мидии . Обнаружено существенное изменение изотопного состава элементов С, О, S, К, С1, Са в наружном и внутреннем слоях раковины. Рассмотрены основные ядерные характеристики исследованных изотопов — спин и магнитный момент ядра, энергия связи нейтрона в ядре, вид ядер. Установлена корреляция между энергией связи нейтронов в ядрах изотопов и аномальным фракционированием изотопов легких элементов в биологическом объекте. Качественно, наблюдаемые в эксперименте, изотопные аномалии объяснены с помощью ядерио-спинового изотопного эффекта. Ил. 4. Табл. 1. Библ, 19 назв. [c.90]
Рассмотрены основные ядерные характеристики исследованных изотопов — спин и магнитный момент ядра, энергия связи нейтрона в ядре, вид ядер. Установлена корреляция между энергией связи нейтронов в ядрах изотопов и аномальным фракционированием изотопов легких элементов в биологическом объекте. Качественно, наблюдаемые в эксперименте, изотопные аномалии объяснены с помощью ядерио-спинового изотопного эффекта. Ил. 4. Табл. 1. Библ, 19 назв. [c.90]
© Laurent Thion/ILL Представьте себе танцовщицу, вращающуюся на кончиках пальцев ног вокруг своей оси, при этом, сама танцовщица находится на вращающейся карусели. При некотором невезении для этой танцовщицы в определенный момент времени ее собственный момент вращения может сложиться с моментом вращения карусели, и на ее тело будет воздействовать нагрузка, которая может привести к травме. Ученые из Венского технологического университета (TU Wien) обнаружили, что подобное явление может возникать и в квантово-механических системах, а обнаружено это было в ходе эксперимента, в котором вращающийся вокруг своей оси нейтрон пересекал вращающееся магнитное поле. Напомним, что под понятием спина элементарной частицы подразумевается угловой момент ее орбитального вращения.
Еще в 1988 году ученые предсказали, как должен себя вести нейтрон, попав внутрь вращающейся среды (магнитного поля в частности). В этом случае должно произойти объединение спина нейтрона и момента вращения магнитного поля, но до последнего времени никому не удавалось продемонстрировать это экспериментально. «Нам же для этого потребовалось несколько лет работы и несколько не очень удачных попыток» — пишут исследователи. В экспериментах нейтрон, подобно вращающемуся танцору на вращающейся карусели, пересекает область, в которой при помощи специальной катушки создается вращающееся магнитное поле. В недрах исследовательской установки нейтронный луч расщепляется на два независимых луча. Один из этих лучей проходит через область вращающегося магнитного поля, а второй не подвергается никаким внешним воздействиям. После этого оба луча вновь объединяются в один луч. Если рассматривать какой-нибудь отдельный нейтрон, то он, согласно причудам квантовой механики, находится одновременно в двух расщепленных лучах, и в первом луче инерциальные эффекты немного изменяют длину волны волновой составляющей этой квантовой частицы. В результате этого после сложения лучей волны или усиливают, или гасят друг друга, создавая картину наподобие интерференционной. Самой сложной задачей, с которой довелось столкнуться исследователям, стала конструкция катушки, способной вырабатывать вращающееся магнитное поле.
Статья опубликована в журнале npj Quantum Information |
СПИН-ОРБИТАЛЬНОЕ ВЗАИМОДЕЙСТВИЕ • Большая российская энциклопедия
В книжной версии
Том 31. Москва, 2016, стр. 75-76
Скопировать библиографическую ссылку:
Авторы: В. П. Павлов
СПИН-ОРБИТА́ЛЬНОЕ ВЗАИМОДЕ́ЙСТВИЕ, взаимодействие заряженных частиц, обладающих спином (и, следовательно, спиновым магнитным моментом) и орбитальным моментом. С.-о. в. – релятивистский эффект; напр., для электрона в атоме водорода энергия $Δℰ$ С.2\hbar c)(\boldsymbol l \boldsymbol s),$$ где $e$, $r$, $m$ – электрич. заряд, радиус-вектор и масса электрона, $\boldsymbol l$ и $\boldsymbol s$ – векторы его орбитального момента и спина, $\hbar$ – постоянная Планка. Поскольку проекция спина электрона на направление $\boldsymbol l$ может принимать только два значения ($±1/2$, в единицах $\hbar$), С.-о. в. приводит к расщеплению уровней энергии в атоме водорода (и водородоподобных атомах) на 2 близких подуровня – к дублетной структуре уровней (см. Тонкая структура). У многоэлектронных атомов картина тонкого расщепления уровней энергии оказывается более сложной. Атомы щелочных металлов, у которых полный спин электронов равен $1/2$, также обладают дублетной структурой уровней энергии.
С.-о. в. существует и у нейтральных частиц, напр. у нейтронов, имеющих и орбитальный, и спиновый механич. моменты. Весьма существенно С.-о. в. в атомных ядрах; его вклад в полную энергию взаимодействия достигает 10%.
Эффект спин-селективной адсорбции водяного параВигасин А.А., Волков А.А., Тихонов В.И., Щелушкин Р.В. Лаборатория спектроскопии межмолекулярных взаимодействий,
Тел.: +7 (095) 132-8165 В работе показано, что адсорбция водяного пара при нормальных условиях позволяет дискриминировать молекулы воды по их спиновому состоянию. Образцы, обогащенные орто- или пара-спин-изомерами воды, могут сохраняться длительное время в конденсированной фазе, не претерпевая спонтанной спин-конверсии. Показано, что нарушение равновесия по спин-модификациям воды в атмосфере может привести к заметному изменению ее радиационных характеристик. Эффект спин-селективной адсорбции водяного пара на поверхности окиси алюминия был обнаружен около 10 лет назад (см., например, [1]). В [2] показано, что данный эффект может быть использован для разделения спин-изомеров воды методом фронтальной хроматографии. Параллельная ориентация спинов водорода в молекуле воды приводит ее в состояние орто-модификации, а антипараллельная – в состояние пара-модификации. Отношение статистических весов для орто- и пара-состояний равняется 3, поэтому в равновесном водяном паре при нормальных условиях содержание орто-изомеров в 3 раза превышает содержание пара-изомеров. Поскольку переходы между орто- и пара-состояниями молекулы запрещены, водяной пар является, по существу, смесью независимых орто- и пара-фракций. В настоящей работе описывается лабораторный эксперимент, в котором методом спин-селективной адсорбции достигается по крайней мере троекратное изменение равновесного 3 : 1 орто/пара-отношения в водяном паре. Предлагается качественное объяснение наблюдаемого явления и показано, что нарушение орто-пара-отношения в условиях реальной атмосферы способно привести к заметным вариациям ее радиационных характеристик. Идея эксперимента состоит в попытке наблюдать нарушение орто-пара-равновесия в воде в результате ее взаимодействия с адсорбентом путем непрерывного слежения за интенсивностью спектральных орто- и пара-линий вращательного спектра молекулы воды. В качестве зонда была выбрана удобная для регистрации пара близкорасположенных интенсивных орто- и пара-линий, относящихся к вращательному участку спектра (рис. 1). Смесь водяного пара с азотом в качестве газа-носителя медленно пропускали сквозь адсорбционную колонку, заполненную пористым углем. Выходящий из колонки газ направлялся в кювету, сопряженную с субмиллиметровым ЛОВ-спектрометром. В кювете рабочую смесь зондировали на частотах 30-40 см-1 пучком перестраиваемого по частоте монохроматического излучения. В кусочно-непрерывном режиме со скоростью 10 точек/с, разрешением 0,0003 см-1 и периодичностью 1 мин записывался коэффициент пропускания газового слоя и наблюдалась картина орто-пара-дублета, представленная на рис. 2. Найдено, что в процессе прохождения водяного пара сквозь адсорбент происходит закономерное и хорошо воспроизводимое перераспределение интенсивностей линий. Парциальное давление водяного пара в нашем эксперименте не превышало 1 Top, что позволяло пренебречь допплеровским уширением и учитывать только столкновительное уширение. Полагалось, что наблюдаемые линии имеют лоренцевскую форму с интегральными интенсивностями и полуширинами соответственно Sort и Spar и gort и g par. Сумма двух лоренцевских контуров в реальном масштабе времени вписывалась в измеряемые линии, что давало количественную оценку изменения интегральных интенсивностей орто- и пара-линий и, соответственно, искомого орто/пара-отношения в водяном паре.
Результирующий вид отношения в зависимости от времени показан на рис. 3. Как видно, орто-молекулы воды обладают большей подвижностью в угольном фильтре. По этой причине в процессе диффузии через адсорбент начальные порции водяного пара обогащались орто-молекулами, а последующие – пара-молекулами. Орто- и пара-обогащенные порции водяного пара в соответствующие моменты времени отбирались из потока и вымораживались с помощью азотной ловушки. Накопленные таким способом пробы спин-модифицированной воды объемом до 50 мл хранились в бытовом холодильнике. Через определенное время их размораживали и подвергали повторному спектральному анализу на орто-пара-содержание. Побывавшая в твердой и жидкой фазах обогащенная по орто-или пара-модификациям вода вновь демонстрировала отличное от равновесного орто/пара-отношение. Время жизни модификаций оценено в десятки минут для жидкой воды и месяцы для льда. Нами также найдено, что помимо угля в качестве спин-модификаторов воды могут выступать многие другие вещества с развитой поверхностью типа цеолитов, силикагеля и т.п. Качественная модель процесса спин-селективной адсорбции может быть представлена следующим образом. Пусть общее число молекул водяного пара равняется N0, из которых N0ort находятся в орто- и N0par в пара-состояниях, так что N0ort+N0par=N0 Если предположить, что скорости адсорбции и десорбции спиновых фракций различны и между ними не происходит взаимной конверсии ни в газовой фазе, ни на поверхности, то процесс диффузии можно описать с помощью следующей системы уравнений: Здесь индексы а и d относятся соответственно к процессам адсорбции и десорбции. Решение этой системы уравнений может быть представлено в виде которое должно удовлетворять начальным условиям термодинамического равновесия. Отсюда для отношения Nort/Npar будем иметь С помощью этого решения можно описать экспериментальные данные (рис. 3), находя константы скорости адсорбции и десорбции с помощью процедуры метода наименьших квадратов. Считаем, что в начальный момент времени отношение N0ort/N0par = 3. Подгонка теории под эксперимент дает в относительных единицах: korta=0,9; kortd=0,08; kpara = 3,5; kpard = 0,5. Видно, что кинетические константы для пара молекул в 3-6 раз превышают константы для орто-молекул. В качестве возможного объяснения этому отличию можно предложить следующее. Для разреженного газа десорбция молекулы с поверхности может рассматриваться как мономолекулярный процесс [З]. Это означает, что молекула десорбируется, когда энергия, превышающая энергию отрыва с поверхности, сосредоточивается на разрываемо связи. Соответствующая константа скорости может представлена в виде: k=(v*W)/Q, здесь v- скорость активации, W – число состояний, имеющих энергию выше порога диссоциации, Q – квантовая статсумма. Основным источником избыточной внутренней энергии является энергия межмолекулярных колебаний, не зависящая от спинового состояния адсорбированной молекулы, поэтому и число состояний W можно полагать не зависящим от спиновой модификации. Напротив, статсумма может включать в себя вращательную составляющую при условии, что адсорбированная молекула совершает заторможенное или свободное вращение в составе комплекса молекула-поверхность. Можно ожидать поэтому, что отношение констант десорбции будет различаться в 3 раза: kortd/kpard=1/3 Для того чтобы охарактеризовать различие в константах адсорбции, введем в рассмотрение константу равновесия Keq, которая, очевидно, равняется Keq =ka/kd=(Qh3O*Qsurf)/Qads . Здесь Qh3O, Qsurf и Qads – статсуммы молекулы воды, поверхности и комплекса молекула-поверхность соответственно. Полагая, что , можно заключтиь, что отношение korta/kpara должно составлять 1/3. Если принять подобные отношения для констант скорости адсорбции и десорбции, не составляет труда аппроксимировать экспериментальную зависимость, представленную на рис. 3 в области орто/пара-отношения, превышающего равновесное
Оказывается невозможным, однако, описать последующее превышение содержания пара фракции над орто-фракцией. Для того чтобы сделать это описание полным, следует предположить, что в действительности отношение констант адсорбции korta/kpara составляет не 1/3 = 0,333(3), а равняется приблизительно 0,5-0,7. Как показано на рис. 3, при таком предположении удается весьма точно передать качественный ход наблюдаемой кинетики орто/пара-отношения. На основе эксперимента и предложенной модели можно предположить, что неравновесное разделение воды на орто- и пара-спин-изомеры естественным образом происходит в различных природных процессах – в живых организмах и окружающей среде. В частности, не исключено, что долговременные флуктуационные нарушения орто/пара-отношения 3 : 1 существуют в атмосфере. Водяной пар в атмосфере постоянно находится в нестационарных условиях, испытывая конденсацию и испарение в объеме воздушной среды на частицах аэрозолей в примесей, в облаках и на земной поверхности. Можно ожидать поэтому, что при определенных условиях в процессе кинетических трансформаций равновесное отношение спиновых модификаций в водяном паре будет нарушено. Представляет интерес оценить, насколько это нарушение может сказаться на функции пропускания атмосферы. Если вариации пропускания атмосферы при нарушенном спиновом составе окажутся значительными, это будет означать, что моделирование радиационных характеристик атмосферы невозможно без детального знания кинетической предыстории водяного пара в атмосфере. Для оценки эффекта мы рассчитали модельный спектр пропускания слоя водяного пара при атмосферных условиях на основе данных о параметрах линий водяного пара, содержащихся в базе данных HITRAN [4]. Расчеты производили для спектральной области вблизи 10 мкм, в которой расположен максимум планковской кривой излучения нагретой поверхности Земли. Помимо “равновесного” коэффициента поглощения aeq, отвечающего прохождению излучения через слой водяного пара с нормальным орто/пара-отношением 3:1, был рассчитан “неравновесный” коэффициент поглощения aneq, отвечающий нарушенному орто/пара-отношению. Оказалось, что поглощение на выделенных длинах волн и интегральное поглощение по участку спектра заметно чувствительны к нарушению орто/пара-равновесия. Нетрудно показать, что в зависимости от степени нарушения равновесного спинового состава, нормированный на равновесное значение коэффициент поглощения водяного пара заключен в фиксированных пределах, а именно, ограничен областью где через х обозначено отношение Nort/Npar (см. рис. 4). Средняя линия, показанная на рис. 4 штриховой линией, характеризует неравновесный коэффициент поглощения, усредненный по участку, содержащему большое количество случайно расположенных орто- и пара-линий поглощения. Таким образом, в настоящей работе показана возможность нарушения равновесного орто/пара-отношения в воде в результате ее контакта с адсорбентом и способность метастабильных орто- и пара-модификаций существовать в виде самостоятельных субстанций на протяжение длительного времени. Высказано предположение о возможном нарушении орто/пара-отношения в естественных процессах. Показано, что эффект нарушения спинового равновесия при конденсации паров воды может иметь важное значение для распространения излучения и радиационного баланса в атмосфере. Работа выполнена при частичной финансовой поддержке гранта Российского фонда фундаментальных исследований 02-05-64529 СПИСОК ЛИТЕРАТУРЫ
|
SPIN MUSIC SERVICE
[10-13/11/2020] 26-я Международная промышленная выставка «Металл-Экспо»
Место: Россия, Москва ВДНХ.
Международная промышленная выставка «Металл-Экспо’2020», на которой представлено все многообразие продукции черной и цветной металлургии, современного оборудования и технологий. 550 компаний более чем из 30 стран мира демонстрируют свои экспозиции в павильонах ВДНХ Подробнее →
[31/10/2020] Halloween
Место: Россия, Москва Березы Парк
31 Октября вечером в Березы Парк, прошло грандиозное событие, которое стало изюминкой в клубной жизни Москвы в этот Уикэнд. Подробнее →
[20/09/2020] Московский Марафон 2020
Место: Россия, Москва Лужники
20 сентября, в Москве состоялся восьмой Московский марафон, который стал крупнейшим беговым событием в России. Подробнее →
[30/08/2020] Фестиваль DELIGHT
Место: Россия, Москва Березы Парк
30 Августа на территории живописнейшего места в пределах города, прошло мероприятие DELIGHT. Организаторами которого выступили Orbita Project , T.L.N. и S.T.C.
Подробнее →
[20/08/2020] Закрытие сезона AtomSkills—2020
Место: Россия, Нововоронеж
В 2020 году Росатом провёл пятый юбилейный Отраслевой чемпионат профессионального мастерства AtomSkills—2020
в открытом формате по 24 профессиональным компетенциям. Подробнее →
[25/07/2020] Z. BOAT NIGHT – “Пространство” & Space Music
Место: Россия, Москва Теплоход РИО-1
25 июля, прошло мероприятие Z.BOAT NIGHT, от легендарного радио шоу “Пространство” и лейбла Space Music. Мероприятие прошло на теплоходе, на нижней̆ палубе. Теплоход отправился от Кутузовского причала и проплыл по ночной Москве. Подробнее →
[08/03/2020] INFINITY
Место: Россия, Москва ГЛАВCLUB
8 Марта в столичном клубе ГлавClub, прошла грандиозная вечеринка, посвященная электронной музыке. Гостями которой стали артисты мирового масштаба, такие как JUNO REACTOR и GREG HILIGHT. Конечно, поддержку иностранным гостям оказали лучшие музыканты и диджеи из России.
⠀
Подробнее →
[08/03/2020] Концерт THERR MAITZ
Место: Россия, Москва ГлавКлуб
Сольный концерт популярной группы THERR MAITZ, возродил традицию группы выступать весной, их концерт безусловно задал настроение не весь сезон. Подробнее →
[01/03/2020] Свадьба
Место: Россия, Москва Гостиный Двор
В самом начале весны, в Гостином дворе прошла красочная, и очень красивая свадьба. Размах декораций и техническое обеспечение поражало своим масштабом. Подробнее →
[24 – 27 /02/2020] выставка CPM – COLLECTION PREMIÈRE MOSCOW
Место: ЦВК «ЭКСПОЦЕНТР», Москва. Россия
CPM – это самая крупная специализированная выставка моды в Восточной Европе, в которой ежегодно принимают участие более чем 1 300 международных брендов. Подробнее →
[17/02/2020] премия Wedding Awards 2019
Место: Россия, Москва Lotte Hotel Moscow
Долгожданная в свадебном мире премия Wedding Awards 2019, прошла уже в 7-ой раз в Lotte Hotel Moscow. Церемония Wedding Awards 2019 посвящённая профессионалам свадебного мира. В этом году появились новые номинации, а все работы участников – источник вдохновения на ближайший год. Подробнее →
[25/01/2020] День студента в Парке Горького
Место: Россия, Москва. Парк Горького
В главный праздник всех студентов и Татьян на катке «Восход» в Парке Горького состоялась большая праздничная программа с танцами, интерактивами и необычными спортивными развлечениями. На сцене катка выступили группа «Nletto», а также репер ST. Подробнее →
[14-17/11/2019] Гран-При по фигурному катанию на коньках 2019
Место: Россия, Москва. Мегаспорт
Жители Москвы посетители выступления спортсменов-фигуристов, которые прошли с 14 по 17 ноября в «Мегаспорте». Российские и зарубежные спортсмены выступили в Москве в рамках российского этапа Гран-при по фигурному катанию. Подробнее →
[13/10/2019] Фестиваль «Белая трость»
Место: Место: Россия, Москва. Государственный кремлевский дворец
В этом году исполняется лет международному фестивалю «Белая трость». Ежегодно на фестиваль приезжают как юные талантливые дети нашей страны, так и дети из стран ближнего и дальнего зарубежья. Подробнее →
[3-6/10/2019] Фестиваль «ИгроМир – 2019»
Место: Россия, Москва. Крокус Экспо
С 3 по 6 октября в московском Крокус Экспо в очередной раз прошёл «ИгроМир» – главный геймерский ивент в России. На выставке было, пожалуй, слишком много интересного: демо-стенды грядущие новинки, эксклюзивные показы геймплея , конкурсы, бесплатный лут, гости, косплееры… Подробнее →
[22-28/09/2019] INCOSAI 2019
Место: Россия, ЦВЗ Манеж
В Москве, на территории манежа прошёл XXIII конгресс Международной организации высших органов финансового контроля INCOSAI 2019.
⠀
INCOSAI – международная организация высших органов аудита, созданная в 1953 году для содействия развитию сотрудничества высших органов аудита и совершенствованию государственного аудита во всём мире.
Подробнее →
[22/09/2019] Абсолют Московский Марафон
Место: Россия, Лужники
22 сентября, в Москве состоялся седьмой Московский марафон, в котором участвовали более 30 тысяч человек из десятков стран мира.
Часть участников пробежала классическую марафонскую дистанцию протяженностью в 42 километра 200 метров. Трасса Московского марафона 2019 проложена в один круг по набережным Москвы, по Садовому и Бульварному кольцам, под стенами Кремля, по Крымскому и по Большому Устьинскому мостам, Водоотводный канал — по Малому Каменному мосту.
Подробнее →
[12-13/09/2019] Московский Финансовый Форум
Место: Россия, Москва. Манеж
Московский финансовый форум — это уникальная площадка для профессиональной дискуссии, посвящённой вопросам финансово-экономической политики России. Подробнее →
[08.09.2019] День города в Царицыно
Место: Россия, Москва. Парк Царицыно
Под слоганом «Москва театральная» прошёл День города в Царицыно в 2019 году. В программе – экскурсии, выставки и много других интересных мероприятий. Подробнее →
[7-8/09/2019] День города, на Ходынском бульваре
Место: Россия, Москва Ходынское поле
В День города в парке Ходынское поле прошёл концерт, на котором жителей столицы с праздником поздравили популярные музыканты и исполнители. В рамках грандиозной праздничной программы ко Дню города для москвичей и гостей столицы подготовлены выступления известных музыкантов, которые сменяли друг друга на сцене до позднего вечера. Зрители в течение первых осенних выходных в парке на «Ходынском поле» смогли наслаждаться любимыми песнями и хитами. Подробнее →
[08/09/2019] День города, на ВДНХ
Место: Россия, Москва ВДНХ. Аллея Космонавтов
В честь 872-летия Москвы в 2019 году на День города на ВДНХ решено устроить яркие праздничные мероприятия. Организаторы провели их 7 и 8 сентября Подробнее →
[04-07/09/2019] CPM – Collection Première Moscow 2019
Место: Россия, Москва Экспо Центр
Collection Première Moscow 2019, международная выставка мужской, женской, детской одежды, белья, свадебной моды и аксессуаров. Ведущее по количеству международных брендов (свыше 700 из 35 стран мира) деловое событие Восточной Европы, Collection Première Moscow становится местом встречи байеров, руководителей отделов закупок в торговых сетях, владельцев магазинов и ателье, категорийных менеджеров, дизайнеров и технологов, стилистов, фэшн-маркетологов и журналистов. Подробнее →
[31/08-01/09/2019] Международный фестиваль идей и технологий Rukami.
Место: Россия, Москва ВДНХ
Международный фестиваль идей и технологий Rukami — один из ключевых проектов кружкового движения НТИ — впервые прошёл в Москве на ВДНХ с 31 августа по 1 сентября. Гости фестиваля смогли окунуться в мир будущего: вместе с мейкерами они смогли создать невероятные устройства, посетить разнообразные мастер-классы, оценить технологические перформансы и арт-инсталляции, а самое главное — они открыли для себя мир технического творчества. Подробнее →
[09-11/08/2019] Всероссийский фестиваль «Сыр Пир Мир»
Место: Россия, Истра, Дубровское
Гастрособытие собрало более 300 фермеров и сыроваров со всей страны. Всего на фестиваль приехали участники из 44 регионов России, которые представили свыше 500 сортов сыра отечественного производства и другую натуральную продукцию. Для гостей приготовили 100 тонн сыра, фирменные колбасы, хлеб, молочную продукцию, мед, квас и множество других продуктов. Все это можно продегустировать и купить. Подробнее →
[03/08/2019] Пикник «Афиши»
Место: Россия, Москва Парк Коломенское
Пикник «Афиши» — крупнейший в Москве музыкальный фестиваль на открытом воздухе, ежегодно собирающий более 60 000 человек. В этом году Хедлайнером фестиваля стала группа The Cure. ⠀
Также в Коломенском появилась новая сцена – зона фестиваля Gazgolder live. Отвечала за нее творческое объединение «Газгольдер». Здесь выступили Баста, проект Скриптонита «Gruppa Skryptonite», T-Fest, Matrang, Смоки Мо, «Вадяра Блюз» и Lucaveros.
Подробнее →
[27/07/2019] Группа «Пелагея» в Зеленом театре ВДНХ
Место: Россия, Москва Зеленый Театр
27 июля в Зеленом театре ВДНХ прошёл долгожданный летний концерт группы Пелагея. Принцесса русского фолка вместе со своей группой приготовила настоящий десерт для музыкальных гурманов. Подробнее →
[25/07/2019] Концертное шоу «Optimystica Orchestra/8 женщин»
Место: Россия, Москва Зеленый театр ВДНХ
В Зеленом театре ВДНХ состоялось уникальное концертное шоу «Optimystica Orchestra/8 женщин». Под открытым небом выступили сразу восемь знаковых артисток независимой российской сцены. Подробнее →
[20/07/2019] Фестиваль «Martini Time»
Место: Россия, Москва “Флакон Север”
20 Июля 2019 года на территории московского пространства «Флакон Север» (бывший «Хлебозавод») прошёл фестиваль гастрономических развлечений Martini Time. Это мероприятие стало редкой возможностью оценить работы лучших шеф-поваров со всего мира. А также чудесная возможность оценить рестораны, в которых обычно выстраиваются очереди, в одном месте и в одно время. На фестивале они совместно с профессионалами российской гастрономической индустрии представили свои фирменные блюда и поделились кулинарными приемами. Подробнее →
[19-22/07/2019] Чемпионат мира по художественной гимнастике
Место: Россия, Москва Гимнастический центр Ирины Винер-Усмановой.
В Москве прошёл чемпионат мира по одному из самых грациозных и зрелищных видов спорта — художественной гимнастике. Это первый в истории мировой турнир среди юниорок, в котором смогли участвовать спортсменки только до 15 лет. Чемпионат проходил у стадиона «Лужники», в новом гимнастическом центре Ирины Винер-Усмановой. Подробнее →
[13/07/2019] Ночной забег
Место: Россия, Москва “Лужники”
13 июля 2019 года в Лужниках прошёл массовый забег по ночной Москве. Всех желающих принять участие в марафоне ждал десятикилометровый незабываемый забег по художественно подсвеченной набережной ночной столицы Старт и финиш находились в одном месте — в «Лужниках». Таким образом, спортсмены смогли не только получить удовольствие от бега в летнюю ночь, но и полюбоваться целым рядом достопримечательностей мегаполиса, которые, как известно, по-настоящему преображаются в темное время суток Подробнее →
[11/07/2019] Фестиваль Клуба путешествий Михаила Кожухова
Место: Россия, Москва “Флакон”
11 июля в городском пространстве “Флакон”, состоялся первый фестиваль Клуба путешествий Михаила Кожухова! На празднике выступили Uma2rman, Андрей Макаревич, Евгений Хавтан (группа “Браво”), Tequilajazzz и Вера Полозкова и Ундервуд. Специальным гостем вечера стала – Чулпан Хаматова. Подробнее →
[05-07/07/29] Фестиваль «Боль»
Место: Россия, Москва Культурный центр ЗИЛ
Фестиваль состоялся в культурном центре ЗИЛ – первом московском дворце культуры и памятнике конструктивизма, органично принявшем “Боль” в своих стенах в 2019 году. На мероприятии выступили более 70 артистов. 2019 год стал пятым по счету и самым продолжительным, ведь именно в этот раз он занял три дня Подробнее →
[05/07/2019] Летний корпоратив Kaspersky
Место: Россия, Завидово
Лето, живая музыка, атмосфера счастья, когда ты забываешь о насущном…и это все -“Летний корпоратив Kaspersky 2019”, тот самый ивент, в котором посчастливилось участвовать нашей компании. Хэдлайнером концерта стала группа БИ-2. Подробнее →
[4-7/07/2019] Moscow Urban Forum
Место: Россия, Парк Зарядье
Московский урбанистический форум — крупнейший международный конгресс, посвященный вызовам развития глобальных мегаполисов. Он собирает вместе представителей администраций городов России и мира, объединяет архитекторов, градостроителей, застройщиков, инвесторов, финансистов, горожан, а также технологические стартапы и медиа. Подробнее →
[22/06/2019] Концерт Наргиз в Зеленом Театре
Место: Россия, Москва Зеленый Театр
На территории ВДНХ в Зеленом Театре прошёл большой сольный концерт Наргиз, на котором певица исполнила свои новые песни и проверенные временем хиты.
Наша компания предоставила современное звуковое и световое оборудование для этого мероприятия.
Подробнее →
[20/06/2019] Выпускные балы
Место: Россия, Москва Президент Отель, Гостиницы: Метрополь и Рэдиссон Славянская
В конце июня по всей России прошли Выпускные балы.
Выпускной бал – день расставания с любимыми учителями и одноклассниками. Он должен пройти ярко и феерично, потому что второго шанса попрощаться с детскими воспоминаниями не будет. Этот день можно сравнить с днем рождения, свадьбой или рождением ребенка, он – единственный и неповторимый.
Подробнее →
[14/06/2019] День Открытие сезона в Зеленом Театре
Место: Россия, Москва Зеленый Театр
14 Июня состоялся концерт с участием известных российских музыкантов, который дал старт сезону в Зеленом театре ВДНХ. Мероприятие получилось одним из самых ярких событий праздничной программы, посвященной 80-летию Главной выставки страны. На сцене выступили любимцы рок и джаз-фестивалей, а также новые музыкальные герои.
Наша компания предоставила современное звуковое, и световое оборудование для этого мероприятия.
Подробнее →
[12/06/2019] День России
Место: Россия, Москва Парк Сокольники
Сотни людей пришли на Фестивальную площадь парка “Сокольники” в Москве, чтобы отпраздновать День России со своими кумирами – топовыми блогерами страны. Героями фестиваля “Блогеры России” стали Карина Лазарьянц, Давид Манукян, Субхан Мамедов, Юрий Кузнецов, а также певица Рита Дакота, чей охват аудитории суммарно – более 16 млн человек. Подробнее →
[09/06/2019] Благотворительный забег при участии Фонда «Жизнь в движении»
Место: Россия, Москва Парк Победы
В рамках XIX Летних игр World Class — ведущей российской фитнес-сети, состоялся открытый забег в Парке Победы на Поклонной горе. В этот день на площадке прошли соревнования по пауэрлифтингу, боксерскому многоборью и боксу. Завершало праздничную церемонию открытия Игр выступление группы Uma2rman. Наша компания предоставила современное звуковое, сценическое, энерготехническое и видео оборудование для этого мероприятия. Подробнее →
[08-09/06/09] FACES&LACES 2019 ОПЕН-ЭЙР и Выставка Локальной уличной культуры
Место: Россия, Москва Торговый Центр Авиапарк
В течение двух дней на этой сцене, стилизованной под гаражную мастерскую, выступили прорывные молодые артисты современной российской панк, рок и рэп-сцены, о которых скоро будут говорить все. На выставке были представлены масштабные экспозиции, объединяющие в себе работы активных уличных художников и автомобильные проекты от топовых локальных кастом-клубов. Подробнее →
[01/06/2019] День Активного гражданина
Место: Россия, Москва Парк Горького
Мероприятие по случаю пятилетия проекта “Активный гражданин” прошли 1 и 2 июня на 13 столичных площадках. Наша компания предоставила современное звуковое и световое оборудование на мероприятии в Парке Горького. На сцене выступила Полина Гагарина, Елена Темникова и другие артисты. Там же зрителям показали мюзикл “Москва! Я люблю тебя!” с участием пользователей “Активного гражданина” Подробнее →
[09/05/2019] 9 Мая Праздничный Концерт ВДНХ
Место: Россия, Москва ВДНХ
9 Мая Праздничный Концерт ВДНХ.
Главная выставка страны в год своего 80-летия приготовила для москвичей и гостей столицы масштабную праздничную программу. На мероприятие гостей ждала большая программа с участием арт-проекта «Тенора XXI века», солистов Алексея Татаринцева, Аскара Абдразакова, симфонического оркестра Москвы «Русская филармония», хора Академии хорового искусства им. В.С. Попова и других. Режиссер праздничного концерта — Гаянэ Шиладжян, почетный деятель искусств города Москвы, лауреат премии Правительства Москвы.
Подробнее →
[30/04/2019] Торжественный запуск Фонтанов
Место: Россия, Москва ВДНХ
Компания SPIN MUSIC SERVICE является генеральным партнером АО «ВДНХ» и участвовала в техническом обеспечении мероприятия “Торжественный запуск фонтанов на территории ВДНХ”. В этом году событие получилось особенно торжественным. Был организован уникальный концерт. Виртуозы исполнили Праздничную увертюру ля мажор Дмитрия Шостаковича. Подробнее →
[20-21/04/019] Champions’Ball – 2019
Место: Россия, Москва ЦМТ
Открытый Международный конкурс среди пар Pro-Am — Champions’ Ball – 2019, организатором которого является Dance Promotion Group при поддержке Международной Ассоциации танцевальных клубов, школ и студий танца (МАСКТ). Champions’ Ball — особенный конкурс со своей уникальной концепцией, потрясающими декорациями, внушительными спецэффектами и живым музыкальным сопровождением, настоящий Бал Чемпионов. Подробнее →
[20/04/2019] Концерт группы LSP
Место: Россия, Москва ВТБ Арена
Компания SPIN MUSIC SERVICE выступила генеральным подрядчиком на концерте популярной группы LSP в ВТБ АРЕНА. Это был первый стадионный концерт LSP в Москве. Тонны Звука и Света обрушились на фанатов группы в этот вечер. Умопомрачительное шоу вместе с новой программой группы не оставили равнодушными никого в этот день. Наша компания предоставила современное звуковое, световое и сценическое оборудование для этого мероприятия. Подробнее →
[30/11/2018] Открытие Катка ВДНХ
Место: Россия, Москва. ВДНХ
30 ноября, на ВДНХ открылся Город зимы — масштабное пространство для активного отдыха. Город работал весь зимний сезон, до 10 марта, и включал десяток различных площадок: два катка, трассу для детских снегоходов, места для командных игр в керлинг и снежки, ярмарки и красочные световые инсталляции. Общая площадь всех объектов Города зимы — более 34 тыс. кв. м. Только совокупный размер обоих катков превышает 13 тыс. кв. м. Подробнее →
[10-13/10/2018] Выставка «Золотая осень»
Место: Россия, Москва ВДНХ
С 10 по 13 октября 2018 года на ВДНХ прошла Российская агропромышленная выставка «Золотая осень», организуемая Министерством сельского хозяйства Российской Федерации.
«Золотая осень» – главное событие российского агропромышленного комплекса. Мероприятие объединяет в себе масштабную экспозицию достижений отечественных сельхозпроизводителей и актуальную деловую программу, в рамках которой обсуждаются перспективы развития отрасли. Подробнее →
[4/10/2018] Международный киберспортивный турнир
Место: Россия, Москва ВТБ Ледовый дворец
Крупнейший киберспортивный турнир EPICENTER по Counter-Strike: Global Offensive возвращается в Москву. Зрителей ждало впечатляющее противостояние лучших команд мира, незабываемое красочное шоу, а также автограф-сессии профессиональных игроков и комментаторов. Подробнее →
[4-7/10/2018] Фестиваль «ИгроМир – 2018»
Место: Россия, МВЦ «Крокус»
Фестиваль «ИгроМир», – это один из самых долгожданных и масштабных выставочных проектов страны в области интерактивных развлечений. Он призван познакомить отечественных фанатов компьютерных игр с последними новинками в этой области.
В рамках фестиваля гостей ждало незабываемое путешествие по виртуальным мирам и масштабная выставка, которая стала для посетителей уникальной возможностью раньше всех оценить новые достижения разработчиков интерактивных игр.
Подробнее →
[23/09/2018] Московский марафон
Место: Россия, Лужники
23 сентября, в Москве состоялся шестой Московский марафон, в котором участвовали 30 тысяч человек из десятков стран мира.
Часть участников пробежала классическую марафонскую дистанцию протяженностью в 42 километра 195 метров. Ну а тем, кто хотел посоревноваться на более короткой дистанции, отрыли забег длиной в 10 километров. Также в рамках Московского марафона прошла корпоративная эстафета и заезд хендбайкеров. В заезде хендбайкеров смогли поучаствовать на велосипедах с ручным приводом люди с ограниченными возможностями.
Подробнее →
[08/09/2018] День Города
Место: Россия, Москва Музей-заповедник «Измайлово»
В рамках празднования Дня Города, в музее-заповеднике «Измайлово», состоялся яркий двухчасовой праздничный концерт «Я люблю тебя, Москва». Подробнее →
[08/09/2018] Праздник «День города в Доме музыки»
Место: Россия, Москва «Московский международный дом музыки»
8 сентября Московский международный Доме музыки отметил главный столичный праздник – День Города. Все желающие смогли принять участие в конкурсах, мастер-классах, интерактивных шоу-программах, а завершением вечера стал праздничный концерт с участием известных артистов – фортепианного трио Bel Suono, Валерия Сюткина и его группы. Гости услышали самые известные и всеми любимые песни музыканта, а также новые композиции. Подробнее →
[04/09/2018] CPM Moscow 2018
Место: Россия, Москва ЦВК «Экспоцентр»
04 сентября 2018 года, свои двери открыл 31-й сезон крупнейшей международной выставки моды Восточной Европы CPM – Collection Premiere Moscow. Байерская сессия, деловой форум и яркие презентации коллекций весна-лето 2019 прошли в ЦВК «Экспоцентр» на протяжении четырех дней. Подробнее →
[26/08/2018] Полумарафон «Лужники»
Место: Россия, Москва «Лужники»
26 августа в Москве состоялся полумарафон «Лужники» дистанцией 21,1 км. Участников ждали живописная трасса по набережным города, беговой праздник с фудкортом, музыкой и развлечениями. Подробнее →
[24/08/2018] Ночь Одноактных балетов
Место: Россия, Москва «Зеленый Театр» ВДНХ Сцена на воде
24 августа в «Зеленом театре ВДНХ. Сцене на воде» состоялась Ночь одноактных балетов — совместный проект ВДНХ и театра «Балет Москва», впервые прошедший в 2016 году и ставший уже традиционным мероприятием в афише Зеленого театра. В этом году, в рамках третьей «Ночи», зрителям были представлены две постановки классической труппы театра: «Три поэмы» хореографа Кирилла Радева и премьерный спектакль «Транскрипция цвета» Хуанхо Аркеса. Вечер прошёл в формате двух отделений. Подробнее →
[17-18/08/2018] Международный Фестиваль Фейерверков
Место: Россия, Москва «Братеевский каскадный парк»
Ведущие пиротехники со всего мира собрались, чтобы удивить зрителей̆ и побороться за звание лучшего. Специально для мероприятия были созданы талисман фестиваля – Змей Горыныч – инсталляция на тему театра, совмещающая в себе интерактивную и развлекательную функции. Подробнее →
[04/08/2018] Пикник Афиши
Место: Россия, Москва парк «Коломенский»
В парке «Коломенский» прошел Пикник «Афиши». Один из крупнейших российских фестивалей уже в 15-й раз собирает жителей и гостей столицы, которые смогли насладиться живой музыкой и приятной атмосферой. Подробнее →
[27/07/2018] IV Международный фестиваль искусств «Вдохновение»
Место: Место: Россия, Москва ВДНХ
В Москве, на территории ВДНХ, прошёл четвертый фестиваль искусств «Вдохновение».
Особенность фестиваля «Вдохновение» состоит в том, что каждый год его программа посвящена одному жанру или одной важной теме в искусстве, а афиша представляет актуальные, необычные и масштабные произведения, открывает разные грани выбранного направления — от признанной классики до удивительных экспериментов.
Подробнее →
[13/07/2018] Финальный этап турнира Nike “Бунтари коробок”
Место: Россия, Москва Парк Горького
В дни проведения чемпионата мира по футболу FIFA в России, в Москве прошёл финальный этап турнира Nike “Бунтари коробок”, а вместе с ним — фантастическое выступление легендарной и популярной группы ЛСП. Яркий насыщенный турнир и не менее яркое выступление музыкантов. Подробнее →
[07/07/2018] Открытие выставки Музеев Катара «Жемчуг: сокровища морей и рек»
Место: Россия, Москва Государственный исторический музей
Всемирно известная коллекция жемчуга Музеев Катара прибыла в Москву в рамках перекрестного Года культуры Катара и России. В экспозицию вошло 100 экспонатов, в том числе 50 ранее не выставлявшихся изделий. Среди них — изысканные украшения Дома Cartier, кольцо с жемчугом, принадлежавшее Элизабет Тейлор, брошь по эскизу Сальвадора Дали и старинные драгоценности монарших домов Европы, в том числе великолепная тиара эрцгерцогини Марии Валерии Австрийской. Подробнее →
[24/06/2018] BMW Опера без границ
Место: Россия, Москва Театральная площадь
Уже 40 лет неотъемлемой частью работы BMW Group является культурная миссия компании. За это время было реализовано более 100 проектов по всему миру. Основное внимание BMW Group сосредоточено на современном искусстве, джазе и классической музыке, архитектуре и дизайне. Сила эмоций и сила искусства — две стихии, которые невозможно сдержать. Подробнее →
[10/06/2018] FIFA Fan Fest 2018
Место: Россия, Москва Воробьевы горы
Открытие Фестиваля болельщиков FIFA Fan Fest 2018 в Москве состоялся 10 июня на Воробьевых Горах! На сцене появился главный трофей Чемпионата мира, который презентовали Александр Кержаков и чемпион мира и Европы, игрок сборной Франции – Марсель Десайи. На открытии Фестиваля болельщиков FIFA Fan Fest 2018 в Москве выступили: ATL, ХЛЕБ, SWANKY TUNES, 25/17, ГРОТ, ST, ЗОМБ, T-KILLAH, ЖАК ЭНТОНИ, LUXOR, SABI MISS, IVAN VALEEV, HOMIE, PIZZA и многие другие. Подробнее →
[02/06/2018] Зеленый театр ВДНХ Сцена на воде
Место: Россия, ВДНХ, Зеленый театр
2 июня на уникальной площадке под открытым небом «Зеленый театр ВДНХ. Сцена на воде» состоялся концерт Государственного духового оркестра России. Его выступление также дало старт IV Фестивалю духовых оркестров. Сценический комплекс под открытым небом начал работу в прошлом году и стал одной из знаковых концертных площадок столицы с неповторимой атмосферой, впервые предоставив москвичам уникальную возможность посещать концерты в формате «музыка на воде». Вся конструкция напоминает удивительный арт-объект и становится местом притяжения для всех посетителей парка. В рамках фестиваля на ВДНХ Государственный духовой оркестр России представит специальную программу современной популярной музыки. Можно будет танцевать, отбивать такт или просто слушать, закрыв глаза, — все композиции разные по стилям и настроению. Заряд оптимизма и радости гарантирован каждому! Подробнее →
[31/05/2018] Startup Village 2018
Место: Россия, Москва «Сколково»
Startup Village – это шестая ежегодная международная стартап-конференция предпринимателей и инноваторов. В этом году Startup Village прошёл с 31 мая по 1 июня и объединил на территории Инновационного центра «Сколково» 20 000 человек из разных стран. Подробнее →
[26/05/2018] Проект “Активный гражданин!”
Место: Россия, Парк Горького
26 мая, проект “Активный гражданин” праздновал свой четвертый день рождения. “День рождения Активного гражданина” — это праздник на открытом воздухе для самых инициативных и активных жителей столицы — тех, кому не все равно, в каком городе они будут жить завтра. В этом году мероприятие прошло в ЦПКиО имени Горького, на сцене выступили современные российские исполнители и диджеи: DJ Fedor Fomin, Алексей Кортнев, Полина Гагарина, Егор Крид, Алексей Воробьев, группа “IOWA”, Вахтанг, Кравец, Сергей Мазаев. Для гостей также выступил детский театр “Домисолька”. Подробнее →
[19/05/2018] Synergy Art Forum
Место: Россия, Москва ЦВЗ Манеж
Synergy Art Forum — первый в стране грандиозный форум, посвящённый современному художественному рынку. В одном пространстве встретились ценители искусства, арт-критики, коллекционеры и предприниматели. Специалисты поделились с гостями опытом и дали практические советы. Эксперты рассказали о ключевых тенденциях области и тонкостях арт-инвестирования, привели примеры удачного арт-сотрудничества и объяснили, как монетизировать свою креативность и с нового ракурса взглянуть на бизнес и творчество. Подробнее →
[04-5/05/2018] Турнир EPICENTER XL
Место: Россия, ВТБ Ледовый дворец
Epic Esports Events провела финальную стадию турнира в период с 27 апреля по 6 мая в Москве. На EPICENTER XL команды разыграли призовой фонд в $ 1 000 000. Это самый крупный призовой фонд в истории киберспортивных соревнований в рамках одной дисциплины, организованных на территории России. Подробнее →
[01/05/2018] 1 Мая Демонстрация
Место: Россия, Москва Красная Площадь
1 мая 2018 года на Красной площади прошла более чем стотысячная демонстрация. Торжественные шествия прошли так же и в центре города. На самом главном, из этих шествий наша компания организовала звуковое сопровождение, торжественной части мероприятия. Подробнее →
[21-22/04/2018] Champions’ Ball 2018
Место: Россия, Москва Конгресс зал Центра Международной торговли
21, 22 апреля в Конгресс-зале Центра Международной торговли в 11-ый раз Москва встречала лучшие танцевальные дуэты Pro Am, среди которых в первых рядах пары, представляющие танцевальные клубы GallaDance. Подробнее →
[20/04/2018] Юбилей Вячеслава Фетисова 60 лет
Место: Россия, Москва ВТБ Ледовый дворец
20 апреля, свой юбилейный 60-ый день рождения, легендарный хоккеист, двукратный олимпийский чемпион Вячеслав Фетисов провел в Парке Легенд!
В ВТБ Ледовом дворце состоялся выставочный матч с участием известных хоккеистов. На льду в составе обеих команд появились такие великие мастера, как Алексей Касатонов, Сергей Макаров, Игорь Ларионов, Павел Буре, Александр Могильный, Валерий Каменский, Виталий Прохоров, а также звезды спорта, общественные и политические деятели. Встреча прошла на Малой арене. Команда Вячеслава Фетисова одержала победу.
Подробнее →
[13/04/2018] Шоу-открытие павильона «Космос»
Место: Россия, Москва ВДНХ
13, 14 и 15 апреля на территории ВДНХ прошёл грандиозный праздник в честь открытия павильона «Космос». В выходные посетители насладились аудиовизуальным театральным шоу и одними из первых увидели новую экспозицию центра «Космонавтика и авиация». Подробнее →
[23-25/03/2018] Московский культурный форум-2018
Место: Россия, Москва Центральный манеж
В Центральном выставочном зале «Манеж» с 23 по 25 марта прошел «Московский культурный форум-2018», на котором собрались деятели культуры и искусства, руководители профильных министерств и ведомств, представители бизнеса, а также все те, кто ценит искусство. Организатор форума – Департамент культуры города Москвы – подготовил для всех желающих насыщенную интерактивную программу. Подробнее →
[22-24/03/2018] Концерт “Зачем молчать, когда есть голос!”
Место: Россия, Спорткомплекс Олимпийский
C 22 по 24 марта 2018 года в СК «Олимпийский» прошли концерты звёзд российской эстрады для молодёжи, впервые принявшей участие в выборах Президента РФ. Егор Крид, Полина Гагарина, Джиган, Дима Билан, Нюша, группа Serebro, L’ONE, Бьянка, Клава Кока и ещё 20 популярных артистов зажгли на сцене спорткомплекса специально для всех пришедших гостей. Подробнее →
[11/03/2018] Гала-концерт «Весна МУЗ-ТВ на катке ВДНХ»
Место: Россия, Москва ВДНХ Каток
11 марта на столичном катке ВДНХ состоялся грандиозный концерт с участием самых ярких звезд телеканала «МУЗ-ТВ». Более 5 000 гостей катка шумно и весело проводили зиму и встретили наступившую весну в компании любимых артистов. Подробнее →
[17/02/2018] Масленица
Место: Россия, Москва ВДНХ
В 2018 году масленичная неделя продлилась с 12 по 18 февраля. ВДНХ традиционно стала одной из основных площадок Москвы, где развернулись народные гуляния. В этот раз центром праздника на Главной выставке страны стала площадь Промышленности. 9 февраля здесь начала работу широкая ярмарка, а 17 и 18 февраля прошли основные активности. В выходные гостей ВДНХ ждала насыщенная программа: творческие мастер-классы, театральные постановки, выступления музыкантов и конкурсы с аниматорами. Подробнее →
[15/05/2017] XXV, юбилейный, фестиваль «Российская студенческая весна»
Место: Россия, г. Тула
Компания «Spin Music Service» выполнила комплексное техническое обеспечение сценическим и световым оборудованием мероприятия – «XXV, юбилейный, фестиваль «Российская студенческая весна», которое прошло с 15 мая 2017 года в городе Тула на территории Тульского Кремля. Подробнее →
[13/04/2017] SAP Форум Москва 2017
Место: Москва, МВЦ «Крокус-Экспо», павильон 3, залы 16 и 20
13 апреля 2017 года в Москве в Международном Выставочном Центре «Крокус-Экспо» состоялось одно из важнейших событий в календаре SAP – ежегодный SAP Форум Москва 2017. Подробнее →
[15/12/2016-15/01/2017] Фестиваль «Путешествие в Рождество»
Место: Москва, площадь Революции
Фестиваль «Путешествие в Рождество» сегодня, 11 января 2017 года, и в последующие три дня с 12 по 14 января показал театральные постановки на льду, которые прошли на площадке «Волшебный ледовый театр» на площади Революции. Подробнее →
[15/01/2017] Гала-ужин «I Love Bayher»
Место: Москва, ТВК «Экспоцентр», 8 павильон, 1 зал
15 января 2017 года в Москве на территории Центрального выставочного комплекса «Экспоцентр» прошло корпоративное мероприятие с символичным названием Гала-ужин «I Love Bayher». Подробнее →
[31/12/2016-01/01/2017] Новогодняя ночь на Главном катке страны
Место: Москва, ВДНХ
В ночь с 31 декабря 2016 года на 1 января 2017 года каток ВДНХ стал одной из центральных праздничных площадок города. Свыше 10 000 человек встретили Новый год на льду Главного катка страны, совершив путешествие по разным уголкам нашей планеты – от Крайнего Севера до солнечного Апеннинского полуострова. Подробнее →
[30/12/2016-01/01/2017] Новогодняя ночь на Аллее Космонавтов
Место: Москва, Северо-Восточный Округ
На праздничных площадках в округах Москвы прошли концерты и театральные представления. С Новым годом 2017 москвичей и гостей города поздравили танцевальные и вокальные коллективы, а также сольные исполнители. А ещё гости праздника увидели спектакли уличных театров. Подробнее →
[28/12/2016-26/02/2017] II-й Новогодний фестиваль «Ледовая Москва. В кругу семьи»
Место: Москва, Парк Победы на Поклонной горе
Новогодние праздники на «Ледовой Москве» прошли шумно и весело! Даже суровые рождественские морозы не смогли испугать наших гостей. Их активно согревали веселые подвижные игры с аниматорами, праздничное шоу, новогоднее представление в кукольном театре и, главное, – катание с разнообразных ледяных горок! Подробнее →
[27-28/08/2016] Первая Всероссийская акция «Ночь кино» у Большого театра
Место: Москва, Teaтpaльнaя площадь, Большой Театр
С 27 на 28 августа 2016 года в Москве на Театральной площади у Большого театра стартовала первая Всероссийская акция «Ночь кино». Акция впервые проходит во всех 85 регионах России. Старт ей дал Министр культуры РФ Владимир Мединский. Событие приурочено ко Дню российского кино и призвано привить любовь к отечественным шедеврам киноискусства. Акция продолжилась концертом с кинохитами в исполнении Дениса Мацуева и Российского национального оркестра. Подробнее →
[19-20/08/2016] Дни Москвы в Тульской области
Место: Тула, Тульский Кремль
19-20 июля 2016 года в городе Тула на территории Тульского Кремля состоялись деловые и праздничные мероприятия, ставшие уже традиционными, «Дни Москвы в Тульской области». Подробнее →
[13-14/05/2016] Уникальный ночной концерт итальянской оперы «Сельская честь» Пьетро Масканьи в Московском метро
Место: Москва, Московский метрополитен, платформа станции метро «Кропоткинская»
Ставшая уже традиционной «Ночь музыки» в столичном метро преподнесла москвичам и гостям города необыкновенный сюрприз под землей. В ночь с 13 на 14 мая 2016 года на станции метро «Кропоткинская» худрук и главный дирижёр Академического большого хора РГГУ Борис Тараканов поставил концертную версию оперы итальянского композитора Пьетро Масканьи «Сельская честь». Подробнее →
[30/04/2016] Открытие летнего сезона фонтанов на ВДНХ
Место: Москва, ВДНХ
30 апреля 2016 года на главной выставке страны ВДНХ стартовал долгожданный летний сезон фонтанов. На площадке между красивейшими фонтанами «Дружба народов» и «Каменный цветок» состоялся светомузыкальный концерт симфонического оркестра Москвы «Русская филармония», который исполнил музыкальные шедевры из любимых фильмов на открытой сцене. Подробнее →
[27/01/2016] Корпоративное мероприятие
Место: Москва, парк «Сокольники»
21 января 2016 года в одном из павильонов парка «Сокольники» прошло ежегодное корпоративное мероприятие одной всемирно известной компании. Подробнее →
[16-19/06/2015] Международный военно-технический форум «АРМИЯ 2015»
Место: Московская область, г. Кубинка, полигон «Алабино», КВЦ ВП ПКиО ВС РФ «Патриот»
С 16 по 19 июня 2015 года состоялось выдающееся событие в жизни российского общества и Вооруженных сил Российской Федерации «Международный военно-технический форум «Армия-2015», который прошёл в городе Кубинка Московской области на территории конгрессно-выставочного центра Военно-патриотического ПКиО ВС РФ «Патриот», что на полигоне Алабино. Подробнее →
[13/09/2014] Фестиваль «Бабье Лето»
Место: Москва, ВДНХ, Зеленый театр
13 сентября 2014 года в Зеленом театре, что на ВДНХ, состоялся концерт, посвященный короткому, но очень приятному осеннему времени. Торжество бабьего лета провозгласили вокалистки, играющие в разных музыкальных стилях, но объединенные большой любовью к музыке. Подробнее →
[16/08-07/09/2014] Суперсерия “Концерты в Зеленом Театре”
Место: Москва, ВДНХ, Зеленый театр
Spin Music Service выступил техническим подрядчиком и выполнил комплексное техническое обеспечение мероприятия – “Суперсерия “Концерты в Зеленом Театре”, которое прошло с 16 августа по 7 сентября 2014 года. Подробнее →
[16/08/2014] Фестиваль «Московское варенье»
Место: Москва, Тверская улица, Лубянская площадь
С 8 по 17 августа 2014 года прошло самое сладкое событие лета в Москве – Фестиваль «Московское варенье» и вся столица России наполнилась вареньем экзотических и невиданных сортов и прочими видами «сахарного» веселья. Подробнее →
[02-08/05/2014] Праздник Весны и Труда
Место: Москва, ул. Тверская, дом 13
Целых шесть дней подряд с 2 до 8 мая 2014 года в Москве на улице Тверская, 13, что напротив здания Правительства г. Москвы, прошло грандиозное мероприятие “Праздник Весны и Труда”. Подробнее →
[01/05/2014] Первомайское шествие и демонстрация
Место: Москва, Красная площадь и Васильевский спуск
1 мая 2014 года с 10-00 утра на Красной площади состоялось Первомайское шествие и демонстрация. Мероприятие в честь Международного дня солидарности трудящихся объединило не только людей разных возрастов и взглядов, но и различные трудовые коллективы, профсоюзные организации, студентов, активистов общественных объединений. Подробнее →
[01/03/2014] Широкая Масленица
Место: Москва, музей-заповедник «Коломенское»
1 и 2 марта 2014 года в музее-заповеднике «Коломенское» прошло празднование Широкой Масленицы и традиционные народные масленичные гуляния: фолк-фестиваль и сожжение самой большой Масленицы. Все желающие смогли поучаствовать в фольклорном празднике проводов зимы на территории старинной русской усадьбы. Подробнее →
[13/10/2013] Гала ужин банка ВТБ
Место: Москва, ЦВК «Экспоцентр»
13 октября 2013 года в центральном выставочном комплексе «Экспоцентр» прошло грандиозное по своим масштабам мероприятие «Гала ужин банка ВТБ». Это было колоссальное шоу от государственного камерного оркестра джазовой музыки имени Олега Лундстрема и гаражный саунд плюс мягкий ритм-н-блюзовый от британского популярного исполнителя Craig David, которые поразили всех гостей, удивили и подарили грандиозные впечатления. Подробнее →
[24-25/08/2013] Фестиваль музыки и спорта BeeKiteCamp 2013 в Анапе
Место: Краснодарский край, Анапский район, Бугазская коса (ст. Благовещенская), площадка BeeKiteCamp
Компания «Спин Мьюзик Сервис» выступила техническим подрядчиком и выполнила комплексное техническое обеспечение мероприятия. Финальный BeeKiteCamp прошел 24-25 августа на Бугазской косе и завершил музыкально-спортивный сезон BeeKiteCamp 2013. Подробнее →
[12/06/2013] Первый фестиваль музыки и спорта BeeKiteCamp Highlights 2013 в Санкт-Петербурге
Место: Санкт-Петербург, Парк 300-летия г. Санкт-Петербурга
Компания «Спин Мьюзик Сервис» выступила генеральным техническим подрядчиком и выполнила комплексное техническое обеспечение мероприятия «Первый фестиваль музыки и спорта BeeKiteCamp Highlights 2013 в Санкт-Петербурге». BeeKiteCamp в Санкт-Петербурге – яркое мероприятие летнего сезона, которое впервые состоялось на берегу Финского залива. Подробнее →
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Селективное управление спиновым угловым моментом фотона с помощью электронно-индуцированного оптического спинового эффекта Холла
Abstract
Развитие оптического спинового эффекта Холла (OSHE) реализует расщепление различных спиновых компонент, способствуя манипулированию спиновым угловым моментом фотона, который действует. как носитель информации для квантовых технологий. Однако в OSHE с оптическим возбуждением отсутствует активный контроль углового момента фотона на глубокой субволновой шкале из-за предела оптической дифракции.Здесь мы экспериментально демонстрируем избирательную манипуляцию спинового углового момента фотона в глубоком субволновом масштабе с помощью электронно-индуцированного OSHE в наноантеннах Au. Инверсия диаграммы направленности OSHE наблюдается с помощью катодолюминесцентной поляриметрии с угловым разрешением со смещением положения электронного удара в пределах 80 нм в одном антенном блоке. Благодаря такому избирательному управлению вращением фотонов мы предлагаем надежное, конфиденциальное и высокоуровневое кодирование информации на глубокой субволновой шкале для будущих квантовых приложений.
ВВЕДЕНИЕ
Квантовая информация с характеристиками большой емкости и высокой скорости обработки успешно применяется в современной передаче сигналов, обработке, памяти и т. Д. ( 1 – 3 ). Эволюция квантовой науки в практическую технологию обещает огромные преимущества для конкретных приложений в вычислениях ( 4 ), моделировании ( 5 ) и криптографии ( 6 ). При развитии квантовой информационной технологии очень важно найти подходящий носитель информации, который должен быть высокоинтегрированным и с большой емкостью хранения, чтобы удовлетворить потребности приложений квантовой информации.Фотоны были подтверждены как носители информации с низким уровнем шума в новаторских работах по квантовой запутанности, телепортации и нелокальности Белла ( 7 – 10 ). По мере увеличения требований к информационной емкости был введен спиновый угловой момент фотона, чтобы обеспечить дополнительные степени свободы для переноса квантовой информации ( 11 – 13 ).
Оптический спиновый эффект Холла (OSHE) обеспечивает уникальный подход к управлению спиновым угловым моментом фотона.Спиновое расщепление фотонов исследовалось с помощью механизма спин-орбитального взаимодействия ( 14 – 18 ) и применялось для плоских микрополостей ( 19 , 20 ), метаматериалов ( 21 – 24 ), прецизионные измерения ( 25 – 27 ) и т. д. Учитывая, что спиновый угловой момент фотона действует как носитель информации с высокой надежностью и большой пропускной способностью, OSHE, по прогнозам, будет иметь потенциал в манипулировании носителем информации для квантовой технологии, особенно в кодировании информации и криптографии с особенностями ортогональности и высокой размерности.Предыдущие исследования по управлению OSHE в основном фокусировались на конструкции структуры ( 28 – 30 ), в которой манипуляция спином фотона может быть реализована с помощью фазового сдвига Панчаратнама-Берри и Рытова-Владимирского-Берри ( 31 – 33 ) , которые были использованы для объяснения физики, лежащей в основе OSHE, со спин-орбитальным взаимодействием света. В недавнем исследовании был предложен метод электрической настройки OSHE в жидкокристаллической микрополости ( 34 ). Однако этот подход трудно интегрировать в наномасштабе.Необходимо предложить эффективное решение для избирательного управления OSHE, чтобы реализовать его потенциал в квантовой информационной технологии и приложениях для устройств ( 35 ), где препятствие, связанное с пределом дифракции света, должно быть устранено для будущей интеграции устройств.
Как один из неинвазивных методов обнаружения с высоким разрешением ( 36 – 40 ), поляриметрия катодолюминесценции (КЛ) с точным контролем положения электронного удара преодолевает предел дифракции света ( 41 ) и успешно применяется. для исследования электромагнитного поля на глубокой субволновой шкале ( 42 , 43 ).При стимуляции электронным пучком глубокий субволновой сдвиг положения возбуждения может напрямую регулировать распределение локальной плотности состояний (LDOS) ( 44 – 46 ), способствуя эволюции излучения КЛ в дальней зоне. КЛ поляриметрия с угловым разрешением как характеристика импульсного пространства фотонов может эффективно определять направление излучения. Следовательно, поляриметрия изображения CL с угловым разрешением может исследовать спин фотона с угловыми диаграммами дальнего поля и позволяет исследовать поляризационно-зависимые явления с высоким пространственным и угловым разрешением.Этот метод определения характеристик преодолевает предел дифракции света; таким образом, его можно использовать для наблюдения OSHE, индуцированного электронами, в глубоком субволновом масштабе, что открывает путь для избирательного управления спином фотона при электронном возбуждении.
В этой работе мы демонстрируем избирательное управление спиновым угловым моментом фотона с помощью электронно-индуцированного OSHE на плазмонной наноантенне с точно сконструированными мультипольными моментами. При сдвиге положения возбуждения электронного луча на глубокой субволновой шкале расщепление спиновых компонент левосторонних циркулярно-поляризованных (LCP) и правосторонних циркулярно-поляризованных (RCP) компонентов спина фотонов можно наблюдать с помощью поляриметрии визуализации CL с угловым разрешением и положения удара электронного луча расположен на краю наноантенны Au.Диаграмма направленности LCP и RCP может быть инвертирована путем изменения положения удара электронного луча, в то время как картина нерасщепления спиновых состояний может быть обнаружена с помощью позиции падения электронов, расположенной в центре наноантенны Au. Переключение спинового расщепления фотона между состояниями «включено» и «выключено» может быть эффективно достигнуто путем изменения интерференции дипольных и квадрупольных моментов, что приводит к избирательной манипуляции спином фотона. Основываясь на этой электронно-индуцированной OSHE, мы реализуем спин-зависимое двоичное кодирование в пределах одной наноантенны Au.Эта возможность возбуждения OSHE электронным пучком обеспечивает отличную платформу для манипулирования спином фотона и открывает путь для будущей обработки квантовой информации и проектирования устройств.
РЕЗУЛЬТАТЫ
Электронно-индуцированный OSHE относится к явлению спинового расщепления фотонов, когда наблюдается асимметричная диаграмма направленности с разделением спиновых компонентов при электронном возбуждении (рис. 1A). Одиночная наноантенна Au была изготовлена размером 200 × 80 нм с использованием электронно-лучевой литографии с нанесением 30 нм Au и 2 нм Ti в качестве адгезионного слоя.Для исследования поведения различных спиновых компонент в дальней зоне представлена схема спинового расщепления фотонов (рис. 1B) для анализа параметров Стокса: S 1 , S 2 и S 3 в пространстве [θ, ϕ] в векторных сферических гармониках (примечание S1), которое является общим представлением поляризации и может использоваться для получения связанной с поляризацией величины ( 47 ). Все измерения КЛ выполняются в сканирующем электронном микроскопе (SEM; FEI Quattro C), оборудованном специализированной системой обнаружения КЛ (Delmic), которая состоит из параболического зеркала, поляриметрической оптики с вращающейся пластиной и высокочувствительного комплементарного металлооксидного полупроводника. (CMOS), как показано на рис.1С. Электронный луч, проходящий через точечное отверстие параболического зеркала, может эффективно возбуждать образец, а излучение КЛ может собираться зеркалом и измеряться с помощью матрицы КМОП. Четвертьволновая пластинка вместе с линейным поляризатором помещается на пути света для выделения различных спиновых составляющих излучения КЛ. Угловые картины различных спиновых компонентов в дальнем поле могут быть получены на целевой длине волны с помощью поляриметрии изображения CL с угловым разрешением.
Инжир.1 Схема обнаружения спиновой компоненты.( A ) Схематическое изображение электронно-индуцированного OSHE. Симметричная нано-прямоугольная антенна из Au при возбуждении электронным пучком на верхнем крае генерирует асимметричное излучение с круговой поляризацией. ( B ) Схематическое изображение спинового анализа фотонов. ( C ) ХЛ поляриметрия с угловым разрешением для измерений циркулярно поляризованного излучения. Четвертьволновая пластинка и линейный поляризатор используются для извлечения компонентов ХЛ излучения с круговой поляризацией.
При возбуждении центра верхнего края ХЛ-излучение наноантенны Au было проанализировано как по спектрам, так и по угловым диаграммам в дальней зоне. Спектры ХЛ с разрешением по круговой поляризации (ЦП) (рис. 2A) показывают, что компоненты LCP и RCP демонстрируют сопоставимые интенсивности ХЛ с их пиками излучения, оба расположены на длине волны около 630 нм, что хорошо согласуется с результатом моделирования (рис. S1), с небольшое красное смещение по сравнению с резонансом LSP (рис. S2). Чтобы охарактеризовать различие состояний поляризации, хиральность ХЛ определяется как | I RCP – I LCP | / ( I RCP + I LCP ), где I LCP ( I RCP ) интенсивность ХЛ излучения LCP (RCP).Вокруг максимальной длины волны 630 нм интенсивности LCP и RCP CL почти эквивалентны с хиральностью CL менее 5%, что соответствует результатам экспериментов по хиральному распределению LDOS (рис. S3).
Рис. 2 Анализ спиновых состояний.( A ) Экспериментальные суммарные, LCP и RCP CL спектры, полученные от наноантенны Au размером 200 × 80 нм при возбуждении электронным пучком 30 кэВ. Положение стимуляции расположено в середине верхнего края наноантенны Au, при этом измеренная хиральность CL соответствует правой ординате.( B ) Измерены угловые диаграммы горизонтальных ( I H слева) и вертикальных ( I V справа) компонентов для сигналов CL. Положение стимуляции находится в середине верхнего края наноантенны Au с длиной волны обнаружения 650 нм. ( C ) Измеренные угловые диаграммы компонентов RCP (слева) и LCP (справа) для сигналов CL. Положение стимуляции и длина волны обнаружения такие же, как в (B). ( D ) Измеренная угловая диаграмма S 0 Параметр Стокса.( E ) Измеренная угловая диаграмма S 3 Параметр Стокса. Все шаблоны нормализованы к 1. Ось в (C) – (E) такая же, как в (B).
Картины дальнего поля различных спиновых компонент были получены с помощью поляриметрии изображений CL с угловым разрешением. Угловая диаграмма, показанная на рис. 2D, отражает всенаправленность излучения КЛ от симметричной металлической наноантенны. Однако анализ различных спиновых компонент излучения КЛ выявляет асимметричные особенности.Хотя наблюдаемое симметричное распределение I H и I V (построенное из декартовых полей I θ и I ϕ ; рис. 2B) указывает на ненаправленную картину горизонтального и вертикального Согласно состояниям, угловые диаграммы дальнего поля I LCP и I RCP демонстрируют очевидную направленность, которые расположены в левой и правой половине полушария, соответственно (рис.2С). Чтобы исследовать поведение компонентов LCP и RCP в дальней зоне, была исследована угловая диаграмма параметра Стокса S 3 , где наблюдалось разделение направлений компонентов LCP и RCP (рис. 2E), что хорошо согласуется с результат моделирования (рис. S4). Этот результат демонстрирует различие в диаграммах дальнего поля между компонентами спина LCP и RCP, которые можно применять для манипулирования спином фотонов, в то время как зондирование того же образца оптическим пятном с дифракционным пределом размывает наблюдаемый OSHE (рис.S5). При дальнейшем анализе рассчитанного сигнала ближнего поля компонентов LCP и RCP было обнаружено четкое пространственное разделение их диаграмм ближнего поля, что привело к разделению компонентов LCP и RCP в дальней зоне. Эта особенность расщепления вместе с эквивалентностью интенсивностей LCP и RCP указывает на существование индуцированного электронами OSHE.
Селективное манипулирование спиновым угловым моментом в глубоком субволновом масштабе с помощью электронно-индуцированного OSHE показано на рис. 3.Были выбраны три положения возбуждения, чтобы проиллюстрировать эту манипуляцию при обнаруженных длинах волн 600 и 650 нм, соответственно (фиг. 3A). Для позиции падения в середине верхнего края угловая диаграмма дальнего поля S 3 показывает расщепление спина фотона с компонентами LCP и RCP, расположенными в левой и правой половинах угловой полусферы, что демонстрирует поворот по состоянию ОГБО. Для положения возбуждения, расположенного в центре наноантенны, расщепление между компонентами LCP и RCP не наблюдается, что свидетельствует о регрессе в состояние выключения OSHE.Для положения возбуждения, расположенного в середине нижнего края, относительное расположение компонентов LCP и RCP инвертируется в шаблоне разделения, что показывает возврат в состояние включения. Переключение из состояния включения в состояние выключения может быть достигнуто за счет сдвига электронного луча в пределах 40 нм, а инверсия угловой диаграммы также может быть реализована за счет сдвига положения возбуждения в пределах 80 нм, демонстрируя эффективную избирательную манипуляцию спин фотона под действием электронно-индуцированного OSHE. Как показано на рис.3B, результаты моделирования показывают эволюцию угловой картины с электронным пучком, перемещающимся по трем выбранным позициям, что согласуется с результатами эксперимента. Для обнаруженных длин волн 550 и 700 нм с большим отклонением от максимальной длины волны (λ 0 ) результаты экспериментов и моделирования (рис. S6) показывают образцы OSHE с более низкой интенсивностью S 3 . Эти результаты показывают, что в угловой диаграмме дальнего поля интенсивность S 3 увеличивается по мере увеличения обнаруженной длины волны λ и уменьшается после λ = λ 0 .Это наблюдение показывает, что подходящая λ для обнаружения OSHE при электронном возбуждении составляет около 630 нм для исследуемой наноантенны Au.
Рис. 3 Манипуляции со спиновым угловым моментом фотона.( A ) Экспериментальные нормализованные угловые CL S 3 паттернов, полученных от наноантенны Au размером 200 × 80 нм, с напряжением электронной стимуляции 30 кэВ. Положения стимуляции, расположенные в середине верхнего края, в центре антенны и в середине нижнего края, которые отмечены красной точкой на изображении наноантенны Au, полученном с помощью сканирующей электронной микроскопии (SEM) в псевдоцвете.Собранные длины волн составляют 600 и 650 нм соответственно. ( B ) Смоделированные угловые CL S 3 диаграмм направленности наноантенны Au. Положения возбуждения электронного луча и собранные длины волн такие же, как в (A). ( C ) Коэффициент рассеяния как функция длины волны для различных положений возбуждения. Горизонтальная штриховая линия соответствует усредненному коэффициенту рассеяния. Столбик ошибки представляет собой неопределенность коэффициента рассеяния в трех экспериментах. ( D ) S 3 отношение (ρ) как функция длины волны для различных положений возбуждения. S 3 отношение (ρ) определяется как | S 3 слева | / S 3 справа , где S 3 слева ( S 3 справа ) – интегрированное S 3 значение левой (правой) половины углового полушария. Горизонтальная штриховая линия соответствует усредненному значению ρ. Столбик ошибки представляет собой неопределенность ρ в трех экспериментах.
Чтобы исследовать направленность спиновых состояний при различных положениях возбуждения, коэффициент рассеяния LCP был получен как функция длины волны, которая определяется как отношение интенсивности полуугловой полусферы с меньшей интенсивностью ко всей угловой полусфере.Экспериментальные данные показывают, что измеренный коэффициент рассеяния остается более 20% при возбуждении на верхнем или нижнем крае (рис. 3C), что указывает на направленность излучения состояния LCP в угловой диаграмме дальнего поля. Чтобы исследовать особенности разделения компонентов LCP и RCP, были получены значения S 3 , интегрированные на левой и правой половинах углового полушария с полосой погрешности для описания неопределенности экспериментов (рис. 3D). Чтобы количественно описать разницу расщепления в угловых шаблонах S 3 , соотношение (ρ) S 3 определяется как | S 3 слева | / S 3 справа , где S 3 слева ( S 3 справа ) – интегрированное S 3 значение левой (правой) половины углового полушария.Результаты экспериментов показывают, что, когда положение электронного возбуждения находится на верхнем крае, ρ остается около 1 в обнаруженном диапазоне длин волн от 550 до 700 нм с отклонением менее 15%. С положением стимуляции, расположенным на нижнем краю, ρ остается около -1 в том же обнаруженном диапазоне длин волн с отклонением менее 12%. Эти анализы отражают разницу в структуре расщепления компонентов LCP и RCP при различных положениях столкновения, что подтверждает управление электронно-индуцированным OSHE со сдвигом положения стимуляции на глубокой субволновой шкале, тем самым реализуя избирательное управление спиновым угловым моментом.
Для изучения механизма OSHE, индуцированного электронным пучком, с помощью КЛ поляриметрии с угловым разрешением были исследованы угловые картины в дальней зоне наноантенн из Au разного размера. Угловые диаграммы параметра Стокса S 3 показаны на рис. 4A, где различимое расщепление компонентов LCP и RCP с эквивалентной интенсивностью (рис. S7) подтверждает существование OSHE в различных наноантеннах. Результаты экспериментов показывают, что при обнаруженной длине волны 650 нм интенсивность S 3 увеличивается с увеличением размера наноантенн Au, что хорошо согласуется с результатами моделирования (рис.4Б).
Рис. 4. Многополярный анализ угловых диаграмм с разрешением CP для наноантенны из золота.( A ) Экспериментальные нормированные угловые S 3 паттернов, полученных из наноантенн Au размером 200 × 80, 200 × 70, 200 × 60, 180 × 60 и 160 × 60 нм. Положение стимуляции расположено в середине верхнего края наноантенны Au, с возбуждением электронным пучком 30 кэВ. Собранная длина волны составляет 650 нм. ( B ) Имитация угловых S 3 диаграмм Au наноантенны разных размеров.Размер наноантенны Au, положение возбуждения и длина собранной волны такие же, как на (A). ( C ) Моделирование интенсивности рассеяния различных мультипольных моментов в наноантенне размером 200 × 80 нм. Спектры соответствуют полной интенсивности и интенсивности моментов P , Q и M . ( D ) Смоделированная интенсивность рассеяния различных компонентов электрического диполя в наноантенне размером 200 × 80 нм. Спектры соответствуют интенсивности компонентов P x , P y , и P z .На вставке: ось ( xyz ) ориентации диполя.
Чтобы выяснить физику, лежащую в основе наблюдаемого OSHE при электронной стимуляции, интенсивность рассеяния различных мультипольных моментов была исследована с помощью мультиполярного разложения, в котором рассчитанное рассеянное поле было разложено на векторные сферические гармоники согласно общей теории мультипольного рассеяния ( 48 – 50 ) I = 2ω43c3∣P∣2 + 2ω43c5∣M∣2 + 4ω53c5 (P · T) + 2ω63c7∣T∣2 + ω65c5∑∣Qαβ∣2 + ω640c7∑∣Mαβ∣2 + O (15c7) ( 1) где P , M , T , Q αβ и M αβ соответствуют электрическому диполю, магнитному диполю, тороидальному диполю, электрическому квадруполю и магнитному квадруполю; c – скорость света в вакууме; α, β = x , y , z. Соответствующие компоненты для торцевого возбуждения: P y , P z , M y и Q αα , которые вычисляются с помощью асимптотических приближений дальнего поля для диполей и квадруполей в наличие субстрата. Компоненты P y и P z имеют характерные тороидальные формы со значительным компонентом E z на краю наноантенны, которые подходят для управления электронным пучком.Компонент M y создает петлю электрического тока на плоскости xz . Q αα квадруполи показывают лепестки мультипольного излучения в диаграмме направленности в дальней зоне. Из данных моделирования во временной области (FDTD) вычисляется интенсивность рассеяния этих мультипольных моментов (рис. 4C), которая отражает вклад моментов P и Q в угловую диаграмму дальнего поля. Этот результат показывает, что в диапазоне длин волн от 550 до 700 нм интерференция моментов P и Q усиливает угловую диаграмму направленности в дальней зоне, где связанная с λ особенность интерференционной моды приводит к эволюции угловой диаграммы с длина волны увеличивается, как показано на рис.3А. Дальнейшие расчеты интенсивности рассеяния электрических дипольных моментов показывают, что P y является основным компонентом излучения в дальней зоне электрического диполя (рис. 4D), где положение стимуляции на оси симметрии препятствует возбуждению P x . Расчет интенсивности рассеяния электрических квадрупольных моментов показывает, что Q xx , Q yy и Q zz являются тремя основными компонентами излучения квадруполя в дальней зоне (рис.S8). С положением возбуждения, расположенным в середине верхнего края наноантенны Au, вклад мод P и Q является доминирующим в угловой диаграмме дальнего поля, где разность фаз π / 2 между квадрупольными и дипольные моменты приводят к этому спиновому расщеплению между компонентами LCP и RCP (примечания S2 и S3). Разница в размерах наноантенн Au приводит к сдвигу пропорций мультипольного момента, где разница пропорций между моментами P и Q увеличивается по мере увеличения размера наноантенны и приводит к эволюции картины расщепления LCP и RCP в дальней зоне. состояния.
Управление OSHE при электронном возбуждении с перемещением положения столкновения в наномасштабе может применяться для зависящего от спина двоичного кодирования, где манипулирование спином фотона, опосредованное смещением луча на глубокой субволновой шкале, несет информацию, что является преимуществом при интеграции модулей. Режим кодирования зависит от параметра Стокса S 3 излучения, где две разные схемы разделения LCP и RCP на левой и правой половинах угловой полусферы определены как 0 и 1.Код стирания, определенный из шаблона нерасщепления, вводится для повышения точности информации. Эти три режима: 0, 1 и код стирания соответствуют положениям возбуждения электронного луча на верхнем крае, нижнем крае и центре блока кодирования (фиг. 5A). Весь процесс кодирования был интегрирован в единый блок на глубокой субволновой шкале.
Рис. 5 Схема спин-зависимого двоичного кодирования.( A ) Функциональный блок для спин-зависимого двоичного кодирования.С положениями возбуждения электронного луча, расположенными в середине верхнего края, середине нижнего края и в центре наноантенны, которые отмечены тремя точками на псевдоцветном СЭМ-изображении наноантенны Au; соответствующие S 3 шаблона определены как 0, 1 и код стирания для двоичного кодирования. ( B ) Коды ASCII, состоящие из заглавных букв «P» и «K» для двоичного кодирования. ( C ) Угловой CL S 3 шаблонов с движением электронного луча по двум траекториям, соответствующим кодам ASCII, которые выводят двоичные последовательности «01010000» и «01001011», соответствующие заглавным буквам «P» и «K». ,” соответственно.
В этом зависящем от спина двоичном кодировании блок кодирования был разработан и изготовлен с размером 200 × 80 нм, где пути сканирования были разработаны в соответствии с кодами ASCII (Американский стандартный код для обмена информацией) (рис. 5B). При перемещении электронного луча по этим двум путям заглавные буквы «P» и «K» кодировались и детектировались дальнее поле (рис. 5C). Это двоичное кодирование вводит спин фотона, а не интенсивность луча в качестве носителя, чтобы повысить способность обработки информации, что увеличивает информационную емкость на основе измерения интенсивности.Разница в хиральном распределении LDOS между компонентами LCP и RCP (рис. S3) представляет информацию, связанную с поляризацией, с различным положением удара свободных электронов. Эквивалентность интенсивности LCP и RCP предотвращает считывание информации с помощью детектирования интенсивности, где несходство угловых паттернов спинового расщепления фотонов является ключом к рассекречиванию сигнала. Кроме того, введение кода стирания повышает надежность процесса кодирования, что способствует созданию надежного решения для кодирования.Это зависящее от спина двоичное кодирование преодолевает предел дифракции света за счет применения электронного возбуждения и реализует глубокое субволновое масштабирование спинового углового момента фотона, которое действует как кодирующая информация, что способствует интеграции будущих квантовых устройств.
Кроме того, спин фотона можно использовать для классического двоичного кодирования информации; Для будущей работы томография квантового состояния с одним кубитом может быть в дальнейшем использована для проверки того, является ли спиновая степень свободы излучаемого света реальным кубитом или смешанным состоянием, что открывает путь для изучения квантовой оптики свободных электронов и расширения квантовой технологии Приложения.С другой стороны, последние достижения в области сверхбыстрой электронной микроскопии также могут быть применены для сверхбыстрой модуляции спин-орбитальной связи с использованием свободных электронов. Если волновой пакет свободных электронов модулируется с фемтосекундным временным разрешением, то эта скорость модуляции может быть передана модуляции поляризации фотона, которая потенциально может способствовать реализации высокоскоростной передачи квантовой информации.
ОБСУЖДЕНИЕ
Таким образом, мы продемонстрировали уникальный подход для избирательного управления спиновым угловым моментом фотона в глубоком субволновом масштабе с помощью электронно-индуцированного OSHE.Переключение между состояниями OSHE «включено» и «выключено» было реализовано со смещением электронного луча в пределах 40 нм, а инверсия диаграммы направленности в дальней зоне наблюдалась при перемещении положения удара в пределах 80 нм, где задействованы мультипольные моменты, возбуждаемые электронами. закономерность эволюции спинового расщепления фотона. Кроме того, поскольку спиновый угловой момент может выступать в качестве отличного носителя информации для приложений квантовой информации, мы демонстрируем зависящее от спина двоичное кодирование в пределах одного блока.Особенности управления в глубокой субволновой шкале, большой объем информации и высокая конфиденциальность делают его многообещающим кандидатом для хранения и обработки квантовой информации, где высокая степень интеграции и надежность повышают применимость этой конструкции в устройствах. Наша работа обеспечивает демонстрацию и экспериментальную конфигурацию управления спином фотона с помощью электронно-индуцированного OSHE, что может вдохновить на исследования современных междисциплинарных дисциплин спин-орбитального взаимодействия, киральной квантовой оптики и связанных приложений в квантовой информационной технологии в сочетании с одиночными излучателями.
МАТЕРИАЛЫ И МЕТОДЫ
Некоторые из следующих методов аналогичны методам, ранее опубликованным в ( 44 ).
Изготовление образцов
Наноструктуры Au были изготовлены на подложке Si / SiO 2 с помощью стандартного процесса EBL (электронно-лучевая литография) с последующим процессом отрыва и облучением ионами Ar. Положительный резист {MircoChem PMMA [поли (метилметакрилат)], A2 950} наносился методом центрифугирования на подложку толщиной ~ 60 нм.Структуры формировали с помощью сфокусированного электронного пучка с энергией 30 кэВ, управляемого модулем системы создания нанограмм, который установлен на SEM (FEI Quanta 450 FEG). Слой Au толщиной 30 нм был нанесен на подложку с помощью электронно-лучевого испарителя (LJUHV E-400 L). Облучение ионами Ar проводили в течение 1 мин для очистки остаточного ПММА в конечном процессе.
измерений CL
угловых диаграмм CL были получены с помощью детекторной системы CL (Delmic SPARC), которая установлена на SEM (Thermo Fisher Scientific Quattro C).Излучение регистрировалось высокочувствительной КМОП-схемой для определения угловой диаграммы направленности в дальней зоне. Угловой диапазон сбора до 1,49π ср, с угловым разрешением <10 мрад. Для обнаружения определенных длин волн КЛ излучения на оптическом пути были размещены различные полосовые фильтры. Для детектирования ХЛ с разрешением CP в модуле анализатора поляризации использовались комбинации четвертьволновой пластинки и линейного поляризатора для различных диапазонов длин волн детектирования. В частности, выбросы LCP и RCP CL можно избирательно собирать, ориентируя быструю ось волновой пластины на ± 45 ° по отношению к оси поляризации поляризатора.
Численное моделирование
Все результаты моделирования в этом отчете были получены с помощью коммерческого решателя методов FDTD (FDTD Solutions, Lumerical). Область моделирования включала структуру с идеально подобранными слоями во всех направлениях. Для расчета рассеяния использовались источники рассеянного поля полного поля с линейной и круговой поляризацией для освещения структуры вдоль оси – z . При расчете эмиссии КЛ электронный пучок, движущийся вдоль оси – z , рассматривался как линейная плотность тока Дж ( r , t ) = ρ v δ ( z + vt ) δ ( x – x 0 ) δ ( y – y 0 ) n z , где ρ – заряд электрона, v – скорость электрона, r = ( x 0 , y 0 , z ) – положение электронного луча, а n z – единичный вектор вдоль направления + z .В частотной области это соответствует плотности тока как Дж ( r , ω) = ρ e – i ω z / v δ ( x – x 0 ) δ ( y – y 0 ) n z , плотность тока моделировалась как серия диполей с временной фазовой задержкой (- z / ν ), связанной со скоростью электронов, ν = 0,34 c , что соответствует энергии электронов 30 кэВ ( c – скорость света в вакууме).Эталонное моделирование (без наноструктуры и подложки) также было выполнено для вычитания любого фонового сигнала, создаваемого электронным пучком, который мог скрыть сигнал от наноструктуры. Спектры ХЛ рассчитывались в дальней зоне путем интегрирования вектора Пойнтинга, нормального к произвольной поверхности в верхней полуплоскости z для длин волн от 400 до 1000 нм. В дальней зоне усредненная по времени величина вектора Пойнтинга в сферических координатах может быть выражена как P всего = ε 0 c (| E θ | 2 + | E φ | 2 ) / 2, P LCP = ε 0 c (| E θ – i E φ | 2 ) / 4 и P RCP = ε 0 c (| E θ + i E φ | 2 ) / 4 для всего, LCP и RCP CL расчет спектров.Дальняя зона задана как вакуум. При моделировании использовались данные Палика для комплексных показателей преломления Au (золото), Si (кремний). Показатель преломления SiO 2 был принят равным 1,5.
Благодарности: Мы благодарны Т. Коэнену из Delmic CL Solutions B.V. за помощь в технической поддержке и З. Дангу, Х. Хе, Д. Лю из Пекинского университета за обсуждение статьи. Финансирование: Работа выполнена при поддержке Национальной программы ключевых исследований и разработок Китая (грант №2020YFA0211300), Национальный научный фонд Китая (грант № 12027807), Пекинский фонд естественных наук (грант № Z180011), Национальная программа фундаментальных исследований Китая (номера грантов 2017YFA025700, 2017YFA0206000 и 2019YFA0210203), NSFC (гранты № 61521004). и 217), а также платформа высокопроизводительных вычислений Пекинского университета. Автор: З.Ф. курировал проект. C.C. и Q.J. задумал и спроектировал проект. C.C. и З.Л. провели все эксперименты. C.C.и Q.J. выполнил все симуляции. C.C. написал рукопись. L.Z. и M.J. обеспечивали техническую поддержку. Все авторы участвовали в научных обсуждениях и исправлениях рукописей. Конкурирующие интересы: Авторы заявляют об отсутствии конкурирующих интересов. Доступность данных и материалов: Все данные, необходимые для оценки выводов в статье, представлены в статье и / или дополнительных материалах. Дополнительные данные, относящиеся к этой статье, могут быть запрошены у авторов.
- Copyright © 2021 Авторы, некоторые права защищены; эксклюзивный лицензиат Американской ассоциации содействия развитию науки. Нет претензий к оригинальным работам правительства США. Распространяется по некоммерческой лицензии Creative Commons Attribution 4.0 (CC BY-NC).
Акустический спиновый эффект Холла в металлах с сильной спин-орбитой
Экспериментальная установка
Тонкопленочные гетероструктуры выращиваются на пьезоэлектрических подложках LiNbO 3 с использованием радиочастотного (ВЧ) магнетронного распыления.Структура пленки суб. / X ( d ) / CoFeB (1) / MgO (2) / Ta (1) с X = W, Pt, Ta и Cu (толщина в нанометрах). В дальнейшем гетероструктуры называются бислоями X / CoFeB. Стандартная оптическая литография используется для моделирования стержней Холла из пленки и электродов / встречно-штыревых преобразователей (IDT) ( 17 ) из проводящих металлов (подробности подготовки образцов см. В разделе «Материалы и методы»).
Схема экспериментальной установки и система координат показаны на рис.1А. Барная стойка расположена между двумя IDT. На рис. 1В показано типичное изображение устройства, полученное с помощью оптического микроскопа. Векторный анализатор цепей (ВАЦ) подключен к IDT, чтобы возбуждать ПАВ типа Рэлея с одного конца и обнаруживать его передачу на другом конце. На рисунке 1C показаны типичные спектры пропускания с двухслойным W / CoFeB, помещенным между IDT. Амплитуда передачи достигает максимума на ∼194 МГц, что соответствует основной частоте возбуждения SAW ( f SAW ), определяемой геометрией IDT и скоростью звука подложки.
Изучены акустоэлектрические свойства пленок в зависимости от магнитного поля. Непрерывный радиочастотный сигнал с фиксированной частотой f и мощностью P подается от одного из портов VNA к соответствующему IDT, который запускает SAW вдоль x , которая распространяется на пленку и вызывает движение решетки. Продольное (вдоль x ) и поперечное (вдоль y ) напряжения стержня Холла, определяемые как V xx и V yx , соответственно, измеряются во время возбуждения ПАВ.Поскольку V xx и V yx содержат аналогичную информацию, здесь мы сосредоточимся на результатах V xx ; характеристики V yx см. в разделе S1. Чтобы извлечь напряжение, возникающее из ПАВ, мы вычитаем среднее напряжение, измеренное в нерезонансных условиях, и получаем акустическое напряжение ΔVxx≡Vxx− 〈Vxxoff〉. 〈Vxxoff〉 – среднее значение V xx , когда f установлено далеко от f SAW (подробности см. В разделе «Материалы и методы»).Мы прикладываем плоское магнитное поле величиной H во время измерения напряжения. Угол между полем и осью x определяется как φ H . Поскольку легкая магнитная ось слоя CoFeB направлена вдоль плоскости пленки, а магнитная анизотропия в плоскости является слабой, мы предполагаем, что ориентация намагниченности следует ориентации магнитного поля.
Рис. 1 Экспериментальная установка для исследования акустического спинового эффекта Холла.( A ) Схематическое изображение экспериментальной установки, включая подложку, пленку, IDT и векторный анализатор цепей.На нижнем изображении показан спиновый ток, вызванный движением решетки, т.е. акустический спиновый эффект Холла. Спиновый ток течет ортогонально распространению ПАВ. Обратите внимание, что направление спинового тока меняется на противоположное, когда направление распространения ПАВ меняется на противоположное. ( B ) Типичное изображение устройства, полученное при оптической микроскопии. Яркие области – это электроды, а серый квадрат в центре – полоса Холла, сделанная из пленки. ( C ) Амплитуда передачи ПАВ от IDT1 к IDT2 (от IDT2 к IDT1) показана как функция частоты ( f ) синей (красной) линией.Между IDT помещается перемычка Холла из бислоя W (2.4) / CoFeB.
Акустическое напряжение
На рисунке 2 (A, C и D) показана зависимость угла поля (φ H ) Δ V xx для W / CoFeB, Pt / CoFeB и Cu / CoFeB двухслойный, когда РЧ-сигнал f ∼ f SAW и P ∼10 дБм применяется к IDT2. Для бислоев W / CoFeB и Pt / CoFeB Δ V xx показывает синусоидальное изменение с периодом 90 ° .Обратите внимание, что знак (т.е. фаза) синусоидального изменения одинаков для двух бислоев, хотя знак угла Холла спина противоположен между Pt и W ( 3 ). Напротив, для бислоя Cu / CoFeB такой вариации не обнаружено. (Мы также обнаружили, что Δ V xx показывает небольшую зависимость от φ H для однослойных пленок W.) На рисунке 2B показано Δ V xx в сравнении с φ H W / Двухслойный CoFeB, когда РЧ-сигнал подается на IDT1.Среднее напряжение смещения и синусоидальное изменение меняют знак при изменении направления распространения ПАВ. Аналогичные особенности наблюдаются для бислоев Pt / CoFeB.
Рис. 2 Зависимость акустического напряжения от угла поля.( A до D ) Зависимость угла магнитного поля (φ H ) от Δ V xx при ВЧ-сигнале f ∼ f SAW и P ∼ 10 дБм применяется к IDT2 (A, C и D) и IDT1 (B).Пленки, помещенные между IDT, представляют собой бислои W (1,8) / CoFeB (A и B), Pt (2,0) / CoFeB (C) и Cu (1,8) / CoFeB (D). Величина магнитного поля зафиксирована на уровне ∼55 мТл. Планки погрешностей, которые представляют стандартное отклонение повторных измерений, меньше символов. Черные линии показывают соответствие данным с формулой. 1.
Мы аппроксимируем зависимость φ H от Δ V xx следующей функцией: ΔVxx = ΔVxx0 + ΔVxx2φcos2φH + ΔVxx4φsin22φH (1), где ΔVxxnφ ( n = 2, 4) представляет собой коэффициент синусоидальная функция с периодом 360 ° / n и ΔVxx0 является независимой от φ H составляющей.ΔVxx0 пропорционально так называемому акустическому току, который возникает в результате выпрямления локализованного электрического поля и плотности заряда ( 18 ).
Зависимость ΔVxx0 f показана на рис. 3A. ΔVxx0 достигает пика при f ∼194 МГц, что соответствует f SAW (см. Рис. 1C), и меняет свой знак при изменении направления распространения SAW ( 19 ). Зависимость f ΔVxx2φ и ΔVxx4φ показана на рис.3 (Б и В) соответственно. ΔVxx4φ значительно больше, чем ΔVxx2φ, и показывает четкий пик при f ∼ f SAW , предполагая, что его появление связано с возбуждением SAW. (Происхождение малого ΔVxx2φ остается неизвестным.) Для всех компонентов (ΔVxx0, ΔVxx2φ и ΔVxx4φ) величина сигнала незначительно меняется в зависимости от направления распространения ПАВ. Поскольку амплитуда передачи ПАВ слабо зависит от направления распространения (см. Рис. 1С), невзаимность системы ( 20 , 21 ) может способствовать асимметрии.Зависимость ΔVxx4φ от мощности ( P ) показана на рис. 3D. ΔVxx4φ линейно увеличивается с P .
Рис. 3 Резонансное возбуждение акустического напряжения.( A до C ) ВЧ-частота ( f ) зависимость ΔVxx0 (A), ΔVxx2φ (B) и ΔVxx4φ (C). Синие (красные) треугольники представляют результаты, когда РЧ-сигнал подается на IDT1 (IDT2). ВЧ-мощность ( P ) зафиксирована на уровне ∼10 дБмВт. ( D ) P Зависимость ΔVxx4φ при изменении f .Сплошные линии показывают соответствие данным с линейной функцией. Верхняя и нижняя панели показывают результаты, когда РЧ-сигнал подается на IDT1 и IDT2 соответственно. (От A до D) Планки погрешностей показывают ошибки аппроксимации Δ V xx с уравнением. 1. Представленные данные получены с использованием бислоя W (2.4) / CoFeB.
Чтобы определить происхождение ΔVxx4φ, мы исследовали его зависимость от толщины слоя X ( d ). В дальнейшем мы используем ΔVxx0 и ΔVxx4φ для представления соответствующего значения при f ∼ f SAW .Поскольку коэффициент пропускания SAW незначительно меняется от устройства к устройству из-за незначительных различий в IDT, мы нормализуем ΔVxx4φ на ΔVxx0 и определяем vxx4φ≡ΔVxx4φ / ΔVxx0. На рис. 4А показана зависимость vxx4φ d для бислоев W / CoFeB. Мы находим, что vxx4φ принимает максимум при d ∼ 2 нм. Такая зависимость vxx4φ d напоминает зависимость спинового холловского магнетосопротивления (SMR) ( 22 , 23 ). Зависимость d отношения КМР rxx2φ≡∣ΔRxx2φ / Rxx0∣ представлена на рис.4Б. ΔRxx2φ представляет собой изменение сопротивления, когда намагниченность слоя CoFeB вращается в плоскости xy ( 24 ), а Rxx0 – это базовое сопротивление, которое не изменяется в зависимости от φ H . Зависимость d vxx4φ и rxx2φ аналогична. Согласно дрейфово-диффузионной модели спинового транспорта в двойных слоях НМ / ферромагнитный металл (ФМ) ( 23 , 24 ) максимум rxx2φ пропорционален квадрату угла Холла спина слоя НМ (θ SH ). ), а толщина слоя НМ в максимуме близка к его спиновой диффузионной длине (λ N ).Используя модель (см. Материалы и методы), мы получаем θ SH ∼ 0,23 и λ N ∼ 0,73 нм из зависимости rxx2φ d для W, которые хорошо согласуются с предыдущими исследованиями ( 24 ) .
Рис. 4 Зависимость акустического напряжения от толщины слоя X, магнитного поля и резонансной частоты.( A ) Нормированное акустическое напряжение vxx4φ = ΔVxx4φ / ΔVxx0 в зависимости от толщины слоя W ( d ) для бислоев W / CoFeB.Радиочастотная частота ( f ) и мощность ( P ) установлены на ∼ f SAW и ∼10 дБм соответственно. ( B ) d Зависимость rxx2φ той же системы, показанная на (A). Черная линия соответствует данным с формулой. 4. ( C ) Зависимость угла поля (φ H ) акустического напряжения Δ V xx , полученная с использованием различной величины поля ( H ). Фиолетовая, зеленая и оранжевая линии соответствуют H, ∼ 8, 14 и 55 мТл соответственно.( D ) ΔVxx4φ в зависимости от H . (C и D) Данные получены с использованием радиочастотного сигнала f ∼ f SAW и P ∼10 дБм, приложенного к IDT1. ( E ) H Зависимость ∣ΔRxx2φ∣. ( F ) Зависимость ΔVxx4φ от резонансной частоты ПАВ ( f SAW ). ВЧ-мощность ( P ) зафиксирована на уровне 10 дБмВт. Сплошные линии показывают линейные посадки, проходящие через начало координат. (C – F) Представленные данные получены с использованием W (2.4) / Двухслойный CoFeB. Синие (красные) треугольники в (A) и (F) представляют результаты, когда РЧ-сигнал подается на IDT1 (IDT2). Столбики ошибок в (A), (D) и (F) показывают ошибки аппроксимации Δ V xx с уравнением. 1.
Сходство в зависимости d vxx4φ и rxx2φ предполагает, что спиновый ток генерируется в X-слое. Тот факт, что vxx4φ почти отсутствует для бислоев Cu / CoFeB (см. Рис. 2D), еще раз подтверждает это мнение: угол Холла спина Cu значительно меньше, чем у Pt и W.Однако обратите внимание, что между акустическим напряжением и SMR есть несколько различий. Во-первых, зависимость этих двух углов от поля различается. Обычно сопротивление из-за SMR изменяется как cos 2φ H [см., Например, ( 22 )], тогда как доминирующий вклад в акустическое напряжение Δ V xx изменяется как sin22φH. Во-вторых, vxx4φ более чем на один порядок больше, чем rxx2φ. В-третьих, мы обнаруживаем заметную разницу в зависимости величины магнитного поля ( H ) между ними.На рис. 4C мы показываем зависимость H Δ V xx от φ H для бислоя W / CoFeB. Как видно, напряжение смещения (ΔVxx0) практически не меняется с H . Напротив, величина ΔVxx4φ увеличивается с уменьшением H . Зависимость ΔVxx4φ H , представленная на рис. 4D, показывает, что ΔVxx4φ масштабируется с 1/ H . Для справки мы показываем на рис. 4E зависимость 900ΔRxx2φ от H . В отличие от ΔVxx4φ, ΔRxx2φ∣ почти постоянна по сравнению с H .
Описание модели
Чтобы учесть эти результаты, мы модифицируем дрейфово-диффузионную модель спинового транспорта, которая используется для описания SMR ( 23 ). Во-первых, мы включаем вызванное ПАВ деформацию FM-слоя и магнитоупругую связь ( 25 , 26 ), которые вызывают изменения направления намагниченности по отношению к магнитному полю ( 27 – 29 ). Следовательно, Δ V xx приобретает дополнительный коэффициент 1Hsin 2φH по сравнению с изменением сопротивления, которое возникает из-за SMR.Затем, чтобы генерировать (выпрямленный) постоянный ток, спиновый ток должен изменяться во времени и пространстве так, чтобы он взаимодействовал с движением магнитных моментов, вызванным деформацией, вызванной ПАВ. Мы обнаружили, что следующая форма спинового тока js, zy (ориентация электронного спина вдоль y и поток вдоль z ) создает выпрямленный постоянный ток и учитывает экспериментальные результаты js, zy = A∂ux∂t (2) где u x – смещение решетки вдоль направления распространения волны ( x ). A – это предварительный фактор, который определяет эффективность генерации спинового тока и пропорционален λ , поэтому , SOI.
Спиновый ток js, zy, генерируемый в слое NM, который изменяется во времени и пространстве синхронно с SAW, дрейфует к интерфейсу NM / FM и вызывает накопление спина. Величина накопления спина на границе раздела зависит от направления намагничивания FM-слоя из-за действия крутящего момента передачи спина ( 22 , 23 ). Накопление спина генерирует спиновой ток обратного потока в слое NM, который преобразуется в ток заряда посредством обратного спинового эффекта Холла ( 11 ).Поскольку направление намагничивания изменяется во времени и пространстве за счет магнитоупругой связи, спиновой ток обратного потока локально выпрямляется и вызывает акустическое напряжение постоянного тока, зависящее от φ H . Таким образом, для наблюдения выпрямленного постоянного акустического напряжения требуется FM-слой со значительной магнитоупругой связью. [См. Раздел S1, где мы показываем, что ΔVxx4φ отсутствует для бислоя W / Py из-за небольшой магнитоупругой связи Py (Ni 81 Fe 19 )]. Результирующее акустическое напряжение показывает (см. Раздел S2) ΔVxx≈cλso2K (d) fSAWP sgn (k) bHMSsin22φH, (3) где c – постоянная, которая зависит от материала и геометрии устройства, K ( d ) характеризует зависимость d , аналогичную зависимости SMR (см.4), k – волновой вектор ПАВ типа Рэлея [sgn ( x ) принимает знак x ], а b и M S – соответственно магнитоупругая связь постоянная и намагниченность насыщения FM-слоя. Знак ( k ) в правой части уравнения. 3 возникает из-за формы индуцированного решеткой спинового тока (уравнение 2).
Уравнение 3 отражает многие особенности акустического напряжения, обнаруженные в экспериментах.Как видно, Δ V xx изменяется как sin22φH. Коэффициент sin22φH в уравнении. 3, эквивалент ΔVxx4φ, меняет свой знак при изменении направления распространения волны (определяется знаком k ), масштабируется с 1H и P , и пропорционален квадрату спин-орбитальной связи НМ слоя и, следовательно, не зависит от знака угла Холла спина слоя НМ. Зависимость ΔVxx4φ от толщины, закодированная как K ( d ), относительно хорошо согласуется с экспериментальными результатами.Мы также исследовали зависимость ΔVxx4φ f SAW для бислоя W / CoFeB; результаты представлены на фиг. 4F. Как видно, ΔVxx4φ масштабируется с f SAW . Мы подчеркиваем, что уравнение. 2 – единственная форма спинового тока, которая может объяснить эти результаты. Обратите внимание, что линейная зависимость ΔVxx4φ с f SAW позволяет исключить вклады спин-зависимой силы инерции ( 30 ) и связанных эффектов в присутствии SOI ( 31 ), которые пропорциональны более высокому порядку. из ф SAW .
Таким образом, эти результаты демонстрируют, что движение решетки индуцирует спиновой ток. Недавние исследования показали, что спин-вращательная связь ( 14 , 15 ) может вызывать накопление спина в слое НМ, что приводит к генерации спинового тока, если толщина слоя НМ больше, чем длина затухания ПАВ (обычно порядка длины волны ПАВ, которая здесь составляет несколько микрометров) ( 16 ). Чтобы прояснить роль спин-вращательной связи, мы исследовали ΔVxx4φ инвертированных структур, бислоев CoFeB / W.Как в двойных слоях W / CoFeB, так и в CoFeB / W, спин-вращательная связь индуцирует спиновую плотность в слое W, что может вызвать поток спинового тока к слою CoFeB, поскольку последний может действовать как спиновый сток. Если бы такой спиновый ток протекал, направление потока было бы противоположным для нормальной (W / CoFeB) и инвертированной (CoFeB / W) структур и, следовательно, привело бы к ΔVxx4φ с противоположным знаком.
Мы обнаружили, что знаки ΔVxx4φ для бислоев W / CoFeB и CoFeB / W одинаковы, демонстрируя, что спин-вращательная связь не является источником спинового тока (см. Разделы S1 и S3).По той же причине мы можем исключить индуцированную ПАВ спиновую накачку ( 27 , 32 ) из слоя CoFeB и обратный спиновый эффект Холла W-слоя. Это также подтверждается тем фактом, что знаки ΔVxx4φ для бислоев W / CoFeB и Pt / CoFeB одинаковы (см. Рис. 2), хотя знак θ SH для W и Pt различен.
На рис. 5A мы суммируем максимальное значение vxx4φ и rxx2φ при изменении d , обозначенное как vxx, max4φ и rxx, max2φ, соответственно, для каждого бислоя (X = Ta, W, Pt).Включены результаты для бислоев CoFeB / W. Обратите внимание, что структура W зависит от условий роста: исходя из удельного сопротивления пленки ( 33 , 34 ), мы считаем, что W образует высокоомную β-фазу в бислое W / CoFeB, тогда как это смесь β -фаза и низкоомная кристаллическая α-фаза в бислое CoFeB / W. Следовательно, отношение SMR (rxx, max2φ) для последнего меньше из-за меньшего θ SH ( 34 – 36 ). Напротив, мы находим, что vxx, max4φ принимает почти одинаковое значение для двух бислоев, указывая на то, что существуют факторы, отличные от θ SH , которые устанавливают величину vxx, max4φ.На рис. 5В мы построили отношение γ≡vxx, max4φrxx, max2φ, чтобы охарактеризовать такой вклад. Мы обнаружили, что γ заметно больше для бислоев с Pt и (β + α) -W (CoFeB / W), чем с β-W (W / CoFeB) и Ta. Поскольку первые два слоя текстурированы, а последние два сильно разупорядочены (т.е. аморфноподобны), мы считаем, что текстура пленок может влиять на γ. Обнаружена небольшая корреляция между γ и объемным модулем X-слоя.
Рис. 5 Эффективность генерации спинового тока, вызванного движением решетки.( A и B ) Максимальные значения нормированного акустического напряжения vxx, max4φ≡∣ΔVxx4φ / ΔVxx0∣max (красные полосы) и максимального отношения SMR rxx, max2φ≡∣ΔRxx2φ / Rxx0∣max (зеленые полосы) (A) и их отношения γ≡vxx, max4φrxx, max2φ (B), полученные для бислоев X / CoFeB (X = Ta, W и Pt) и бислоев CoFeB / W. W (β) и W (β + α) представляют бислои W / CoFeB и CoFeB / W соответственно.
Физика тенниса | Вращение мяча в полете
Когда мяч в теннисе ему часто придают вращение влияют на его траекторию и отскок.Три самых распространенные способы удара по теннисному мячу плоские (нет спин), топспином или нарезкой (ударьте нижнее / обратное вращение). Тип отжима на мяч влияет на его траекторию в воздухе, а также как он подпрыгивает. Мы рассмотрим эффекты и физика этих трех типов спина. За наших объяснения, мы определим вращательное движение теннисного мяча в направлении топспина прямое вращение / вращение и вращательное движение в направление подкрутки назад вращение / вращение.Однако сначала мы должны рассмотреть Эффект Магнуса, который вызывает различия в двигательном поведении во время полета шары, совершающие разные вращения.
Эффект Магнуса:
Магнус
Эффект – это физическое явление, которое
дополнительная сила на вращающийся объект. В
вращение шара вызывает силы сопротивления на
верх и низ шара должны быть неравными.в
случай обратного вращения (на фото), сопротивление
нижняя часть шара больше, чем верхняя
мяч, потому что тангенциальная скорость
нижняя часть мяча находится в том же направлении, что и
скорость траектории мяча. Это означает
низ шара имеет большую величину
скорость относительно воздуха вокруг него, чем у остальных
мяча, что приводит к увеличению сопротивления
сила.Точно так же перетаскивание вверху
мяч уменьшается, так как верхняя часть мяча имеет
более низкая скорость относительно окружающего воздуха, чем
остальной мяч. Эти силы сопротивления могут быть
считается оказанием неравного давления на
мяч, с большим сопротивлением, соответствующим большему
давление. Результирующий перепад давления тогда
вызывает чистую силу на мяч в направлении
низкое давление.В случае обратного вращения это
приводит к восходящей силе на мяч, а для
верхнее вращение это приводит к действию направленной вниз силы на
мяч. Это похоже на то, как аэродинамический профиль создает
поднимать.
Источник : [2]
Flat Hit:
Удар по мячу без вращения, также
известен как плоский удар, не вращается ни с одним
значительная угловая скорость при пролете
воздух.2где CC это сопротивление
коэффициент,
ρ \ rho
плотность воздуха,
AA
площадь поперечного сечения объекта,
мм
масса объекта,
gg
– ускорение свободного падения, а
vxv_x
а также
vyv_y
– горизонтальная и вертикальная скорости
проект соответственно.В отличие от движения снаряда в
вакуум, горизонтальная и вертикальная составляющие
ускорения не независимы друг от друга
поскольку
axa_x
зависит от
vyv_y
и наоборот.
Источник : [3]
Img Src: https: //www.linkedin.com / today / post / article / 20140920022202-82311677-виртуальная-теннис-академия-урок-1-кусочек-топспин-в-теннисе
Топспин:
Источник изображения:
http://twu.tennis-warehouse.com/learning_center/aerodynamics2.php
Для удара по мячу топспином
игрок поворачивает головку ракетки над
вершина мяча во время удара.Это оказывает
крутящий момент вокруг центра шара, который вызывает
мяч вращается вперед во время его
полет. Как показано на диаграмме выше, топспин равен
характеризуется тангенциальной скоростью
вершина шара, указывающая в том же направлении, что и
траектория мяча.
Удар по мячу топспином
заставляет силу Магнуса воздействовать на мяч
перпендикулярно скорости мяча в
нисходящее направление.Потому что есть дополнительный
направленная вниз сила на мяч, теннисисты могут ударить
мяч с большей скоростью и приземлится
суд, если они применяют топспин к мячу, когда
ударяя по нему. Кроме того, шары можно бить выше
над сеткой, что затрудняет выполнение удара
возврат, потому что дополнительная нисходящая сила тянет
мяч вниз.Это также приводит к более высокому
отскок за мяч.
Источник : [1]
Источник изображения:
http://twu.tennis-warehouse.com/learning_center/aerodynamics2.php
Подспор (обратное вращение):
Чтобы попасть в
мяч с нижним или обратным вращением, игрок
откидывает ракетку назад и засовывает ее под
мяч при ударе по нему.Этот тип выстрела
называется срез. Он оказывает крутящий момент на
центр мяча, который заставляет мяч
вращаться с обратным вращением во время полета.
Как показано на диаграмме выше, нижнее вращение
характеризуется тангенциальной скоростью
вершина мяча направлена в противоположную сторону
направление как траектория полета мяча.
Удар по мячу топспином
заставляет силу Магнуса воздействовать на мяч
перпендикулярно скорости мяча в
восходящее направление.Потому что есть дополнительный
сила, направленная вверх на мяч, кажется, что мяч
«парить» по воздуху во время полета. Срезные снимки
таким образом, как правило, достигают более низкого значения, чем чистая и
с относительно низкой скоростью, чтобы сохранить
им от выхода за пределы двора.
Это приводит к более низкому отскоку мяча.
Кроме того, разрезание мяча позволяет игроку
попасть по мячу в точное место в
суд противников.Однако из-за способа срезать
выстрелы попадают, если игрок пытается разрезать
мяч, который движется слишком быстро, или нанесенный удар
слишком сильно, он или она может легко выбить мяч
границ.
Источник : [1]
Источник изображения: http://twu.tennis-warehouse.com/learning_center/aerodynamics2.php
Наблюдение антиферромагнитного спинового эффекта Холла
Като Ю.К., Майерс Р.С., Госсард А.С. и Авшалом Д.Д. Наблюдение спинового эффекта Холла в полупроводниках. Наука 306 , 1910–1913 (2004).
CAS Статья Google Scholar
Kimata, M. et al. Магнитные и магнитные обратные спиновые эффекты Холла в неколлинеарном антиферромагнетике. Природа 565 , 627–630 (2019).
CAS Статья Google Scholar
Nan, T. X. et al. Управление поляризацией спинового тока посредством неколлинеарного антиферромагнетизма. Nat. Commun. 11 , 4671 (2020).
CAS Статья Google Scholar
Baek, S.C. et al. Спиновые токи и спин-орбитальные моменты в ферромагнитных трехслойных слоях. Nat. Матер. 17 , 509–513 (2018).
CAS Статья Google Scholar
Мирон И. М. и др. Перпендикулярное переключение одиночного ферромагнитного слоя, вызванное инжекцией тока в плоскости. Природа 476 , 189–193 (2011).
CAS Статья Google Scholar
Liu, L. et al. Спиново-моментное переключение с гигантским спин-эффектом Холла тантала. Наука 336 , 555–558 (2012).
CAS Статья Google Scholar
Kurebayashi, H. et al. Антидемпфирующий вращающий момент на орбите, возникающий из-за кривизны Берри. Nat. Nanotechnol. 9 , 211–217 (2014).
CAS Статья Google Scholar
Юнгвирт, Т., Марти, X., Уодли, П., Вундерлих, Дж.Антиферромагнитная спинтроника. Nat. Nanotechnol. 11 , 231–241 (2016).
CAS Статья Google Scholar
Chen, X. Z. et al. Управление спин-орбитальным моментом Нееля в антиферромагнетике электрическим полем. Nat. Матер. 18 , 931–935 (2019).
CAS Статья Google Scholar
Manchon, A. et al.Индуцированные током спин-орбитальные моменты в ферромагнитных и антиферромагнитных системах. Ред. Мод. Phys. 91 , 035004 (2019).
CAS Статья Google Scholar
MacNeill, D. et al. Управление спин-орбитальными моментами за счет симметрии кристалла в двойных слоях WTe 2 / ферромагнетик. Nat. Phys. 13 , 300–305 (2017).
CAS Статья Google Scholar
Song, P. et al. Сосуществование большого обычного и плоского спинового эффекта Холла с большой длиной спиновой диффузии в низкосимметричном полуметалле при комнатной температуре. Nat. Матер. 19 , 292–298 (2020).
CAS Статья Google Scholar
Sinova, J. et al. Универсальный собственный спиновый эффект Холла. Phys. Rev. Lett. 92 , 126603 (2004).
Артикул Google Scholar
Zhang, W. et al. Гигантский зависящий от граней спин-орбитальный момент и спин-холловская проводимость в треугольном антиферромагнетике IrMn 3 . Sci. Adv. 2 , e1600759 (2016).
Артикул Google Scholar
Oh, Y. W. et al. Бесполевое переключение перпендикулярной намагниченности за счет спин-орбитального момента в структурах антиферромагнетик / ферромагнетик / оксид. Nat. Nanotechnol. 11 , 878 (2016).
CAS Статья Google Scholar
Liu, Y. et al. Накопление спина вне плоскости на поверхности (001) антиферромагнетика IrMn 3 под действием тока. Phys. Ред. Заявка 12 , 064046 (2019).
CAS Статья Google Scholar
Fukami, S. et al. Переключение намагниченности спин-орбитальным моментом в двухслойной системе антиферромагнетик – ферромагнетик. Nat. Матер. 15 , 535–541 (2016).
CAS Статья Google Scholar
Zhang, W. et al. Спиновые эффекты Холла в металлических антиферромагнетиках. Phys. Rev. Lett. 113 , 196602 (2014).
Артикул Google Scholar
Z˘elezný, J., Zhang, Y., Felser, C. & Yan, B. Спин-поляризованный ток в неколлинеарных антиферромагнетиках. Phys. Rev. Lett. 119 , 187204 (2017).
Артикул Google Scholar
González-Hernández, R. et al. Магнитный спиновый эффект Холла в коллинеарном антиферромагнетике. Препринт на https://arxiv.org/abs/2002.07073 (2020).
Bodnar, Y. S. et al. Запись и чтение антиферромагнетика Mn 2 Au с помощью спин-орбитальных моментов Нееля и большого анизотропного магнитосопротивления. Nat.Commun. 9 , 348 (2018).
Артикул Google Scholar
Wadley, P. et al. Электрическое переключение антиферромагнетика. Наука 351 , 587–590 (2016).
CAS Статья Google Scholar
Чжан, Ю., Лю, К., Мяо, Б. Ф., Дин, Х. Ф. и Ван, X. Р. Анатомия электрических сигналов и форма линии постоянного напряжения в спин-крутящем ферромагнитном резонансе. Phys. Ред. B 99 , 064424 (2019).
CAS Статья Google Scholar
Лю Л., Морияма Т., Ральф Д. и Бурман Р. Ферромагнитный резонанс со спиновым моментом, индуцированный спиновым эффектом Холла. Phys. Rev. Lett. 106 , 036601 (2011).
Артикул Google Scholar
Bodnar, Y. S. et al. Визуализация индуцированного током переключения вектора Нееля в антиферромагнетике Mn 2 Au. Phys. Ред. B 99 , 140409 (2019).
CAS Статья Google Scholar
Fukami, S. et al. Схема переключения крутящего момента спин-орбиты с коллинеарной магнитной осью легкого перемещения и текущей конфигурацией. Nat. Nanotechnol. 11 , 621–625 (2016).
CAS Статья Google Scholar
Shi, S. et al. Полностью электрическое переключение намагниченности и взаимодействие Дзялошинского – Мория в гетероструктурах WTe 2 / ферромагнетик. Nat. Nanotechnol. 14 , 945–949 (2019).
CAS Статья Google Scholar
Saglam, H. et al. Независимость спин-орбитальных моментов от направления обменного смещения в бислоях Ni 81 Fe 19 / IrMn. Phys. Ред. B 98 , 094407 (2018).
CAS Статья Google Scholar
Holanda, J.и другие. Модуляция магнитного затухания в IrMn 3 / Ni 80 Fe 20 посредством магнитного спинового эффекта Холла. Phys. Rev. Lett. 124 , 087204 (2020).
CAS Статья Google Scholar
Zhou, X. F. et al. От полевого момента до антидемпфирующего момента в антиферромагнетике Mn 2 Au. Phys. Ред. Заявка 11 , 054030 (2019).
CAS Статья Google Scholar
Wang, Y. et al. Перемагничивание при комнатной температуре в топологических гетероструктурах изолятор – ферромагнетик спин-орбитальными моментами. Nat. Commun. 8 , 1364 (2017).
CAS Статья Google Scholar
Спиновый фотогальванический эффект в двумерных коллинеарных антиферромагнетиках
Модельные и возможные материалы
Коллинеарный АСМ-материал состоит из двух FM-подрешеток с противоположными намагниченностями.Эти две подрешетки обычно соединяются операцией симметрии, что приводит к нулевой суммарной намагниченности. Одной из наиболее распространенных операций симметрии для компенсации намагниченности является симметрия \ (\ widehat T \ widehat I \), как показано на рис. 1a. В таком АСМ-материале, несмотря на то, что симметрия относительно обращения времени (\ (\ widehat T \)) и симметрии пространственной инверсии (\ (\ widehat I \)) нарушена, объединенная \ (\ widehat T \ widehat I \) симметрия все еще сохраняется и связывает магнитные подрешетки с противоположными намагниченностями.Эта симметрия заставляет энергетические зоны двух подрешеток быть вырожденными. В отсутствие эффекта SOC спин является хорошим квантовым числом, т. Е. Сохраняющейся величиной. Это позволяет нам исследовать SPGE АФМ-материалов с сохранением \ (\ widehat T \ widehat I \) в двух подрешетках с намагниченностью со спином вверх и вниз по отдельности, используя модель, предложенную Юнгом и др. 23 .
Рис. 1: Принцип работы SPGE.a Схема материала AFM с симметрией \ ({\ hat T} {\ hat I} \) (вверху) и соответствующей симметричной полосовой структурой (внизу). b , c Спин-поляризованные подрешетки и связанные с ними синглетно-зонные структуры соответственно. Свет генерирует ток PGE в каждой подрешетке (вверху), а соответствующий оптический переход происходит в спиновой подзоне (внизу). Ситуация для подрешетки с намагниченностями со спином вверх и вниз показана в ( b ) и ( c ) соответственно. d Устройство спинтроники на основе СПГЭ с двумерным коллинеарным АСМ материалом.
Сначала опишем фотогальванический эффект (ФГЭ) в одной спиновой подрешетке.c ({\ boldsymbol {k}}) \ delta \ left [{\ omega _ {mn} ({\ mathbf {k}}) – \ omega} \ right]}, \ end {array} $$
(2)
где \ (f_ {nm} ({\ mathbf {k}}) = f_n ({\ mathbf {k}}) – f_m ({\ mathbf {k}}) \) – разница коэффициентов занятости, \ (\ hbar \ omega _ {mn} ({\ mathbf {k}}) = {\ it {\ epsilon}} _ m ({\ mathbf {k}}) – {\ it {\ epsilon}} _ n ({\ mathbf {k}}) \) – разность энергий полос, а \ (\ omega \) – частота света. Функция \ (\ delta \) возникает из квантового времени жизни электронов (см. Дополнительное примечание 5).\ downarrow \), что приводит к SPGE в материале AFM со слабым эффектом SOC. Используемая здесь модель включает только межзонный оптический переход и подходит для всех полупроводников AFM. Для коллективизированных АСМ материалов должен быть нелинейный эффект Друде (внутризонный переход), возникающий из-за диполя кривизны Берри 28,29 . Поскольку все обнаруженные 2D ван-дер-ваальсовы антиферромагнетики до сих пор являются полупроводниками, их внутризонный оптический переход в SPGE отсутствует и в нашей работе игнорируется.
Таким образом, мы можем сконструировать спинтронное устройство на основе SPGE, как показано на рис. 1d: лазерный луч излучает двумерный коллинеарный материал AFM с симметрией \ ({\ widehat T} {\ widehat I} \), и генерирует чистый спиновой ток J s без каких-либо зарядных токов J c , который может вводить спиновой ток в подключенный терминал бесконтактным и сверхбыстрым способом. Ожидается, что спиновый ток, генерируемый этим механизмом, будет иметь большую длину диффузии спина по сравнению с генерируемым механизмами, связанными с эффектом SOC 15,16,17,18,19,20,21,22 .Это связано с сохранением спина и отсутствием поля SOC, зависящего от импульса, которые не приводят к декогеренции спина по механизму Дьяконова – Переля 30 во время рассеяния. Спиновый ток может иметь интересные взаимодействия с локальными магнитными моментами 31 , что заслуживает дальнейшего изучения.
Богатая коллекция слоистых магнитных материалов 32,33,34 . Однако не все эти магнитные порядки поддерживают требуемую симметрию. Чтобы определить подходящий порядок АСМ для SPGE, мы используем модель сотовой решетки, которую применяют большинство 2D коллинеарных материалов АСМ.На рис. 2 показаны четыре распространенных магнитных порядка. Соответствующие материалы приведены в дополнительной таблице 1. Порядки АСМ зигзагообразного и полосчатого типа, такие как MPS 3 (M = Fe, Co, Ni) 35,36,37,38,39 и MSiSe 3 (M = V, Fe, Ni) 40 показаны на рис. 2а, б соответственно. Симметрия \ (\ widehat I \) каждой подрешетки может быть ясно видна для этих порядков AFM, предотвращая PGE в каждой подрешетке и SPGE решеток AFM. На рис. 2в показан порядок АСМ типа Нееля, в котором соседние магнитные моменты связаны друг с другом антипараллельно.Такой порядок АСМ был обнаружен в монослое MnPS 3 7,8,41,42,43 и MnPSe 3 44 в экспериментах. В этом АФМ-порядке симметрия \ (\ widehat I \) каждой подрешетки нарушается, и две подрешетки связаны симметрией \ (\ widehat T \ widehat I \). Этот тип AFM-порядка удовлетворяет симметрии SPGE. В отличие от вышеупомянутых порядков АСМ, существующих в однослойных 2D-материалах, существует АСМ-порядок A-типа, который может возникать только в многослойных 2D-магнитах (рис.2d), например CrX 3 (X = Cl, Br, I) 2,3,4 и MnBi 2 Te 4 5,6 . В этих материалах магнитные атомы расположены в порядке FM внутри слоя и в порядке AFM между соседними слоями. Хотя \ (\ widehat I \) симметрия сохраняется для монослоя, в бислое она вынуждена нарушаться из-за межслойного наложения, что заставляет АСМ-материалы A-типа сохранять \ ({\ widehat T} {\ widehat I} \ ) симметричность и совместимость для реализации SPGE.На основании проведенного выше анализа мы можем выбрать подходящие 2D-магнитные материалы. В качестве конкретных примеров мы берем монослой MnPS 3 типа Нееля и двухслойный CrCl 3 типа A в качестве двух репрезентативных материалов. Два экспериментально синтезированных двумерных коллинеарных АСМ материала обладают незначительными эффектами SOC и подходящей шириной запрещенной зоны для SPGE.
Рис. 2: Схема четырех порядков АСМ в двумерной сотовой решетке.a зигзагообразного типа, b полосатого типа, c типа Néel и d A-типа.На вставке ( d ) показан вид сбоку АСМ A-типа.
Результаты расчетов из первых принципов
Трихалькогенид переходного металла MnPS 3 представляет собой АСМ материал с температурой Нееля ( T N ) 78 K в массе 45,46 . Он имеет слоистую структуру, в которой атомы Mn образуют сотовую решетку в каждом слое. В центре каждого шестиугольника Mn расположен узел в форме гантели P 2 S 6 (рис. 3a).Магнитные моменты ближайших соседних атомов Mn антипараллельны друг другу, образуя АФМ-порядок неелевского типа. Недавно он был успешно расслоен до однослойного 7,8,41,42,43 , и порядок АСМ типа Нееля может быть сохранен. Магнитные подрешетки в монослое MnPS 3 имеют нецентросимметричную структуру с точечной группой D 3 , которая содержит симметрию вращения C 3 по оси z и C 2 ось вращения вокруг направления y , как показано на рис.3а. Симметрия \ ({\ widehat T} {\ widehat I} \), которая соединяет две подрешетки, четко отражается в рассчитанной спиновой плотности (рис. 3b). Оказывается, что рассчитанные спиновые плотности немагнитных атомов P и S идентичны для двух спиновых состояний. Тем не менее, спиновые плотности атомов Mn распределены асимметрично для противоположных спиновых состояний, что приводит к нарушенной симметрии \ (\ widehat I \) в двух спиновых состояниях. Плотности противоположных спиновых подрешеток могут быть преобразованы друг в друга применением симметрии \ ({\ widehat T} {\ widehat I} \).На рисунке 3c показана рассчитанная зонная структура монослоя MnPS 3 , которая согласуется с предыдущими работами 40,47,48 . Прямая запрещенная зона 2,50 эВ находится в точках K 47 . Полосы, вносимые электронами со спином вверх и вниз, являются вырожденными и также демонстрируют незначительный эффект SOC (см. Дополнительный рисунок 1). Эти характеристики поддерживают СПГЭ в монослое MnPS 3 .
Рис. 3: Результаты расчета монослоя MnPS 3 .a Вид сверху (слева) и вид сбоку (справа) монослоя MnPS 3 .2 \) при 3,36 эВ, что сопоставимо с заявленным зарядом PGE в монослое SnTe 49,50,51,52 и двухслойном WTe 2 29 , а также с обычными 3D сегнетоэлектриками (такими как BiTiO 3 27 и PbTiO 3 26 ). Мы замечаем, что топологические полуметаллы Вейля 53,54,55 , такие как TaAs, имеют очень большие коэффициенты PGE из-за существования конусов Вейля 56 . Точно так же мы предполагаем, что топологические полуметаллы AFM обладают большим SPGE, если выполняется симметрия, что заслуживает дальнейшего изучения.\ uparrow \) при 3,36 эВ на рис. 3д. Можно обнаружить, что горячие точки (области, где абсолютные значения k -разрешенных коэффициентов PGE велики) появляются в k точках в направлении \ ({\ Gamma} {\ mathrm {M}} \) и близко к точке М. Это может происходить из-за фотоперехода из второй валентной зоны в первую зону проводимости вблизи точки M, как показано на рис. 3c, где валентная зона имеет плоский характер. Кроме того, симметрия \ ({\ widehat T} {\ widehat I} \) гарантирует, что коэффициенты PGE для состояния со спином вниз противоположны таковым для состояния со спином вверх.\ downarrow \), как ожидается, будет значительным и может быть легко обнаружен при энергии видимого света с помощью магнитооптического эффекта Керра или обратного спинового эффекта Холла. Кроме того, SPGE не ограничивается монослоем, поскольку многослойный MnPS 3 также обладает необходимой симметрией (см. Дополнительное примечание 4).
Далее рассмотрим СПГЭ в бислое CrCl 3 . Объемный CrCl 3 – это АСМ полупроводник с T N = 15,5 K 57 .Недавно он был успешно использован до атомного предела, и порядок АСМ A-типа поддерживается вплоть до двухслойного 13,14,58 . В каждом монослое атомы Cr образуют сотовую структуру, а шесть атомов Cl в октаэдрической координации окружают каждый атом Cr. При наложении монослоев возникает межслойный сдвиг (рис. 4а). Магнитные моменты атомов Cr ферромагнитно связаны в одном слое, в то время как антиферромагнитно связаны между соседними слоями, образуя АФМ-порядок A-типа.Хотя монослой CrCl 3 центросимметричен, двухслойное наложение нарушает симметрию \ (\ widehat I \). Эта нарушенная симметрия \ (\ widehat I \) ясно показана в рассчитанных плотностях для двух различных спиновых состояний, как показано на рис. 4b.
Рис. 4: Результаты расчета двухслойного CrCl 3 .a Кристаллическая структура двухслойного CrCl 3 . Левая панель показывает структуру одного слоя, а правая панель показывает двухслойное наложение (показаны только атомы Cr). b Расчетные плотности (виды сбоку, изоповерхность 0,09 э / Å 3 ) для состояний со вращением вверх (вверху) и вниз (внизу) двухслойного CrCl 3 . c Расчетная ленточная структура. d Коэффициенты PGE подрешетки спин-вверх двухслойного CrCl 3 .
На рис. 4в показана рассчитанная зонная структура двухслойного CrCl 3 . Получена ширина запрещенной зоны 2,61 эВ. Крамерсовское вырождение зонной структуры является результатом симметрии \ ({\ widehat T} {\ widehat I} \).{\ uparrow (\ downarrow)}) \). Коэффициенты PGE состояний со спином вниз противоположны коэффициентам состояний со спином вверх из-за симметрии \ ({\ widehat T} {\ widehat I} \), что приводит к SPGE в двухслойном CrCl 3 . Аналогичный СПГЭ ожидается и в ровном слое CrCl 3 . Тогда как для CrCl 3 с нечетными слоями симметрия \ (\ widehat I \) восстанавливается, что препятствует СПГР. Это указывает на интересный характер нечетно-четного слоя SPGE в немногослойном CrCl 3 .
Эффекты фазы отжима? – Вопросы и ответы в МРТ
Эффекты фазы вращения Что такое спин-фазовые эффекты? |
| Эффекты спиновой фазы относятся к изменениям угла (фазы) прецессии, которым подвергаются протоны, когда они движутся в пределах градиента.Важной функцией градиентов магнитного поля является пространственное кодирование MR-сигнала. Если протон меняет положение во время применения этих градиентов, он приобретает или теряет фазу по сравнению с неподвижной тканью. В рутинной визуализации эффекты спиновой фазы в первую очередь ответственны за потерю сигнала для потока в плоскости и в областях турбулентности сосудов. Эффекты спин-фазы, не являющиеся чисто деструктивным явлением, также можно количественно оценить и использовать для создания МР-ангиограмм и измерения сосудистого или спинномозгового кровотока. | Низкий сигнал об артериальном кровотоке в плоскости из-за спин-фазовых эффектов |
Чтобы получить представление о величине спин-фазовых эффектов, давайте вычислим фазу, набираемую протоном, движущимся через градиент магнитного поля. Для простоты предположим, что протон движется с постоянной скоростью ( v ) в течение времени ( t ) в пределах градиента, имеющего постоянную величину G .Положение протона будет тогда x = vt , а его резонансная частота смещения f, будет линейной функцией времени, задаваемой формулой
f = γGx = γGvt
Поскольку общий коэффициент усиления фазы представляет собой сумму возрастающих изменений частоты во времени, чистый фазовый сдвиг этого протона, Φ (t) , , можно записать как
Φ (t) = ∫ f dt = ∫ (γGvt) dt = γGv ∫ t dt = ½γGvt²
Таким образом, это уравнение демонстрирует важную (но не интуитивно понятную) концепцию: фазовый сдвиг, испытываемый движущимся вращением, будет пропорционален его скорости, силе приложенного градиента и квадрату отрезка времени, в котором он движется. этот градиент.
Hahn EL. Обнаружение движения морской воды по ядерной прецессии. J. Geophys Res, 1960; 65: 776-777. (Помимо спиновых эхо-сигналов, Хан также обнаружил градиентные эхо-сигналы, возникающие при обращении градиентного поля, описанном в этой статье. Он даже пошел дальше, чтобы показать, как можно измерить скорость на основе индуцированных градиентом фазовых сдвигов, основы современного фазового контраста.

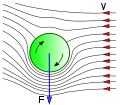
 При этом, спин нейтрона до входа в магнитное поле и после выхода из него остается неизменным. Инерционные эффекты, воздействующие на нейтрон, проявляются только в области магнитного поля и это можно обнаружить только при помощи квантовой механики.
При этом, спин нейтрона до входа в магнитное поле и после выхода из него остается неизменным. Инерционные эффекты, воздействующие на нейтрон, проявляются только в области магнитного поля и это можно обнаружить только при помощи квантовой механики. При этом, в самой катушке должно было быть маленькое окошко, через которое нейтронный луч проникал в область создаваемого ею магнитного поля. Подходящая геометрия обмоток этой катушки была получена при помощи компьютерного моделирования, а система была изготовлена и первоначально испытана на источнике нейтронов в Венском технологическом университете. Окончательные же эксперименты и измерения проводились на установке ILL, Гренобль, Франция.
При этом, в самой катушке должно было быть маленькое окошко, через которое нейтронный луч проникал в область создаваемого ею магнитного поля. Подходящая геометрия обмоток этой катушки была получена при помощи компьютерного моделирования, а система была изготовлена и первоначально испытана на источнике нейтронов в Венском технологическом университете. Окончательные же эксперименты и измерения проводились на установке ILL, Гренобль, Франция. org, sci-dig.ru
org, sci-dig.ru