Физика mg: Что такое mg в Физике? Прошу помогите(((
- Сила тяжести – в чем измеряется? Чему равна?
- MG — Научно-исследовательский портал Уральского федерального университета
- Влияние физико-химических свойств растворов Mg, Na и K на процессы фотохимического образования комплексов урана с органическими лигандами
- Шеляпина Марина Германовна – ЯФМИ
- Потенциальная энергия: определение, виды, формулы
- Nanodispersed Mg-based Powders Received in a Hydrogen-argon Plasma Flow and Estimation of their Application Prospects as Hydrogen Storage Materials
- Урок 15. основы гидромеханики – Физика – 10 класс
- Обзор силы гравитации Рона Куртуса
- Масса, вес, плотность
- Плотность
- Законы движения Ньютона
- ГЛАВА 4
- Нормальные, растягивающие и другие примеры сил
- Физика лифта
Сила тяжести – в чем измеряется? Чему равна?
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Сила тяготения
В 1682 году Исаак Ньютон открыл Закон Всемирного тяготения
 Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.Формула силы тяготения согласно этому закону выглядит так:
Закон Всемирного тяготения F = GMm/R2 F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6.67 × 10-11 м3 кг-1 с-2 |
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря Закону Всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей
Несколько лет назад ученые открыли такое явление, как гравитационные волны — но это не тоже самое, что гравитация:
Источник: YouTube-канал «Это работает»
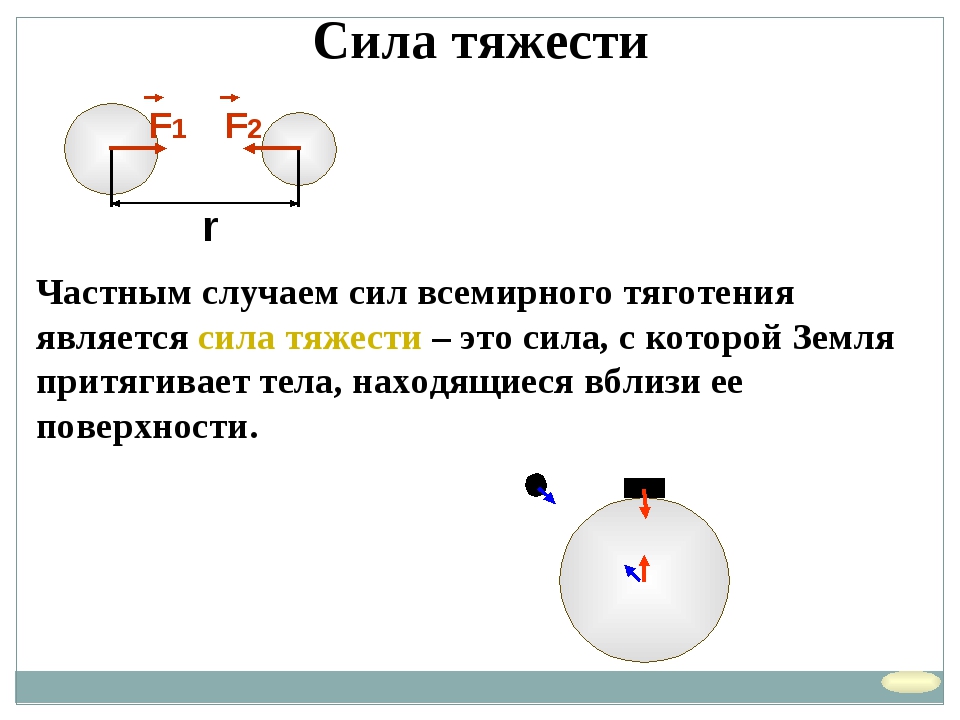
Сила тяжести
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести F = mg F — сила тяжести [Н] m — масса тела [кг] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2 |
На первый взгляд сила тяжести очень похожа на вес тела.
Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Но разница все-таки есть, давайте разбираться.Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также, важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. Вес зависит также от ускорения, с которым движутся тело или опора.
Например, в лифте вес тела зависит от того, куда и с каким ускорением движется тело. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения.
F = mg
F = GMm/R2
Приравниваем правые части:
mg = GMm/R2
Делим на массу левую и правую части:
g = GM/R2
Это и будет формула ускорения свободного падения.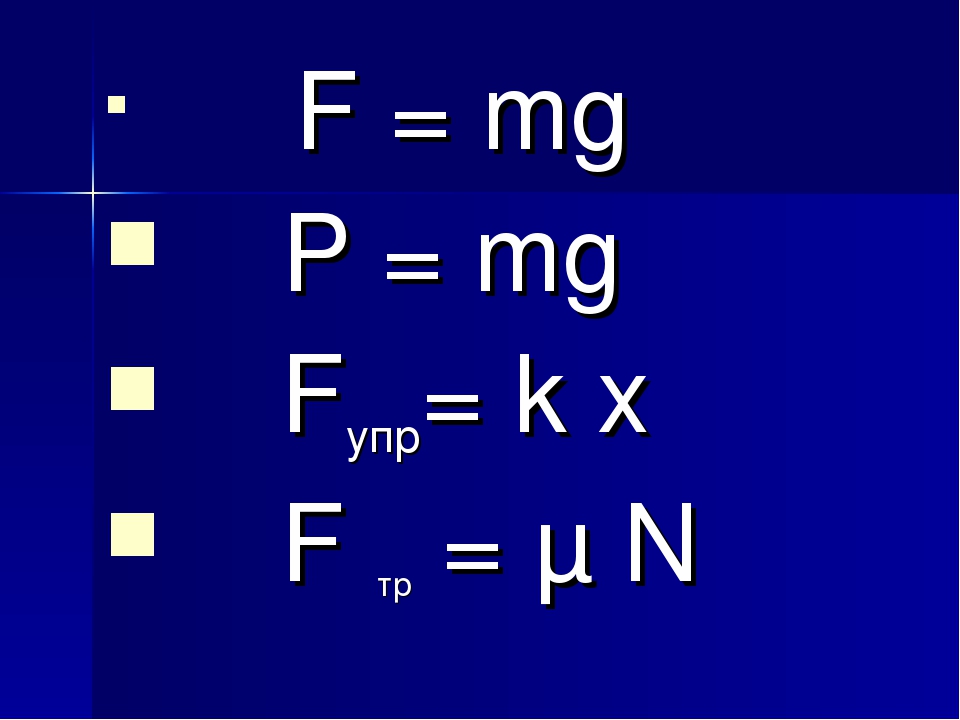 Ускорение свободного падения для каждой планеты уникально, эта формула нужна.
Ускорение свободного падения для каждой планеты уникально, эта формула нужна.
Формула для ускорения свободного падения g = GM/R2 F — сила тяготения [Н] M — масса планеты [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6.67 × 10-11 м3 кг-1 с-2 |
А теперь задачка
Определить силу тяжести, действующую на тело массой 80 кг.
Решение:
Не смотря на кажущуюся простоту, тут есть над чем подумать.Вроде бы просто нужно взять формулу F = mg, подставить числа и дело в шляпе.
Да, но есть один нюанс: в значении ускорения свободного падения для Земли очень много знаков после запятой.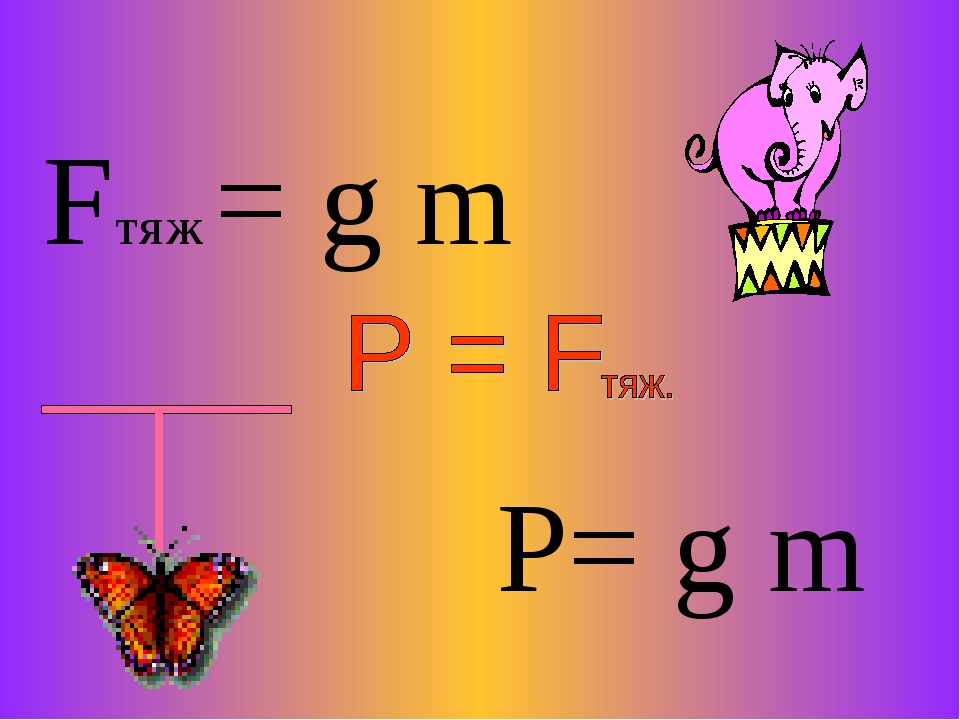
В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Итак, F = mg.
F = 80*10 = 800 Н
Ответ: 800 Н.
Учимся летать
В серии книг Дугласа Адамса «Автостопом по Галактике» говорится, что летать — это просто промахиваться мимо Земли. Если ты промахнулся мимо Земли и достиг первой космической скорости 7,9 км/с, то ты стал искусственным спутником Земли.
Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него так получалось, аппарат должен иметь начальную скорость, равную или большую первой космической скорости.
Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.
Подробнее о возможностях полетов и невесомости читайте в нашей статье про вес тела.
Научить летать по-настоящему физика, конечно, не может, но обмануть систему и найти лазейки — это всегда пожалуйста. Запишите ребенка на бесплатный вводный урок в современную школу Skysmart: покажем, как у нас все устроено, определим план развития и влюбим в науку!
MG — Научно-исследовательский портал Уральского федерального университета
TY – JOUR
T1 – НИЗКОТЕМПЕРАТУРНАЯ ЛЮМИНЕСЦЕНЦИЯ И ТЕРМОСТИМУЛИРОВАННАЯ ЛЮМИНЕСЦЕНЦИЯ МОНОКРИСТАЛЛОВ BEO : MG
AU – Огородников, Игорь Николаевич
AU – Петренко, Максим Дмитриевич
AU – Иванов, Владимир Юрьевич
PY – 2018
Y1 – 2018
N2 – Люминесценция и термостимулированная люминесценция (ТСЛ) кристаллов BeO : Mg исследованы при T=6-380 K. Получены кривые ТСЛ, а также спектры люминесценции (1.2-6.5 eV), возбуждения и отражения (3.7-20 eV). Установлено, что внедрение изовалентной примеси магния в BeO приводит к появлению трех новых широких полос люминесценции при 6.2-6.3, 4.3-4.4 и 1.9-2.6 eV. Первые две отнесены к излучательной аннигиляции релаксированного околопримесного (Mg) экситона, возбужденное состояние которого формируется в результате переноса энергии свободными экситонами. Примесные ВУФ- и УФ-полосы сопоставлены с таковыми для собственной люминесценции BeO, обусловленной излучательной аннигиляцией автолокализованных экситонов (АЛЭ) двух типов: в BeO : Mg полоса при 6.2-6.3 eV сопоставлена с полосой BeO при 6.7 eV (АЛЭ1), а полоса при 4.3-4.4 eV — с полосой BeO при 4.9 eV (АЛЭ2). В видимой области спектр люминесценции обусловлен суперпозицией внутрицентровых переходов в примесном комплексе, включающем ион магния. Проявление полос рентгенолюминесценции BeO : Mg при T=6 K свидетельствует об их возбуждении при переходах зона–зона и в рекомбинационных процессах.
Получены кривые ТСЛ, а также спектры люминесценции (1.2-6.5 eV), возбуждения и отражения (3.7-20 eV). Установлено, что внедрение изовалентной примеси магния в BeO приводит к появлению трех новых широких полос люминесценции при 6.2-6.3, 4.3-4.4 и 1.9-2.6 eV. Первые две отнесены к излучательной аннигиляции релаксированного околопримесного (Mg) экситона, возбужденное состояние которого формируется в результате переноса энергии свободными экситонами. Примесные ВУФ- и УФ-полосы сопоставлены с таковыми для собственной люминесценции BeO, обусловленной излучательной аннигиляцией автолокализованных экситонов (АЛЭ) двух типов: в BeO : Mg полоса при 6.2-6.3 eV сопоставлена с полосой BeO при 6.7 eV (АЛЭ1), а полоса при 4.3-4.4 eV — с полосой BeO при 4.9 eV (АЛЭ2). В видимой области спектр люминесценции обусловлен суперпозицией внутрицентровых переходов в примесном комплексе, включающем ион магния. Проявление полос рентгенолюминесценции BeO : Mg при T=6 K свидетельствует об их возбуждении при переходах зона–зона и в рекомбинационных процессах. Определены энергетические характеристики примесных состояний в BeO : Mg, выявлено влияние изовалентной примеси на флуктуационную перестройку структуры BeO : Mg в области термической трансформации АЛЭ_1-> АЛЭ2. Работа выполнена при частичной финансовой поддержке постановления N 211 Правительства Российской Федерации (контракт N 02.A03.21.0006, ключевой центр превосходства “Радиационные и ядерные технологии”) и Министерства образования и науки Российской Федерации (базовая часть госзадания на выполнение НИР для УрФУ им. Б.Н. Ельцина).
Определены энергетические характеристики примесных состояний в BeO : Mg, выявлено влияние изовалентной примеси на флуктуационную перестройку структуры BeO : Mg в области термической трансформации АЛЭ_1-> АЛЭ2. Работа выполнена при частичной финансовой поддержке постановления N 211 Правительства Российской Федерации (контракт N 02.A03.21.0006, ключевой центр превосходства “Радиационные и ядерные технологии”) и Министерства образования и науки Российской Федерации (базовая часть госзадания на выполнение НИР для УрФУ им. Б.Н. Ельцина).
AB – Люминесценция и термостимулированная люминесценция (ТСЛ) кристаллов BeO : Mg исследованы при T=6-380 K. Получены кривые ТСЛ, а также спектры люминесценции (1.2-6.5 eV), возбуждения и отражения (3.7-20 eV). Установлено, что внедрение изовалентной примеси магния в BeO приводит к появлению трех новых широких полос люминесценции при 6.2-6.3, 4.3-4.4 и 1.9-2.6 eV. Первые две отнесены к излучательной аннигиляции релаксированного околопримесного (Mg) экситона, возбужденное состояние которого формируется в результате переноса энергии свободными экситонами. Примесные ВУФ- и УФ-полосы сопоставлены с таковыми для собственной люминесценции BeO, обусловленной излучательной аннигиляцией автолокализованных экситонов (АЛЭ) двух типов: в BeO : Mg полоса при 6.2-6.3 eV сопоставлена с полосой BeO при 6.7 eV (АЛЭ1), а полоса при 4.3-4.4 eV — с полосой BeO при 4.9 eV (АЛЭ2). В видимой области спектр люминесценции обусловлен суперпозицией внутрицентровых переходов в примесном комплексе, включающем ион магния. Проявление полос рентгенолюминесценции BeO : Mg при T=6 K свидетельствует об их возбуждении при переходах зона–зона и в рекомбинационных процессах. Определены энергетические характеристики примесных состояний в BeO : Mg, выявлено влияние изовалентной примеси на флуктуационную перестройку структуры BeO : Mg в области термической трансформации АЛЭ_1-> АЛЭ2. Работа выполнена при частичной финансовой поддержке постановления N 211 Правительства Российской Федерации (контракт N 02.A03.21.0006, ключевой центр превосходства “Радиационные и ядерные технологии”) и Министерства образования и науки Российской Федерации (базовая часть госзадания на выполнение НИР для УрФУ им.
Примесные ВУФ- и УФ-полосы сопоставлены с таковыми для собственной люминесценции BeO, обусловленной излучательной аннигиляцией автолокализованных экситонов (АЛЭ) двух типов: в BeO : Mg полоса при 6.2-6.3 eV сопоставлена с полосой BeO при 6.7 eV (АЛЭ1), а полоса при 4.3-4.4 eV — с полосой BeO при 4.9 eV (АЛЭ2). В видимой области спектр люминесценции обусловлен суперпозицией внутрицентровых переходов в примесном комплексе, включающем ион магния. Проявление полос рентгенолюминесценции BeO : Mg при T=6 K свидетельствует об их возбуждении при переходах зона–зона и в рекомбинационных процессах. Определены энергетические характеристики примесных состояний в BeO : Mg, выявлено влияние изовалентной примеси на флуктуационную перестройку структуры BeO : Mg в области термической трансформации АЛЭ_1-> АЛЭ2. Работа выполнена при частичной финансовой поддержке постановления N 211 Правительства Российской Федерации (контракт N 02.A03.21.0006, ключевой центр превосходства “Радиационные и ядерные технологии”) и Министерства образования и науки Российской Федерации (базовая часть госзадания на выполнение НИР для УрФУ им. Б.Н. Ельцина).
Б.Н. Ельцина).
UR – http://elibrary.ru/item.asp?id=32737390
U2 – 10.21883/FTT.2018.01.45300.171
DO – 10.21883/FTT.2018.01.45300.171
M3 – Статья
VL – 60
SP – 132
EP – 144
JO – Физика твердого тела
JF – Физика твердого тела
SN – 0367-3294
IS – 1(15)
ER –
| Abstract: | Методом электронного поглощения исследовано влияние физико-химических свойств растворов Mg, Na и K на процессы фотохимического образования нанокластеров комплексов трех-, четырех- и пятивалентного урана с органическими лигандами при светодиодном облучении растворов UO2(ClO4)2⋅5h3O в ацетоне (область 420–440 нм). Установлены закономерности таких процессов. В системах UO2(ClO4)2⋅5h3O в ацетоне с добавлением ацетонового раствора катионов Mg, Na при облучении происходит фотополимеризация ацетона, а катализатором процесса являются возбужденные комплексы уранила.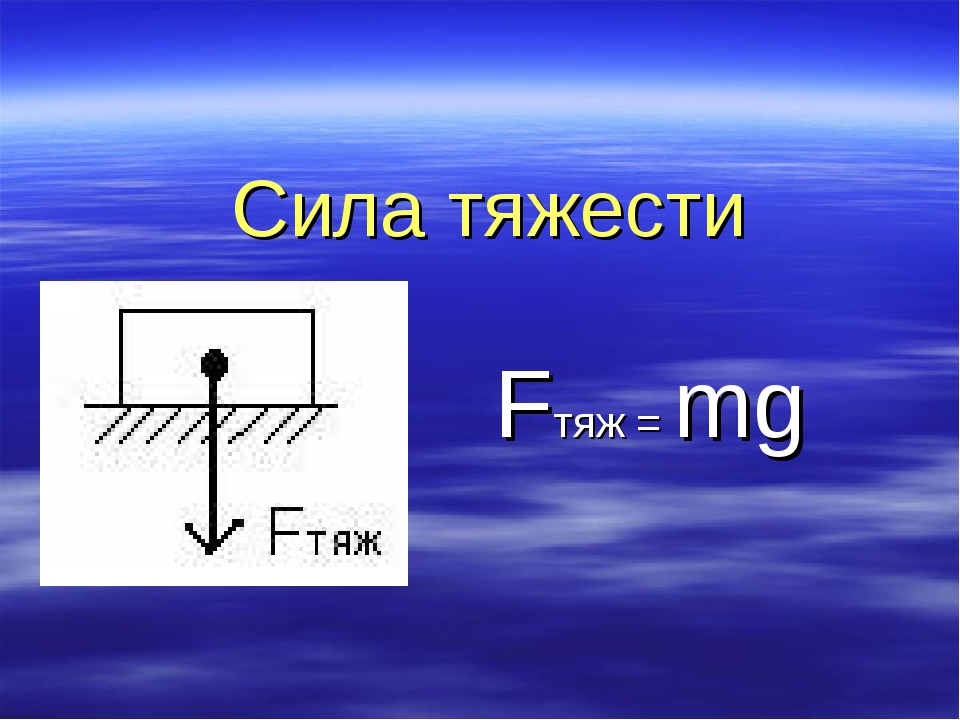 В полимере, который представляет собой очень вязкую темно-коричневую жидкость, уран находится в виде нанокластеров соединений пяти- и четырехвалентного урана, образующихся в результате фотохимических превращений. В спектрах образцов растворов UO2(ClO4)2⋅5h3O в ацетоне с добавлением водного раствора катионов Mg, K в воде наблюдается появление полос, принадлежащих комплексам трех-, четырех- и пятивалентного урана. В растворе с добавлением катионов Mg наблюдается образование и слабоокрашенного темно-коричневого раствора. Процессы образования и виды комплексов урана переменной валентности зависят от физико-химических свойств добавляемых растворов. Добавление K и Mg в воде смещает положение полос в спектре в длинноволновую сторону по сравнению с Na и Mg в ацетоне, а около 900 нм обнаруживается полоса поглощения комплексов трехвалентного урана. Проанализированы процессы изменения состава и структуры первой координационной сферы уранила. = Using the electron absorption method, the effect of the physicochemical properties of Mg, Na, and K solutions on the photochemical formation of nanoclusters of three-, tetra-, and pentavalent uranium with organic ligands has been studied when solutions of UO2(ClO4)2⋅5h3O in acetone were illuminated by light-emitting diodes (LED) in the region from 420 to 440 nm. В полимере, который представляет собой очень вязкую темно-коричневую жидкость, уран находится в виде нанокластеров соединений пяти- и четырехвалентного урана, образующихся в результате фотохимических превращений. В спектрах образцов растворов UO2(ClO4)2⋅5h3O в ацетоне с добавлением водного раствора катионов Mg, K в воде наблюдается появление полос, принадлежащих комплексам трех-, четырех- и пятивалентного урана. В растворе с добавлением катионов Mg наблюдается образование и слабоокрашенного темно-коричневого раствора. Процессы образования и виды комплексов урана переменной валентности зависят от физико-химических свойств добавляемых растворов. Добавление K и Mg в воде смещает положение полос в спектре в длинноволновую сторону по сравнению с Na и Mg в ацетоне, а около 900 нм обнаруживается полоса поглощения комплексов трехвалентного урана. Проанализированы процессы изменения состава и структуры первой координационной сферы уранила. = Using the electron absorption method, the effect of the physicochemical properties of Mg, Na, and K solutions on the photochemical formation of nanoclusters of three-, tetra-, and pentavalent uranium with organic ligands has been studied when solutions of UO2(ClO4)2⋅5h3O in acetone were illuminated by light-emitting diodes (LED) in the region from 420 to 440 nm. The characteristic features of these processes have been established. With the addition of Mg, Na cations, in systems of UO2(ClO4)2⋅5h3O in acetone such illumination leads to photopolymerization of acetone, the excited uranyl complexes being catalysts of the process. The polymer representing a very viscous liquid, dark brown in color, includes nanoclusters of penta- and tetravalent uranium compounds formed due to the photochemical transformations. Spectra for the samples of UO2(ClO4)2⋅5h3O solutions in acetone upon the addition of Mg, K cations into water reveal the bands attributed to complexes of three-, tetra-, and pentavalent uranium. On the addition of Mg into the solution one can also observe the formation of a lighter-colored brown solution as well. The formation processes and types of the variable-valence uranium complexes are dependent on the physicochemical properties of the solutions added. The added K и Mg cations in water are responsible for shifting of the bands to the long-wavelength region as compared to the case of Na and Mg in acetone; the absorption band for three-valent uranium complexes is observed close to 900 nm. The characteristic features of these processes have been established. With the addition of Mg, Na cations, in systems of UO2(ClO4)2⋅5h3O in acetone such illumination leads to photopolymerization of acetone, the excited uranyl complexes being catalysts of the process. The polymer representing a very viscous liquid, dark brown in color, includes nanoclusters of penta- and tetravalent uranium compounds formed due to the photochemical transformations. Spectra for the samples of UO2(ClO4)2⋅5h3O solutions in acetone upon the addition of Mg, K cations into water reveal the bands attributed to complexes of three-, tetra-, and pentavalent uranium. On the addition of Mg into the solution one can also observe the formation of a lighter-colored brown solution as well. The formation processes and types of the variable-valence uranium complexes are dependent on the physicochemical properties of the solutions added. The added K и Mg cations in water are responsible for shifting of the bands to the long-wavelength region as compared to the case of Na and Mg in acetone; the absorption band for three-valent uranium complexes is observed close to 900 nm. Changes in the composition and structure of the first coordination sphere in uranyl have been analyzed. Changes in the composition and structure of the first coordination sphere in uranyl have been analyzed. |
Шеляпина Марина Германовна – ЯФМИ
Дата и место рождения: 03 октября 1972 года, г. Ленинград
Организационная деятельность:
- Секретарь кафедры ЯФМИ по международной деятельности
- Зам. руководителя программы “Прикладные математика и физика”
- Член научно-технического совета “Образовательного ресурсного центра по направлению физика”
- Зам. председателя оргкомитета Международного Симпозиума и Летней Школы “Nuclear Magnetic Resonance in Condensed Matter” (NMRCM)
Ученые степени и звания:
- Кандидат физико-математических наук, Научно-исследовательский институт физики Санкт-Петербургского государственного университета (2000), Тема: Исследование квадрупольных взаимодействий в кристаллах LiNbO3, LiTaO3 и KNbO3 методами ЯМР и компьютерного моделирования, специальность 01.
 04.03 – радиофизика, Руководитель: В.С. Касперович
04.03 – радиофизика, Руководитель: В.С. Касперович - Доцент по кафедре (2010)
Образование:
- 1989-1993 бакалавриат СПбГУ, физический факультет, кафедра радиофизики
- 1993-1995 магистратура СПбГУ, физический факультет, кафедра квантовых магнитных явлений
- 1995-1999 аспирантура СПбГУ, физическй факультет, специальность 01.04.03 – радиофизика
Дополнительное образование и стажировки:
- Диплом международной школы HERCULES (2003)
- Лаборатория Кристаллографии, Национальный центр научных исследований Франции, Гренобль, Франция (1996, 2001, 2002, 2003, 2004, 2006)
- Институт Неэля, Национальный центр научных исследований Франции, Гренобль, Франции (2007, 2008, 2010, 2012)
- Мюнхенский университет, Германия (2004)
Опыт работы:
- 2014- доцент, СПбГУ, физический факультет, кафедра ядерно-физических методов исследований
- 2004-2013 доцент, СПбГУ, физический факультет, кафедра квантовых магнитных явлений
- 2003-2004 старший преподаватель, СПбГУ, физический факультет, кафедра квантовых магнитных явлений
- 2000-2003 ассистент, СПбГУ, физический факультет, кафедра квантовых магнитных явлений
Область научных интересов:
- Магнитный резонанс в твердых телах (ЯМР, ЯКР, ЭПР)
- Неэмпирические расчеты
- X-ray, нейтронография
- Гидриды металлов – материалы для хранения водорода: стабильность, фазовые переходы, подвижность водорода
- Исследование парамагнитных ионов и металлических кластеров в пористых матрицах (цеолитах)
- Структура, электронные и магнитные свойства интерметаллических соединений
Учебная деятельность:
Курсы лекций
- Физика конденсированного состояния
- Резонансные методы исследования конденсированного состояния
- ЯМР высокого разрешения в твердых телах
- Альтернативные источники энергии
- Ядерный квадрупольный резонанс
- ЯМР в магнитоупорядоченных соединениях
Руководство кандидатскими, магистерскими и бакалаврскими работами
Кандидатские диссертации
- А.
 Выводцева (защита – октябрь 2016)
Выводцева (защита – октябрь 2016) - К. Клюкин (защита – октябрь 2015)
- Ю. Жуков (защита – октябрь 2015)
- О. Баврина (защита – октябрь 2015)
Магистерские диссертации
- Определение состояние ионов меди в мордените по данным ЭПР и неэмпирических расчетов. А. Ковалев (защита – июнь 2014)
- Моделирование системы дисульфид молибдена – оксид графена. Е. Михеенко (защита – июнь 2014)
- Исследование подвижности водорода в решетке неупорядоченных сплавов переходных металлов методом ядерного магнитного резонанса. А. Выводцева (2013)
- Электронная структура и магнитное упорядочение в тройных системах железо-кобальт-бор. В. Шахардин (2013)
- Моделирование наноразмерных магниево-углеродных комплексов – материалов для хранения водорода. Э. Велиев (2013)
- Моделирование тонких пленок Mg/M (M = переходный металл) – материалов для хранения водорода. К. Клюкин (2012)
- Исследование гидридов сплавов Ti-V методом протонного ядерного магнитного резонанса.
 Е. Куренкова (2012)
Е. Куренкова (2012) - Исследование магнитного упорядочения атомов в новых материалах. И. Шихман (2012)
- Магнитное упорядочение атомов железа и ванадия в системе 1-12 по данным неэмпирических расчётов. Н. Кривко (2012)
- Исследование гидридов сплавов Ti-V-Cr методом протонного ядерного магнитного резонанса. Б. Харьков (2011)
- Электронная структура и стабильность гидридов на основе магния. М. Сирецкий (2010)
- Электронная структура и стабильность системы Mg-Ni-Ca по данным неэмпирических расчётов. К. Харченко (2010)
Бакалаврские работы
- Исследования слоистых перовскитоподобных соединений методами ядерного магнитного резонанса и теории функционала плотности. Д. Иванов (2012)
- Электронная структура и стабильность гидридов сплавов магний-железо-кобальт. Е. Михеенко (2012)
- Теоретическое исследование аномальных магнитных свойств замещённого галлата лантана. В. Бессонов (2011)
- Моделирование нанокомпозитов магний-углерод – материалов для хранения водорода.
 Э. Велиев (2011)
Э. Велиев (2011) - Электронная стуктура и стабильность гидрированных кластеров магния с добавками переходных металлов. Е. Рузич (2011)
- Структура и стабильность тонких плёнок Mg/Ti и Mg/Nb: неэмпирические расчёты. К. Клюкин (2010)
- Релаксация протонов в кристаллических и аморфных гидридах интерметаллидов. Е. Куренкова (2010)
- Влияние каталитических добавок на подвижность водорода в сплаве Ti-V-Cr. В. Осипов (2010)
- Взаимное упорядочение магнитных моментов железа и ванадия в наноразмерных интерметаллических комплексах по данным неэмпирических расчётов. И. Шихман (2010)
- Электронная структура и магнитные свойства цементита Fe3C. Н. Кривко (2009)
- Исследование электронной структуры гидридов Ti-V-H методами KKR и FLAPW. К. Харченко (2008)
- Влияние атомов переходных металлов на геометрию кластеров магния. М. Сирецкий (2008)
- Исследование гидридов сплавов Ti-V-Cr методом 1H ЯМР.
 Б. Харьков (2008)
Б. Харьков (2008) - Курсовые работы
- Теоретическое исследование аномальных магнитных свойств замещённого галлата лантана. В. Бессонов (2010)
- Моделирование процесса дегидрирования кластеров гидрида магния. Э. Велиев (2010)
- Моделирование кластеров AlnHm. Е. Рузич (2010)
- Моделирование тонких пленок Mg/Ti. К. Клюкин (2009)
- Магнитные свойства тонких пленок Fe/V: ab initio расчёты. И. Шихман (2009)
Награды:
- Почетная грамота Министерства образования и науки Российской Федерации (2012)
- 1-я премия научно-исследовательских работ ФУНЦ СПбГУ (2012)
- 1-я премия научно-исследовательских работ ФУНЦ СПбГУ (2005)
- IUPAP grant for women in physics (2004)
Основные публикации:
2014
- V.I. Chizhik, Y.S. Chernyshev, A.V. Donets, V.V. Frolov, A.V. Komolkin, M.G. Shelyapina, Magnetic Resonance and Its Applications.
 Springer (2014) 788 p. 234 illus.
Springer (2014) 788 p. 234 illus. - A.V. Vyvodtceva, M.G. Shelyapina, A.F. Privalov, Yu.S. Chernyshev, D. Fruchart. 1H NMR study of hydrogen self-diffusion in ternary Ti–V–Cr alloys. J. Alloys Compd. 614 (2014) 364-367.
2013
- K. Klyukin, Marina G. Shelyapina, D. Fruchart.Hydrogen induced phase transition in magnesium: An Ab initio study. J. Alloys Compd. 580 (2013) S10-S12
- N. Skryabina, D. Fruchart, M.G. Shelyapina, S. Dolukhanyan, A. Aleksanyan.Phase transformations in Ti–V hydrides. J. Alloys Compd. 580 (2013) S94-S97.
- E. Kurenkova, A. Vyvodtseva, M. G. Shelyapina, V.I. Chizhik, A.V. Ievlev, N.Ye. Skryabina, A.G. Aleksanyan, D. Fruchart. 1H NMR Study of Hydrogen Site Occupancy in Hydrides of Disordered Ti-V and Ti-V-Cr Alloys. Sol. State Phen. 194 (2013) 254-257.
- I.A. Shikhman, M.G. Shelyapina, G.S. Kupriyanova. A Density Functional Theory Study of the Fe(001)/Fe3O4(001) Interface. Sol. State Phen.
 194 (2013) 288-291.
194 (2013) 288-291.
2012
2011
- M.G. Shelyapina, D. Fruchart. Role of Transition Elements in Stability of Magnesium Hydride: A Review of Theoretical Studies. Sol. State Phen. 170 (2011) 227-231.
- K. Klyukin, M.G. Shelyapina, D. Fruchart. Modelling of Mg/Ti and Mg/Nb Thin Films for Hydrogen Storage. Sol. State Phen. 170 (2011) 298-301.
- N. Skryabina, D. Fruchart, S. Miraglia, P. de Rango, M.G. Shelyapina. Phase Transformations in Ti-V-Cr-H Composition.Sol. State Phen. 170 (2011) 302-306.
- V.I. Chizhik, V.S. Kasperovich, M.G. Shelyapina, Yu. S. Chernyshev. Exchange model for proton relaxation in disordered metallic hydrides. Int. J. Hydrogen Energy 36 (2011) 1601-1605.
- М. Г. Шеляпина, D. Fruchart, S. Miraglia, G. Girard. Электронная структура и стабильность гидридов Mg6TiMh26 (M = Mg, Al, Zn). ФТТ 53 (2011) 8-14.
- В.С. Касперович, Б.Б. Харьков, И.А. Рыков, С.А. Лавров, М.Г. Шеляпина, Ю.
 С. Чернышев, В.И. Чижик, Н.Е. Скрябина, D. Fruchart, S. Miraglia. Спин-решёточная релаксация и подвижность протонов в решетке сплава TiV0.8Cr1.2. ФТТ 53 (2011) 214-221.
С. Чернышев, В.И. Чижик, Н.Е. Скрябина, D. Fruchart, S. Miraglia. Спин-решёточная релаксация и подвижность протонов в решетке сплава TiV0.8Cr1.2. ФТТ 53 (2011) 214-221. - V.S. Kasperovich, M.G. Shelyapina, B. Khar’kov, I. Rykov, V. Osipov, E. Kurenkova, A.V. Ievlev, N.E. Skryabina, D. Fruchart, S. Miraglia, P. de Rango. NMR study of metal-hydrogen systems for hydrogen storage. J. Alloys Compd. 509 (2011) S804–S808.
2010
2009
- M.Yu. Siretskiy, M.G. Shelyapina, D. Fruchart, S. Miraglia, N.E. Skryabina. Influence of a transition metal atom on the geometry and electronic structure of Mg and Mg–H clusters. J. Alloys Compd. 480 (2009) 114-116.
- П.М. Бородин, Н.М. Вечерухин, В.С. Касперович, А.В. Комолкин, А.В. Мельников, В.В. Москалев, В.В. Фролов, Ю.С. Чернышев, В.И. Чижик, М.Г. Шеляпина. «Квантовая радиофизика. Магнитный резонанс и его приложения.» Учебное пособие Под ред. В.И. Чижика. СПбГУ (2009) 699 с.
2008
2007
- М.
 Г. Шеляпина, В.С.Касперович, Н.Е.Скрябина, D.Fruchart. Неэмпирические расчеты стабильности неупорядоченных твердых растворов Ti-V-Cr и их гидридов. ФТТ 49 (2007) 385-388.
Г. Шеляпина, В.С.Касперович, Н.Е.Скрябина, D.Fruchart. Неэмпирические расчеты стабильности неупорядоченных твердых растворов Ti-V-Cr и их гидридов. ФТТ 49 (2007) 385-388. - V.A. Romaka, Yu.K. Gorelenko, Yu.V. Stadnyk, L.P. Romaka, M. Shelyapina, D. Fruchart, V.F. Chekurin. Conductivity Mechanisms in ZrNiSn Intermetallic Semiconductors Highly Doped by Co. II. Electronic Structure Simulation. Phys. Chem. Solid State 8 (2007) 446-471.
- S. Miraglia, D. Fruchart, N. Skryabina, M. Shelyapina, B. Ouladiaf, E.K. Hlil, P. de Rango, J. Charbonnier. Hydrogen-induced structural transformation in TiV0.8Cr1.2 studied by in situ neutron diffraction. J. Alloys Compd. 442 (2007) 49-54.
- D. Fruchart, V.A. Romaka, Yu.V. Stadnyk, L.P. Romaka, Yu.K. Gorelenko, M.G. Shelyapina, V.F. Chekurin. Conductivity mechanisms in heavy-doped n-ZrNiSn intermetallic semiconductors. J. Alloys Compd. 438 (2007) 8-14.
2006
- В.С.Касперович, Н.Г.Содель, М.
 Г.Шеляпина. Неэмпирические кластерные расчеты тензора градиентов электрического поля в иттрий-алюминиевом гранате Y3Al5O12. Физика Твердого Тела 48 (2006) 1593-1597.
Г.Шеляпина. Неэмпирические кластерные расчеты тензора градиентов электрического поля в иттрий-алюминиевом гранате Y3Al5O12. Физика Твердого Тела 48 (2006) 1593-1597. - Yu.V. Stadnyk, V.A. Romaka, M.G. Shelyapina, D. Fruchart, Yu. K. Gorelenko, L.P. Romaka, A.V. Tkachuk, V.F. Chekurin. Impurity band effect on TiCo1-xNixSb conduction. Donor impurities. J. Alloys Compd. 421 (2006) 19-23.
- L.P. Romaka, M.G. Shelyapina, Yu.V. Stadnyk, D. Fruchart, E.K. Hlil and V.A. Romaka. Peculiarity of metal–insulator transition due to composition change in the semiconducting TiCo1−xNixSb solid solution: I. Electronic structure calculations. J. Alloys Compd. 416 (2006) 46-50.
- M. G. Shelyapina, V. S. Kasperovich, P. Wolfers. Electronic Structure and Electric-Field-Gradients Distribution in Y3Al5O12 : an ab initio Study. J. Phys. Chem. Solids 67 (2006) 720-724.
- N. Klinduhov, M.G. Shelyapina, V.S. Kasperovich, E.K. Hlil and D. Fruchart. Electronic structure and magnetic couplings in iron–cobalt borides compounds.
 J. Magn. Magn. Mater. 300 (2006) e563-e566.
J. Magn. Magn. Mater. 300 (2006) e563-e566. - В.А. Ромака, М.Г. Шеляпина, Ю.К.Гореленко, Д.Фрушарт, Ю.В.Стаднык, Л.П.Ромака, В.Ф.Чекурин. Особенности механизмов проводимости сильно легированных интерметаллических полупроводников n-ZrNiSn. ФТП 40 (2006) 676-682.
- В.А. Ромака, Ю.В.Стаднык, М.Г. Шеляпина, Д.Фрушарт, В.Ф.Чекурин, Л.П.Ромака, Ю.К.Гореленко. Особенности перехода проводимости металл-диэлектрик в узкощелевых полупроводниках структурного типа MgAgAs. ФТП 40 (2006) 136-141.
- В.А. Ромака, М.Г. Шеляпина, Ю.В.Стаднык, Д.Фрушарт, Л.П.Ромака, В.Ф.Чекурин. Роль примесной зоны при переходе диэлектрик-металл при изменении состава сильно легированного и компенсированного полупроводникового твердого раствора TiCo1-xNixSb. Донорные примеси. ФТП 40 (2006) 796-801.
- В.А.Ромака, Д.Фрушарт, Ю.В.Стаднык, Я.Тобола, Ю.К.Гореленко, М.Г.Шеляпина, Л.П.Ромака, В.Ф.Чекурин. Условия достижения максимальных значений коэффициента термоэлектрической мощности в интерметаллических полупроводниках структурного типа MgAgAs.
 ФТП 40 (2006) 1309-1315.
ФТП 40 (2006) 1309-1315.
2005
2004
- M. G. Shelyapina, D. Fruchart, E. K. Hlil, N. Skryabina, J. Tobola and P. Wolfers. First principles study of induced magnetic moments in Fe1−xMx disordered alloys and in Fe/M (0 0 1) superlattices with M = V, Nb, Ta, Mo. J. Alloys Compd. 383 (2004) 157-161.
- M. G. Shelyapina, M. Morales, M. Bacmann, F. Baudelet, D. Fruchart, C. Giorgetti, E. K. Hlil, G. Krill, N. Skryabina and P. Wolfers. X-ray magnetic circular dichroism study of the RMn12−xFex series with R = Y, Er and Lu. J. Alloys Compd. 383 (2004) 152-156.
- M. G. Shelyapina, M. Morales, M. Bacmann, F. Baudelet, D. Fruchart, C. Giorgetti, E. K. Hlil, G. Krill and P. Wolfers. Magnetic properties of RMn12−xFex type compounds: I. X-ray magnetic circular dichroism study of the ErMn12−xFex series with x=0, 7, 8 and 9. J. Alloys Compd. 368 (2004) 84-93.
2003
- N. Koblyk, M.G. Shelyapina, L.P. Romaka, G.
 Melnyk, O. Bodak, D. Fruchart, El. K. Hlil, and J. Tobola. Transport properties and electronic structure of M2CuSb3 compounds with M = Ti, Zr, Hf. J. Alloys Compd. 354/1-2 (2003) 6-12.
Melnyk, O. Bodak, D. Fruchart, El. K. Hlil, and J. Tobola. Transport properties and electronic structure of M2CuSb3 compounds with M = Ti, Zr, Hf. J. Alloys Compd. 354/1-2 (2003) 6-12. - M. G. Shelyapina, D. Fruchart, S. Miraglia, D. S. dos Santos, S. S. M. Tavares, J. Toboła. KKR-CPA study of the electronic and magnetic structures of disordered Pd1-yNiy alloy and its hydride. J. Alloys Compd. 356-357 (2003) 218-222.
- M. G. Shelyapina, V. S. Kasperovich, B. F. Shchegolev, and E. V. Charnaya. Cluster calculations of electric-field-gradient at the Ta site for the ferroelectric LiTaO3 crystal. Ferroelectrics 282 (2003) 1-7.
2002
- О.Е. Квятковский, М.Г. Шеляпина, Б.Ф. Щеголев, Л.С. Воротилова, И.Б. Захарова. Кластерные ab initio расчеты для галогено-фуллеренов C60F24, C60Cl24, C60Br24. ФТТ 44 (2002) 557-559.
- M.G. Shelyapina, V.S. Kasperovich, V.S. Baranov, M. Morales, P. Wolfers, M. Bacmann, D. Fruchart. Caracterisation by EPR analysis of the magnetic phase diagram of RFe12-xMxXy compounds (R = rare earth metal, M = transition metals, X = H, C).
 J. Alloys Compd. 343/1-2 (2002) 1-4.
J. Alloys Compd. 343/1-2 (2002) 1-4. - M.G. Shelyapina, N. Koblyuk, L. Romaka, Yu. Stadnyk, O. Bodak, E. K. Hlil, P. Wolfers, D. Fruchart, and J. Tobola. Electronic structure of MCuSn compounds with M = Ti, Zr and Hf. J. Alloys Compd. 347 (2002) 43-51.
2001
1999
1998
Дополнительно:
- Замужем, двое детей: Сонечка и Никитос
Потенциальная энергия: определение, виды, формулы
Определение потенциальной энергии
Энергия, говоря простым языком, это возможность что-либо сделать, возможность совершить работу. То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.
А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.
Энергию, связанную с взаимодействием тел, называют ПОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ. Иначе говоря, если тело за счёт взаимодействия с другим телом может совершить некоторую работу, то оно будет обладать потенциальной энергией, и при совершении работы будет происходить изменение этой энергии. Обозначают механическую потенциальную энергию чаще всего — Еп.
Виды потенциальной энергии
Существуют различные виды потенциальной энергии. К примеру, любое тело на Земле находится в гравитационном взаимодействии с Землёй, а значит обладает потенциальной энергией гравитационного взаимодействия. И ещё пример — витки растянутой или сжатой пружины находятся в упругом взаимодействии друг с другом, а значит сжатая или растянутая пружина будет обладать потенциальной энергией упругого взаимодействия.
И ещё пример — витки растянутой или сжатой пружины находятся в упругом взаимодействии друг с другом, а значит сжатая или растянутая пружина будет обладать потенциальной энергией упругого взаимодействия.
Далее мы рассмотрим только виды механической потенциальной энергии и формулы, по которым их можно рассчитать. Но в дальнейшем вы узнаете и о других видах потенциальной энергии — к примеру, о потенциальной энергии электрического взаимодействия заряженных тел, о потенциальной энергии взаимодействия электрона с атомным ядром.
Знакомьтесь: наш мир. Физика всего на свете.
Книга адресована школьникам старших классов, студентам, преподавателям и учителям физики, а также всем тем, кто хочет понять, что происходит в мире вокруг нас, и воспитать в себе научный взгляд на все многообразие явлений природы. Каждый раздел книги представляет собой, по сути, набор физических задач, решая которые читатель укрепит свое понимание физических законов и научится применять их в практически интересных случаях.
Формулы потенциальной энергии
Перед тем как приступить к выводу формул потенциальной энергии, ещё раз вспомним, что совершённая телом или над телом работа равна изменению его энергии. При этом, если само тело совершает работу, то его энергия уменьшается, а если над телом совершают работу, то его энергия увеличивается. К примеру, если спортсмен поднимает штангу, то он сообщает ей потенциальную энергию гравитационного взаимодействия, а если он отпускает штангу и она падает, то потенциальная энергия гравитационного взаимодействия штанги с Землёй уменьшается. Также, если вы открываете дверь, растягивая пружину, то вы сообщаете пружине потенциальную энергию упругого взаимодействия, но если потом дверь закрывается, благодаря сжатию пружины в начальное состояние, то и энергия упругой деформации пружины уменьшается до нуля.
А) Чтобы вывести формулу потенциальной энергии гравитационного взаимодействия, рассмотрим, какую работу совершает тело, двигаясь под действием силы тяжести:
А = F*s = mg*s = mg*(h1
— h2) = mgh1
— mgh2
= Eп1
— Еп2, то есть, мы получили, что потенциальная энергия гравитационного взаимодействия тела с Землёй может быть вычислена по формуле: Еп = mgh.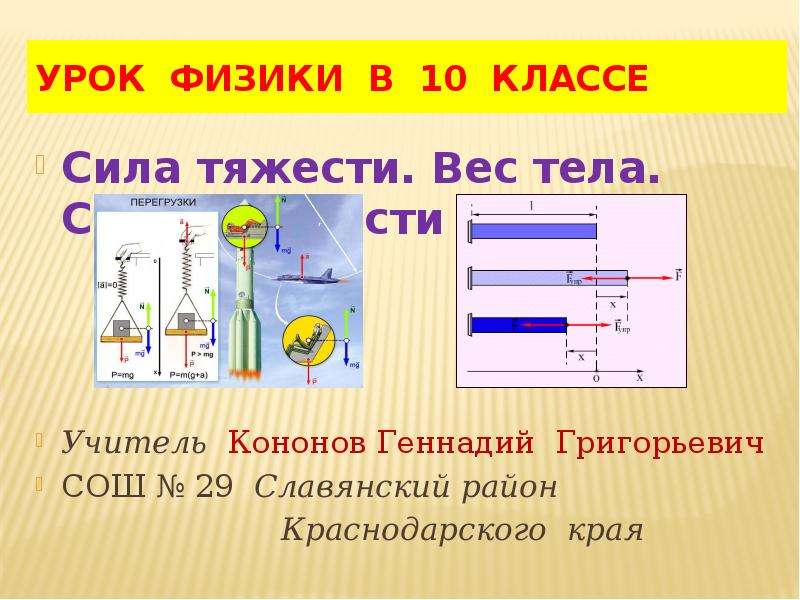
Здесь важно отметить, что поверхность Земли принимается за начало отсчёта высоты, то есть для тела, находящегося на поверхности Земли Еп = 0, для тела, поднятого над Землёй Еп > 0, а для тела, находящегося в яме глубиной h, Еп < 0.
Отметим также и то, что в формуле работы отсутсвовал cosa. Это не случайно. Ведь если тело движется по сложной траектории, то, какой бы сложной она ни была, её можно разбить на множество вертикальных и горизонтальных участков. Но на горизонтальных участках работа силы тяжести будет равна нулю, так как угол между силой тяжести и перемещением будет прямым, а значит работа будет совершаться только на вертикальных участках траектории, для которых cosa = 1 или cosa = −1.
Тогда можно сделать ещё один важный вывод — работа силы тяжести не зависит от формы траектории, а только от расположения начальной и конечной точки. А это не случайность — это свойство любых сил, сообщающих телам потенциальную энергию. Такие силы называют потенциальными и сила тяжести — одна из них. К потенциальным силам относится и сила упругости.
Такие силы называют потенциальными и сила тяжести — одна из них. К потенциальным силам относится и сила упругости.
Б) Чтобы вывести формулу потенциальной энергии упругой деформации, рассмотрим, какую работу нужно совершить, чтобы растянуть пружину, изменив её длину на х (х = l — l0):
А = –Fупр(ср.)*s,
Во-первых, знак минус в формуле стоит потому, что угол между силой упругости и перемещением свободного конца пружины равен 180 градусов и cosa = −1.
Во-вторых, возникающая при растяжении пружины сила упругости является переменной силой, в отличие от силы тяжести, поэтому в формуле работы стоит средняя сила упругости. При этом величина силы упругости, в соответствии с законом Гука, прямо пропорциональна изменению длины пружины, а значит её среднее значение можно определить так:
Fупр(ср.) = (Fупр(нач.) + Fупр(конеч.))/2
И так как Fупр(нач.) = 0, а Fупр(конеч. ) = kх, то:
) = kх, то:
А = —kх*s/2
Но s = x, поэтому: А = —kx2/2 = 0 — kх2/2 = Еп1 — Еп2.
В итоге, мы получили формулу потенциальной энергии упругой деформации: Еп = kx2/2.
Что еще почитать?
Методические советы учителям
1) Обязательно обратите внимание учащихся на связь энергии и работы.
2) Не давайте учащимся формулы потенциальной энергии без вывода.
3) Обратите внимание учащихся на то, что оба вида потенциальной энергии зависят от выбора начальной точки, то есть от системы координат.
4) При выводе формул потенциальной энергии обязательно поясните учащимся почему отсутствует cosa в формуле работы.
5) Отметьте, что и работа силы тяжести, и работа силы упругости не зависят от формы траектории и, следовательно равны нулю на замкнутой траектории — это общее и важное свойство всех потенциальных сил.
Nanodispersed Mg-based Powders Received in a Hydrogen-argon Plasma Flow and Estimation of their Application Prospects as Hydrogen Storage Materials
Author:
Melnikova, Evgenia I.
Kolonenko, Andrey L.
Glushenko, Gari A.
Vnukova, Natalya G.
Churilov, Grigory N.
Zhizhaev, Anatoly M.
Мельникова, Евгения И.
Колоненко, Андрей Л.
Глушенко, Гари А.
Внукова, Наталья В.
Чурилов, Григорий Н.
Жижаев, Анатолий М.
Journal Name:
Журнал Сибирского федерального университета. Математика и физика. Journal of Siberian Federal University. Mathematics & Physics;2017 10 (1)Abstract:
Nanodispersed powders, consisting of Mg, Mg and Ni, Mg and Pd, were synthesized in a water-cooled chamber in a hydrogen-helium mixture at atmospheric pressure. Plasma generation was carried out in HF arc discharge in an argon flow with one hollow electrode and the other — crucible with molten metal. The resulting powders were investigated by scanning electron microscopy, X-ray fluorescence analysis
and X-ray analysis. When adding nickel during the synthesis, magnesium particles with nickel coating
were obtained. Synthesis with palladium resulted in producing magnesium particles with dispersed fine
palladium inclusions. However, since the saturated steam pressure of palladium is 2–3 orders lower than
that of nickel, then obtaining particles coated with palladium is only possible at higher palladium melt
temperatures that we could achieve in this laboratory setup variant. As a possible application of the
synthesized powders the possibility of their hydrogen storage usage was experimentally evaluated
The resulting powders were investigated by scanning electron microscopy, X-ray fluorescence analysis
and X-ray analysis. When adding nickel during the synthesis, magnesium particles with nickel coating
were obtained. Synthesis with palladium resulted in producing magnesium particles with dispersed fine
palladium inclusions. However, since the saturated steam pressure of palladium is 2–3 orders lower than
that of nickel, then obtaining particles coated with palladium is only possible at higher palladium melt
temperatures that we could achieve in this laboratory setup variant. As a possible application of the
synthesized powders the possibility of their hydrogen storage usage was experimentally evaluatedНанодисперсные порошки, состоящие из Mg, Mg и Ni, Mg и Pd, были синтезированы в охлаждае- мой водой камере, в гелии, смешанном с водородом при атмосферном давлении. Генерация плазмы осуществлялась в ВЧ-дуговом разряде в потоке аргона с одним полым электродом и другим — тиглем с расплавленным металлом.
 Полученные порошки исследовались методами растровой
электронной микроскопии, рентгенофлуоресцентного анализа и рентгенофазового анализа. При
одновременном распылении магния и никеля образовывались порошки, состоящие из частиц маг-
ния, покрытых никелевой оболочкой. При одновременном распылении магния и палладия порошки
состояли из смеси частиц магния и частиц палладия. Однако так как давление насыщенных
паров палладия на 2–3 порядка ниже, чем давление насыщенных паров никеля, то получение ча-
стиц, покрытых оболочкой палладия, возможно только при более высоких температурах распла-
ва палладия, чем мы могли достигнуть в данном варианте нашей лабораторной установки. В
качестве возможного применения синтезированных порошков экспериментально была оценена
возможность их использования в виде аккумуляторов водорода
Полученные порошки исследовались методами растровой
электронной микроскопии, рентгенофлуоресцентного анализа и рентгенофазового анализа. При
одновременном распылении магния и никеля образовывались порошки, состоящие из частиц маг-
ния, покрытых никелевой оболочкой. При одновременном распылении магния и палладия порошки
состояли из смеси частиц магния и частиц палладия. Однако так как давление насыщенных
паров палладия на 2–3 порядка ниже, чем давление насыщенных паров никеля, то получение ча-
стиц, покрытых оболочкой палладия, возможно только при более высоких температурах распла-
ва палладия, чем мы могли достигнуть в данном варианте нашей лабораторной установки. В
качестве возможного применения синтезированных порошков экспериментально была оценена
возможность их использования в виде аккумуляторов водорода
Урок 15. основы гидромеханики – Физика – 10 класс
Физика, 10 класс
Урок 15. Основы гидромеханики
Перечень вопросов, рассматриваемых на уроке:
1. Сила давления
Сила давления
2.Давление
3.Закон Паскаля
4.Гидростатическое давление
5.Атмосферное давление
6.Закон Архимеда
Глоссарий по теме
Гидростатика – раздел механики, в котором изучается равновесие покоящихся жидкостей и их давление на погруженные в них тела.
Давление – это величина равная отношению силы давления к площади поверхности, на которую эта сила действует.
Нормальное атмосферное давление – это величина давления, равная 760 мм рт. ст. или 101325 Па.
Сила Архимеда –выталкивающая сила, действующая на тело, погруженное в жидкость или газ
Основная и дополнительная литература по теме урока:
Грачев А.В., Погожев В.А., Салецкий А.М., Боков П.Ю. Физика.10 класс. М.: Вентана-Граф, 2017. – С. 222 – 229.
Е.А. Марон, А.Е. Марон Сборник качественных задач по физике. М., Просвещение, 2006, С.36-50.
Основное содержание урока
Силой давления называется сила, действующая перпендикулярно некоторой поверхности.
Результатом действия силы давления является давление.
Отношение модуля силы давления F к площади поверхности S, на которую эта сила действует, называется давлением
Закон Паскаля.
Силы давления в данной точке покоящейся жидкости (газа) действуют во всех направлениях одинаково. При ведём простое доказательство закона.
Выделим в какой-нибудь точке покоящейся жидкости её малый объём в форме прямоугольного параллелепипеда или куба.
Если кубик покоится, значит сумма сил, действующих на его 6 граней равна нулю. Это означает, что силы, действующие попарно на противоположные грани куба, равны по модулю, а, следовательно, и давления будут равны по всем направлениям.
Ввиду произвольности ориентации выбранного нами малого объёма жидкости, очевидно, что давление по всем направлениям должно быть одинаково.
Гидростатическое давление. Атмосферное давление.
Это давление, оказываемое «столбом» жидкости на уровне плоскости своего нижнего основания.
Выделим в покоящейся жидкости «столб» – цилиндр высотой h и площадью основания S, верхнее основание которого совпадает со свободной поверхностью жидкости.
По первому закону Ньютона сумма проекций трех сил, действующих на столб жидкости: силы атмосферного давления, силы тяжести и силы давления жидкости- равна нулю
Fp– mg – Fатм = 0;
Но так как mg=ρ·V·g=ρ·S·h·g; Fp = p·S; Fатм = pатм ·S,
Получим p = pатм+ ρ·g·h;
где pатм – атмосферное давление; ρ – плотность жидкости; g – ускорение свободного падения; h – глубина.
Величина ρ·g·h называется гидростатическим давлением.
Атмосферное давление – это давление в какой-нибудь точке атмосферы.
Нормальное или среднее значение атмосферного давления равно 760 мм ртутного столба, что соответствует 101325 Па. Т.е. 1 мм рт. ст. = 133,322 Па.
Зависимость атмосферного давления от высоты имеет сложный вид из-за сжимаемости воздуха (в отличие от жидкостей).
Закон Архимеда. Сила Архимеда.
Выделим в жидкости объем прямоугольного параллелепипеда, ориентированного для удобства анализа так, чтобы нижняя и верхняя грани были параллельны поверхности жидкости
На тело в жидкости действуют сила тяжести и силы давления со стороны жидкости. Давление на боковые стенки равны. Сила давления снизу больше, чем сила давления сверху. Разность этих двух сил и есть выталкивающая сила – сила Архимеда.
FA=p2 S – p1 S =S( p2 – p1) = ρ g S(h2 – h1) = ρ gV
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости.
где – плотность жидкости; g – ускорение свободного падения; Vm – объём погруженной в жидкость части тела
Разбор тренировочных заданий
1. Найдите силу нормального атмосферного давления на грань куба с ребром 1 м. Округлите до целых кПа.
Варианты ответов:
1) 100;
2) 125;
3) 101;
4) 110
Решение. По определению сила давления равна F = p x S;
Нормальное атмосферное давление p = 101325 Па; площадь грани куба (1м)2 = 1м2;
Получим значение силы давления F = (101325 Н/м2 ) х (1 м2) = 101325 Н =101,325 кН.
Ответ: 3) 101
2. В первой строке таблицы приведены значения атмосферного давления на разных высотах. Занесите во вторую строку соответствующие значения высот из перечня: h1, h2, h3, h4, если известно, что h3 > h4 > h1 > h2
P (мм рт. ст.) | 738 | 750 | 550 | 525 |
h(м) |
Решение. Как известно, давление атмосферы падает с высотой. Выпишем в порядке убывания давления: 750,738,550,525. Из приведённого неравенства имеем, что наименьшая высота h2, затем h1, h4 и h3. Наименьшей высоте соответствует наибольшее давление и т.д. Высота растёт, давление падает. Или наоборот. В таблицу теперь под каждым давлением впишем соответствующее значение высоты.
Из приведённого неравенства имеем, что наименьшая высота h2, затем h1, h4 и h3. Наименьшей высоте соответствует наибольшее давление и т.д. Высота растёт, давление падает. Или наоборот. В таблицу теперь под каждым давлением впишем соответствующее значение высоты.
Ответ:
P (мм рт. ст.) | 738 | 750 | 550 | 525 |
h(м) | h1 | h2 | h4 | h3 |
Обзор силы гравитации Рона Куртуса
SfC Home> Физика> Гравитация>
, Рон Куртус (редакция 14 апреля 2020 г.)
Гравитация – это сила , которая притягивает объекты к Земле. Это приближение силы тяжести , которая притягивает объекты массы друг к другу на больших расстояниях.
( Примечание : Гравитация на Луне – это сила, которая притягивает объекты к поверхности Луны.
)
Уравнение силы тяжести: F = mg , где g – ускорение свободного падения. Единицы могут быть обозначены в метрической (СИ) или английской системе. Уравнение также указывает вес объекта ( Вт = мг).
Основной особенностью этой силы является то, что все объекты падают с одинаковой скоростью, независимо от их массы. Гравитация на Луне и на других планетах имеет разные значения ускорения свободного падения. Однако эффекты силы похожи.
Вопросы, которые могут у вас возникнуть:
- Что такое уравнение гравитации?
- Какая самая выдающаяся характеристика гравитации?
- Что такое гравитация в другом месте?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Уравнение гравитации
Согласно закону всемирного тяготения Ньютона , гравитация – это сила, притягивающая объекты друг к другу.Для объектов, относительно близких к Земле, эта сила называется гравитацией, и ее уравнение:
F = мг
где
- F – сила, притягивающая объекты к Земле
- м – масса объекта
- g – ускорение свободного падения; это число постоянно для всех масс вещества
- мг – произведение м умноженное на г
Примечание : Для проверки того, что сила тяжести равна силе тяжести для объектов, близких к Земле, см.
Постоянные факторы гравитации.
Ускорение свободного падения
Ускорение силы тяжести на Земле обозначено g . Его значение:
г = 9.807 метров на секунду в квадрате (м / с 2 ) в метрической системе измерения или системе СИ
г = 32,2 фута на секунду в квадрате (фут / с 2 ) в английской системе измерения
Примечание : Поскольку в большинстве учебников используется g = 9.8 м / с 2 и 32 фут / с 2 , в этих уроках мы также будем использовать округленную версию.
В уравнении F = mg вы должны использовать ту же систему измерения для массы, m , что и для g .
Примечание: Некоторые учебники небрежно определяют g как ускорение силы тяжести . Это неверно и вводит в заблуждение, поскольку сила тяжести не ускоряется.Выражение должно быть – ускорение за счет силы тяжести , что является правильным описанием g .
Следует проявлять осторожность при определении научных терминов.
Масса и масса
Вес объекта данной массы – это сила тяжести, действующая на этот объект:
w = мг
где
- w – вес в ньютонах (Н) или фунт-сила (фунт)
- м – масса в килограммах или фунт-масса (фунт-масса)
Примечание : Часто возникает путаница относительно обозначения веса и массы.
Хотя килограмм считается единицей массы, он часто используется для обозначения веса. Вы должны знать, что вес 1 кг массы равен w = 9,8 ньютона.
Кроме того, фунт считается силой, но его часто называют массой. Масса 1 фунт-сила равна 1/32 массы фунта.
Опять же, вы должны быть точными в формулировке научных терминов.
Взвешивание объекта
Вы можете определить вес объекта на откалиброванных весах – обычно с пружиной, сопротивляющейся силе груза.
Массу объекта можно измерить с помощью весов, сравнивая с объектом данной массы.
Объекты падают с одинаковой скоростью
Наиболее выдающейся характеристикой силы тяжести является тот факт, что все объекты падают с одинаковой скоростью – если предположить, что влияние сопротивления воздуха незначительно. Это связано с тем, что ускорение свободного падения g является постоянным для всех объектов, независимо от их массы.
Это кажется нелогичным, поскольку можно ожидать, что тяжелый предмет упадет быстрее, чем предмет, который весит меньше.Но это факт. Попробуйте уронить два объекта одновременно с одинаковой высоты, убедившись, что они достаточно тяжелые, чтобы на них не влияло сопротивление воздуха. Вы увидите, что они одновременно упали на землю.
( Для получения дополнительной информации см. Принцип эквивалентности силы тяжести. )
Гравитация в другом месте
Когда вы говорите о гравитации, вы имеете в виду гравитацию около Земли. Однако то же самое уравнение гравитации справедливо для объектов вблизи Луны или других планет, за исключением того, что значение g другое.В таких случаях вы обычно указываете, где находится гравитация, например «гравитация на Луне» или «гравитация на Марсе».
Однако то же самое уравнение гравитации справедливо для объектов вблизи Луны или других планет, за исключением того, что значение g другое.В таких случаях вы обычно указываете, где находится гравитация, например «гравитация на Луне» или «гравитация на Марсе».
Гравитация на Луне
Сила тяжести на Луне составляет примерно 1/6 силы тяжести на Земле для данной массы. Таким образом:
F м = мг м
где
- F м – сила или вес на Луне
- м – масса объекта
- g m – ускорение свободного падения на Луне
Значение для г м равно 1.6 м / с 2 или 5,3 фут / с 2 .
Вес и масса на Луне
Значение для г м составляет примерно 1/6 значения для г на Земле. Таким образом, объект на Луне будет весить около 1/6 своего веса на Земле.
Используя пружинные весы, если вы весите на Земле 60 кг (132 фунта), то на Луне вы будете весить всего 10 кг (22 фунта). Однако, используя шкалу баланса и на Земле, и на Луне, ваша масса будет одинаковой.
Упавшие предметы
Если вы уроните на Луну два объекта разного веса, они упадут на землю с одинаковой скоростью. Вам не придется беспокоиться о влиянии сопротивления воздуха, поскольку на Луне нет воздуха.
Поскольку g m = g /6, объекты будут падать с меньшей скоростью.
( См. Уравнения силы тяжести для падающих объектов, а затем примените g м , чтобы получить другие значения.)
Сводка
Гравитация – это сила, притягивающая объекты к Земле. Это частный случай гравитации. Уравнение силы тяжести: F = мг, в результате чего все объекты падают с одинаковой скоростью, независимо от их массы. Гравитация на Луне и гравитация на других планетах имеют разные значения ускорения свободного падения, но эффекты силы схожи.
Будьте как можно лучше
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Гравитационные ресурсы
Сила гравитации – Журнал “Вселенная сегодня”
Притяжение Земли – Википедия
Как работает гравитация? – Как работает материал
Стандартная сила тяжести – Среднее значение по сравнению с вариацией из-за положения на Земле – Википедия
Международная формула силы тяжести – Изменение силы тяжести в зависимости от расстояния от экватора – Отдел геофизики.Университет Оклахомы
Я чувствую себя легче, когда поднимаюсь в гору, но разве я? – Национальная физическая лаборатория FAQ
Книги
Книги с самым высоким рейтингом по простой науке о гравитации
Книги с самым высоким рейтингом по продвинутой физике гравитации
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.
Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_overview.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Гравитационные темы
Обзор силы тяжести
Вес объекта определяется как сила тяжести на объекте и может быть рассчитана как масса, умноженная на ускорение свободного падения, w = mg.Поскольку вес – это сила, ее единицей СИ является ньютон. Для объекта, находящегося в свободном падении, когда на него действует только сила тяжести, выражение для веса следует из второго закона Ньютона. Вы можете спросить, как и многие, «Почему вы умножаете массу на ускорение свободного падения, когда масса покоится на столе?». Значение g позволяет определить чистую силу тяжести, если было в свободном падении, а чистая сила тяжести равна весу.Другой подход состоит в том, чтобы рассматривать “g” как меру интенсивности гравитационного поля в ньютонах / кг в вашем местоположении. Вы можете рассматривать вес как меру массы в кг, умноженную на интенсивность гравитационного поля, 9,8 Н / кг при стандартных условиях. Данные можно ввести в любое из полей ниже. Затем щелкните за пределами поля, чтобы обновить другие количества. У поверхности Земли, где g = 9,8 м / с 2 :
| Индекс А как насчет состояния невесомости? |
Плотность
Падающее яблоко
Гравитация повсюду вокруг нас. Он может, например, заставить яблоко упасть на землю:
Гравитация постоянно действует на яблоко, поэтому оно движется все быстрее и быстрее … другими словами, оно ускоряется.
Если не учитывать сопротивление воздуха, его скорость увеличивается на 9. 8 метров в секунду каждую секунду . То есть два лота «в секунду» и пишется:
8 метров в секунду каждую секунду . То есть два лота «в секунду» и пишется:
9,8 м / с 2
9,8 м / с 2 – ускорение свободного падения у поверхности Земли. Почти все в нашей жизни происходит вблизи поверхности Земли, поэтому это значение часто используется и записывается как small g :
г = 9,8 м / с 2
Среднее значение г равно 9.80665 м / с 2 , но значения в разных странах разные, например, в Калькутте 9,78548, Лондоне 9,81599 и Токио 9,79805.
Таким образом, большинство людей просто используют 9,8 м / с 2
Чтобы удержать яблоко против силы тяжести, нужна сила.
Сила – это масса, умноженная на ускорение ( F = m a ), и в этом случае ускорение составляет g :
F = m г
Пример: сколько силы удерживать яблоко массой 0.
 1 кг?
1 кг?F = m г
F = 0,1 кг × 9,8 м / с 2
F = 0,98 кг м / с 2
Сила измеряется в Ньютонах ( Н ), что совпадает с кг м / с 2
F = 0,98 N
Итак, чтобы удерживать яблоко, требуется сила около 1 Ньютона .
Мы также говорим, что вес яблока равен 0.98 Н.
Чтобы преобразовать массу в кг в силу в Ньютонах, умножьте на 9,8 м / с 2
Другой пример:
Пример: стальная балка весом 100 кг равномерно установлена на двух опорах. Сколько силы приходится на каждую опору?
На балку действует сила тяжести, направленная вниз:
F = m г
F = 100 кг × 9,8 м / с 2 = 980 Н
Поскольку каждая опора равномерно расположена на опоре, она выдерживает половину веса (980/2 = 490):
Но что такое гравитация?
Теперь вы знаете, как справиться с гравитацией здесь, на Земле (просто умножьте массу на 9. 8 м / с 2 , чтобы получить силу), но что такое гравитация на самом деле?
8 м / с 2 , чтобы получить силу), но что такое гравитация на самом деле?
Что ж, масса и энергия делают пространство искривленным (или искаженным), поэтому для объектов естественно следовать по пути навстречу друг другу.
Здесь объект естественным образом следует за пространством-временем в направлении
Земля
Это приводит к тому, что объекты притягиваются друг к другу , что мы называем Gravity .
Гравитация : притяжение объектов с массой или энергией друг к другу.
Это притяжение проявляется в виде силы:
- меньше для удаленных объектов
- больше для объектов большей массы (таких как Солнце)
Представьте себе всего два шара:
Каждый шар состоит из множества кусочков массы и энергии, которые притягиваются друг к другу:
(на самом деле нужно лота на частиц больше!)
Но мы обычно упрощаем это, представляя, что масса и энергия каждого шара находятся в его центре, называемом Центром тяжести.
(Но помните, что мы просто представляем, что вся масса находится в центре, чтобы упростить вычисления.)
Ньютон разработал формулу силы притяжения:
- F – сила (в Ньютонах), равная, но противоположная в направлении для обоих объектов
- G – гравитационная постоянная, приблизительно 6,674 × 10 -11 Н · м 2 / кг 2
- m 1 и m 2 – две массы (в кг)
- d – расстояние между центрами каждой массы (в метрах)
Пример: две машины массой 800 кг и 1500 кг находятся на расстоянии 3 м друг от друга
Гравитационное притяжение между двумя автомобилями :
F = G м 1 м 2 д 2
F = 6.674 × 10 -11 Н м 2 / кг 2 × 800 кг × 1500 кг (3 м) 2
F ≈ 0,000009 N
Они очень слабо (всего 9 миллионных долей Ньютона) притягиваются друг к другу!
Пример: Яблоко и Земля
Яблоко массой 0,1 кг
Земля имеет массу 5,972 × 10 24 кг
От центра яблока до центра Земли составляет 6371 км (6. 371 × 10 6 м)
371 × 10 6 м)
F = G м 1 м 2 д 2
F = 6,674 × 10 -11 Н м 2 / кг 2 × 0,1 кг × 5,972 × 10 24 кг (6,371 × 10 6 м) 2
F = 0,98 N
(Это то же значение, что и в предыдущем расчете, так что это кажется вполне правильным!)
В обе стороны
Яблоко тянет и Землю!
Но Земля настолько невероятно массивна, что почти не влияет на нее.
Рассчитаем ускорение для яблока и для Земли:
Пример (продолжение): Зная, что сила равна 0,98 Н, каково ускорение яблока
и Земли?Для яблока :
| F = m a | ||
| Мы знаем, что F составляет 0,98 Н, а m равно 0,1 кг | 0.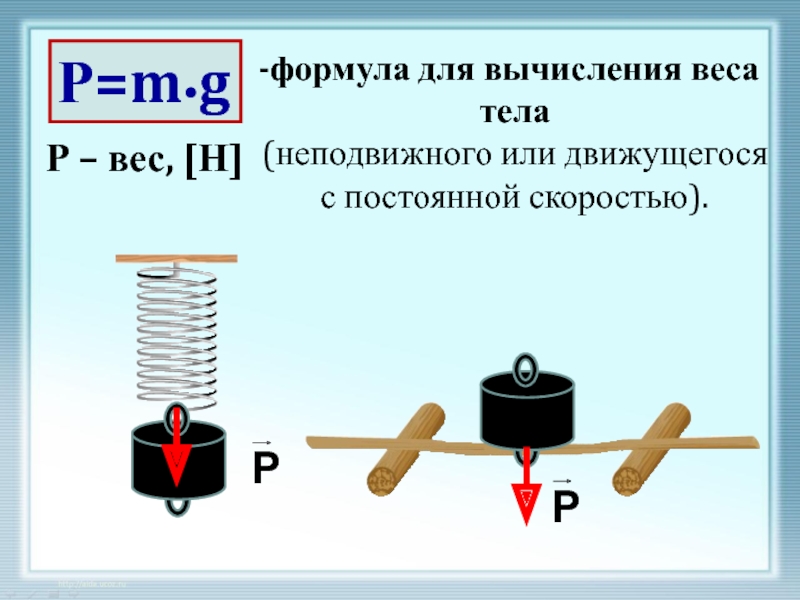 98 Н = 0,1 кг а 98 Н = 0,1 кг а | |
| Разделите обе стороны на 0,1 кг | 0,98 Н / 0,1 кг = а | |
| Смена сторон | a = 0,98 Н / 0,1 кг | |
| Ответ: | a = 9,8 м / с 2 |
Это ускорение свободного падения g, которое мы все испытываем каждый день.
А для Земли :
| F = m a | ||
| F составляет 0,98 Н, а m равно 5,972 × 10 24 кг | 0,98 N = 5,972 × 10 24 кг a | |
| Разделите обе стороны на 5,972 × 10 24 кг | 0,98 Н / 5,972 × 10 24 кг = а | |
| Смена сторон | a = 0. 98 Н / 5.972 × 10 24 кг 98 Н / 5.972 × 10 24 кг | |
| Ответ: | a = 1,64 × 10 -25 м / с 2 |
Это очень маленькое ускорение , неудивительно, что мы не замечаем, как Земля движется из-за яблока.
Но гораздо более крупный объект, такой как Луна (с массой 7.342 × 10 22 кг ), действительно оказывает заметное влияние на Землю.
Луна вращается вокруг Земли на расстоянии около 384000 км каждые 27,3 дня
И Земля также имеет “орбиту” (больше похожую на колебание) с Луной около 5000 км (что на самом деле меньше радиуса Земли), также каждые 27,3 дня.
Ваша очередь: попробуйте вычислить силу притяжения между Землей и Луной.
Играй
Поиграйте с гравитацией в Gravity Freeplay.
Сводка
- Пространство кривой массы и энергии, которое естественным образом заставляет объекты двигаться навстречу друг другу
- этот аттракцион мы называем гравитацией
- Это постоянное притяжение заставляет объекты ускоряться навстречу друг другу
- ускорение имеет соответствующую силу ( F = m a )
- у поверхности Земли ускорение свободного падения составляет 9.
 8 м / с 2
8 м / с 2 - , так что массой 1 кг испытывает гравитационное притяжение 9,8 ньютонов силы
Законы движения Ньютона
Теперь, когда мы знаем законов движения Ньютона, как нам применить их? Как они могут позволить нам предсказать движение? объекта, если мы знаем все силы, действующие на него? Как может они позволяют нам предсказать силы, действующие на объект, если мы знаем его движение?
Сказать, что остальная часть этого конечно, просто ищет хитрые способы применить
F = м аПример 1: Представьте, что ящик тянут по трение меньше пол (хотя такой пол найти очень трудно, он все равно Помогите нам понять концепцию и , мы можем вернуться к этому ситуация позже, после с учетом трения, и решить ее более реалистично).
Представьте, что ящик тянут по горизонтали,
трение меньше пол.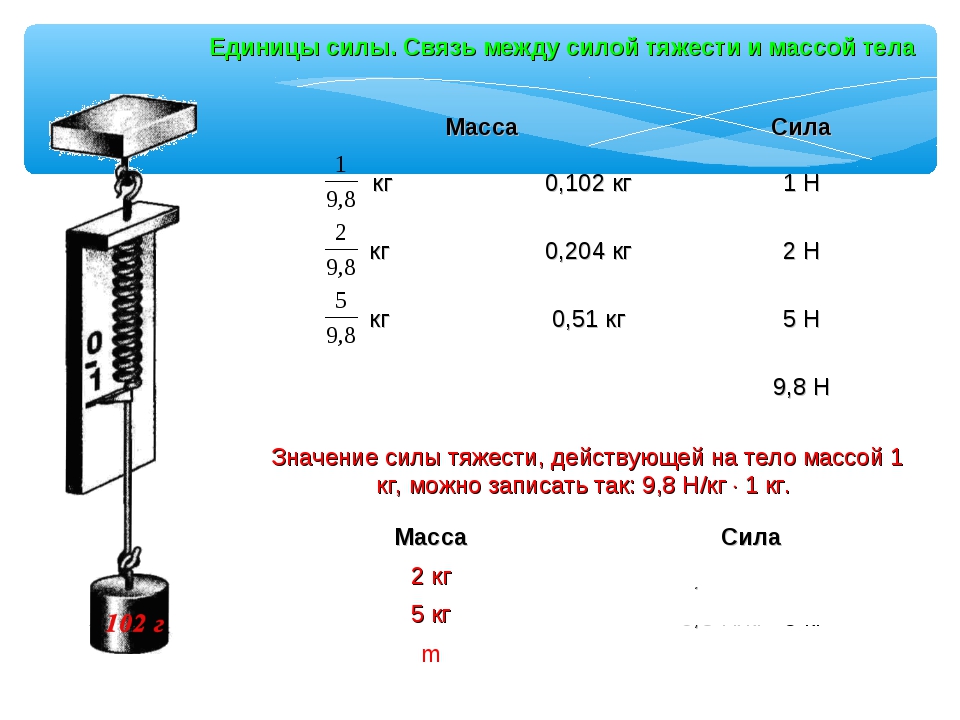 Вокруг него привязана веревка и мужчина
тянет трос с усилием Т. Т – натяжение в
веревка. Что происходит с ящиком?
Вокруг него привязана веревка и мужчина
тянет трос с усилием Т. Т – натяжение в
веревка. Что происходит с ящиком?
Прежде, чем мы сможем применить Второй закон Ньютона,
F = m aмы должны найти чистую силу – вектор сумму все силы – действующие на объект.В добавок к сила T , действующая на веревку, какие другие силы действуют на объект ?
Как обсуждалось в классе, в Механике мы можем ограничить внимание к «контактным» силам и «гравитации». Это означает гравитацию тянет вниз на этом ящике с силой, равной его весу, Вт . Но пол поддерживает обрешетку. Пол отвечает толкая вверх на ящике с силой, которую мы называем нормальным сила .«Нормальный» означает «перпендикулярный». Мы назовем эту силу № ; вы также можете встретить его с надписью N или Ф. № .
Эти силы показаны на «диаграмме свободного тела» выше. Мы
втянули в все силы, действующие на объект.
Чистая сила – это вектор сумма этих сил.
Мы
втянули в все силы, действующие на объект.
Чистая сила – это вектор сумма этих сил.
где, греческое заглавное «сигма» означает «сумма».Помни, хотя, векторная запись всегда элегантная сокращенная запись. Когда пишем
F нетто = F = T + n + wмы действительно написали
F нетто, x = F x = T x + n x + w хи
F net, y = F y = T y + n y + w yЧто это за x- и y-составляющие сил T, n, и w ? Для этого первого простого примера мы можем найти – по осмотр – что этих компонентов
Т х = ТT y = 0
n x = 0
n y = n
w x = 0
w y = – w
Теперь мы готовы применить
F = m aНо сначала это нужно записать в терминах компонентов,
F x = F сеть, x = F x = m a xF x = F net, x = F x = T x + n x + w x = T = m а x
T = м x
a x = т / м
Ящик имеет горизонтальное ускорение , равное .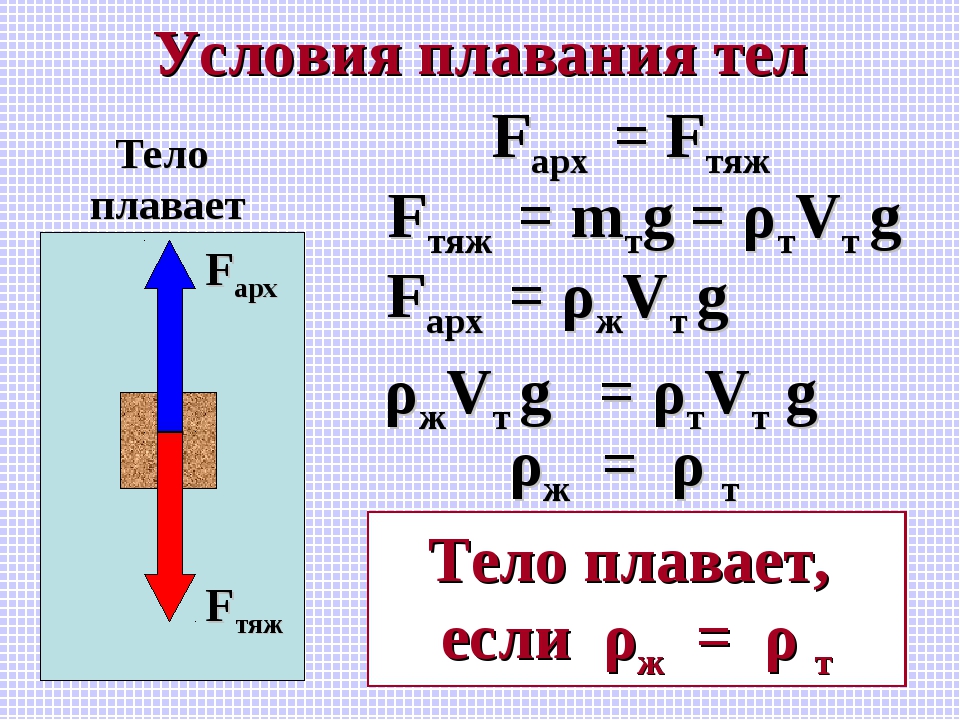 напряжение Т, деленное на m, массу обрешетки.Что насчет
силы в вертикальном направлении?
напряжение Т, деленное на m, массу обрешетки.Что насчет
силы в вертикальном направлении?
F y = F net, y = F y = T y + n y + w y = n – w = m a y
н – ш = м а л
Поскольку мы знаем, что ящик не ускоряется в направлении оси Y – не отрывается от пола и не зарывается в пол – мы знаем, что y = 0, поэтому
п = шНаправляющая вверх нормальная сила, прилагаемая полом к ящику, в в этой ситуации, равна весу, сила, направленная вниз сила тяжести.
Пример 2: Какие силы действуют на книгу, если вы толкаете вниз на нем с силой F пока он сидит на гладком, горизонтальный стол, как показано на рисунке ниже?
Втянуть все силы. Это называется «свободное тело». диаграмму “. В этом курсе механики мы ограничимся
«контактные силы» и сила тяжести. Контактные силы, для
в этом случае будет “нормальная” сила – перпендикулярная сила
– проявляется таблицей – обозначенной на схеме n – и
сила F приложенная рукой.Гравитация проявляет силу
вниз, назвал вес и обозначил w . Как и в
в предыдущем примере мы можем сразу написать
диаграмму “. В этом курсе механики мы ограничимся
«контактные силы» и сила тяжести. Контактные силы, для
в этом случае будет “нормальная” сила – перпендикулярная сила
– проявляется таблицей – обозначенной на схеме n – и
сила F приложенная рукой.Гравитация проявляет силу
вниз, назвал вес и обозначил w . Как и в
в предыдущем примере мы можем сразу написать
, но это действительно элегантное сокращение для
F x = F сеть, x = F x = m xи
F y = F net, y = F y = m a yВ этом примере, хотя ничего не происходит по горизонтали. направление. Все силы имеют только по вертикали компонентов, так что все, что у нас действительно есть, это
F y = F net, y = F y = m a yСчитая положительным, имеем
F y = F net, y = F y = п – ш – F Поскольку книга лежит на столе, мы знаем, что она не ускоряется. поэтому y = 0. Это означает
поэтому y = 0. Это означает
п = ш + ж
Мы можем использовать законы Ньютона для определения значения нормального сила n.
Эта же идея и техника могут быть использованы немного по-другому. ситуация
Пример 3: Рассмотрим лампу, висящую на цепи. Что такое натяжение в цепи?
Как всегда, начнем с «диаграммы свободного тела». Напряжение Т воздействует на лампу вверх , в то время как сила тяжести тянет вниз с силой Вт , вес лампы. Чистая сила – это векторная сумма этих двух сил.Лампа не ускоряется , поэтому сила вверх должна равняется силе вниз . По величине это означает
Т = шНапряжение: Напряжение равно величине силы осуществляется цепью, веревкой или веревкой. Направление этого сила зависит от остальной ситуации и объекта, который мы концентрируемся на данный момент.
 Если мы сосредоточимся на
цепи, показанной ниже, направленная вниз сила T ‘ – сила
воздействует на цепь лампой, а направленная вверх сила Т ” сила, действующая на цепь со стороны потолка.Здесь нет
замена хороших диаграмм свободного тела.
Если мы сосредоточимся на
цепи, показанной ниже, направленная вниз сила T ‘ – сила
воздействует на цепь лампой, а направленная вверх сила Т ” сила, действующая на цепь со стороны потолка.Здесь нет
замена хороших диаграмм свободного тела.Пример 4: Рассмотрим светофор, подвешенный на шнурах, как показано на рисунке ниже. Какое напряжение в каждом из этих шнуры?
Натяжение Т 3 легко, так что рассмотрим первое. В виде мы видели в двух предыдущих примерах; это напряжение в Вертикальный шнур, поддерживающий вес, как раз равен весу. В на диаграмме ниже мы нарисовали силы, действующие на светофор.Единственные силы, действующие на светофор: w , груз, действующий вниз, и T 3 , восходящая сила из-за вертикального троса. Т 3 – это напряжение в этом кабеле. Ясно
Т 3 = ш Но как насчет напряжения в двух других кабелях, T 2 и Т 1 ? Чтобы найти их, мы должны посмотреть на перекресток
где соединяются три кабеля. Этот перекресток находится в
равновесие так
Этот перекресток находится в
равновесие так
F нетто = F = Т 1 + Т 2 + Т 3 = 0
Однако мы должны помнить, что этот единственный вектор уравнение – элегантное сокращенное обозначение для двух скалярных уравнения,
F net, x = F x = T 1 x + T 2 x + T 3 x = 0F net, y = F y = T 1 y + T 2 y + T 3 y = 0
Итак, мы должны разложить все эти силы на их x- и y-компоненты,
T 1x = – T 1 cos 37 o = – 0.8 T 1T 1y = T 1 sin 37 o = 0,6 Т 1
T 2x = T 2 cos 53 o = 0,6 Т 2
T 2y = T 2 sin 53 o = 0,8 Т 2
Т 3x = 0
T 3 года = – T 3 = – w
Знаки являются важными для ! Теперь мы можем вернуться к
уравнения компонентов и решите для натяжения T 1 и
Т 2 .
T 1 x + T 2 x + T 3 x = 0
– 0,8 т. 1 + 0,6 т. 2 + 0 = 0
Т 1 = 0,75 Т 2
F net, y = F y = T 1 y + T 2 y + T 3 y = 0
T 1 год + T 2 года + T 3 года = 0
0.6 T 1 + 0,8 T 2 2 – w = 0
0,6 T 1 + 0,8 T 2 = w
0,6 (0,75 T 2 ) + 0,8 T 2 = w
1,25 T 2 = w
T 2 = 0,8 w
T 1 = 0,75 (0,8 ширины)
T 1 = 0,6 Вт
Теперь мы расширяем наши приложения и смотрим на Atwoods.
 Станок
Станок Пример 5 : Рассмотрим машину Этвудса, показанную здесь, с масс m 1 и m 2 .Они прикреплены легкий шнур поверх шкива, как показано на рисунке. Какое ускорение системы?
Можно сказать «ускорение системы» для масс 1 и 2 будут иметь такое же ускорение , поскольку они прикреплены шнурком. Если m 2 > m 1 и Этвуды машина выпущена из покоя, масса m 1 будет разгон до при массе m 2 ускоряет вниз на стойку.Собственно, это будет их ускорения независимо от того, выпущена ли система из состояния покоя или двигается. Вероятно, это будет легче визуализировать, если вы представьте, что система выходит из состояния покоя. Как мы можем применить F = m a ? Применим F = m a к массам, по одной
время. | |
Посмотрите на меньшую массу, м 1 .Какие силы, действующие на эту массу? Натяжение струны создает силу вверх в то время как сила тяжести опускает . Мы ожидаем этого масса, чтобы иметь ускорение от до . Там нет горизонтальных сил. Возьмем до как положительный . F нетто = F = T – w 1 = m 1 aF нетто = F = T – м 1 г = м 1 a т – м 1 г = м 1 a Это одно уравнение имеет два неизвестных – напряжение T и ускорение a.Значит нам нужно еще информация . | |
Мы получаем эту дополнительную информацию, просматривая
силы, действующие на более тяжелую массу, м 2 , и
применяя Второй закон Ньютона, F = m a , чтобы
эта масса. Натяжение струны создает силу вверх в то время как сила тяжести опускает .Мы ожидаем этого масса, чтобы иметь ускорение, равное против . Мы Вы можете позвонить вниз “положительно” для этой массы или мы можем позвонить до “положительно”, а затем мы ожидаем эта масса должна иметь ускорение – a. Любой выбор Это хорошо. На этот раз выберем вниз как «положительный». F нетто = F = w 2 – T = m 2 aF нетто = F = m 2 г – T = m 2 a м 2 г – T = м 2 a Конечно, это одно уравнение также имеет два
неизвестные – напряжение Т и ускорение а. |
Но теперь у нас есть два уравнения с двумя неизвестными и этого достаточно. Мы можем найти напряжение T в первое уравнение,
Т – м 1 г = м 1 аT = m 1 g + m 1 a
, а затем подставим это во второе уравнение
м 2 г – T = м 2 ам 2 г – (м 1 г + м 1 а) = м 2 а
м 2 г – м 1 г – м 1 a = м 2 а
м 2 г – м 1 г = м 1 a + м 2 а
(м 2 – м 1 ) г = (м 1 + м 2 ) а
(м 1 + м 2 ) a = (м 2 – м 1 ) г
a = (m 2 – m 1 ) г / (m 1 + м 2 )
Пример 6: Теперь рассмотрим наклонную машину Атвудса.
 Масса m 1 и m 2 соединены струной.
который проходит по шкиву, а масса m 2 сидит на гладком
наклонная плоскость. Помните, что «гладкий» – это просто кодовое слово для
«без трения»; мы скоро перейдем к трениям. Этот склонный
Здесь схематически изображена машина Этвудса:
Масса m 1 и m 2 соединены струной.
который проходит по шкиву, а масса m 2 сидит на гладком
наклонная плоскость. Помните, что «гладкий» – это просто кодовое слово для
«без трения»; мы скоро перейдем к трениям. Этот склонный
Здесь схематически изображена машина Этвудса:Теперь мы хотим применить Второй закон Ньютона, F = m а . Второй закон Ньютона описывает влияние сил на один объект. Поэтому мы должны изолировать все силы от массы м 1 и нанести его.Затем мы изолируем все силы от массы m 2 и снова нанести. Это требует хорошего свободного тела диаграммы.
Висящая масса m1 воздействует только на две силы; веревка тянет вверх с силой, которую мы обозначаем T, в то время как гравитация тянет вниз с силой мы маркируем w:
Мы ожидаем, что ускорение будет восходящим, и нарисовали его.
рядом с диаграммой свободного тела.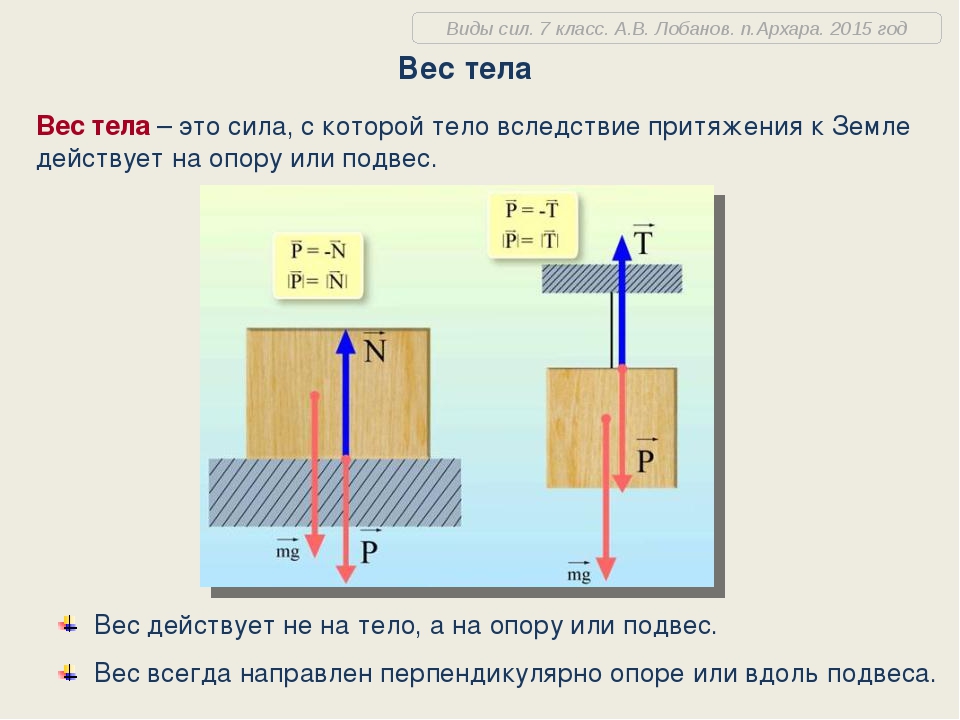 Как всегда, теперь мы готовы подать заявку F = m a этим силам, действующим на этот объект.
Как всегда, теперь мы готовы подать заявку F = m a этим силам, действующим на этот объект.
Т – м 1 г = м 1 a
Как и следовало ожидать, это одно уравнение имеет два неизвестные – напряжение Т и ускорение а – так что надо смотреть в другом месте для получения дополнительной информации. Конечно, где смотреть находится в другой массе.
Тщательно постройте диаграмму свободного тела, показывающую все силы
действующая на массу m 2 .Действуют три силы на эту массу – струна действует с силой Т ,
(без трения) наклонная плоскость оказывает «нормальную» силу н ,
и сила тяжести тянет вниз с силой w 1 = m 1 г. Чтобы найти чистую силу , мы должны решить
эти векторы на их компоненты. Поскольку ускорение будет
быть по направлению плоскости, мы выбрали это направление
как ось абсцисс.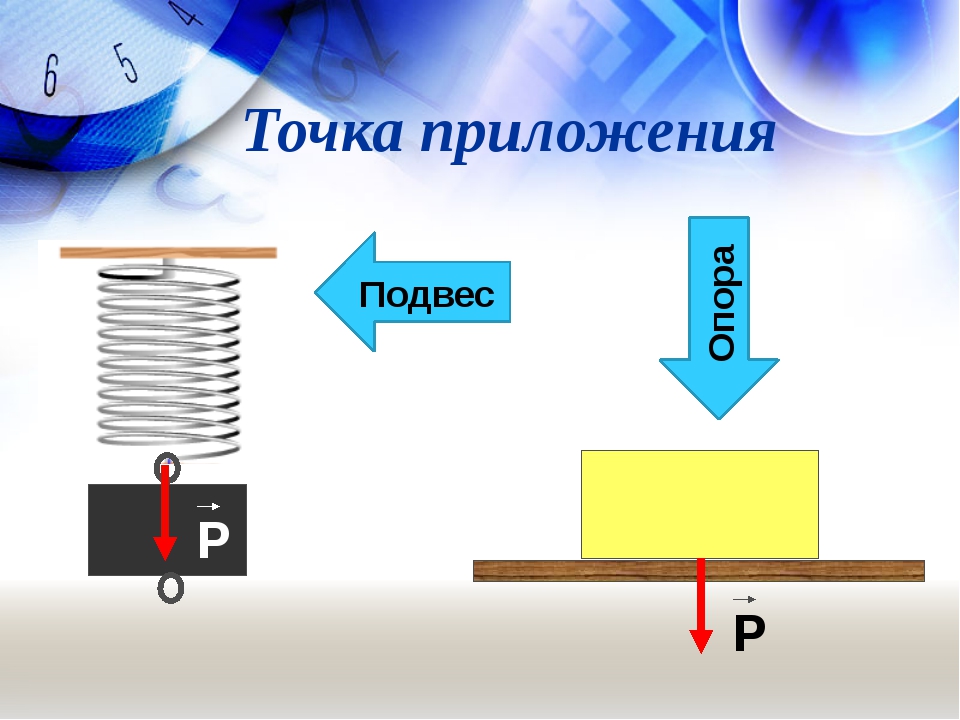
Обратите внимание, что угол в эта диаграмма отсчитывается от оси Y . Это означает вес имеет составляющие
w x = m 2 g sinw y = – m 2 g cos
А у нас
п х = 0n y = n
и
Т x = – Т
T y = 0
Убедитесь, что вы понимаете знаки и синусы! Не продолжай пока вам не будут понятны все эти составляющие!
Теперь мы можем применить Второй закон Ньютона к этой массе:
F = m aF = F нетто = T + n + w = m a
F x = F net, x = F x = м 2 a x
F x = T x + n x + w x = m 2 a x
– Т + 0 + м 2 г sin = м 2 a x = м 2 a
, где мы использовали
х = а, поскольку ускорение происходит только в положительном направлении оси x.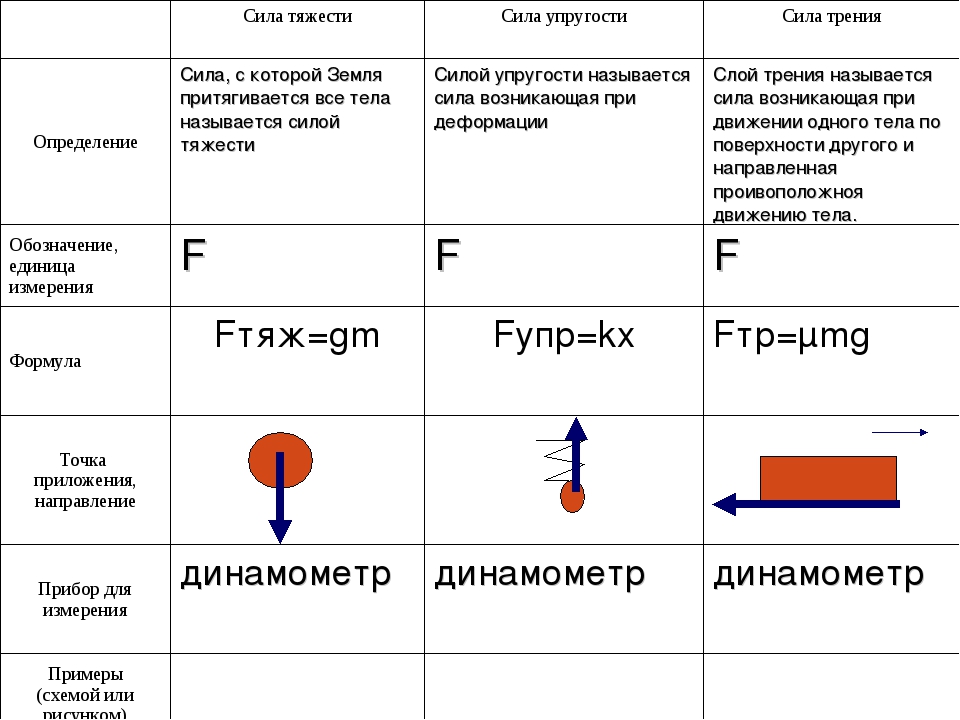
Это предоставляет всю информацию, которая нам нужна для решения T и a. Как и раньше, мы можем решить одно из этих уравнений относительно T и подставьте это в другое уравнение и решите относительно a.
T = m 2 г sin – м 2 а[м 2 г sin – m 2 a] – m 1 g = m 1 a
м 1 a + m 2 a = m 2 г sin – м 1 г
(m 1 + m 2 ) a = (m 2 sin – м 1 ) г
a = (м 2 sin – м 1 ) г / (м 1 + м 2 )
Как насчет y-компонентов сил, действующих на массу? м 2 , на наклонной плоскости?
F y = F net, y = F y = m 2 a yF y = T y + n y + w y = m 2 a y = 0
, где мы использовали
а y = о, поскольку ускорение происходит только в положительном направлении оси x и
нет ускорения перпендикулярно плоскости.
0 + n – м 2 г cos = 0
n = m 2 г cos
Из y-составляющих сил на массу m 2 , мы можно решить для нормальной силы. Это будет важно, когда мы принять во внимание трение .
Пример 7: Два блока масс m 1 и м 2 размещены в контакте друг с другом на гладкой, горизонтальная плоскость, как показано здесь.Постоянная горизонтальная сила F применяется к m 1 . Какое ускорение каждая масса?
В каком-то смысле мы можем (почти) решить этот пример интуитивно – в нашей голове. Сила F приложена к объекту массой m = м 1 + м 2 . Значит, его ускорение должно быть
а = Ф / мили
а = F / (м 1 + м 2 ) Это правильный ответ! Но разве в этом больше ничего нет?
вопрос? Простые вопросы – интуитивно очевидные – делают
замечательные шаблоны или примеры для более сложных задач.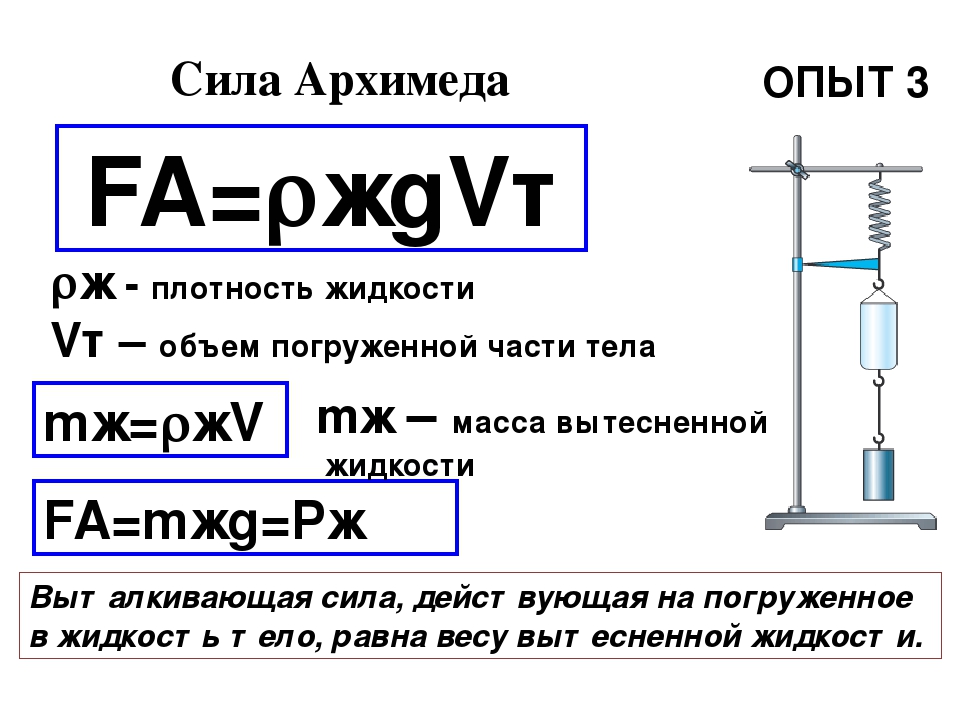
Посмотрите все силы на м . Сделайте хорошее свободное тело диаграмма сил, действующих на м 1 .
Конечно, внешняя сила F толкает вправо на масса m 1 . Гравитация тянет вниз с силой w 1 = m 1 g и самолет отвечает нормальной силой н 1 . Но другой масса – m 2 – действует на массу m 1 .Эта сила обозначена P ‘ и указывает налево. Мы можем применить Второй закон Ньютона к силам y-компоненты и найти, что n 1 = w 1 1. Но теперь есть дополнительный и неизвестная сила в x-компоненте Второго закона Ньютона,
F 1, сетка = F – P ‘= m 1 aНам нужно на больше информации , поэтому перейдем к другой массе, м 2
Первая масса m1 оказывает на эту массу, m2 силу P .Применяя y-компонент F = m a , мы легко найти
n 2 = w 2Для x-компонентов только сила , действующая на m2, равна P так
F 2, сетка = P = m 2 aОднако из Третьего закона Ньютона F 12 = – F 21 , мы знаем, что P = P ‘, поэтому
F – P ‘= м 1 аF – м 2 a = м 1 a
F = m 1 a + m 2 a
F = (м 1 + м 2 ) a
a = F / (м 1 + м 2 )
Это тот же ответ, который мы так быстро нашли ранее, но этот
может предоставить шаблон для использования в более сложных ситуациях.
Пример 8: Этот конкретный пример сформулирован в терминах взвешивание рыбы в ускоряющем элеваторе. Это тоже весело представить себе вес в ускоряющемся лифте. Когда лифт разгоняется до ступеней? Когда лифт разогнаться вниз палаты?
Силы, действующие на рыбу, показаны в свободном теле. диаграмма. T – это напряжение на шкале. Это ценность весы читают.Мы можем назвать это видимым весом рыбы. Чистое усилие на рыбу
. F net = T – wили
F нетто = T – мгЧистая сила ( всегда! ) равна массе, умноженной на ускорение. Эта рыба движется вместе с лифтом. В этом На диаграмме мы взяли ускорение от до , так что это положительный.
F нетто = T – m g = m aT = m g + m a
Т = м (г + а)
В то время как лифт ускоряет вверх по стойке , кажущийся
вес рыбы на больше ее истинного веса на ,
мг.
Что происходит, когда лифт ускоряется с вниз по палате ?
Силы, действующие на рыбу, снова показаны в свободном теле. диаграмма,
F net = T – wили
F нетто = T – мгЧистая сила ( всегда! ) равна массе, умноженной на ускорение. Эта рыба движется вместе с лифтом. Теперь ускорение должно быть до , то есть отрицательное .
F net = T – m g = m (- a)T = м г – м а
Т = м (г – а)
В то время как лифт ускоряется на вниз по стойке , кажущийся вес рыбы на меньше ее истинного веса, мг.
Попробуйте сами на элеваторе – не взвешивая рыбу, ставим обращая внимание на собственный кажущийся вес !
c) 2002 год, Дуг Дэвис; все права защищеныГЛАВА 4
ГЛАВА 4
12.Запишем F = м a из силовой диаграммы для автомобиля:
y -компонент: F T мг = ma , или
F T = м ( a + g ) = (1200 кг) (0,80 м / с2 + 9,80 м / с2)
= 1,3 104 Н.
28. ( а )
( b ) Поскольку скорость постоянна, ускорение равно нулю.
Запишем F = м a из силовой диаграммы для косилки:
x -компонент: F cos
q F fr = ma = 0, что даетF
fr = (88,0 Н) cos 45 = 62,2 Н.( c ) y -компонент: F
N мг F sin q = ma = 0, что даетF
fr = (14.5 кг) (9,80 м / с2) + (88,0 Н) sin 45 = 204 Н.( d ) Мы можем найти ускорение от движения косилки:
a = v / t = (1,5 м / с 0) / (2,5 с) = 0,60 м / с
2.Для компонента x из F = м a теперь у нас
F cos
q F fr = ma ;F cos 45 62,2 N = (14,5 кг) (0.60 м / с
2), что дает F = 100 Н.30. ( a ) Поскольку ковши находятся в состоянии покоя, ускорение равно нулю.
Запишем F = м a из диаграммы сил для каждого ковша:
нижний ковш: F
T2 м 2 г = м 2 a = 0, что даетF T2 = м 2 г = (3.0 кг) (9,80 м / с2) = 29 Н.
верхний ковш: F T1 F T2 м 1 г = м 1 a = 0, что дает
F T1 = F T2 + м 1 г = 29 Н + (3,0 кг) (9,80 м / с2) = 58 Н.
( b ) У двух ковшей должно быть одинаковое ускорение.
Запишем F = м a из диаграммы сил для каждого ковша:
нижний ковш: F T2 м 2 г = м 2 a , что дает
F T2 = м 2 ( г + a )
= (3.0 кг) (9,80 м / с2 + 1,60 м / с2) = 34 Н.
верхний ковш: F T1 F T2 м 1 г = м 1 a , что дает
F T1 = F T2 + м 1 ( г + a )
= 34 Н + (3,0 кг) (9,80 м / с2 + 1,60 м / с2) = 68 Н.
32. ( a ) Поскольку скорость постоянна, ускорение равно нулю.
Запишем F = м a из силовой диаграммы:
F
T + F T мг = мА = 0, что даетF
T =! мг =! (65 кг) (9.80 м / с2) = 3,2 102 Н.( b ) Теперь имеем:
F
T + F T мг = мА ;2 (1,10) (
! мг ) мг = мА , что даетa = 0,10 г = 0,10 (9,80 м / с2) = 0,98 м / с2.
40. ( а ) ( б ) ( в )
В ( a ) трение статическое и противодействует приближающемуся движению вниз по плоскости.
В ( b ) трение кинетическое и препятствует движению вниз по плоскости.
В ( c ) трение кинетическое и препятствует движению вверх по плоскости.
56. Пока коробка скользит вниз, трение будет вверх
самолет, противодействующий движению. Из диаграммы сил для
коробка, имеем F = м а :
x -компонент: мг sin q F fr = ma .
y -компонент: F N мг cos q = 0.
Из уравнения x получаем
F fr = мг sin q ma = m ( g sin q a )
= (18,0 кг) [(9,80 м / с2) sin 37,0 (0,270 м / с2)]
= 101 Н.
Поскольку трение кинетическое, имеем
F fr = м k F N = m k мг cos q ;
101.3 N = м k (18,0 кг) (9,80 м / с2) cos 37,0, что дает м k = 0,719.
58. Для каждого объекта мы принимаем направление ускорения как
.положительное направление. Кинетическое трение из таблицы
будет противодействовать движению чаши.
( a ) Из силовых диаграмм имеем F = м a :
x -компонент (чаша): F T F fr = м чаша a ;
y -компонент (чаша): F N м чаша г = 0;
y -компонент (cat): m cat g F T = m cat a .
С F fr = m k F N, имеем
F T = F fr = м чаша a + м k м чаша г .
Когда мы исключаем F T, получаем
( м кот м к м чаша) г = ( м кот + м чаша) а ;
[(5,0 кг) (0,44) (11 кг)] (9,80 м / с2) = (5.0 кг + 11 кг) a , что дает a = 0,098 м / с2.
( b ) Находим время, за которое чаша дойдет до края стола с
x = x 0 + v 0 t +! по адресу 2;
0,9 м = 0 + 0 +! (0,098 м / с2) т 2, что дает т = 4,3 с.
74. Берем положительное направление вверх.
Весы показывают силу, которую человек оказывает на весы. С
Третий закон Ньютона, это также величина нормального
сила, действующая на человека. Эффективная масса по шкале
м масштаб = F N / г .
Запишем F = м a из силовой диаграммы для человека:
y -компонент: F N мг = ma , или
м масштаб = F N / г = м ( a + г ) / г .
( a ) Когда лифт находится в состоянии покоя, a = 0:
м масштаб = м (0 + г ) / г = м = 75,0 кг.
( b ) Когда лифт поднимается с постоянной скоростью, a = 0:
м масштаб = м (0 + г ) / г = м = 75,0 кг.
( c ) Когда лифт падает с постоянной скоростью, a = 0:
м масштаб = м (0 + г ) / г = м = 75.0 кг.
( d ) Когда лифт ускоряется вверх, a положительный:
м масштаб = м ( a + г ) / г = (75,0 кг) (3,0 м / с2 + 9,80 м / с2) / (9,80 м / с2) = 98,0 кг.
( e ) Когда лифт ускоряется вниз, a отрицательно:
м масштаб = м ( a + г ) / г = (75,0 кг) (3.0 м / с2 + 9,80 м / с2) / (9,80 м / с2) = 52,0 кг.
Нормальные, растягивающие и другие примеры сил
Пример 1. Вес на уклоне, двумерная задача
Рассмотрим лыжника на склоне, показанном на рисунке 2. Ее масса, включая снаряжение, составляет 60,0 кг. а) Каково ее ускорение, если трение незначительно? (b) Каково ее ускорение, если известно, что трение составляет 45,0 Н?
Рис. 2. Поскольку движение и трение параллельны склону, наиболее удобно проецировать все силы в систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника). N перпендикулярно откосу, а f параллельно склону, но w имеет компоненты вдоль обеих осей, а именно w ⊥ и [латекс] \ textbf {w} _ {\ parallel} [ /латекс]. N равно по величине w ⊥ , так что нет движения перпендикулярно склону, но f меньше w∥, так что есть ускорение вниз по склону (вдоль параллельной оси).
СтратегияЭто двумерная задача, поскольку силы, действующие на лыжника (интересующая система), не параллельны.Подход, который мы использовали в двумерной кинематике, также здесь очень хорошо работает. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав две связанных одной -мерной задачи, которую нужно решить. Самая удобная система координат для движения по наклонной поверхности – это та, в которой одна координата параллельна склону, а другая – перпендикулярна склону. (Помните, что движения по взаимно перпендикулярным осям независимы.) Мы используем символы ⊥ и ∥ для обозначения перпендикуляра и параллельности соответственно.Такой выбор осей упрощает этот тип проблемы, потому что нет движения, перпендикулярного уклону, и потому что трение всегда параллельно поверхности между двумя объектами. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и поддержка склона, обозначенные соответственно w , f и N на рисунке 2. N всегда перпендикулярно склону, а f параллельно ему. Но w не находится в направлении ни одной из осей, и поэтому первый шаг, который мы делаем, – проецируем его на компоненты вдоль выбранных осей, определяя w ∥ как компонент веса, параллельный наклону, и w ⊥ составляющая веса, перпендикулярная уклону. {\ circ}) – f} {m} [/ latex].{2} [/ латекс]
, что соответствует ускорению, параллельному наклону, при противоположном трении 45,0 Н.
ОбсуждениеПоскольку трение всегда противостоит движению между поверхностями, ускорение меньше при трении, чем при его отсутствии. Фактически, общий результат заключается в том, что если трение на уклоне незначительно, то ускорение вниз по уклону составляет a = g sin θ , независимо от массы .Это связано с ранее обсуждавшимся фактом, что все объекты падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).
Физика лифта
Физика лифтаФизика лифта
Представьте, что вы находитесь в лифте. Нарисуйте отдельные схемы свободного тела для вас, лифта как такового и вашей комбинированной системы плюс лифт для этих трех ситуаций:
- лифт не имеет ускорения (стоит на месте или движется с постоянной скоростью)
- лифт имеет восходящее ускорение (ускорение вверх или замедление при движении вниз)
- лифт имеет ускорение вниз (ускорение вниз или замедление при движении вверх)
В этой ситуации нет новых сил, действующих при ускорении – одна или несколько сил просто изменяют размер, чтобы вызвать ускорение.
На диаграмме свободного тела есть две силы: сила тяжести и сила, направленная вверх, нормальная, исходящая от лифта.
На схеме свободного тела лифта есть три силы: сила тяжести, направленная вниз нормальная сила, исходящая от вас, и восходящая сила, обусловленная натяжением троса, удерживающего лифт.
Комбинированная система «вы + лифт» имеет две силы: комбинированную силу тяжести и натяжение троса.
Рассмотрим нормальную силу, действующую на вас со стороны лифта:
- N = мг, если лифт находится в покое или движется с постоянной скоростью
- Н = мг + ма, если лифт имеет восходящее ускорение
- N = mg – ma, если лифт имеет ускорение вниз
Нормальная сила равна вашему кажущемуся весу.Таким образом, вы действительно чувствуете себя немного тяжелее, чем обычно, когда лифт ускоряется вверх, и легче, чем обычно, когда ускорение уменьшается. В более экстремальных ситуациях это намного очевиднее.

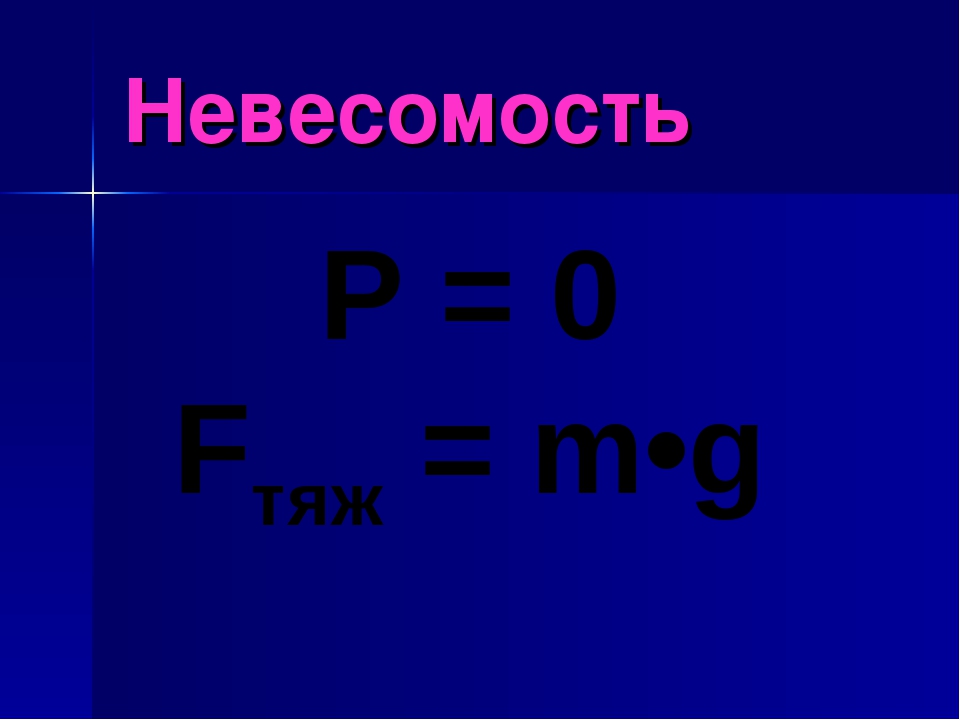 04.03 – радиофизика, Руководитель: В.С. Касперович
04.03 – радиофизика, Руководитель: В.С. Касперович Выводцева (защита – октябрь 2016)
Выводцева (защита – октябрь 2016) Е. Куренкова (2012)
Е. Куренкова (2012)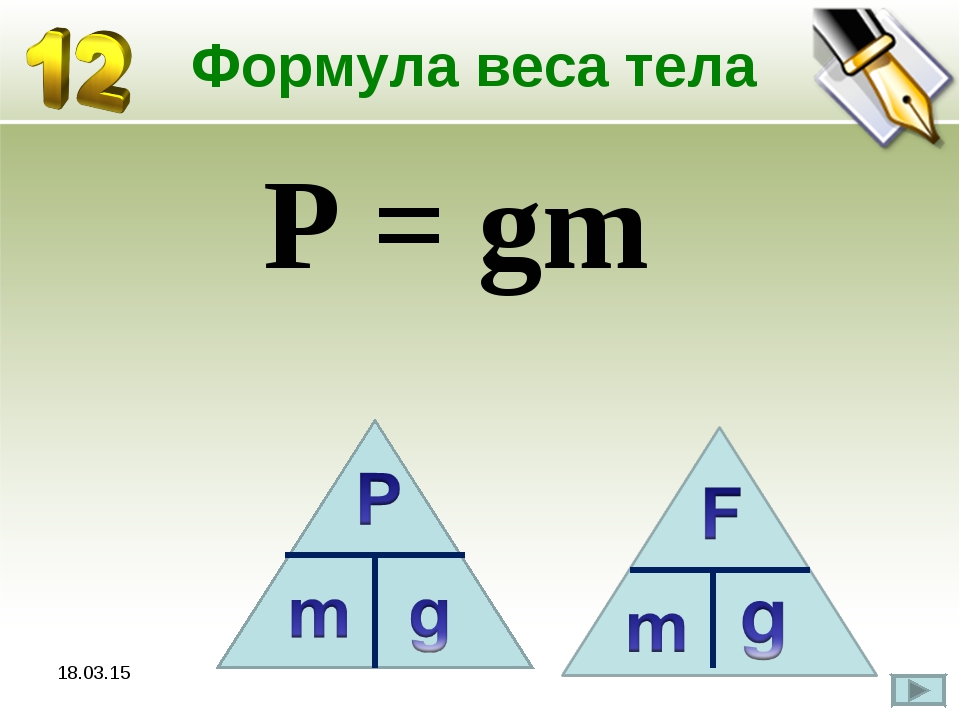 Э. Велиев (2011)
Э. Велиев (2011) Б. Харьков (2008)
Б. Харьков (2008) Springer (2014) 788 p. 234 illus.
Springer (2014) 788 p. 234 illus. 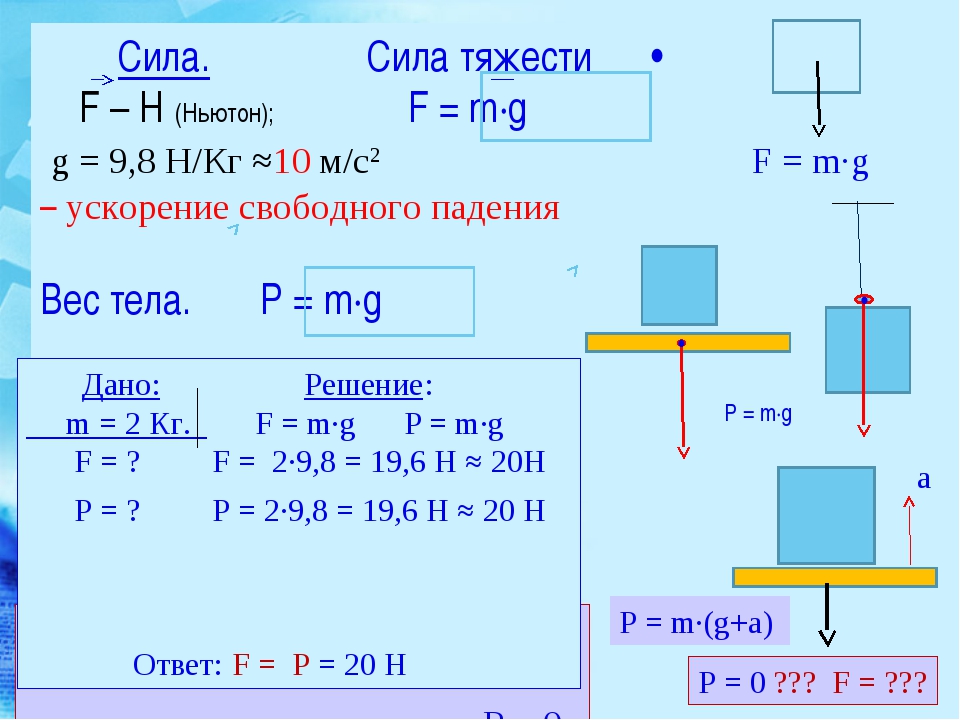 194 (2013) 288-291.
194 (2013) 288-291. С. Чернышев, В.И. Чижик, Н.Е. Скрябина, D. Fruchart, S. Miraglia. Спин-решёточная релаксация и подвижность протонов в решетке сплава TiV0.8Cr1.2. ФТТ 53 (2011) 214-221.
С. Чернышев, В.И. Чижик, Н.Е. Скрябина, D. Fruchart, S. Miraglia. Спин-решёточная релаксация и подвижность протонов в решетке сплава TiV0.8Cr1.2. ФТТ 53 (2011) 214-221. Г. Шеляпина, В.С.Касперович, Н.Е.Скрябина, D.Fruchart. Неэмпирические расчеты стабильности неупорядоченных твердых растворов Ti-V-Cr и их гидридов. ФТТ 49 (2007) 385-388.
Г. Шеляпина, В.С.Касперович, Н.Е.Скрябина, D.Fruchart. Неэмпирические расчеты стабильности неупорядоченных твердых растворов Ti-V-Cr и их гидридов. ФТТ 49 (2007) 385-388. Г.Шеляпина. Неэмпирические кластерные расчеты тензора градиентов электрического поля в иттрий-алюминиевом гранате Y3Al5O12. Физика Твердого Тела 48 (2006) 1593-1597.
Г.Шеляпина. Неэмпирические кластерные расчеты тензора градиентов электрического поля в иттрий-алюминиевом гранате Y3Al5O12. Физика Твердого Тела 48 (2006) 1593-1597.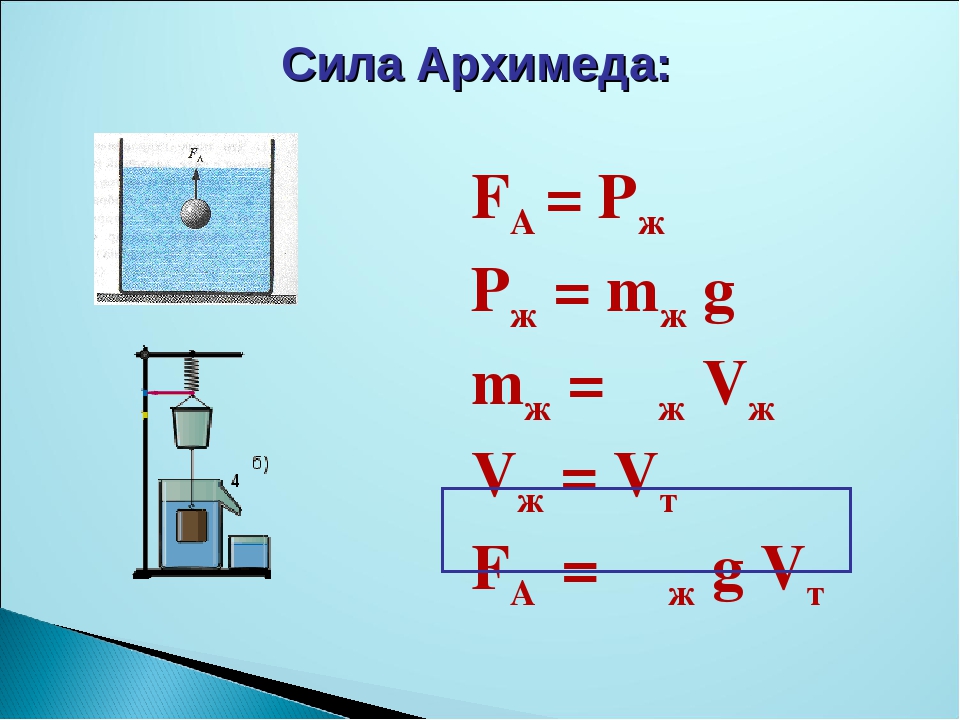 J. Magn. Magn. Mater. 300 (2006) e563-e566.
J. Magn. Magn. Mater. 300 (2006) e563-e566.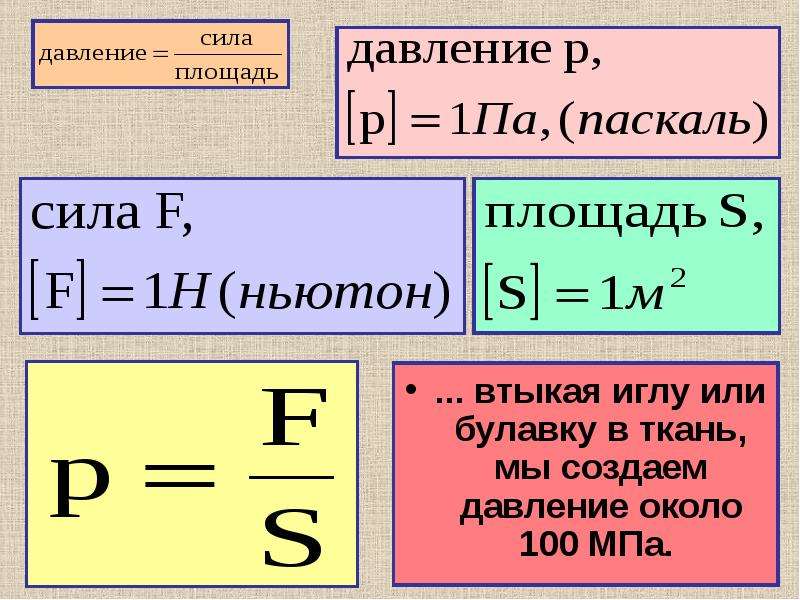 ФТП 40 (2006) 1309-1315.
ФТП 40 (2006) 1309-1315. Melnyk, O. Bodak, D. Fruchart, El. K. Hlil, and J. Tobola. Transport properties and electronic structure of M2CuSb3 compounds with M = Ti, Zr, Hf. J. Alloys Compd. 354/1-2 (2003) 6-12.
Melnyk, O. Bodak, D. Fruchart, El. K. Hlil, and J. Tobola. Transport properties and electronic structure of M2CuSb3 compounds with M = Ti, Zr, Hf. J. Alloys Compd. 354/1-2 (2003) 6-12. J. Alloys Compd. 343/1-2 (2002) 1-4.
J. Alloys Compd. 343/1-2 (2002) 1-4. )
) Постоянные факторы гравитации.
Постоянные факторы гравитации.

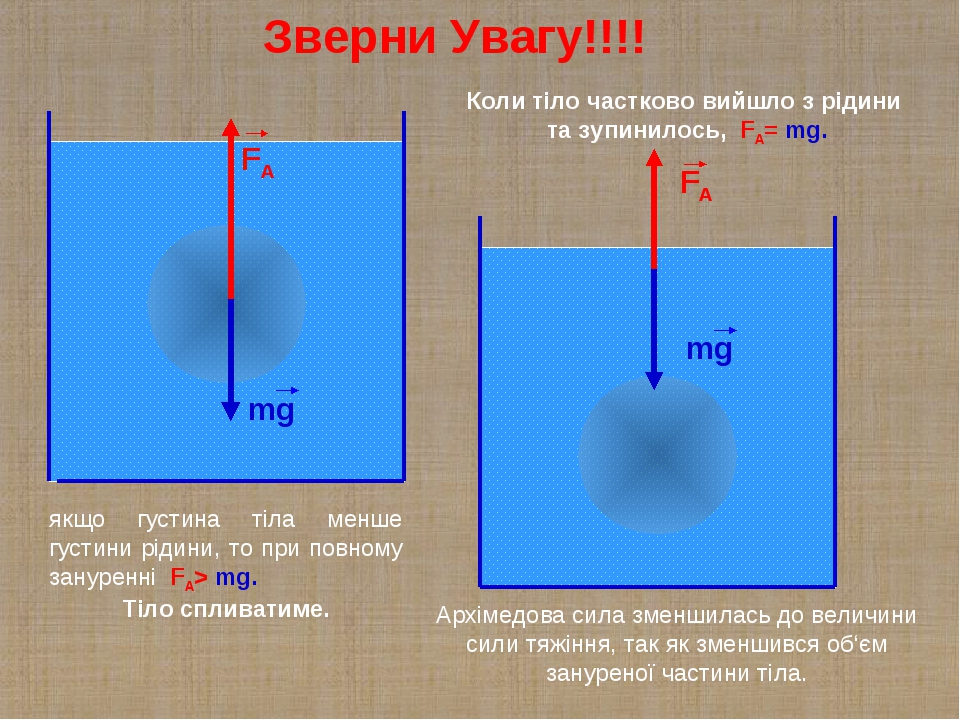 Соответствующая единица измерения силы и веса в системе СИ – это Ньютон, при этом 1 килограмм весит 9,8 Ньютона при стандартных условиях на поверхности Земли. Однако в общепринятых единицах США фунт является единицей силы (и, следовательно, веса). Фунт – широко используемая единица измерения в торговле. Использование фунтовой силы ограничивает единицу массы неудобно большой единицей измерения, называемой «снарядом». Не рекомендуется использовать эту единицу, и настоятельно рекомендуется использование исключительно единиц СИ для всей научной работы.
Соответствующая единица измерения силы и веса в системе СИ – это Ньютон, при этом 1 килограмм весит 9,8 Ньютона при стандартных условиях на поверхности Земли. Однако в общепринятых единицах США фунт является единицей силы (и, следовательно, веса). Фунт – широко используемая единица измерения в торговле. Использование фунтовой силы ограничивает единицу массы неудобно большой единицей измерения, называемой «снарядом». Не рекомендуется использовать эту единицу, и настоятельно рекомендуется использование исключительно единиц СИ для всей научной работы.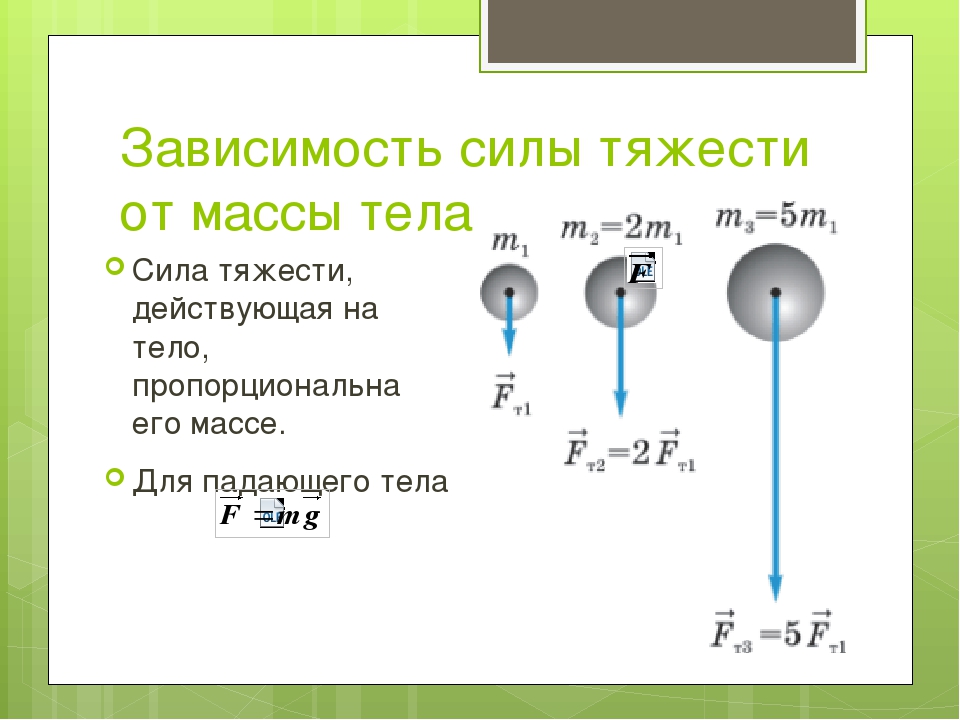 8 м / с 2
8 м / с 2 
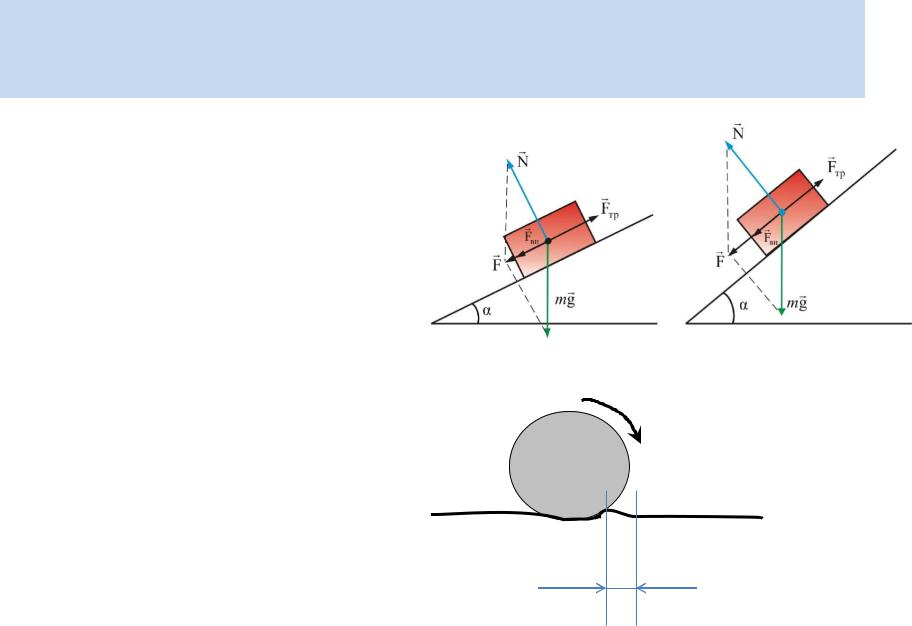 Горизонтальных сил нет.
Горизонтальных сил нет.