18.12.201907.07.2019

Как через эдс найти напряжение – Формула связи между ЭДС (электродвижущей силой) и напряжением.

• by alexxlab
• Комментариев к записи Как через эдс найти напряжение – Формула связи между ЭДС (электродвижущей силой) и напряжением. нет
• Разное

Формула связи между ЭДС (электродвижущей силой) и напряжением.

В задачах на электрический ток в качестве дано или найти присутствуют напряжение и ЭДС (электродвижущая сила). Есть достаточно простая связь между этими параметрами. Введём любую цепь (рис. 1).

Рис. 1. Связь между ЭДС и напряжением

Пусть дан источник с ЭДС 

, напряжение во внешней цепи . Внутреннее сопротивление источника — , а сопротивление внешней цепи — . В данной системе течёт электрический ток . Тогда:

(1)

(2)

Логично предположить, что количество электронов, сгенерированных источником, равно количеству электронов, ушедших в цепь, тогда приравниваем (1) и (2):

Откуда:

(3)

Соотношение (3) — связь между ЭДС и напряжением в полной цепи постоянного тока.

В условиях идеальной цепи (внутреннее сопротивление источника равно нулю 

), ЭДС численно равно напряжению.

Вывод: приведенные соотношения помогают в ряде задач, в которых даны параметры источника тока/напряжения, а необходимо найти силу тока или напряжения на каком-либо элементе цепи (резистор, катушка, лампа и т.д.), и наоборот.

Поделиться ссылкой:

www.abitur.by

ЭДС и напряжение. Внутреннее сопротивление источников питания.

РадиоКот >Обучалка >Аналоговая техника >Основы электроники >

ЭДС и напряжение. Внутреннее сопротивление источников питания.

Ликбез так ликбез!
Несмотря на то, что многие из посетителей этого сайта являются продвинутыми радиокотами и уже успешно занимаются программированием и конструированием, существуют еще отдельные котята, у которых возникают иногда вопросы, связанные с азами радио- (или даже электро) техники.

Итак, вернемся к азам… По азу- я всех везу! Ой! Это из другой оперы…

Закон Ома. Вот я о чем.

О законе Ома мы уже говорили. Поговорим еще раз – с несколько иной стороны. Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. ( электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.

Переведя сие заклинание на язык сухих формул получаем:

I=E/R

где:
I – сила тока,
E – Э.Д.С. – электродвижущая сила
R – сопротивление

Ток измеряется в амперах, э.д.с. – в вольтах, а сопротивление носит гордое имя товарища Ома.
Э.д.с. – это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):

I=U/R

где:
U – напряжение источника непосредственно на его клеммах.

Рассмотрим простой пример.

Представим себе обычную батарейку в виде источника э.д.с. и включенного последовательно с ним некоего резистора, который будет олицетворять собой внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр. Его входное сопротивление значительно больше внутреннего сопротивления батарейки, но не бесконечно большое – то есть, через него потечет ток. Величина напряжения, которую покажет вольтметр будет меньше величины э.д.с. как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.

Но, тем не менее именно эта величина и принимается за напряжение батарейки.

Формула конечного напряжения при этом будет иметь следующий вид:

U(бат)=E-U(внутр)

Так как со временем у всех элементов питания внутреннее сопротивление увеличивается, то и падение напряжения на внутреннем сопротивлении тоже увеличивается. При этом напряжение на клеммах батарейки уменьшается. Мяу!

Разобрались!

Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер.

Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке. Или как мы, радиокоты, любим выражаться – к просадке напруги.

Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму.

Можно так подобрать элементы последовательной цепи, чтобы на каком-нибудь из них получить напряжение, уменьшенное, по сравнению с исходным, во сколько угодно раз.

Простейший делитель напряжения состоит из двух резисторов.
Чем меньшую часть исходного напряжения мы хотим получить и передать в нагрузку, тем меньше должно быть сопротивление резистора, с которого оно снимается. Кроме того, сопротивление этого резистора должно быть значительно меньше, чем сопротивление нагрузки, иначе подключение нагрузки изменит сопротивление всего участка, и напряжение на нем изменится.

Частенько вместо одного из резисторов делителя используют саму нагрузку. В этом случае второй резистор, на котором гасится избыток напряжения, называют гасящим сопротивлением.

Подключив резистор параллельно нагрузке, можно уменьшить идущий через нее ток. Резистор, который включается для ответвления лишнего тока, порядочные коты называют шунтом (ШУНТ в переводе на русский – обходной путь).

Нормальные герои всегда идут шунтом! (Шутка!)

Чем меньше сопротивление шунта, тем большая часть тока пойдет через него и меньшая через нагрузку.
Уф! Запарилась писать такие объемы на своей КПКошке…
Вопросы есть? Будут – пишите. Может, чего еще из школьной программы вспомню.

<<–Вспомним пройденное—-Поехали дальше–>>

---

Как вам эта статья?	Заработало ли это устройство у вас?

www.radiokot.ru

Электродвижущая сила и конечное напряжение

Физика > ЭДС и конечное напряжение

 

Рассмотрите связь электродвижущей силы и конечного напряжения в электрической цепи: роль внутреннего сопротивления, разность потенциалов, формула и схемы.

Конечное напряжение

(напряжение на выходе источника) основывается на электродвижущей силе и внутреннем сопротивлении.

Задача обучения

• Переведите соотношение между ЭДС и конечным напряжением в формулу.

Основные пункты

• Электродвижущая сила отображает разность потенциалов источника в момент, когда ток лишен движения.
• Конечное напряжение – выход напряжения в устройстве, измеренное через клеммы.
• Формула расчета: V = ЭДС – Ir.

Термины

• Конечное напряжение – выход напряжения в устройстве, измеряемое на клеммах.
• Электродвижущая сила (ЭДС) – напряжение, сформированное батареей или магнитной силой в соответствии с законом Фарадея.
• Разность потенциалов – отличие в показателях потенциальной энергии между двумя точками в электрическом поле.

Если вы забудете выключить фары на машине, то со временем они потускнеют. Причина – разряд батареи. Почему же они просто не мигают при потере энергии? Постепенное затухание говорит о том, что конечное напряжение снижается по мере расхода заряда. Все дело в том, что у всех источников напряжения есть две главные части: источник электрической энергии и внутреннее сопротивление.

Электродвижущая сила

Все источники напряжения формируют разность потенциалов и могут отправлять ток при подключении к сопротивлению. Если брать небольшой масштаб, то из-за этого отличия создается электрическое поле, влияющее на заряды и вызывающее ток. Мы называем это отличие электродвижущей силой (ЭДС). Но не думайте, что перед нами «сила» в привычном понятии. Это особая разновидность разности потенциалов источника, когда ток лишен движения. Измеряется в вольтах.

ЭДС связана с источником разности потенциалов, но отличается от конечного напряжения при проходе тока. К примеру, напряжение на аккумуляторе будет меньшим, чем ЭДС. Если конечное напряжение можно вычислить без подачи тока, то оно приравнивается к ЭДС.

Конечное напряжение

Выход напряжения из устройства измеряется на клеммах и именуется конечным напряжением (V). Его вычисляют по формуле:

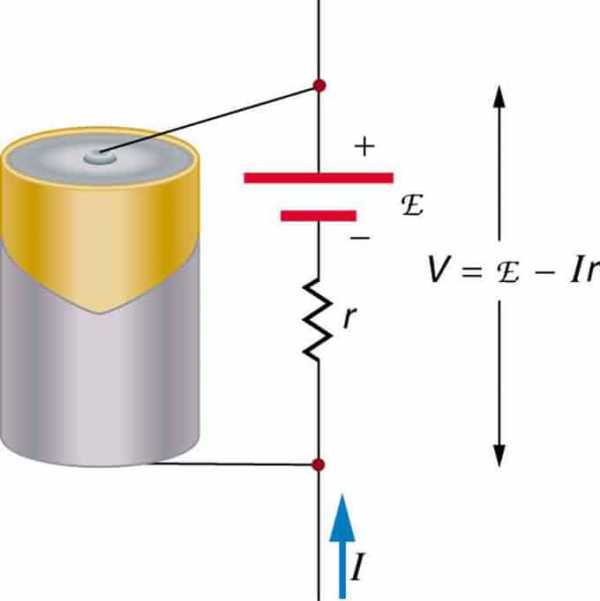
Любой источник напряжения обладает ЭДС, связанной с источником разности потенциалов. Также оно настраивается на сопротивление (r), связанное с конструкцией. Здесь видны выходные клеммы, по которым измеряют конечное напряжение (V). Так как V = ЭДС – Ir, конечное напряжение приравнивается к ЭДС, если ток отсутствует

V = ЭДС – Ir (r – внутреннее сопротивление, I – протекающий во время измерения ток).

I положителен, если ток течет от положительной клеммы. Чем больше ток, тем меньше конечное напряжение. Также конечное напряжение уменьшается при росте внутреннего сопротивления.

---

v-kosmose.com

Напишите формулу нахождения ЭДС, если дано напряжение и сила тока, и чему равно внутреннее сопротивление?

Здесь работает закон Ома для полной цепи: I=E / (R+r), где: R — сопротивление нагрузки r — внутриннее сопротивление мсточника питания От сюда выводим E: I*(R+r) = E E = IR+Ir – это формула нахождения ЭДС Из этой формулы выводим внутреннее сопротивление r: Ir = E-IR Только в условии нет сопротивления нагрузки R!!

Если это ток короткого замыкания, то внутреннее сопротивление равно частному от деления напряжения на ток. А ЭДС равна этому напряжению.

I=(U+ЭДС) /R следовательно ЭДС=I*R-U это для неоднородного участка цепи, где U=(ф1-ф2), т. е цепь, содержащая источник ЭДС…. внутреннее сопротивление рассчитывается так: r=U/I, где U – напряжение в режиме холостого хода, т. е. при нулевом токе нагрузки, а I – ток нагрузки в режиме короткого замыкания

в однородном магнитном поле эдс=BS/t

touch.otvet.mail.ru

Расчет простых цепей постоянного тока

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.  

Пример 1

  Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов  R₁ = 20 и R₂ = 32 Ом. Определить ток в цепи и напряжения на резисторах.

 

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи. 

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов. 

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. 

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. 

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

Пример 2

  Общий ток цепи, содержащей два соединенных параллельно резистора R₁=70 Ом и R₂=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов. 

Токи в резисторах 

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи 

А затем напряжение 

Зная напряжения, найдем токи, протекающие через резисторы 

Как видите, токи получились теми же.

Пример 3

  В электрической цепи, изображенной на схеме R₁=50 Ом, R₂=180 Ом, R₃=220 Ом. Найти мощность, выделяемую на резисторе R₁, ток через резистор R₂, напряжение на резисторе R₃, если известно, что напряжение на зажимах цепи 100 В.

 

Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R₁, необходимо определить ток I₁, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.

Эквивалентное сопротивление и ток в цепи 

Отсюда мощность, выделяемая на R₁ 

Ток I₂ определим с помощью формулы делителя тока, учитывая, что ток I₁ для этого делителя является общим 

Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U₃, как напряжение на резисторе R₂ 

Таким образом производится расчет простых цепей постоянного тока.

Просмотров: 28159

electroandi.ru

---