Как взять частную производную – .
1) Найти частные производные данных функций по каждой из независимых переменных (х, у – переменные)
Решение
Найдем частную производную функции по переменной х, а переменную у в этом случае будем считать постоянной:
.
Найдем частную производную функции по переменной у, а переменную х в этом случае будем считать постоянной:
.
2) Вычислить приближённо, заменяя приращение функции дифференциалом
Решение
Полагая, что есть частное значение функции в точке и что вспомогательная точка будет , получим
;
,
,
; .
Подставляя в формулу , найдем
.
Ответ:
3) Исследовать на максимум и минимум следующую функцию ,
Решение
Найдем частные производные и :
,
.
Решим систему уравнений Которая в данном случае примет вид:
Решения и не удовлетворяют условию
Определим частные производные второго порядка:
, , .
Найдем значение в точке :
, , .
Тогда . и функция в точке имеет экстремум.
Так как , то в точке функция имеет минимум и .
Ответ: т. – точка минимума,
4) Найти наибольшее и наименьшее значение функции в области ,
Решение
Функция непрерывна в замкнутом квадрате . Поэтому, согласно теореме Вейерштрасса, она на этом множестве достигает своих наибольшего и наименьшего, значений функции.
Найдём все решения системы уравнений:
Имеем
Все решения находятся в области
Найдём значения функции в найдённых стационарных точках:
На границе области
А) . Отсюда
Б) . Отсюда ,
С) . Отсюда
D) . Отсюда ,
Найдем значения функции в точках пересечения линий, ограничивающих область .
Выберем наибольшее и наименьшее значения:
,
5) Найти условные экстремумы функции при
Решение
Составим функцию Лагранжа
Имеем
Система имеет единственное решение
Далее
Найдём дифференциал второго порядка в точке :
Тогда
Из уравнения ограничения
При поэтому функция в точке имеет условный минимум,
Ответ: в точке имеет условный минимум,
| < Предыдущая | Следующая > |
|---|
matica.org.ua
12. Частные производные высших порядков
Пусть функция имеет в некоторой области
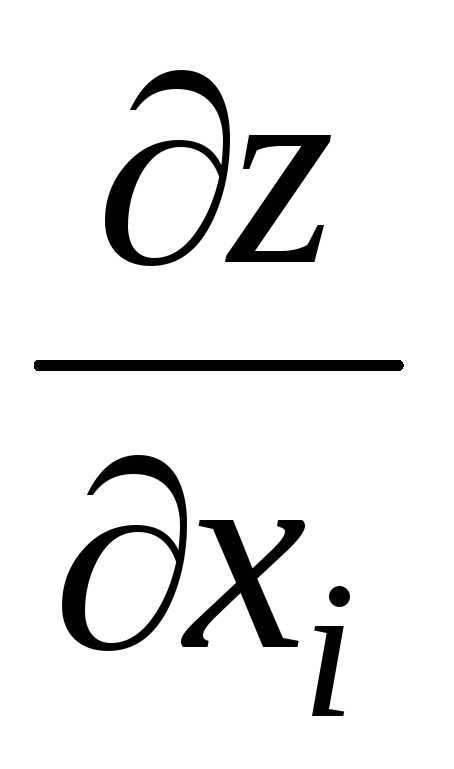 (она называется также частной производной
первого порядка). Тогда эта производная,
сама являясь функцией тех же переменных,
может иметь в некоторой точке
(она называется также частной производной
первого порядка). Тогда эта производная,
сама являясь функцией тех же переменных,
может иметь в некоторой точке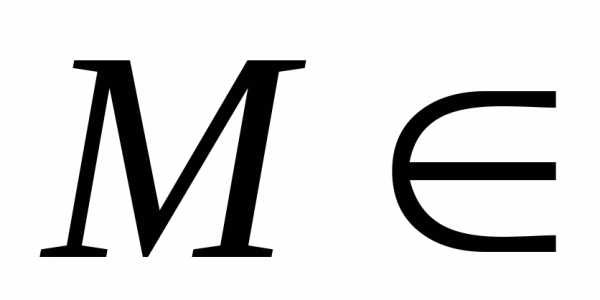 Dчастные производные
по той же
Dчастные производные
по той же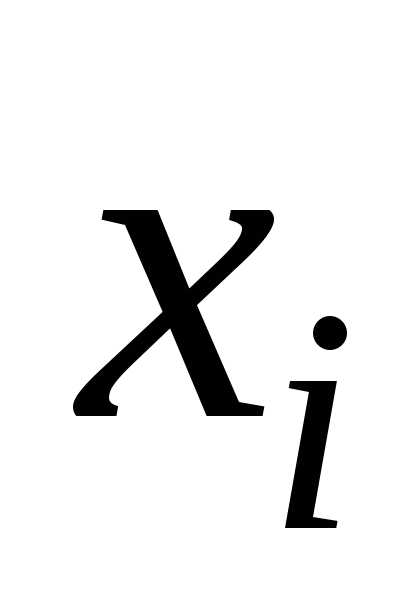 или по любой другой переменной
или по любой другой переменной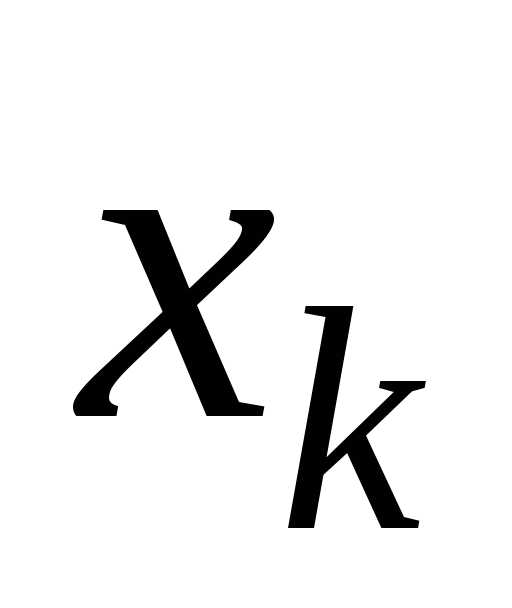 .
Для исходной функцииэти производные будут ужепроизводными
второго порядка (иливторыми частными производными). Производнаявторого
порядка функции по аргументам
.
Для исходной функцииэти производные будут ужепроизводными
второго порядка (иливторыми частными производными). Производнаявторого
порядка функции по аргументам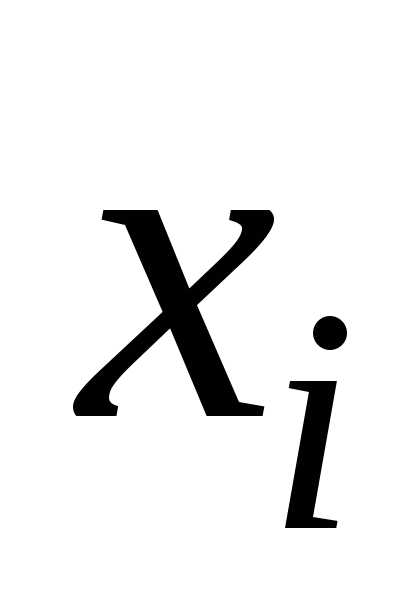 и
и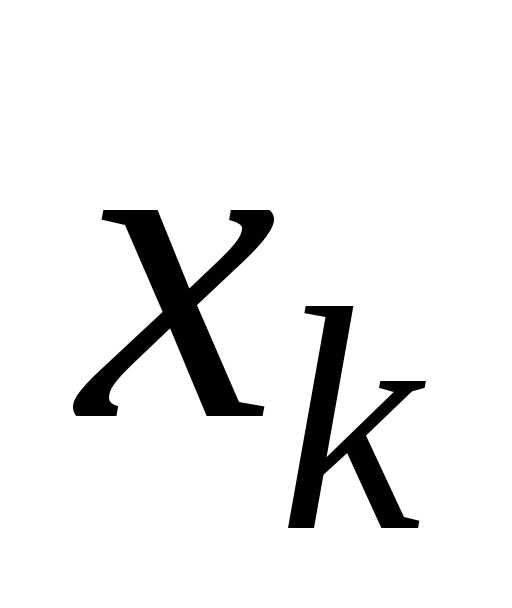 в точке
в точке обозначается одним из следующих
символов:
обозначается одним из следующих
символов: Если 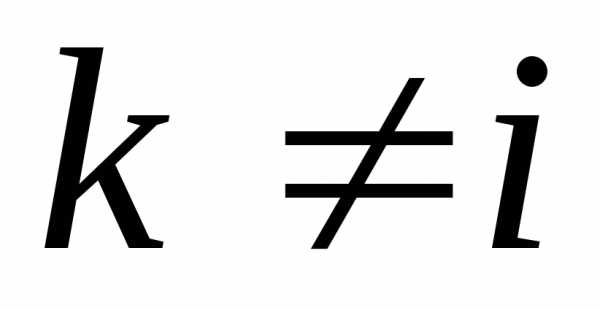 ,
точастная
производная второго порядка называется смешанной.
Если
,
точастная
производная второго порядка называется смешанной.
Если 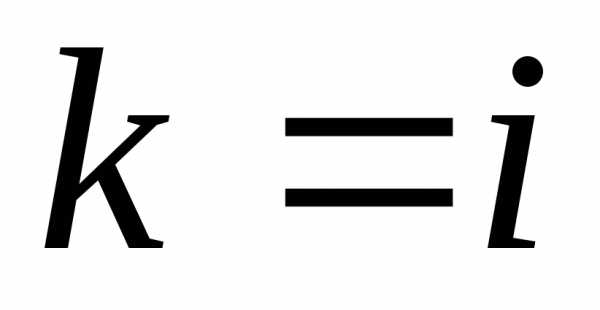 ,
то частная производная второго порядка
обозначается
,
то частная производная второго порядка
обозначается
Частные производные третьего порядка определяются как частные производные от частных производных второго порядка и т.д.
Следует отметить свойство смешанных частных производных:
Теорема. Если в точке Dсмешанные частные
производные
Dсмешанные частные
производные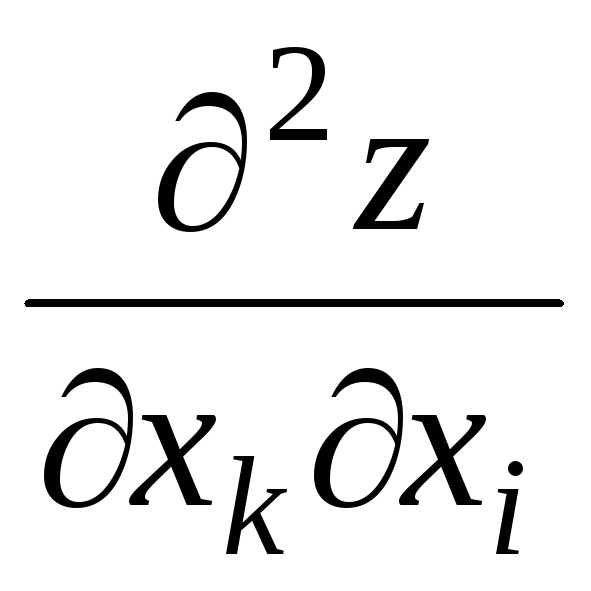 и
и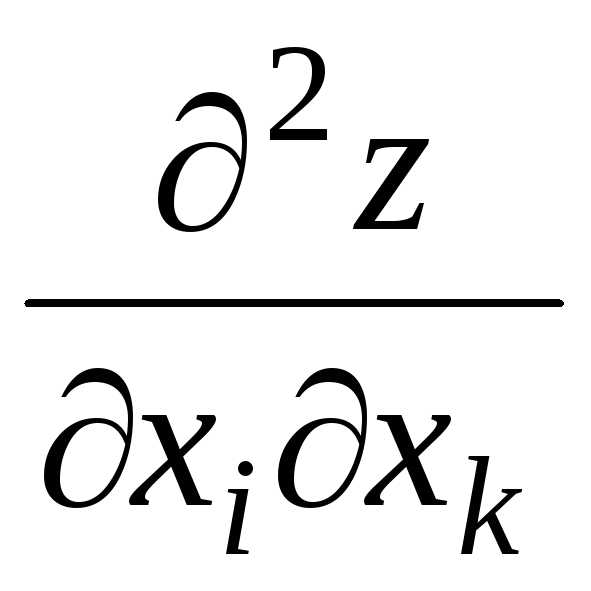 непрерывны, то они равны между собой в
этой точке, т.е.
непрерывны, то они равны между собой в
этой точке, т.е.
,
или значение смешанной производной не зависит от того порядка, в котором производится дифференцирование.
Это свойство верно и для смешанных производных любого порядка.
Теорема. Если функция
определена в некоторой областиDи имеет в этой
области всевозможные частные производные
до  го
порядка включительно инепрерывные
в Dсмешанные
производные
го
порядка включительно инепрерывные
в Dсмешанные
производные 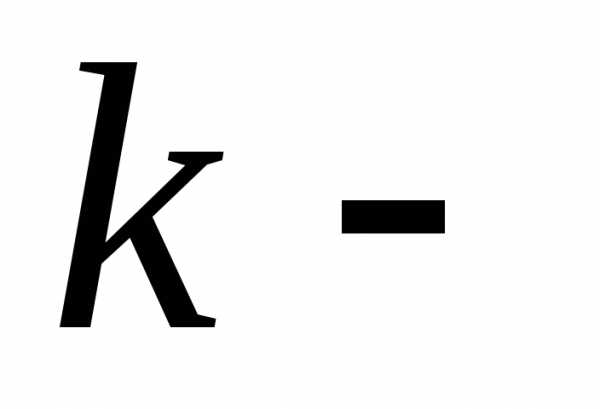 го
порядка, то значение любой
го
порядка, то значение любой 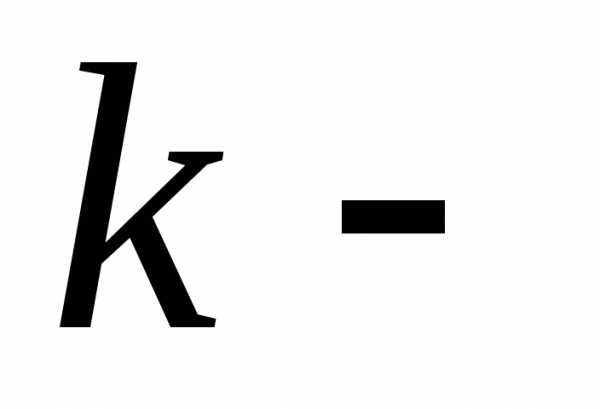 той
смешанной производной не зависит от
того порядка, в котором производятся
последовательные дифференцирования.
той
смешанной производной не зависит от
того порядка, в котором производятся
последовательные дифференцирования.
Пример
5. Найти
частные производные второго порядка
функции  .
.
Решение. Частные производные первого порядка для этой функции мы нашли раньше, рассматривая пример 1:
Найдем теперь частные производные от частных производных первого порядка, получим тем самым частные производные второго порядка заданной функции:
На примере убеждаемся, что смешанные частные производные не зависят от порядка дифференцирования, поэтому в дальнейшем будем находить только одну из них.
13. Дифференциалы высших порядков
Пусть функция
определена в некоторой областиD и имеет в этой области непрерывные
частные производные первого порядка.
Тогда она имеет и полный дифференциал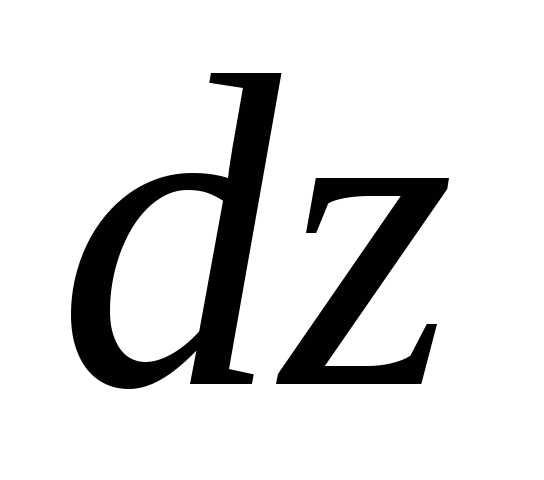 :
:
,
который,
в свою очередь, является некоторой
функцией от тех же переменных. Если
предположить существование непрерывных
частных производных второго порядка
для функции 
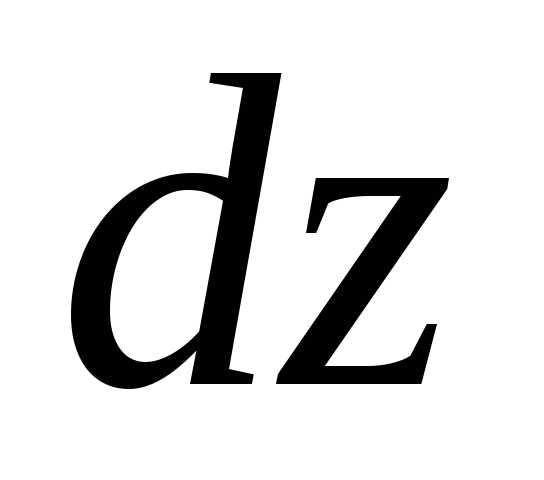 будет иметь непрерывные частные
производные первого порядка, и можно
будет говорить о дифференциале от этого
дифференциала:
будет иметь непрерывные частные
производные первого порядка, и можно
будет говорить о дифференциале от этого
дифференциала: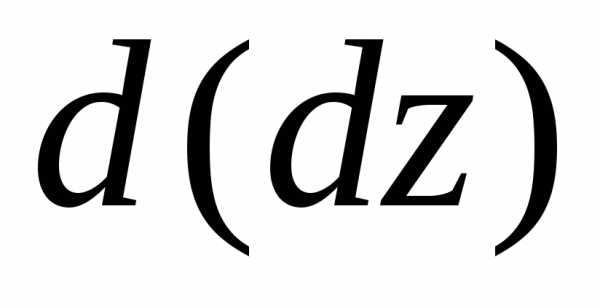 ,
который называетсядифференциалом
второго порядка (или вторым
дифференциалом)
функции
и обозначается.
,
который называетсядифференциалом
второго порядка (или вторым
дифференциалом)
функции
и обозначается.Замечание. Приращения при этом рассматриваются какпостоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Следовательно, дифференциалы любого порядка выше первого от независимых переменных равны нулю, т.е.
,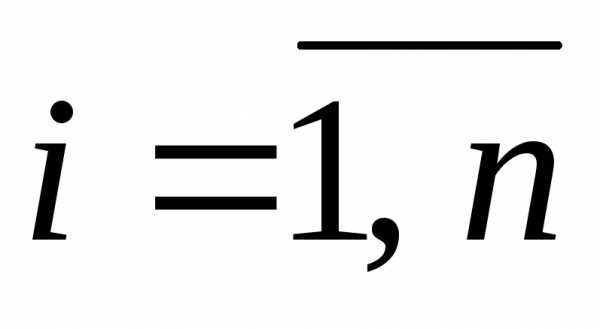 .
(7)
.
(7)
Поэтому, применяя правила дифференцирования и помня о равенстве смешанных производных по одному и тому же набору переменных, получим:
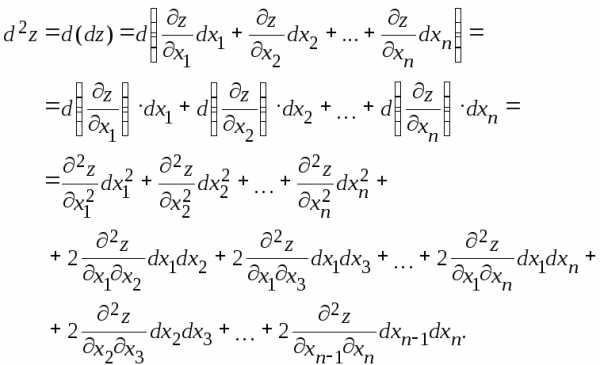
Здесь
и далее
,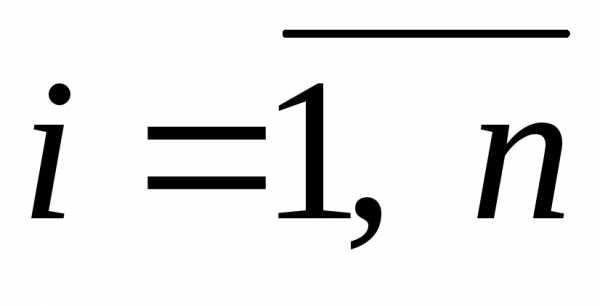 .
.
Аналогично
определяются дифференциалы
третьего 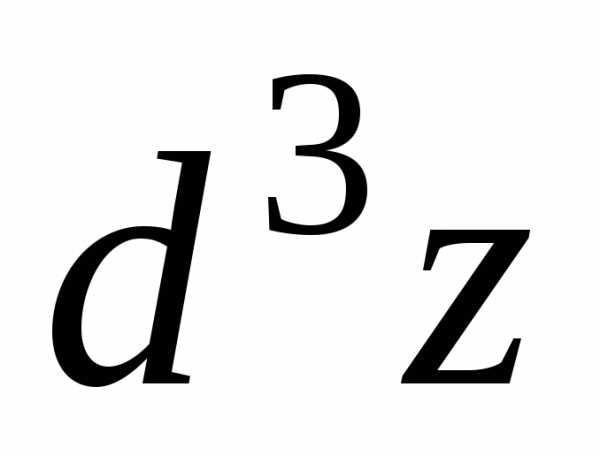 ,четвертого
,четвертого 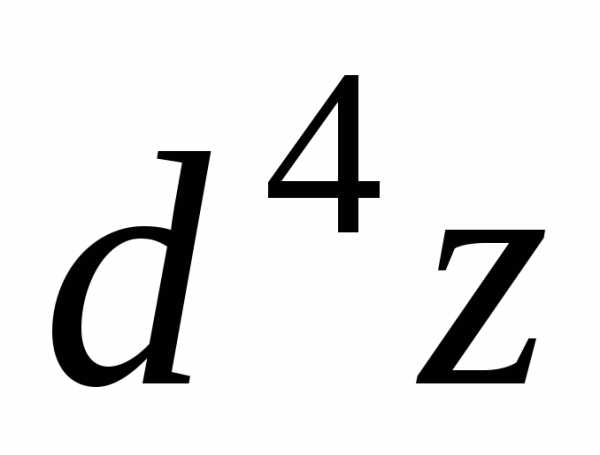 и т.д.порядков. Если определен
дифференциал
и т.д.порядков. Если определен
дифференциал 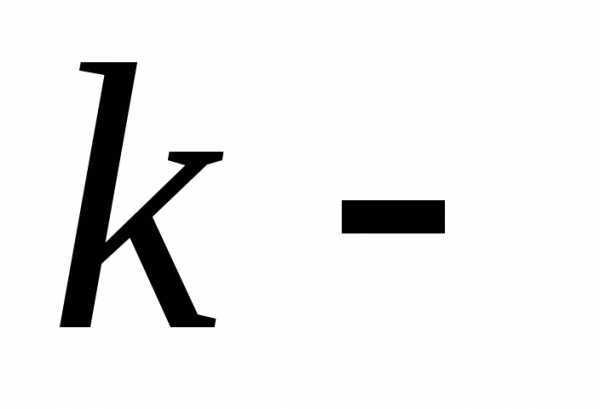 го
порядка
го
порядка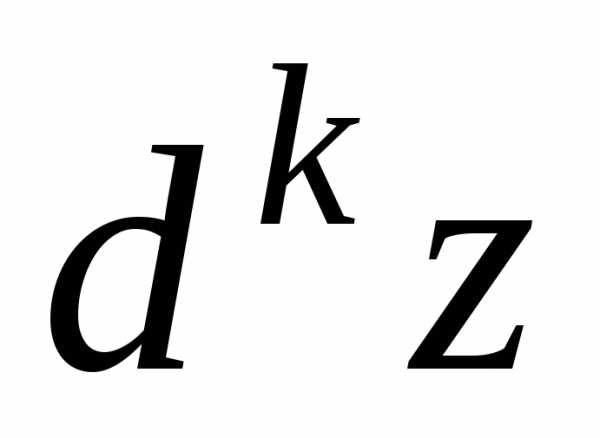 ,
то дифференциал
,
то дифференциал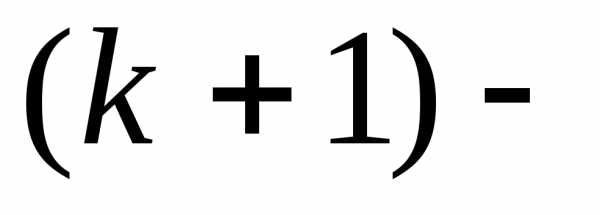 го
порядка определяется как полный
дифференциал от дифференциала
го
порядка определяется как полный
дифференциал от дифференциала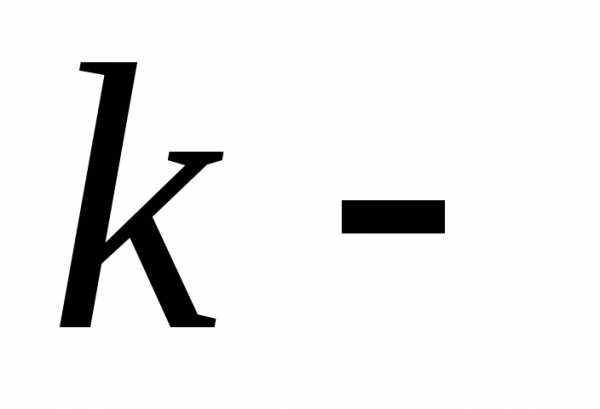 го
порядка:
го
порядка:
.
Сложность выражения для дифференциала зависит как от количества переменных, так и от его порядка. Поэтому проще запомнить
,
которое
нужно понимать следующим образом:
сначала многочлен, стоящий в скобках, формальнопо правилам алгебры
возводится в степень, затем все полученные
члены «умножаются» на ,
т.е.
,
т.е. дописывается в числителе каждой дроби
при
дописывается в числителе каждой дроби
при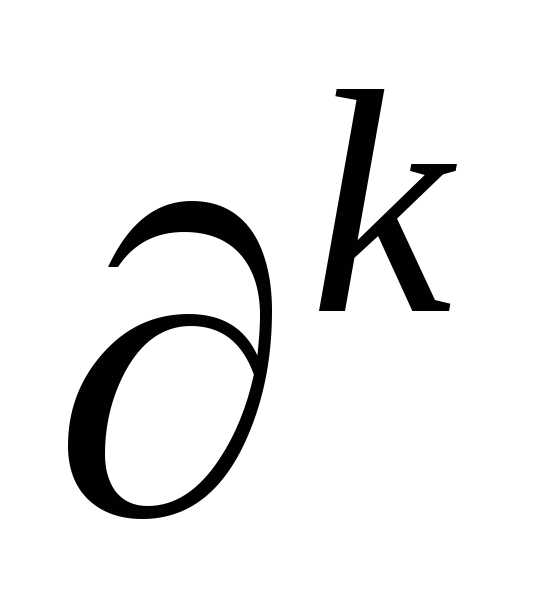 ,
а после этого всем символам возвращается
их значение производных и дифференциалов.
,
а после этого всем символам возвращается
их значение производных и дифференциалов.
Например, если , то
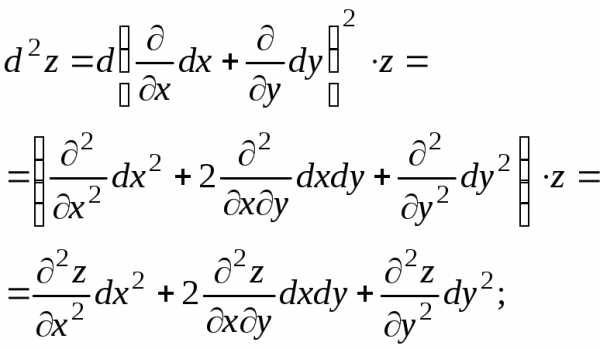
т.е.
(8)
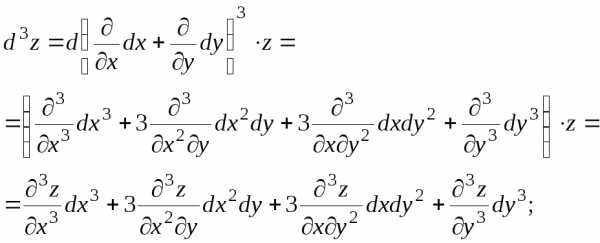
таким образом,
(9)
и т.д.
Пример 6. Найти дифференциалы до третьего порядка включительно функции
.Решение. Для нахождения дифференциалов функции воспользуемся свойствами дифференциала, выраженными формулами (6) (дифференциал суммы, разности, произведения двух функций и т.д.) и определением дифференциала второго, третьего и т.д. порядков:
Теперь дифференцируем полученное выражение, помня, что дифференциалы независимых переменных есть константы, т.е. дифференциалы любого порядка выше первого от независимых переменных равны нулю (см. формулу (7)):
Дифференцируя третий раз, применяя те же правила, получим:
Здесь
.
Для дифференциалов второго и третьего порядка данной функции мы получили бы те же самые выражения, если бы воспользовались для их нахождения формулами (8) и (9), т.е. если бы сначала нашли все частные производные нужных порядков, а потом подставили их в эти формулы. Проверьте и сравните.
Из полученных выражений для дифференциалов заданной функции мы можем теперь записать выражения для частных производных этой функции любого порядка, по любым независимым переменным, сопоставляя полученное с формулами (8) и (9), например:
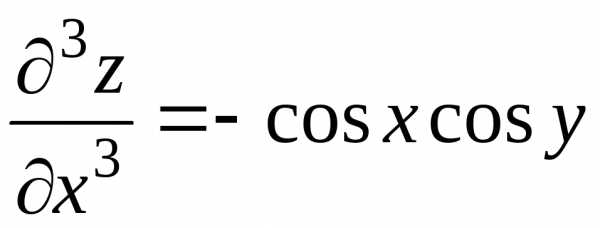 ,
, 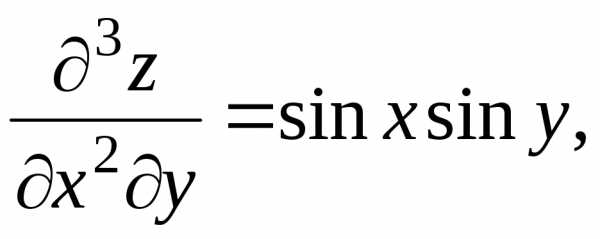
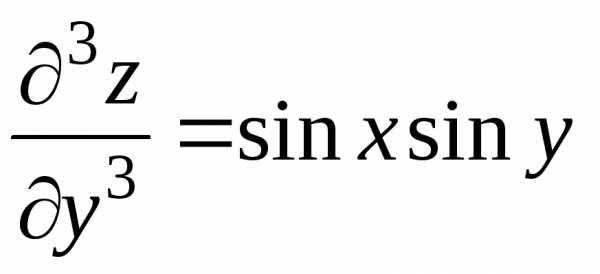 ,
.
,
.
Пример 7. Найти дифференциалы до третьего порядка включительно функции .
Решение. Так как все частные
производные данной функции по переменной ,
начиная со второй, равны нулю, то здесь
легко сразу воспользоваться формулами
(3) и (4):
,
начиная со второй, равны нулю, то здесь
легко сразу воспользоваться формулами
(3) и (4):
.
studfiles.net
Частные производные высшего порядка. Смешанные производные.
Как уже отмечали, что производные и называют частными производными первого порядка или первыми частными производными. Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные, так называемые повторные, производные по x, и y или смешанные частные производные.
Так, частные производных второго обозначаются следующим образом:
или ; или ;
или ; или ;.
Аналогично определяются частные производные 3-го, 4-го и более высоких порядков. Например, для функции z=f(x, y) имеем:
, Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными. Для функции таковыми являются производные . Заметим, что в случае, когда смешанные производные непрерывны, то имеет место равенство .
Пример 5. Найти частные производные второго порядка функции
.
Решение. Частные производные первого порядка для данной функции найдены в примере 3:
Дифференцируя и по переменным х и y, получим
,
;
;
.
5. Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y. Они называютсявторыми частными производными или частными производными второго порядка и обозначаются zxx , zyy’ , zxy или. Согласно определению ; . Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная . Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности
вычислялись частные производные по x и по y.
Похожие статьи:
poznayka.org
