05.05.202016.08.2019

Лекция метод гаусса – 8. —

• by alexxlab
• Комментариев к записи Лекция метод гаусса – 8. — нет
• Разное

Лекция № 4

Вопрос 1. Системы линейных алгебраических уравнений слу (Основные понятия и определения).

1. Системой m линейных уравнений с nнеизвестными называется система уравнений вида:

2. Решением системы уравнений (1) называется совокупность чисел x₁, x₂, … , x_n, обращающая каждое уравнение системы в тождество.

3. Система уравнений (1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной.

4. Система уравнений (1) называется определенной, если она имеет только одно решение, и неопределенной, если у нее более одного решения.

5. В результате элементарных преобразований система (1) преобразуется к равносильной ей системе (т.е. имеющей то же множество решений).

К элементарным преобразованиям систем линейных уравнений относятся:

1. Отбрасывание нулевых строк.

2. Изменение порядка строк.

3. Прибавление к элементам любой строки элементов другой строки, умноженных на одно число.

Вопрос 2. Методы решения систем линейных уравнений.

1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.

Системой n линейных уравнений с n неизвестными называется система уравнений вида:

Запишем систему (2) в матричном виде, для этого введем обозначения.

Матрица коэффициентов перед переменными:

X = ‒ матрица переменных.

В = ‒ матрица свободных членов.

Тогда система (2) примет вид:

A×X = B ‒ матричное уравнение.

Решив уравнение, получим:

X = A

-1×B

Пример:

; ;

1) │А│= 15 + 8 ‒18 ‒9 ‒12 + 20 = 4  0 матрицаА^-1 существует.

2) A^T= ;

3)

à =

4) А^-1 = × Ã =;

Х = А^-1 × B

Ответ:

2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.

Рассмотрим систему 2 ‒ х линейных уравнений с 2 ‒ мя неизвестными:

Решим эту систему методом подстановки:

Из первого уравнения следует:

Подставив во второе уравнение, получим:

Подставляем значение в формулу для, получим:

=

Определитель Δ — определитель матрицы системы;

Δ x₁ — определитель переменной x₁;

Δ x₂ — определитель переменной x₂;

Формулы:

x ₁ =;x ₂ =;…,x_n = ;Δ  0;

‒ называются формулами Крамера.

При нахождении определителей неизвестных х₁, х₂,…, х_nзаменяется столбец коэффициентов при той переменной, определитель которой находят, на столбец свободных членов.

Пример: Решить систему уравнений методом Крамера

Решение: 

Составим и вычислим сначала главный определитель этой системы:

Так как Δ ≠ 0, то система имеет единственное решение, которое можно найти по правилу Крамера:

где Δ ₁, Δ ₂, Δ ₃ получаются из определителя Δ путем замены 1‒ го, 2 ‒ го или 3 ‒ го столбца, соответственно, на столбец свободных членов.

Таким образом:

Лекция № 5

Вопрос 1. Метод Гаусса решения систем линейных уравнений.

Рассмотрим систему:

Расширенной матрицей системы (1) называется матрица вида:

Метод Гаусса – это метод последовательного исключения неизвестных из уравнений системы, начиная со второго уравнения по m – тое уравнение.

При этом путем элементарных преобразований матрица системы приводится к треугольной (если m = n и определитель системы ≠ 0) или ступенчатой (если m < n) форме.

Затем, начиная с последнего по номеру уравнения, находятся все неизвестные.

studfiles.net

Алгоритм метода Гаусса:

1) Составить расширенную матрицу системы, включающую столбец свободных членов.

2) Если а₁₁  0, то первую строку делим на а₁₁ и умножаем на (– a₂₁) и прибавляем вторую строку. Аналогично дойти до m–той строки:

I стр. делим на а₁₁ и умножаем на (– а_m1) и прибавляем m – тую стр.

При этом из уравнений, начиная со второго по m – тое, исключится переменная x₁.

3) На 3 ‒ м шаге вторая строка используется для аналогичных элементарных преобразований строк с 3 ‒ й по m – тую. При этом исключится переменная x_{2 ,} начиная с 3 ‒ й строки по m – тую, и т. д.

В результате этих преобразований система приведется к треугольной или ступенчатой форме (в случае треугольной формы под главной диагональю нули).

Приведение системы к треугольной или ступенчатой форме называется прямым ходом метода Гаусса

, а нахождение неизвестных из полученной системы называется обратным ходом.

Пример:

Прямой ход. Приведём расширенную матрицу системы

с помощью элементарных преобразований к ступенчатому виду. Переставим первую и вторую строки матрицыA_b, получим матрицу:

Сложим вторую строку полученной матрицы с первой, умноженной на (‒2), а её третью строку – с первой строкой, умноженной на (‒7). Получим матрицу

К третьей строке полученной матрицы прибавим вторую строку, умноженную на (‒3), в результате чего получим ступенчатую матрицу

Таким образом, мы привели данную систему уравнений к ступенчатому виду:

,

Обратный ход. Начиная с последнего уравнения полученной ступенчатой системы уравнений, последовательно найдём значения неизвестных:

Вопрос 2. Исследование систем линейных уравнений.

Теорема Кронекера – Капелли, базисные решения.

Теорема 1. Система m – линейных уравнений с n – неизвестными совместна только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

r (A) = r (A_в)

Пример:

│А│= = 58 0, r (А) = 3;

A_B= =r (A_B) ≤ 3, так как

= ‒ 8 + 45 + 144 ‒ 40 + 72 ‒ 18 = 195 =r (A_B) = 3 =

r(A) = r (A_B) => по теореме Кронекера ‒ Капелли система совместна.

Теорема 2. Если ранг матрицы совместной системы равен числу неизвестных, т. е. r(A) = n, то система имеет единственное решение.

Если ранг матрицы системы меньше числа неизвестных, т. е. r (

A) <n, то переменные х₁, х₂, …, х_rназываются базисными, если минор, составленный из коэффициентов при этих неизвестных  0.

Остальные (n – r) – неизвестных называются свободными.

Пример: найти базисное решение системы уравнений.

Решение:

х₁, х₂, х₃ – базисные, х₄ – свободное.

Пусть х₄= C = const; х₃= 2, тогда

2 х₂+ 2 + 2 C= 0 | · 2

х₂= – C – 1

х₁ – C – 1 + 2 + C= 2;

х₁= 1

Ответ:

х₁= 1;

х₂= – C – 1;

х₃ = 2;

х₄= C.

Найдем частное решение:

Пусть C = 1, тогда

х₁= 1;

х₂= – 2;

х₃ = 2;

х₄= 1.

Проверка:

Подставим значения х₁, х₂, х₃, и х₄ в систему уравнений

,

Получим

Лекция № 6

Вопрос 1. Системы линейных однородных уравнений.

Исследование решений. Фундаментальная система решений.

Однородной системы m – линейных уравнений с n – неизвестными называется система уравнений вида:

Теорема. Система (3) всегда имеет хотя бы одно тривиальное решение: х₁= х₂ = … = х_n= 0.

При решении однороднойсистемылинейных уравнений возможны следующие случаи:

1) Если m = n и определитель матрицы системы ∆  0, то ∆ x₁ = ∆ x₂ = = … = ∆ x_n= 0. Тогда система (3) имеет единственное тривиальное решение по формулам Крамера.

2) Если m = n, но определитель матрицы системы ∆ = 0, то система (3) имеет множество решений.

3) Если m<n, то система (3) имеет множество решений.

Определение. Система линейно независимых решений e_l, е₂, …, е_k называется фундаментальной, если каждое решение системы (3) является линейной комбинацией решений e_l, е₂ , …, е_k.

Теорема. Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений (3) меньше числа пере­менных

n, то всякая фундаментальная система решений систе­мы (3) состоит из n – r решений.

Пример:

m = 3; n = 4.

х₁, х₂, х₃ – базисные, x₄ – свободное.

Пустьх₄= C, тогда

х₃ = х₄=>х₃= C

х₂– 7C– 14C= 0

х₂= 21C

х₁– 21C + 2C + 5C = 0

х₁= 14C

Ответ:

х₁= 14C;

х₂= 21C;

х₃= C;

х₄= C.

studfiles.net

Лекция 3. Понятие системы линейных уравнений. Метод Гаусса. Метод Крамера.

Элементы линейной алгебры.

Лекция 3. Понятие СЛУ. Метод Гаусса. Метод Крамера

Лекция 3. Понятие системы линейных уравнений. Метод Гаусса. Метод Крамера.

1.1 Понятие системы линейных уравнений.

Определение 1. Системой линейных уравнений, содержащей m уравнений и n неизвестных, называется система вида

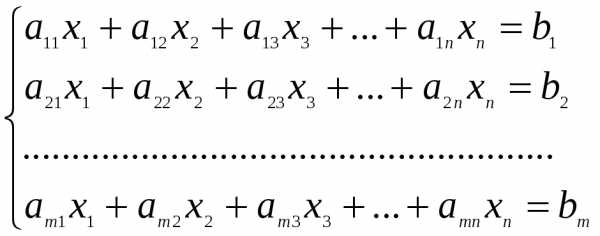
где числа a_ij – называются коэффициентами системы, числа b_ij – свободными членами.

Определение 2. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Определение 3. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

В последенем случае каждое решение системы называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или несовместна. Если совместна, найти ее общее решение.

1.2 Решение систем линейных уравнений. Метод Гаусса.

Пусть дана система m линейных уравнений с n неизвестными:

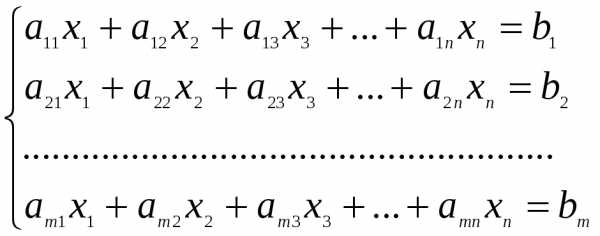
Матрица А = , составленная из коэффициентов при неизвестных х_i (i = 1,2,…n), называется матрицей системы.

Матрица B = 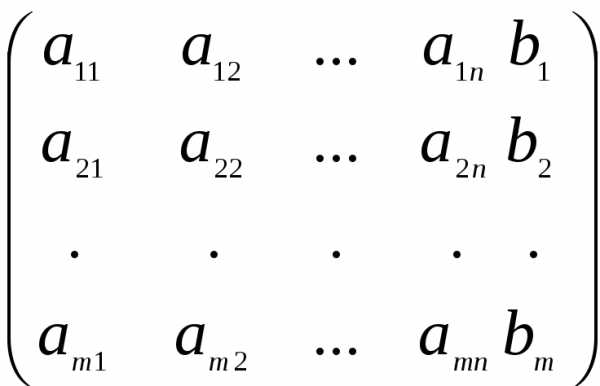, составленная из коэффициентов при неизвестных и свободных членов, называется расширенной матрицей.

Определение 4. Матрица А называется матрицей треугольного вида, если все ее элементы выше (ниже) главной диагонали равны нулю.

Например, А = или В = – матрицы треугольного вида.

Метод Гаусса удобно использовать при решении систем с большим количеством уравнений. Этот метод заключается в последоваетльном исключении неизвестных. Систему линейных уравнений приводят к системе с треугольной матрицей с помощью эквивалентных преобразований. Затем из полученной системы переменные находят с помощью последовательных подстановок.

К эквивалентным преобразованиям относят следующие:

• умножение и деление коэффициентов и свободных членов на одно и тоже число, отличное от нуля.

• Сложение и вычитание уравнений.

• Перестановка уравнений.

• Исключение из системы уравнений, в которых все коэффициенты равны нулю.

Пример 1

Решить систему линейных уравнений методом Гаусса:

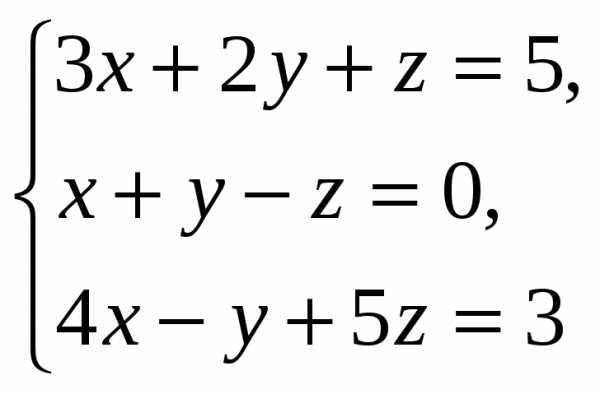
Выпишем расширенную матрицу системы:

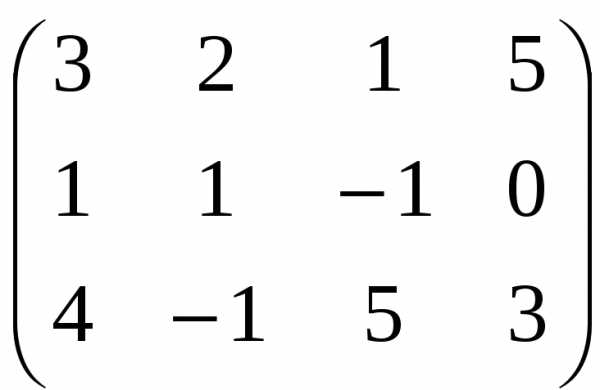
Для упрощения вычислений поменяем первую и вторую строки местами:

Умножим первую строку на –3 и сложим ее со второй строкой. Первую строку умножим на –4 и сложим с третьей сторокой, получим эквивалентную матрицу:

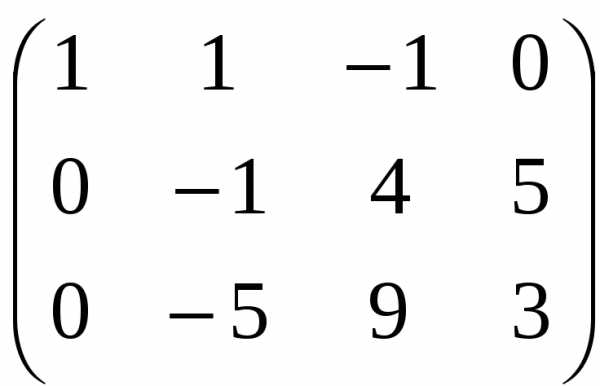
Умножим вторую строку на –1:

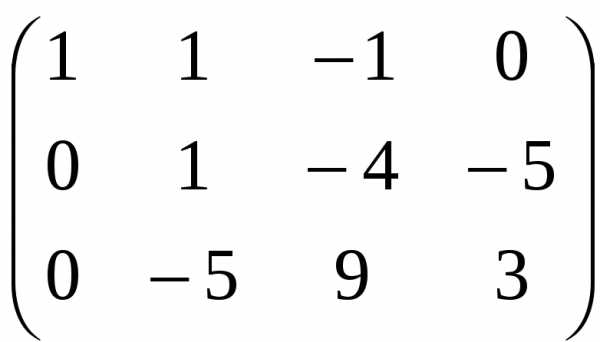
Умножим вторую строку на 5 и сложим с третьей строкой:

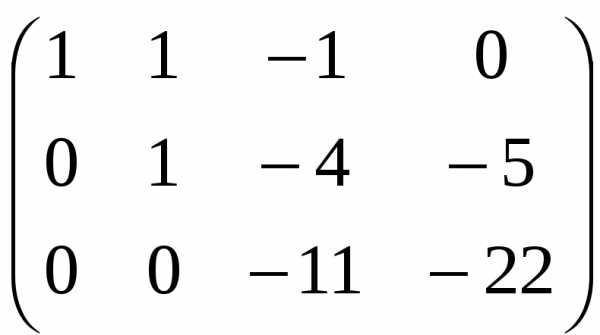
Разделим третью строку на –11:

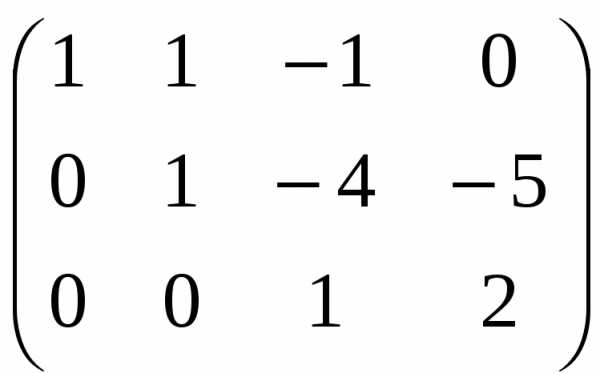
Получили матрицу треугольного вида (все элементы ниже главной диагонали равны нулю). Выпишем систему уравнений треугольного вида:

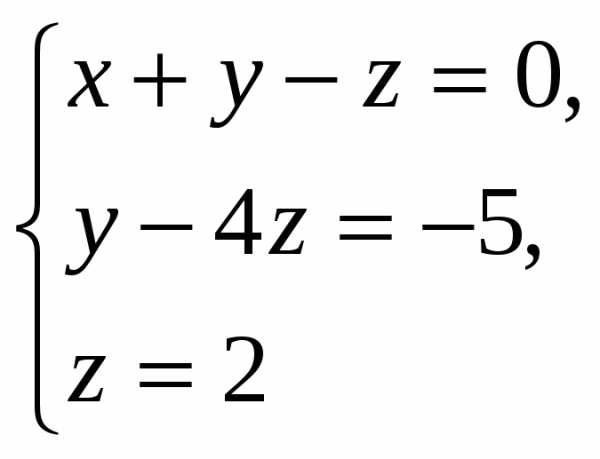
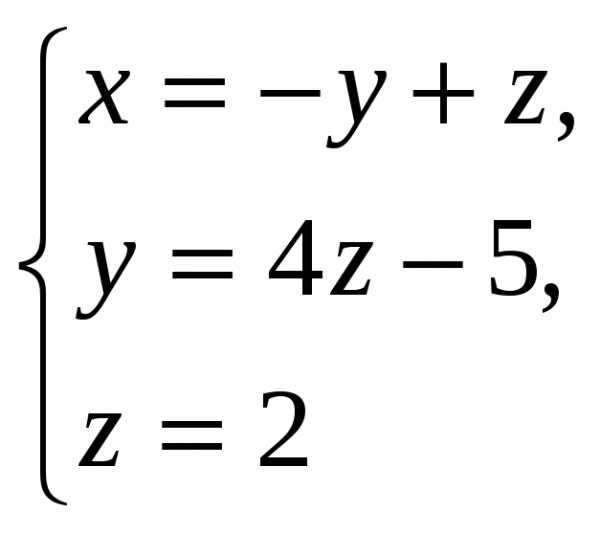
Ответ: х = -1, у = 3, z = 2

1.3 Решение систем линейных уравнений методом Крамера.

Для решения систем линейных уравнений с большим количеством уравнений применяют метод Гаусса. Если же уравнений в системе не так много, то удобнее использовать метод Крамера. Этот метод основан на вычислении определителей.

Пусть дана система n линейных уравнений с n неизвестными:

Составим определитель матрицы системы:

Заменим в определителе  первый столбик, соответствующий переменной х₁, на столбец свободных членов b₁, b₂, …,b_n, получим определитель _х1:

Заменим в определителе  второй столбик, соответствующий переменной х₂, на столбец свободных членов b₁, b₂, …,b_n, получим определитель _х2:

Аналогично поступаем с третьим, четвертым, …, n –ым столбцами определителя . В итоге получим n+1 определитель. Для того, чтобы найти неизвестные х₁, х₂ , …, х_n используем формулы Крамера:

, , …,

При вычислении определителей могут возникнуть следующие случаи:

• если определитель матрицы системы  отличен от 0, то система линейных уравнений имеет единственное решение;

• если определитель матрицы системы  равен 0, а среди определителей _х1, _х2, …, _хn есть хотя один отличный от 0, то система линейных уравнений не имеет решений;

• если определитель матрицы системы  равен 0 и все определители _х1, _х2, …, _хn равны 0, то система линейных уравнений имеет бесконечно много решений.

Пример 3.

Решить систему линейных уравнений методом Крамера:

Выпишем определитель матрицы системы  и вычислим его:

Так как 0, то система имеет единственное решение.

Заменим в определителе  первый столбик на столбец свободных коэффициентов, получим _х :

Заменим в определителе  второй столбик на столбец свободных коэффициентов, получим _у :

Найдем значения переменных х и у по формулам Крамера:

,

Ответ: (-3;1)

Пример 4.

Решить систему линейных уравнений методом Крамера:

Выпишем определитель матрицы системы  и вычислим его:

Так как 0, то система имеет единственное решение.

Заменим в определителе  первый столбик на столбец свободных коэффициентов, получим _х :

Заменим в определителе  первый столбик на столбец свободных коэффициентов, получим _у :

Заменим в определителе  первый столбик на столбец свободных коэффициентов, получим _z :

Найдем значения переменных х , у и z по формулам Крамера:

, ,

Ответ: (-1; 1; -2)

7

multiurok.ru

Метод Гаусса лекция по математике

Определитель n-го порядка F044 F0 3D

F0 E7

F0 41

F0 EA

F0 3D

F0 E7a ij F 0E 7, составленный из

коэффициентов при неизвестных , называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи. a). Если F044

F0 B9

F0 30, то система (1) имеет единственное решение, которое может

быть найдено методом ГАУССА . б). Если F044

F0 3D

F0 30 , то система (1) либо имеет бесконечное множество решений ,

либо несовместна ,т.е. решений нет.

2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ 1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.

(2).

Метод Гаусса решения системы (2) состоит в следующем: Разделим все члены первого уравнения на , а затем ,умножив полученное уравнение на , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное будет исключено ,и получиться система вида:

(3)

Теперь разделим второе уравнение системы (3) на , умножим полученное уравнение на и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное будет исключено и получиться система треугольного вида :

(4) Из последнего уравнения системы (4) находим ,подставляя найденное подставляя найденное значение в первое уравнение , находим .

3. ПРИМЕР. Методом Гаусса решить систему:

Решение: Разделив уравнение (а) на 2 , получим систему

Вычтем из уравнения (b) уравнение , умноженное на 3, а из уравнения (c) – уравнение , умноженное на 4.

Разделив уравнение() на -2,5 , получим : Вычтем из уравнения () уравнение , умноженное на -3:

Из уравнения находим Z=-2; подставив это значение в уравнение , получим Y=0,2-0,4Z=0,2-0,4(-2)=1; наконец , подставив значение Z=-2 и Y=1 в уравнение (a1) , находим X=0,5-0,5Y-Z=0,5-0,5 1 – (-2)=2. Итак, получаем ответ X=2, Y=1, Z=-2 .

www.docsity.com

---