Магнитная индукция постоянного магнита – – ,
Сила магнитного поля постоянного магнита
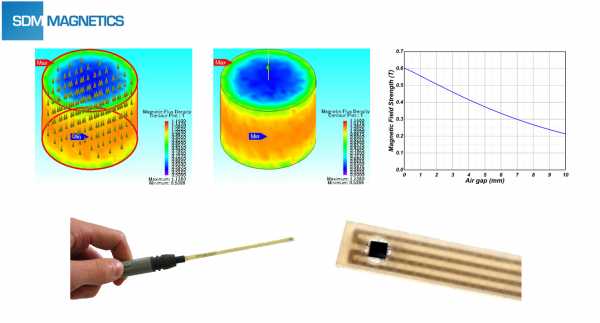
Для пользователей магнитов, как подтвердить класс и магнитные свойства, все еще остается проблемой. Большинство пользователей не могут самостоятельно получить значение основных магнитных параметров. В этом случае наилучшим решением является относительное измерение магнитных свойств. Относительное измерение магнитных свойств включает в себя напряженность магнитного поля, магнитный поток и магнитный момент. Для испытаний магнитного потока и магнитного момента в разных спецификациях требуется различная испытательная катушка, и именно по этой причине сила магнитного поля является самым популярным методом тестирования среди относительных измерений.
Как получить магнитное поле магнита?
Сила магнитного поля магнита может быть измерена измерителем Гаусса или измерителем Тесла. Теперь у многих пользователей магнитов есть свой собственный измеритель Гаусса, а также устанавливаются критерии приемки напряженности магнитного поля. Для многополярного магнита напряженность магнитного поля будет измеряться с помощью Magnet Analyzer.
Как рассчитать напряженность магнитного поля магнита?
Для простого магнита формы мы можем рассчитать его приблизительную напряженность магнитного поля по закону Био-Савара.
Для формы цилиндра:
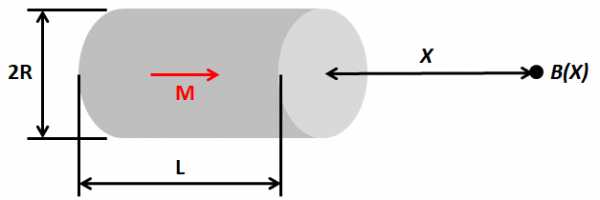
Где Br – остаточная индукция магнита; X – воздушный зазор между испытательной точкой и поверхностью магнита.
Для формы блока:
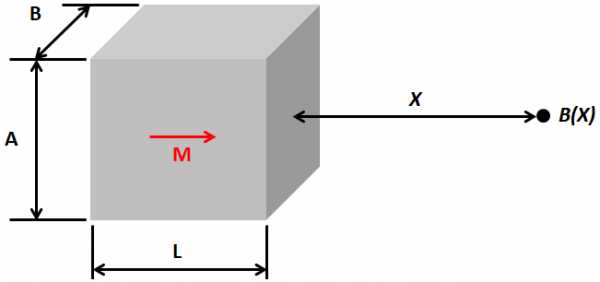
Где Br – остаточная индукция магнита; X – воздушный зазор между испытательной точкой и поверхностью магнита.
Для формы кольца:
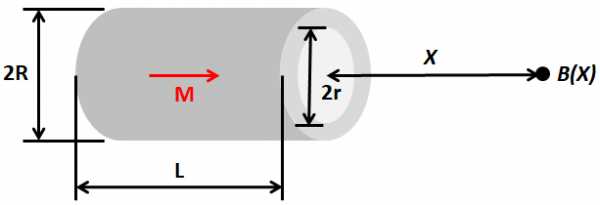
Где Br – остаточная индукция магнита; X – воздушный зазор между испытательной точкой и поверхностью магнита.
Согласно вышеприведенному уравнению, значение напряженности магнитного поля зависит от степени, размера и места измерения магнита. Следует отметить, что измеренное значение напряженности магнитного поля магнита, покрытого никелем, будет ниже, чем значение моделирования Биота-Савара из-за эффекта экранирования от ферромагнетизма. Покрытие никелем.
Для многополюсной намагниченности и сложных условий дизайнер будет изучать его прочность и распределение магнитного поля с помощью программного обеспечения для анализа конечных элементов (FEA или FEM), а затем точно оценить состояние намагниченности и распределение потока всей системы магнитных цепей. Анализ конечных элементов является мощным инструментом на этапе разработки продукта с магнитом.
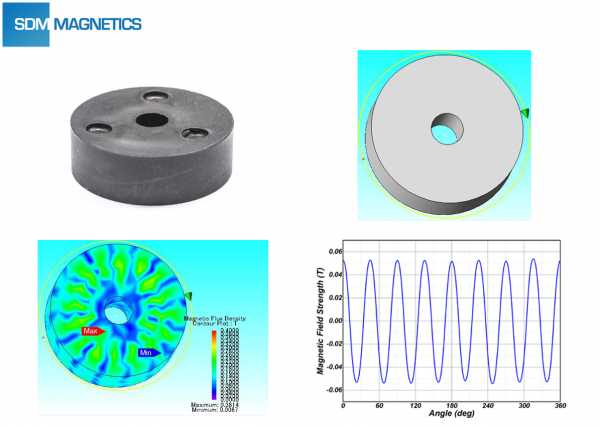
Технология анализа конечных элементов широко используется при проектировании сенсорного магнита, магнитной сборки и комплексной магнитной системы. SDM Magnetics обладают большим опытом в анализе конечных элементов приложения магнитов. SDM Magnetics стремится предоставить техническое решение для заказчика на стадии разработки и снижения издержек.
Вычисленные значения и результаты моделирования приведены только для справки и отклонения между измеренным значением и расчетным значением по разным причинам. Оператору необходимо избегать отклонения от инструмента и процесса работы.
Чтобы обеспечить отсутствие элемента холла без трещин, изготовитель инструмента обычно изготавливает покрытие из эпоксидной смолы на элемент зала. Это покрытие также создает воздушный зазор, и этот воздушный зазор часто пропускается во время расчета и моделирования.
ru.magnet-sdm.com
Тайны постоянного магнита
Сейчас объясню: По жизни так уж повелось, что особо сильно нельзя, — то особо ( просто жуть, как ) и хочется… А дело здесь в следующем. Какой-то рок судьбы навис над «постоянниками», аура тайны и недоговорённости. Все физики ( дядьки и тётки разные ) в постоянных магнитах совершенно не рубят ( проверенно неоднократно, лично ), и всё, наверное, потому, что во всех учебниках физики этот вопросик обходится стороной. Электромагнетизм — это да, это, пожалуйста, а вот о постоянниках ни слова…Посмотрим, что можно выжать из самой умной книжки «И.В.Савельев. Курс общей физики. Том 2. Электричество и магнетизм», — круче этой макулатуры, вы вряд ли сможете что-либо откопать. Значит так, в 1820 году некий чувак под фамилией Эрстед замутил опыт с проводником, и рядом стоящей с ним компасной стрелкой. Пуская электрический ток по проводнику в разных направлениях, он убедился в том, что стрелка чётко сориентируется понятно с чем. Из опыта баклан заключил, что магнитное поле имеет направленный характер. В более позднее время выяснили ( интересно, как ? ), что магнитное поле в отличие от электрического не оказывает действия на покоящийся заряд. Сила возникает лишь тогда, когда заряд движется ( возьмём на заметку ). Движущиеся заряды ( токи ) изменяют свойства окружающего их пространства и создают в нём магнитное поле. То есть отсюда следует, что магнитное поле порождается движущимися зарядами.
Вот видите, всё дальше в электричество уклоняемся. Ведь в магните-то ни фига не двигается и ток в нём не течёт. Вот, что по этому поводу сморозил Ампер: он предположил, что в молекулах вещества циркулируют круговые токи ( молекулярные токи ). Каждый такой ток обладает магнитным моментом и создаёт в окружающем пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю ( прикольно, да ? ). Но этого мало: В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. — Чувствуете, как ересь всё крепчает и крепчает ? ? Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается — его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле. Ура !
Ну, каково ?! — Оказывается материал магнетика всё время намагничен ( ! ), только хаотично. То есть, если начать делить большой кусок на более маленькие, и добравшись до самых микро-при-микро дребеней, получим таки нормально работающие магниты ( намагниченные ) без какого бы то ни было намагничивания !!! — Вот, ведь бред.
Небольшая справка, так, для общего развития: Намагничение магнетика характеризуется магнитным моментом единицы объёма. Эту величину называют намагниченностью и обозначают буквой «J».
Продолжим наше погружение. Маленько из электричества: А вы знаете, что линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей ? Нет ? — Теперь знайте, но не верьте. По-простому если сказать, то представьте зонтик. Ручка зонтика это направление тока, а вот край самого зонтика ( к примеру ), т.е. окружность — это, типа, линия магнитной индукции. Причём начинается такая линия из воздуха, и заканчивается, понятно, тоже нигде ! — Вы себе этот бред физически представляете ? Под это дело подписали целых трех мужиков: закон Био-Савара-Лапласа называется. Вся запарка идёт оттого, что где-то неправильно представили саму сущность поля, — почему оно появляется, что оно есть, собственно, где начинается, куда и как распространяется.
Даже в абсолютно простых вещах они ( эти злобные физики ) морочат всем головы: Направленность магнитного поля характеризуют векторной величиной ( «В» — измеряется в теслах ). Логично бы было по аналогии с напряжённостью электрического поля «Е» назвать «В» напряжённостью магнитного поля ( типа, функции у них похожие ). Однако ( внимание ! ) основную силовую характеристику магнитного поля назвали магнитной индукцией… Но и этого им показалось мало, и чтобы окончательно всё запутать, название «напряжённость магнитного поля» присвоили вспомогательной величине «Н», аналогичной вспомогательной характеристике «D» электрического поля. Каково…
Далее выясняя силу Лоренца, приходят к выводу, что магнитная сила слабее кулоновской на множитель, равный квадрату отношения скорости заряда к скорости света ( т.е. магнитная составляющая силы меньше электрической составляющей ). Таким образом приписывая магнитным взаимодействиям релятивистский эффект !!! Для совсем маленьких поясню: Жил в начале века дядя Эйнштейн и придумал он теорию относительности, привязав все процессы к скорости света ( чистейший бред ). То есть, если разогнаться до скорости света, то время остановится, а если превысить её, то пойдёт вспять… Всем уже давно понятно, что это была просто мировая наколка шутника Эйнштейна, и что всё это, мягко сказать, — неправда. Вот теперь ещё и магниты с их свойствами к этой лабудятине приковали, — за что же их так ?…
Ещё маленькая справка: Господин Ампер вывел замечательную формулу, и оказалось, что если к магниту поднести провод, ну или железяку, какую, то магнит не провод притягивать будет, а заряды, которые движутся по проводнику. Назвали это пафосно: «Закон Ампера» ! Маленько не учли, что если проводник к батарейке не подключён и ток по нему не течёт, то он всё равно к магниту прилипает. Отмазку такую придумали, что, мол, заряды всё равно есть, только двигаются хаотично. Вот они-то к магниту и липнут. Интересно, это же откуда там, в микрообъёмах ЭДС берётся, чтобы эти заряды хаотично колбасить. Это же просто вечный двигатель ! И ведь не нагреваем ничего, — энергией не накачиваем… Или вот ещё прикол: К примеру, алюминий — тоже металл, а вот зарядов у него, почему-то, хаотичных нет. Ну НЕ ЛИПНЕТ алюминий к магниту !!! … или сделан он из дерева…
Ах, да ! Я же ещё не рассказал, как направлен вектор магнитной индукции ( такое надо знать ). Так вот, вспомнив наш зонтик, представим, что по окружности ( край зонта ) мы пустили ток. В результате этой простенькой операции вектор направлен нашей мыслью в сторону ручки точно по центру палочки. Если же проводник с током имеет неправильные очертания, то всё пропало, — простота испаряется. Появляется дополнительный векторок под названием дипольный магнитный момент ( в случае с зонтиком он тоже есть, просто направлен туда же, куда и вектор магнитной индукции ). Начинается страшный расколбас в формулах, — всякие интегралы по контуру, синусы-косинусы и т.д. — Кому надо, может сам поинтересоваться. И ещё стоит упомянуть, что ток надо пускать по правилу правого буравчика, т.е. по часовой стрелке, тогда вектор будет от нас. Это связано с понятием положительной нормали. Ладно, едем дальше…
Товарищ Гаусс подумал маленько и решил, что отсутствие в природе магнитных зарядов ( на самом деле Дирак предположил, что они есть, только их ещё не обнаружили ) приводит к тому, что линии вектора «В» не имеют ни начала, ни конца. Поэтому число пересечений, возникающих при выходе линий «В» из объёма, ограниченного некоторой поверхностью «S», всегда равно числу пересечений, возникающих при входе линий в этот объём. Следовательно, поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Интерпретируем теперь всё в нормальный русский язык: Любая поверхность, как легко представит
www.o000o.ru
МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
Содержание статьиМАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА. Простейшие проявления магнетизма известны очень давно и знакомы большинству из нас. Однако объяснить эти, казалось бы, простые явления на основе фундаментальных принципов физики удалось лишь сравнительно недавно.
Существуют магниты двух разных видов. Одни – так называемые постоянные магниты, изготовляемые из «магнитно-твердых» материалов. Их магнитные свойства не связаны с использованием внешних источников или токов. К другому виду относятся так называемые электромагниты с сердечником из «магнитно-мягкого» железа. Создаваемые ими магнитные поля обусловлены в основном тем, что по проводу обмотки, охватывающей сердечник, проходит электрический ток.Магнитные полюса и магнитное поле.
Магнитные свойства стержневого магнита наиболее заметны вблизи его концов. Если такой магнит подвесить за среднюю часть так, чтобы он мог свободно поворачиваться в горизонтальной плоскости, то он займет положение, примерно соответствующее направлению с севера на юг. Конец стержня, указывающий на север, называют северным полюсом, а противоположный конец – южным полюсом. Разноименные полюса двух магнитов притягиваются друг к другу, а одноименные взаимно отталкиваются.
Итак, магнит притягивает другие магниты и предметы из магнитных материалов, не находясь в соприкосновении с ними. Такое действие на расстоянии объясняется существованием в пространстве вокруг магнита магнитного поля. Некоторое представление об интенсивности и направлении этого магнитного поля можно получить, насыпав на лист картона или стекла, положенный на магнит, железные опилки. Опилки выстроятся цепочками в направлении поля, а густота линий из опилок будет соответствовать интенсивности этого поля. (Гуще всего они у концов магнита, где интенсивность магнитного поля наибольшая.)
М.Фарадей (1791–1867) ввел для магнитов понятие замкнутых линий индукции. Линии индукции выходят в окружающее пространство из магнита у его северного полюса, входят в магнит у южного полюса и проходят внутри материала магнита от южного полюса обратно к северному, образуя замкнутую петлю. Полное число линий индукции, выходящих из магнита, называется магнитным потоком. Плотность магнитного потока, или магнитная индукция (В), равна числу линий индукции, проходящих по нормали через элементарную площадку единичной величины.
Магнитной индукцией определяется сила, с которой магнитное поле действует на находящийся в нем проводник с током. Если проводник, по которому проходит ток I, расположен перпендикулярно линиям индукции, то по закону Ампера сила
где F – сила в ньютонах, I – ток в амперах, l – длина в метрах. Единицей измерения магнитной индукции является тесла (Тл) (см. также ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ).
Гальванометр.
Гальванометр – чувствительный прибор для измерения слабых токов. В гальванометре используется вращающий момент, возникающий при взаимодействии подковообразного постоянного магнита с небольшой токонесущей катушкой (слабым электромагнитом), подвешенной в зазоре между полюсами магнита. Вращающий момент, а следовательно, и отклонение катушки пропорциональны току и полной магнитной индукции в воздушном зазоре, так что шкала прибора при небольших отклонениях катушки почти линейна.
Намагничивающая сила и напряженность магнитного поля.
Далее следует ввести еще одну величину, характеризующую магнитное действие электрического тока. Предположим, что ток проходит по проводу длинной катушки, внутри которой расположен намагничиваемый материал. Намагничивающей силой называется произведение электрического тока в катушке на число ее витков (эта сила измеряется в амперах, так как число витков – величина безразмерная). Напряженность магнитного поля Н равна намагничивающей силе, приходящейся на единицу длины катушки. Таким образом, величина Н измеряется в амперах на метр; ею определяется намагниченность, приобретаемая материалом внутри катушки.
В вакууме магнитная индукция B пропорциональна напряженности магнитного поля Н:
где m0 – т.н. магнитная постоянная, имеющая универсальное значение 4pЧ10–7 Гн/м. Во многих материалах величина B приблизительно пропорциональна Н. Однако в ферромагнитных материалах соотношение между B и Н несколько сложнее (о чем будет сказано ниже).
На рис. 1 изображен простой электромагнит, предназначенный для захвата грузов. Источником энергии служит аккумуляторная батарея постоянного тока. На рисунке показаны также силовые линии поля электромагнита, которые можно выявить обычным методом железных опилок.
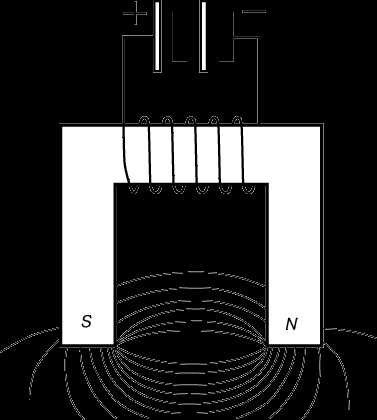
Крупные электромагниты с железными сердечниками и очень большим числом ампер-витков, работающие в непрерывном режиме, обладают большой намагничивающей силой. Они создают магнитную индукцию до 6 Тл в промежутке между полюсами; эта индукция ограничивается лишь механическими напряжениями, нагреванием катушек и магнитным насыщением сердечника. Ряд гигантских электромагнитов (без сердечника) с водяным охлаждением, а также установок для создания импульсных магнитных полей был сконструирован П.Л.Капицей (1894–1984) в Кембридже и в Институте физических проблем АН СССР и Ф.Биттером (1902–1967) в Массачусетском технологическом институте. На таких магнитах удавалось достичь индукции до 50 Тл. Сравнительно небольшой электромагнит, создающий поля до 6,2 Тл, потребляющий электрическую мощность 15 кВт и охлаждаемый жидким водородом, был разработан в Лосаламосской национальной лаборатории. Подобные поля получают при криогенных температурах.
Магнитная проницаемость и ее роль в магнетизме.
Магнитная проницаемость m – это величина, характеризующая магнитные свойства материала. Ферромагнитные металлы Fe, Ni, Co и их сплавы обладают очень высокими максимальными проницаемостями – от 5000 (для Fe) до 800 000 (для супермаллоя). В таких материалах при сравнительно малых напряженностях поля H возникают большие индукции B, но связь между этими величинами, вообще говоря, нелинейна из-за явлений насыщения и гистерезиса, о которых говорится ниже. Ферромагнитные материалы сильно притягиваются магнитами. Они теряют свои магнитные свойства при температурах выше точки Кюри (770° С для Fe, 358° С для Ni, 1120° С для Co) и ведут себя как парамагнетики, для которых индукция B вплоть до очень высоких значений напряженности H пропорциональна ей – в точности так же, как это имеет место в вакууме. Многие элементы и соединения являются парамагнитными при всех температурах. Парамагнитные вещества характеризуются тем, что намагничиваются во внешнем магнитном поле; если же это поле выключить, парамагнетики возвращаются в ненамагниченное состояние. Намагниченность в ферромагнетиках сохраняется и после выключения внешнего поля.
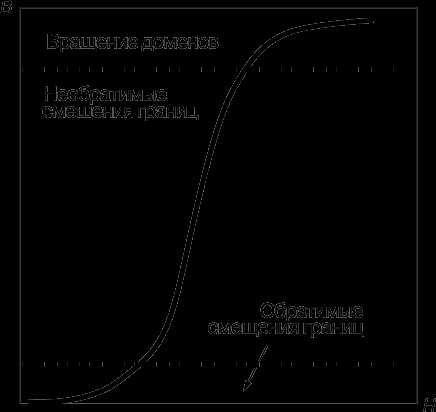
На рис. 2 представлена типичная петля гистерезиса для магнитно-твердого (с большими потерями) ферромагнитного материала. Она характеризует неоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1–2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1–3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)–(4) соответствует коэрцитивной силе, препятствующей размагничиванию. Дальнейший рост значений (-H) приводит кривую гистерезиса в третий квадрант – участок 4–5. Следующее за этим уменьшение величины (-H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.
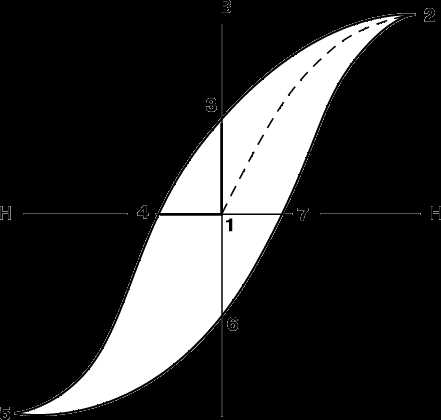
Магнитно-твердые материалы характеризуются широкой петлей гистерезиса, охватывающей значительную площадь на диаграмме и потому соответствующей большим значениям остаточной намагниченности (магнитной индукции) и коэрцитивной силы. Узкая петля гистерезиса (рис. 3) характерна для магнитно-мягких материалов – таких, как мягкая сталь и специальные сплавы с большой магнитной проницаемостью. Такие сплавы и были созданы с целью снижения обусловленных гистерезисом энергетических потерь. Большинство подобных специальных сплавов, как и ферриты, обладают высоким электрическим сопротивлением, благодаря чему уменьшаются не только магнитные потери, но и электрические, обусловленные вихревыми токами.
Магнитные материалы с высокой проницаемостью изготовляются путем отжига, осуществляемого выдерживанием при температуре около 1000° С, с последующим отпуском (постепенным охлаждением) до комнатной температуры. При этом очень существенны предварительная механическая и термическая обработка, а также отсутствие в образце примесей. Для сердечников трансформаторов в начале 20 в. были разработаны кремнистые стали, величина m которых возрастала с увеличением содержания кремния. Между 1915 и 1920 появились пермаллои (сплавы Ni с Fe) с характерной для них узкой и почти прямоугольной петлей гистерезиса. Особенно высокими значениями магнитной проницаемости m при малых значениях H отличаются сплавы гиперник (50% Ni, 50% Fe) и му-металл (75% Ni, 18% Fe, 5% Cu, 2% Cr), тогда как в перминваре (45% Ni, 30% Fe, 25% Co) величина m практически постоянна в широких пределах изменения напряженности поля. Среди современных магнитных материалов следует упомянуть супермаллой – сплав с наивысшей магнитной проницаемостью (в его состав входит 79% Ni, 15% Fe и 5% Mo).
Теории магнетизма.
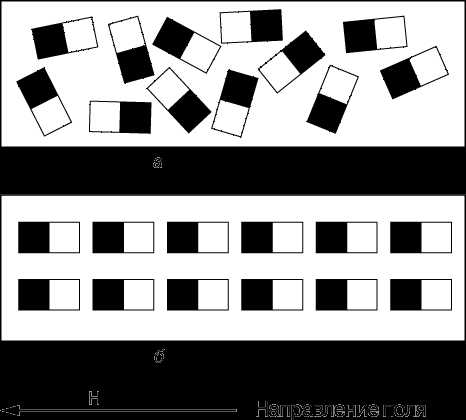
Впервые догадка о том, что магнитные явления в конечном счете сводятся к электрическим, возникла у Ампера в 1825, когда он высказал идею замкнутых внутренних микротоков, циркулирующих в каждом атоме магнита. Однако без какого-либо опытного подтверждения наличия в веществе таких токов (электрон был открыт Дж.Томсоном лишь в 1897, а описание структуры атома было дано Резерфордом и Бором в 1913) эта теория «увяла». В 1852 В.Вебер высказал предположение, что каждый атом магнитного вещества представляет собой крошечный магнит, или магнитный диполь, так что полная намагниченность вещества достигается, когда все отдельные атомные магниты оказываются выстроенными в определенном порядке (рис. 4,б). Вебер полагал, что сохранять свое упорядочение вопреки возмущающему влиянию тепловых колебаний этим элементарным магнитам помогает молекулярное или атомное «трение». Его теория смогла объяснить намагничивание тел при соприкосновении с магнитом, а также их размагничивание при ударе или нагреве; наконец, объяснялось и «размножение» магнитов при разрезании намагниченной иглы или магнитного стержня на части. И все же эта теория не объясняла ни происхождения самих элементарных магнитов, ни явлений насыщения и гистерезиса. Теория Вебера была усовершенствована в 1890 Дж.Эвингом, заменившим его гипотезу атомного трения идеей межатомных ограничивающих сил, помогающих поддерживать упорядочение элементарных диполей, которые составляют постоянный магнит.
Подход к проблеме, предложенный когда-то Ампером, получил вторую жизнь в 1905, когда П.Ланжевен объяснил поведение парамагнитных материалов, приписав каждому атому внутренний нескомпенсированный электронный ток. Согласно Ланжевену, именно эти токи образуют крошечные магниты, хаотически ориентированные, когда внешнее поле отсутствует, но приобретающие упорядоченную ориентацию после его приложения. При этом приближение к полной упорядоченности соответствует насыщению намагниченности. Кроме того, Ланжевен ввел понятие магнитного момента, равного для отдельного атомного магнита произведению «магнитного заряда» полюса на расстояние между полюсами. Таким образом, слабый магнетизм парамагнитных материалов обусловлен суммарным магнитным моментом, создаваемым нескомпенсированными электронными токами.
В 1907 П.Вейс ввел понятие «домена», ставшее важным вкладом в современную теорию магнетизма. Вейс представлял домены в виде небольших «колоний» атомов, в пределах которых магнитные моменты всех атомов в силу каких-то причин вынуждены сохранять одинаковую ориентацию, так что каждый домен намагничен до насыщения. Отдельный домен может иметь линейные размеры порядка 0,01 мм и соответственно объем порядка 10–6 мм3. Домены разделены так называемыми блоховскими стенками, толщина которых не превышает 1000 атомных размеров. «Стенка» и два противоположно ориентированных домена схематически изображены на рис. 5. Такие стенки представляют собой «переходные слои», в которых происходит изменение направления намагниченности доменов.
В общем случае на кривой первоначального намагничивания можно выделить три участка (рис. 6). На начальном участке стенка под действием внешнего поля движется сквозь толщу вещества, пока не встретит дефект кристаллической решетки, который ее останавливает. Увеличив напряженность поля, можно заставить стенку двигаться дальше, через средний участок между штриховыми линиями. Если после этого напряженность поля вновь уменьшить до нуля, то стенки уже не вернутся в исходное положение, так что образец останется частично намагниченным. Этим объясняется гистерезис магнита. На конечном участке кривой процесс завершается насыщением намагниченности образца за счет упорядочения намагниченности внутри последних неупорядоченных доменов. Такой процесс почти полностью обратим. Магнитную твердость проявляют те материалы, у которых атомная решетка содержит много дефектов, препятствующих движению междоменных стенок. Этого можно достичь механической и термической обработкой, например путем сжатия и последующего спекания порошкообразного материала. В сплавах алнико и их аналогах тот же результат достигается путем сплавления металлов в сложную структуру.
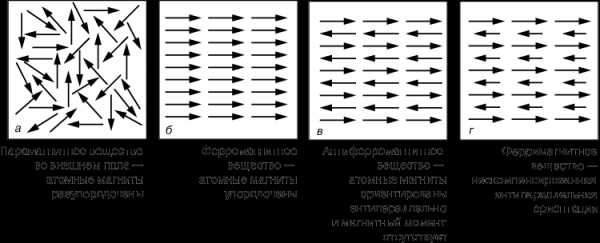
Кроме парамагнитных и ферромагнитных материалов, существуют материалы с так называемыми антиферромагнитными и ферримагнитными свойствами. Различие между этими видами магнетизма поясняется на рис. 7. Исходя из представления о доменах, парамагнетизм можно рассматривать как явление, обусловленное наличием в материале небольших групп магнитных диполей, в которых отдельные диполи очень слабо взаимодействуют друг с другом (или вообще не взаимодействуют) и потому в отсутствие внешнего поля принимают лишь случайные ориентации (рис. 7,а). В ферромагнитных же материалах в пределах каждого домена существует сильное взаимодействие между отдельными диполями, приводящее к их упорядоченному параллельному выстраиванию (рис. 7,б). В антиферромагнитных материалах, напротив, взаимодействие между отдельными диполями приводит к их антипараллельному упорядоченному выстраиванию, так что полный магнитный момент каждого домена равен нулю (рис. 7,в). Наконец, в ферримагнитных материалах (например, ферритах) имеется как параллельное, так и антипараллельное упорядочение (рис. 7,г), итогом чего оказывается слабый магнетизм.
Имеются два убедительных экспериментальных подтверждения существования доменов. Первое из них – так называемый эффект Баркгаузена, второе – метод порошковых фигур. В 1919 Г.Баркгаузен установил, что при наложении внешнего поля на образец из ферромагнитного материала его намагниченность изменяется небольшими дискретными порциями. С точки зрения доменной теории это не что иное, как скачкообразное продвижение междоменной стенки, встречающей на своем пути отдельные задерживающие ее дефекты. Данный эффект обычно обнаруживается с помощью катушки, в которую помещается ферромагнитный стерженек или проволока. Если поочередно подносить к образцу и удалять от него сильный магнит, образец будет намагничиваться и перемагничиваться. Скачкообразные изменения намагниченности образца изменяют магнитный поток через катушку, и в ней возбуждается индукционный ток. Напряжение, возникающее при этом в катушке, усиливается и подается на вход пары акустических наушников. Щелчки, воспринимаемые через наушники, свидетельствует о скачкообразном изменении намагниченности.
Для выявления доменной структуры магнита методом порошковых фигур на хорошо отполированную поверхность намагниченного материала наносят каплю коллоидной суспензии ферромагнитного порошка (обычно Fe3O4). Частицы порошка оседают в основном в местах максимальной неоднородности магнитного поля – на границах доменов. Такую структуру можно изучать под микроскопом. Был предложен также метод, основанный на прохождении поляризованного света сквозь прозрачный ферромагнитный материал.
Первоначальная теория магнетизма Вейса в своих основных чертах сохранила свое значение до настоящего времени, получив, однако, обновленную интерпретацию на основе представления о нескомпенсированных электронных спинах как факторе, определяющем атомный магнетизм. Гипотеза о существовании собственного момента у электрона была выдвинута в 1926 С.Гаудсмитом и Дж.Уленбеком, и в настоящее время в качестве «элементарных магнитов» рассматриваются именно электроны как носители спина.
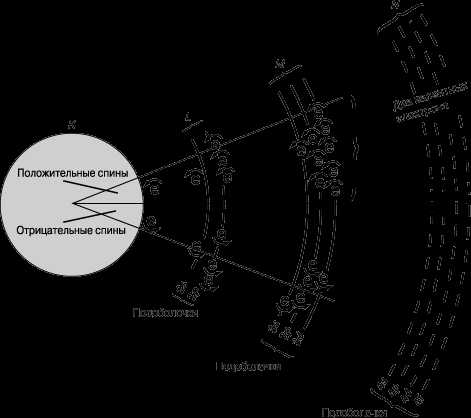
Для пояснения этой концепции рассмотрим (рис. 8) свободный атом железа – типичного ферромагнитного материала. Две его оболочки (K и L), ближайшие к ядру, заполнены электронами, причем на первой из них размещены два, а на второй – восемь электронов. В K-оболочке спин одного из электронов положителен, а другого – отрицателен. В L-оболочке (точнее, в двух ее подоболочках) у четырех из восьми электронов положительные, а у других четырех – отрицательные спины. В обоих случаях спины электронов в пределах одной оболочки полностью компенсируются, так что полный магнитный момент равен нулю. В M-оболочке ситуация иная, поскольку из шести электронов, находящихся в третьей подоболочке, пять электронов имеют спины, направленные в одну сторону, и лишь шестой – в другую. В результате остаются четыре нескомпенсированных спина, чем и обусловлены магнитные свойства атома железа. (Во внешней N-оболочке всего два валентных электрона, которые не дают вклада в магнетизм атома железа.) Сходным образом объясняется магнетизм и других ферромагнетиков, например никеля и кобальта. Поскольку соседние атомы в образце железа сильно взаимодействуют друг с другом, причем их электроны частично коллективизируются, такое объяснение следует рассматривать лишь как наглядную, но весьма упрощенную схему реальной ситуации.
Теорию атомного магнетизма, основанную на учете спина электрона, подкрепляют два интересных гиромагнитных эксперимента, один из которых был проведен А.Эйнштейном и В.де Гаазом, а другой – С.Барнеттом. В первом из этих экспериментов цилиндрик из ферромагнитного материала подвешивался так, как показано на рис. 9. Если по проводу обмотки пропустить ток, то цилиндрик поворачивается вокруг своей оси. При изменении направления тока (а следовательно, и магнитного поля) он поворачивается в обратном направлении. В обоих случаях вращение цилиндрика обусловлено упорядочением электронных спинов. В эксперименте Барнетта, наоборот, так же подвешенный цилиндрик, резко приведенный в состояние вращения, в отсутствие магнитного поля намагничивается. Этот эффект объясняется тем, что при вращении магнетика создается гироскопический момент, стремящийся повернуть спиновые моменты по направлению собственной оси вращения.
За более полным объяснением природы и происхождения короткодействующих сил, упорядочивающих соседние атомные магнитики и противодействующих разупорядочивающему влиянию теплового движения, следует обратиться к квантовой механике. Квантово-механическое объяснение природы этих сил было предложено в 1928 В.Гейзенбергом, который постулировал существование обменных взаимодействий между соседними атомами. Позднее Г.Бете и Дж.Слэтер показали, что обменные силы существенно возрастают с уменьшением расстояния между атомами, но по достижении некоторого минимального межатомного расстояния падают до нуля.
МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
Одно из первых обширных и систематических исследований магнитных свойств вещества было предпринято П.Кюри. Он установил, что по своим магнитным свойствам все вещества можно разделить на три класса. К первому относятся вещества с резко выраженными магнитными свойствами, подобными свойствам железа. Такие вещества называются ферромагнитными; их магнитное поле заметно на значительных расстояниях (см. выше). Во второй класс попадают вещества, называемые парамагнитными; магнитные свойства их в общем аналогичны свойствам ферромагнитных материалов, но гораздо слабее. Например, сила притяжения к полюсам мощного электромагнита может вырвать из ваших рук железный молоток, а чтобы обнаружить притяжение парамагнитного вещества к тому же магниту, нужны, как правило, очень чувствительные аналитические весы. К последнему, третьему классу относятся так называемые диамагнитные вещества. Они отталкиваются электромагнитом, т.е. сила, действующая на диамагнетики, направлена противоположно той, что действует на ферро- и парамагнетики.
Измерение магнитных свойств.
При изучении магнитных свойств наиболее важное значение имеют измерения двух типов. Первый из них –измерения силы, действующей на образец вблизи магнита; так определяется намагниченность образца. Ко второму относятся измерения «резонансных» частот, связанных с намагничением вещества. Атомы представляют собой крошечные «гироскопы» и в магнитном поле прецессируют (как обычный волчок под влиянием вращающего момента, создаваемого силой тяжести) с частотой, которая может быть измерена. Кроме того, на свободные заряженные частицы, движущиеся под прямым углом к линиям магнитной индукции, действует сила, как и на электронный ток в проводнике. Она заставляет частицу двигаться по круговой орбите, радиус которой дается выражением
R = mv/eB,
где m – масса частицы, v – ее скорость, e – ее заряд, а B – магнитная индукция поля. Частота такого кругового движения равна
где f измеряется в герцах, e – в кулонах, m – в килограммах, B – в теслах. Эта частота характеризует движение заряженных частиц в веществе, находящемся в магнитном поле. Оба типа движений (прецессию и движение по круговым орбитам) можно возбудить переменными полями с резонансными частотами, равными «естественным» частотам, характерным для данного материала. В первом случае резонанс называется магнитным, а во втором – циклотронным (ввиду сходства с циклическим движением субатомной частицы в циклотроне).
Говоря о магнитных свойствах атомов, необходимо особо остановиться на их моменте импульса. Магнитное поле действует на вращающийся атомный диполь, стремясь повернуть его и установить параллельно полю. Вместо этого атом начинает прецессировать вокруг направления поля (рис. 10) с частотой, зависящей от дипольного момента и напряженности приложенного поля.
Прецессия атомов не поддается непосредственному наблюдению, поскольку все атомы образца прецессируют в разной фазе. Если же приложить небольшое переменное поле, направленное перпендикулярно постоянному упорядочивающему полю, то между прецессирующими атомами устанавливается определенное фазовое соотношение и их суммарный магнитный момент начинает прецессировать с частотой, равной частоте прецессии отдельных магнитных моментов. Важное значение имеет угловая скорость прецессии. Как правило, это величина порядка 1010 Гц/Тл для намагниченности, связанной с электронами, и порядка 107 Гц/Тл для намагниченности, связанной с положительными зарядами в ядрах атомов.
Принципиальная схема установки для наблюдения ядерного магнитного резонанса (ЯМР) представлена на рис. 11. В однородное постоянное поле между полюсами вводится изучаемое вещество. Если затем с помощью небольшой катушки, охватывающей пробирку, возбудить радиочастотное поле, то можно добиться резонанса на определенной частоте, равной частоте прецессии всех ядерных «гироскопов» образца. Измерения сходны с настройкой радиоприемника на частоту определенной станции.
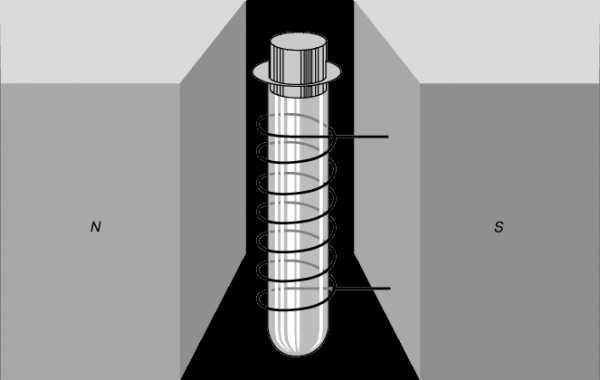
Методы магнитного резонанса позволяют исследовать не только магнитные свойства конкретных атомов и ядер, но и свойства их окружения. Дело в том, что магнитные поля в твердых телах и молекулах неоднородны, поскольку искажены атомными зарядами, и детали хода экспериментальной резонансной кривой определяются локальным полем в области расположения прецессирующего ядра. Это и дает возможность изучать особенности структуры конкретного образца резонансными методами.
Расчет магнитных свойств.
Магнитная индукция поля Земли составляет 0,5Ч10–4 Тл, тогда как поле между полюсами сильного электромагнита – порядка 2 Тл и более.
Магнитное поле, создаваемое какой-либо конфигурацией токов, можно вычислить, пользуясь формулой Био – Савара – Лапласа для магнитной индукции поля, создаваемого элементом тока. Расчет поля, создаваемого контурами разной формы и цилиндрическими катушками, во многих случаях весьма сложен. Ниже приводятся формулы для ряда простых случаев. Магнитная индукция (в теслах) поля, создаваемого длинным прямым проводом с током I (ампер), на расстоянии r (метров) от провода равна
Индукция в центре кругового витка радиуса R с током I равна (в тех же единицах):
Плотно намотанная катушка провода без железного сердечника называется соленоидом. Магнитная индукция, создаваемая длинным соленоидом c числом витков N в точке, достаточно удаленной от его концов, равна
Здесь величина NI/L есть число ампер (ампер-витков) на единицу длины соленоида. Во всех случаях магнитное поле тока направлено перпендикулярно этому току, а сила, действующая на ток в магнитном поле, перпендикулярна и току, и магнитному полю.
Поле намагниченного железного стержня сходно с внешним полем длинного соленоида с числом ампер-витков на единицу длины, соответствующим току в атомах на поверхности намагниченного стержня, поскольку токи внутри стержня взаимно компенсируются (рис. 12). По имени Ампера такой поверхностный ток называется амперовским. Напряженность магнитного поля Ha, создаваемая амперовским током, равна магнитному моменту единицы объема стержня M.
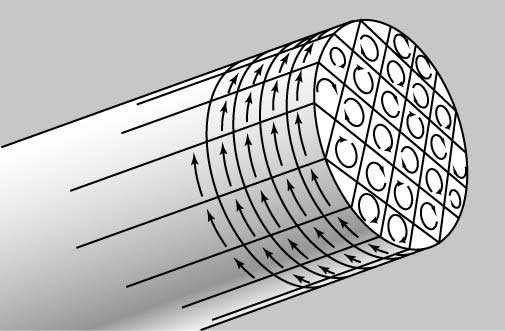
Если в соленоид вставлен железный стержень, то кроме того, что ток соленоида создает магнитное поле H, упорядочение атомных диполей в намагниченном материале стержня создает намагниченность M. В этом случае полный магнитный поток определяется суммой реального и амперовского токов, так что B = m0(H + Ha), или B = m0(H + M). Отношение M/H называется магнитной восприимчивостью и обозначается греческой буквой c ; c – безразмерная величина, характеризующая способность материала намагничиваться в магнитном поле.
Величина B/H, характеризующая магнитные свойства материала, называется магнитной проницаемостью и обозначается через ma, причем ma = m0m, где ma – абсолютная, а m – относительная проницаемости,
В ферромагнитных веществах величина c может иметь очень большие значения –до 104ё106. Величина c у парамагнитных материалов немного больше нуля, а у диамагнитных – немного меньше. Лишь в вакууме и в очень слабых полях величины c и m постоянны и не зависят от внешнего поля. Зависимость индукции B от H обычно нелинейна, а ее графики, т.н. кривые намагничивания, для разных материалов и даже при разных температурах могут существенно различаться (примеры таких кривых приведены на рис. 2 и 3).
Магнитные свойства вещества весьма сложны, и для их глубокого понимания необходим тщательный анализ строения атомов, их взаимодействий в молекулах, их столкновений в газах и их взаимного влияния в твердых телах и жидкостях; магнитные свойства жидкостей пока наименее изучены.
www.krugosvet.ru
Изучение магнитного поля постоянного магнита — КиберПедия
Цель работы: измерение индукции магнитного поля постоянного магнита; экспериментальное построение линий магнитной индукции.
Теоретическое введение
Магнитная стрелка в каждой точке поверхности Земли – (при отсутствии помех) принимает строго определенное направление: одним концом она приблизительно указывает в направлении геофизического севера, и другим – на юг. Конец магнитной стрелки, который указывает на север, условно называется северным (N), а противоположный – южным (S).
Если в некоторой области пространства на магнитную стрелку действуют силы, стремящиеся установить ее в определенном направлении, то мы говорим, что там имеется магнитное поле. Поведение стрелки компаса в магнитном поле (Земли или любою другого источника) позволяет ввести линии магнитной индукции по аналогии с силовыми линиями электрического поля. В каком-то смысле это даже лучше: стрелка сама указывает направление силовой линии в точке, где она находится. Основной характеристикой магнитного поля является вектор магнитной индукции , касательный к силовой линии, проходящей через данную точку. Эта величина пропорциональна силе, которая действует на северный конец бесконечно малой магнитной стрелки, помещенной в данную точку магнитного поля. В различных точках поля индукция по величине и направлению имеет различные значения. Линии магнитной индукции, в отличие от силовых линий электростатического поля, всегда замкнуты. Изображение магнитного поля с помощью силовых линий дает некоторое представление не только о направлении, но и величине магнитной индукции. Принято силовые линии магнитного поля, как и электрического, прочерчивать с такой густотой, чтобы число линий, пересекающих единицу площади поверхности, перпендикулярной к ним, было пропорционально величине магнитной индукции в пределах этой поверхности (поверхность предполагается достаточно малой). При этом в местах увеличения магнитной индукции силовые линии сгущаются, а в местах ослабления – разрежаются.
На рис.13.1 показан вид линий магнитной индукции простейших магнитных полей – поля прямого проводника и соленоида. Видно, что линии магнитной индукции охватывают проводник с током, создающий поле. Вблизи проводника они лежат в плоскостях, перпендикулярных проводнику. Направление линий индукции определяется по правилу правого винта (буравчика): если ввинчивать буравчик по направлению вектора плотности тока в проводнике, то направление движения рукоятки буравчика укажет направление линий магнитной индукции.
На рис.13.2,а представлены силовые линии поля постоянного полосового магнита. Принято считать, что линии выходят из северного полюса магнита, входят в южный и замыкаются внутри магнита.
 |
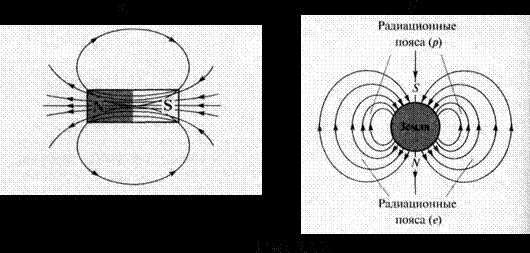На основании опыта установлено, что разноименные полюса притягиваются, одноименные отталкиваются. В этом смысле взаимодействие магнитов похоже на взаимодействие заряженных тел. Поведение стрелки компаса означает, что существует земной магнетизм, подобно тому, как существует гравитационное поле Земли, обусловленное ее массой. Поскольку обращаемый к северу конец стрелки назвали северным полюсом, а притягиваются разноименные полюса, то вблизи северного географического полюса Земли находится южный магнитный. Иными словами, магнитное поле Земли (вне Земли) направлено с географического юга на север (рис. 13.2.б).
Из сопоставления рис.13.1,в и 13.2,а видно, что магнитное поле вне соленоида подобно магнитному полю полосового магнита. Северный полюс магнита совпадает с тем концом соленоида, из которого ток в витках виден идущим против часовой стрелки. Линии магнитной индукции постоянного магнита выходят из его северного полюса и входят в южный. На первый взгляд кажется, что здесь имеется полная аналогия с линиями напряженности электростатического поля, причем полюсы магнита играют роль магнитных зарядов, создающих магнитное поле. Электростатическое поле Е порождается электрическими зарядами и воздействует на них, что символически изобразим как:
электрический заряд → → электрический заряд.
Два полюса магнита наводят на мысль о симметричном соотношении:
магнитный заряд → → магнитный заряд.
Оказалось, однако, что симметрия между магнитными и электрическими явлениями не столь прямолинейна. Если отдельные тела можно зарядить либо только положительно, либо только отрицательно, поскольку существуют элементарные заряженные частицы – носители электрических зарядов двух разных видов, – то отделить один из магнитных полюсов от противоположного невозможно. Если разрезать на две части магнит, то каждая часть будет снова вести себя как самостоятельный магнит, имеющий на своих концах противоположные полюсы (рис. 13.3).
Что произойдет, если при делении дойти до того, что разбить магнит на отдельные атомы? Можно ли тогда отделить северный полюс от южного? Нет, даже отдельные атомы ведут себя как микроскопические, но тем не менее «полноценные» магниты с северным и южным полюсами. Оказывается, что даже отдельные элементарные частицы (например, электроны) представляют собой микромагниты. В настоящее время отсутствуют какие-либо экспериментальные доказательства того, что в природе могут существовать отдельные магнитные заряды (монополи), подобные электрическим. В отличие от электрических зарядов свободных магнитных “зарядов” в природе не существует. Нет их и в полюсах постоянных магнитов. Поэтому линии магнитной индукции не могут обрываться на полюсах.
Полная аналогия между магнитными полями полосовых магнитов и соленоидов позволила французскому физику А.Амперу высказать (1821-1822) гипотезу о том, что магнитные свойства постоянных магнитов обусловлены существующими в них микротоками. О природе и характере этих микротоков Ампер ничего не мог сказать, так как в то время учение о строении вещества находилось еще в начальной стадии. Лишь после открытия электрона и выяснения строения атомов и молекул, то есть спустя почти 100 лет, гипотеза Ампера была блестяще подтверждена и легла в основу современных представлений о магнитных свойствах вещества. Гипотетические микротоки Ампера получили простое и наглядное истолкование: они связаны с движением электронов в атомах, молекулах и ионах.
Оказалось, что магнитное поле порождается движущимися электрическими зарядами и, в свою очередь, оказывает воздействие на них, так что наша схема принимает вид:
движущийся электрический заряд → → движущийся электрический заряд.
В быту мы обычно имеем дело с малыми электростатическими зарядами. В то же время заряд, протекающий через сечение проводника даже при небольшом токе, велик из-за огромной концентрации электронов в металле. Поэтому неудивительно, что первые экспериментальные наблюдения связи электрических и магнитных явлений были реализованы по схеме:
электрический ток → → электрический ток.
Если понимать под стрелкой экспериментальное подтверждение указанной связи, то первую из них (порождение магнитного поля током) «провел» датский ученый Г. X. Эрстед.
В 1820 г. Эрстедом было экспериментально установлено, что проводники, по которым текут токи, также взаимодействуют с магнитной стрелкой. Положение магнитной стрелки, помещенной около проводника с током, изменяется с изменением величины и направления тока, но стрелка совершенно не реагирует на неподвижные электрические заряды. Отсюда, действительно, можно сделать вывод, что способностью создавать магнитное поле обладают лишь движущиеся электрические заряды (электрический ток), а вокруг неподвижных зарядов существует только электростатическое поле. Магнитное поле, возникающее в пространстве около проводников с током, как и электрическое поле, обусловленное неподвижными зарядами, является одним из видов материи.
Дадим теперь количественное определение вектора магнитной индукции . Опыты показывают, что сила , действующая со стороны магнитного поля на движущуюся в этом поле заряженную частицу, подчиняется следующим закономерностям:
а) сила всегда перпендикулярна вектору скорости частицы;
б) отношение не зависит ни от заряда q частицы, ни от модуля ее скорости;
в) при изменении направления скорости частицы в данной точке поля модуль силы изменяется от ) до максимального значения Fmax, которое зависит не только от ,но также от значения в данной точке силовой характеристики поля – вектора магнитной индукции . По определению, модуль вектора равен:
. (13.1)
Итак, магнитная индукция численно равна отношению силы, действующей на заряженную частицу со стороны магнитного поля, к произведению абсолютного значения заряда и скорости частицы, если направление скорости частицы таково, что эта сила максимальна. Вектор направлен перпендикулярно вектору силы и вектору скорости , причем векторы , и образуют правую тройку.
По формуле (13.1) можно найти силу, действующую со стороны магнитного поля на движущуюся в нем заряженную частицу, только если скорость частицы перпендикулярна вектору . В общем случае эта сила равна:
. (13.2)
Модуль силы равен:
, (13.3)
где α – угол между векторами и .
Сила направлена перпендикулярно скорости заряженной частицы и сообщает частице только нормальное ускорение, то есть не совершает работы и вызывает только искривление траектории частицы.
Сила, описываемая формулой (13.2) является магнитной составляющей силы Лоренца, действующей на частицу в электромагнитном поле. В общем случае, когда на частицу действуют и электрическое, и магнитное поля, результирующая сила, называемая силой Лоренца, равна сумме двух составляющих – электрической и магнитной:
. (13.4)
Иногда под силой Лоренца понимают только магнитную составляющую силы . Разделение силы Лоренца на электрическую и магнитную составляющие относительно, то есть эти составляющие зависят от выбора системы отсчета.
На проводники с электрическим током, находящиеся в магнитном поле, действуют силы Ампера. Сила Ампера , приложенная к малому элементу проводника с током I, равна векторной сумме сил, которые действуют со стороны магнитного поля на движущиеся в проводнике носители тока. Если поперечное сечение проводника равно S, а его длина – dl, то в данном объеме dV=Sdl сосредоточено dN=ndV=nSdl носителей тока (n – концентрация носителей тока). Их полный заряд равен , где q0 – заряд каждого носителя тока. Скорость движения i-го носителя тока складывается из скорости беспорядочного теплового движения и скорости направленного движения : . Сила, действующая на i-ый заряд со стороны магнитного поля с индукцией , равна . Искомая сила Ампера равна сумме сил для всех dN носителей:
. (13.5)
Здесь учтено, что вследствие беспорядочности теплового движения носителей заряда . Так как – плотность тока, а – сила тока, то из (13.5) получаем силу Ампера:
, (13.6)
где – вектор элемента тока, проведенный в направлении электрического тока. Величина силы Ампера
, (13.6а)
где α – угол между и .
Мы получили выражение для силы, действующей на элемент проводника . Для определения полной силы, действующей на проводник, надо проинтегрировать (13.6) вдоль его длины. Такое интегрирование становится тривиальным для прямолинейного проводника в однородном магнитном поле:
, (13.7)
, (13.7а)
где α – угол между и . Направление силы Ампера определяется правилом векторного произведения: поступательное движение правого винта покажет направление вектора силы, если в плоскости ( , ) вращать винт от к .
Из закона Ампера (13.6) следует, что сила максимальна, если элемент проводника с током расположен перпендикулярно линиям магнитной индукции:
,
откуда
. (13.7)
Таким образом, магнитная индукция численно равна максимальной силе, действующей на единичный элемент тока.
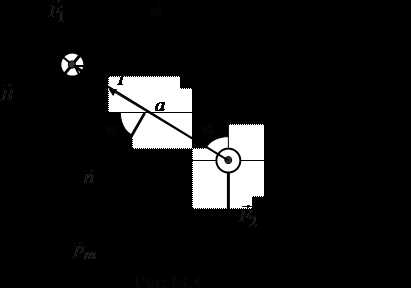
Пусть прямоугольный контур с током помещен в магнитное поле (рис.13.4). Силы, действующие на стороны рамки длиной а, лежащие в плоскости рисунка, равны друг другу и направлены в противоположные стороны по одной прямой, перпендикулярной плоскости рисунка, так что полностью уравновешивают друг друга. Стороны, имеющие длину l, перпендикулярны , так что на каждую из них действует сила Ампера, равная F=F1=F2=IlB. Эти силы противоположны по направлению, но не направлены вдоль одной прямой, они стремятся повернуть контур таким образом, чтобы его плоскость стала перпендикулярна (при этом единичный вектор нормали к контуру станет параллелен , угол между нормалью и станет равным нулю: α=0; это – положение равновесия рамки). Момент пары сил и равен
, (13.8)
где – плечо пары сил. Произведение al=S – это площадь контура. Величина, численно равная произведению силы тока I, протекающего в контуре, на площадь контура S, называется магнитным моментом: . Магнитный момент контура – векторная величина. Направление совпадает с положительным направлением нормали к плоскости контура, которое определяется правилом буравчика: если рукоятка вращается по направлению тока в контуре, то поступательное движение буравчика показывает направление вектора . Таким образом,
. (13.9)
 |
Из (13.8) получим:
и . (13.10)
Действие магнитного поля на помещенный в него небольшой виток с током (в пределах достаточно малого витка магнитное поле можно считать однородным) часто используют в качестве основы для определения силовой характеристики магнитного поля – вектора . Величина момента сил максимальна при α=900: . Магнитная индукция численно равна максимальному вращающему моменту сил, действующему на рамку с током с единичным магнитным моментом:
. (13.11)
Экспериментальная часть
Приборы и оборудование: постоянный магнит, датчик, блок питания, амперметр.
Методика измерений
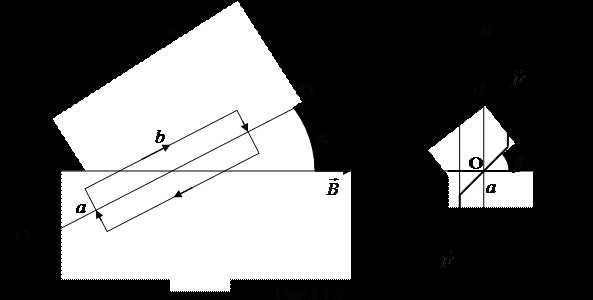
Рассмотрим прямоугольную рамку, расположенную в горизонтальной плоскости и закреплённую на упругой нити. Закреплённая ось ОО (рис.13.5) вращения рамки параллельна одной из сторон рамки и составляет угол α с линиями магнитной индукции, также горизонтальными. Силы Ампера, действующие на стороны a рамки, проходят через ось вращения ОО и вращающего момента относительно этой оси не дают. Силы, действующие на стороны b, равны:
(13.12)
и направлены перпендикулярно плоскости рис.13.5,а. Момент этой пары сил относительно оси ОО равен
, (13.13)
поскольку плечо пары равно стороне рамки а. Под действием этого вращающего момента рамка начинает вращаться относительно оси ОО, упругая нить закручивается, и в ней возникает возвращающий момент упругих сил, пропорциональный углу поворота рамки β:
, (13.14)
где – модуль кручения нити. При повороте рамки на угол β величина сил Ампера (13.12) не изменится, так как не изменяется угол α между сторонами b рамки и индукцией поля ; однако изменится плечо пары (рис.13.5,б):
. (13.15)
Из (13.12) и (13.15) получим:
. (13.16)
Равновесное положение рамки достигается при таких углах β, когда момент сил Ампера уравновешивается моментом упругих сил:
. (13.17)
Экспериментальная установка
Постоянный магнит 1 (рис.13.6) создаёт между полюсами индукцию магнитного поля . Датчик 2 – это по существу прибор магнито-электрической системы, в котором отсутствует постоянный магнит. Рамка 3 прибора шириной а, длиной b имеет N витков.
 |
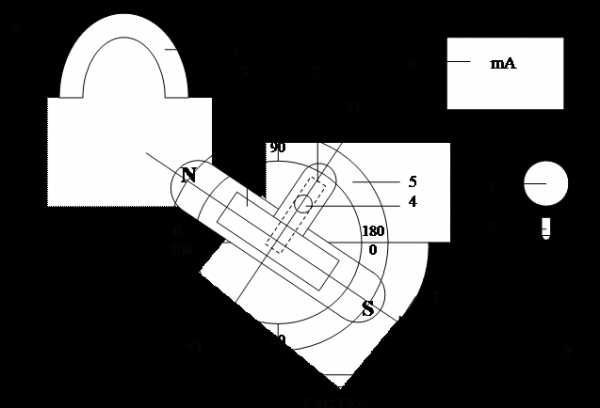С осью рамки связана стрелка прибора, показывающая угол поворота рамки относительно закреплённой оси ОО под действием магнитного поля постоянного магнита. Поскольку зависимость индукции поля B от угла поворота рамки β нелинейная (13.17), то шкала прибора также нелинейна и проградуирована в относительных единицах d, пропорциональных отношению ( ), а значит, и индукции поля:
,
или
. (13.18)
Коэффициент является константой прибора и равен:
.
На датчике установлен компас 4, который показывает направление линий индукции поля постоянного магнита. Датчик закреплён на подставке 5, поворачивающейся на вертикальной оси, проходящей через центр рамки. Основание датчика имеет шкалу, разделенную на 360 градусов. По шкале производится отсчёт угла поворота датчика γ относительно оси OX.
Блок питания обеспечивает постоянный ток, проходящий через рамку. Регулировка тока (от 2 мА до 20 мА) производится регулятором 7 и контролируется миллиамперметром 6. Переключатель 8 даёт возможность изменять направление тока в рамке.
Внимание! 1. Величина индукции магнитного поля постоянного магнита такова, что при приближении к нему Ваши обычные наручные часы и калькуляторы испортятся.
cyberpedia.su
Постоянные магниты, их описание и принцип действия :: SYL.ru
Наряду с электризующимися трением кусочками янтаря постоянные магниты были для древних людей первым материальным свидетельством электромагнитных явлений (молнии на заре истории определенно относили к сфере проявления нематериальных сил). Объяснение природы ферромагнетизма всегда занимало пытливые умы ученых, однако и в настоящее время физическая природа постоянной намагниченности некоторых веществ, как природных, так и искусственно созданных, еще не до конца раскрыта, оставляя немалое поле деятельности для современных и будущих исследователей.
Традиционные материалы для постоянных магнитов
Они стали активно использоваться в промышленности, начиная с 1940 года с появления сплава алнико (AlNiCo). До этого постоянные магниты из различных сортов стали применялись лишь в компасах и магнето. Алнико сделал возможным замену на них электромагнитов и применение их в таких устройствах, как двигатели, генераторы и громкоговорители.
Это их проникновение в нашу повседневную жизнь получило новый импульс с созданием ферритовых магнитов, и с тех пор постоянные магниты стали обычным явлением.
Революция в магнитных материалах началась около 1970 года, с созданием самарий-кобальтового семейства жестких магнитных материалов с доселе невиданной плотностью магнитной энергии. Затем было открыто новое поколение редкоземельных магнитов на основе неодима, железа и бора с гораздо более высокой плотностью магнитной энергии, чем у самарий-кобальтовых (SmCo) и с ожидаемо низкой стоимостью. Эти две семьи редкоземельных магнитов имеют такие высокие плотности энергии, что они не только могут заменить электромагниты, но использоваться в областях, недоступных для них. Примерами могут служить крошечный шаговый двигатель на постоянных магнитах в наручных часах и звуковые преобразователи в наушниках типа Walkman.
Постепенное улучшение магнитных свойств материалов представлено на диаграмме ниже.
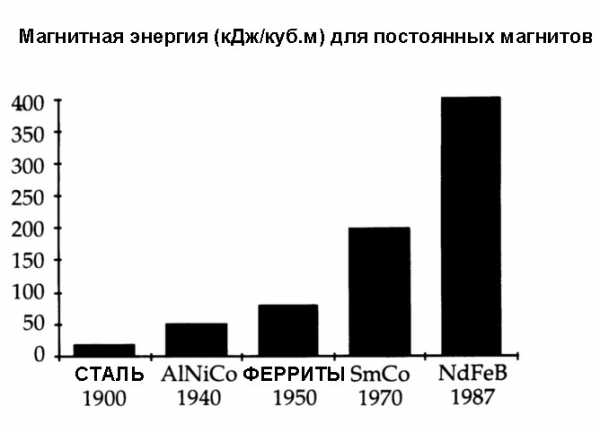
Неодимовые постоянные магниты
Они представляют новейшее и наиболее значительное достижение в этой области на протяжении последних десятилетий. Впервые об их открытии было объявлено почти одновременно в конце 1983 года специалистами по металлам компаний Sumitomo и General Motors. Они основаны на интерметаллическом соединении NdFeB: сплаве неодима, железа и бора. Из них неодим является редкоземельным элементом, добываемым из минерала моназита.
Огромный интерес, которые вызвали эти постоянные магниты, возникает потому, что в первый раз был получен новый магнитный материал, который не только сильнее, чем у предыдущего поколения, но является более экономичным. Он состоит в основном из железа, которое намного дешевле, чем кобальт, и из неодима, являющегося одним из наиболее распространенных редкоземельных материалов, запасы которого на Земле больше, чем свинца. В главных редкоземельных минералах моназите и бастанезите содержится в пять-десять раз больше неодима, чем самария.
Физический механизм постоянной намагниченности
Чтобы объяснить функционирование постоянного магнита, мы должны заглянуть внутрь его до атомных масштабов. Каждый атом имеет набор спинов своих электронов, которые вместе формируют его магнитный момент. Для наших целей мы можем рассматривать каждый атом как небольшой полосовой магнит. Когда постоянный магнит размагничен (либо путем нагрева его до высокой температуры, либо внешним магнитным полем), каждый атомный момент ориентирован случайным образом (см. рис. ниже) и никакой регулярности не наблюдается.
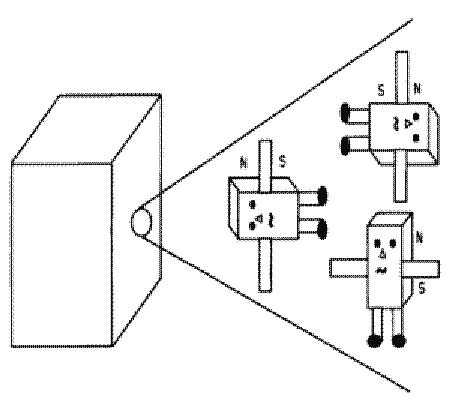
Когда же он намагничен в сильном магнитном поле, все атомные моменты ориентируются в направлении поля и как бы сцепляются «в замок» друг с другом (см. рис. ниже). Это сцепление позволяет сохранить поле постоянного магнита при удалении внешнего поля, а также сопротивляться размагничиванию при изменении его направления. Мерой силы сцепления атомных моментов является величина коэрцитивной силы магнита. Подробнее об этом позже.
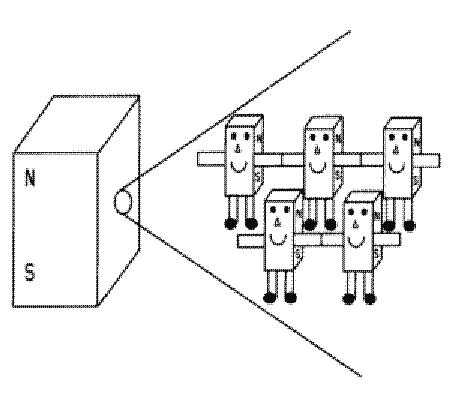
При более глубоком изложении механизма намагничивания оперируют не понятиями атомных моментов, а используют представления о миниатюрных (порядка 0,001 см) областях внутри магнита, изначально обладающих постоянной намагниченностью, но ориентированных при отсутствии внешнего поля случайным образом, так что строгий читатель при желании может отнести вышеизложенный физический механизм не к магниту в целом. а к отдельному его домену.
Индукция и намагниченность
Атомные моменты суммируются и образуют магнитный момент всего постоянного магнита, а его намагниченность M показывает величину этого момента на единицу объема. Магнитная индукция B показывает, что постоянный магнит является результатом внешнего магнитного усилия (напряженности поля) H, прикладываемого при первичном намагничивании, а также внутренней намагниченности M, обусловленной ориентацией атомных (или доменных) моментов. Ее величина в общем случае задаётся формулой:
B = µ0 (H + M),
где µ0 является константой.
В постоянном кольцевом и однородном магните напряженность поля H внутри него (при отсутствии внешнего поля) равна нулю, так как по закону полного тока интеграл от нее вдоль любой окружности внутри такого кольцевого сердечника равен:
H∙2πR = iw=0 , откуда H=0.
Следовательно, намагниченность в кольцевом магните:
M= B/µ0.
В незамкнутом магните, например, в том же кольцевом, но с воздушным зазором шириной lзаз в сердечнике длиной lсер, при отсутствии внешнего поля и одинаковой индукции B внутри сердечника и в зазоре по закону полного тока получим:
Hсер l сер + (1/ µ0)Blзаз = iw=0.
Поскольку B = µ0(Hсер + Мсер), то, подставляя ее выражение в предыдущее, получим:
Hсер(l сер + lзаз) + Мсер lзаз=0,
или
Hсер = ─ Мсер lзаз(l сер + lзаз).
В воздушном зазоре:
Hзаз = B/µ0,
причем B определяется по заданной Мсер и найденной Hсер.
Кривая намагничивания
Начиная с ненамагниченного состояния, когда Н увеличивается от нуля, вследствие ориентации всех атомных моментов по направлению внешнего поля быстро увеличиваются М и B, изменяясь вдоль участка «а» основной кривой намагничивания (см. рисунок ниже).
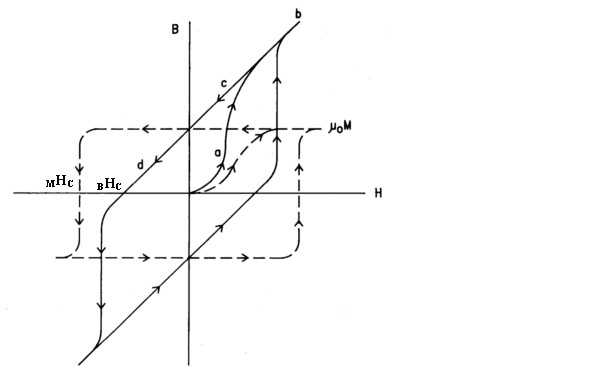
Когда выровнены все атомные моменты, М приходит к своему значению насыщения, и дальнейшее увеличение В происходит исключительно из-за приложенного поля (участок b основной кривой на рис. ниже). При уменьшении внешнего поля до нуля индукция В уменьшается не по первоначальному пути, а по участку «c» из-за сцепления атомных моментов, стремящегося сохранить их в том же направлении. Кривая намагничивания начинает описывать так называемую петлю гистерезиса. Когда Н (внешнее поле) приближается к нулю, то индукция приближается к остаточной величине, определяемой только атомными моментами:
Вr = μ0 (0 + Мг).
После того как направление H изменяется, Н и М действуют в противоположных направлениях, и B уменьшается (участок кривой «d» на рис.). Значение поля, при котором В уменьшается до нуля, называется коэрцитивной силой магнита BHC. Когда величина приложенного поля является достаточно большой, чтобы сломать сцепление атомных моментов, они ориентируются в новом направлением поля, а направление M меняется на противоположное. Значение поля, при котором это происходит, называется внутренней коэрцитивной силой постоянного магнита МНC. Итак, есть две разных, но связанных коэрцитивных силы, связанных с постоянным магнитом.
На рисунке ниже показаны основные кривые размагничивания различных материалов для постоянных магнитов.
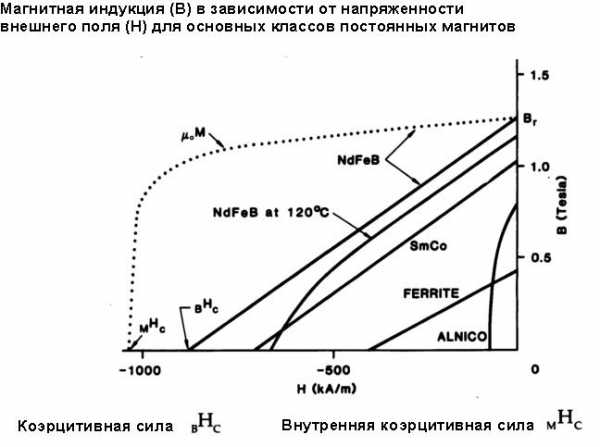Из него видно, что наибольшей остаточной индукцией Br и коэрцитивной силой (как полной, так и внутренней, т. е. определяемой без учета напряженности H, только по намагниченности M) обладают именно NdFeB-магниты.Поверхностные (амперовские) токи
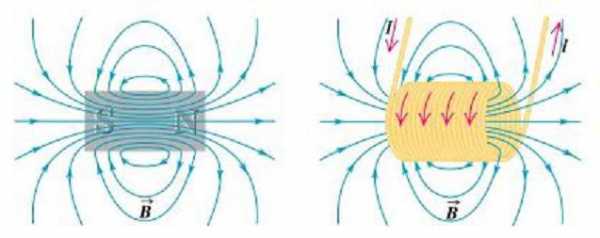
Магнитные поля постоянных магнитов можно рассматривать как поля некоторых связанных с ними токов, протекающих по их поверхностям. Эти токи называют амперовскими. В обычном смысле слова токи внутри постоянных магнитов отсутствуют. Однако, сравнивая магнитные поля постоянных магнитов и поля токов в катушках, французский физик Ампер предположил, что намагниченность вещества можно объяснить протеканием микроскопических токов, образующих микроскопические же замкнутые контуры. И действительно, ведь аналогия между полем соленоида и длинного цилиндрического магнита почти полная: имеется северный и южный полюс постоянного магнита и такие же полюсы у соленоида, а картины силовых линий их полей также очень похожи (см. рисунок ниже).
Есть ли токи внутри магнита?
Представим себе, что весь объем некоторого стержневого постоянного магнита (с произвольной формой поперечного сечения) заполнен микроскопическими амперовскими токами. Поперечный разрез магнита с такими токами показан на рисунке ниже.
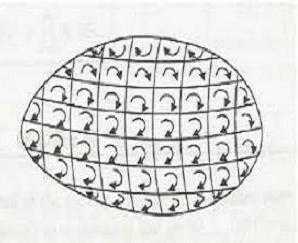Каждый из них обладает магнитным моментом. При одинаковой ориентации их по направлению внешнего поля они образуют результирующий магнитный момент, отличный от нуля. Он и определяет существование магнитного поля при кажущемся отсутствии упорядоченного движения зарядов, при отсутствии тока через любое сечение магнита. Легко также понять, что внутри него токи смежных (соприкасающихся) контуров компенсируются. Нескомпенсированными оказываются только токи на поверхности тела, образующие поверхностный ток постоянного магнита. Плотность его оказывается равной намагниченности M.Как избавиться от подвижных контактов
Известна проблема создания бесконтактной синхронной машины. Традиционная ее конструкция с электромагнитным возбуждением от полюсов ротора с катушками предполагает подвод тока к ним через подвижные контакты – контактные кольца со щетками. Недостатки такого технического решения общеизвестны: это и трудности в обслуживании, и низкая надежность, и большие потери в подвижных контактах, особенно если речь идет о мощных турбо- и гидрогенераторах, в цепях возбуждения которых расходуется немалая электрическая мощность.
Если сделать такой генератор на постоянных магнитах, то проблема контакта сразу же уходит. Правда, появляется проблема надежного крепления магнитов на вращающемся роторе. Здесь может пригодиться опыт, накопленный в тракторостроении. Там уже давно применяется индукторный генератор на постоянных магнитах, расположенных в пазах ротора, залитых легкоплавким сплавом.
Двигатель на постоянных магнитах
В последние десятилетия широкое распространение получили вентильные двигатели постоянного тока. Такой агрегат представляет собой собственно электродвигатель и электронный коммутатор его обмотки якоря, выполняющий функции коллектора. Электродвигатель представляет собой синхронный двигатель на постоянных магнитах, расположенных на роторе, как и на рис. выше, с неподвижной обмоткой якоря на статоре. Электронный коммутатор схемотехнически представляет собой инвертор постоянного напряжения (или тока) питающей сети.
Основным преимуществом такого двигателя является его бесконтактность. Специфическим его элементом является фото-, индукционный или холловский датчик положения ротора, управляющий работой инвертора.
www.syl.ru
ПОСТОЯННЫЙ МАГНИТ • Большая российская энциклопедия
-
В книжной версии
Том 27. Москва, 2015, стр. 267-268
-
Скопировать библиографическую ссылку:
Авторы: И. Д. Подольский
Рис. 1. Картина магнитного поля постоянных магнитов: а – без магнитопровода; б – с магнитопроводом; 1 – постоянный магнит; 2 – магнитопровод; 3 – рабочий объём; N и S – полюса постоянного магнита. Стр…
ПОСТОЯ́ННЫЙ МАГНИ́Т, изделие из магнитотвёрдого материала, сохраняющее после намагничивания и стабилизации значит. намагниченность при воздействии внешних магнитных полей, повышенных температур, ударов, вибрации и др. Предшественники П. м. из природного магнетита, получившего намагниченность в поле Земли, использовались в Древнем Китае и цивилизации майя в судовых компасах, а также в ритуальных целях. «Геркулесовым камнем» в античном мире называли куски магнетита, притягивающие железные предметы. П. м. из совр. магнитотвёрдых материалов (МТМ) способны удерживать груз, в 100 раз и более превышающий их собств. вес. При намагничивании внешним постоянным или импульсным магнитным полем П. м. приобретает намагниченность, интенсивность которой зависит от марки МТМ. Одновременно у торцов П. м. возникает пара разноимённых магнитных полюсов, на которых замыкаются линии магнитной индукции, образующие внешний магнитный поток П. м. (рис. 1, а). Магнитное поле полюсов в теле П. м. частично размагничивает его (коэф. размагничивания зависит от марки МТМ, формы и соотношения размеров магнита). Для уменьшения размагничивания к торцам П. м. присоединяют магнитопровод из магнитомягкого материала, в результате магнитный поток концентрируется в огранич. воздушном зазоре (рис. 1, б). Совр. П. м., обладающие высокой устойчивостью к размагничиванию (напр., на основе сплава неодим – железо – бор), могут использоваться практически без магнитопровода, что значительно уменьшает габаритные размеры и массу мн. устройств. Широко применяются кольцевые магниты с несколькими парами разноимённых полюсов, для создания которых используют спец. приёмы намагничивания.
В зависимости от технологии получения МТМ (методом литья, пластич. деформации, порошковой металлургии или вакуумного напыления) П. м. подразделяются на литые, деформируемые, спечённые и плёночные. П. м. практически не имеют ограничений по форме и размерам, выпускаются в виде призм, цилиндров, дисков, колец, стержней, сегментов, скоб и т. п.
П. м. подразделяются по области применения, типу МТМ и геометрич. форме. Для снижения необратимых магнитных потерь в П. м. используют магнитную стабилизацию, заключающуюся в предварит. нормированном нагревании П. м. или воздействии на него размагничивающего поля; обратимые потери могут быть уменьшены выбором соответствующей марки МТМ и оптимальной магнитной цепи. В качестве контрольных параметров П. м. обычно используют магнитную индукцию в зазоре эквивалентной (по осн. параметрам) магнитной системы или контрольного магнитопровода, а также магнитный поток и момент П. м. в разомкнутой магнитной цепи и др.
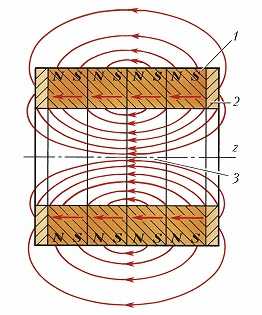
Рис. 2. Двухполюсные кольцевые магниты с аксиальной магнитной текстурой и однонаправленным (вдоль оси z) осесимметричным магнитным полем, предназначенные для фокусировки электронных пучков (все обозна…
П. м. широко применяются в качестве автономных источников магнитного поля в устройствах автоматики, робототехники, СВЧ- и вычислит. техники, в приводах, электродвигателях и генераторах, в медицинских, измерит. приборах и др. Напр., в радарах с помощью П. м. осуществляют фокусировку электронных пучков (рис. 2). Практич. значимость П. м. непрерывно растёт в связи с совершенствованием и появлением новых типов МТМ, с одной стороны, и развитием перспективных областей применения – с другой.
bigenc.ru
Постоянный магнит. Магнитное поле. Линии индукции. Вектор
Постоянным магнитом называется тело, обладающее собственным постоянным магнитным полем. Классический школьный магнит — параллелепипед, каждая из половин которого выкрашена в свой цвет (синий и красный). Такое цветовое решение не случайно: для любого магнита характерно наличие двух полюсов (концов): южный (S, красный) и северный (N, синий).
Визуализируем (рис. 1):
Рис. 1. Магнит
В школе проводят эксперимент с магнитной стрелкой. Сама магнитная стрелка представляет собой малый магнит установленный на подставке с тонкой иголкой, которая позволяет стрелке свободно вращаться. Тогда, если установить несколько магнитных стрелок вокруг основного магнита, они будут ориентированы по-разному (рис. 2).
Рис. 2. Магнитная стрелка в поле постоянного магнита
Ориентация стрелок зависит от их положения относительно магнита и магнитного поля этого источника. Мы можем ввести гипотетические гладкие линии, которые проходят через магнитные стрелки вдоль острия стрелок (рис. 3).
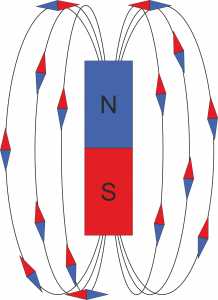
Рис. 3. Визуализация магнитного поля
Данные гипотетические линии назовём линиями магнитной индукции. Линии магнитной индукции замкнуты внутри магнита. Договоримся, что они начинаются на северном полюсе магнита (N) и заканчиваются на южном (S) (рис. 4).
Рис. 4. Поле постоянного магнита
Линии магнитной индукции на рисунке обладают некоторой информативностью: чем больше плотность линий в единице площади, тем сильнее магнитное поле (рис. 5).
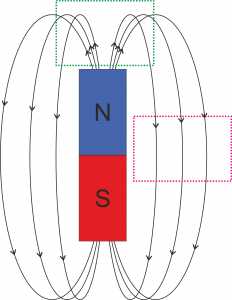
Рис. 5. Поле постоянного магнита (плотность)
Выберем одинаковые по площади прямоугольники (зелёный и розовый) в различных точках магнитного поля. Заметно, что количество линий и их «густота» в зелёном прямоугольнике выше, чем в розовом. Это значит, что магнитное поле в зелёном прямоугольнике сильнее, чем в розовом.
Для математического описания величины поля используется вектор магнитной индукции.
Поделиться ссылкой:
www.abitur.by
