25.04.202016.08.2019

Предел математика – как понять, вычислить, подробное объяснение с решением

• by alexxlab
• Комментариев к записи Предел математика – как понять, вычислить, подробное объяснение с решением нет
• Разное

Высшая математика. Первый семестр/Пределы — Викиучебник

Материал из Викиучебника — открытых книг для открытого мира

Пусть задана некоторая меняющаяся величина y{\displaystyle y}, зависящая от переменного x{\displaystyle x}. Предположим, что это переменное x{\displaystyle x} можно менять так, что выполняется некоторое условие B{\displaystyle {\mathcal {B}}}: переменное «приближается» («стремится») к чему-нибудь (что это означает, мы уточним позже при помощи строгих определений). Тогда встаёт вопрос о том, не ведёт ли себя величина y{\displaystyle y} каким-либо «правильным» образом, тоже «стремясь» к чему-нибудь, например, к числу L{\displaystyle L}. Если это так, то это «что-то» называется пределом величины y{\displaystyle y} при данном условии B{\displaystyle {\mathcal {B}}} для x{\displaystyle x} и обозначается

limBy.{\displaystyle \displaystyle \lim _{\mathcal {B}}y.}

Дадим теперь строгие определения предела в некоторых частных случаях, а потом перейдём к обсуждению общего определения.

ru.wikibooks.org

Предел (математика) — Википедия. Что такое Предел (математика)

Преде́л — одно из основных понятий математического анализа. Различают предел последовательности и предел функции.

Понятие предела на интуитивном уровне использовалось ещё во второй половине XVII века Ньютоном, а также математиками XVIII века, такими как Эйлер и Лагранж. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.

История

Основной источник: ^[1]

Интуитивное понятие о предельном переходе использовалось еще учеными Древней Греции при вычислении площадей и объемов различных геометрических фигур. Методы решения таких задач в основном были развиты Архимедом.

При создании дифференциального и интегрального исчислений математики XVII века (и, прежде всего, Ньютон) также явно или неявно использовали понятие предельного перехода. Впервые определение понятия предела было введено в работе Валлиса «Арифметика бесконечных величин» (XVII век), однако исторически это понятие не лежало в основе дифференциального и интегрального исчислений.

Лишь в XIX веке в работах Коши теория пределов была использована для строгого обоснования математического анализа. Дальнейшей разработкой теории пределов занимались Вейерштрасс и Больцано.

С помощью теории пределов во второй половине XIX века было, в частности, обосновано использование в анализе бесконечных рядов, которые явились удобным аппаратом для построения новых функций.

Предел последовательности

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.

Число a{\displaystyle a} называется пределом последовательности x1,x2,…,xn,…{\displaystyle x_{1},x_{2},…,x_{n},…}

, если

∀{\displaystyle \forall } ϵ>0{\displaystyle \epsilon >0} , ∃{\displaystyle \exists } N(ϵ){\displaystyle N(\epsilon )} , ∀{\displaystyle \forall } n>N(ϵ){\displaystyle n>N(\epsilon )}: |xn−a|<ϵ{\displaystyle |x_{n}-a|<\epsilon }.

Предел последовательности обозначается limn→+∞xn{\displaystyle \lim _{n\to +\infty }x_{n}}. Куда именно стремится n{\displaystyle n}, можно не указывать, поскольку n{\displaystyle n} ∈N{\displaystyle \in \mathbb {N} }, оно может стремиться только к +∞{\displaystyle +\infty }.

Свойства:

Предел функции

График функции, предел которой при аргументе, стремящемся к бесконечности, равен L{\displaystyle L}.

Функция f(x){\displaystyle f(x)} имеет предел A{\displaystyle A} в точке x0{\displaystyle x_{0}}, если для всех значений x{\displaystyle x}, достаточно близких к x0{\displaystyle x_{0}}, значение f(x){\displaystyle f(x)} близко к A{\displaystyle A}.

Число b называется пределом функции f(x) в точке a, если ∀ϵ>0{\displaystyle \forall \epsilon >0} существует δ>0{\displaystyle \delta >0}, такое что ∀x,0<|x−a|<δ{\displaystyle \forall x,0<|x-a|<\delta } выполняется |f(x)−b|<ϵ{\displaystyle |f(x)-b|<\epsilon }.

Для пределов функций справедливы аналогичные свойства, как и для пределов последовательностей, например, limx→x0(f(x)+g(x))=limx→x0f(x)+limx→x0g(x){\displaystyle \lim _{x\to x_{0}}(f(x)+g(x))=\lim _{x\to x_{0}}f(x)+\lim _{x\to x_{0}}g(x)}, если все члены существуют.

Обобщенное понятие предела последовательности

Пусть X{\displaystyle X} — некоторое множество, в котором определено понятие окрестности U{\displaystyle U} (например, метрическое пространство). Пусть xi∈X{\displaystyle x_{i}\in X} — последовательность точек (элементов) этого пространства. Говорят, что x∈X{\displaystyle x\in X} есть предел этой последовательности, если в любой окрестности точки x{\displaystyle x} лежат почти все члены последовательности то есть ∀U(x)∃n∀i>nxi∈U(x){\displaystyle \forall U(x)\exists n\forall i>nx_{i}\in U(x)}

См. также

Примечания

1. ↑ А.Г. Цыпкин. Справочник по математике, 1983, Москва «Наука».

wiki.sc

Пределы. Понятие пределов. Вычисление пределов.

Понятие пределов рассмотрим на показательных примерах.

Пусть х – числовая переменная величина, Х – область ее изменения. Если каждому числу х, принадлежащему Х, поставлено в соответствие некоторое число у, то говорят, что на множестве Х определена функция, и записывают у = f(x).
Множество Х в данном случае – плоскость, состоящая из двух координатных осей – 0X и 0Y. Для примера изобразим функцию у = х². Оси 0X и 0Y образуют Х – область ее изменения. На рисунке прекрасно видно, как ведет себя функция. В таком случае говорят, что на множестве Х определена функция у = х

2.

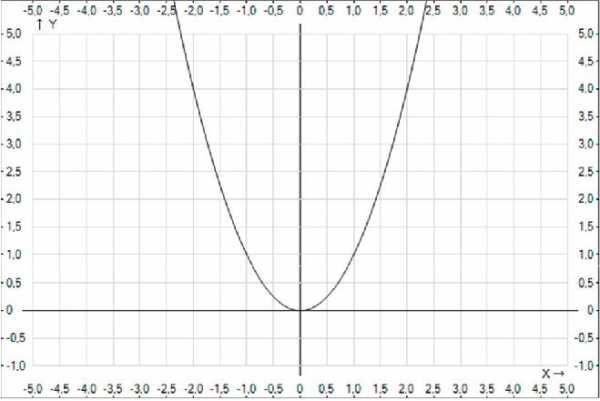
Совокупность Y всех частных значений функции называется множеством значений f(x). Другими словами, множество значений – это промежуток по оси 0Y, где определена функция. Изображенная парабола явно показывает, что f(x) > 0 , т.к. x2 > 0. Поэтому область значений будет [0; +]. Множество значений смотрим по 0Y.

Совокупность всех х называется областью определения f(x). Множество определений смотрим по 0X и в нашем случае областью допустимых значений является [-; +].

Точка а (а принадлежит или Х) называется предельной точкой множества Х, если в любой окрестности точки а имеются точки множества Х, отличные от а.

Пришла пора понять – что же такое предел функции?

Чисто b, к которому стремится функция при стремлении х к числу а, называется пределом функции. Записывается это следующим образом:

Например, f(x) = х². Нам надо узнать, к чему стремится (не равна) функция при х 2. Сначала запишем предел:

Посмотрим на график.

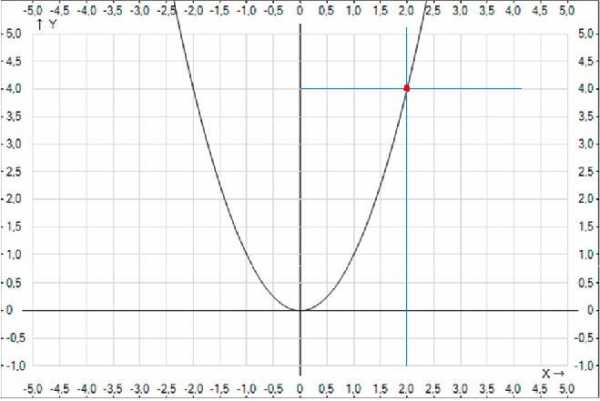
Проведем параллельно оси 0Y линию через точку 2 на оси 0X. Она пересечет наш график в точке (2;4). Опустим из этой точки на ось 0Y перпендикуляр – и попадем в точку 4. Вот к чему стремится наша функция при х 2. Если теперь подставить в функцию f(x) значение 2, то ответ будет таким же.

Теперь прежде чем перейти к вычислению пределов, введем базовые определения.

Понятие пределов введено французским математиком Огюстеном Луи Коши в XIX веке.

Допустим, функция f(x) определена на некотором интервале, в котором содержится точка x = A, однако совсем не обязательно, чтобы значение f(А) было определено.

Тогда, согласно определению Коши, пределом функции

f(x) будет некое число B при x, стремящимся к А, если для каждого C > 0 найдется число D > 0, при котором

Т.е. если функция f(x) при x А ограничена пределом В, это записывается в виде

.

Пределом последовательности называется некое число А, если для любого сколь угодно малого положительного числа В > 0 найдется такое число N, при котором все значения в случае n > N удовлетворяют неравенству

Такой предел имеет вид .

Последовательность, у которой есть предел, будем называть сходящейся, если нет – расходящейся.

Как Вы уже заметили, пределы обозначаются значком lim, под которым записывается некоторое условие для переменной, и далее уже записывается сама функция. Такой набор будет читаться, как «предел функции при условии…». Например:

– предел функции при х, стремящимся к 1.

Выражение «стремящимся к 1» означает, что х последовательно принимает такие значения, которые бесконечно близко приближаются к 1.

Теперь становится ясно, что для вычисления данного предела достаточно подставить вместо х значение 1:

Ответ: -3.

Кроме конкретного числового значения х может стремиться и к бесконечности. Например:

Выражение х означает, что х постоянно возрастает и неограниченно близко приближается к бесконечности. Поэтому подставив вместо х бесконечность станет очевидно, что функция 1- х будет стремиться к , но с обратным знаком:

Таким образом, вычисление пределов сводится к нахождению его конкретного значения либо определенной области, в которую попадает функция, ограниченная пределом.

Исходя из вышеизложенного следует, что при вычислении пределов важно пользоваться несколькими правилами:

1. Сперва попытаемся подставить в функцию число. Результат вычисление и будет ответом.
2. Если х стремиться не к числу, например в пределах вида или , то такие пределы решаются сразу, т.к число деленное на бесконечность всегда дает ноль, а деленное на 0 всегда бесконечность. Если у вас затруднено понимание понятий бесконечность и 0 в пределах, то вы можете подставлять вместо бесконечности – бесконечно большое число – например 1000 000, или вместо 0 – бесконечно малое – к примеру 0,000001 и прикинуть к чему будет стремиться ответ.
3. Есть еще одна интересная группа пределов, где мы и в числите и в знаменателе при подстановке получаем или 0 или бесконечность. Так называемые пределы с неопределенностью, часть из которых замечательные. Их мы рассматриваем отдельно в статьях “Вычисление пределов. Пределы с неопределенностью” и “Замечательные пределы: Первый и второй замечательный предел”.

Понимая

сущность предела и основные правила вычисления пределов, вы получите ключевое представление о том, как их решать. Если какой предел будет вызывать у вас затруднения, то пишите в комментарии и мы обязательно вам поможем.

Заметка: Юриспруденция – наука о законах, помогающее в конфлитных и других жизненных трудностях.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

reshit.ru

Предел (математика) — Википедия

У этого термина существуют и другие значения, см. Предел.

Преде́л — одно из основных понятий математического анализа. Различают предел последовательности и предел функции.

Понятие предела на интуитивном уровне использовалось ещё во второй половине XVII века Ньютоном, а также математиками XVIII века, такими как Эйлер и Лагранж. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.

История

Основной источник: ^[1]

Интуитивное понятие о предельном переходе использовалось еще учеными Древней Греции при вычислении площадей и объемов различных геометрических фигур. Методы решения таких задач в основном были развиты Архимедом.

При создании дифференциального и интегрального исчислений математики XVII века (и, прежде всего, Ньютон) также явно или неявно использовали понятие предельного перехода. Впервые определение понятия предела было введено в работе Валлиса «Арифметика бесконечных величин» (XVII век), однако исторически это понятие не лежало в основе дифференциального и интегрального исчислений.

Лишь в XIX веке в работах Коши теория пределов была использована для строгого обоснования математического анализа. Дальнейшей разработкой теории пределов занимались Вейерштрасс и Больцано.

С помощью теории пределов во второй половине XIX века было, в частности, обосновано использование в анализе бесконечных рядов, которые явились удобным аппаратом для построения новых функций.

Видео по теме

Предел последовательности

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.

Число a{\displaystyle a} называется пределом последовательности x1,x2,…,xn,…{\displaystyle x_{1},x_{2},…,x_{n},…} , если

∀{\displaystyle \forall } ϵ>0{\displaystyle \epsilon >0} , ∃{\displaystyle \exists } N(ϵ){\displaystyle N(\epsilon )} , ∀{\displaystyle \forall } n>N(ϵ){\displaystyle n>N(\epsilon )}: |xn−a|<ϵ{\displaystyle |x_{n}-a|<\epsilon }.

Предел последовательности обозначается limn→+∞xn{\displaystyle \lim _{n\to +\infty }x_{n}}. Куда именно стремится n{\displaystyle n}, можно не указывать, поскольку n{\displaystyle n} ∈N{\displaystyle \in \mathbb {N} }, оно может стремиться только к +∞{\displaystyle +\infty }.

Свойства:

Предел функции

График функции, предел которой при аргументе, стремящемся к бесконечности, равен L{\displaystyle L}.

Функция f(x){\displaystyle f(x)} имеет предел A{\displaystyle A} в точке x0{\displaystyle x_{0}}, если для всех значений x{\displaystyle x}, достаточно близких к x0{\displaystyle x_{0}}, значение f(x){\displaystyle f(x)} близко к A{\displaystyle A}.

Число b называется пределом функции f(x) в точке a, если ∀ϵ>0{\displaystyle \forall \epsilon >0} существует δ>0{\displaystyle \delta >0}, такое что ∀x,0<|x−a|<δ{\displaystyle \forall x,0<|x-a|<\delta } выполняется |f(x)−b|<ϵ{\displaystyle |f(x)-b|<\epsilon }.

Для пределов функций справедливы аналогичные свойства, как и для пределов последовательностей, например, limx→x0(f(x)+g(x))=limx→x0f(x)+limx→x0g(x){\displaystyle \lim _{x\to x_{0}}(f(x)+g(x))=\lim _{x\to x_{0}}f(x)+\lim _{x\to x_{0}}g(x)}, если все члены существуют.

Обобщенное понятие предела последовательности

Пусть X{\displaystyle X} — некоторое множество, в котором определено понятие окрестности U{\displaystyle U} (например, метрическое пространство). Пусть xi∈X{\displaystyle x_{i}\in X} — последовательность точек (элементов) этого пространства. Говорят, что x∈X{\displaystyle x\in X} есть предел этой последовательности, если в любой окрестности точки x{\displaystyle x} лежат почти все члены последовательности то есть ∀U(x)∃n∀i>nxi∈U(x){\displaystyle \forall U(x)\exists n\forall i>nx_{i}\in U(x)}

См. также

Примечания

1. ↑ А.Г. Цыпкин. Справочник по математике, 1983, Москва «Наука».

wiki2.red

Предел (математика) Википедия

У этого термина существуют и другие значения, см. Предел.

Преде́л — одно из основных понятий математического анализа. Различают предел последовательности и предел функции.

Понятие предела на интуитивном уровне использовалось ещё во второй половине XVII века Ньютоном, а также математиками XVIII века, такими как Эйлер и Лагранж. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.

История[ | ]

Основной источник: ^[1]

Интуитивное понятие о предельном переходе использовалось еще учеными Древней Греции при вычислении площадей и объемов различных геометрических фигур. Методы решения таких задач в основном были развиты Архимедом.

При создании дифференциального и интегрального исчислений математики XVII века (и, прежде всего, Ньютон) также явно или неявно использовали понятие предельного перехода. Впервые определение понятия предела было введено в работе Валлиса «Арифметика бесконечных величин» (XVII век), однако исторически это понятие не лежало в основе дифференциального и интегрального исчислений.

Лишь в XIX веке в работах Коши теория пределов была использована для строгого обоснования математического анализа. Дальнейшей разработкой теории пределов занимались Вейерштрасс и Больцано.

С помощью теории пределов во второй половине XIX века было, в частности, обосновано использование в анализе бесконечных рядов, которые явились удобным аппаратом для построения новых функций.

Предел последовательности[ | ]

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.

Число a{\displaystyle a} называется пределом последовательности x1,x2,…,xn,…{\displaystyle x_{1},x_{2},…,x_{n},…} , если

∀{\displaystyle \forall } ε>0{\displaystyle \varepsilon >0} , ∃{\displaystyle \exists } N(ε){\displaystyle N(\varepsilon )}

ru-wiki.ru

Предел (математика) Википедия

У этого термина существуют и другие значения, см. Предел.

Преде́л — одно из основных понятий математического анализа. Различают предел последовательности и предел функции.

Понятие предела на интуитивном уровне использовалось ещё во второй половине XVII века Ньютоном, а также математиками XVIII века, такими как Эйлер и Лагранж. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.

История

Основной источник: ^[1]

Интуитивное понятие о предельном переходе использовалось еще учеными Древней Греции при вычислении площадей и объемов различных геометрических фигур. Методы решения таких задач в основном были развиты Архимедом.

При создании дифференциального и интегрального исчислений математики XVII века (и, прежде всего, Ньютон) также явно или неявно использовали понятие предельного перехода. Впервые определение понятия предела было введено в работе Валлиса «Арифметика бесконечных величин» (XVII век), однако исторически это понятие не лежало в основе дифференциального и интегрального исчислений.

Лишь в XIX веке в работах Коши теория пределов была использована для строгого обоснования математического анализа. Дальнейшей разработкой теории пределов занимались Вейерштрасс и Больцано.

С помощью теории пределов во второй половине XIX века было, в частности, обосновано использование в анализе бесконечных рядов, которые явились удобным аппаратом для построения новых функций.

Предел последовательности

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.

Число a{\displaystyle a} называется пределом последовательности x1,x2,…,xn,…{\displaystyle x_{1},x_{2},…,x_{n},…} , если

∀{\displaystyle \forall } ε>0{\displaystyle \varepsilon >0} , ∃{\displaystyle \exists } N(ε){\displaystyle N(\varepsilon )} , ∀{\displaystyle \forall } n>N(ε){\displaystyle n>N(\varepsilon )}: |xn−a|<ε{\displaystyle |x_{n}-a|<\varepsilon }.

Предел последовательности обозначается limn→+∞xn{\displaystyle \lim _{n\to +\infty }x_{n}}. Куда именно стремится n{\displaystyle n}, можно не указывать, поскольку n{\displaystyle n} ∈N{\displaystyle \in \mathbb {N} }, оно может стремиться только к +∞{\displaystyle +\infty }.

Свойства:

Предел функции

График функции, предел которой при аргументе, стремящемся к бесконечности, равен L{\displaystyle L}.

Функция f(x){\displaystyle f(x)} имеет предел A{\displaystyle A} в точке x0{\displaystyle x_{0}}, если для всех значений x{\displaystyle x}, достаточно близких к x0{\displaystyle x_{0}}, значение f(x){\displaystyle f(x)} близко к A{\displaystyle A}.

Число b называется пределом функции f(x) в точке a, если ∀ε>0{\displaystyle \forall \varepsilon >0} существует δ>0{\displaystyle \delta >0}, такое что ∀x,0<|x−a|<δ{\displaystyle \forall x,0<|x-a|<\delta } выполняется |f(x)−b|<ε{\displaystyle |f(x)-b|<\varepsilon }.

Для пределов функций справедливы аналогичные свойства, как и для пределов последовательностей, например, limx→x0(f(x)+g(x))=limx→x0f(x)+limx→x0g(x){\displaystyle \lim _{x\to x_{0}}(f(x)+g(x))=\lim _{x\to x_{0}}f(x)+\lim _{x\to x_{0}}g(x)}, если все члены существуют.

Обобщенное понятие предела последовательности

Пусть X{\displaystyle X} — некоторое множество, в котором определено понятие окрестности U{\displaystyle U} (например, метрическое пространство). Пусть xi∈X{\displaystyle x_{i}\in X} — последовательность точек (элементов) этого пространства. Говорят, что x∈X{\displaystyle x\in X} есть предел этой последовательности, если в любой окрестности точки x{\displaystyle x} лежат почти все члены последовательности то есть ∀U(x)∃n∀i>nxi∈U(x){\displaystyle \forall U(x)\exists n\forall i>nx_{i}\in U(x)}

См. также

Примечания

1. ↑ А.Г. Цыпкин. Справочник по математике, 1983, Москва «Наука».

wikiredia.ru

---