Решение интегралов 1 рода решение – .
Криволинейный интеграл первого рода | Вычисление криволинейный интеграл 1 рода
Определение: Пусть в каждой точки гладкой кривой L = AB в плоскости Oxy задана непрерывная функция двух переменных f(x,y). Произвольно разобьем кривую L на n частей точками A = М0, М1, М2, … Мn = B. Затем на каждой из полученных частей выберем любую точку и составим сумму
где — дуга дуги . Полученная сумма называется интегральной суммой первого рода для функции f(x,y), заданой на кривой L.
Обозначим через d наибольшую из длин дуг (таким образом, d = ). Если при d ? 0 существует предел интегральных сумм Sn (не зависящих от способа разбиения кривой L на части и выбора точек ), то этот предел называется криволинейным интегралом первого порядка от функции f(x,y) по кривой L и обозначается
Можно доказать, что если функция f(x,y)
Свойства криволинейного интеграла 1 рода
Криволинейный интеграл первого рода обладает свойствами, аналогичными соответствующим свойства определеннного интеграла:
- аддитивность,
- линейность,
- оценка модуля,
- теорема о среднем.
Однако есть отличие:
т.е. криволинейный интеграл первого рода не зависит от направления интегрирования.
Вычисление криволинейных интегралов первого рода
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла. А именно:
- Если кривая L задана непрерывно дифференцируемой функцией y=y(x), x [a,b], то
при этом выражение называется дифференциалом длины дуги.
- Если крива L задана параметрически, т.е. в виде x=x(t), y=y(t), где x(t), y(t) — непрерывно дифференцируемые функции на некотором отрезке , то
Это равенство распространяется на случай пространственной кривой L, заданной параметрически: x=x(t), y=y(t), z=z(t), . В этом случае, если f(x,y,z) — непрерывная функция вдоль кривой L, то
- Если плоская кривая L задана полярным уравнением r=r( ), , то
Криволинейные интегралы 1 рода — примеры
Пример 1
Вычислить криволинейный интеграл первого рода
где L дуга параболы y2=2x, заключенная между точками (2,2) и (8,4).
Решение: Найдем дифференциал дуги dl для кривой . Имеем:
Следовательно данный интеграл равен:
Пример 2
Вычислить криволинейный интеграл первого рода , где L — окружность x2+y2=ax (a>0).
Решение: Введем полярные координаты: , . Тогда поскольку x2+y2=r2, уравнение окружности имеет вид: , то есть , а дифференциал дуги
.
При этом . Следовательно,
15. Несобственные интегралы. Несобственные интегралы первого рода
Выше был определён интеграл для ограниченных и заданных на ограниченном отрезке функций. Распространим понятие интеграла на случаи, когда одно или оба этих условия нарушаются.
Определение. Пусть задана на бесконечном промежутке и для всякого существует интеграл Предел называется несобственным интегралом первого рода (интегралом по неограниченному промежутку) и обозначается Если существует и конечен, то несобственный интеграл первого рода называется сходящимся, если же он не существует или равен Бесконечности, то несобственный интеграл первого рода называется расходящимся.
Примеры.
1. Рассмотрим . Пусть Тогда Таким образом, рассмотренный интеграл при расходится. Пусть теперь Тогда
И мы окончательно получили, что рассматриваемый интеграл при расходится и при сходится. Этот интеграл часто используется в признаке сравнения в качестве эталонного.
2. Выясним сходимость интеграла .
Имеем
. Следовательно, интеграл сходится и его значение равно .
3. Выяснить сходимость интеграла . По определению получаем
.
Следовательно, интеграл сходится и его значение равно .
4. Для интеграла имеем
.
Следовательно, интеграл расходится.
5. Для интеграла по определению имеем
.
Следовательно, интеграл сходится и его значение равно 1.
6. Выяснить сходимость интеграла , .
По определению
Следовательно, интеграл сходится и его значение равно .
Задание 2.4
Вычислить несобственные интегралы первого рода или доказать их расходимость.
1. ; 2.; 3. ; 4. ;
5. ; 6. .
Ответы: 1. ; 2. расходится; 3. ; 4. расходится; 5. расходится; 6. .
Нам в дальнейшем понадобится следующий важный результат.
Теорема 2.8. (Критерий Коши). Несобственный интеграл первого рода сходится тогда и только тогда, когда для всякого существует Такое, что для всех выполнено неравенство
Доказательство этого результата опустим.
Определение. Несобственный интеграл первого рода называется абсолютно сходящимся, если сходится интеграл
Отметим, что если несобственный интеграл первого рода сходится абсолютно, то он сходится. Действительно, тогда для интеграла выполнен критерий Коши, а в силу справедливости неравенства , критерий Коши выполнен и для интеграла
Обратное утверждение неверно.
Сходимость несобственного интеграла определяется аналогично. Предлагается проделать это самостоятельно.
Для несобственного интеграла можем записать и назвать этот интеграл сходящимся, если сходятся оба слагаемых. Если хотя бы один из этих интегралов расходится, то будем считать интеграл расходящимся. В качестве точки выбирают обычно 0.
Пример. Рассмотрим интеграл По определению сходимости этого интеграла получаем
Так как оба слагаемых расходятся, то исходный интеграл расходится. Получаемая при этом неопределённость при разных скоростях стремления к и к даёт разные результаты. В частности, если , , то
.
Если , , то абсолютно аналогично показывается, что этот предел равен . Подобрав скорости стремления к и к можно получить в пределе любое заранее заданное число от до .
С другой стороны, при согласованном стремлении верхнего и нижнего пределов к можем записать
Это дает возможность ввести новое понятие.
Определение. Говорят, что несобственный интеграл первого рода сходится в смысле главного значения Коши, если существует и конечен предел .
Рассмотренный выше пример показывает, что несобственный интеграл первого рода может сходиться в смысле главного значения Коши и расходиться в обычном смысле.
Отметим несколько свойств несобственных интегралов первого рода
1. Если интеграл сходится, то для всякого интеграл сходится и
2. Если интеграл сходится, то сходится интеграл и имеет место равенство
3. Если интегралы и сходятся, то сходятся интегралы и имеет место равенство
Обратное утверждение неверно, то есть, если интеграл от алгебраической суммы функций сходится, то интегралы от слагаемых сходиться не обязаны. Например, интегралы и расходятся, а интеграл , как будет показано позднее, сходится.
Для других типов несобственных интегралов первого рода свойства аналогичны.
Сходимость не всех несобственных интегралов первого рода просто выяснить по определению. Поэтому часто используют так называемые признаки сравнения в непредельной и предельной формах.
Теорема 2.9. Пусть для всякого Выполнено неравенство . Тогда, если интеграл абсолютно сходится, то интеграл абсолютно сходится, а если интеграл абсолютно расходится, то интеграл абсолютно расходится.
Доказательство. Действительно, в условиях теоремы для всех имеем . Тогда, если интеграл сходится, то есть монотонно возрастающая ограниченная сверху функция от и поэтому имеет предел при . Если интеграл расходится, то и поэтому .
Теорема 2.10. Если и – бесконечно малые в одного порядка малости, то есть , то интегралы И либо оба абсолютно сходятся, либо оба абсолютно расходятся.
Доказательство. Так как , то . Возьмем . По определению предела существует такое, что для всех выполнено неравенство а, следовательно, и неравенство Из последнего неравенства и теоремы 2.9 получаем утверждение теоремы.
Замечание. После изучения теоремы 2.10 может сложиться впечатление, что для сходимости несобственного интеграла первого рода, в том числе и абсолютной, необходимо, чтобы подынтегральная функция была бесконечно малой при . То, что это не так, показывает следующий пример [15].
Возьмем функцию, график которой состоит из отрезков прямых, соединяющих точки , , , . Ее аналитическое выражение имеет вид
Площадь, заключенная между графиком этой функции и осью , равна сумме площадей треугольников с вершинами в точках , , , . Так как площадь каждого такого треугольника равна , , то . Заметим, что условие ограниченности функции несущественно, так как вершины треугольников можно взять, например, в точках , , , ..
Примеры
1. Выяснить сходимость интеграла
Так как для всех а интеграл сходится, то и исходный интеграл тоже сходится.
2. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 2 и так как сходится, то исходный интеграл сходится.
3. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 1,5 и так как сходится, то исходный интеграл сходится.
4. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен И, следовательно, интеграл сходится.
5. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 1,5 и, следовательно, интеграл сходится.
6. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 0,5 и, следовательно, интеграл расходится.
7. Интеграл сходится, так как имеет место оценка для всех , а интеграл , как было показано ранее, сходящийся.
8. Интеграл расходится, так как имеет место оценка для всех , а интеграл, как было показано ранее, расходится.
Задание 2.5
Используя признак сравнения выяснить сходимость несобственных интегралов. В ответе указана сходимость и порядок малости подынтегральной функции относительно .
1. ; 2. ; 3. ; 4. ; 5. ; 6. .
Ответы: 1. сходится, ; 2. сходится, ;
3. расходится, ; 4. сходится, ; 5. сходится, ;
6. сходится, ;
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Вычисление поверхностных интегралов: теория и примеры
Поверхностный интеграл – обобщение понятия криволинейного интеграла на случаи, когда интегрирование происходит не по отрезку кривой, а по ограниченной поверхности. Как и криволинейные интегралы, поверхностные интегралы бывают первого рода и второго рода.
Поверхностный интеграл первого рода записывается в виде
,
где f(M) = f(x,y,z) – функция трёх переменных, а поверхность σ – область интегрирования этой функции. Если f(x,y,z) равна единице, то поверхностный интеграл равен площади поверхности.
Представьте себе довольно большой подсолнух с очень-очень маленькими семечками. Тогда по сумме поверхностей очень-очень маленьких семечек, расположенных на поверхности подсолнуха, можно вычислить поверхность подсолнуха – таким может быть упрощённое толкование поверхностного интеграла. Почему так?
Давайте перейдём к более формальному определению поверхностного интеграла. Поверхность σ разбита на n частей с площадями Δσ1, Δσ2, …, Δσn. Если выбрать на каждой частичной поверхности (семечке) произвольную точку Mi с координатами (ζi, ηi, ςi,), то можно составить сумму
.
Эта сумма называется интегральной суммой для функции f(M) по поверхности σ. Теперь будем максимально увеличивать число таких маленьких частей, а наибольший диаметр Δσi – наоборот, уменьшать. Если интегральная сумма при стремлении наибольшего из диаметров частей к нулю (то есть, как мы уже отмечали, все части очень маленькие) имеет предел, то этот предел и называется поверхностным интегралом первого рода от функции f(M) по поверхности σ.
Вычисление поверхностного интеграла первого рода производится сводением к двойному интегралу.
Пусть поверхность σ задана уравнением z = z(x, y), её проекцией на плоскость xOy является область Dxy, при этом функция z = z(x, y) и её частные производные и непрерывны в области Dxy.
Тогда
Это и есть формула, выражающая поверхностный интеграл первого рода через двойной интеграл по проекции поверхности σ на плоскость xOy.
Пример 1. Вычислить поверхностный интеграл первого рода
где σ – часть плоскости в первом октанте.
Решение. Чертёж:
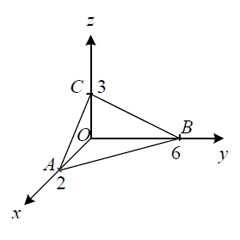
Из уравнения плоскости получаем выражение “зет”: .
Тогда частные производные: , и
.
Поверхность σ является изображённым на чертеже треугольником ABC, а его проекцией на плоскость xOy – треугольником AOB, который ограничен прямыми x = 0, y = 0 и 3x + y = 6. От поверхностного интеграла перейдём к двойному интегралу и решим его:
.
Прежде чем перейти к определению поверхностного интеграла второго рода, требуется познакомиться с понятиями стороны поверхностей и ориентированных поверхностей.
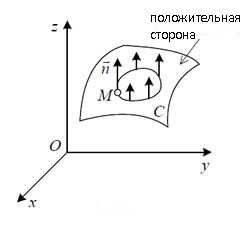
Пусть в пространстве дана гладкая поверхность σ. На этой поверхности выберем произвольную точку M и проведём через неё вектор нормали к поверхности. Через точку M проведём также на поверхности σ произвольный контур, не имеющий общих точек с границей поверхности σ. Точку M вместе с вектором нормали будем перемещать по контуру так, чтобы вектор нормали постоянно был перпендикулярен поверхности σ. По возвращении точки M в начальное положение возможны два случая: направление вектора нормали сохранится или же поменяется на противоположное.
Если направление вектора нормали не поменяется, то поверхность σ называется двусторонней. Если же при обходе контура направление вектора нормали поменяется на противоположное, то поверхность называется односторонней. Двусторонние поверхности называются ориентированными поверхностями, односторонние – неориентированными поверхностями.
Пример односторонней поверхности – лист Мёбиуса (на рисунке выше), который можно сделать из полоски бумаги, одна сторона которой повёрнута на 180 градусов, и затем концы склеены. И вот что здесь важно: для односторонней поверхности понятие поверхностного интеграла второго рода не вводится.
Так что будем рассматривать только двусторонние поверхности. Примеры двусторонних поверхностей – плоскости, сфера, эллипсоил, параболоид.
Положительную сторону двустороней поверхности определяет направление вектора нормали. Противоположная сторона поверхности называется отрицательной. Положительной стороной поверхности называется её верхняя сторона. Если единичные векторы нормали составляют острые углы с осью Oz, то выбрана верхняя сторона поверхности z = z(x, y), если углы тупые, то нижняя сторона поверхности.
Как и в случае поверхностного интеграла первого рода, поверхность можно разбить на n частей. При формулировке понятия поверхностного интеграла первого рода в интегральной сумме присутствовали площади каждой из частей, на которые умножаются значения функции f(Mi). В случае поверхностного интеграла второго рода берутся площади не самих частей, а площади их проекций на координатные плоскости. А функцию трёх переменных для отличия от интеграла первого рода обозначим R(x,y,z). Тогда интегральная сумма запишется так:
,
где Δsi – площади упомянутых проекций частей стороны поверхности на координатную ось (пока будем считать, что на ось xOy).
При таких соглашениях и обозначениях определение поверхностного интеграла второго рода аналогично определению интеграла первого рода. А именно: поверхностным интегралом второго рода называется предел данной интегральной суммы при стремлении к нулю наибольшего из диаметров частей рассматриваемой поверхности.
Записывается он так:
.
В данном случае функция R(x,y,z) интегрируема по переменным x и y, так как части поверхности проецировались на плоскость xOy.
Аналогично можно записать и два других поверхностных интеграла второго рода:
(функция P(x,y,z) интегрируема по переменным y и z, так как части поверхности проецируются на плоскость yOz),
(функция Q(x,y,z) интегрируема по переменным z и x, так как части поверхности проецируются на плоскость zOx).
Сумма этих интегралов
называется общим поверхностным интегралом второго рода и обозначается
Поверхностный интеграл второго рода вычисляется путём разложения общего поверхностного интеграла второго рода на сумму поверхностных интегралов (см. окончание предыдущего параграфа) и сведением каждого из них к двойному интегралу.
Рассмотрим подробно вычисление интеграла
.
Пусть поверхность σ задана уравнением z = z(x, y). Положительную сторону поверхности обозначим , отрицателную , а проекцию на плоскость xOy – Dxy.
Таким образом, получаем формулу для вычисления поверхностного интеграла второго рода:
.
Если выбрана отрицательная сторона поверхности, то знак интеграла меняется:
.
Аналогично вычисляются два других отдельных интеграла – слагаемых общего:
,
.
Пример 2. Вычислить поверхностный интеграл второго рода
,
где σ – верхняя сторона части плоскости , отсечённая плоскостями y = 0 и y = 4 и находящаяся в первом октанте.
Решение. Чертёж – на рисунке сверху. По определению получаем сумму трёх двойных интегралов:
Второй интеграл равен нулю, так как плоскость σ параллельна оси Oy. Поэтому найдём первый и третий интегралы:
Остаётся лишь сложить все отдельные интегралы и получить общий поверхностный интеграл второго рода:
.
Если требуется вычислить поверхностный интеграл второго рода по замкнутой поверхности, можно перейти к тройному интегралу, используя формулу Остроградского. Тогда, если функции P(x,y,z), Q(x,y,z) и R(x,y,z) и их частные производные , , – непрерывные функции в области W, которую ограничивает замкнутая поверхность σ, то при интегрировании по внешней стороне поверхности в силе равенство
Пример 4. Вычислить поверхностный интеграл первого рода
,
где σ – боковая поверхность конуса при .
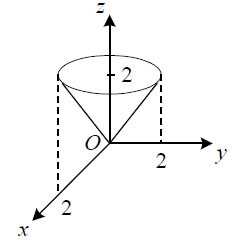
Решение. Так как частные производные , , то
Сводим данный поверхностный интеграл к двойному:
.
Проекцией поверхности на плоскость xOy является круг с центром в начале координат и радиусом R = 2, поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:
Получаем следующий интеграл, который окончательно и решаем:
Пример 5. Вычислить поверхностный интеграл второго рода
,
где σ – верхняя часть треугольника, образованного пересечением плоскости с координатными плоскостями.
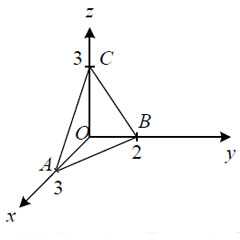
Решение. Данный поверхностный интеграл разделим на сумму двух интегралов
, где
,
.
Чтобы вычислить интеграл I1, построим проекцию поверхности σ на плоскость yOz. Проекцией является треугольник OCB, который на плоскости yOz ограничивают прямые или , y = 0 и z = 0. Из уравнения плоскости выводится . Поэтому можем вычислить интеграл I1:
Чтобы вычислить интеграл I2, построим проекцию поверхности σ на плоскость zOx. Проекцией является треугольник AOC, который ограничивают прямые или , x = 0 и z = 0. Вычисляем:
Складываем два полученных интеграла и окончательно получаем данный поверхностный интеграл:
.
Пример 6. Вычислить поверхностный интеграл второго рода
,
где σ – внешняя поверхность пирамиды, образованной плоскостью и координатными плоскостями.
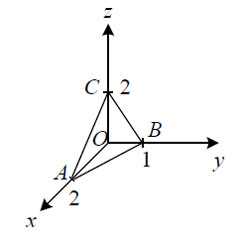
Решение. Данный поверхностный интеграл вычислим двумя способами
1) интегрируя по каждой грани пирамиды;
2) используя формулу Остроградского.
1) Вычисление интегрированием по каждой грани пирамиды.
а) Вычислим интеграл по треугольнику ABC. Для этого разделим интеграл на сумму трёх интегралов, которые отдельно решим:
;
Складываем и получаем:
.
б) Вычислим поверхностный интеграл по треугольнику AOB, который находится в плоскости z = 0. Тогда dz = 0 и, учитывая, что нормальный вектор плоскости образует с осью Oz тупой угол, получаем
в) Треугольник AOC находится в плоскости y = 0, таким образом, dy = 0 и (нормальный вектор плоскости образует с осью Oy тупой угол) получаем
г) Осталось вычислить поверхностный интеграл по треугольнику CBO находится в плоскости x = 0, таким образом, dx = 0 и получаем
.
В результате получаем данный поверхностный интеграл второго рода:
.
2) Используя формулу Остроградского, от поверхностного интеграла по замкнутой поверхности перейдём к тройному интегралу, где W – область, ограниченная поверхностью σ. Так как P = xz, Q = 1, R = 2y, то частные производные , , .
Получаем следующее решение данного поверхностного интеграла:
В последнем примере вернёмся к вычислению поверхностного интеграла первого рода.
Пример 7. Вычислить площадь поверхности параболоида во внутренней части сферы .
Решение. Определим, при каком значении z данные поверхности пересекаются:
Значение −3 не подходит, поэтому остаётся только z = 1.
Обозначим через C часть поверхности данного параболоида во внутреней стороне сферы. Проекция поверхности C (обозначим её D) на плоскость xOy является кругом с центром в начале координат и радиусом √2, так как при z = 1 получаем уравнение окружности . Решаем поверхностный интеграл первого рода:
.
Так как
то
.
Проекцией поверхности на плоскость xOy является круг, поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:
Получаем окончательное решение данного поверхностного интеграла:
Кратные и криволинейные интегралы
Поделиться с друзьями
function-x.ru
МА. Криволинейные интегралы первого рода и поверхностные интегралы первого рода
Теоретический минимумКриволинейные и поверхностные интегралы часто встречаются в физике. Они бывают двух видов, первый из которых рассматривается здесь. Этот
тип интегралов строится согласно общей схеме, по которой вводятся определённые, двойные и тройные интегралы. Коротко напомним эту схему.
Имеется некоторый объект, по которому проводится интегрирование (одномерный, двумерный или трёхмерный). Этот объект разбивается на малые части,
в каждой из частей выбирается точка. В каждой из этих точек вычисляется значение подынтегральной функции и умножается на меру той части, которой
принадлежит данная точка (длину отрезка, площадь или объём частичной области). Затем все такие произведения суммируются, и выполняется предельный
переход к разбиению объекта на бесконечно малые части. Получающийся предел и называется интегралом.
1. Определение криволинейного интеграла первого рода
Рассмотрим функцию , определённую на кривой . Кривая предполагается спрямляемой. Напомним, что это означает, грубо говоря,
что в кривую можно вписать ломаную со сколь угодно малыми звеньями, причём в пределе бесконечно большого числа звеньев длина ломаной должна оставаться
конечной. Кривая разбивается на частичные дуги длиной и на каждой из дуг выбирается точка . Составляется произведение ,
проводится суммирование по всем частичным дугам . Затем осуществляется предельный переход с устремлением длины наибольшей
из частичных дуг к нулю. Предел является криволинейным интегралом первого рода
.
Важной особенностью этого интеграла, прямо следующей из его определения, является независимость от направления интегрирования, т.е.
.
2. Определение поверхностного интеграла первого рода
Рассмотрим функцию , определённую на гладкой или кусочно-гладкой поверхности . Поверхность разбивается на частичные области
с площадями , в каждой такой области выбирается точка . Составляется произведение , проводится суммирование
по всем частичным областям . Затем осуществляется предельный переход с устремлением диаметра наибольшей из всех частичных
областей к нулю. Предел является поверхностным интегралом первого рода
.
3. Вычисление криволинейного интеграла первого рода
Методика вычисления криволинейного интеграла первого рода просматривается уже из формальной его записи, а фактически следует непосредственно из
определения. Интеграл сводится к определённому, только нужно записать дифференциал дуги кривой, вдоль которой проводится интегрирование.
Начнём с простого случая интегрирования вдоль плоской кривой, заданной явным уравнением . В этом случае дифференциал дуги
.
Затем в подынтегральной функции выполняется замена переменной , и интеграл принимает вид
,
где отрезок отвечает изменению переменной вдоль той части кривой, по которой проводится интегрирование.
Очень часто кривая задаётся параметрически, т.е. уравнениями вида . Тогда дифференциал дуги
.
Формула эта очень просто обосновывается. По сути, это теорема Пифагора. Дифференциал дуги – фактически длина бесконечно малой части кривой.
Если кривая гладкая, то её бесконечно малую часть можно считать прямолинейной. Для прямой имеет место соотношение
.
Чтобы оно выполнялось для малой дуги кривой, следует от конечных приращений перейти к дифференциалам:
.
Если кривая задана параметрически, то дифференциалы просто вычисляются:
и т.д.
Соответственно, после замены переменных в подынтегральной функции криволинейный интеграл вычисляется следующим образом:
,
где части кривой, по которой проводится интегрирование соответствует отрезок изменения параметра .
Несколько сложнее обстоит дело в случае, когда кривая задаётся в криволинейных координатах. Этот вопрос обычно обсуждается в рамках дифференциальной
геометрии. Приведём формулу для вычисления интеграла вдоль кривой, заданной в полярных координатах уравнением :
.
Приведём обоснование и для дифференциала дуги в полярных координатах. Подробное обсуждение построения координатной сетки полярной системы координат
см. здесь. Выделим малую дугу кривой, расположенную по отношению к координатным линиям так, как показано на рис. 1. В силу малости всех фигурирующих
дуг снова можно применить теорему Пифагора и записать:
.
Отсюда и следует искомое выражение для дифференциала дуги.
С чисто теоретической точки зрения достаточно просто понять, что криволинейный интеграл первого рода должен сводиться к своему частному случаю –
определённому интегралу. Действительно, выполняя замену, которая диктуется параметризацией кривой, вдоль которой вычисляется интеграл, мы устанавливаем
взаимно-однозначное отображение между частью данной кривой и отрезком изменения параметра . А это и есть сведение к интегралу
вдоль прямой, совпадающей с координатной осью – определённому интегралу.
4. Вычисление поверхностного интеграла первого рода
После предыдущего пункта должно быть ясно, что одна из основных частей вычисления поверхностного интеграла первого рода – запись элемента поверхности ,
по которой выполняется интегрирование. Опять-таки начнём с простого случая поверхности, заданной явным уравнением . Тогда
.
Выполняется замена в подынтегральной функции, и поверхностный интеграл сводится к двойному:
,
где – область плоскости , в которую проектируется часть поверхности, по которой проводится интегрирование.
Однако часто задать поверхность явным уравнением невозможно, и тогда она задаётся параметрически, т.е. уравнениями вида
.
Элемент поверхности в этом случае записывается уже сложнее:
.
Соответствующим образом записывается и поверхностный интеграл:
,
где – область изменения параметров, соответствующая части поверхности , по которой проводится интегрирование.
5. Физический смысл криволинейного и поверхностного интегралов первого рода
Обсуждаемые интегралы обладают очень простым и наглядным физическим смыслом. Пусть имеется некоторая кривая, линейная плотность которой не является
константой, а представляет собой функцию точки . Найдём массу этой кривой. Разобьём кривую на множество малых элементов,
в пределах которых её плотность можно приближённо считать константой. Если длина маленького кусочка кривой равна , то его масса
, где – любая точка выбранного кусочка кривой (любая, так как плотность в пределах
этого кусочка приближённо предполагается постоянной). Соответственно, масса всей кривой получится суммированием масс отдельных её частей:
.
Чтобы равенство стало точным, следует перейти к пределу разбиения кривой на бесконечно малые части, но это и есть криволинейный интеграл первого рода.
Аналогично разрешается вопрос о полном заряде кривой, если известна линейная плотность заряда .
Эти рассуждения легко переносятся на случай неравномерно заряженной поверхности с поверхностной плотностью заряда . Тогда
заряд поверхности есть поверхностный интеграл первого рода
.
Замечание. Громоздкая формула для элемента поверхности, заданной параметрически, неудобна для запоминания. Другое выражение получается в дифференциальной геометрии,
оно использует т.н. первую квадратичную форму поверхности.
Примеры вычисления криволинейных интегралов первого рода
Пример 1. Интеграл вдоль прямой.
Вычислить интеграл
вдоль отрезка прямой, проходящей через точки и .
Сначала запишем уравнение прямой, вдоль которой проводится интегрирование: . Найдём выражение для :
.
Вычисляем интеграл:
Пример 2. Интеграл вдоль кривой на плоскости.
Вычислить интеграл
по дуге параболы от точки до точки .
Заданные точки и позволяют выразить переменную из уравнения параболы: .
Вычисляем интеграл:
.
Однако можно было проводить вычисления и иначе, пользуясь тем, что кривая задана уравнением, разрешённым относительно переменной .
Если принять переменную за параметр, то это приведёт к небольшому изменению выражения для дифференциала дуги:
.
Соответственно, интеграл несколько изменится:
.
Этот интеграл легко вычисляется подведением переменной под дифференциал. Получится такой же интеграл, как и в первом способе вычисления.
Пример 3. Интеграл вдоль кривой на плоскости (использование параметризации).
Вычислить интеграл
вдоль верхней половины окружности .
Можно, конечно, выразить из уравнения окружности одну из переменных, а затем провести остальные вычисления стандартно. Но можно использовать и
параметрическое задание кривой. Как известно, окружность можно задать уравнениями . Верхней полуокружности
отвечает изменение параметра в пределах . Вычислим дифференциал дуги:
.
Таким образом,
Пример 4. Интеграл вдоль кривой на плоскости, заданной в полярных координатах.
Вычислить интеграл
вдоль правого лепестка лемнискаты .
На чертеже выше изображена лемниската. Вдоль её правого лепестка нужно проводить интегрирование. Найдём дифференциал дуги для кривой :
.
Следующий шаг – определение пределов интегрирования по полярному углу. Ясно, что должно выполняться неравенство , а потому
.
Вычисляем интеграл:
Пример 5. Интеграл вдоль кривой в пространстве.
Вычислить интеграл
вдоль витка винтовой линии , соответствующего пределам изменения параметра .
Вычисляем дифференциал дуги:
.
Подставляем в интеграл:
.
Примеры вычисления поверхностных интегралов первого рода
Пример 6. Интеграл по поверхности, заданной явно.
Вычислить интеграл
по поверхности тела .
Поверхность интегрирования состоит из двух частей: части плоскости , которую обозначим и поверхности , заданной
уравнением . Эта поверхность представляет собой верхнюю половину конуса второго порядка. Проекция той её части,
по которой проводится интегрирование, на плоскость представляет собой круг, ограниченный окружностью .
Запишем элемент поверхности:
.
Таким образом, поверхностный интеграл сводится к следующему двойному:
где – круг . Такой интеграл проще всего вычислять в полярных координатах:
.
Теперь интегрируем по плоскости . Это совсем простое интегрирование, так как поверхностный интеграл сразу превращается
в двойной без каких-либо дополнительных вычислений. Он будет отличаться только множителем от только что вычисленного.
Окончательный ответ получается суммированием двух вычисленных интегралов:
.
Пример 7. Интеграл по сфере.
Вычислить интеграл
по верхней полусфере .
Можно выразить явно, например, аппликату из уравнения сферы и проводить вычисления дальше, но при интегрировании по сфере удобно использовать
сферические координаты. Тем более элемент поверхности сферы в этом случае хорошо известен:
.
Осталось только выполнить замену в подынтегральной функции:
.
Пример 7. Интеграл по параметрически заданной поверхности.
Вычислить интеграл
по части поверхности геликоида , отвечающей границам изменения параметров .
Поверхность интегрирования задана параметрически, поэтому для написания элемента поверхности нужно предварительно вычислить три якобиана:
.
Таким образом, элемент поверхности
.
Следовательно, поверхностный интеграл сводится к следующему двойному:
.
Детали вычисления определённого интеграла здесь опущены: они не имеют отношения к теме. Тем более, сам интеграл достаточно простой.
corum.mephist.ru
6. Криволинейный интеграл первого рода
Пусть
на плоскости дана непрерывная простая
спрямляемая кривая 
,
вдоль которой расположены массы, причём
известна их линейная плотность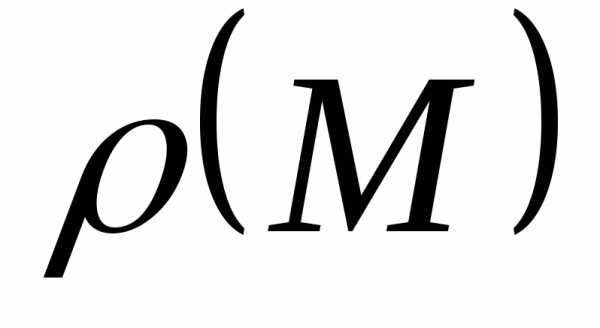
во всех точках
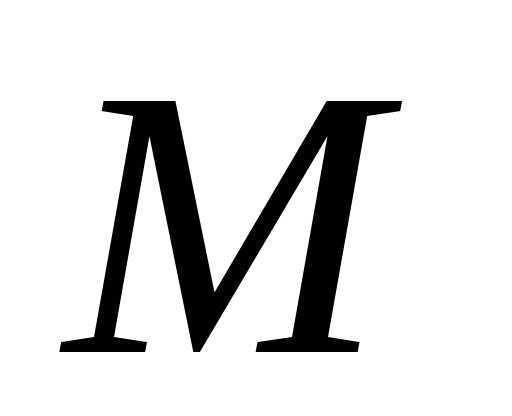кривой. Требуется определить массу
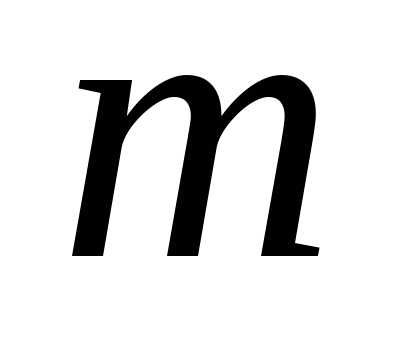всей кривой.
С
этой целью разобьём кривую на отрезки
точками
,
причем
начальная точка кривой,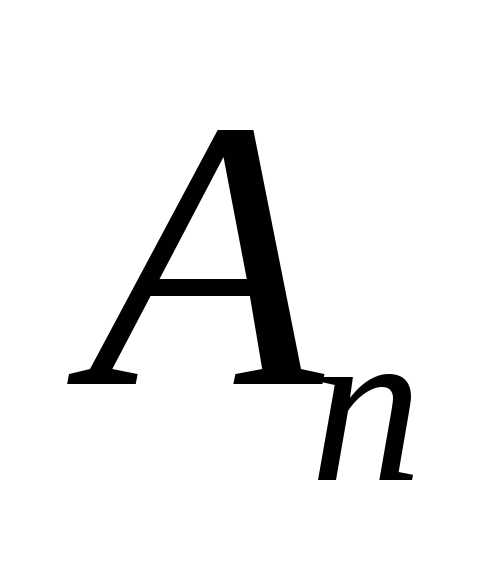 
конечная точка;
длина 
-го
отрезка кривой. Фиксируем произвольно
точку
на отрезке
и будем считать, что плотность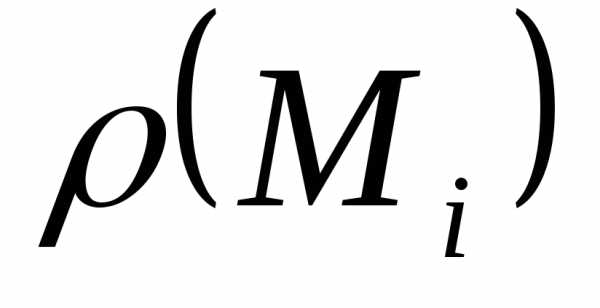
сохраняет свое значение во всех точках
отрезка.
Тогда
масса отрезка 
,
а масса всей кривой
Погрешность
последнего выражения будет стремиться
к нулю, если длины всех отрезков 
стремятся к нулю. Обозначив через
наибольшую из длин
,
точное значение массы кривой получим
в результате предельного перехода:
.
Отвлекаясь
от задачи о массе кривой, можно рассмотреть
функцию точки
,
заданную на кривой
,
и повторив рассуждения, аналогичные
проведенным выше, получить интегральную
сумму:
. (6.1)
Определение. Конечный
предел
,
если он существует для любого разбиения
кривой
на отрезки
и не зависит от выбора точек,
называется криволинейным интегралом
первого рода от функции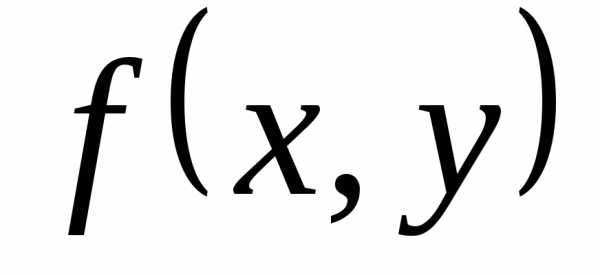
по кривой
и обозначается символом
. (6.2)
(Здесь 
есть длина дуги кривой, а
«дифференциал дуги».)
Криволинейный
интеграл первого рода по пространственной
кривой 
определяется аналогично:
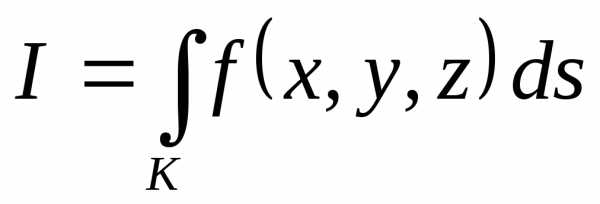. (6.3)
Свойства криволинейного интеграла первого рода
Криволинейный интеграл первого рода не зависит от выбора направления на пути интегрирования:
;
2. ;
3. .
Если путь интегрирования
разбит на части,
то
разбит на части,
то.
Рис. 6.1
Дифференциал
дуги 
приближенно
можно выразить в соответствии с теоремой
Пифагора (рис. 6.1):
для
случая кривой 
,
принадлежащей плоскости, или
для трёхмерного случая. При эти выражения становятся точными.
Пусть
кривая 
задана в параметрической форме:
,
причём,
функции 
и
непрерывны вместе со своими производными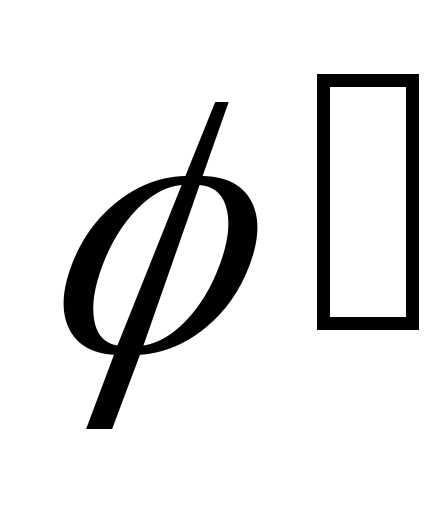
и,
то есть кривая
гладкая или кусочно-гладкая. Если кратных
точек на кривой нет, она спрямляемая.
Криволинейный интеграл (6.2) существует,
если подынтегральная функция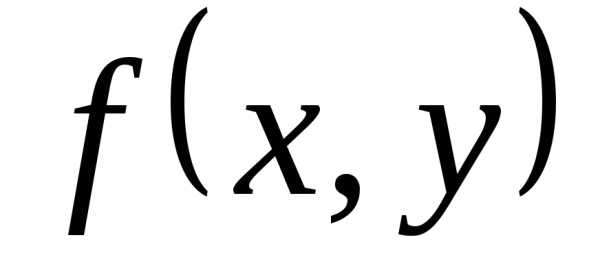 
непрерывная.
Дифференциал дуги в этом случае имеет следующий вид:
.
Подставив в интеграл (6.2), получим:
. (6.4)
В
случае кривой 
,
заданной явным уравнением в декартовых
координатах
,
формула (6.2) принимает вид:
. (6.5)
Пусть
кривая 
задана в полярных координатах:
,
тогда:
,
.
Следовательно, дифференциал дуги
,
а интеграл (6.2) принимает вид
.
Пример 6.1. Вычислить интеграл:
,
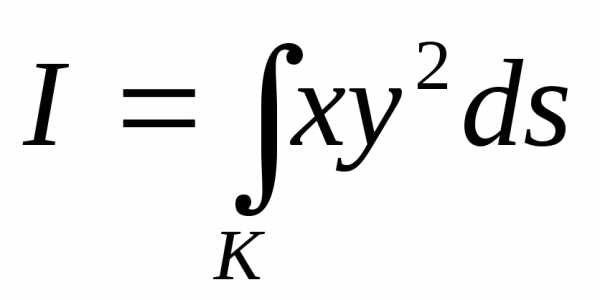если 
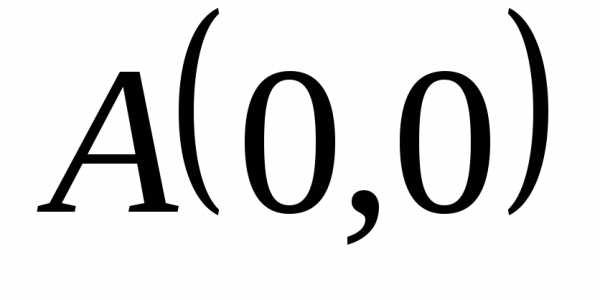отрезок прямой между точками 
и
.
Решение.
Направляющий вектор прямой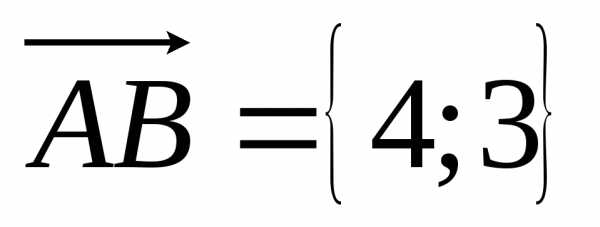 
.
Уравнение прямой
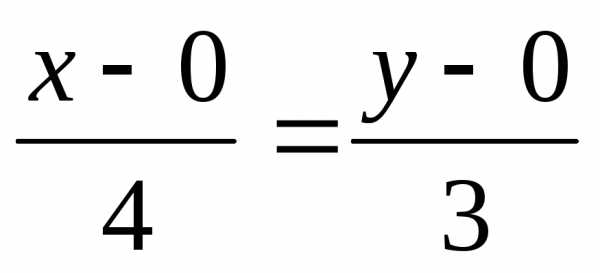или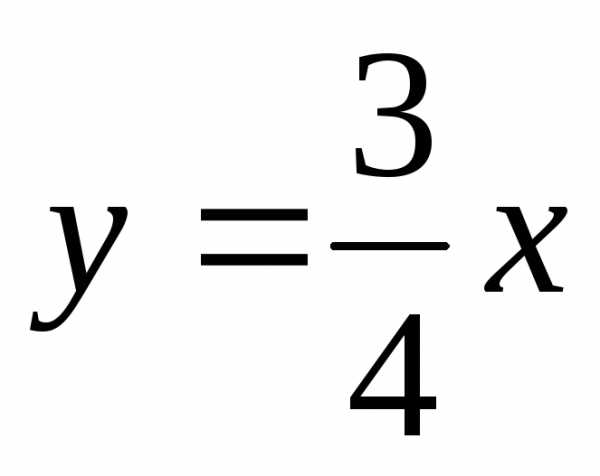 
.
Дифференциал дуги
.
.
Пример 6.2. Вычислить интеграл
,
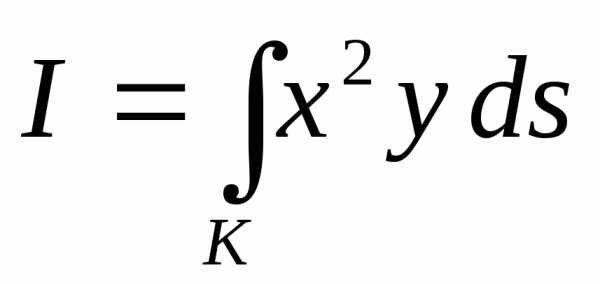если 
есть дуга окружности
,
принадлежащая первой четверти (рис. 6.2).
Решение.
.
Рис. 6.2
Подставим найденные выражения в интеграл и вычислим его:
.
Пример 6.3. Вычислить длину первой арки циклоиды:
.
(Циклоида представляет собой траекторию точки катящегося колеса, изображенную на рис. 6.3.)
Решение. Длину кривой можно найти, вычислив криволинейный интеграл
.
Рис. 6.3
Подставив в интеграл производные
получим:
.
Пример 6.4. Вычислить длину винтовой линии, заданной уравнениями
.
Решение.
.
.
Пример 6.5. Вычислить длину спирали Архимеда (рис.6.4).
от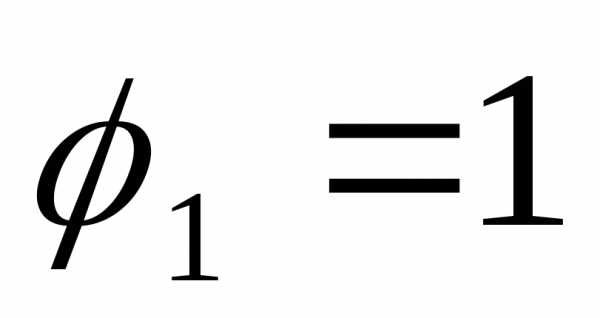 
до
.
(Угол 
здесь выражен в радианах).
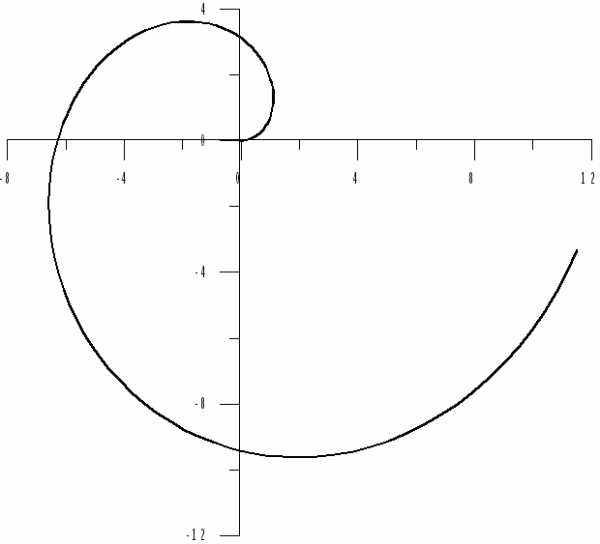
Рис. 6.4
Решение.
.
Первый интеграл в последней строке совпадает с исходным интегралом. Перенесём его влево и разделим на 2 полученный результат:
.
Решить самостоятельно: [1] № 3770, 3772, 3774, 3775, 3777.
studfiles.net
∫ Решение определённых интегралов – Калькулятор Онлайн
Введите функцию, для которой необходимо вычислить интеграл
Калькулятор предоставляет ПОДРОБНОЕ решение определённых интегралов.
Этот калькулятор находит решение определенного интеграла от функции f(x) с данными верхними и нижними пределами.
Примеры
С применением степени
(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)
Квадратный корень
sqrt(x)/(x + 1)
Кубический корень
cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
x*arcsin(x)
Арккосинус
x*arccos(x)
Применение логарифма
x*log(x, 10)
Натуральный логарифм
ln(x)/x
Экспонента
exp(x)*x
Тангенс
tg(x)*sin(x)
Котангенс
ctg(x)*cos(x)
Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)
Арктангенс
x*arctg(x)
Арккотангенс
x*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число – “Пи”, которое примерно равно 3.14
- sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- – умножение
- 3/x
- – деление
- x^3
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
www.kontrolnaya-rabota.ru
21.1. Криволинейные интегралы первого рода
Рассмотрим пространственную кусочно-гладкую кривую, ограниченную точкамиИ(рис. 21.1), и определенную на ней непрерывную функцию Где- точка кривой. ДугуРазобьем точками
НаЭлементарных дуг
Длины которых обозначим соответственно черезА
Наибольшую из этих длин-через.На каждой из элементарных дугВыберем произвольно
Одну точкуИ составим сумму
(21.1)
Называемую интегральной суммой для функции По длине дуги кривой Криволинейным интегралом первого родаили криволинейным интегралом по дуге кривойОт функцииНазывается предел интеграль – Рис – 21.1
Ной суммы (21.1) при
На кривойЦеликом лежащей на плоскостиФункцияОт координаты не зависит, поэтому по определению имеем
Если подынтегральную функциюРассматривать как линейную
Плотность кривойТо криволинейный интеграл первого рода представляет собой массу этой кривой.
Основные свойства криволинейного интеграла первого рода следующие.
1. Криволинейный интеграл первого рода не зависит от направления пути интегрирования:
4. Если йуть интегрированияРазбит на части, то
Вычисление 1фиволинейного интеграла первого рода сводится к вычислению определенного интеграла.
Если пространственная криваяЗадана параметрическими уравнениями
, то
(21.2)
Если криваяЛежит в плоскости, то
(21.3)
В частности, для плоской кривой, заданной уравнениемИмеем
(21.4)
Если плоская кривая задана уравнениемВ полярных
Координатах, то
(21.5)
Если кривая задана уравнением, то криволинейный интеграл
Вычисляется по формуле
(21.6)
Пример 21.1. Вычислить криволинейный интеграл, где
– дуга кривойМежду точками, для которых
Поскольку,И на дуге кривойФункция
, то по формуле (21.4) находим
Пример 21.2. ВычислитьГде- дуга кривой
Между точками, для которых
Применяем формулу (2J.6). В данном случае
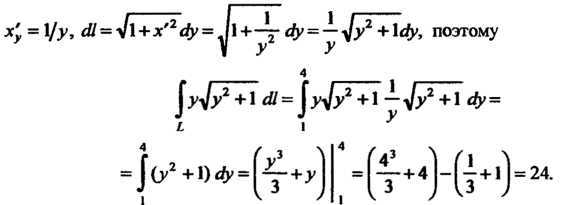
Пр имер 21.3. Вычислить криволинейный интегралГде-
Контур треугольника(рис. 21.2) с вершинами
В соответствии со свойством 4) криволинейного интегра первого рода имеем
На отрезкеПоэтому
На отрезкеНа отрезке
Принимая во внимание свойство 1) криволинейного интеграла, используя формулы (21.4) и (21.6), получаем
Пример 21.4. ВычислитьГде- лепесток лемнискаты
Расположенный в первом координатном углу.
ЛинияЗадана уравнением в полярных координатах, поэтому здесь целесообразно воспользоватьсяформулой (21.S).
Так какТо
Заметив еще, чтоТ. е.По формуле (21.5) получим
Пример 21.5. ВычислитьГде- отрезок прямой
Между точками
Составим сначала уравнения прямой, проходящей через точкиИ
Или
Таким образом, получаем параметрические уравнения прямой:
ТочкаПробегает отрезок, когдаИзменяется отДо 1, т. е.
Так какТо
По формуле (21.2) находим
Пример 21.6. ВычислитьГде-дуга винтовой линии
Отраниченной точками, для которых Применяем формулу (21.2). Поскольку
И
| < Предыдущая | Следующая > |
|---|
matica.org.ua
