Решение задач по физике с блоками: Подвижный и неподвижный блок, с примерами задач
- Комментариев к записи Решение задач по физике с блоками: Подвижный и неподвижный блок, с примерами задач нет
- Разное
- Подвижный и неподвижный блок, с примерами задач
- силы и блоки, 8 класс.
- Подвижные и неподвижные блоки. Физика, 7 класс: уроки, тесты, задания.
- Блоки.
- 100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
- Урок решения задач по теме: “Блоки. Наклонная плоскость”
- Физика 7 класс. Простые механизмы. Блок :: Класс!ная физика
- Страница не найдена | MIT
- ньютоновской механики – Задача блока на блоке с трением
- домашних заданий и упражнений – Парадокс в задаче двух блоков
- 2.4: Решение проблем – Физика LibreTexts
- Задачи двух тел
- Двойные проблемы: две проблемы тела
- 6.1 Решение проблем с помощью законов Ньютона – Университетская физика, том 1
Подвижный и неподвижный блок, с примерами задач
Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.
Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).
Неподвижный блок
Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.
Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:
Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:
так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.
Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:
при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:
Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.
Комбинация неподвижных блоков
Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения.
Условие равновесия для рычага на рис.2 станет формула:
Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
Подвижный блок
Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:
Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:
Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:
Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.
В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.
Золотое правило механики
Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.
В виде формулы «золотое правило№ можно записать так:
где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы .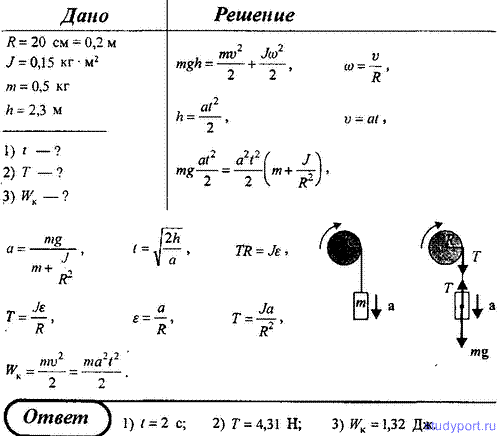
Золотое правило является самой простой формулировкой закона сохранения энергии. Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:
Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:
Если силы и уравновешены, то блок покоится или движется равномерно.
Примеры решения задач
силы и блоки, 8 класс.
Продолжаем подготовку к олимпиадам. Сегодня закрепляем тему «статика». Поговорим про блоки, посчитаем силы, установим равновесие.
Задача 1. Черный ящик, привязанный через систему блоков и нитей к стенке, покоится на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть его с места, непосредственно к нему необходимо приложить горизонтальную силу чуть больше Н. Какую минимальную силу надо прикладывать к черному ящику, чтобы он оставался неподвижным, если к веревке приложена сила Н? Ответ дать в Ньютонах, округлив до целых. Считать, что м/c.
Считать, что м/c.
Рисунок 1
Расставим силы:
Рисунок 2
Теперь видно, что на блок действуют три силы , поэтому общая сила равна 45 Н. 16 из них «съест» сила трения, поэтому, чтобы удержать такой ящик, не хватает Н.
Ответ: 29 Н.
Задача 2. Все блоки в системе, представленной на рисунке − невесомые. Масса левого тела кг. При какой массе правого тела система останется в равновесии? Ответ дать в килограммах, округлив до целых. Считать, что м/c.
Рисунок 3
Расставим силы:
Рисунок 4
Теперь запишем условия равновесия:
Откуда
И
Ответ: 2 кг.
Задача 3. Спасатели с помощью веревок, перекинутых через систему блоков, перемещают равномерно и прямолинейно массивную плиту так, как показано на рисунке. С какой результирующей силой верёвки действуют на плиту? Спасатели тянут свой конец веревки с силой Н. Массами веревок и блоков пренебречь. Ответ дать в Н, округлив до целых. Считать, что м/c.
Ответ дать в Н, округлив до целых. Считать, что м/c.
Замечание: требуется найти только силу, с которой нити действуют непосредственно на плиту. Силу, действующую на плиту со стороны верхнего крепления в ответ включать не надо.
Рисунок 5
Расставим силы:
Рисунок 6
Теперь видно, что «за нитки» плиту тянут Н, а полная сила (с учетом верхнего крепления – Н.
Ответ: 600 Н.
Задача 4. Какую горизонтальную силу надо прикладывать к шкафу, чтобы удержать его на месте? Массы грузов равны кг, кг. Ответ дать в Ньютонах, округлив до целых. Считать, что м/c.
Рисунок 7
На шкаф действуют две силы тяжести: первого груза (20 Н) и второго (50 Н). Итого 70 Н.
Ответ: 70 Н.
Задача 5. Два ящика покоятся на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть с места левый ящик, к нему необходимо приложить горизонтальную силу чуть больше 26 Н. Чтобы сдвинуть правый − чуть больше 14 Н. Ящики соединили нитью, переброшенной через блоки, прикреплённые к ящикам так, как показано на рисунке. Какую минимальную силу надо приложить к концу нити, чтобы расстояние между ящиками начало уменьшаться? Ответ дать в Ньютонах, округлив до целых.
Ящики соединили нитью, переброшенной через блоки, прикреплённые к ящикам так, как показано на рисунке. Какую минимальную силу надо приложить к концу нити, чтобы расстояние между ящиками начало уменьшаться? Ответ дать в Ньютонах, округлив до целых.
Рисунок 8
Расстояние будет уменьшаться при сдвиге любого из ящиков, поэтому нужно выяснить, какой легче сдвинуть. Для этого расставляем силы:
Рисунок 9
Теперь видно, что на левый ящик действует сила , а на правый – . Если
То Н, а если
То Н. Поэтому ответ – 7 Н. Этого будет достаточно, чтобы сдвинуть правый ящик и тем самым сократить расстояние.
| 1. |
Блок, определение экономии силы
Сложность: лёгкое |
1 |
2.
|
Блок, показания динамометров в системе блоков
Сложность: лёгкое |
3 |
| 3. |
Показания динамометров в разных положениях
Сложность: лёгкое |
2 |
4.
|
Системы неподвижных блоков
Сложность: лёгкое |
1 |
| 5. |
Показания динамометров в системах неподвижных блоков с одним или двумя грузиками
Сложность: лёгкое |
1 |
6.
|
Системы из двух блоков
Сложность: лёгкое |
2 |
| 7. |
Рычаг и подвижный блок
Сложность: среднее |
4 |
8.
|
Неподвижный и подвижный блоки
Сложность: среднее |
2 |
| 9. |
Вес подвижного блока и груза
Сложность: среднее |
2 |
10.
|
Система неподвижного и подвижного блока
Сложность: среднее |
2 |
| 11. |
Масса груза (подвижный блок)
Сложность: среднее |
4 |
12.
|
Сила, с которой давит на землю рабочий (неподвижный блок)
Сложность: среднее |
3 |
| 13. |
Система из двух подвижных и двух неподвижных блоков
Сложность: сложное |
2 |
14.
|
Давление на опору (подвижный блок)
Сложность: сложное |
5 |
| 15. |
Простые механизмы
Сложность: сложное |
5 |
Блоки.
 Условие равновесия блоков
Условие равновесия блоков«Кто овладел творениями Архимеда,
будет меньше удивляться открытиям
самых великих людей нашего времени»
Г.В. Лейбниц
Данная тема посвящена решению задач на тему «Блоки. Условие равновесия блоков».
Задача 1. Какую минимальную силу нужно приложить к концу веревки для подъема мешка цемента массой 50 кг с помощью данной системы блоков? На какую высоту будет поднят мешок при совершении этой силой работы в 2500 Дж? Считать блоки идеальными.
|
ДАНО: |
РЕШЕНИЕ: Подвижный блок, позволяет получить выигрыш в силе в два раза. Значит, минимальная сила, которую нужно приложить к концу веревки для подъема мешка цемента, равна половине веса этого мешка Вес мешка цемента: Тогда минимальная сила Работа силы определяется по формуле Согласно «Золотому правилу
механики», если мы выигрываем в силе, то во столько же раз проигрываем в
пути. Высоту подъема точки приложения силы определим как отношение работы, совершенной силой, к модулю этой силы Тогда искомая высота |
Ответ: 250 Н; 5 м.
Задача 2. В системе, изображенной на рисунке, масса самого правого груза равна 1,5 кг, а массы всех блоков одинаковы и равны 0,4 кг. Система уравновешена и неподвижна. Определите массы остальных грузов, если массой троса и трением в блоках можно пренебречь.
|
ДАНО: |
РЕШЕНИЕ: Если трос является невесомым и нерастяжимым, а так же при отсутствии трения в блоках, силы натяжения троса должны быть равны между собой Поскольку система уравновешена, то: С другой стороны, трос передает производимое на него воздействие
равномерно по всей своей длине. Поскольку система уравновешена, то: |
Ответ: 2,6 кг.
Задача 3. Плита массой 120 кг была равномерно поднята с помощью подвижного блока на высоту 16 м за 40 с. Считая КПД механизма 80%, а массу блока — 10 кг, определите полную работу и развиваемую мощность. Считать, что в блоке отсутствуют силы трения.
|
ДАНО: |
РЕШЕНИЕ: Коэффициента полезного действия механизма определяется отношением полезной работы механизма ко всей затраченной им работе Полезная работа: Сила тяжести плиты и блока: Тогда Затраченная работа: Затраченная мощность: |
Ответ: 26
кДж; 650 Вт.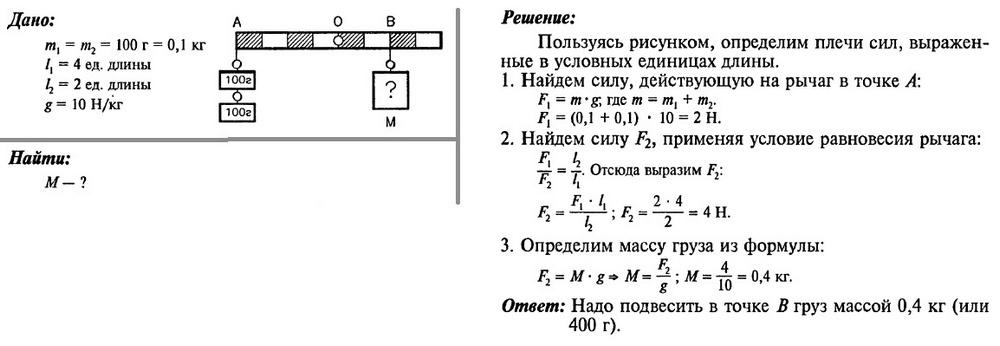
Задача 4. На рисунке изображена система грузов. Массы тел соответственно равны 0,2 кг и 0,4 кг. Определите силу натяжения нити. Считать нить и блоки идеальными?
|
ДАНО: |
РЕШЕНИЕ: Так как нить и блоки идеальны, то: На основании II закона Ньютона: Так как блок 2 подвижный: Тогда получаем Выразим из второго уравнения ускорение a2, подставим полученное выражение в первое уравнение Преобразуем полученное уравнение и выразим из него искомую силу натяжения нити
|
Ответ: 2 Н.
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Урок решения задач по теме: “Блоки. Наклонная плоскость”
Ирина Павловна Нерода,
учитель физики МБОУ «СШ №16»
г.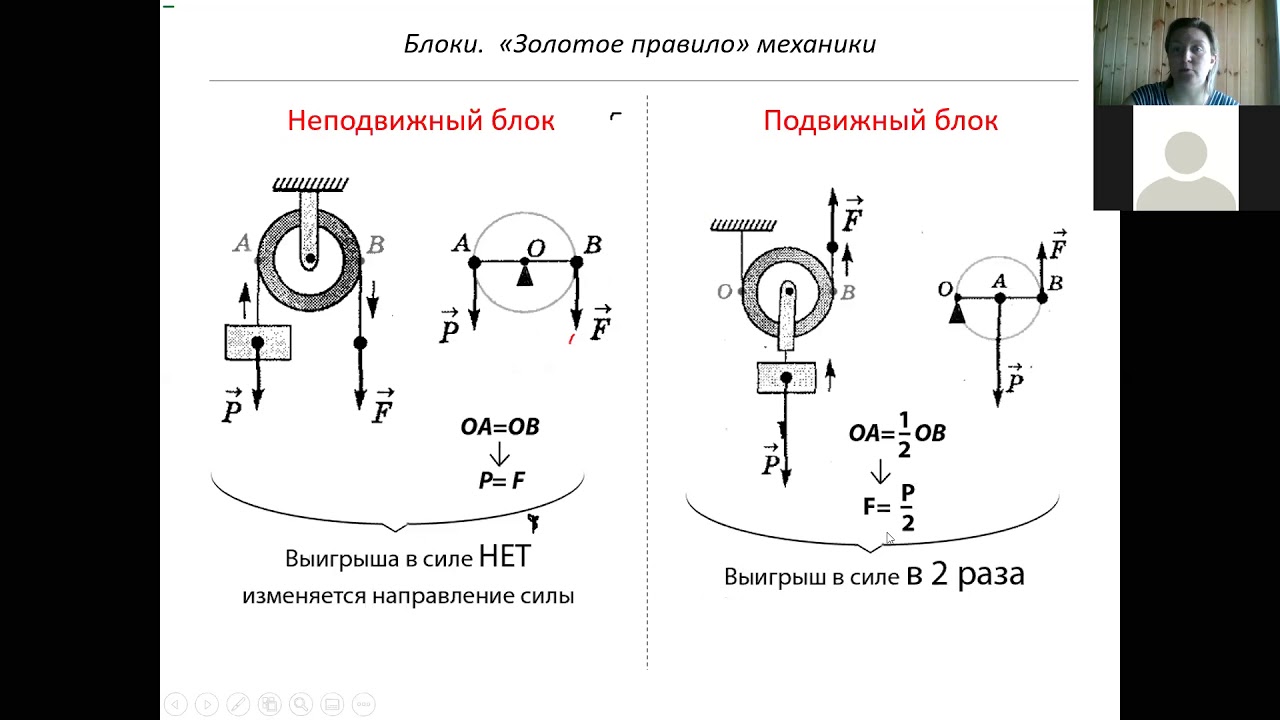 Ачинск
Ачинск
Тема урока: Решение задач по теме: «Блоки. Наклонная плоскость»»
Цель урока: применять знания на правило моментов сил, нахождение выигрыша с силе.
Задачи урока: закрепить практические навыки и умения по определению выигрыша в силе, нахождения приложенной силы по правилу моментов сил.
Познавательные учебные действия:
выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
рефлексия способов и условий действия, контроль и оценку процесса и результатов деятельности;
умение строить речевые высказывания в устной и письменной речи.
Личностные учебные действия:
Регулятивные учебные действия:
целеполагание, как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно;
составление плана и последовательности действий;
контроль в форме сравнения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
оценка – выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;
волевая саморегуляция, как способность к волевому усилию, к преодолению препятствий.

Универсальные учебные действия:
анализ;
синтез;доказательство, установление причинно – следственных связей, построение логической цепи рассуждений.
Ключевые понятия: блок, наклонная плоскость, сила, момент сил, выигрыш в силе.
Учебник: Физика 7 Л.Э Генденштейн, А.А. Булатова, И.Н.Корнильев, А.В.Кошкина
План урока
Работа в парах и последующее фронтальное обсуждение вопросов:Назовите виды простых механизмов.
Приведите примеры простых механизмов и назовите, для чего их используют?
Что называется блоком?
Какие бывают блоки? Все ли они дают выигрыш в силе?
2
Изучение нового материала
Решение задачи у доски из учебника §24 №5
На рисунках изображен подъем груза силой F с помощью неподвижного и подвижного блоков. В обоих случаях груз поднимают на 50см. На какое расстояние перемещают в каждом случае конец троса, к которому приложена сила F?
3
Этап закрепления и первичной проверки
Решение похожих задач самостоятельно и последующая проверка:
§24 №6
На рисунке изображен подъем груза с помощью системы блоков.
А) Сколько в этой системе подвижных блоков и сколько неподвижных;
Б) Получается ли при этом выигрыш в силе, и если да, то какой?
3
Изучение нового материала
Решение задачи у доски из учебника §24 №8
1. Тележку массой 1 кг равномерно поднимают по наклонной плоскости длиной 2 м, прикладывая силу F. Высота наклонной плоскости 1 м. Трением пренебречь.
А) Какой выигрыш в силе получается с помощью данной наклонной плоскости?
Б) Дает ли выигрыш использование блока, и если да, то какой?
В) Какую силу надо приложить к свободному концу троса, чтобы равномерно поднимать тележку по наклонной плоскости?
Г) На какое расстояние нужно опустить свободный конец троса. Чтобы поднять тележку вдоль всей плоскости?
2. На рисунке схематично изображены наклонные плоскости. Какая из них дает наибольший выигрыш в силе?
3
Этап закрепления и первичной проверки
Решение похожих задач самостоятельно и последующая проверка:
§24 №9
Тележку равномерно поднимают по наклонной плоскости, прикладывая к свободному концу тороса силу F, равную по модулю 10Н. Длина наклонной плоскости 3 м, а высота-75см. Чему равна масса тележки? Трением и массой блока пренебречь.
6
Рефлексия
Выставление оценок. Обсуждение того, что вызвало затруднения на уроке.
7
Домашнее задание
§24 ,
Нарисуйте схемы, с помощью которых можно получить выигрыш в силе в 5 раз, состоящие из подвижных и неподвижных блоков. Придумайте, как с помощью имеющихся дома предметов изготовить данные схемы (детский конструктор, катушки ниток).
Литература:
Формирование УУД на уроках физики согласно ФГОС
( kopilkaurokov.ru)
Физика 7 Л.Э Генденштейн, А.А. Булатова, И.Н.Корнильев, А.В.Кошкина
Физика 7 класс. Простые механизмы. Блок :: Класс!ная физика
Физика 7 класс. ПРОСТЫЕ МЕХАНИЗМЫ
В современной технике для переноса грузов на стройках и предприятиях широко используются грузоподъемные механизмы, незаменимыми составными частями которых можно назвать простые механизмы. Среди них древнейшие изобретения человечества: блок и рычаг. Древнегреческий ученый Архимед облегчил труд человека, дав ему при использовании своего изобретения выигрыш в силе, и научил менять направление действия силы.Блок – это колесо с желобом по окружности для каната или цепи, ось которого жестко прикреплена к стене или потолочной балке. Грузоподъемные устройства обычно используют не один, а несколько блоков. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспаст.
Подвижный и неподвижный блок – такие же древнейшие простые механизмы, как и рычаг. Уже в 212 г.до н.эры с помощью крюков и захватов, соединенных с блоками, сиракузцы захватывали у римлян средства осады. Сооружением военных машин и обороной города руководил Архимед.
Неподвижный блок Архимед рассматривал как равноплечий рычаг.
Момент силы, действующей с одной стороны блока, равен моменту силы, приложенной с другой стороны блока. Одинаковы и силы, создающие эти моменты.
Выигрыш в силе при этом отсутствует, но такой блок позволяет изменить направление действия силы, что иногда необходимо.
Подвижный блок Архимед принимал за неравноплечий рычаг, дающий выигрыш в силе в 2 раза. Относительно центра вращения действуют моменты сил, которые при равновесии должны быть равны.
Архимед изучил механические свойства подвижного блока и применил его на практике. По свидетельству Афинея, “для спуска на воду исполинского корабля, построенного сиракузским тираном Гиероном, придумывали много способов, но механик Архимед, применив простые механизмы, один сумел сдвинуть корабль с помощью немногих людей. Архимед придумал блок и посредством него спустил на воду громадный корабль”.
Блок не дает выигрыша в работе, подтверждая “золотое правило” механики. В этом легко убедиться, обратив внимание на расстояния, пройденные рукой и гирей.
Спортивные парусные суда, как и парусники прошлого,
Устали? – Отдыхаем!
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
ньютоновской механики – Задача блока на блоке с трением
Причина, по которой вы находите это не интуитивно понятным, заключается в том, что вы предполагаете, что приложенная сила к верхнему блоку заставит нижний блок испытывать ту же силу из-за трения, что неверно.
Например, рассмотрим два блока A, и B , которые сидят бок о бок на гладком столе. Если вы приложите силу F к A , то можно ошибочно сказать, что сила, которую испытывает B , также равна F . Но это было бы неправильно. На самом деле это меньше, чем F .
То же верно и для вашего примера. Сила трения, испытываемая нижним блоком, меньше действительной силы, приложенной к верхнему блоку.Следовательно, чтобы нижний блок испытывал максимальную силу статического трения, необходимо приложить силу, превышающую эту. Обратите внимание, что эта «сила трения» возникает из-за самого верхнего блока, и, следовательно, ваш пример аналогичен приведенному выше примеру.
Но почему нижний блок вообще испытывает меньшую силу? Это потому, что «остальная» сила (или, точнее говоря: остальная часть импульса) используется для перемещения самого верхнего блока. Если верхний блок массивный, вам нужно будет приложить еще большую силу, чтобы заставить верхний блок ускоряться с той же скоростью, что и нижний блок.Большая часть переданного импульса (силы) здесь передается верхнему блоку, а остальная часть – нижнему блоку. Если верхний блок легкий, то очень небольшая часть передаваемого импульса (силы) используется для перемещения верхнего блока, а остальная часть передается нижнему блоку. Следовательно, в этом случае требуемая сила будет близка к максимальной силе статического трения.
Вы можете увидеть это в своем выражении: $ F = \ frac {(m_1 + m_2) F_ {sf}} {m_2} $
при $ m_1 \ to 0 $ требуемая сила приближается к силе трения.
Однако в этом выражении: $ F = \ frac {m_1} {m_2} \ mu_s (m_1 + m_2) g $
как $ m_1 \ to 0 $, сила также приближается к $ 0 $. Это потому, что это выражение включает тот факт, что максимальная сила трения уменьшается по мере уменьшения массы верхнего блока (чем легче верхний блок, тем меньше нормальная сила между двумя блоками). Следовательно, когда масса верхнего блока приближается к $ 0 $, максимальная сила, которую вы можете приложить, также приближается к $ 0 $.
домашних заданий и упражнений – Парадокс в задаче двух блоков
Закрыто. Это вопрос не по теме. В настоящее время он не принимает ответы.Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме Physics Stack Exchange.
Закрыт 6 лет назад.
ОБНОВЛЕНИЕ(относительно дубликата):
Этот вопрос не дублирует другой вопрос.Конечно, ситуация в обоих вопросах одинакова, и, да, оба вопроса в конечном итоге предоставляют методологию для решения проблемы и нахождения правильного значения трения, но модератор должен понимать, что здесь я НЕ просил о методе решения для Трение . Проблема заключалась в том, что я даже не понимал, что придется решать по трению.
Я решил много таких задач еще в школе, и у меня появилась привычка считать статическое трение равным и противоположным любой силе, прилагаемой к трению (вплоть до максимального предела трения).Это была грубая ошибка, которую я сделал, и именно поэтому она выглядела как «парадокс». Более того, как оказалось, я задал ту же задачу нескольким своим друзьям, и многие из них совершили ту же ошибку.
Итак, по сути, «другая» проблема – это просто запрос общей методологии для решения таких проблем, в то время как эта проблема похожа на головоломку, которая представляет пользователю методологию решения проблемы путем рассмотрения различных систем и противоречий, которые возникают из-за них. . Я считаю, что пользователь, который знает общую методологию, представленную в другом вопросе, подвержен путанице / парадоксу, который представляет эта проблема.2 $$
Это парадоксально. Почему значение ускорения оказывается другим, если мы рассматриваем только второй блок в нашей задаче?
2.4: Решение проблем – Физика LibreTexts
Далее мы сосредоточимся на элементах решения проблем. У нас есть все необходимые инструменты, так что это не будет связано с какой-либо новой физикой, но идея состоит в том, чтобы познакомить вас с некоторыми общими темами, которые возникают в задачах физики и механики.
Шкивы
Шкив – одно из любимых устройств для решения физических задач.Как было сказано в описании силы натяжения, для начала мы используем простейшую модель, что означает, что мы будем предполагать, что шкивы безмассовые и без трения. Шкивы становятся особенно интересными в ситуациях, подобных следующему примеру, когда хотя бы один из шкивов может двигаться. Два блока остаются неподвижными в системе тросов и шкивов, показанной на схеме. Учитывая эту информацию, можете ли вы сделать вывод, как сравниваются две массы?
Рисунок 2.4.1 – Блоки, подвешенные на нескольких шкивах
К настоящему времени мы знаем, что когда дело доходит до анализа сил, присутствующих в системе, нет лучшего инструмента, чем FBD.Начнем там:
Рисунок 2.4.2 – FBD блока и шкива
[Мы взяли на себя смелость определять системы координат в наших FBD – вверх это направление \ (+ y \) – для обоих – что нам понадобится в ближайшее время.]
Может возникнуть вопрос, почему для шкива нарисовано два вектора силы натяжения. Самый простой ответ – подумать о том, что вы почувствуете, если перережете веревку с обеих сторон шкива и держите по одному концу в каждой руке. Очевидно, вы почувствуете, как оба конца веревки тянут вниз.Следовательно, согласно третьему закону Ньютона, оба конца веревки натягиваются на шкиве. Для шкива без массы и без трения эти две силы натяжения также должны быть равны, что объясняет, почему они обозначены одинаково. Обратите внимание, что вектор натяжения на блоке также помечен тем же именем переменной. Это потому, что это та же веревка , , и наше предположение о безмассовых шкивах без трения гарантирует, что везде, где мы измеряем натяжение одного куска веревки, оно будет одинаковым.
Предупреждение
Если бы мы изобразили вектор силы натяжения, тянущий вверх на правом шкиве, мы не смогли бы обозначить его так же. Не все векторы натяжения в одной физической системе равны, только величины всех векторов натяжения, полученные от одной и той же веревки.
Еще один любопытный аспект этого FBD – это весовая этикетка левого шкива. Технически эта сила действует на блок, и блок тянет за шкив. В этом случае сила натяжения шкива блоком равна весу блока, а сам шкив не имеет собственного веса, так что мы вправе пойти по этому пути.Другой способ обосновать это – рассматривать блок + шкив как единую систему, а сила тяжести, действующая на систему, – это показанный вектор силы.
Следующим шагом в нашем анализе является суммирование сил для каждого объекта и применение второго закона Ньютона, который в данном случае предполагает нулевое ускорение. При вычислении суммы сил мы должны позаботиться о том, чтобы правильно использовать нашу систему координат:
\ [\ left. \ begin {array} {l} 0 = a_1 = \ dfrac {F_ {net \; 1}} {m_1} = \ dfrac {2T – m_1 g} {m_1} \; \; \; \Правая стрелка \;\;\; T = \ dfrac {m_1 g} {2} \\ 0 = a_2 = \ dfrac {F_ {net \; 2}} {m_2} = \ dfrac {T – m_2 g} {m_2} \; \; \; \; \Правая стрелка \;\;\; T = m_2 g \\ \ end {array} \ right \} \; \; \; \Правая стрелка \;\;\; м_1 = 2 м_2 \]
Обратите внимание, что легкий \ (m_2 \) выдерживает более тяжелый, потому что размещение шкива позволяет нам использовать натяжение одной и той же веревки дважды на более тяжелую массу.Этот трюк можно повторять сколько угодно раз (на шкиве может быть несколько дорожек), и это позволяет нам поднимать очень тяжелые веса с очень небольшой силой. Данное изобретение называется блоком и захватом . Они используются для плавания на парусных судах (тяжелые паруса и гика можно затянуть сильнее), подъема блоков двигателей и многих других задач.
Ограничения
Затем мы рассмотрим сложную концепцию, известную как ограничение s. Ограничение – это условие, которое существует для физической системы, которое ограничивает ее поведение.Что делает концепцию «сложной», так это то, что они, в конечном счете, играют математическую роль в решении проблемы, но эту роль часто трудно извлечь из постановки задачи. Проще говоря, ограничения связывают переменные в задаче друг с другом, обеспечивая дополнительные уравнения (помимо второго закона Ньютона), с которыми можно работать. Мы уже видели пример ограничения. Это соотношение между силой трения и нормальной силой. Для кинетического трения это дает уравнение, которое связывает эти две силы, в то время как для статического трения он устанавливает верхний предел величины трения для данной нормальной силы.
Один из наиболее распространенных примеров ограничения относится к канатам, движущимся через шкивы. Это ограничение связывает движение одного объекта с движением другого, когда они соединены системой шкивов. Вернемся к системе, показанной на рисунке 2.4.1, и зададим следующий вопрос: если блок \ (m_2 \) падает на расстояние \ (\ Delta y \), что происходит с блоком \ (m_1 \)?
Прежде всего, должно быть ясно, что \ (m_1 \) возрастает по мере того, как \ (m_2 \) падает, поэтому вопрос только в том, как далеко? Сначала это может быть неочевидным, но подумайте об этом так: когда шкив, удерживающий \ (m_1 \), поднимается на 1 единицу, оба сегмента струны, идущие вверх от шкива, становятся короче на 1 единицу.Эти две единицы строки не просто исчезают, и фактически они принимаются свободным концом строки, который прикреплен к \ (m_2 \). Это означает, что когда \ (m_2 \) падает на расстояние \ (\ Delta y \), \ (m_1 \) должен подниматься только на половину этого расстояния.
Что это говорит о сравнении скоростей и ускорений двух блоков? Что ж, они должны двигаться одновременно, поэтому каждая единица длины, отброшенная на \ (m_2 \), соответствует увеличению \ (m_1 \) на половину, а это означает, что \ (m_1 \) всегда перемещается на половину скорость и разгоняется вдвое меньше, чем \ (m_2 \).Если эта система не сбалансирована (как это было выше), то применение второго закона Ньютона к обоим блокам включает в себя два ускорения, но они ограничены, связаны друг с другом в два раза, что дает нам дополнительное ограничение уравнение :
\ [2 \ осталось | a_1 \ right | = \ left | a_2 \ справа | \]
Что с абсолютными значениями, спросите вы? Что ж, эти переменные могут иметь положительные или отрицательные значения, и мы должны быть осторожны, когда дело касается знаков.в частности, мы должны посмотреть, как наше ограничение связано с нашим выбором систем координат для двух блоков. На рисунке 2.4.2 мы выбрали «вверх» в качестве положительного направления для обоих блоков. Поэтому нам нужно спросить себя: «Если один блок испытывает положительное смещение, каков знак смещения другого блока?» В этом случае ясно, что смещения двух блоков имеют противоположные знаки. Следовательно, уравнение ограничения для ускорений блока:
\ [2a_1 = -a_2 \]
Обратите внимание, что совершенно нормально установить разные системы координат для двух блоков – каждый FBD имеет право на свою собственную индивидуальную систему координат.То, как системы координат соотносятся друг с другом, влияет на уравнение связи. Так, например, если бы мы вместо этого выбрали нисходящее направление + \ (y \) – для блока № 2 (но оставили вверх как положительное значение для другого блока), тогда не было бы необходимости в знаке минус в ограничении уравнение – положительные смещения одного блока соответствуют положительным смещениям другого блока. Мы видим, что, следовательно, нет «правильного» выбора системы координат, но мы должны позаботиться о том, чтобы когда придет время объединить уравнения из двух FBD, чтобы уравнения ограничений правильно связывали переменные.В следующем примере мы увидим еще более яркий пример выбора системы координат.
Пример \ (\ PageIndex {1} \)
Высота двух блоков на диаграмме ниже отличается на 36 см. Когда они выходят из состояния покоя, верхний блок падает, а нижний блок поднимается. Один из блоков имеет массу, в три раза превышающую массу другого блока, шкивы безмассовые и без трения, а струна не растягивается.
- Какой блок тяжелее? Объяснять.
- Найдите расстояние, на которое поднимается нижний блок, когда два блока выровнены.
- Найдите время, необходимое для выравнивания двух блоков.
- Решение
а. Натяжение струны, продетой через шкивы, везде одинаково, поэтому на нижний блок действует в три раза больше силы натяжения, чем на верхний. Если бы нижний блок был в три раза тяжелее верхнего блока, тогда система была бы сбалансирована, и ни одна масса не могла бы ускоряться.[Вы должны попробовать выполнить математику части (c) с массами другим способом и продемонстрировать себе, что это ускорение должно быть равно нулю.] Учитывая, что система ускоряется, это должен быть более высокий блок с большим масса.
г. Когда верхний блок тянет струну вниз с одной стороны большого шкива, то же количество струны, которое набирается с левой стороны шкива, теряется с правой стороны. Струна с правой стороны большого шкива разделена между тремя сегментами, удерживающими другой блок.Следовательно, нижний блок перемещается на одну треть вверх по мере того, как верхний блок перемещается вниз. Если нижний блок поднимается на расстояние \ (y \), то верхний блок опускается на расстояние \ (3y \), и, поскольку они достигают той же высоты, сумма этих изменений составляет 36 см, что означает, что нижний блок поднимается на расстояние длины \ (y = 9 \) см.
г. Чтобы узнать время, необходимое им для выравнивания, нам нужно использовать их ускорения. Мы уже знаем их относительные ускорения: нижний блок ускоряется на одну треть скорости верхнего блока.Поэтому мы будем называть ускорение верхнего блока «\ (3a \)», делая ускорение нижнего блока равным \ (a \). Но нам нужны законы Ньютона, чтобы пойти дальше. FBD двух задействованных систем выглядит так:
Более высокая масса в три раза больше меньшей массы, поэтому мы будем называть \ (m_2 \) просто «\ (m \)», что делает \ (m_1 \) равным \ (3m \). Включение всего во второй закон Ньютона для обоих FBD дает следующие уравнения:
\ [\ left.\ begin {array} {l} a_1 = \ dfrac {F_ {net \; 1}} {m_1} \; \; \; \Правая стрелка \;\;\; 3a = \ dfrac {-T + 3mg} {3m} \\ a_2 = \ dfrac {F_ {net \; 2}} {m_2} \; \; \; \Правая стрелка \;\;\; a = \ dfrac {3T – mg} {m} \\ \ end {array} \ right \} \; \; \; \Правая стрелка \;\;\; a = \ frac {2} {7} g \ nonumber \]
С помощью ускорения нижнего блока, расстояния, которое он проходит, и того факта, что он начинается в состоянии покоя, мы можем вычислить время, необходимое для совершения поездки:
\ [y = v_o t + \ frac {1} {2} at ^ 2 \; \; \; \Правая стрелка \;\;\; t = \ sqrt {\ dfrac {7y} {g}} = \ в коробке {0.25s} \ nonumber \]
Наклонные плоскости
Шкивы(и, в частности, блокиратор и захват) являются примером того, что часто называют простым механизмом . Это потому, что мы можем использовать такое устройство для подъема тяжелого веса с силой, меньшей, чем сам вес. Другой пример простой машины – наклонная плоскость . Эти устройства также позволяют выполнять задачу по подъему тяжелого объекта на более высокое положение с использованием меньшего усилия, чем было бы необходимо при прямом подъеме.Основная особенность задач, связанных с наклонными плоскостями, – это система координат, используемая для объекта на наклонной плоскости. Давайте посмотрим на пример. Как обычно, мы начинаем с самого простого примера и усложняем его по ходу дела – блок массы \ (M \) на плоскости без трения, наклоненной под углом \ (\ theta \):
Рисунок 2.4.3 – Блок на наклонной плоскости
Начнем наш анализ, как всегда, с диаграммы свободного тела.Ни один FBD не будет полным без выбора системы координат, поэтому мы должны выбрать ее здесь. Если мы выберем нашу систему координат горизонтальной и вертикальной, как мы обычно делаем, тогда, когда блок скользит по плоскости, его ускорение будет иметь как компоненты \ (x \), так и \ (y \). Это, конечно, нормально, но работать с этим может быть немного неудобно. В горизонтальном и вертикальном направлениях нет ничего сакрального, так почему бы не выбрать систему координат, параллельную и перпендикулярной плоскости?
Рисунок 2.4.4 – Система координат наклонной плоскости
На средней диаграмме на рисунке 2.4.4 показана сумма нормальных и гравитационных сил между хвостом и головой, приводящая к результирующей силе, параллельной плоскости и вниз по плоскости, как и должно быть, поскольку мы знаем, в каком направлении будет двигаться блок. ускоряться. На правой диаграмме показана сила тяжести, разбитая на ее компоненты \ (x \) и \ (y \) в выбранной системе координат (вы должны сами проверить геометрию, которая приводит к заключению, что угол на этой диаграмме совпадает с углом наклон составляет горизонталь).Обратите внимание: поскольку блок не ускоряется перпендикулярно плоскости, мы можем сделать вывод, что \ (N = Mg \ cos {\ theta} \). Также ясно, что чистая сила – это \ (x \) – компонент силы тяжести, в результате чего ускорение вниз по плоскости равно \ (a = g \ sin {\ theta} \).
Предположим, мы хотим поднять этот блок на новую высоту. Чтобы заставить его двигаться вверх по плоскости, нам нужно приложить силу, превышающую чистую силу, показанную выше, которая меньше силы, которую нам пришлось бы приложить, чтобы поднять его прямо вверх.Как и в случае с блоком и снастью, эта «простая машина» помогает нам выполнять работу с меньшими усилиями, чем требуется, если она выполняется более непосредственно. В случае блока и снасти, чтобы поднять груз на некоторое расстояние, другой конец веревки нужно было протянуть на большее расстояние. В этом случае мы видим аналогичную вещь – расстояние, на которое мы должны толкнуть блок, является гипотенузой треугольника, чтобы поднять его на высоту вертикального катета треугольника. Это обычная тема для простых машин – требуется меньшее усилие, но оно должно применяться на большем расстоянии.В следующей главе мы увидим, почему это так.
Мы можем значительно усложнить этот простой пример. Самая естественная регулировка – включить трение. Из-за природы двух типов трения добавление статического трения (которое входит в неравенство) может быть особенно проблематичным. Чтобы понять, почему, давайте рассмотрим следующую проблему:
Система, изображенная на рисунке 2.4.5, показывает два блока, которые остаются в состоянии покоя, которые прикреплены безмассовой струной к безмассовому шкиву без трения.Плоскость наклонена под углом \ (тета \) вверх от горизонтали, а ее поверхность шероховатая (т.е.не имеет трения). Приведены масса подвесного блока, угол наклона и коэффициент статического трения. По этим величинам определите минимально возможное значение массы блока на плоскости.
Рисунок 2.4.5 – Механическая система
Начиная (как всегда) с FBD (включая систему координат) для каждого блока, мы имеем:
Рисунок 2.4.6 – Схемы блоков со свободным телом
Давайте прокомментируем направление силы статического трения. Напомним, что сила статического трения просто реагирует на «попытку» движения объекта по поверхности. В этом случае, если блок «пытался» скользить по плоскости, то сила статического трения должна быть вверх по плоскости. Здесь он направлен вниз по плоскости, что означает, что другие силы должны быть такими, чтобы ускорять его вверх по плоскости… Откуда мы знаем, что это так? Ответ заключается в постановке вопроса: мы ищем минимальную массу блока на плоскости. Представьте себе блок, масса которого уравновешивает систему. если к блоку добавляется или вычитается небольшая масса, система может оставаться в покое, поскольку статическое трение удерживает баланс. Если мы добавим этому блоку слишком много массы, статическое трение достигнет своего предела, и блок начнет скользить вниз, а если мы уберем слишком много массы, он будет скользить вверх по плоскости.Статическое трение будет противодействовать намеченному движению, поэтому для минимальной массы сила статического трения должна быть направлена вниз по плоскости.
Предупреждение
Хотя мы можем определить направление статического трения для этой задачи, во многих задачах это невозможно. Если вы знаете, что сила статического трения присутствует (или может быть), просто втяните ее в любом направлении. Когда проблема решена, если вы решите значение этой силы, она будет положительной, если вы выбрали правильное направление, и отрицательной, если вы этого не сделали.FBD – это просто инструмент, и в конечном итоге вы получите ответ, поэтому не тратьте энергию на то, чтобы получить правильное направление на диаграмме.
Разбиение векторов на компоненты в выбранных нами системах координат и применение второго закона Ньютона (для нулевого ускорения) дает:
\ [\ begin {array} {l} block \; на \; плоскости: \; \; \ begin {array} {l} x – направление \; силы: \; \; 0 = a_x = \ dfrac {f – T + Mg \ sin {\ theta}} {M} \\ y – направление \; силы: \; \; 0 = {a_y} = \ dfrac {N – Mg \ cos {\ theta}} {M} \ end {array} \\ висит \; блок: \; \; \; y – направление \; силы: \; \; 0 = {a_y} = \ dfrac {T – mg} {m} \ end {array} \]
Затем примените ограничение, которое связывает максимальную силу трения покоя (которая возникает, когда минимальная масса находится на плоскости) и нормальную силу:
\ [f \ le \ mu_S N \; \; \; \Правая стрелка \;\;\; (максимум \; f \; для \; минимум \; M) \; \; \; \Правая стрелка \;\;\; f = \ mu_S N \]
Остальное – алгебра с четырьмя системными уравнениями, результат которых:
\ [M_ {min} = \ frac {m} {\ mu _S \ cos \ theta + \ sin \ theta} \]
Теперь мы должны проверить, имеет ли этот ответ смысл.o \) случае (горизонтальная поверхность, где нормальная сила равна весу блока на поверхности) потребует, чтобы сила трения равнялась весу подвесного блока. То есть мы должны иметь \ (mg = f = \ mu_S N = \ mu_S Mg \; \; \ Rightarrow \; \; m = \ mu_S M \), что мы получаем, когда подставляем ноль для \ ( \ тета \).
Эта задача могла бы так же легко запросить максимальное возможное значение для \ (M \). Читателю предлагается попробовать это в качестве упражнения.
С этой проблемой было связано много всего, но главное – делать это шаг за шагом и выполнять следующие предписанные шаги:
- нарисовать схему
- выделите соответствующие объекты и начертите для них диаграммы свободного тела
- выберите системы координат для схем, которые удобны
- разбивает силы на компоненты в выбранной системе координат
- суммируйте силы в направлениях \ (x \) и \ (y \) и примените второй закон Ньютона для обоих направлений
- применить ограничения
- решить алгебру
Пример \ (\ PageIndex {2} \)
Трос закреплен на 50.Блок 0 кг в двух местах и проходит через систему из двух шкивов, как показано на схеме ниже. Блок опирается на шероховатую (коэффициент трения покоя 0,400) горизонтальную поверхность. Затем больший шкив тянет вверх с постепенно увеличивающейся силой. Оба шкива безмассовые и без трения, канат также безмассовый. Меньший шкив прикреплен к полу, и оба шкива расположены так, что веревка перпендикулярна полу на одном конце и параллельна ему на другом.Когда тяговое усилие достигает определенной величины, блок едва начинает скользить вправо. Вычислите величину этой тянущей силы.
- Решение
В этой задаче нет наклонной плоскости (хотя она может быть!), Но это хороший пример важности следования указанным выше предписаниям. Начните с диаграмм свободного тела и систем координат. FBD меньшего шкива не принесет нам ничего полезного, поэтому нужно нарисовать только два FBD.Обратите внимание, что натяжение на стороне блока происходит от той же веревки, что и натяжение на верхней части блока, поэтому они равны:
Блок вообще не ускоряется (как и шкив), поэтому сумма сил в каждом из направлений \ (x \) и \ (y \) равна нулю.
Блок \ [\ begin {array} {l}: \; \; \ begin {array} {l} x – направление \; силы: \; \; 0 = T – f \\ y – направление \; силы: \; \; 0 = T + N-mg \ end {array} \\ шкив: \; \; y – направление \; силы: \; \; 0 = тянуть – 2T \ end {array} \ nonumber \]
Если нам нужно тянуть «достаточно сильно», чтобы заставить блок двигаться, то это происходит, когда горизонтальное усилие равно максимальной силе статического трения, что дает нам уравнение ограничения:
\ [f = \ mu_S N \ nonumber \]
Обратите внимание, что блок должен начать скользить, прежде чем он начнет подниматься, потому что для подъема требуется, чтобы нормальная сила была равна нулю, и он будет скользить, когда сила статического трения мала, но не равна нулю.Теперь решите уравнения одновременно, чтобы получить:
\ [pull = \ boxed {280N} \ nonumber \]
Включая движение
Мы сделали два примера с системами, для которых ускорение равно нулю. Но, конечно, возможно, что проблема действительно связана с ускорением объектов. Иногда нас просят найти это ускорение, а иногда ускорение – это часть информации, которая дается. Ускорение может быть задано напрямую, или, возможно, оно может быть вычислено другим способом, возможно, исходя из кинематики или если движение является круговым.Знание чего-либо о движении объекта подпадает под категорию «ограничений», потому что движение задано (ограничено), что приводит к уравнениям, которые не являются результатом второго закона Ньютона. Мы рассмотрим пример, в котором используются шаги для решения задач механики, которые также включают дополнительное ограничение кругового движения. Прежде чем мы это сделаем, попробуйте следующий пример:
Пример \ (\ PageIndex {3} \)
Блок прикреплен к одному концу безмассовой пружины, другой конец которой прикреплен к вертикальному неподвижному штифту на горизонтальной поверхности без трения.Блок вращается по кругу, и в результате этого движения пружина растягивается. Фактически, чем быстрее движение, тем больше растягивается пружина. Чтобы растянуть любую пружину, нужно одновременно тянуть за оба конца. Ясно, что колышек натягивает один конец пружины, когда блок движется по кругу, но какая сила тянет блок наружу, чтобы растянуть пружину?
- Решение
Блок не вытащил наружу ! Он только втягивается внутрь (пружиной).Чтобы растянуть пружину, нужно вытянуть наружу не блок, а пружину, которую нужно потянуть таким образом. Пружина втягивает блок внутрь (поддерживая его центростремительное ускорение), и сила третьего закона пары блока на пружине – это то, что тянет пружину наружу.
Возможно, это лучше, чем любой другой пример, указывает на важность изоляции объектов с помощью силовых диаграмм. Блок здесь не является проводником для какой-то таинственной силы, вытягивающей пружину – это объект, вытягивающий пружину.Вам нужно полностью доверять третьему закону, чтобы получить силу между пружиной и блоком, и вам нужно полностью доверять второму закону, чтобы понять, что блок не требует дополнительной силы, воздействующей на него наружу, чтобы уравновесить силу пружины, потому что это ускоряется.
Теперь об обещанном примере, который включает движение в соответствии с пошаговыми инструкциями, приведенными ранее. Что делает эту проблему интересной, так это информация, которая скрыта внутри формулировки …
Камень на тетиве летает по кругу в вертикальной плоскости (при наличии земной силы тяжести) так, что едва достигает вершины (струна остается натянутой на всю длину, но нет натяжения) продолжая свой круговой путь.Найдите скорость камня по длине струны.
- выделить соответствующие объекты и нарисовать для них диаграммы свободного тела
- выбрать системы координат для схем, которые удобны
В качестве положительного направления \ (y \) выберем вниз.
- силы разрыва на компоненты в выбранной системе координат
Здесь нет необходимости.
- суммируйте силы в направлениях \ (x \) и \ (y \) и примените второй закон Ньютона в обоих направлениях
\ [a = \ dfrac {\ sum {F_y}} {m} = \ dfrac {T + mg} {m} \]
Первое ограничение состоит в том, что скала почти не перемещается. Что это значит? Чтобы ответить на этот вопрос, подумайте, что бы произошло, если бы камень двигался медленнее … Он выпал бы из круга, а это значит, что струна не останется прямой. Это означало бы, что напряжение равно нулю.2} {l} \]
Достаточно просто:
\ [v = \ sqrt {gl} \]
Хотя это довольно простой пример с точки зрения предпринятых шагов, он указывает на один очень важный аспект этих проблем. Если вы не тратите некоторое время на размышления о том, что происходит физически, вы, скорее всего, упустите из виду «скрытую» информацию в формулировке проблемы. Это не уловка, чтобы сбить вас с толку – это именно то, с чем вы сталкиваетесь в реальном мире, когда вам нужно решить реальную проблему.Вам необходимо уметь преобразовывать описательные аспекты системы в математически анализируемые величины.
Пример \ (\ PageIndex {4} \)
Тетербол вращается вокруг шеста, делая полный круг каждые 1,5 секунды. Общая длина веревки – 2,4 м. Вычислите угол θ, который веревка образует с шестом. Веревка имеет незначительную массу.
- Решение
Начните с диаграммы силы мяча, включая систему координат:
Затем сложите силы по осям \ (x \) и \ (y \) и примените второй закон Ньютона:
\ [\ begin {array} {l} a_x = \ dfrac {T \ sin \ theta} {m} \\ a_y = \ dfrac {T \ cos \ theta – mg} {m} \ end {array} \ nonumber \]
Ускорение в направлении \ (x \) является центростремительным, с радиусом его кругового движения, равным горизонтальному участку прямоугольного треугольника, гипотенуза которого равна длине струны.o} \ nonumber \]
Задачи двух тел
В блоке законов Ньютона введена тема задач двух тел. Была обсуждена пара стратегий решения проблем, которые были применены для решения трех примеров проблем. Такие проблемы с двумя телами обычно включают решение для ускорения объектов и силы, действующей между объектами. Одна из стратегий решения задач двух тел включает использование системного анализа для определения ускорения в сочетании с анализом отдельного объекта для определения силы, передаваемой между объектами.Вторая стратегия заключалась в использовании анализа двух отдельных объектов с целью разработки системы из двух уравнений для решения двух неизвестных величин. При необходимости найдите время, чтобы просмотреть страницу о решении задач двух тел. Эта страница будет основываться на уроках, извлеченных ранее в разделе «Законы Ньютона».
В этом уроке мы проанализируем задачи о двух телах, в которых объекты движутся в разных направлениях. В этих задачах два объекта связаны цепочкой, которая передает силу одного объекта другому.Струна наматывается на шкив, который изменяет направление приложения силы без изменения величины. В качестве иллюстрации того, как работает шкив, рассмотрим схему справа. Объект A связан с объектом B строкой. Веревка наматывается на шкив в конце стола. Объект A подвешен в воздухе, а объект B лежит на столе. В этой ситуации объект А упадет вниз под действием силы тяжести, потянув вниз один конец струны, к которой он подсоединен.Согласно закону действия-противодействия Ньютона, этот нижний конец струны будет тянуть вверх на объект A. Противоположный конец струны соединен с объектом B. Этот конец струны тянет вправо на объект B. соединение двух объектов тянет оба объекта с одинаковой силой, но в разных направлениях. Трос тянет вверх на объект A и вправо на объект B. Шкив изменил направление приложения силы.
Проблемы, связанные с двумя объектами, соединительными струнами и шкивами, характеризуются объектами, которые движутся (или даже ускоряются) в разных направлениях.Они движутся или ускоряются с одинаковой скоростью, но в разных направлениях. Таким образом, при решении таких задач становится важным выбрать другую систему отсчета и систему осей для каждого объекта. Следует обратить внимание на такой выбор системы осей, чтобы оба объекта ускорялись вдоль оси в положительном направлении. С осями, правильно определенными для каждого отдельного объекта, можно построить диаграмму свободного тела. Затем к каждой диаграмме можно применить законы Ньютона, чтобы получить систему из двух уравнений для решения двух неизвестных.Этот процесс решения проблем будет продемонстрирован на трех различных примерах задач.
Пример задачи 1Масса 200,0 грамма (m 1 ) и масса 50,0 грамма (m 2 ) соединены веревкой. Струна натянута на шкив. Определите ускорение масс и натяжение струны.
Как это часто бывает, в этом примере проблема запрашивает информацию о двух неизвестных – ускорении объектов и силе, действующей между объектами.В такой ситуации, как эта, когда два объекта подвешены на шкиве, более массивный объект будет ускоряться вниз, а наименее массивный объект будет ускоряться вверх. Величина ускорения будет одинаковой для каждого объекта. Система координат, выбранная для m 1 , имеет положительную ось y, направленную вниз; система координат, выбранная для m 2 , имеет положительную ось y, направленную вверх. При таком выборе осей направление ускорения будет положительным для каждого объекта.Диаграммы свободного тела для каждой индивидуальной массы показаны ниже. Каждый объект испытывает нисходящую силу тяжести, которая рассчитывается как 1 • g и 2 • g соответственно. Каждый объект также испытывает восходящую силу натяжения, которая притягивает два объекта друг к другу.
Уравнение второго законаНьютона (F net = m • a) можно применить к обеим диаграммам, чтобы написать два уравнения для двух неизвестных. F net будет выражаться как сила в направлении ускорения минус сила, которая ему противодействует.Таким образом, для массы 200,0 грамм F net записывается как 1,960 N – F десятки . Для массы 50,0 грамм F net записывается как F десятки – 0,490 Н. Уравнения 1 и 2 являются результатом применения уравнения второго закона Ньютона к массам 200,0 и 50,0 граммов. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
1.960 – F десятки = 0,2000 • a
F десятки – 0,490 = 0,0500 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 2 можно переформулировать, чтобы получить выражение для F десятков , записанное в терминах ускорения.
F десятки = 0,0500 • a + 0,490
Это выражение для F десятков теперь можно подставить в уравнение 1, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
1,96 – (0,0500 • a + 0,490) = 0,2000 • a
1,96 – 0,0500 • а – 0,490 = 0,2000 • а
1,47 = 0,2500 •
a = 1,47 / 0,2500 = 5,88 м / с 2
Теперь, когда ускорение было найдено из уравнения 1, его значение можно подставить в уравнение 3, чтобы определить натяжение.
F десятков = 0.0500 • (5,88) + 0,490
F десятков = 0,784 Н
Проанализированную здесь шкивную систему иногда называют машиной Атвуда. Подход к решению проблем – это стандартный подход, который будет использоваться на этой странице для решения двух неизвестных. Он будет повторен в примере проблемы 2, чтобы решить то, что обычно называют модифицированной машинной проблемой Этвуда.
Рассмотрим ситуацию с двумя телами справа.20,0-граммовый подвесной груз (m 2 ) прикреплен к 250-граммовому планеру с воздушным гусеничным ходом (m 1 ). Определите ускорение системы и натяжение струны.
Как и в примере задачи 1, эту систему необходимо сначала проанализировать концептуально, чтобы определить направление ускорения двух объектов. Это позволит назначить оси координат для каждого объекта. Поскольку ничто не толкает m 1 влево, мы могли бы предположить, что он будет ускоряться вправо из-за натяжения струны.Висящая масса (m 2 ) будет явно ускоряться вниз под действием силы тяжести. Таким образом, система координат выбрана для m 2 имеет положительную ось y, направленную вниз; система координат, выбранная для m 1 , имеет положительную ось x, направленную вправо. При таком выборе осей направление ускорения будет положительным для каждого объекта.
Диаграмма свободного тела для каждой отдельной массы показана ниже. Каждый объект испытывает нисходящую силу тяжести (F grav ), рассчитываемую как m 1 • g и m 2 • g соответственно.Планер (m 1 ) испытывает восходящую опорную силу (воздух толкает его вверх), чтобы уравновесить силу тяжести. Планер также испытывает горизонтальную силу – силу натяжения (F десятки ) вправо. Висящая масса (m 2 ) испытывает восходящую силу натяжения (F десятки ), которая оказывает некоторое сопротивление нисходящей силе тяжести.
Уравнение второго законаНьютона (F net = m • a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных.F net будет выражаться как сила в направлении ускорения минус все, что ему противодействует. Для параплана массой 250,0 грамм (0,250 кг) F net – это просто неуравновешенная сила натяжения (F десятки ). Для подвешенной массы 20,0 грамм (0,020 кг) F net записывается как 0,196 N – F десятки . Уравнения 4 и 5 являются результатом применения уравнения второго закона Ньютона к 250,0-граммовому планеру и 20,0-граммовой висящей массе. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях.Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
F десятки = 0,2500 • a
0,196 – F десятки = 0,0200 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 4 выражает значение F десятков с точки зрения ускорения. Это выражение для F tens можно подставить в уравнение 5, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
0,196 – 0,2500 • а = 0,0200 • а
0,196 = 0,2700 •
a = 0,196 / 0,2700 = 0,72593 м / с 2
а = ~ 0,726 м / с 2
Теперь, когда ускорение было найдено из уравнения 5, его значение можно подставить в уравнение 4, чтобы определить натяжение.
F десятки = 0,2500 • (0.72593) = 0,18148
F десятков = ~ 0,181 Н
Система шкивов, проанализированная в примере задачи 2, иногда упоминается как модифицированная машина Атвуда. Анализ немного сложнее, чем машина Атвуда в примере задачи 1. Последний пример задачи будет представлять собой случай модифицированной машины Атвуда с поверхностью, наклоненной, как показано ниже. Подход к решению проблем будет таким же.
Пример задачи 3
Рассмотрим ситуацию с двумя телами справа.Ящик 2,50×10 3 кг (m 1 ) стоит на наклонной плоскости и соединен кабелем с массой 4,00×10 3 кг (m 2 ). Эта вторая масса (m 2 ) подвешена на шкиве. Угол наклона 30,0 °, поверхность не имеет трения. Определите ускорение системы и натяжение троса.
Как и предыдущая задача, первая задача включает анализ ситуации, чтобы определить, в каком направлении объекты будут ускоряться.Такой анализ позволит присвоить каждому объекту систему координатных осей. В этом случае висящая масса (m 2 ) могла ускоряться вверх или вниз. Направление его ускорения зависит от сравнения его веса (силы тяжести) с противоположной силой, действующей на другую массу (m 1 ). Масса на наклонной плоскости сталкивается с тремя силами – силой тяжести, нормальной силой и силой натяжения. Сила тяжести направлена вниз (как обычно) и рассчитывается как m 1 • g.Нормальная сила направлена перпендикулярно поверхности (как обычно). Сила натяжения направлена вверх и вправо – параллельно наклонной плоскости и в той же ориентации, что и струна, обеспечивающая эту силу. Как обсуждалось на предыдущей странице, объекты, размещенные на наклонных плоскостях, анализируются путем разделения силы тяжести на два компонента. Один компонент направлен параллельно плоскости (и вниз под этим углом), а другой компонент направлен перпендикулярно плоскости (и вверх под этим углом).Это параллельная составляющая силы тяжести, которая пытается увести m 1 вниз по наклонной плоскости. Как упоминалось ранее, этот компонент может быть вычислен путем умножения веса объекта (m 1 • g) на синус угла наклона (30 °). Значение для F parallel составляет
. F параллельно = м 1 • g • синус (θ) = (2500 кг) • (9,8 Н / кг) • синус (30 °)
F параллельно = 12250 Н
Этот параллельный компонент силы тяжести пытается тянуть m 1 вниз по наклонной плоскости.Так как m 1 прикреплен кабелем к m 2 , подвесная масса будет тянуться вместе с ним. Однако есть противоположное действие силы тяжести, тянущее m 2 вниз; это противоположное действие, если оно будет доминирующим, перетащит объект m 1 вверх по наклонной плоскости. Сила тяжести на м 2 составляет
F grav-2 = m 2 • g = (4000 кг) • (9,8 Н / кг) = 39200 Н
Эта сила тяжести на m 2 является доминирующей силой.Таким образом, m 1 будет ускоряться вверх по наклонной плоскости, а m 2 будет ускоряться вниз. Оси координат назначаются соответственно так, чтобы каждый объект имел положительное ускорение.
На схемах ниже показаны эти оси координат и силы, действующие на два объекта. Три силы на m 1 уже обсуждались. На схеме показаны два компонента F grav . Как упоминалось на предыдущей странице, перпендикулярная составляющая силы тяжести рассчитывается как
F перпендикуляр = m 1 • g • cosθ = (2500 кг) • (9.8 Н / кг) • cos (30 °)
F перпендикуляр = 21218 Н
Нормальная сила (F norm ), действующая на m 1 , уравновешивает F перпендикуляр , так что нет ускорения, перпендикулярного наклонной плоскости. Значение нормы для F также составляет 21218 Н. Висящая масса (m 2 ) испытывает только две силы – силу тяжести, направленную вниз, и силу натяжения вверх.
Теперь уравнение второго закона Ньютона (F net = m • a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных.F net выражается как сила в направлении ускорения за вычетом любой силы, которая ему противодействует. Для груза массой 2500 кг на уклоне (m 1 ), F net – это просто сила натяжения (F десятки ) за вычетом параллельной составляющей силы тяжести. Для подвешенной массы 4000 кг (m 2 ) F net – это сила тяжести (39200 Н) за вычетом силы натяжения (F десятки ). Уравнения 6 и 7 являются результатом применения уравнения второго закона Ньютона к m 1 и m 2 .(Обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
F десятки – 12250 = 2500 • a
39200 – F десятки = 4000 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 6 можно изменить, чтобы получить выражение для F десятков , выраженное в единицах ускорения.
F десятки = 2500 • a + 12250
Это выражение для F tens можно подставить в уравнение 7, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
39200 – (2500 • a + 12250) = 4000 • a
39200 – 2500 • a – 12250 = 4000 • a
26950 = 6500 •
a = 26950/6500 = 4,1462 м / с 2
а = ~ 4,15 м / с 2
Теперь, когда ускорение было найдено из уравнения 7, его значение можно подставить в уравнение 8, чтобы определить силу натяжения (F десятки ).
F десятков = 2500 • a + 12250 = 2500 • (4,1462) + 12250 = 22615 N
F десятков = ~ 2,26 x 10 4 N
Проблемы с двумя телами, подобные этим трем примерам задач, могут быть довольно сложной задачей. Системный подход, применяемый к каждой проблеме, упрощает анализ. Хорошее концептуальное понимание, приверженность использованию диаграмм свободного тела и твердое понимание второго закона Ньютона – вот основные составляющие успеха.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора машины Этвуда. Вы можете найти его в разделе Physics Interactives на нашем сайте. Тренажер позволяет исследовать двухмассовые системы, ускоряемые подвешенной массой.
1. Рассмотрим ситуацию с двумя телами справа. 100,0-граммовый подвешенный груз (m2) прикрепляют к 325-граммовой массе (m1), покоящейся на столе. Коэффициент трения между 325,0-граммовой массой и столом составляет 0,215. Определите ускорение системы и натяжение струны.
2. Рассмотрим ситуацию с двумя телами справа.Ящик 3,50×10 3 кг (m 1 ) стоит на наклонной плоскости и соединен кабелем с массой 1,00×10 3 кг (m 2 ). Эта вторая масса (m 2 ) подвешена на шкиве. Угол наклона составляет 30,0 °, а поверхность имеет коэффициент трения 0,210. Определите ускорение системы и натяжение троса.
Двойные проблемы: две проблемы тела
Наше исследование до сих пор ограничивалось анализом отдельных объектов, движущихся под действием законов Ньютона.Но что произойдет, если два объекта так или иначе связаны вместе? Например, эвакуатор может тянуть машину по шоссе. Как проводится такой анализ? Как определяется ускорение эвакуатора и автомобиля? А как насчет силы, действующей между эвакуатором и автомобилем? В этой части Урока 3 мы попытаемся проанализировать такие ситуации. Мы обнаружим, что анализ проводится таким же общим образом, как и при наличии одного объекта – с использованием диаграмм свободного тела и законов Ньютона.
Базовый подходСитуации с двумя объектами часто называют ситуациями двух тел. Будучи физическими задачами, задачи двух тел характеризуются набором двух неизвестных величин. Чаще всего (хотя и не всегда) двумя неизвестными являются ускорение двух объектов и сила, передаваемая между двумя объектами. К двум телесным проблемам обычно можно подойти, используя один из двух основных подходов.Один из подходов включает комбинацию системного анализа и индивидуального анализа тела. В системном анализе два объекта рассматриваются как один объект, движущийся (или ускоряющийся) вместе как единое целое. Масса системы – это сумма масс двух отдельных объектов. Если задействовано ускорение, ускорение системы такое же, как и у отдельных объектов. Системный анализ обычно выполняется для определения ускорения системы. Системный анализ совмещен с анализом отдельного объекта.При анализе отдельных объектов один из двух объектов изолирован и рассматривается как отдельный независимый объект. Строится диаграмма свободного тела, определяются и вычисляются отдельные силы, действующие на объект. Анализ отдельного объекта обычно выполняется для определения значения любой силы, действующей между двумя объектами, например, контактных сил или сил натяжения.
Двойная комбинация системного анализа и анализа отдельного объекта – это один из двух подходов, которые обычно используются для анализа задач двух тел.Второй подход предполагает использование двух отдельных анализов отдельных объектов. При таком подходе диаграммы свободного тела строятся независимо для каждого объекта, и второй закон Ньютона используется для связи отдельных значений силы с массой и ускорением. Анализ каждого отдельного объекта генерирует уравнение с неизвестным. В результате получается система двух уравнений с двумя неизвестными. Система уравнений решается с целью определения неизвестных значений.
В качестве первого примера из двух подходов к решению задач двух тел рассмотрим следующий пример задачи.
Коробка 5,0 кг и коробка 10,0 кг соприкасаются друг с другом. К 5-килограммовому ящику прилагается горизонтальная сила 45,0 Н для ускорения обоих ящиков по полу. Не обращайте внимания на силы трения и определите ускорение коробок и силу, действующую между коробками.
Первый подход к этой проблеме предполагает двойное сочетание системного анализа и анализа отдельного объекта.Как уже упоминалось, системный анализ используется для определения ускорения, а анализ отдельного объекта используется для определения сил, действующих между объектами. В системном анализе два объекта рассматриваются как один объект. Разделительная линия, разделяющая объекты, игнорируется. Масса системы из двух объектов 15,0 кг. Схема свободного тела для системы показана справа. На систему действуют три силы – сила тяжести (Земля тянет вниз на 15.0 кг массы), нормальная сила (пол толкает систему вверх, чтобы выдержать ее вес) и приложенная сила (рука давит на заднюю часть системы). Сила, действующая между ящиком 5,0 кг и ящиком 10,0 кг, не учитывается в системном анализе, так как это внутренняя сила . Так же, как силы, удерживающие вместе атомы внутри объекта, не включены в диаграмму свободного тела, так и силы, удерживающие вместе части системы, игнорируются. Это считается внутренними силами; при построении диаграмм свободного тела учитываются только внешние силы.Величина силы тяжести составляет m • g или 147 Н. Величина нормальной силы также составляет 147 Н, поскольку она должна выдерживать вес (147 Н) системы. Приложенная сила составляет 45,0 Н. Второй закон Ньютона (a = F net / м) можно использовать для определения ускорения. При 45,0 Н для F , нетто и 15,0 кг для м, ускорение составляет 3,0 м / с 2 .
Теперь, когда ускорение определено, для каждого объекта можно выполнить анализ отдельного объекта, чтобы определить силу, действующую между ними.Неважно, какой объект выбран; результат будет одинаковым в любом случае. Здесь анализ отдельного объекта проводится на объекте массой 10,0 кг (только потому, что на него действует на одну силу меньше). Справа показана диаграмма свободного тела для объекта весом 10,0 кг. На него действуют только три силы: сила тяжести на 10,0 кг, сила опоры (от пола, толкающая вверх) и сила правого контакта (F , контакт ). По мере того как объект весом 5,0 кг ускоряется вправо, он будет толкать вправо на 10.0-килограммовый объект; это известно как контактная сила (или нормальная сила, или приложенная сила, или…). Вертикальные силы уравновешивают друг друга, поскольку нет вертикального ускорения. Единственная неуравновешенная сила, действующая на объект весом 10,0 кг, – это Fcontact. Эта сила представляет собой чистую силу и равна m • a, где m равно 10,0 кг (поскольку этот анализ предназначен для объекта весом 10,0 кг), а a уже было определено равным 3,0 м / с 2 . Чистая сила равна 30,0 Н. Эта чистая сила представляет собой силу, с которой объект массой 5,0 кг толкает 10.Объект весом 0 кг справа; она имеет величину 30,0 Н. Таким образом, ответы на два неизвестных для этой проблемы: 3,0 м / с 2 и 30,0 Н.
Теперь рассмотрим решение этой же проблемы, используя второй подход – использование анализа двух отдельных объектов. В процессе этого второго подхода мы проигнорируем тот факт, что знаем ответы, и будем предполагать, что решаем проблему впервые. При таком подходе выполняются два отдельных анализа диаграмм свободного тела.На диаграммах ниже показаны диаграммы свободного тела для двух объектов.
Обратите внимание, что на объект массой 5,0 кг сзади действуют четыре силы. Две вертикальные силы – F grav и F norm – очевидные силы. Приложенная сила 45,0 Н (F приложение ) является результатом давления руки на задний объект, как описано в формулировке проблемы и показано на диаграмме. Сила левого контакта на 5.Объект весом 0 кг – это сила, с которой объект весом 10,0 кг толкает влево объект весом 5,0 кг. Когда делается попытка подтолкнуть задний объект (объект весом 5,0 кг) вперед, передний объект (объект весом 10,0 кг) толкает его назад. Эта сила равна и противоположна заднему объекту, толкающему вперед передний объект. Эта сила просто обозначена как F , контакт для обеих диаграмм свободного тела. На диаграмме свободного тела для объекта массой 10,0 кг присутствуют только три силы. Еще раз, две вертикальные силы – F grav и F norm – очевидные силы.Горизонтальная сила – это просто объект весом 5,0 кг, толкающий вперед объект весом 10,0 кг. Приложенная сила 45,0 Н не действует на этот объект весом 10,0 кг; оно применяется к объекту массой 5,0 кг и уже было рассмотрено на предыдущей диаграмме свободного тела.
Теперь цель этого подхода состоит в том, чтобы создать систему из двух уравнений, которую можно решить для двух неизвестных значений. Использование F net = m • a с диаграммой свободного тела для объекта массой 5,0 кг даст уравнение 1 ниже:
45.0 – Контакт F = 5,0 • a
Использование F net = m • a с диаграммой свободного тела для объекта массой 10,0 кг даст уравнение 2 ниже:
F контакт = 10,0 • a
(Обратите внимание, что единицы были исключены из Уравнений 1 и 2, чтобы очистить уравнения до .) Если выражение 10.0 • a подставляется в Уравнение 1 для F контакта , тогда Уравнение 1 сводится к единственному уравнение с одной неизвестной.Уравнение принимает вид
45,0 – 10,0 • a = 5,0 • a
Пара шагов алгебры приводит к значению ускорения 3,0 м / с 2 . Это значение a можно подставить обратно в уравнение 2, чтобы определить контактное усилие:
Контакт F = 10,0 • a = 10,0 • 3,0
Контакт F = 30,0 Н
Как можно видеть, использование второго подхода к решению двух телесных задач дает те же два ответа для двух неизвестных.Теперь мы попробуем те же два подхода к очень похожей задаче, которая включает в себя силу трения.
Пример проблемы 2:
Коробка 5,0 кг и коробка 10,0 кг соприкасаются друг с другом. К 5-килограммовому ящику прилагается горизонтальная сила 45,0 Н для ускорения обоих ящиков по полу. Коэффициент кинетического трения 0.200. Определите ускорение и контактное усилие.
Наше первое решение этой проблемы будет включать двойную комбинацию системного анализа и анализа отдельного объекта. Как вы, вероятно, заметили, пример проблемы 2 аналогичен примеру проблемы 1, за исключением того, что поверхность не лишена трения в примере задачи 2. Поэтому при проведении анализа системы в этом втором примере необходимо учитывать трение в системе весом 15 кг. . Итак, диаграмма свободного тела для системы теперь включает четыре силы – те же три, что и в примере задачи 1, плюс левую силу трения.Сила трения в системе может быть рассчитана как μ • F norm , где F norm – нормальная сила, испытываемая системой. Норма F системы равна силе тяжести, действующей на систему массой 15,0 кг; это значение составляет 147 Н. Итак,
F frict = μ • F norm = (0.200) • (147 N) = 29.4 N
Вертикальные силы уравновешивают друг друга – в соответствии с тем фактом, что нет вертикального ускорения.Горизонтальные силы не уравновешивают друг друга. Чистая сила может быть определена как векторная сумма F app и F frict . То есть F net = 45,0 Н, правая + 29,4 Н, левая; они добавляют к 15,6 Н, верно. Теперь ускорение можно рассчитать, используя второй закон Ньютона.
a = F , нетто / м = (15,6 Н / 15,0 кг) = 1,04 м / с 2
Теперь, когда системный анализ был использован для определения ускорения, можно выполнить анализ отдельного объекта для любого объекта, чтобы определить силу, действующую между ними.Опять же, не имеет значения, какой объект выбран; результат будет одинаковым в любом случае. Объект массой 10 кг выбран для анализа отдельного объекта, поскольку на него действует на одну силу меньше; это упрощает решение. На объект весом 10,0 кг действуют четыре силы. Две вертикальные силы очевидны – сила тяжести (98,0 Н) и нормальная сила (равная силе тяжести). Горизонтальные силы – это сила трения слева и сила 5,0-килограммового объекта, толкающего 10.0-килограммовый объект вперед; на схеме свободного тела он обозначен как F , контакт . Чистую силу – векторную сумму всех сил – всегда можно найти, сложив силы в направлении ускорения и вычтя те, которые действуют в противоположном направлении. Этот F net равен F contact – F frict . Применение второго закона Ньютона к этому объекту дает уравнение:
F контакт – F frict = (10,0 кг) • (1.04 м / с 2 )
Сила трения на этом объекте весом 10,0 кг отличается от силы трения в системе (поскольку система весила кг и ). Значение F frict можно вычислить как μ • F norm , где F norm – нормальная сила, испытываемая объектом весом 10,0 кг. Норма F для 10,0-кг объекта равна силе тяжести, действующей на 10-килограммовый объект; это значение 98.0 Н. Итак,
F frict = μ • F norm = (0.200) • (98,0 Н) = 19,6 Н
Итак, теперь значение 19,6 Н может быть подставлено в приведенное выше уравнение и F контакт может быть вычислен:
F контакт – 19,6 Н = (10,0 кг) • (1,04 м / с 2 )
Контакт F = (10,0 кг) • (1,04 м / с 2 ) + 19,6 Н
Контакт F = 30,0 Н
Таким образом, использование двойной комбинации системного анализа и индивидуального анализа тела позволяет нам определить два неизвестных значения – 1.04 м / с 2 для ускорения и 30,0 Н для контакта F . Теперь мы увидим, как два анализа отдельных объектов могут быть объединены, чтобы сгенерировать систему из двух уравнений, способных разрешить две неизвестные. Мы еще раз начнем анализ, предполагая, что мы решаем проблему впервые и не знаем ни ускорение, ни контактную силу. Диаграммы свободного тела для отдельных объектов показаны ниже.
Теперь пять сил на 5.Объект весом 0 кг сзади. Две вертикальные силы – F grav и F norm – очевидные силы. Приложенная сила 45,0 Н (F , приложение ) является результатом давления руки на задний объект. Сила левого контакта с объектом массой 5,0 кг – это сила, с которой объект массой 10 кг толкает влево объект массой 5,0 кг. Его значение такое же, как сила контакта, прилагаемая к переднему объекту весом 10,0 кг задним объектом весом 5,0 кг. Эта сила просто обозначена как F , контакт для обеих диаграмм свободного тела.Наконец, сила трения влево является результатом трения о пол, по которому движется объект весом 5,0 кг. На диаграмме свободного тела для объекта весом 10,0 кг теперь четыре силы. Две вертикальные силы – F grav и F norm – очевидны. Правое контактное усилие (F contact ) – это просто объект весом 5,0 кг, толкающий вперед объект весом 10,0 кг. А сила трения влево – это результат трения о пол. И снова на этот 10 не действует приложенная сила 45,0 Н.0-килограммовый объект; оно применяется к объекту массой 5,0 кг и уже было рассмотрено на предыдущей диаграмме свободного тела. Сила трения для каждого объекта может быть определена как μ • Fnorm, где F norm – нормальная сила, испытываемая отдельными объектами. Каждый объект испытывает нормальную силу, равную его весу (поскольку вертикальные силы должны уравновешиваться). Таким образом, силы трения для объекта весом 5,0 кг (вес 49,0 Н) и объекта весом 10,0 кг (вес 98,0 Н) составляют 0,200 • 49,0 Н и 0,200 • 98,0 Н соответственно.
Используя эти значения F frict и второй закон Ньютона, можно записать систему из двух уравнений, позволяющую найти два неизвестных значения. Использование F net = m • a с диаграммой свободного тела для объекта массой 5,0 кг даст уравнение 3 ниже:
45,0 – F контакт – 9,8 = 5,0 • a
Использование F net = m • a с диаграммой свободного тела для объекта массой 10,0 кг даст уравнение 4 ниже:
F контакт – 19.6 = 10,0 •
(Обратите внимание, что единицы были исключены из Уравнений 3 и 4, чтобы очистить уравнения до .) Из Уравнения 4, контакт F = 10,0 • a + 19,6. Подставляя это выражение для контакта F в уравнение 3 и выполняя правильные алгебраические манипуляции, получаем значение ускорения:
45,0 – (10,0 • a + 19,6) – 9,8 = 5,0 • a
45,0 – 19,6 – 9,8 = 15,0 •
15,6 = 15,0 •
а = (15,6 / 15.0) = 1,04 м / с 2
Это значение ускорения можно подставить обратно в выражение для F contact , чтобы определить контактное усилие:
Контакт F = 10,0 • a + 19,6 = 10,0 • (1,04) + 19,6
Контакт F = 30,0 Н
Опять же, мы обнаруживаем, что второй подход с использованием анализа двух отдельных объектов дает тот же набор ответов для двух неизвестных. Последний пример задачи будет включать вертикальное движение.Подходы останутся прежними.
Пример задачи 3:Мужчина входит в лифт с двумя коробками – одна на другой. Верхний ящик имеет массу 6,0 кг, а нижний – 8,0 кг. Мужчина ставит две коробки по метрической шкале на пол. При ускорении вверх из состояния покоя мужчина замечает, что шкала показывает значение 166 Н; это сила, направленная вверх на нижнюю коробку.Определите ускорение лифта (и ящиков) и определите силы, действующие между ящиками.
Для решения этой проблемы будут использоваться оба подхода. Первый подход предполагает двойное сочетание системного анализа и анализа отдельного объекта. Для системного анализа две коробки считаются единой системой массой 14,0 кг. На эту систему действуют две силы – сила тяжести и нормальная сила. Схема свободного тела показана справа.Сила тяжести рассчитывается обычным образом с использованием массы 14,0 кг.
F grav = m • g = 14,0 кг • 9,8 Н / кг = 137,2 Н
Поскольку существует вертикальное ускорение, вертикальные силы не уравновешиваются; F grav не соответствует значению F norm . Нормальная сила указана в формулировке задачи. Эта нормальная сила 166 Н представляет собой направленную вверх силу, действующую на нижнюю коробку; он служит силой для системы, поскольку нижний ящик является частью системы.Чистая сила – это векторная сумма этих двух сил. Итак,
F net = 166 N, вверх + 137,2 N, вниз = 28,8 N, вверх
Ускорение можно рассчитать, используя второй закон Ньютона:
a = F нетто / м = 28,8 Н / 14,0 кг = 2,0571 м / с 2 = ~ 2,1 м / с 2
Теперь, когда системный анализ был использован для определения ускорения, можно выполнить анализ отдельного объекта для любого блока, чтобы определить силу, действующую между ними.Как и в предыдущих задачах, не имеет значения, какой ящик выбран; результат будет одинаковым в любом случае. Верхний ящик используется в этом анализе, поскольку он встречает на одну силу меньше. Схема свободного тела показана справа. Сила тяжести на верхнем ящике равна m • g, где m = 6,0 кг. Сила тяжести составляет 58,8 Н. Сила, направленная вверх, неизвестна, но может быть рассчитана, если сетка F = m • уравнение применяется к диаграмме свободного тела. Поскольку ускорение направлено вверх, сторона Fnet уравнения будет равна силе в направлении ускорения (F контакт ) минус сила, которая ему противодействует (F grav ).Итак,
F контакт – 58,8 Н = (6,0 кг) • (2,0571 м / с2)
(Обратите внимание, что здесь используется неокругленное значение ускорения; округление произойдет, когда будет определен окончательный ответ.) Решение для контакта F дает 71,14 Н. Это число может быть округлено до двух значащих цифр – 71 Н. Таким образом, двойное Комбинация системного анализа и индивидуального анализа тела приводит к ускорению 2,1 м / с 2 и силе контакта 71 Н.
Теперь второй подход к решению проблемы будет использован для решения той же проблемы. В этом решении два анализа отдельных объектов будут объединены для создания системы двух уравнений, способных решить для двух неизвестных. Мы начнем этот анализ с предположения, что мы решаем проблему впервые и не знаем ни ускорение, ни контактную силу. Диаграммы свободного тела для отдельных объектов показаны ниже.
Обратите внимание, что значения F grav для двух ящиков были включены в диаграмму.Они были рассчитаны с использованием F grav = m • g, где m = 6,0 кг для верхнего ящика и m = 8,0 кг для нижнего ящика. Контактная сила (F , контакт ) на верхнем блоке направлена вверх, поскольку нижний блок толкает его вверх, когда система из двух объектов ускоряется вверх. Контактное усилие (F контакт ) на нижнем блоке направлено вниз, поскольку верхний блок толкает вниз нижний блок, когда происходит ускорение. Эти две контактные силы равны друг другу, поскольку они возникают в результате взаимодействия между двумя коробками.Третья сила на нижнем ящике – это сила, с которой весы толкают его вверх с силой 166 Н; это значение было указано в постановке задачи.
Применение второго закона Ньютона к этим двум диаграммам свободного тела приводит к уравнению 5 (для контейнера весом 6,0 кг) и уравнению 6 (для контейнера весом 8,0 кг).
F контакт – 58,8 = 6,0 • a
166 – F контакт – 78,4 = 8,0 • a
Теперь, когда разработана система двух уравнений, алгебру можно использовать для решения двух неизвестных.Уравнение 5 можно использовать для записи выражения для контактной силы (F , контакт ) через ускорение (a).
F контакт = 6,0 • a + 58,8
Это выражение для контакта F можно затем подставить в уравнение 6. Уравнение 6 тогда преобразуется в
.166 – (6,0 • a + 58,8) – 78,4 = 8,0 • a
Следующие алгебраические шаги выполняются над приведенным выше уравнением, чтобы найти ускорение.
166 – 6,0 • a – 58,8 – 78,4 = 8,0 • a
166 – 58,8 – 78,4 = 8,0 • а + 6,0 • а
28,8 = 14,0 а
a = 2,0571 м / с 2 = ~ 2,1 м / с 2
Теперь значение ускорения (a) можно подставить обратно в выражение для F контакт (F контакт = 6.0 • a + 58.8), чтобы найти F контакт . Контактное усилие составляет 71,14 Н (~ 71 Н).
Следует отметить, что второй подход к этой проблеме дает те же численные ответы, что и первый подход.Студентам предлагается использовать наиболее удобный для них подход.
Для дополнительной практики рассмотрите следующие задачи с двумя телами. Для каждой проблемы была предоставлена сокращенная версия решения . К теме задач двух тел мы вернемся в следующей главе, когда мы рассмотрим ситуации, в которых шкивы и объекты движутся в разных направлениях.
Проверьте свое понимание1.Грузовик везет машину по пересеченной местности. Масса грузовика 4,00х10 3 кг, масса автомобиля 1,60х10 3 кг. Если сила тяги, возникающая в результате поворота колес грузовика, составляет 2,50×10 4 Н, то определите ускорение автомобиля (или грузовика) и силу, с которой грузовик тянет на автомобиль. Предположим, что силы сопротивления воздуха незначительны.
2. Ящик весом 7,00 кг прикреплен к 3.Ящик массой 00 кг на веревке 1. Ящик массой 7,00 кг тянут веревкой 2 с усилием 25,0 Н. Определите ускорение ящиков и натяжение веревки 1. Коэффициент трения между землей и ящиками составляет 0,120 .
3. Трактор тащит два больших бревна через поле. Цепочка соединяет бревна друг с другом; переднее бревно соединяется с трактором отдельной цепью. Масса лобового бревна 180 кг.Масса заднего бревна 220 кг. Коэффициент трения между бревнами и полем составляет примерно 0,45. Натяжение цепи, соединяющей трактор с передним бревном, составляет 1850 Н. Определите ускорение бревен и натяжение цепи, соединяющей два бревна.
4. Два ящика скреплены прочной проволокой и прикреплены к потолку лифта вторым проводом (см. Схему).Масса приставки 14,2 кг; масса нижнего ящика 10,4 кг. Лифт поднимается вверх со скоростью 2,84 м / с 2 . (Предположим, что провод относительно безмассовый .)
(a) Найдите натяжение верхнего троса (точки соединения A и B).
(b) Найдите натяжение нижней проволоки (точки соединения C и D).6.1 Решение проблем с помощью законов Ньютона – Университетская физика, том 1
Сила сопротивления на барже
Два буксира толкают баржу под разными углами (рис. 6.4). Первый буксир прикладывает силу 2,7 × 105 Н2,7 × 105 Н в направлении x , а второй буксир прикладывает силу 3,6 × 105 Н3,6 × 105 Н в направлении y . Масса баржи составляет 5,0 × 106 кг 5,0 × 106 кг, а ее ускорение составляет 7,5 × 10–2 м / с27,5 × 10–2 м / с2 в указанном направлении. Какова сила сопротивления воды барже, сопротивляющейся движению? ( Примечание: Сила сопротивления – это сила трения, создаваемая жидкостями, такими как воздух или вода.Сила сопротивления препятствует движению объекта. Поскольку баржа имеет плоское дно, можно предположить, что сила сопротивления направлена в направлении, противоположном движению баржи.) Рис. 6.4 (a) Вид сверху двух буксиров, толкающих баржу. (b) Схема свободного тела для корабля содержит только силы, действующие в плоскости воды. В нем не учитываются две вертикальные силы – вес баржи и подъемная сила поддерживающей ее воды, которые не показаны. Обратите внимание, что F → appF → app – это общая приложенная сила буксиров.Стратегия
Направления и величины ускорения и приложенных сил показаны на Рисунке 6.4 (а). Мы определяем общую силу буксиров на барже как F → appF → app так, чтобы F → приложение = F → 1 + F → 2.F → приложение = F → 1 + F → 2.Сопротивление воды F → DF → D направлено в направлении, противоположном направлению движения лодки; эта сила, таким образом, действует против F → app, F → app, как показано на диаграмме свободного тела на Рисунке 6.4 (b). Здесь представляет интерес система баржа, поскольку на нее действуют силы, а также ее ускорение.Поскольку приложенные силы перпендикулярны, оси x и y находятся в том же направлении, что и F → 1F → 1 и F → 2.F → 2. Проблема быстро становится одномерной в направлении F → appF → app, поскольку трение происходит в направлении, противоположном F → app.F → app. Наша стратегия состоит в том, чтобы найти величину и направление чистой приложенной силы F → appF → app, а затем применить второй закон Ньютона для определения силы сопротивления F → D.F → D.
Решение
Поскольку FxFx и FyFy перпендикулярны, мы можем определить величину и направление F → appF → app напрямую.Во-первых, результирующая величина определяется теоремой Пифагора: Fapp = F12 + F22 = (2.7 × 105N) 2+ (3.6 × 105N) 2 = 4.5 × 105N. Fapp = F12 + F22 = (2.7 × 105N) 2+ (3.6 × 105N) 2 = 4.5 × 105N.Угол равен
θ = tan − 1 (F2F1) = tan − 1 (3,6 × 105N2,7 × 105N) = 53,1 °. θ = tan − 1 (F2F1) = tan − 1 (3,6 × 105N2,7 × 105N) = 53,1 °.Из первого закона Ньютона мы знаем, что это то же направление, что и ускорение. Мы также знаем, что F → DF → D находится в противоположном направлении от F → app, F → app, поскольку он замедляет ускорение. Следовательно, чистая внешняя сила имеет то же направление, что и F → app, F → app, но ее величина немного меньше, чем F → app.F → приложение. Проблема теперь одномерная. Из диаграммы свободного тела видно, что
Fnet = Fapp-FD.Fnet = Fapp-FD.Однако второй закон Ньютона гласит, что
Таким образом,
Fapp-FD = ma.Fapp-FD = ma.Это может быть решено для величины силы сопротивления водного FDFD в виде известных величин:
FD = Fapp-ma. FD = Fapp-ma.Подстановка известных значений дает
FD = (4,5 × 105 Н) – (5,0 × 106 кг) (7,5 × 10–2 м / с2) = 7,5 × 104 Н. FD = (4,5 × 105 Н) – (5,0 × 106 кг) (7,5 × 10–2 м / с2) = 7,5 × 104 Н.Направление F → DF → D уже определено как направление, противоположное F → app, F → app, или под углом 53 ° 53 ° к югу от запада.

 Так как подвижный блок дает нам выигрыш в силе в два раза, то в пути мы
проиграем также в два раза, то есть высота подъема мешка цемента будет в два
раза меньше высоты подъема точки приложения силы
Так как подвижный блок дает нам выигрыш в силе в два раза, то в пути мы
проиграем также в два раза, то есть высота подъема мешка цемента будет в два
раза меньше высоты подъема точки приложения силы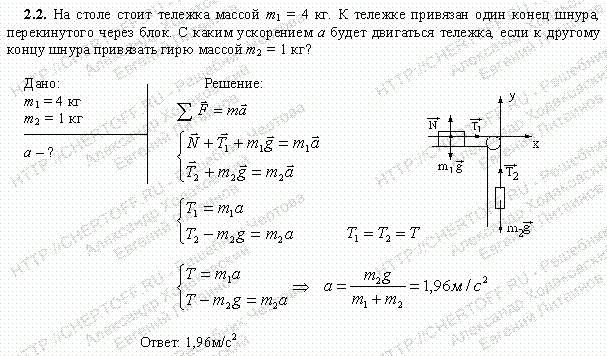 Так как на блоки с обеих сторон действуют
силы натяжения T, а на ось каждого блока
действует вес подвешенного на него груза и вес самого блока, то получаем, что
в равновесии сила тяжести, действующая на каждый из блоков с грузом,
уравновешивается удвоенной силой натяжения троса
Так как на блоки с обеих сторон действуют
силы натяжения T, а на ось каждого блока
действует вес подвешенного на него груза и вес самого блока, то получаем, что
в равновесии сила тяжести, действующая на каждый из блоков с грузом,
уравновешивается удвоенной силой натяжения троса