Теоремы физики – Категория:Физические теоремы — Википедия
- Теорема Гаусса
- Основная теорема физики
- Теоретическая физика — Википедия
- Третье начало термодинамики (тепловые теоремы Нернста и Планка) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
- Теорема Карно | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
- О теореме вириала и ее физическом смысле
- Эренфеста теоремы – Физическая энциклопедия
Теорема Гаусса
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора на площадь ΔS и на косинус угла α между вектором и нормалью к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 1.3.1):
| ΔΦ = E ΔS cos α = En ΔS, |
где En – модуль нормальной составляющей поля
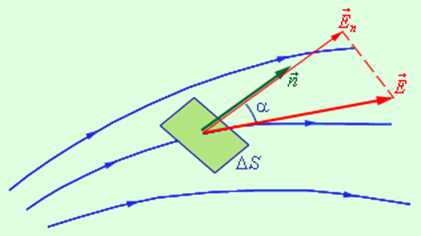 |
| Рисунок 1.3.1. К определению элементарного потока ΔΦ |
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки ΔΦi поля через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора через замкнутую поверхность S (рис. 1.3.2):
В случае замкнутой поверхности всегда выбирается внешняя нормаль.
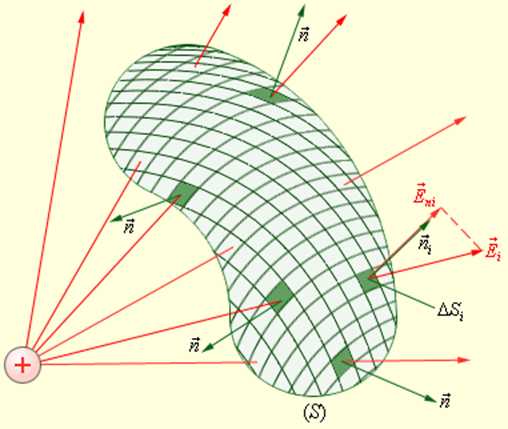 |
| Рисунок 1.3.2. Вычисление потока Ф через произвольную замкнутую поверхность S |
Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
Для доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю
где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR2. Следовательно,
Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R0 (рис. 1.3.3).
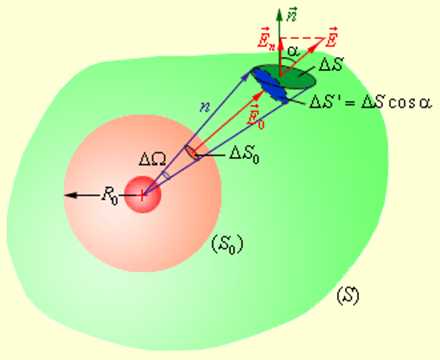 |
| Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд |
Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки одинаковы. Действительно,
| ΔΦ0 = E0ΔS0, ΔΦ = EΔS cos α = EΔS ‘. |
Здесь ΔS’ = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Так как , a , следовательно Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φi электрических полей отдельных зарядов. Если заряд qi оказался внутри поверхности S, то он дает вклад в поток, равный если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
Таким образом, теорема Гаусса доказана.
Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.
Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.
Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R. Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
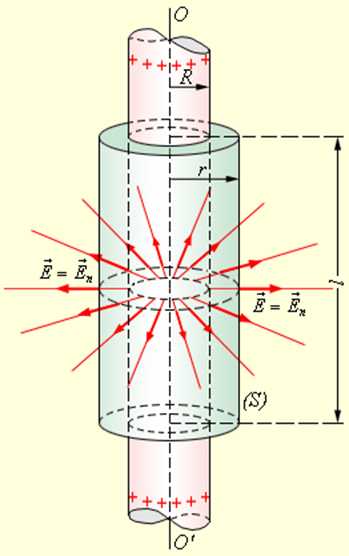 |
| Рисунок 1.3.4. Вычисление поля однородно заряженного цилиндра. OO’ – ось симметрии |
При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:
где τ – заряд единицы длины цилиндра. Отсюда
Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.
Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).
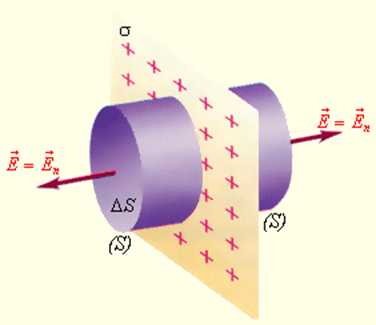 |
| Рисунок 1.3.5. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность |
В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает:
где σ – поверхностная плотность заряда, т. е. заряд, приходящийся на единицу площади.
Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.
questions-physics.ru
Основная теорема физики
Бывают ли теоремы в физике? Да, мы знаем, что 1) учащимся и учителям непривычно воспринимать слово “теорема” применительно к физике. Но, что делать, если здесь будет много геометрии. 2) Мы знаем, что теорема – это суждение, справедливость которого требуется доказать и придется доказывать, потому что с нашей стороны доказательств не будет, мы лишь опишем те наблюдения, которые нам удалось сделать. 3) Задача, которую мы вам предложим, содержит геометрический чертеж, а это еще один мотив для нашего заголовка. Речь идет о задаче № 1.2 из “Сборника избранных задач по физике” М.П. Шаскольский и Э.А. Эльцина стр.(5, 67): “Какую экспозицию нужно делать при фотографировании автомобиля, движущегося со V=36 км/ч, чтобы его изображение на негативе не размывалось, если для этого смещение X изображения должно быть не более 0,1 мм (рис.1).
Рис. 1
Для автомобиля L=3м, а размер изображения на негативе
получается равным l=1,5 см. Пусть искомое время равно t секунд, тогда автомобиль
успеет проехать за это время расстояние, равное V•t. За это же время смещение
изображения должно быть не более 0,1 мм. Отношение этих величин должно,
очевидно, равняться отношению длины автомобиля к размеру его изображения, т.е.
L/l=300/1,5=200. Следовательно, t=(200•0,01)/10
• или
Если подменить слагаемое V•t другим , то равенство нарушится
Введем обозначение X‘ и запишем равенство
или
Предположим, что существует такое V‘, что справедливо равенство
Мы видим, что появление новой величины влечет за собой появление новой величины .
Теперь получается формула
(1)
Если, теперь, открыть справочник по физике, содержащий данные по СТО, там найдется формула Эйнштейна
(2)
Как пишут в детективных в детективных романах “все совпадения считать случайными”. Но мы и не претендуем на многое, а всего лишь отмечаем, что оба равенства (1) и (2) имеют одинаковую структуру. “Основная теорема” теперь может быть сформулирована. Можно ли вывести (2) из (1), и наоборот (1) из (2)?
Если вам не нравятся новые элементы и , то заметим, что в их появлении состоит эвристический прием, который называется: введение вспомогательных элементов. Приведем пример: решим уравнение
+12•=10
Сразу видно, что выражение нельзя преобразовать в более простой вид. Однако, зная, что
+=1
и что 52+122=132, разделив все члены уравнения на 13, получим
+•=
Введем вспомогательный элемент , где 0<<90°
Тогда . Уравнение принимает такой вид
+= или
Это один из методов решения задач. Всего их три: разбиение задачи на подзадачи, преобразование (моделирование) задачи и уже упоминавшимся методом вспомогательных элементов. Так, во всяком случае, утверждается в книге Л.М. Фридмана и Е.Н. Турецкого “Как научиться решать задачи”. Процитируем из книги Л.М. Фридмана и Е.Н. Турецкого: Психология уже свыше ста лет занимается исследованием процессов решения задач человеком. В результате этих исследований открыто много интересных закономерностей и найдены важные характеристики процессов решения задач. Особый интерес представляет общая характеристика этого процесса, данная известным советским психологом С.В. Рубинштейном (1889-1960). Он характеризовал решение задач человеком как процесс их переформулирования, в котором непрерывно производится анализ условий и требований задачи через синтетический акт соотнесения.
Естественно возникает вопрос: а в чем состоит это переформулирование? Что получаем? Какими средствами производится переформулирование?”. Речь в этом отрывке шла о моделировании, как методе решения задачи. Применительно к нашему случаю переформулирвание (моделирование) может осуществляться вращением фотоаппарата вокруг собственной оси (воображаемой конечно).
Но, что говорят авторы о подзадачах. Они приводят такой пример.
Найти чему равна разность
–
Подзадачи получаются из вопросов:
1. Почему под знаком первого квадратного корня стоит модуль разности ?
2. Нельзя ли избавиться от этого модуля, что для этого нужно сделать?
3. Каким числом: положительным или отрицательным является заданная разность?
Авторы исходят из концепции (способ понимания), что анализ это задавание вопросов вычленяющих какую-либо особенность. Анализ и есть вычленение. Применительно к нашему случаю можно предложить подзадачу. Что будет, если автомобиль будет двигаться по синусоидальному закону, а фотографирование производится в произвольные промежутки времени, т.е. случайно? Так и хочется забросить этот вопрос специалистам по квантовой механике (начинающим).
Подведем краткий итог нашему рассказу. На интересной проблемной задаче мы рассказали учащимся о средствах и приемах, которые помогут им осознанно ориентироваться в учебном материале.
urok.1sept.ru
Теоретическая физика — Википедия
Материал из Википедии — свободной энциклопедии
Теорети́ческая фи́зика — раздел физики, в котором в качестве основного способа познания природы используется создание теоретических (в первую очередь математических) моделей явлений и сопоставление их с реальностью. В такой формулировке теоретическая физика является самостоятельным методом изучения природы, хотя её содержание, естественно, формируется с учётом результатов экспериментов и наблюдений за природой.
Методология теоретической физики[1] состоит в выделении ключевых физических понятий (таких, как атом, масса, энергия, энтропия, поле и т. д.) и формулировки на математическом языке законов природы, связывающих эти понятия; объяснении наблюдаемых явлений природы на основе сформулированных законов природы; предсказании новых явлений природы, которые могут быть обнаружены.
Близким аналогом является математическая физика, которая исследует свойства физических моделей на математическом уровне строгости, однако не занимается вопросами выбора физических понятий и сопоставления моделей с реальностью (хотя вполне может предсказать новые явления).
Теоретическая физика не рассматривает вопросы вида «почему математика должна описывать природу?». Она принимает за постулат то, что, в силу неких причин, математическое описание природных явлений оказывается крайне эффективным[2], и изучает последствия этого постулата. Строго говоря, теоретическая физика изучает не свойства самой природы, а свойства предлагаемых теоретических моделей. Кроме того, часто теоретическая физика изучает какие-либо модели «сами по себе», без привязки к конкретным природным явлениям.
Однако основной задачей теоретической физики остаётся открытие и понимание наиболее общих законов природы, управляющих какой-либо областью физических явлений, и, во-вторых, исходя из этих законов, описание ожидаемого поведения тех или иных физических систем в реальности. Почти специфической особенностью теоретической физики в отличие от других естественных наук является предсказание ещё неизвестных физических явлений и точных результатов измерений.
Продуктом теоретической физики являются физические теории. Поскольку теоретическая физика работает именно с математическими моделями, крайне важным требова
ru.wikipedia.org
Третье начало термодинамики (тепловые теоремы Нернста и Планка) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Третье начало термодинамики — это утверждение о принципиальной недостижимости абсолютного нуля температуры. Самое «молодое» из термодинамических начал, оно было сформулировано только в начале XX в. Третье начало завершает аксиоматическое построение термодинамики.
Третье начало утверждает, что при абсолютном нуле температуры энтропия обращается в нуль. Отсюда следует категорический запрет на существование физических объектов с температурой, равной абсолютному нулю:
T ≠ 0 K = -273,16 °C.
В отличие от потенциальной энергии гравитационного поля или электростатического потенциала, энтропия определяется однозначно. Это позволяет рассматривать термодинамику как формально замкнутую схему рассуждений, не нуждающуюся во внешних по отношению к ней доказательствах.
Обсудим сначала характер недостижимости нуля, который существует уже в рамках второго начала. Рассмотрим холодильную машину, отбирающую теплоту Q2 у тела с температурой T2. Из второго начала в форме Карно следует, что холодильный коэффициент любой тепловой машины не превышает холодильного коэффициента обратимой машины:
χ = Q2 / A = Q2 / (Q1 — Q2) <= 2 / (T1 — T2).
| Установка для получения сверхнизких температур |
Если T2 → 0 K, то и χ ∞ 0, а, следовательно, необходимая для отбора теплоты работа стремится к бесконечности:
A = Q1 — Q2 → ∞.
Это означает, что мы не можем изготовить тепловой резервуар (термостат) с T = 0 K путем охлаждения реального физического тела. Остается, правда, открытым вопрос о существовании в природе уже готовых термостатов с нулевой температурой. Вот их отсутствие и постулируется в третьем начале термодинамики, которое формулируется в двух вариантах: в узком смысле («Тепловая теорема Нернста») и в широком смысле («Тепловая теорема Планка»).
Согласно тепловой теореме Нернста (1906 г.), при абсолютном нуле все изменения энтропии
limT→0ΔS = 0.
Тепловая теорема Планка (1910 г.) более радикальна: при абсолютном нуле S обращается в нуль:
limT→0S = 0.
| Шкала температур кипения и затвердевания некоторых веществ |
Для чисто термодинамического подхода достаточно теоремы Нернста. В статистической физике более естественен подход Планка, а теорема Нернста уже не является аксиомой, а получается автоматически, как следствие статистического подхода.
Из третьего начала в формулировке Нернста следует, что все термодинамические процессы, протекающие при температуре, стремящейся к абсолютному нулю, не сопровождаются изменением энтропии. Другими словами, изотерма T = 0 K совпадает с предельной адиабатой
S = S0 (dQ = TdS = 0),
т.е. верно утверждение о недостижимости абсолютного нуля с помощью адиабатических процессов. Действительно, любая адиабата с S ≠ S0не пересекается с адиабатой S = S0, которая, в силу теоремы Нернста, совпадает с изотермой T = 0 K.
Так как любой термодинамический процесс может быть представлен как совокупность адиабатических и изотермических процессов, то абсолютный нуль никогда не может быть достигнут!
Третье начало в формулировке Планка устраняет неопределенность в задании энтропии, связанную с произволом в выборе начальной константы. Действительно, выбирая в качестве начальной точки процесса состояние с T = 0 K, получим:
S0 = limT→0S = 0 ⇒ S = S0 + ∫T0(dQ / T) = ∫T0(dQ / T).
Третье начало термодинамики накладывает определенные ограничения на уравнения состояния. В частности, калорическое уравнение идеального газа оказывается непригодным вблизи абсолютного нуля. Запишем изохорную теплоемкость как функцию от энтропии:
CV = dQ / T [V = const] = TdS / T [V = const] ⇒ dS = CVdT / T.
В силу третьего начала, при T → 0 изменение энтропии ΔS → 0 и, следовательно, изохорная теплоемкость также должна стремиться к нулю:
limT→0CV = 0. Материал с сайта http://worldofschool.ru
В термодинамической системе, именуемой одноатомным идеальным газом,
PV = RT;
CV = 3R / 2,
это условие явно нарушается!
Доказать какое-либо утверждение в математике, например теорему о равенстве треугольников в геометрии, означает вывести ее с помощью логических переходов из некоторых аксиом. Математики могут использовать различные системы аксиом, обсуждать их независимость и непротиворечивость друг другу, но справедливость самих аксиом не обсуждается и не доказывается (их не из чего выводить!). Начала термодинамики — это те же аксиомы, но физики, а не математики. Следовательно, имеется способ доказательства, отсутствующий в математике, — Его Величество Опыт! Начала термодинамики являются обобщением огромного количества опытных данных и в этом смысле доказаны (с точки зрения физики). Можно, конечно, использовать эквивалентные формулировки начал термодинамики (эквивалентность надо доказывать!) и выбирать наиболее удобные, наглядные или красивые из них (к сожалению, это обычно различные формулировки).
На этой странице материал по темам:Задачи на теорему нернста
Задачи по теореме нернста с решениями
Физика теорема нернста-планка
Математическое выражение теоремы нернста
Третий закон термодинамики физика формула
worldofschool.ru
Теорема Карно | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема: Физические теоремы
Все равновесные процессы являются обратимыми.
Это означает, что они могут протекать как в прямом, так и в обратном направлениях, причем система при этом проходит через одни и те же состояния и ни в самой системе, ни в окружающей среде не возникает никаких остаточных изменений. Такое полное отсутствие «памяти» встречается очень редко, и большинство реальных процессов в природе не удовлетворяет этим условиям, т. е. являются необратимыми. Тепловые машины, работающие по равновесным (обратимым) циклам, называются обратимыми машинами.
Рассмотрим проблему конструирования «наилучшего двигателя всех времен и народов». Машина Карно (конкретное ее устройство нас, как последовательных термодинамиков, не интересует!) — кандидат на это звание. Она является обратимой машиной, содержит термодинамически очень выгодные, адиабатические и изотермические процессы. Остается, правда, открытым вопрос о числе и последовательности этих процессов, обеспечивающих максимальный КПД (может быть, надо использовать более сложные циклы, чем Карно?). Оказывается, что конкретное устройство обратимой машины и тип рабочего тела не важны. Имеет место следующее утверждение, известное как теорема Карно:
«КПД двух обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от конструкции машин». Материал с сайта http://worldofschool.ru
Реальные циклы тепловых двигателей необратимы и в действительности даже незамкнуты, так как в них рабочее тело (сгоревшая смесь газов) по окончании цикла выбрасывается наружу! Тем не менее, идеальные обратимые машины чрезвычайно важны для теоретических построений. Предположим, что одна из двух машин, рассмотренных выше, является необратимой. Тогда «КПД необратимой машины не может превышать КПД обратимой машины».
На этой странице материал по темам:О теореме карно
Teorema karno
worldofschool.ru
О теореме вириала и ее физическом смысле
Home / Публикации / Статьи / О теореме вириала и ее физическом смысле
Известная нам физика и химия основана на законах и правилах, называемых разнообразно то принципами, то постулатами или исходными сущностями. Наиболее яркими примерами аксиом в физике являются законы механики и принцип эквивалентности Ньютона, постулаты Бора и принцип неопределенности Гейзенберга, ОТО и СТО Эйнштейна, Теория большого взрыва и т.д. и т.п.
В химии такой подход демонстируют правила Льюиса, Периодический закон, теория резонанса и т д. Общим для данного способа движения научной мысли является отсутствие причинно – следственных связей, описываемых в приведенных выше названиях. В настоящее время формирование таких правил, законов и теорий считается подавляющей массой научных сотрудников, а также людей далеких от науки, конечной целью (достижением) физики и химии.
Согласно истории науки такая ситуация существует со времени ее становления.
Наряду с подавляющим числом людей, считающих эти достижения конечным результатом науки, во все времена существовали также люди, глубинно интересующиеся наукой и пытающиеся найти причинно – следственные связи между явлениями. Для нас только поиск причин и следствий является истинно научным подходом, и фортуна нам благоволила. В предыдущих работах нам удалось выяснить причинно – следственные связи в целом ряде физических и химических явлений (подробнее см. сайты itchem.ru, fphysics.com).
В настоящее время корректность теоремы вириала не вызывает сомнения ни в печатных публикациях, ни в интернете. Как в физике, так и в химии, как в классической науке, так и в квантовой, эта теорема считается доказанной. Соответственно, она широко используется, например, при описании атома водорода.
В своей книге (Как образуется химическая связь и протекают химические реакции, стр. 29) мы писали:
«Электроны притягиваются к ядру за счет электростатических сил взаимодействия. Однако электроны не падают на ядро, поскольку вращаются вокруг него с определенной скоростью, т.е. имеют определенную кинетическую энергию. В простейшем виде доказательство теоремы вириала состоит в следующем: электрон находится на определенном расстоянии от ядра так как обе силы – центростремительная Fцс и центробежная Fцб – уравновешивают друг друга на этом расстоянии, т.е.
Fцс = Fцб». ( 1)
Или, если подставить формулы для этих сил, получится
где me ,Vи RH -центробежная сила, масса электрона, скорость движения электрона по орбите и радиус орбиты атома водорода, а ε0 и q – электрическая постоянная, заряд электрона и протона, соответственно.
В этом выражении левой части стоит классическая ньютоновская масса, а в правой только электрические величины. Такое равенство носит мистический характер, так как не связано с физическим механизмом. Поэтому и теорема вириала не имела физического объяснения, т.е. приведенное равенство не является доказательством физической корректности теоремы вириала.
В современных учебниках центробежная сила считается вообще фиктивной силой. Так например в Курсе физики Т.И. Трофимовой, выдержившей уже в 2001 г. семь изданий на стр. 43 написано:
“Возникает вопрос о «реальности» или «фиктивности» сил инерции. В ньютоновской механике, согласно которой сила есть результат взаимодействия тел, на силы инерции можно смотретькак на «фиктивные», «исчезающие» в инерциальных системах отсчета. ” Зависимость центробежных сил от системы отсчета увеличивает мистический характер центробежных сил.
В более ранних работах мы показали, что инерционные свойства тела определяются зарядом, а не массой, и что незаряженных тел нет. Поэтому мы сделали второй расчет, в котором используется электромагнитная инерционная масса.
Сила центробежная расчитывалась по уравнению
F цб = me v2/rH = 9,1*10-31 *(2,2*106)2/0,53*10-10 = 0.83*10-7Н.
Центростремительная (в случае атома водорода – Кулоновская сила) описывается уравнением:
(3)
Отметим, что определить радиус атома водорода можно из экспериментального значения первого потенциала ионизации (ППИ) [см. Как образуется химическая связь и протекают химические реакции, стр. 32]. Потенциальная энергия электрона в атоме водорода
Ее= 2ППИ (4)
Используем эту величину в формуле для радиуса
| R= | = |
| =5,29· 10-11=0,529Å | (5) |
Подставляем следующие численные значения в эту формулу 1/4πε0=8.99*109 Н*м2/с2– электрическая постоянная, 0.16*10-18 Кл- заряд электрона и протона, 0.529*10-10м – радиус атома водорода и получаем, что сила Кулона (центростремительная сила) в атоме водорода равна 0.82*10 -7Н.
Fк =8.99*109* (0.16*10-18)2/(0.529*10-10)2 =0.82*10 -7Н
Кроме того, мы рассчитали численное значение ускорений под действием Кулоновских сил и значение центробежного ускорения.
Расчет, сделанный нами (в первом приближении предполагалось, что ядро атома неподвижно), дал следующие значения: ускорение, приобретаемое под действием силы Кулона
| aкул.= | · | (6) |
| akул.=8,99 · 109 | · 1,76 · 10 -11 | ≈0,904*1023м/с2 |
Центробежное ускорение, вычисленное по формуле ацб= v2/RH, равно
При расчетах мы не использовали значение массы электрона, но взяли другую, уже более 100 лет измеренную, величину q/m= -1.76×10-11 Кл/кг. Значения для постоянных характеристик электрона взяты с http://2mb.ru/fizika/konstanty/elektron/ и Википедии. В различных источниках приводятся разные значения для скорости электрона, либо 2.22×106м/с http://naukaland.ru/discuss/783-chemu-ravna-skorost-elektrona-skolko-oborotov.html либо 2.22×106м/с http://www.medelk.kharkov.ua/chemia2/chemia37.htm или 2,18×106м/с http://nasedkin.ru/Root_Russian/Arithmetic/Arithmetic-02.html, именно этим обусловлено неточное равенство расчетных значений ускорений.
Давайте подробнее рассмотрим, какой физический смысл несет масса в одном и другом случае.
С точки зрения физического смысла первый расчет воспринимается как магический постулат, физический смысл (причинно – следственные связи) которого не ясен.
До открытия атомно – молекулярного строения материи и законов электромагнитных явлений (в первую очередь, законов Фарадея) физические причины, раскрывающие такие совпадения, и не могли быть определены. Действительно, до этих открытий нельзя было даже в виде гипотезы предложить существования причинно – следственной связи между Ньютоновской массой и силами Кулона, не говоря уже ничего о численном совпадении.
С другой стороны, уже после открытия ядерно – атомно – молекулярного строения материи и законов электромагнитных явлений использование приведенного выше первого расчета и сохранение Ньютоновского физического смысла параметра m можно объяснить только инерцией мышления и верой в авторитеты (прежде всего в непререкаемый авторитет Ньютона).
В отличие от первого, второй расчет является прекрасной демонстрацией возможности и необходимости исключения механической Ньютоновской массы из исходных сущностей, как это было сделано с теплородом и флогистоном по ходу развития химии и физики. Второй расчет имеет физический механизм. Согласно цитируемуму выше учебнику Трофимовой (стр. 177) при движении заряда с ускорением возникает ЭДС, εi электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э. д. с. εi не зависит от способа изменения магнитного потока.
Под действием Кулоновских сил электрон приобретает линейное ускорение. Равенство центробежного и центростремительного ускорений является демонстрацией того, что законы электродинамики не зависят от вида ускорения. Т.е. оно не зависит ни от знака ускорения (положительное оно, или отрицательное) ни от типа движения (поступательно-линейное или центростремительно-криволинейное), ни от того, какая именно сила привела к ускоренному движению.
После прекращения воздействия силы, вызывающей ускоренное движение тела, постепенно прекращается и действие силы, вызванной ЭДС, и тело продолжает двигаться с достигнутой скоростью.
В предыдущих работах, выясняя причины инерциальных свойств электрона, мы пришли к заключению, что инерциальные свойства материи обусловлены зарядом и, следовательно, инерциальная масса имеет электромагнитное происхождение. С другой стороны, в последующих работах (прежде всего в статье «Масса» и данной работе ) мы склоняемся к выводу, что m это параметр, скорее всего, зависящий и от строения заряда. Для электронов он в 1837 меньше, чем для нуклонов.
Такое существенное различие в инерциальных свойствах электронов и нуклонов позволяет говорить, что инерциальные свойства вещества обусловлены в основном нуклонами.
Приведенное в статье «Принцип эквивалентности» уравнение, рассчитывающее атомный вес элемента,
M=1,00732*Z+1,0087*N,
где Z-количество протонов, N-количество нейтронов.
Это уравнение является арифметическим доказательством того, что инерциальная масса нуклонов численно определяет атомный вес элемента и, соответственно, его вес по второму закону Ньютона и следовательно, постулируемой ньютоновской инертной массы не существует.
Уравнение в статье «Масса» для расчета инерциальной массы
m = qH2R/v = qH1H2R/E
является доказательством того, что инерциальная масса определяется зарядом частиц, видом (строением) этих частиц, что незаряженных частиц материи не существует и, что инерционная масса атома пропорциональна заряду ядра.
Исключение ньютоновской массы, из фундаментальных физических сущностей идентично изменению формулировки Периодического закона после открытия Г.Мозли. До открытия Мозли Периодический закон формулировался Д. Менделеевым следующим образом: свойства химических элементов не произвольны, а находятся в периодической зависимости от атомной массы. После открытия Мозли Периодический закон формулировался следующим образом: заряд ядра является важнейшим свойством элемента, определяющим его химические свойства.
Теперь мы можем говорить, что инерциальные свойства вещества обусловлены зарядом!
Важным результатом этой работы стали
- дополнительное доказательство, что Ньютоновской массы не существует и, соответственно, не существует гравитационного притяжения в представлении Ньютона. Объединение ньютоновской гравитации с электродинамическими взаимодействиями было одной из нерешаемых задач при создании единой теории поля.
- очередной вклад в обоснование электродинамической природы массы.
- развернутая демонстрация (в дополнение к предыдущим нашим работам), что центробежные силы – это не фиктивные силы, а электро – магнитные силы, вызванные ЭДС, появляющейся при движении зарядов с ускорением.
Хотя считается, что теорема вириала доказана, и Солнечная система описывается теоремой вириала, однако, до сих пор известная задача 300-летней давности об устойчивости этой системы не имеет однозначного аналитического решения. Ньютон считал, что устойчивость Солнечной системы в конечном счёте обеспечивается сверхестественными силами. Неустойчивость модели атома водорода Бора-Резерфорда явилась одной из основных причин, что привели Бора к признанию квантово – механического описания атома и признанию идей Гейзенберга и Шредингера. Существовавшие до сей поры доказательства, в отличие от нашего, не давали физического объяснения этим явлениям.
В чем основное отличие этой статьи от предыдущих.
В большинстве статей наших книг и размещенных на сайтах fphysics.com и itchem.ru (кроме статей “Масса”,”Принцип Эквивалентности”, “Расчет ковалентного радиуса атома водорода”) дают феноменологическое объяснение инерциальной массы, основыванное на законах электродинамики (главным образом, на законах Фарадея).
Для того, чтобы убедиться в корректности этого объяснения, нам в свое время, надо было понять и поверить (преодолеть инерцию мышления)
1) в корректности нашего объяснения электропроводности (см. «Общая химия XXI век», гл.Феноменологическое объяснение электропроводности);
2) что законы Фарадея, открытые им в экспериментах на проводниках и магнитах, распространяются и на конвекционные токи;
3) что движущийся одиночный заряд является конвекционным током;
4) что одиночный заряд, двигающийся с ускорением, есть переменный ток, и что этот переменный ток обладает самоиндукцией, как и всякий другой ток (см. Как образуется химическая связь и протекают химические реакции, стр. 244).
И даже после преодоления инерции мышления во всех перечисленных вопросах мы имели только феноменологическое качественное объяснение, т.к. коэффициент самоиндукции конвекционного тока не мог быть рассчитан количественно.
В данной статье доказывается что заряд, двигающийся с ускорением, вызывает появление ЭДС, действующей на заряд силой равной по величине силе, вызвавшей движение заряда с ускорением и противоположной ей по направлению. Это и есть центробежная сила, действующая на заряд.
Равенство по величине центростремительной силы, вызвавшей движение заряда с ускорением, центробежной силе доказывает, что силой, вызвавшей движение заряда с ускорением, является сила Лоренца. Обобщенная сила Лоренца описывает движение зарядов в электрических и магнитных полях (Кулоновская сила +магнитная составляющая силы Лоренца). В случае атомов и молекул эти поля создаются заряженными частицами (ядрами и электронами), а магнитные взаимнодвижущимися этими же частицами.
В рамках электродинамики было доказано, что заряд, двигающийся с ускорением, вызывает появление электродвижущей силы (далее ЭДС), воздействующей на этот заряд.
Величина электродвижущей силы не зависит от вида силы, вызвавшей движение заряда с ускорением. Этой силой может быть и Ньютоновская сила гравитации (притяжение масс), и сила Лоренца. Ускорение также может быть любым (центростремительным и линейным).
Для магнитной составляющей силы Лоренца характерно, что направление ее действия подчиняется правилу Ленца.
Из этого правила мы можем сделать обобщение, согласно которому действие ЭДС на заряд направлено на сохранение величины ускорения (и центробежного и центростремительного) заряда, вызвавшего появление ЭДС. Величина ускорения заряда определяет орбиту заряда в атоме, а также орбиты в молекулярных и планетарных случаях.
Силой Лоренца можно объясняснить устойчивость орбит электронов в атомах и закрыть дискуссию о фиктивности центробежной силы. Экспериментальным подтверждением этого вывода является устойчивость орбиты электрона в атоме.
Сила Лоренца – центростремительная сила. Она является единственной причиной ускоренного движения заряда. Согласно электродинамике вызванная ею ЭДС действует на заряд
с силой равной по величине силе, вызвавшей движение заряда с ускорением
в направлении противоположном этой силе
Более того, можно сказать, что устойчивость этих систем доказывает, что в них действует сила Лоренца. Соответственно, в этих системах взаимодействуют электрические и магнитные поля, как микрочастиц, так и космических объектов.
21-10-2011
itchem.ru
Эренфеста теоремы – Физическая энциклопедия
ЭРЕНФЕСТА ТЕОРЕМЫ -теоремы,
утверждающие, что ср. значения величин (координат, импульса, энергии), характеризующих
движение частицы в квантовой механике, а также ср. значение силы, действующей
на частицу, связаны между собой ур-ниями, аналогичными соответствующим ур-ниям
классич. механики. Установлены П. Эрен-фестом (P. Ehrenfest, 1927) на основе
сопоставления частице пакета волн де Бройля y(x, t)(см. Волновой
пакет). В случае одной пространств. координаты (х), учитывая, что
|y(х, t)|2 есть плотность вероятности обнаружить
частицу в нек-рой точке х, естественно вводится понятие “центра
(тяжести)” волнового пакета как ср. значения координаты:
при этом считается, что
y (х, t)достаточно быстро спадает при
и нормирована
на единицу. Вычисление производной по времени от (1) с учётом Шрёдингера
уравнения для одночастичного случая доказывает, что имеет место первая
теорема Эренфеста: центр волнового пакета движется со скоростью, равной
ср. импульсу частицы, отнесённому к её массе:
Отсюда, в частности, можно
вывести явный вид самосопряжённых оператора импульса
и оператора координаты .
Вторая производная от (1)
по времени приводит ко второй теореме Эренфеста: производная по времени
от ср. импульса частицы равна ср. значению силы <Fx>= -<dU/dx>, приложенной к частице, т.е.
Т. о., при условии, что
размерами волнового пакета по сравнению с характерным масштабом изменения потенциала U(x)можно пренебречь, центр волнового пакета будет двигаться точно по
законам классич. механики, записанным для ср. значений соответствующих физ.
величин, т. е. соотношение между скоростью и импульсом частицы и 2-й закон Ньютона
классич. механики выполняются в квантовой механике лишь для ср. значений физ.
величин.
Для случая 3-мерных волновых
пакетов Э.т. (2) и (3) записываются соответственно в виде
Пределы применимости Э.
т. (т. е. справедливости классич. законов для квантовых средних) выводятся,
в частности, из разложения ф-ции U(x)в окрестности “центра (тяжести)”
достаточно
узкого пакета в ряд Тейлора и вычисления соответствующих квантовомеханич. средних.
Если ограничиться первыми тремя членами разложения, то должны выполняться условия
где ,
т. е. потенциал U должен достаточно плавно зависеть от .
Кроме того, из сравнения выражений для кинетич. энергий классич. и квантовых
частиц можно сделать вывод, что они сопоставимы лишь при достаточно больших
импульсах, т. е. когда
из неопределённостей
соотношения
с учётом (4) и (5) выводится
ещё одно условие, необходимое, чтобы квантовая частица подчинялась классич.
законам:
Выбор достаточно узких
волновых пакетов приводит к большому разбросу по импульсам, что, в свою очередь,
влечёт за собой быстрое “расплывание” пакетов (квадратичный по времени
закон “расплывания”). Т.о., волновой пакет можно сопоставить с частицей
только для очень коротких временных промежутков. Поиск нерасплывающихся волновых
пакетов или частицеподобных решений приводит к рассмотрению нелинейных обобщений
ур-ний динамики (см. Солитон).
Лит.: Борисоглебский
Л. А., Квантовая механика, 2 изд., Минск, 1988; Матвеев А. Н., Атомная физика,
М., 1989; Рыбаков Ю. П., Терлецкий Я. П., Квантовая механика, М., 1991.
В. И. Санюк.
Предметный указатель >>
www.femto.com.ua
