15.05.202005.07.2019

Уравнение идеального газа формула – Формула идеального газа

• by alexxlab
• Комментариев к записи Уравнение идеального газа формула – Формула идеального газа нет
• Разное

Уравнение состояния идеального газа | Все формулы

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

•  — давление,
•  — молярный объём,
•  — универсальная газовая постоянная
•  — абсолютная температура,К.

Так как , где—количество вещества, а , где— масса,—молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.

 — Закон Гей-Люссака.

 — закон 

Шарля (второй закон Гей-Люссака, 1808 г.).А в форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое. С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объёмводородасоединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:

1 Объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:

— закон Бойля — Мариотта. Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году. В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

где —показатель адиабаты, — внутренняя энергия единицы массы вещества.Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений.

С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки. С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведениеувеличивается.

xn--b1agsdjmeuf9e.xn--p1ai

Уравнение состояния идеального газа. Газовые законы.

Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона).
Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние. В 1834 г. французский физик Б.  Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеаль­ного газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул.
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m. Мы знаем, что . Следовательно, . Учитывая, что , получим: .
Произведение постоянных величин есть величина постоянная, следовательно:  – универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).
Таким образом, имеем:  – уравнение состояния (уравнение Менделеева – Клапейрона).
Другие формы записи уравнения состояния идеального газа.
1.Уравнение для 1 моля вещества. Если n=1 моль, то, обозначив объем одного моля Vм, получим: . Для нормальных условий получим:
2. Запись уравнения через плотность: – плотность зависит от температуры и давления!
3.  Уравнение Клапейрона. Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда:
Эта запись означает, что  для данной массы данного газа справедливо равенство:
Для постоянной массы идеального газа отношение произве­дения давления на объем к абсолютной  температуре в данном состоянии есть величина постоянная: .
Газовые законы.
1.      Закон Авогадро. В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов). Условие: V1=V2=…=Vn;  p1=p2=…=pn; T1=T2=…=Tn
Доказательство:   Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.
2.      Закон Дальтона. Давление смеси газов равно сумме парциальных (частных) давлений каждого газа. Доказать: p=p1+p2+…+pn Доказательство:
3.      Закон Паскаля. Давление, производимое на жидкость или газ, передается во все стороны без изменения.

www.eduspb.com

Уравнение состояния идеального газа Менделеева-Клапейрона с выводом

Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.

P – давление [Па]

V- объем [м³]

ν – количество вещества [моль]

R – универсальная газовая постоянная, 8,31 [Дж/(моль · К)]

T – температура [K]

Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.

Вывод уравнения Менделеева-Клапейрона

Давление идеального газа зависит от концентрации частиц и температуры тела:

n – концентрация частиц [м^-3]

k – константа Больцмана k = 1,38 · 10^-23 [Дж/К]

Т – абсолютная температура, в кельвинах [К]

Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:

Подставим nkT вместо давления и выразим кинетическую энергию:

Концентрация частиц газа n равна:

N – число молекул газа в емкости объемом V [м³]. N также можно представить как произведение количества вещества ν и числа Авогадро NA:

Подставим эти величины в уравнение давления идеального газа (p=nkT):

Произведение числа Авогадро N_A и константы Больцмана k дает универсальную газовую постоянную R, которая равна 8,31 [Дж/(моль · К)]. Используя это, упростим уравнение давления и получим искомое уравнение состояния идеального газа:

Учитывая, что количество вещества ν также можно определить, если известны масса вещества m и его молярная масса M:

можно привести уравнение к следующему виду:

Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Всего этих частных случаев 3.

Закон Бойля-Мариотта – изотермический процесс

Проходит при постоянной температуре: T= const.

P·V = const, то есть для конкретного вещества произведение давления на объем остается постоянным:

P₁·V₁ = P₂·V₂.

Закон Гей-Люссака – изобарный процесс

Проходит при постоянном давлении: P = const.

V/T = const, то есть для конкретного вещества отношение объема и температуры остается постоянным:

V₁/T₁ = V₂/T₂.

Закон Шарля – изобарный процесс

Проходит при постоянном объеме: V = const.

P/T = const, то есть для конкретного вещества отношение давления и температуры остается постоянным:

P₁/T₁ = P₂/T₂.

Понравилась статья, расскажите о ней друзьям:

Скорее всего, Вам будет интересно:

people-ask.ru

Уравнение состояния идеального газа – Класс!ная физика

Уравнение состояния идеального газа

«Физика – 10 класс»

В этой главе речь пойдёт о следствиях, которые можно извлечь из понятия температуры и других макроскопических параметров. Основное уравнение молекулярнокинетической теории газов вплотную приблизило нас к установлению связей между этими параметрами.

Как можно рассчитать массу воздуха в кабинете физики?
Какие параметры воздуха будут необходимы для определения этой массы?

Мы детально рассмотрели поведение идеального газа с точки зрения молекулярно-кинетической теории. Была определена зависимость давления газа от концентрации его молекул и температуры (см. формулу (9.17)).

На основе этой зависимости можно получить уравнение, связывающее все три макроскопических параметра р, V и Т, характеризующие состояние идеального газа данной массы.

Формулой (9.17) можно пользоваться только до давления порядка 10 атм.

Уравнение, связывающее три макроскопических параметра р, V и Т, называют уравнением состояния идеального газа.

Подставим в уравнение р = nkT выражение для концентрации молекул газа. Учитывая формулу (8.8), концентрацию газа можно записать так:

где N_A — постоянная Авогадро, m — масса газа, М — его молярная масса. После подстановки формулы (10.1) в выражение (9.17) будем иметь

Произведение постоянной Больцмана k и постоянной Авогадро N_A называют универсальной (молярной) газовой постоянной и обозначают буквой R:

R = kN_A = 1,38 • 10^-23 Дж/К • 6,02 • 10²³ 1/моль = 8,31 Дж/(моль • К). (10.3)

Подставляя в уравнение (10.2) вместо kN_A универсальную газовую постоянную R, получаем уравнение состояния идеального газа произвольной массы

Единственная величина в этом уравнении, зависящая от рода газа, — это его молярная масса.

Из уравнения состояния вытекает связь между давлением, объёмом и температурой идеального газа, который может находиться в двух любых состояниях.

Если индексом 1 обозначить параметры, относящиеся к первому состоянию, а индексом 2 — параметры, относящиеся ко второму состоянию, то согласно уравнению (10.4) для газа данной массы

Правые части этих уравнений одинаковы, следовательно, должны быть равны и их левые части:

Известно, что один моль любого газа при нормальных условиях (р₀ = 1 атм = 1,013 • 10⁵ Па, t = 0 °С или Т = 273 К) занимает объём 22,4 л. Для одного моля газа, согласно соотношению (10.5), запишем:

Мы получили значение универсальной газовой постоянной R.

Таким образом, для одного моля любого газа

Уравнение состояния в форме (10.4) было впервые получено великим русским учёным Д. И. Менделеевым. Его называют уравнением Менделеева—Клапейрона.

Уравнение состояния в форме (10.5) называется уравнением Клапейрона и представляет собой одну из форм записи уравнения состояния.

Б. Клапейрон в течение 10 лет работал в России профессором в институте путей сообщения. Вернувшись во Францию, участвовал в постройке многих железных дорог и составил множество проектов по постройке мостов и дорог.

Его имя внесено в список величайших учёных Франции, помещённый на первом этаже Эйфелевой башни.

Уравнение состояния не надо выводить каждый раз, его надо запомнить. Неплохо было бы помнить и значение универсальной газовой постоянной:

R = 8,31 Дж/(моль • К).

До сих пор мы говорили о давлении идеального газа. Но в природе и в технике мы очень часто имеем дело со смесью нескольких газов, которые при определённых условиях можно считать идеальными.

Самый важный пример смеси газов — воздух, являющийся смесью азота, кислорода, аргона, углекислого газа и других газов. Чему же равно давление смеси газов?

Для смеси газов справедлив закон Дальтона.

Закон Дальтона

Давление смеси химически невзаимодействующих газов равно сумме (ЦЩй их парциальных давлений

p = p₁ + p₂ + … + p_i + … .

где р_i — парциальное давление i-й компоненты смеси.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основные положения МКТ. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика

Почему тепловые явления изучаются в молекулярной физике — Основные положения молекулярно-кинетической теории. Размеры молекул — Примеры решения задач по теме «Основные положения МКТ» — Броуновское движение — Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел — Идеальный газ в МКТ. Среднее значение квадрата скорости молекул — Основное уравнение молекулярно-кинетической теории газов — Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» — Температура и тепловое равновесие — Определение температуры. Энергия теплового движения молекул — Абсолютная температура. Температура — мера средней кинетической энергии молекул — Измерение скоростей молекул газа — Примеры решения задач по теме «Энергия теплового движения молекул» — Уравнение состояния идеального газа — Примеры решения задач по теме «Уравнение состояния идеального газа» — Газовые законы — Примеры решения задач по теме «Газовые законы» — Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»

class-fizika.ru

§ 27. Уравнение состояния идеального газа.

Определение:Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры.

Определение:Уравнением Клайперона называется соотношение, справедливое для постоянной массы идеального газа: .

Определение:Молярной массой любого тела называется физическая величина, равная отношению массы тела к количеству  молей, которое в нём содержится:  = m/,   = m/ ;  = 10 ^–3  m/m_o , где m  масса молекулы данного тела, m_o  масса одной двенадцатой массы атома углерода.

Определение:Молярным объёмом называется физическая величина, равная отношению объёма газа к числу молей, содержащихся в газе: V_ =V/ .

Уравнение состояния идеального газа одного моля p V_ = R T.

Rуниверсальная газовая постояннаяR = 8,31 Дж/(K  моль).

Определение:Уравнением МенделееваКлайперона называется соотношение, справедливое для любого идеального газа: .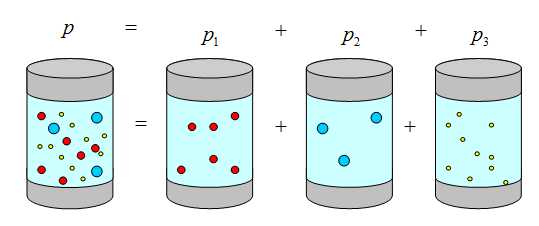

Постоянная Больцмана .

Использование постоянной Больцмана, молярного объёма в уравнении МенделееваКлайперона приведёт к следующему результату:эта формула также является уравнением состояния идеального газа, гдеn₀концентрация молекул идеального газа, т.е. их число в единице объёма. Применяя формулу плотности вещества получим ещё один вариант уравнения состояния идеального газа:

.

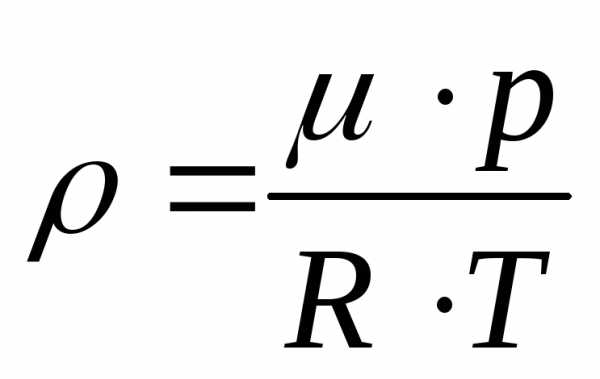§ 28. Основное уравнение кинетической энергии газов.

Определение:Основным уравнение кинетической энергии газов есть соотношение: .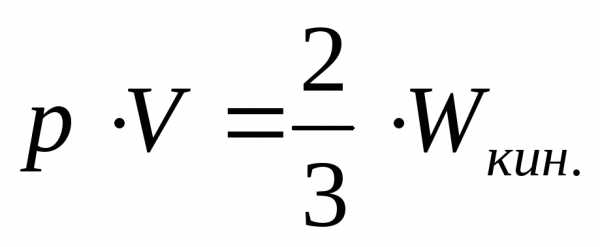

Это уравнение выполняется при N = constобщее число молекул в газе, то есть при отсутствии химических реакций; газ может состоять из разнородных молекул.

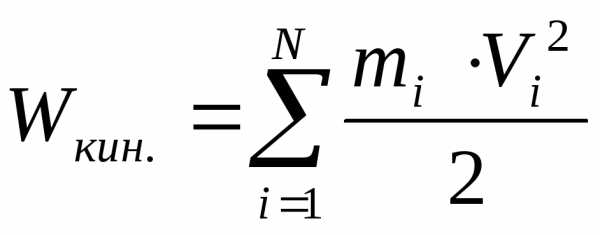 суммарная энергия поступательного движения молекул газа, находящихся в сосуде, гдеm_iмасса, аV_iскорость«i  ой» молекулы.

Для однородного газа m_i=m_o, тогда.

Введём средне квадратичную скорость V_квадр.поступательного движения молекул газа:.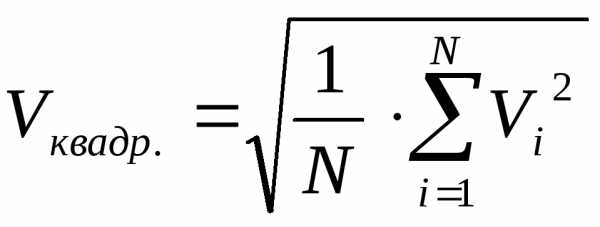

Тогда

Подставим данный результат в основное уравнение кинетической теории газов

(*),mмасса всего газа.

Сопоставим полученный результат с уравнением МенделееваКлайперона:

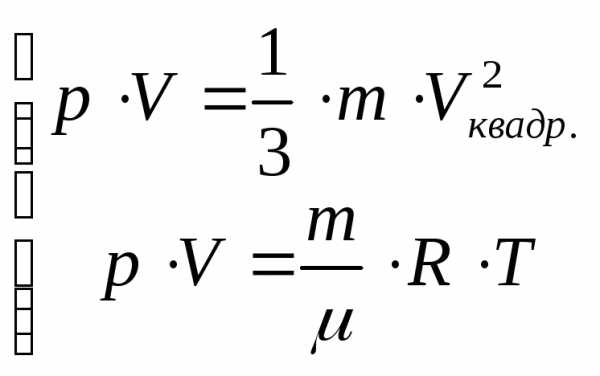, здесь использовалось полезное соотношение:.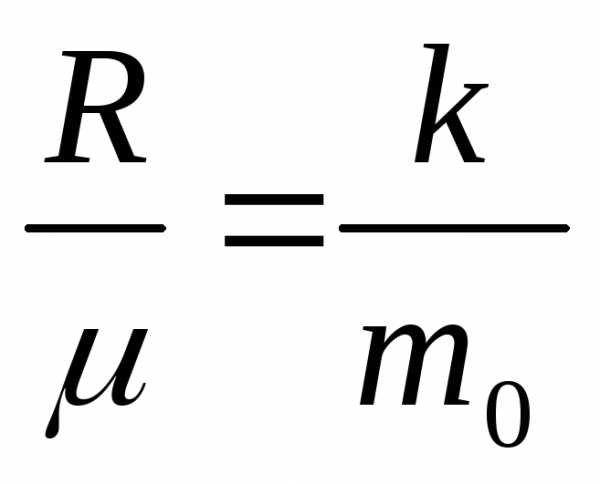

Связь давления, плотности газа и средней квадратичной скорости следует (*):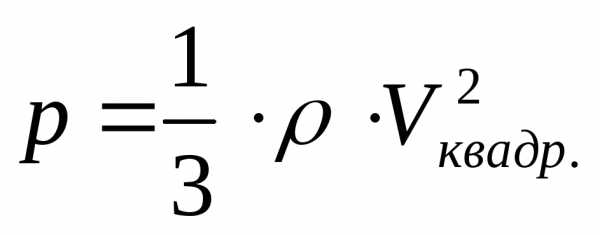

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа:

.

После подстановки явного выражения для средней квадратичной скорости, получим: .

§ 29. Закон распределения молекул идеального газа по скоростям Максвелла.

Закон распределения молекул идеального газа по скоростям определяет долевое участие молекул однородного газа в тепловом движении при данной температуре со скоростями, заключёнными в интервале от V доV +V. Он выведен теоретически:,

где nчисло молекул в единице объёма (концентрация молекул),

n число молекул из общего их числа, скорости которых лежат в интервале скоростей:,

m₀масса одной молекулы,

kпостоянная Больцмана,

Tтемпература газа.

Чем меньше по величине выбирается интервал скоростей, тем более точный результат даёт данная формула.

Nв единицу объёма, которые[,+]

Графическая иллюстрация данной формулы приведена на графике зависимости относительной концентрации молекул n/Vидеального однородного газа от скорости

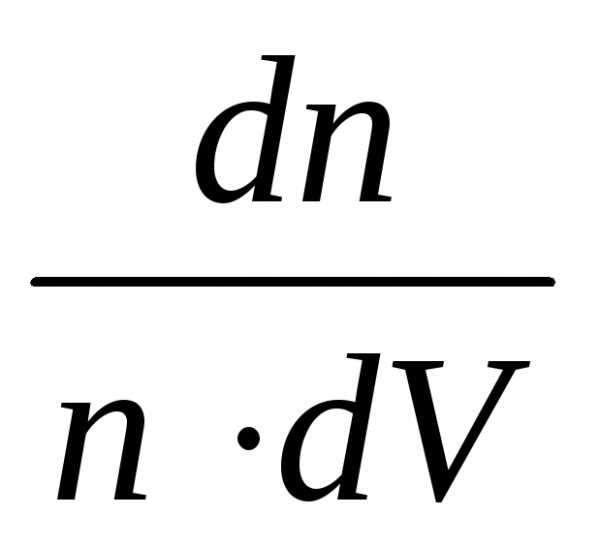
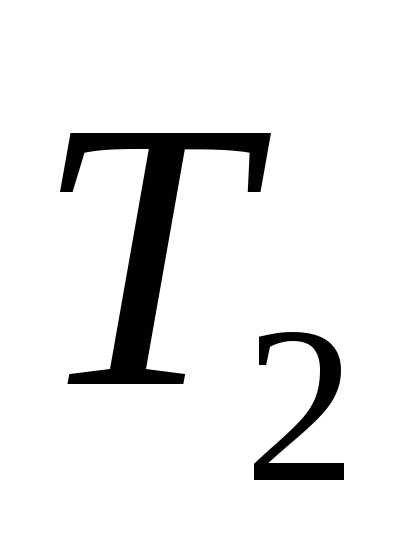
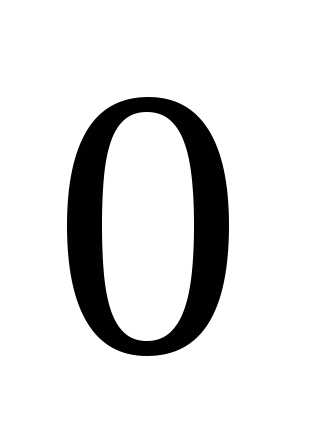
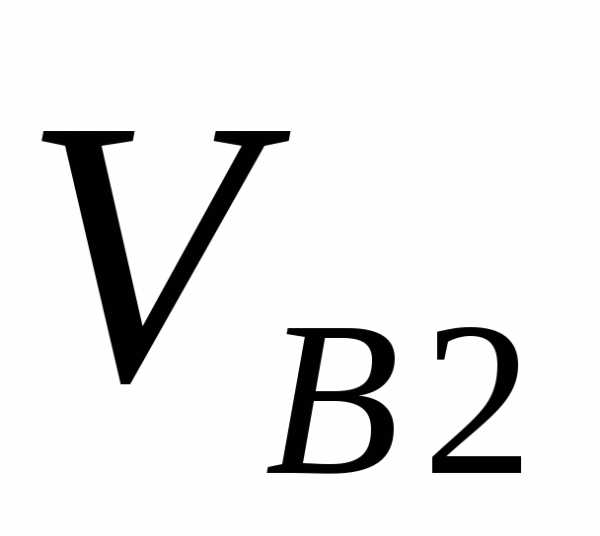
Функцией распределения молекул идеального газа по скоростям Максвелла называется выражение:

.

С помощью этой функции можно найти все статистически необходимые величины, характеризующие состояние идеального газа.

Вначале найдём наивероятнейшую скорость, т.е. значение скорости, соответствующее максимуму функции Максвелла. С точки зрения физики это такое значение скорости, к которому близки значения скорости большей части молекул. Воспользуемся методом нахождения экстремума функции, т.е. вначале возьмём производную от функции распределения Максвелла по скорости, а затем приравняем полученное выражение к нулю:

.

Последнее уравнение имеет три решения, т.к. необходимо равенство нулю каждого из множителей:

1. это не физический случай;

2. 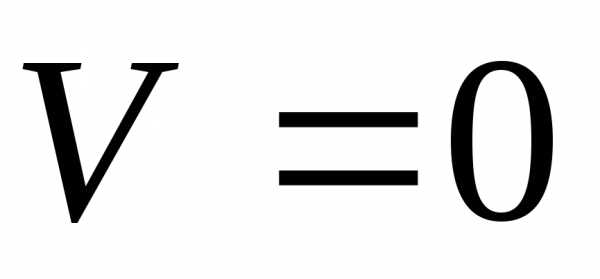тривиальный случай;

3.

Средне квадратичную и средне арифметическую скорости находятся интегрированием:

,.

studfiles.net

Уравнение состояния идеального газа в физике

Молекулы свободно движутся и лишь иногда сталкиваются между собой и со стенками сосуда, в котором находятся. Это значит, что в таком газе можно пренебречь потенциальной энергией его молекул в сравнении с кинетической. Газы можно считать идеальными с достаточной степенью точности в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых превращений.

Уравнение состояния идеального газа

Параметры, с помощью которых описывают состояние идеального газа, как макросистемы это давление (p), объем (V), температура по шкале Кельвина (T). Очевидно, что уравнение, которое их связывает, является очень значимым с точки зрения теории и практики. Называется оно уравнением состояния идеального газа (иногда просто уравнением идеального газа):

   

где Дж/К – постоянная Больцмана,

   

n- число молекул в единице объема газа ( концентрация частиц вещества), N — число его молекул в заданном объеме.

Уравнению (1) можно придать известную форму уравнения Клапейрона (Надо отметить, что от изменения формы записи уравнения (2), (3) не перестают быть уравнениями состояния идеального газа):

   

или

   

где — количество молей газа, R=8,3 Дж/(моль•К) – молярная (универсальная) газовая постоянная, ( моль^-1 (постоянная Авогадро)), – молярная масса газа, – плотность газа.

Уравнение состояния для смеси газов

Если газ представляет собой смесь газов, то уравнение (состояния) идеального газа принимает вид:

   

где число молей i-го компонента смеси.

Для произвольной массы газа (m) с молярной массой уравнение (состояния) идеального газа имеет вид:

   

Это уравнение называют уравнением Менделеева – Клапейрон и оно, опять таки, является уравнением идеального газа, точнее одной из форм записи этого уравнения.

Примеры решения задач

ru.solverbook.com

3.Уравнение состояния идеального газа.

В любом из равновесных состояний параметры Р, Т и Vтермодинамической системы (т.е. газа, жидкости или твердого тела), как показывает опыт, закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение другого. Функциональная связь между давлением, объемом и температурой

f(P,V,N) = 0 (1)

называется уравнением состояния вещества. Если разрешить (1) относительно какого-либо из параметров, например, Р, то уравнение состояния примет вид

Р = Р(V, Т). (2)

Опыт показывает, что для жидкости и твердых тел характер зависимости Р = Р(V, Т) крайне индивидуален. Иначе обстоит дело в случае разреженных газов. Все достаточно разреженные газы подчиняются одному и тому же уравнению состояния –уравнению Клапейрона-Менделеева, которое может быть установлено, как на основе известных опытных газовых законов Бойля-Мариотта (РV = constдля данной массы газа), Гей-Люсака [V_t = V₀ (1 + t)для постоянных массы и давлении газа] и Авогадро (при одинаковых Т и Р в равных объемах любого газа содержится одинаковое число молекул), так и на основе молекулярно-кинетической теории строения вещества. Это уравнение имеет вид

PV=MRT/(3)

или P=MRT/V=RT/,

где М – масса газа, - молярная масса,R– газовая постоянная,R=8,31 Дж/мольК,- плотность газа.

Отношение Z= М/- число молей газа. Тогда

PV=ZRT(4)

В случае газовой смеси величина Zв уравнении (4) равна полному числу молей всех газов, входящих в смесь

Z = Z₁ + Z₂ +….+ Z_n= М₁/₁+ М₂/₂+ …+ М_n/_n(5)

где М₁, М₂, …,М_n– массы отдельных газов, а₁,₂, …_n– молярные массы этих газов.

Реальные газы подчиняются уравнению Клапейрона-Менделеева лишь приближенно – при достаточно низких давлениях и высоких температурах. При больших же Р и низких Т у всех газов наблюдаются отклонения от этого уравнения. Газ, который вполне точно подчиняется уравнению Клапейрона-Менделеева, в термодинамике называют идеальным газом. Такого газа в действительности нет, он является некоторой абстракцией, носвойства всех реальных газов приближаются к свойствам идеального газа при малых давлениях. Любой газ в пределе при Р0 неотличим от идеального. Большинство газов уже при атмосферном давлении и комнатной Т близки к идеальному.

Преобразуем (3). Обозначив массу одной молекулы через m, будем иметь М =mNи=mN_А, гдеN– общее число молекул газа, аN_А– число Авогадро. Тогда (3) можно записать в виде

PV = NRT/N_A,

но отношение k=R/N_A=1,3810^-23Дж/К – постоянная Больцмана. Тогда

PV=NkT(6)

В виде (6) уравнение состояния справедливо независимо от того имеем мы дело с химически однородным газом или с произвольной смесью, т.к. оно совершенно не зависит от химической природы газа.

Выражая из (6) Р, получим

Р = NkT/V, ноN/V=n– число молекул в единице объема газа, тогда

P=nkT(7)

т.е. давление газа зависит только от его температуры и числа молекул в единице объема газа.

4. Барометрическая формула и распределение больцмана.

Если на молекулы газа не действуют никакие внешние силы, то вследствие теплового движения они равномерно распределяются по всему объему сосуда, так что в каждой единице объема содержится в среднем одинаковое число молекул. При одинаковой во всех частях объема температуре в газе устанавливается всюду одинаковое давление Р = nkT = const (в соответствии с законом Паскаля).

Иначе обстоит дело, когда газ находится в некотором силовом поле, в котором на каждую частицу газа действует внешняя сила, толкающая ее в определенном направлении. Под действием такой силы молекулы будут собираться преимущественно в тех областях пространства, куда их заталкивают внешние силы, и там концентрация частиц, а значит, и давление газа будут возрастать. Т.е. действие внешних сил на молекулы газа противоположно тому действию, которое оказывает на них беспорядочное тепловое движение.

В результате одновременного действия внешних сил и теплового движения молекул в газе при заданной температуре устанавливается некоторое неравномерное распределение молекул в пространстве, не изменяемое во времени. Это значит, что при действии внешних сил плотность идеального газа, находящегося в равновесных условиях, будет различной в различных местах пространства, т.е. она будет некоторой функцией координат

n= n(X,Y,Z).

Примером внешних сил является поле силы тяжести, а примером газа в таком силовом поле является земная атмосфера. Молекулы газов, составляющие атмосферный воздух, под влиянием теплового движения рассеялись бы в мировом пространстве, если бы отсутствовала сила тяжести. Напротив, если бы отсутствовало тепловое движение молекул, то под действием силы тяжести все молекулы воздуха упали бы на землю, и весь воздух собрался бы тончайшим слоем у поверхности Земли. Таким образом, само существование атмосферы является результатом одновременного действия силы притяжения молекул к Земле и их теплового движения. При этом в атмосфере устанавливается некоторое неравномерное распределение молекул воздуха по высоте. Соответственно этому распределению молекул устанавливается и определенный закон изменения давления с высотой.

Если бы земная атмосфера находилась в состоянии теплового равновесия, т.е. температура атмосферы была бы одинаковой на всех высотах, то в ней бы установилось так называемое барометрическое распределение плотности и давления с высотой.

Для определения барометрического закона изменения давления и плотности идеального газа с высотой рассмотрим вертикальный столб газа с площадью поперечного сечения S= 1, находящийся при постоянной температуре, рис.1.

Z

dZ P-dP

Z P

0 P₀

Х

Рис.1.

Обозначим давление газа на некотором нулевом уровне Z= 0 (уровне моря, поверхности земли, дне сосуда и т.д.) через Р₀, а давление на высотеZнад нулувым уровнем через Р. При увеличении высоты наdZдавление газа уменьшится на некоторую величинуdР. Это уменьшение давления равно весу столба газа высотойdZс площадью основанияS= 1

dP = – g dZ, (1)

где – - плотность газа. На основании уравнения состояния идеального газа, его плотностьравна

 = P/RT(2)

Следовательно,

dP = – (P/RT)g dZ,

откуда

dP/P = – (/RT)g dZ.

Интегрируя это выражение, находим

р z

 dP/P = – /R  g dZ/Т

p₀ 0

или z

ln P/P₀ = – /R  g dZ/Т (3)

0

На небольших высотах над поверхностью земли ускорение силы тяжести gможно считать постоянным, не зависящим от высотыZ, и вынести его за знак интеграла. Кроме тего, если газ находится в тепловом равновесии при постоянной, не зависящей от высотыZтемпературе Т, то и Т можно вынести за знак интеграла. В этом случае получим

ln P/P₀ = – gZ/RT,

откуда

Р/Р₀=е ^{– gZ/RT}

или

Р = Р₀ е ^{– gZ/RT}. (4)

Формула (4) характеризует изменение давления газа с высотой и называетсябарометрической формулой. Она показывает, что давление газа с высотой убывает по экспоненциальному закону. Характер этого убывания графически можно представить следующим образом, рис.2. Р

Р₀

Z

Рис.2.

Прибор для определения высоты над земной поверхностью называется высотомером (илиальтиметром). Принцип его действия основан на использовании формулы (4). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.

Принимая во внимание, что =mN_AиR=kN_A, мы можем переписать барометрическую формулу в виде

Р = Р₀ е ^{– mgZ/ kT}.

Так как P=nkT, то эта барометрическая формула выражает такжезакон убывания плотности газа с высотой

n = n₀ е ^{– mgZ/ kT} (5)

где nиn₀– числа молекул в единице объема газа в точках, разность высот между которыми равнаZ. Ввиду чрезвычайно малой массы газовых молекул убывание плотности газа и его давления заметно только при значительных изменениях высоты. В случае небольшого изменения высоты изменение давления и плотности газа оказываются весьма малыми. Поэтому в случае газа, заключенного в сосуд небольшой высоты, действием силы тяжести на молекулы газа можно пренебречь. Поскольку температура атмосферы Земли не постоянна и изменяется с высотой, то для более точного описания изменений ее давления и плотности с высотой в формулы (4) и (5) необходимо вводить соответствующие поправки на изменение температуры.

Поскольку входящая в формулу (5) величина mgZпредставляет собой потенциальную энергию молекул в поле тяготения, то эту формулу можно переписать в виде

n = n₀ е ^{– U(Z) /kT} (6)

т.е. она выражает закон распределения молекул идеального газа по величине их потенциальной энергии в поле тяготения. Причем величина n₀имеет смысл числа частиц с потенциальной энергией равной нулю(n = n₀ при U = 0).

В середине 19 века Больцман показал, что для идеального газа, находящегося влюбом силовом поле, число частиц, обладающих заданной потенциальной энергиейU, определяется формулой, имеющей тот же вид, что и формула (6). Поскольку, в произвольном силовом поле потенциальная энергия частицы может зависеть от всех трех координат, характеризующих ее положение в пространстве, а не только от одной, как это имело место в частном случае поля тяготения, т.е.n=n(X,Y,Z) и соответственно этомуU=U(X,Y,Z). Таким образом, в любом силовом поле распределение частиц в пространстве выражается законом

n(X,Y,Z) = n₀ е ^{– U(X,Y,Z) / kT} – закон Больцмана (7)

где U(X,Y,Z) – потенциальная энергия частиц во внешнем силовом поле, зависящая от координат той точки, в которой находится частица;n(X,Y,Z) – концентрация частиц в точке с координатамиX,Y,Z;n₀– число частиц в единице объема (концентрация) в том месте пространства, где их потенциальная энергия равна 0.

Больцман показал, что при постоянной Т концентрация частиц убывает с ростом Uи возрастает с убываниемU, т.е.частицы концентрируются преимущественно в местах с меньшей потенциальной энергией.

Закон Больцмана (8) является весьма общим законом, применимым не только к идеальному газу, но и ко многим другим системам невзаимодействующих частиц.

studfiles.net

---