Архимеда закон кратко – Блог Юрия Ретромана.Архимед. Закон Архимеда – Блог Юрия Ретромана.Архимед. Закон Архимеда
- Комментариев к записи Архимеда закон кратко – Блог Юрия Ретромана.Архимед. Закон Архимеда – Блог Юрия Ретромана.Архимед. Закон Архимеда нет
- Советы абитуриенту
Эврика! Закон Архимеда
Архимед – греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед обучался в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.
 Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
По легенде, Архимеду принадлежит множество удивительных технических изобретений, которые завоевали ему славу среди современников. Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.
Архимеду также приписывают изобретение катапульты, военной метательной машины, конструирование планетария, в котором планеты двигались. Учёный создал винт для подъёма воды (Архимедов винт), который до сих пор используется и представляет собой водоподъемную машину, вал с винтовой поверхностью, находящийся в наклонной трубе, погруженной в воду. Во время вращения винтовая поверхность вала перемещает воду по трубе на разные высоты.
Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.
Свой знаменитый закон Архимед открыл при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не подмешивали ли ювелиры серебро к золоту, когда изготавливали корону. Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.
 Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!
Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!
Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую его поместили.
Закон Архимеда гласит: на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Закон Архимеда: формула и примеры решений
Закон Архимеда представляет собой физический принцип, который гласит, что на тело, которое погружено полностью или частично в жидкость, в покое действует вертикально направленная сила, которая по своей величине равна весу жидкости, вытесненной этим телом. Эта сила называется гидростатической или архимедовой. Как и любая сила в физике, она измеряется в ньютонах.
Греческий ученый Архимед

Архимед вырос в семье, которая была связана с наукой, поскольку его отец, Фидий, был великим астрономом своего времени. С раннего детства Архимед стал проявлять интерес к наукам. Учился он в Александрии, где завел дружбу с Эратосфеном из Кирены. Вместе с ним Архимед впервые измерил окружность земного шара. Благодаря влиянию Эратосфена, в юном Архимеде также появился интерес к астрономии.
После возвращения в свой родной город Сиракузы ученый посвящает большое количество времени изучению математики, физики, геометрии, механики, оптики и астрономии. Во всех этих областях науки Архимед совершил различные открытия, понимание которых оказывается трудным даже для современного образованного человека.
Открытие Архимедом своего закона

Согласно исторической справке свой закон Архимед открыл интересным образом. Витрувий в своих трудах описывает, что сиракузский тиран Гиерон Второй поручил одному из мастеров отлить ему золотую корону. После того как корона была готова, он решил проверить, не обманул ли его мастер, и не добавил ли в золото более дешевое серебро, которое имеет меньшую плотность, чем царь металлов. Эту задачу он задал решить Архимеду. Ученому нельзя было нарушать целостность короны.
Однажды принимая ванну, Архимед обратил внимание, что уровень воды в ней поднимается. Этот эффект он решил использовать для вычисления объема короны, знание которого, а также массы короны, позволяло ему вычислить плотность предмета. Это открытие сильно поразило Архимеда. Витрувий описал его состояние так: он бежал по улице абсолютно раздетым, и кричал “Эврика!”, что с древнегреческого переводится “Я нашел!”. В итоге плотность короны оказалась меньше, чем чистого золота, и мастер был казнен.
Архимед создал труд, который называется “О плавающих телах”, где впервые подробно описывает открытый им закон. Отметим, что формулировка закона Архимеда, которую сделал сам ученый, практически не изменилась.
Объем жидкости, находящийся в равновесии с остальной жидкостью
В школе в 7 классе закон Архимеда начинают изучать. Чтобы понять смысл этого закона, следует сначала рассмотреть силы, которые действуют на определенный объем жидкости, находящейся в равновесии в толще остальной жидкости.
Сила, действующая на какую-либо поверхность рассматриваемого объема жидкости, равна p*dS, где p – давление, которое зависит только от глубины, dS – площадь этой поверхности.
Поскольку выделенный объем жидкости находится в равновесии, значит результирующая сила, действующая на поверхности этого объема, и связанная с давлением, должна уравновешиваться весом этого объема жидкости. Эта результирующая сила называется силой выталкивания. Точка приложения ее находится в центре тяжести этого объема жидкости.
Поскольку давление в жидкости вычисляется по формуле p =ro*g*h, где ro – плотность жидкости, g – ускорение свободного падения, h – глубина, то равновесие рассматриваемого объема жидкости определяется уравнением: вес тела = ro*g*V, где V – объем рассматриваемой части жидкости.
Замещение жидкости твердым телом

Рассматривая далее закон Архимеда в физике 7 класса, уберем рассматриваемый объем жидкости из ее толщи, а на свободное место поместим твердое тело того же объема и той же формы.
При этом результирующая сила выталкивания, которая зависит только от плотности жидкости и ее объема, останется прежней. Вес же тела, а также центр его тяжести в общем случае изменятся. В итоге на тело будут действовать изначально две силы:
- Сила выталкивания ro*g*V.
- Вес тела m*g.
В самом простом случае, если тело является однородным, тогда его центр тяжести совпадает с точкой приложения силы выталкивания.
Природа закона Архимеда и пример решения для полностью погруженного в жидкость тела
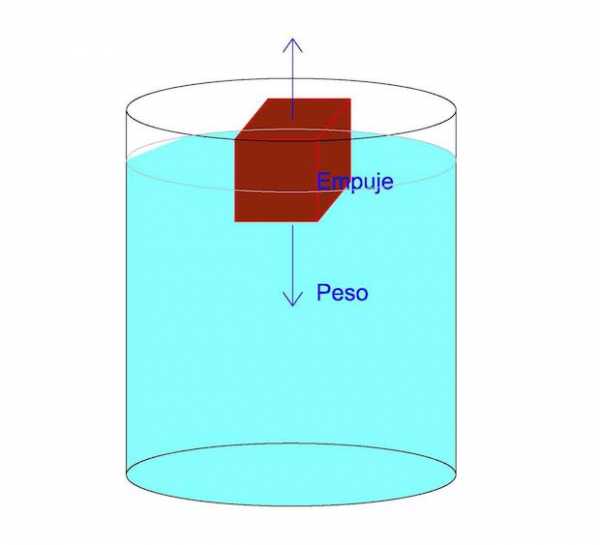
Предположим, что однородное тело массой m погрузили в жидкость с плотностью ro. При этом тело имеет форму параллелепипеда с площадью основания S и высотой h.
Согласно закону Архимеда на тело будут действовать следующие силы:
- Сила ro*g*x*S, которая обусловлена давлением, приложенным к верхней поверхности тела, где x – расстояние от верхней поверхности тела до поверхности жидкости. Эта сила направлена вертикально вниз.
- Сила ro*g*(h+x)*S, которая связана с давлением, действующим на нижнюю поверхность параллелепипеда. Она направлена вертикально вверх.
- Вес тела m*g, который действует вертикально вниз.
Давление, которое создает жидкость на боковые поверхности погруженного тела, равны друг другу по модулю и противоположны по направлению, поэтому в сумме дают нулевую силу.
В случае равновесия имеем: m*g + ro*g*x*S = ro*g*(h+x)*S, или m*g = ro*g*h*S.
Таким образом, природа выталкивающей силы или силы Архимеда заключается в разнице давлений, которые оказывает жидкость на верхнюю и нижнюю поверхности погруженного в нее тела.
Замечания к закону Архимеда

Природа выталкивающей силы позволяет сделать некоторые выводы из данного закона. Приведем важные выводы и замечания:
- Если плотность твердого тела будет больше плотности жидкости, в которую оно погружается, то архимедовой силы будет недостаточно, чтобы вытолкнуть это тело из толщи жидкости, и тело будет тонуть. Наоборот, тело будет плавать на поверхности жидкости только в том случае, если его плотность меньше плотности этой жидкости.
- В условиях невесомости для объемов жидкости, которые не могут создавать ощутимое гравитационное поле самостоятельно, не существует градиентов давления в толще этих объемов. В таком случае понятие о выталкивающей силе перестает существовать, и закон Архимеда оказывается неприменимым.
- Сумму всех гидростатических сил, действующих на погруженное в жидкость тело произвольной формы, можно свести к одной силе, которая направлена вертикально вверх и приложена к центру тяжести тела. Таким образом, в действительности не существует единой силы, приложенной к центру тяжести, такое представления является лишь математическим упрощением.
fb.ru
Закон Архимеда – это… Что такое Закон Архимеда?
Зако́н Архиме́да — один из главных законов гидростатики и статики газов.
Формулировка и пояснения
Закон Архимеда формулируется следующим образом[1]: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:
где — плотность жидкости (газа), — ускорение свободного падения, а — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.
где PA, PB — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.
В теоретической физике также применяют закон Архимеда в интегральной форме:
- ,
где — площадь поверхности, — давление в произвольной точке, интегрирование производится по всей поверхности тела.
В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: проводящее тело вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление жидкости на глубине есть . При этом считаем давление жидкости и напряжённость гравитационного поля постоянными величинами, а — параметром. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат , причём выберем направление оси z совпадающим с направлением вектора . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку . На неё будет действовать сила давления жидкости направленная внутрь тела, . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
Получаем, что модуль силы Архимеда равен , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Условие плавания тел
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести и силы Архимеда , которые действуют на это тело. Возможны следующие три случая:
- — тело тонет;
- — тело плавает в жидкости или газе;
- — тело всплывает до тех пор, пока не начнет плавать.
Другая формулировка (где — плотность тела, — плотность среды, в которую оно погружено):
- — тело тонет;
- — тело плавает в жидкости или газе;
- — тело всплывает до тех пор, пока не начнет плавать.
См. также
Примечания
- ↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, вблизи поверхности планеты).
Ссылки
dic.academic.ruИсследование границ применимости закона Архимеда
li:before{content:”” counter(lst-ctn-kix_list_2-6,decimal) “. “}#doc8809912 .lst-kix_list_2-7>li:before{content:”” counter(lst-ctn-kix_list_2-7,lower-latin) “. “}#doc8809912 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc8809912 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc8809912 ul.lst-kix_list_1-0{list-style-type:none}#doc8809912 .lst-kix_list_2-4>li:before{content:”” counter(lst-ctn-kix_list_2-4,lower-latin) “. “}#doc8809912 .lst-kix_list_2-5>li:before{content:”” counter(lst-ctn-kix_list_2-5,lower-roman) “. “}#doc8809912 .lst-kix_list_2-8>li:before{content:”” counter(lst-ctn-kix_list_2-8,lower-roman) “. “}#doc8809912 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc8809912 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc8809912 ul.lst-kix_list_1-3{list-style-type:none}#doc8809912 ul.lst-kix_list_1-4{list-style-type:none}#doc8809912 ul.lst-kix_list_1-1{list-style-type:none}#doc8809912 ul.lst-kix_list_1-2{list-style-type:none}#doc8809912 ul.lst-kix_list_1-7{list-style-type:none}#doc8809912 ul.lst-kix_list_1-8{list-style-type:none}#doc8809912 ul.lst-kix_list_1-5{list-style-type:none}#doc8809912 ul.lst-kix_list_1-6{list-style-type:none}#doc8809912 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc8809912 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc8809912 .lst-kix_list_2-3>li{counter-increment:lst-ctn-kix_list_2-3}#doc8809912 .lst-kix_list_2-6>li{counter-increment:lst-ctn-kix_list_2-6}#doc8809912 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc8809912 ol.lst-kix_list_2-2{list-style-type:none}#doc8809912 ol.lst-kix_list_2-3{list-style-type:none}#doc8809912 ol.lst-kix_list_2-4{list-style-type:none}#doc8809912 ol.lst-kix_list_2-5{list-style-type:none}#doc8809912 ol.lst-kix_list_2-0{list-style-type:none}#doc8809912 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc8809912 ol.lst-kix_list_2-1{list-style-type:none}#doc8809912 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc8809912 .lst-kix_list_1-0>li:before{content:”\0025cf “}#doc8809912 ol.lst-kix_list_2-6{list-style-type:none}#doc8809912 .lst-kix_list_1-1>li:before{content:”o “}#doc8809912 .lst-kix_list_1-2>li:before{content:”\0025aa “}#doc8809912 ol.lst-kix_list_2-0.start{counter-reset:lst-ctn-kix_list_2-0 0}#doc8809912 ol.lst-kix_list_2-7{list-style-type:none}#doc8809912 ol.lst-kix_list_2-8{list-style-type:none}#doc8809912 .lst-kix_list_1-3>li:before{content:”\0025cf “}#doc8809912 .lst-kix_list_1-4>li:before{content:”o “}#doc8809912 .lst-kix_list_1-7>li:before{content:”o “}#doc8809912 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc8809912 .lst-kix_list_1-5>li:before{content:”\0025aa “}#doc8809912 .lst-kix_list_1-6>li:before{content:”\0025cf “}#doc8809912 .lst-kix_list_2-0>li:before{content:”” counter(lst-ctn-kix_list_2-0,decimal) “. “}#doc8809912 .lst-kix_list_2-1>li:before{content:”” counter(lst-ctn-kix_list_2-1,lower-latin) “. “}#doc8809912 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc8809912 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc8809912 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc8809912 .lst-kix_list_1-8>li:before{content:”\0025aa “}#doc8809912 .lst-kix_list_2-2>li:before{content:”” counter(lst-ctn-kix_list_2-2,lower-roman) “. “}#doc8809912 .lst-kix_list_2-3>li:before{content:”” counter(lst-ctn-kix_list_2-3,decimal) “. “}#doc8809912 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc8809912 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc8809912 ol{margin:0;padding:0}#doc8809912 .c1{padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;text-align:justify;direction:ltr}#doc8809912 .c5{padding-top:0pt;padding-bottom:0pt;line-height:1.0;orphans:2;widows:2;direction:ltr}#doc8809912 .c27{padding-top:0pt;padding-bottom:36pt;line-height:1.0;orphans:2;widows:2;direction:ltr}#doc8809912 .c25{vertical-align:baseline;font-size:18pt;font-family:”Times New Roman”;font-weight:bold}#doc8809912 .c6{vertical-align:baseline;font-size:16pt;font-family:”Times New Roman”;font-weight:bold}#doc8809912 .c8{vertical-align:sub;font-size:14pt;font-family:”Times New Roman”;font-weight:normal}#doc8809912 .c7{vertical-align:baseline;font-size:14pt;font-family:”Times New Roman”;font-weight:bold}#doc8809912 .c0{vertical-align:baseline;font-size:14pt;font-family:”Times New Roman”;font-weight:normal}#doc8809912 .c15{vertical-align:baseline;font-size:12pt;font-family:”Times New Roman”;font-weight:normal}#doc8809912 .c32{vertical-align:baseline;font-size:16pt;font-family:”Times New Roman”;font-weight:normal}#doc8809912 .c30{vertical-align:baseline;font-size:18pt;font-family:”Times New Roman”;font-weight:normal}#doc8809912 .c31{vertical-align:baseline;font-size:13pt;font-family:”Times New Roman”;font-weight:normal}#doc8809912 .c10{background-color:#ffffff;max-width:506.5pt;padding:45pt 42.5pt 56.7pt 63pt}#doc8809912 .c11{margin-left:6.2pt;text-indent:7.7pt;margin-right:7.2pt}#doc8809912 .c19{margin-left:6.2pt;text-indent:9.4pt;margin-right:6.7pt}#doc8809912 .c2{margin-left:5pt;text-indent:9.1pt;margin-right:7.2pt}#doc8809912 .c23{margin-left:132.5pt;text-indent:200.5pt}#doc8809912 .c12{margin-left:333pt;text-indent:2.5pt}#doc8809912 .c3{text-indent:9.1pt;height:11pt}#doc8809912 .c9{text-decoration:underline;font-style:italic}#doc8809912 .c13{margin-left:1.4pt;text-indent:9.1pt}#doc8809912 .c4{height:11pt}#doc8809912 .c20{margin-left:0.5pt}#doc8809912 .c28{font-style:italic}#doc8809912 .c24{text-align:center}#doc8809912 .c22{text-decoration:underline}#doc8809912 .c16{text-indent:9.1pt}#doc8809912 .c17{text-indent:8.8pt}#doc8809912 .c18{margin-right:12.9pt}#doc8809912 .c21{text-indent:9.3pt}#doc8809912 .c26{margin-left:333pt}#doc8809912 .c14{text-indent:10.1pt}#doc8809912 .c29{text-indent:9.6pt}#doc8809912 .title{padding-top:24pt;color:#000000;font-weight:bold;font-size:36pt;padding-bottom:6pt;font-family:”Arial”;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 .subtitle{padding-top:18pt;color:#666666;font-size:24pt;padding-bottom:4pt;font-family:”Georgia”;line-height:1.15;page-break-after:avoid;font-style:italic;orphans:2;widows:2;text-align:left}#doc8809912 li{color:#000000;font-size:11pt;font-family:”Arial”}#doc8809912 p{margin:0;color:#000000;font-size:11pt;font-family:”Arial”}#doc8809912 h2{padding-top:24pt;color:#000000;font-weight:bold;font-size:24pt;padding-bottom:6pt;font-family:”Arial”;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h3{padding-top:18pt;color:#000000;font-weight:bold;font-size:18pt;padding-bottom:4pt;font-family:”Arial”;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h4{padding-top:14pt;color:#000000;font-weight:bold;font-size:14pt;padding-bottom:4pt;font-family:”Arial”;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h5{padding-top:12pt;color:#000000;font-weight:bold;font-size:12pt;padding-bottom:2pt;font-family:”Arial”;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h5{padding-top:11pt;color:#000000;font-weight:bold;font-size:11pt;padding-bottom:2pt;font-family:”Arial”;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 h6{padding-top:10pt;color:#000000;font-weight:bold;font-size:10pt;padding-bottom:2pt;font-family:”Arial”;line-height:1.15;page-break-after:avoid;orphans:2;widows:2;text-align:left}#doc8809912 ]]>МОУ Краснореченская ООШ
Исследование границ применимости закона Архимеда
Выполнил: ученик 8 класса
Ширинкин Виктор
Руководитель: учитель физики
Санин Ю.В.
2015
Оглавление:
1.Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3
2. Погрешности узкого сосуда. . . . . . . . . . . . . . . . . . . . . . . . .4-6
3. «Прилипание» к дну и стенкам . . . . . . . . . . . . . . . . . . . ….6-7
4. Закон Архимеда в невесомости . . . . .. . . . . . . . . . . . . . . . 7-8
5. Ускорение и сила Архимеда . . . . . . . . . . . . . . . . . . . . . . . 8-9
6. Выводы . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . .. . 9
7. Литература . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . .. . . 10
1. Введение
В школе изучается много различных законов. Большинство из них имеют те или иные границы применимости. Знания о границах применимости позволяют безошибочно применять законы в различных ситуациях. Проводя некоторые опыты и получая не совпадающие с теорией результаты, возникла идея о выяснении условий, при которых закон гидростатики не выполняется. Чтобы тщательно изучить этот вопрос, необходимо было найти и обработать большое количество информации, провести ряд опытов. Вся эта работа- внесение своего вклада в науку. Возможно, данный материал не имеет практической значимости, но работать над этим материалом было очень интересно.
2. Чтобы детально разобраться в вопросе о границах применимости закона Архимеда, нужно начать с рассмотрения необходимой, возможно знакомой всем, информации.
Закон Архимеда впервые был упомянут им в трактате “О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Этот закон, едва ли не первый физический закон, с которым мы знакомимся в школе. Он справедлив не только для жидкостей, но и для газов. Сила, выталкивающая погруженное тело, называется архимедовой, или гидростатической, подъемной силой. Появляется она потому, что верхняя и нижняя поверхности тела находятся на разной глубине и, следовательно, испытывают разные силы давления со стороны выше лежащих слоев газа или жидкости.
Воздух сжимаем, у поверхности Земли его плотность заметно выше, чем на высоте нескольких километров. Поэтому воздушный шар, увлекаемый вверх архимедовой силой, остановится, дойдя до некоторой высоты, на которой вес вытесненного воздуха станет равным весу шара. Вода практически несжимаема, поэтому в ней такой картины наблюдать нельзя: если тело начало тонуть, то оно опустится до самого дна.
Всё кажется простым и знакомым. Но всё ли так просто, как кажется? Чтобы ответить на этот вопрос, попробуем объяснить результаты одного эксперимента.
Эксперимент. Оборудование: широкий сосуд (таз), песок, два сосуда, вода.
Ход выполнения: 1. Наполним широкий сосуд водой на ¾ объема.
Два других сосуда необходимо подобрать таких размеров, чтобы один входил в другой с небольшим зазором. Для наглядности эксперимента можно взять градуированную стеклянную банку и цилиндрическую мензурку, но можно использовать и два любых сосуда, для которых выполняются те же условия (небольшой зазор).
2. В меньший сосуд (банку) насыплем такое количество песка, чтобы она держалась на плаву в широком сосуде с водой.
3.Отметим на стенке мензурки глубину её погружения.
4.Определим примерное значение веса банки с песком.
Если в эксперименте используется сосуд с делениями, то объём вытесненной воды можно примерно принять равным величине деления на сосуде, до которого произошло погружение. (В др.случае можно воспользоваться измерительным цилиндром и отливным сосудом для определения объёма вытесненной жидкости.)
Поскольку банка находится в состоянии равновесия, плавает, то, значит, ее вес скомпенсирован выталкивающей силой, равной весу вытесненной жидкости. По количеству вытесненной воды можно определить вес банки с песком. (Примерное значение.)
5. Наполним цилиндрическую мензурку водой так, чтобы её вес был в 1,5-2 раза меньше веса банки с песком и опустим в неё банку с песком. Будет ли плавать эта банка с песком в сосуде (мензурке) немного большего диаметра, в который налито воды меньше, чем необходимо для плавания тела по закону Архимеда? (снимок I)
Естественно предположить, что выталкивающей силы уже не хватит на то, чтобы скомпенсировать вес банки и что банка с песком просто встанет на дно. Чтобы выяснить это, продолжим эксперимент.
7. Наблюдая за банкой убеждаемся в том, что банка, как и в опыте с широким сосудом плавает, погрузившись до того же, деления, что и при плавании в широком сосуде.
Это неожиданный результат. В чем же здесь дело? Почему она плавает?
Чтобы ответить на эти вопросы, нужно вспомнить другой закон гидростатики, открытый в XVII веке французским ученым Б. Паскалем и носящий его имя: «Давление, создаваемое внешними силами, передаетcя без изменения в каждую точку жидкости». В жидкости, находящейся под действием только одной силы тяжести, давление одинаково во всех точках любой горизонтальной плоскости. Эти плоскости называются поверхностями уровня или поверхностями равного давления. Пример такой плоскости – горизонтальная поверхность уровня в сообщающихся сосудах, например, в чайнике и его носке. Давление на любом уровне зависит только от высоты столба жидкости над ним и не зависит от ее массы. Поэтому общая сила F, которая давит на дно сосуда (она равна произведению давления Р на площадь дна S), может быть и больше и меньше веса воды, налитой в сосуд (см, рисунок), в зависимости от формы сосуда. Это на первый взгляд странное явление, открытое Б. Паскалем, получило название «гидростатический парадокс». Оно наводит на мысль, что в сосуде определённой формы можно получить огромные силы давления очень малым количеством жидкости. Сам Паскаль демонстрировал это с помощью бочки с водой и присоединённой к ней тонкой вертикальной трубки, длиной несколько метров. Когда в трубку влили пару кружек воды, наполнив ее доверху, бочка лопнула под действием силы давления F, равной весу столба воды высотой в несколько метров
(давление Р) и диаметром с бочку (площадь S)! Давление в жидкости передается во все стороны одинаково, поэтому струи воды из щелей хлынули во все стороны практически с равной силой,
Гидростатический парадокс приводит к разгадке «неправильного» поведения банки с песком в опыте с «узким» сосудом. Тонкий слой воды, оставшийся между стенками сосудов (банки с песком и мензурки), оказывает такое же давление на дно банки с песком, что и столб воды той же высоты в сосуде большого объема. Именно это давление и заставляет банку плавать.
Следовательно, чем уже зазор между стенками, тем меньшее количество воды вытеснит плавающее тело, тем сильнее нарушается закон Архимеда. Если бы не силы поверхностного натяжения, которые могут играть заметную роль при очень узком зазоре, любое тело можно было бы заставить плавать, в любом, сколь угодно малом количестве воды. Кажется непонятным, что о столь заметном нарушении закона Архимеда не упоминается ни в одном из многочисленных учебников и справочников по физике. Ведь это явление следовало бы, наверное, учитывать при гидростатическом взвешивании, когда определяют вес тела, погруженного в жидкость, при работе с ареометром, которым измеряют плотность жидкости и в других случаях.
Возникает вопрос о поправках к закону Архимеда, о границах его применимости. Но при более детальном рассмотрении этого вопроса становится ясно, что на самом деле эти поправки не нужны.
Если в опыте с «узким» сосудом мензурку наполнить водой до краев и опустить в него банку с песком, то собранной вылившейся воды будет столько, сколько и должно было быть вытеснено по закону Архимеда.
Учитывая это можно прийти к общепризнанному выводу о том, что закон Архимеда – частный случай закона Паскаля, справедливый только для больших объемов жидкости. Поэтому определение выталкивающей силы (равна весу вытесненной жидкости), которое дал Архимед, не подходит к случаю плавания тел в малых объёмах жидкости. Следовательно, в случае с малыми объёмами жидкости, применение закона Архимеда ограничено.
3.Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем одной из сторон прижато ко дну или стенке сосуда.
При рассмотрении закона Архимеда мы считали, что тело полностью погружено в жидкость и вся его поверхность соприкасается с жидкостью. Если же часть поверхности тела плотно прилегает к стенке или дну сосуда, так, что между ними нет прослойки жидкости, то закон Архимеда неприменим. Яркой иллюстрацией сказанного служит опыт, когда ровную нижнюю поверхность деревянного кубика натирают парафином и плотно приставляют ко дну сосуда. Затем осторожно наливают воду. Брусок не всплывает, так как со стороны воды на него действует сила, не выталкивающая его вверх, а прижимающая ко дну (рис.)
Это явление учитывается при подъёме затонувших кораблей. Прежде чем приступить к подъёму, затонувшее судно вначале «отрывают» от дна и только затем приступают непосредственно к подъёму.
4. Тело, погруженное в жидкость, вытеснит часть этой жидкости. На нее, со стороны окружающей жидкости будет действовать такая же выталкивающая сила, как и на погруженное тело. По третьему закону Ньютона выделенная в объеме тела жидкость будет действовать на окружающую жидкость с той же самой по модулю, но противоположно направленной силой. Это — вес вытесненного объема жидкости. Вспомним, что весом тела, неподвижного в некоторой системе отсчета, называется сила, с которой тело вследствие его притяжения к Земле действует на подставку или подвес. В нашем случае роль подставки для выделенного объема жидкости играет окружающая жидкость.
Итак, выталкивающая сила, действующая на погруженное в жидкость тело, равна по модулю и противоположна по направлению весу вытесненной жидкости. Это и есть закон Архимеда. Заметим, что в формулировке закона говорится именно о весе вытесненной жидкости, а не о силе тяжести. И это весьма существенно, так как вес тела (по модулю) не всегда совпадает с силой тяжести. Например, ящик массой m в кабине поднимающегося с ускорением а лифта давит на пол с силой m(g + a). Это значит, что вес ящика равен Р = m(g + a), в то время как сила тяжести, действующая на ящик, равна mg. Когда же кабина лифта опускается с тем же ускорением, вес ящика оказывается равным Р = m(g – a).
Из последнего выражения ясно, что выталкивающая сила появляется тогда, когда нет состояния невесомости, то есть любое тело (в том числе и жидкость) имеет вес. Если сосуд с жидкостью свободно падает, то жидкость находится в состоянии невесомости и на погруженное в нее тело сила Архимеда не действует. Не действует эта сила и в космическом корабле, движущемся с выключенными двигателями. Подтверждением этого служит отсутствие в невесомости явления естественной конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.
В земных условиях убедиться в том, что закон Архимеда в невесомости не действует, можно с помощью опыта с «картезианским водолазом». Нажмите на корпус бутылки так, чтобы водолаз опустился на дно. Затем «поместите его в невесомость»: подбросив (или уронив) бутылку, не изменяя её вертикального положения. Следите за поведением водолаза во время свободного полёта: всплывёт он или нет. В эти краткие мгновения на бутылку действует только сила тяжести (силой сопротивления воздуха можно пренебречь) и её содержимое находится в невесомости. Для получения более точных данных нужно повторить опыт несколько раз и можно самостоятельно сделать вывод о действии закона Архимеда в невесомости.
5. Рассмотрим ситуацию, в которой сила Архимеда девствует на тело, движущееся с ускорением внутри жидкости. Будет ли в этом случае выполняться закон Архимеда? Представим себе легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= ρ Vg и сила натяжения нити T, а вверх — сила гидростатического давления F=FАрх= -ρVg, (*)
где ρт- плотность тела, ρ – плотность жидкости. Условие равновесия тела
-ρVg +T+ ρтVg =0. (1)
Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вверх (всплывать) с некоторым ускорением a, которое можно найти из уравнения движения
F+ ρтV g = ρV a. (2)
Предположив, что в этом случае можно использовать закон Архимеда, подставим – -ρVg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение
a = – g (ρ- ρт)/ ρт (3)
Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.
Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости)
6. Выводы:
В окружающем нас мире происходит огромное количество различных по своей природе явлений. Некоторые из них, даже при современном уровне развития науки, остаются загадками для человека. Много тайм хранит в себе бескрайняя вселенная и микромир. Но всё это многообразие явлений подчиняется вполне определённым законам, которые мы уже открыли и которые ещё предстоит открыть. Поэтому при изучении законов не может быть мелочей и выяснение границ применимости – тоже очень важно. Эти знания помогут понять, где и как можно применять тот или иной закон, расширят кругозор.
Выполняя данную работу можно сделать следующие выводы:
1. Применение закона Архимеда ограничено к случаю плавания тел в малых объёмах жидкости.
2. Закон Архимеда не распространяется на тела, находящиеся в состоянии невесомости.
3.При ускоренном движении тела, находящегося в жидкости или газе, расчёт силы Архимеда затруднён.
7.Литература:
Учебно-методическое пособие. ИДУ Татьянкин Б.А. и др
Журнал «Наука и жизнь» №7 1983г.
portfolio.1september.ru
elementy.ru›Энциклопедия›21067
http://www.physbook.ru/index.php/Kvant._Выталкивающая_сила
http://www.phys.spbu.ru/library/schoollectures/manida
nsportal.ru
Закон Архимеда Википедия
Зако́н Архиме́да — один из законов статики жидкостей (гидростатики) и газов (аэростатики): на тело, погружённое в жидкость или газ, действует выталкивающая или подъёмная сила, равная весу объёма жидкости или газа, вытесненного частью тела, погружённой в жидкость или газ. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой или гидростатической подъёмной силой[1][2].
В соответствии с законом Архимеда для выталкивающей силы выполняется[3]:
- FA=ρgV,{\displaystyle F_{A}=\rho gV,}
где:
Дополнения
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.
FA=Fp;{\displaystyle F_{A}=F_{p};}
ρж g Vж = ρт g Vт
Например, воздушный шарик объёмом V{\displaystyle V}, наполненный гелием, летит вверх из-за того, что плотность гелия (ρH{\displaystyle \rho _{H}}) меньше плотности воздуха (ρO{\displaystyle \rho _{O}}):
FA>Fp;{\displaystyle F_{A}>F_{p};}
ρOgV>ρHgV.{\displaystyle \rho _{O}gV>\rho _{H}gV.}
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление (PA{\displaystyle P_{A}}) и сила давления (FA{\displaystyle F_{A}}), действующие на верхнюю грань тела, равны:
- PA=ρghA;{\displaystyle P_{A}=\rho gh_{A};}
- FA=ρghAS,{\displaystyle F_{A}=\rho gh_{A}S,}
где:
Давление (PB{\displaystyle P_{B}}) и сила давления (FB{\displaystyle F_{B}}), действующие на нижнюю грань тела, равны:
- PB=ρghB;{\displaystyle P_{B}=\rho gh_{B};}
- FB=ρghBS,{\displaystyle F_{B}=\rho gh_{B}S,}
где:
- PB{\displaystyle P_{B}} — давление, оказываемое жидкостью или газом на нижнюю грань тела, Па;
- FB{\displaystyle F_{B}} — сила давления, действующая на нижнюю грань тела и направленная вверх, Н;
- hB{\displaystyle h_{B}} — расстояние между поверхностью жидкости или газа и нижней гранью тела, м.
Сила давления жидкости или газа на тело определяется разностью сил FB{\displaystyle F_{B}} и FA{\displaystyle F_{A}}:
- FB−FA=ρghBS−ρghAS=ρg(hB−hA)S=ρghS=ρgV,{\displaystyle F_{B}-F_{A}=\rho gh_{B}S-\rho gh_{A}S=\rho g\left(h_{B}-h_{A}\right)S=\rho ghS=\rho gV,}
где:
- h=hB−hA{\displaystyle h=h_{B}-h_{A}} — расстояние между верхней и нижней гранями тела (в случае частичного погружения высота части тела, погружённой в жидкость или газ), м;
- V{\displaystyle V} — объём тела, погружённого в жидкость или газ (в случае частичного погружения объём части тела, погружённой в жидкость или газ), м3.
Разница давлений:
- PB−PA=ρghB−ρghA=ρgh.{\displaystyle P_{B}-P_{A}=\rho gh_{B}-\rho gh_{A}=\rho gh.}
В отсутствие гравитационного поля, то есть, в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление p{\displaystyle p} на глубине h{\displaystyle h}, оказываемое жидкостью плотностью ρ{\displaystyle \rho } на тело, есть p=ρgh{\displaystyle p=\rho gh}. Пусть плотность жидкости (ρ{\displaystyle \rho }) и напряжённость гравитационного поля (g{\displaystyle g}) — постоянные величины, а h{\displaystyle h} — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат Oxyz{\displaystyle Oxyz}, причём выберем направление оси z совпадающим с направлением вектора g→{\displaystyle {\vec {g}}}. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку dS{\displaystyle dS}. На неё будет действовать сила давления жидкости направленная внутрь тела, dF→A=−pdS→{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
- F→A=−∫SpdS→=−∫SρghdS→=−ρg∫ShdS→=∗−ρg∫Vgrad(h)dV=∗∗−ρg∫Ve→zdV=−ρge→z∫VdV=(ρgV)(−e→z).{\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z}).}
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
- ∗h(x,y,z)=z;{\displaystyle {}^{*}h(x,y,z)=z;}
- ∗∗grad(h)=∇h=e→z.{\displaystyle ^{**}grad(h)=\nabla h={\vec {e}}_{z}.}
Получаем, что модуль силы Архимеда равен ρgV{\displaystyle \rho gV}, и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Условие плавания тел
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести FT{\displaystyle F_{T}} и силы Архимеда FA{\displaystyle F_{A}}, которые действуют на это тело. Возможны следующие три случая:
- FT>FA{\displaystyle F_{T}>F_{A}} — тело тонет;
- FT=FA{\displaystyle F_{T}=F_{A}} — тело плавает в жидкости или газе;
- FT<FA{\displaystyle F_{T}<F_{A}} — тело всплывает до тех пор, пока не начнёт плавать.
Другая формулировка (где ρt{\displaystyle \rho _{t}} — плотность тела, ρs{\displaystyle \rho _{s}} — плотность среды, в которую тело погружено):
- ρt>ρs{\displaystyle \rho _{t}>\rho _{s}} — тело тонет;
- ρt=ρs{\displaystyle \rho _{t}=\rho _{s}} — тело плавает в жидкости или газе;
- ρt<ρs{\displaystyle \rho _{t}<\rho _{s}} — тело всплывает до тех пор, пока не начнёт плавать.
См. также
Видеоурок: закон АрхимедаПримечания
Ссылки
wikiredia.ru
Архимед и его законы
Несомненно, Архимед (около 287—212 до н. э.) — самый гениальный учёный Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими математиками всех времён. Его труды посвящены не только математике. Он сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью.
Сын астронома Фидия, написавшего сочинение о диаметрах Солнца и Луны, Архимед родился и жил в греческом городе Сиракузы на Сицилии. Он был приближён ко двору царя Гиерона II и его сына-наследника.
Хорошо известен рассказ о жертвенном венце Гиерона. Архимеду поручили проверить честность ювелира и определить, сделан венец из чистого золота или с примесями других металлов и нет ли внутри него пустот. Однажды, размышляя об этом, Архимед погрузился в ванну, и заметил, что вытесненная его телом вода пролилась через край. Гениального учёного тут же осенила яркая идея, и с криком «Эврика, эврика!» он, как был нагой, бросился проводить эксперимент.
Идея Архимеда очень проста. Тело, погружённое в воду, вытесняет столько жидкости, каков объём самого тела. Поместив венец в цилиндрический сосуд с водой, можно определить, какое количество жидкости он вытеснит, т. е. узнать его объём. А, зная объём и взвесив венец, легко вычислить удельную массу. Это и даст возможность установить истину:
ведь золото — очень тяжёлый металл, а более лёгкие примеси, и тем более пустоты, уменьшают удельную массу изделия.
Но Архимед на этом не остановился. В труде «О плавающих телах» он сформулировал закон, который гласит: «Тело, погружённое в жидкость, теряет в своём весе столько, каков вес вытесненной жидкости». Закон Архимеда является (наряду с другими, позже открытыми фактами) основой гидравлики — науки, изучающей законы движения и равновесия жидкостей. Именно этот закон объясняет, почему стальной шар (без пустот) тонет в воде, тогда как деревянное тело всплывает. В первом случае вес вытесненной воды меньше веса самого шара, т. е. архимедова «выталкивающая» сила недостаточна для того, чтобы удержать его на поверхности. А тяжело гружёный корабль, корпус которого сделан из металла, не тонет, погружаясь только до так называемой ватерлинии. Поскольку внутри корпуса корабля много пространства, заполненного воздухом, средняя удельная масса судна меньше плотности воды и выталкивающая сила удерживает его на плаву. Закон Архимеда объясняет также, почему воздушный шар, заполненный тёплым воздухом или газом, который легче воздуха (водородом, гелием), улетает ввысь.
Знание гидравлики позволило Архимеду изобрести винтовой насос для выкачивания воды. Такой насос (кохля) до недавнего времени применялся на испанских и мексиканских серебряных рудниках.
Из курса физики всем знакомо Архимедово правило рычага. Согласно преданию, учёный произнёс крылатую фразу: «Дайте мне точку опоры, и я подниму Землю!». Конечно, Архимед имел в виду применение рычага, но, он был несколько самоуверен: кроме точки опоры ему понадобился бы и совершенно фантастический рычаг — невероятно длинный и при этом несгибаемый стержень.
Достоверные факты и многочисленные легенды говорят о том, что Архимед изобрёл немало интересных машин и приспособлений.
mirznanii.com
Закон Архимеда • Джеймс Трефил, энциклопедия «Двести законов мироздания»
«Эврика!» («Нашел!») — именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда — то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории. В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, — и корабль плывет.
elementy.ru



