Что называется общим решением дифференциального уравнения – , .

Дифференциальные уравнения Основные понятия

Уравнения, связывающие независимую переменную, искомую функцию и ее производные, называются дифференциальными.

Общий вид дифференциальных уравнений: F (x,y,y’,y’’..y’’’) = 0

Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Наивысший порядок производной, входящей в ДУ, называется порядкомэтого уравнения.

Процесс отыскания решения ДУ называется его интегрированием.

Дифференциальные уравнения первого порядка

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида F(x, y, y‘ )=0, где F — известная функция трех переменных, x — независимая переменная, y(

x) — искомая функция, y‘(x) — ее производная.  Если уравнение F(x, y, y‘ )=0 можно разрешить относительно y‘, то его записывают в виде y‘=f(x, y)

Уравнение y‘=f(x, y) устанавливает связь между координатами точки (x, y) и угловым коэффициентом y‘ касательной к интегральной кривой, проходящей через эту точку.

Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:

P(x;y)dx+Q(x;y)dy=0,

Где P(x;y) и Q(x;y) – известные функции. Уравнение P(x;y)dx+Q(x;

y)dy=0 удобно тем, что переменные в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.

 

Если дифференциальное уравнение первого порядка y‘=f(x, y), имеет решение, то   решений у него, вообще говоря, бесконечно много и эти решения могут быть записаны в виде y=φ(x,C), где C — произвольная константа.

Функция y=φ(x,C) называется общим решением дифференциального уравнения 1-го порядка. Она содержит одну произвольную постоянную и удовлетворяет условиям:

  1. Функция y=φ(x,C) является решением ДУ при каждом фиксированном значении С.

  2. Каково бы ни было начальное условие y(x0)= y0, можно найти такое значение постоянной С=С0 , что

    функция y=φ(x,C0) удовлетворяет данному начальному условию.

Частным решением ДУ первого порядка называется любая функция y=φ(x,C0), полученная из общего решения y=φ(x,C) при конкретном значении постоянной С=С0.

Задача отыскания решения ДУ первого порядка P(x;y)dx+Q(x;y)dy=0, удовлетворяющего заданному начальному условию y(x0)= y0 , называется задачей Коши.

Теорема(существования и единственности решения задачи Коши).

Если в уравнении y‘=f(x, y) функция f(x, y) и ее частная производная f‘y(

x, y) непрерывны в некоторой области D, содержащей точку (x0 ; y0 ), то существует единственное решение y=φ(x) этого уравнения, удовлетворяющее начальному условию y(x0)= y0 . (без доказательства)

Уравнения с разделяющимися переменными

Наиболее простым ДУ первого порядка является уравнение вида

P(x)dx+Q(y)dy=0.

В нем одно слагаемое зависит только от x, а другое – от y. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:

∫ P(x)dx+∫Q(y)dy=с – его общий интеграл.

Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:

P1(x) . Q1(y) . dx+ P2(x) . Q2(y) . dy=0.

Особенность этого уравнения в том, что коэффициенты представляют собой произведения двух функций, одна из которых зависит только от х другая – только от у.

Уравнение P1(x) . Q1(y) . dx+ P2(x) . Q2(y) . dy=0 легко сводится к уравнению P(x)dx+Q

(y)dy=0. путем почленного деления его на Q1(y) . P2(x)≠0. Получаем:

, – общий интеграл.

 

studfiles.net

Основные понятия и определения дифференциальных уравнений

Дифференциальным уравнением называется уравнение, связывающее независимую переменную [cbm]x[/cbm] , искомую функцию [cbm]y=f(x)[/cbm] и её производные [cbm]y’,y”,\ldots,y^{(n)}[/cbm] , т. е. уравнение вида

[cbm]F(x,y,y’,y”,\ldots,y^{(n)})=0.[/cbm]

Если искомая функция [cbm]y=y(x)[/cbm] есть функция одной независимой переменной [cbm]x[/cbm] , дифференциальное уравнение называется обыкновенным; например,

[cbm]\mathsf{1)}~\frac{dy}{dx}+xy=0, \quad \mathsf{2)}~y”+y’+x=\cos{x}, \quad \mathsf{3)}~(x^2-y^2)\,dx-(x+y)\,dy=0.[/cbm]

Когда искомая функция [cbm]y[/cbm] есть функция двух и более независимых переменных, например, если [cbm]y=y(x,t)[/cbm] , то уравнение вида

[cbm]F\!\left(x,t,y,\frac{\partial{y}}{\partial{x}},\frac{\partial{y}}{\partial{t}},\ldots,\frac{\partial^m{y}}{\partial{x^k}\partial{t^l}}\right)=0[/cbm]


называется уравнением в частных производных. Здесь [cbm]k,l[/cbm] — неотрицательные целые числа, такие, что [cbm]k+l=m[/cbm] ; например

[cbm]\frac{\partial{y}}{\partial{t}}-\frac{\partial{y}}{\partial{x}}=0, \quad \frac{\partial{y}}{\partial{t}}=\frac{\partial^2y}{\partial{x^2}}.[/cbm]

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение [cbm]y’+xy=e^x[/cbm] — уравнение первого порядка, дифференциальное уравнение [cbm]y”+p(x)y=0[/cbm] , где [cbm]p(x)[/cbm] — известная функция, — уравнение второго порядка; дифференциальное уравнение [cbm]y^{(9)}-xy”=x^2[/cbm] — уравнение 9-го порядка.

Решением дифференциального уравнения n-го порядка на интервале [cbm](a,b)[/cbm] называется функция [cbm]y=\varphi(x)[/cbm] , определенная на интервале [cbm](a,b)[/cbm] вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции [cbm]y=\varphi(x)[/cbm] в дифференциальное уравнение превращает последнее в тождество по [cbm]x[/cbm] на [cbm](a,b)[/cbm] . Например, функция [cbm]y=\sin{x}+\cos{x}[/cbm] является решением уравнения [cbm]y”+y=0[/cbm] на интервале [cbm](-\infty,+\infty)[/cbm] . В самом деле, дифференцируя функцию дважды, будем иметь

[cbm]y’=\cos{x}-\sin{x}, \quad y”=-\sin{x}-\cos{x}.[/cbm]

Подставляя выражения [cbm]y”[/cbm] и [cbm]y[/cbm] в дифференциальное уравнение, получим тождество

[cbm]-\sin{x}-\cos{x}+\sin{x}+\cos{x}\equiv0[/cbm]

График решения дифференциального уравнения называется интегральной кривой этого уравнения.

Общий вид уравнения первого порядка

[cbm]F(x,y,y’)=0.[/cbm]

(1)

Если уравнение (1) удается разрешить относительно [cbm]y'[/cbm] , то получится уравнение первого порядка, разрешенное относительно производной.

[cbm]y’=f(x,y).[/cbm]

(2)

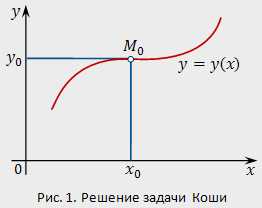
Задачей Коши называют задачу нахождения решения [cbm]y=y(x)[/cbm] уравнения [cbm]y’=f(x,y)[/cbm] , удовлетворяющего начальному условию [cbm]y(x_0)=y_0[/cbm] (другая запись [cbm]y|_{x=x_0}=y_0[/cbm] ).

Геометрически это означает, что ищется интегральная кривая, проходящая через заданную
точку [cbm]M_0(x_0,y_0)[/cbm] плоскости [cbm]xOy[/cbm] (рис. 1).

Теорема существования и единственности решения задачи Коши

Пусть дано дифференциальное уравнение [cbm]y’=f(x,y)[/cbm] , где функция [cbm]f(x,y)[/cbm] определена в некоторой области [cbm]D[/cbm] плоскости [cbm]xOy[/cbm] , содержащей точку [cbm](x_0,y_0)[/cbm] . Если функция [cbm]f(x,y)[/cbm] удовлетворяет условиям

а) [cbm]f(x,y)[/cbm] есть непрерывная функция двух переменных [cbm]x[/cbm] и [cbm]y[/cbm] в области [cbm]D[/cbm] ;

б) [cbm]f(x,y)[/cbm] имеет частную производную [cbm]\frac{\partial{f}}{\partial{y}}[/cbm] , ограниченную в области [cbm]D[/cbm] , то найдется интервал [cbm](x_0-h,x_0+h)[/cbm] , на котором существует единственное решение [cbm]y=\varphi(x)[/cbm] данного уравнения, удовлетворяющее условию [cbm]y(x_0)=y_0[/cbm] .

Теорема дает достаточные условия существования единственного решения задачи Коши для уравнения [cbm]y’=f(x,y)[/cbm] , но эти условия не являются необходимыми. Именно, может существовать единственное решение уравнения [cbm]y’=f(x,y)[/cbm] , удовлетворяющее условию [cbm]y(x_0)=y_0[/cbm] , хотя в точке [cbm](x_0,y_0)[/cbm] не выполняются условия а) или б) или оба вместе.

Рассмотрим примеры.

1. [cbm]y’=\frac{1}{y^2}[/cbm] . Здесь [cbm]f(x,y)=\frac{1}{y^2},~\frac{\partial{f}}{\partial{y}}=-\frac{2}{y^3}[/cbm] . В точках [cbm](x_0,0)[/cbm] оси [cbm]Ox[/cbm] условия а) и б) не выполняются (функция [cbm]f(x,y)[/cbm] и её частная производная [cbm]\frac{\partial{f}}{\partial{y}}[/cbm] разрывны на оси [cbm]Ox[/cbm] и неограниченны при [cbm]y\to0[/cbm] ), но через каждую точку оси [cbm]Ox[/cbm] проходит единственная интегральная кривая [cbm]y=\sqrt[3]{3(x-x_0)}[/cbm] (рис. 2).

2. [cbm]y’=xy+e^{-y}[/cbm] . Правая часть уравнения [cbm]f(x,y)=xy+e^{-y}[/cbm] и ее частная производная [cbm]\frac{\partial{f}}{\partial{y}}=x-e^{-y}[/cbm] непрерывны по [cbm]x[/cbm] и [cbm]y[/cbm] во всех точках плоскости [cbm]xOy[/cbm] . В силу теоремы существования и единственности областью, в которой данное уравнение имеет единственное решение
является вся плоскость [cbm]xOy[/cbm] .

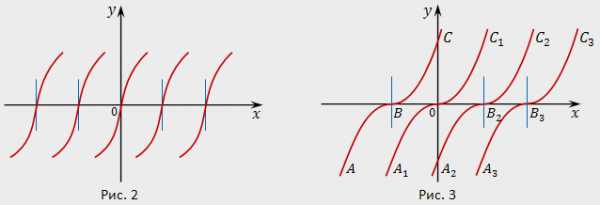
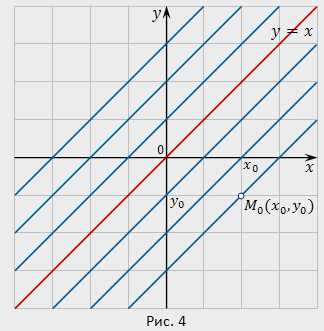
3. [cbm]y’=\frac{3}{2}\sqrt[3]{y^2}[/cbm] . Правая часть уравнения [cbm]f(x,y)=\frac{3}{2}\sqrt[3]{y^2}[/cbm] определена и непрерывна во всех точках плоскости [cbm]xOy[/cbm] . Частная производная [cbm]\frac{\partial{f}}{\partial{y}}=\frac{1}{\sqrt[3]{y}}[/cbm] обращается в бесконечность при [cbm]y=0[/cbm] , т.е. на оси [cbm]Ox[/cbm] , так что при [cbm]y=0[/cbm] нарушается условие б) теоремы существования и единственности. Следовательно, в точках оси [cbm]Ox[/cbm] возможно нарушение единственности. Легко проверить, что функция [cbm]y=\frac{(x+c)^3}{8}[/cbm] есть решение данного уравнения. Кроме этого, уравнение имеет очевидное решение [cbm]y\equiv0[/cbm] . Таким образом, через каждую точку оси [cbm]Ox[/cbm] проходит по крайней мере две интегральные линии и, следовательно, действительно в точках этой оси нарушается единственность (рис. 3).

Интегральными линиями данного уравнения будут также линии, составленные из кусков кубических парабол [cbm]y=\frac{(x+c)^3}{8}[/cbm] и отрезков оси [cbm]Ox[/cbm] , например, [cbm]ABOC_1,[/cbm] [cbm]ABB_2C_2,[/cbm] [cbm]A_2B_2x[/cbm] и др., так что через каждую точку оси [cbm]Ox[/cbm] проходит бесконечное множество интегральных линий.

Условие Липшица

Замечание. Условие ограниченности производной [cbm]\partial{f}/\partial{y}[/cbm] , фигурирующее в теореме существования и единственности решения задачи Коши, может быть несколько ослаблено и заменено так называемым условием Липшица.

Говорят, что функция [cbm]f(x,y)[/cbm] , определенная в некоторой области [cbm]D[/cbm] , удовлетворяет в [cbm]D[/cbm] условию Липшица по [cbm]y[/cbm] , если существует такая постоянная [cbm]L[/cbm] (постоянная Липшица), что для любых [cbm]y_1,y_2[/cbm] из [cbm]D[/cbm] и любого [cbm]x[/cbm] из [cbm]D[/cbm] справедливо неравенство

[cbm]|f(x,y_2)-f(x,y_1)| \leqslant L|y_2-y_1|.[/cbm]

Существование в области [cbm]D[/cbm] ограниченной производной [cbm]\frac{\partial{f}}{\partial{y}}[/cbm] достаточно для того, чтобы функция [cbm]f(x,y)[/cbm] удовлетворяла в [cbm]D[/cbm] условию Липшица. Напротив, из условия Липшица не вытекает условие ограниченности [cbm]\frac{\partial{f}}{\partial{y}}[/cbm] ; последняя может даже не существовать. Например, для уравнения [cbm]y’=2|y|\cos{x}[/cbm] функция [cbm]f(x,y)=2|y|\cos{x}[/cbm] не дифференцируема по [cbm]y[/cbm] в точке [cbm](x_0,0),x_0\ne\frac{\pi}{2}+k\pi,k\in\mathbb{Z}[/cbm] , но условие Липшица в окрестности этой точки выполняется. В самом деле,

[cbm]{|f(x,y_2)-f(x,y_1)|=L|2|y_2|\cos{x}-2|y_1|\cos{x}|=2|\cos{x}|\,||y_2|-|y_1||\leqslant2|y_2-y_1|.}[/cbm]

поскольку [cbm]|\cos{x}|\leqslant1,[/cbm] а [cbm]||y_2|-|y_1||\leqslant|y_2-y_1|[/cbm] . Таким образом, условие Липшица выполняется с постоянной [cbm]L=2[/cbm] .

Теорема. Если функция [cbm]f(x,y)[/cbm] непрерывна и удовлетворяет условию Липшица по [cbm]y[/cbm] в области [cbm]D[/cbm] , то задача Коши

[cbm]\frac{dy}{dx}=f(x,y), \quad y|_{x=x_0}=y_0, \quad (x_0,y_0)\in{D}.[/cbm]


имеет единственное решение.

Условие Липшица является существенным для единственности решения задачи Коши. В качестве примера рассмотрим уравнение

[cbm]\frac{dy}{dx}=\begin{cases}\dfrac{4x^3y}{x^4+y^4},&x^2+y^2>0,\\0,&x=y=0.\end{cases}[/cbm]

Нетрудно видеть, что функция [cbm]f(x,y)[/cbm] непрерывна; с другой стороны,

[cbm]f(x,Y)-f(x,y)=\frac{4x^3(x^4+yY)}{(x^4+y^2)(x^4+Y^2)}(Y-y).[/cbm]

Если [cbm]y=\alpha x^2,~Y=\beta x^2,[/cbm] то

[cbm]|f(x,Y)-f(x,y)|=\frac{4}{|x|}\frac{1-\alpha\beta}{(1+\alpha^2)(1+\beta^2)}|Y-y|,[/cbm]


и условие Липшица не удовлетворяется ни в одной области, содержащей начало координат [cbm]O(0,0)[/cbm] , так как множитель при [cbm]|Y-y|[/cbm] оказывается неограниченным при [cbm]x\to0[/cbm] .

Данное дифференциальное уравнение допускает решение [cbm]y=C^2-\sqrt{x^4+C^4},[/cbm] где [cbm]C[/cbm] — произвольная постоянная. Отсюда видно, что существует бесконечное множество решений, удовлетворяющих начальному условию [cbm]y(0)=0.[/cbm]

Общим решением дифференциального уравнения (2) называется функция

[cbm]y=\varphi(x,C),[/cbm]

(3)


зависящая от одной произвольной постоянной [cbm]C[/cbm] , и такая, что

1) она удовлетворяет уравнению (2) при любых допустимых значениях постоянной [cbm]C;[/cbm]

2) каково бы ни было начальное условие

[cbm]\Bigl.{y}\Bigr|_{x=x_0}=y_0,[/cbm]

(4)


можно подобрать такое значение [cbm]C_0[/cbm] постоянной [cbm]C[/cbm] , что решение [cbm]y=\varphi(x,C_0)[/cbm] будет удовлетворять заданному начальному условию (4). При этом предполагается, что точка [cbm](x_0,y_0)[/cbm] принадлежит области, где выполняются условия существования и единственности решения.

Частным решением дифференциального уравнения (2) называется решение, получаемое из общего решения (3) при каком-либо определенном значении произвольной постоянной [cbm]C[/cbm] .

Пример 1. Проверить, что функция [cbm]y=x+C[/cbm] есть общее решение дифференциального уравнения [cbm]y’=1[/cbm] и найти частное решение, удовлетворяющее начальному условию [cbm]y|_{x=0}=0[/cbm] . Дать геометрическое истолкование результата.

Решение. Функция [cbm]y=x+C[/cbm] удовлетворяет данному уравнению при любых значениях произвольной постоянной [cbm]C[/cbm] . В самом деле, [cbm]y’=(x+C)’=1.[/cbm]

Зададим произвольное начальное условие [cbm]y|_{x=x_0}=y_0[/cbm] . Полагая [cbm]x=x_0[/cbm] и [cbm]y=y_0[/cbm] в равенстве [cbm]y=x+C[/cbm] , найдем, что [cbm]C=y_0-x_0[/cbm] . Подставив это значение [cbm]C[/cbm] в данную функцию, будем иметь [cbm]y=x+y_0-x_0[/cbm] . Эта функция удовлетворяет заданному начальному условию: положив [cbm]x=x_0[/cbm] , получим [cbm]y=x_0+y_0-x_0=y_0[/cbm] . Итак, функция [cbm]y=x+C[/cbm] является общим решением данного уравнения.

В частности, полагая [cbm]x_0=0[/cbm] и [cbm]y_0=0[/cbm] , получим частное решение [cbm]y=x[/cbm] .

Общее решение данного уравнения, т.е. функция [cbm]y=x+C[/cbm] , определяет в плоскости [cbm]xOy[/cbm] семейство параллельных прямых с угловым коэффициентом [cbm]k=1[/cbm] . Через каждую точку [cbm]M_0(x_0,y_0)[/cbm] плоскости [cbm]xOy[/cbm] проходит единственная интегральная линия [cbm]y=x+y_0-x_0[/cbm] . Частное решение [cbm]y=x[/cbm] определяет одну из интегральных кривых, а именно прямую, проходящую через начало координат (рис.4).

Пример 2. Проверить, что функция [cbm]y=Ce^x[/cbm] есть общее решение уравнения [cbm]y’-y=0[/cbm] и найти частное решение, удовлетворяющее начальному условию [cbm]y|_{x=1}=-1.[/cbm] .

Решение. Имеем [cbm]y=Ce^x,~y’=Ce^x[/cbm] . Подставляя в данное уравнение выражения [cbm]y[/cbm] и [cbm]y'[/cbm] , получаем [cbm]Ce^x-Ce^x\equiv0[/cbm] , т. е. функция [cbm]y=Ce^x[/cbm] удовлетворяет данному уравнению при любых значениях постоянной [cbm]C[/cbm] .

Зададим произвольное начальное условие [cbm]y|_{x=x_0}=y_0[/cbm] . Подставив [cbm]x_0[/cbm] и [cbm]y_0[/cbm] вместо [cbm]x[/cbm] и [cbm]y[/cbm] в функцию [cbm]y=Ce^x[/cbm] , будем иметь [cbm]y_0=Ce^{x_0}[/cbm] , откуда [cbm]C=y_0e^{-x_0}[/cbm] . Функция [cbm]y=y_0e^{x-x_0}[/cbm] удовлетворяет начальному условию. Действительно, полагая [cbm]x=x_0[/cbm] , получим [cbm]y=y_0e^{x_0-x_0}=y_0[/cbm] . Функция [cbm]y=Ce^x[/cbm] есть общее решение данного уравнения.

При [cbm]x_0=1[/cbm] и [cbm]y_0=-1[/cbm] получим частное решение [cbm]y=-e^{x-1}[/cbm] .

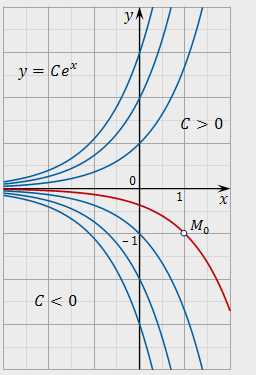
С геометрической точки зрения общее решение определяет семейство интегральных кривых, которыми являются графики показательных функций; частное решение есть интегральная кривая, проходящая через точку [cbm]M_0(1;-1)[/cbm] (рис.5).

Соотношение вида [cbm]\Phi(x,y,C)=0[/cbm] , неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.

Соотношение, получаемое из общего интеграла при конкретном значении постоянной [cbm]C[/cbm] , называется частным интегралом дифференциального уравнения.

Задача решения или интегрирования дифференциального уравнения состоит в нахождении общего решения или общего интеграла данного дифференциального уравнения. Если дополнительно задано начальное условие, то требуется выделить частное решение или частный интеграл, удовлетворяющие поставленному начальному условию.

Так как с геометрической точки зрения координаты [cbm]x[/cbm] и [cbm]y[/cbm] равноправны, то наряду с уравнением [cbm]\frac{dx}{dy}=f(x,y)[/cbm] мы будем рассматривать уравнение [cbm]\frac{dx}{dy}=\frac{1}{f(x,y)}[/cbm] .

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!