Давление идеального газа формула через кинетическую энергию – 21.Основные газовые законы и область их применения. Идеальный газ. Выводы закона Клапейрона-Менделеева. Универсальная газовая постоянная.

Содержание

Основное уравнение МКТ в физике

Определение и формула уравнения МКТ

Основное уравнение МКТ наглядно объясняет, каким образом идеальный газ создает давление на окружающие его стенки сосуда. Молекулы все время ударяются о стенку, воздействуя на нее с некоторой силой F. Тут следует вспомнить третий закон Ньютона: когда молекула ударяется о предмет, на нее действует сила -F, вследствие чего молекула «отбивается» от стенки. При этом мы считаем соударения молекул со стенкой абсолютно упругими: механическая энергия молекул и стенки полностью сохраняется, не переходя во внутреннюю энергию тел. Это значит, что при соударениях изменяются только скорости молекул, а нагревания молекул и стенки не происходит.

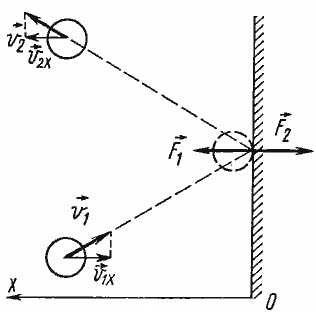
Зная, что соударение со стенкой было упругим, мы можем предсказать, как изменится скорость молекулы после столкновения. Модуль скорости останется таким же, как и до соударения, а направление движения изменится на противоположное относительно оси Ох (считаем, что Ох – это та ось, которая перпендикулярна стенке).

Молекул газа очень много, движутся они хаотично и о стенку ударяются часто. Найдя геометрическую сумму сил, с которой каждая молекула воздействует на стенку, мы узнаём силу давления газа. Чтобы усреднить скорости молекул, необходимо использовать статистические методы. Именно поэтому в основном уравнении МКТ используют усредненный квадрат скорости молекул , а не квадрат усредненной скорости : усредненная скорость хаотично движущихся молекул равна нулю, и в этом случае никакого давления мы бы не получили.

Теперь ясен физический смысл уравнения: чем больше молекул содержится в объеме, чем они тяжелее и чем быстрее движутся – тем большее давление они создают на стенки сосуда.

Основное уравнение МКТ для модели идеального газа

Следует заметить, что основное уравнение МКТ выводилось для модели идеального газа с соответствующими допущениями:

  1. Соударения молекул с окружающими объектами абсолютно упругие. Для реальных же газов это не совсем так; часть кинетической энергии молекул всё-таки переходит во внутреннюю энергию молекул и стенки.
  2. Силами взаимодействия между молекулами можно пренебречь. Если же реальный газ находится при высоком давлении и сравнительно низкой температуре, эти силы становятся весьма существенными.
  3. Молекулы считаем материальными точками, пренебрегая их размером. Однако размеры молекул реальных газов влияют на расстояние между самими молекулами и стенкой.
  4. И, наконец, основное уравнение МКТ рассматривает однородный газ – а в действительности мы часто имеем дело со смесями газов. Как, например, воздух.

Однако для разреженных газов это уравнение дает очень точные результаты. Кроме того, многие реальные газы в условиях комнатной температуры и при давлении, близком к атмосферному, весьма напоминают по свойствам идеальный газ.

Как известно из законов динамики, кинетическая энергия любого тела или частицы . Заменив произведение массы каждой из частичек и квадрата их скорости в записанном нами уравнении, мы можем представить его в виде:

   

Также кинетическая энергия газовых молекул выражается формулой , что нередко используется в задачах. Здесь k – это постоянная Больцмана, устанавливающая связь между температурой и энергией. k=1,38•10-23 Дж/К.

Основное уравнение МКТ лежит в основе термодинамики. Также оно используется на практике в космонавтике, криогенике и нейтронной физике.

Примеры решения задач

ru.solverbook.com

19.Изобразите шкалы температур Кельвина и Цельсия.

20.Что такое идеальный газ? Идеальный газ – физическая модель, в которой молекулы представляются упругими частицами, не взаимодействующими друг с другом.

Давление идеального газа зависит от массы молекул, концентрации молекул.

21.Напишите основное уравнение молекулярно – кинетической теории. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).

22.Что такое концентрация молекул? Концентрация частиц — физическая величина, равная отношению числа частиц N к объёму V, в котором они находятся:

23.Что такое средняя квадратическая скорость молекул? Так как молекулы газа движутся с разной скоростью, используют вероятностную усредненную величину, характеризующую кинетическую энергию молекул газа. Это среднее от квадратов скоростей. Среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа

24.Напишите выражение средней кинетической энергии молекул идеального газа.

25.Напишите выражение давления идеального газа через среднюю кинетическую энергию движения его молекул.

26.Чему равна постоянная Больцмана? Каков ее физический смысл? Постоянная Больцмана

 — физическая постоянная, определяющая связь между температурой и энергией.  Её экспериментальное значение в системе СИ равно

 Дж/К.

27.Напишите уравнение Менделеева — Клапейрона Уравнение состояния идеального газа (или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

,

где

  • —давление,

  • —молярный объём,

  • —универсальная газовая постоянная

  • —абсолютная температура, К.

Или

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

28. Сформулируйте закон Бойля-Мариотта Утверждение закона Бойля — Мариотта состоит в следующем:

При постоянных температуре и массе газа произведение давления газа на его объём постоянно.

В математической форме это утверждение записывается в виде формулы

где — давление газа;— объём газа, а— постоянная в оговоренных условиях величина. В общем случае значениеопределяется химической природой, массой и температурой газа.

Очевидно, что если индексом 1 обозначить величины, относящиеся к начальному состоянию газа, а индексом 2 — к конечному, то приведённую формулу можно записать в виде

.

29.Какой процесс описывает закон Бойля — Мариотта? Какая из величин постоянная? Закон Бойля — Мариотта утверждает, что давление газа в изотермическом процессе обратно пропорционально занимаемому газом объёму. Иначе говоря, давление данной, массы газа при постоянной температуре изменяется обратно пропорционально его объему.   — постоянная в оговоренных условиях величина. В общем случае значение определяется химической природой, массой и температурой газа.

30.Изопроцесс, протекающий при постоянной температуре, называется изотермическим. При постоянной температуре произведение давления газа на объем для данной массы газа есть величина постоянная.

  1. Закон Гей-Люссака — закон пропорциональной зависимости объёма газа от абсолютной температуры при постоянном давлении. При постоянном давлении, объём постоянной массы газа пропорционален абсолютной температуре. Математически закон выглядит так:

где — объём данного количества газа при температуре 100 °C;— объём того же газа при 0 °C;— константа, одинаковая для всех газов при одинаковом давлении.

Гей-Люссак дал для константы значение1⁄266 66, что достаточно близко к современному значению, равному 1⁄273 15.

  1.   — константа, одинаковая для всех газов при одинаковом давлении. Из предыдущего взять процесс, который описывает закон

  2. Изопроцесс, протекающий в идеальном газе, в ходе которого давление остается постоянным, называется изобарным.

Объем газа данной массы при постоянном давлении возрастает линейно с увеличением температуры (закон Гей-Люссака)

  1. Зако́н Ша́рля — один из основных газовых законов, описывающий соотношение давления и температуры для идеального газа. 

Если температура газа увеличивается, то и его давление тоже увеличивается, если при этом масса и объём газа остаются неизменными. Закон имеет особенно простой математический вид, если температура измеряется по абсолютной шкале, например, в градусах Кельвина. Математически закон записывают так:

где:

P — давление газа,

T — температура газа (в градусах Кельвина),

k — константа.

  1. Зависимость давления газа от температуры при постоянном объёме. k — константа.

  2. Изопроцесс, протекающий в газе, при котором объем остается постоянным, называется изохорным.

Давление газа данной массы при постоянном объеме возрастает линейно с увеличением температуры (закон Шарля)

  1. Термодинамика — раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. (Термодинамика – это учение о превращении одних форм энергии в другие.)

  2. Внутренняя энергия — это энергия движения и взаимодействия частиц, из которых состоит тело. Внутренняя энергия зависит от температуры тела, его агрегатного состояния, от химических, атомных и ядерных реакций. Она не зависит ни от механического движения тела, ни от положения этого тела относительно других тел. Внутреннюю энергию можно изменить путем совершения работы и теплопередачи. Если над телом совершается работа, то внутренняя энергия тела увеличивается; если же это тело совершает работу, то его внутренняя энергия уменьшается. т. е. чтобы изменить внутреннюю энергию тела, нужно изменить его температуру.

  3. Вну́тренняя эне́ргия термодинамической системы (обозначается как E или U) — это сумма энергий теплового движения молекул и межмолекулярных взаимодействий Внутренняя энергия идеального газа не зависит от давления или объёма. Так как внутренняя энергия идеального газа является функцией только от температуры, то

.

  1. Первый закон термодинамики – закон сохранения энергии для тепловых процессов – устанавливает связь между количеством теплоты Q, полученной системой, изменением ΔU ее внутренней энергии и работой A, совершенной над внешними телами. Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами. ΔU = Q – A;   Q = ΔU + A.

  2. По формуле первого начала термодинамики , где Q – количество теплоты (Дж), A – совершаемая работа (Дж).Т.к. НАД газом совершили работу, у работы знак отрицательный

  1. Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю (невозможно построить замкнутый цикл, проходящий через точку с нулевой температурой).

  1. Адиабати́ческий, или адиаба́тный проце́сс  — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена () системы со средой сводится только к последним двум процессам. Поэтому,первое начало термодинамики в этом случае приобретает вид

где —изменение внутренней энергии тела, — работа, совершаемая системой.

  1. Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:

Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:

,

то есть вся теплота, которую получает газ идёт на изменение его внутренней энергии.

  1. В изохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно, 

    Q = ΔU = U (T2) – U (T1).

  2. Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

  1. В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.

Первый закон термодинамики для изотермического процесса выражается соотношением 

Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.

  1. Электромагнитные волны — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля.

Среди электромагнитных полей вообще, порождённых электрическими зарядами и их движением, принято относить собственно к излучению ту часть переменных электромагнитных полей, которая способна распространяться наиболее далеко от своих источников — движущихся зарядов, затухая наиболее медленно с расстоянием.

  1. Название диапазона

    Источники

    Радиоволны

    Атмосферные и магнитосферные явления. Радиосвязь.

    Инфракрасное излучение

    Излучение молекул и атомов при тепловых и электрических воздействиях.

    Видимое излучение

    Ультрафиолетовое

    Излучение атомов под воздействием ускоренных электронов.

    Рентгеновские

    Атомные процессы при воздействии ускоренных заряженных частиц.

    Гамма

    Ядерные и космические процессы, радиоактивный распад.

  2. Скорость электромагнитных волн в вакууме  равна скорости света, в различных средах она может быть как меньше, так и больше скорости света.

    Диапазоны

    Название группы волн (или частот)

    Основные способы получения и применения

    Низкочастотные

    волны

    Инфранизкие частоты

    Генераторы специальных конструкций

     

    Низкие частоты

    Промышленные частоты

     

     

    Звуковые частоты

    Генераторы переменного тока;

    большинство электрических

    приборов и двигателей

    питается переменным током 50-60 гц.

    Звуковые генераторы.

    Используются в электроакустике

    (микрофоны), кино, радиовещании.

    Радиоволны

    Длинные

    Генераторы электрических колебаний различных конструкций.

    Используются в телеграфии, радиовещании,

    телевидении, радиолокации и т.д.

    Метровые и дециметровые волны используются

    для исследования свойств вещества.

    Средние

    Короткие

    Метровые

    Дециметровые

    Сантиметровые

    Миллиметровые

    Переходные

    Получаются в магнетронных, клистронных

    генераторах и мазерах.

    Применяются в радиолокации,

    радиоспектроскопии и радиоастрономии.

    Инфракрасные

    лучи

    Декамикронные

    Микронные

    Излучение нагретых тел (газоразрядные лампы и т.п.)

    Используются в инфракрасной спектроскопии,

    при фотографировании в темноте (в инфракрасных лучах)

    Световые лучи.

    Ультрафиолетовые

    лучи

    Ближние

    Крайние

    Излучение Солнца, ртутных ламп и т.п.

    Используются в ультрафиолетовой

    микроскопии, в медицине.

    Рентгеновские

    лучи

    Ультрамягкие

    Получаются в рентгеновских трубках и в других приборах,

    где происходит торможение электронов с энергией более 105 эв.

    Используются в медицине, для изучения строения вещества,

    в дефектоскопии

    Мягкие

    Жесткие

    Гамма

    излучение

     

    Возникают при радиоактивных распадах ядер,

    при торможении электронов энергией более 105 эв

    и при других взаимодействиях элементарных частиц.

    Используются в гамма-дефектоскопии,

    при изучении свойств вещества.

  3. Радиосвязь – разновидность беспроводной связи, при которой в качестве носителя сигнала используются радиоволны, свободно распространяемые в пространстве.

  4. Передача происходит следующим образом: на передающей стороне (в радиопередатчике) формируются высокочастотные колебания (несущий сигнал) определенной частоты. На него накладывается сигнал, который нужно передать (звука, изображения и т. д.) — происходит модуляция несущей полезным сигналом. Сформированный таким образом высокочастотный сигнал излучается антенной в пространство в виде радиоволн. На приёмной стороне радиоволны наводят модулированный сигнал в приемной антенне, он поступает в радиоприёмник. Здесь система фильтров выделяет из множества наведенных в антенне токов от разных передатчиков сигнал с нужной несущей частотой, а детектор выделяет из него модулирующий полезный сигнал. Получаемый сигнал может несколько отличаться от передаваемого передатчиком вследствие влияния разнообразных помех.

Личность первоначального изобретателя радио является спорной. Ключевое изобретение в начале «беспроводной передачи данных, использующей весь частотный спектр», известное как передатчик с искровым разрядником, приписывается Александру Попову, Никола

Тесла, Гульельмо Маркони.

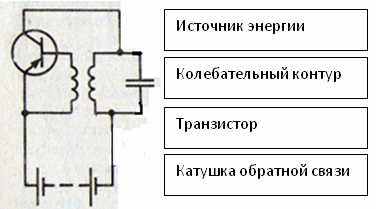
  1. Модуляция  — процесс изменения одного или нескольких параметров высокочастотного несущего колебания по закону низкочастотного информационного сигнала (сообщения).

Передаваемая информация заложена в управляющем (модулирующем) сигнале, а роль переносчика информации выполняет высокочастотное колебание, называемое несущим. Модуляция, таким образом, представляет собой процесс «посадки» информационного колебания на заведомо известную несущую.

В результате модуляции спектр низкочастотного управляющего сигнала переносится в область высоких частот. Это позволяет при организации вещания настроить функционирование всех приёмо-передающих устройств на разных частотах с тем, чтобы они «не мешали» друг другу.

Детектирование – преобразование электрических колебаний, в результате которого получаются колебания более низкой частоты или постоянный ток. Наиболее распространённый случай Д. – демодуляция – состоит в выделении низкочастотного модулирующего сигнала из модулированных высокочастотных колебаний . Д. применяется в радиоприёмных устройствах для выделения колебаний звуковой частоты, в телевидении – сигналов изображения и т. д.

studfiles.net

Основное уравнение молекулярно-кинетической теории (МКТ) с выводом

В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.

Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ – разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:

  • молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости
  • при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания

Основное уравнение молекулярно-кинетической теории

Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа – это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:

p – давление молекул газа на границы емкости,

m0 – масса одной молекулы,

n – концентрация молекул, число частиц N в единице объема V;

v2 – средне квадратичная скорость молекул.

Вывод основного уравнения МКТ

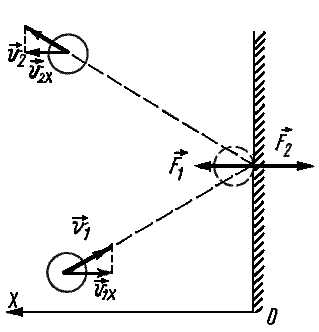
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция vx скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:

Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv1x = –mvx на mv2x = mvx.

Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:

Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:

S – площадь этой стенки

n – концентрация частиц

Давление p равно отношению силы F к площади S, на которую действует эта сила:

Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:

Исходя из вышенаписанного получаем:

Тогда

Если заменить среднее значение кинетической энергии поступательного движения молекул – E:

и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:

Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.

Понравилась статья, расскажите о ней друзьям:

Скорее всего, Вам будет интересно:

people-ask.ru

21.Основные газовые законы и область их применения. Идеальный газ. Выводы закона Клапейрона-Менделеева. Универсальная газовая постоянная.

Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют малые собственные размеры. Это идеализированная модель, согласно которой:

1. Собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда;

2. Между молекулами газа отсутствуют силы взаимодействия;

3. Столкновение молекул газа между собой и со стенками сосуда абсолютно упругие.

Уравнением Клайперона называется соотношение, справедливое для постоянной массы идеального газа:. R=C\v – молярная газовая постоянная, согласно закону Авогадро (при одинаковых давлениях и температурах молярные объемы различных газов также одинаковы). Отсюда следует, что R одинаково у всех газов. Поэтому ее принято называть универсальной газовой постоянной. R = 8, 31 Дж/(K моль)

Молярной массой любого тела называется физическая величина, равная отношению массы тела к количеству  молей, которое в нём содержится:  = m/,   = m/ ;  = 10 –3  m/mo , где m  масса молекулы данного тела, mo  масса одной двенадцатой массы атома углерода.

Молярным объёмом называется физическая величина, равная отношению объёма газа к числу молей, содержащихся в газе: V =V/ .

Вывод уравнения Менделеева – Клайперона.

V =V/, перепишем уравнение состояния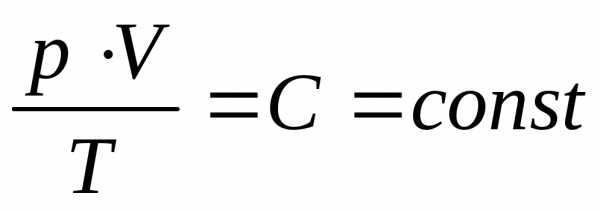в форме учтя чтоR=C\, получим P V = RT отсюда PV = RT.

22.Вывод основного уравнения молекулярно кинетической теории газов для давления. Средняя квадратичная скорость молекул. Средняя кинетическая энергия поступательного движения молекул газа.

Основным уравнение кинетической энергии газов есть соотношение: .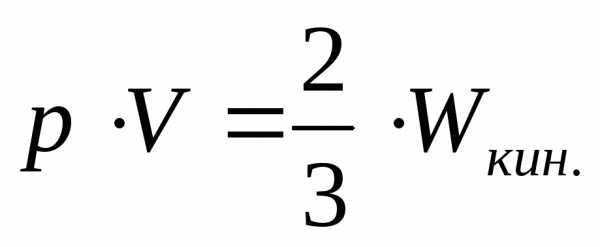

Это уравнение выполняется при N = const  общее число молекул в газе, то есть при отсутствии химических реакций; газ может состоять из разнородных молекул.

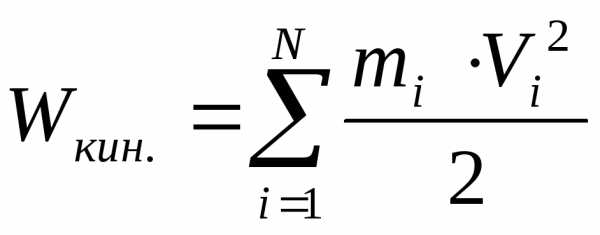суммарная энергия поступательного движения молекул газа, находящихся в сосуде, где mi  масса, а Vi  скорость «i ой» молекулы.

Для однородного газа mi = mo , тогда.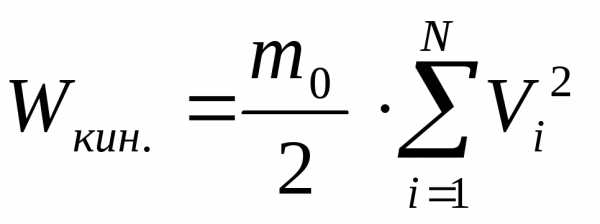

Средняя кинетическая энергия поступательного движения молекул газа.

Введём средне квадратичную скорость V квадр.поступательного движения молекул газ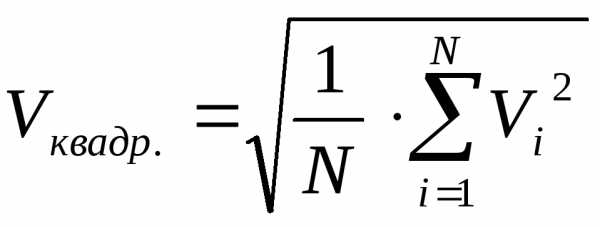а: . Тогда

Подставим данный результат в основное уравнение кинетической теории газов

(*), m  масса всего газа.

Сопоставим полученный результат с уравнением МенделееваКлайперона:

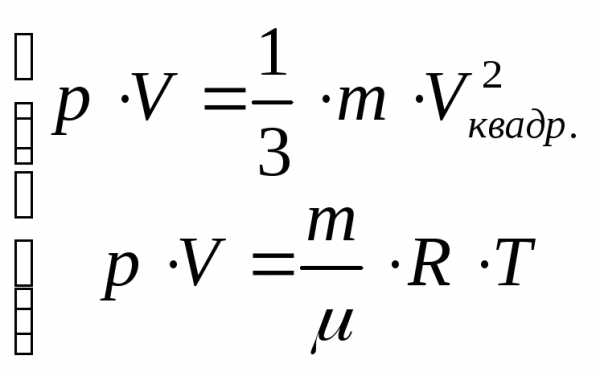, здесь использовалось полезное соотношение: 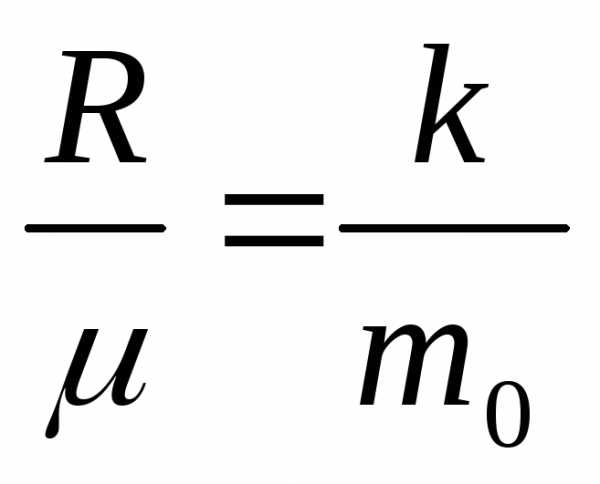. Связь давления, плотности газа и средней квадратичной скорости следует (*):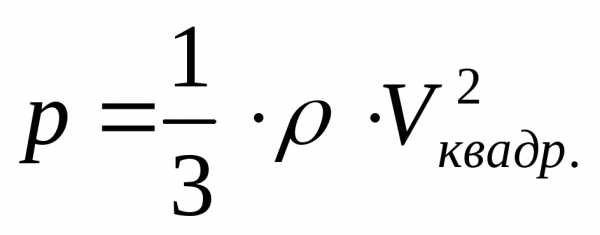

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа:

.После подстановки явного выражения для средней квадратичной скорости, получим: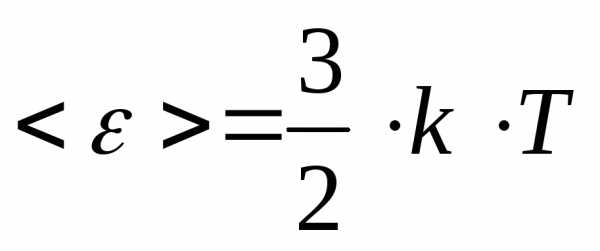

Наиболее вероятная скорость vB – соответствует максимуму f.

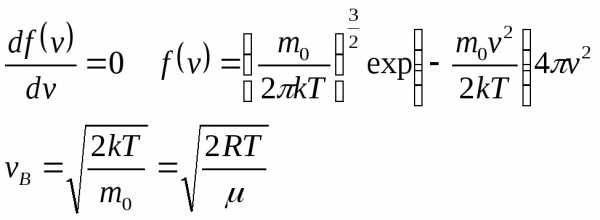
23.Распределение скоростей молекул по Максвеллу. Наиболее вероятная скорость, средняя арифметическая скорость. Опыт Штерна.

Закон распределения молекул идеального газа по скоростям определяет долевое участие молекул однородного газа в тепловом движении при данной температуре со скоростями, заключёнными в интервале от V до V + V. Он выведен теоретически: ,

где n  число молекул в единице объёма (концентрация молекул),

n число молекул из общего их числа, скорости которых лежат в интервале скоростей: ,

m0  масса одной молекулы,

k  постоянная Больцмана,

T  температура газа.

Чем меньше по величине выбирается интервал скоростей, тем более точный результат даёт данная формула.

N в единицу объёма, которые [,+ ]

Графическая иллюстрация данной формулы приведена на графике зависимости относительной концентрации молекул n/V идеального однородного газа от скорости.Функцией распределения молекул идеального газа по скоростям Максвелла называется выражение:.С помощью этой функции можно найти все статистически необходимые величины, характеризующие состояние идеального газа.

Вначале найдём наивероятнейшую скорость, т.е. значение скорости, соответствующее максимуму функции Максвелла. С точки зрения физики  это такое значение скорости, к которому близки значения скорости большей части молекул. Воспользуемся методом нахождения экстремума функции, т.е. вначале возьмём производную от функции распределения Максвелла по скорости, а затем приравняем полученное выражение к нулю:

.

Последнее уравнение имеет три решения, т.к. необходимо равенство нулю каждого из множителей:

1. это не физический случай;

2. V=0  тривиальный случай;

3.

Средне квадратичную и средне арифметическую скорости находятся интегрированием:

, .

Штерна опыт

        экспериментальное определение скоростей теплового движения молекул газа, осуществленное О.Штерном в 1920. Ш. о. подтвердил правильность основ кинетической теории газов Исследуемым газом в опыте служили разреженные пары серебра, которые получались при испарении слоя серебра, нанесённого на платиновую проволоку, нагревавшуюся электрическим током. Проволока располагалась в сосуде, из которого воздух был откачан, поэтому атомы серебра беспрепятственно разлетались во все стороны от проволоки. Для получения узкого пучка летящих атомов на их пути была установлена преграда со щелью, через которую атомы попадали на латунную пластинку, имевшую комнатную температуру. Атомы серебра осаждались на ней в виде узкой полоски, образуя серебряное изображение щели. Специальным устройством весь прибор приводился в быстрое вращение вокруг оси, параллельной плоскости пластинки. Вследствие вращения прибора атомы попадали в др. место пластинки: пока они пролетали расстояние l от щели до пластинки, пластинка смещалась. Смещение растет с угловой скоростью ω прибора и уменьшается с ростом скорости v атомов серебра. Зная ω и l, можно определить v. Т. к. атомы движутся с различными скоростями, полоска при вращении прибора размывается, становится шире. Плотность осадка в данном месте полоски пропорциональна числу атомов, движущихся с определённой скоростью. Наибольшая плотность соответствует наиболее вероятной скорости атомов. Полученные в Ш. о. значения наиболее вероятной скорости хорошо согласуются с теоретическим значением, полученным на основе Максвелла распределения (См.Максвелла распределение) молекул по скоростям.

        

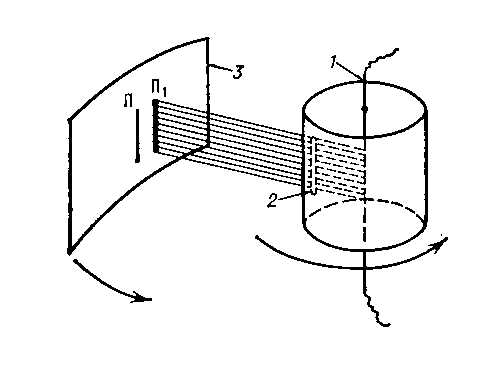
        Схема опыта Штерна: 1 — платиновая проволока с нанесённым на неё слоем серебра; 2 — щель, формирующая пучок атомов серебра; 3 — пластинка, на которой осаждаются атомы серебра; П и П1 — положения полосок осажденного серебра при неподвижном приборе и при вращении прибора.

studfiles.net

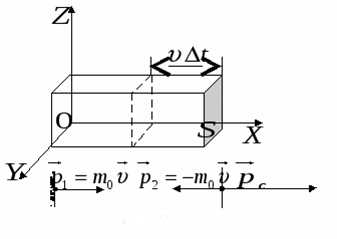
Давление и средняя кинетическая энергия молекул идеального газа

 

В сосуде находиться идеальный газ. Газ оказывает давление при соударении молекул, массой mо каждая, со стенками сосуда площадью S. Вычислим, какое давление газ оказывает на стенку сосуда. Каждая молекула при соударении передает стене импульс 2movx

vx  – это проекция вектора скорости v на ось OX, перпендикулярную стенке.

От всех молекул за одну секунду стенка получит суммарный импульс, который равен 2movxZ .

Z – число столкновений всех молекул со стенкой за одну секунду. Z пропорциональна концентрации молекул n, площади стенки S и проекции скорости  vx.

Формулы и вычисления

Молекулы газа движутся хаотично, поэтому все направления движения молекул равновероятны. Значит, из всех молекул, имеющих  составляющую скорости vx, половина молекул движется в сторону стенки AB, другая половина, в противоположную ей сторону, в сторону стенки CD.

Переданный стенке за одну секунду полный импульс будет равен:

За секунду изменение импульса точки (тела) равно действующей на него силе

Поскольку в сосуде содержится достаточно большое количество молекул и движутся они с разными скоростями, то следует усреднить силу

Видим, что сила зависит от среднего квадрата скорости 

Так как движение хаотично, то все направления проекции квадрата скорости равны

Также известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому

Усредним это выражение по всем молекулам, с учетом выше представленных формул получим

Откуда можно получить:

Силу тогда можно определить по следующей формуле:

Зная силу, определяем давление на стенку сосуда

Это выражение называется основным уравнением молекулярно-кинетической теории.

С помощью данного уравнения можно получить связь между средней кинетической энергией молекул и давлением.

 

 ,средняя кинетическая энергия молекул газа

Давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

fizikatyt.ru

Давление газа

Разделив левую и правую части уравнения (4.4.8) на SΔt и учитывая соотношение (4.3.6), найдем давление газа

(4.4.9)

Это и есть основное уравнение молекулярно-кинетической теории идеального газа*.

* Это уравнение — первое количественное соотношение, полученное в молекулярно-кинетической теории. Поэтому его принято называть основным.

Давление идеального газа пропорционально произведению массы молекулы на концентрацию молекул и средний квадрат их скорости.

Формула (4.4.9) связывает макроскопическую величину — давление, которое может быть измерено манометром, — с микроскопическими величинами, характеризующими молекулы, и является как бы мостом между двумя мирами: макроскопическим и микроскопическим.

Если через обозначить среднюю кинетическую энергию поступательного движения молекулы: 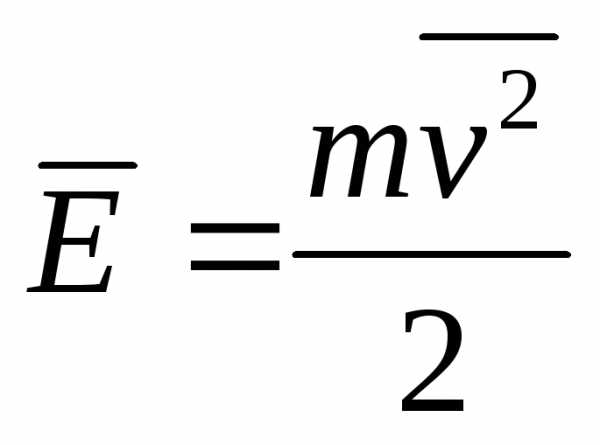, то уравнение (4.4.9) можно записать в форме:

(4.4.10)

Отметим в заключение, что хотя расчет произведен без явного учета столкновений молекул, это не означает, что столкновения совсем не учитывались нами. Именно огромное число столкновений приводит к тому, что движение молекул является хаотическим. Равенства (4.3.4) и (4.3.6) выполняются с большой точностью как раз вследствие громадного числа столкновений.

Нам удалось вычислить давление идеального газа на стенки сосуда. Оно зависит от концентрации молекул. Кроме того, давление газа пропорционально средней кинетической энергии молекул. Это и есть главный факт.

§ 4.5. Температура— мера средней кинетической энергии молекул

Из основного уравнения молекулярно-кинетической теории газа вытекает важное следствие: температура есть мера средней кинетической энергии молекул. Докажем это.

Для простоты будем считать количество газа равным 1 моль. Молярный объем газа обозначим через VM. Произведение молярного объема на концентрацию молекул представляет собой постоянную Авогадро NA, т. е. число молекул в 1 моль.

Умножим обе части уравнения (4.4.10) на молярный объем VM и учтем, что nVM = NA. Тогда

(4.5.1)

Формула (4.5.1) устанавливает связь макроскопических параметров — давления р и объема VM — со средней кинетической энергией поступательного движения молекул.

Вместе с тем полученное опытным путем уравнение состояния идеального газа для 1 моль имеет вид:

(4.5.2)

Левые части уравнений (4.5.1) и (4.5.2) одинаковы, значит, должны быть равны и их правые части, т. е.

Отсюда вытекает связь между средней кинетической энергией поступательного движения молекул и температурой:

(4.5.3)

Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре. Чем выше температура, тем быстрее движутся молекулы.

Соотношение между температурой и средней кинетической энергией поступательного движения молекул (4.5.3) установлено для разреженных газов. Однако оно оказывается справедливым для любых веществ, движение атомов или молекул которых подчиняется законам механики Ньютона. Оно верно для жидкостей, а также для твердых тел, у которых атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решетки.

При приближении температуры к абсолютному нулю энергия теплового движения молекул также приближается к нулю*.

* При очень низких температурах (вблизи абсолютного нуля) движение атомов и молекул уже не подчиняется законам Ньютона. Согласно более точным законам движения микрочастиц — законам квантовой механики — абсолютный нуль соответствует минимальному значению энергии движения, а не полному прекращению какого-либо движения вообще.

studfiles.net

Молекулярно-кинетическая теория идеального газа Основные формулы

  • Основное уравнение молекулярно-кинетической теории:

,

где 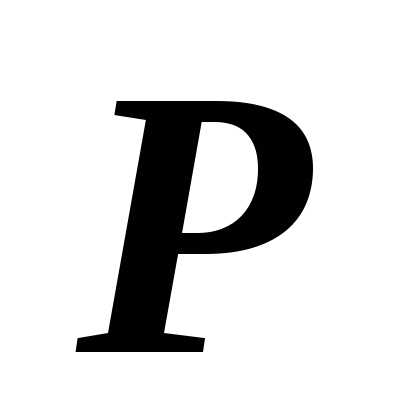– давление газа, – концентрация молекул, 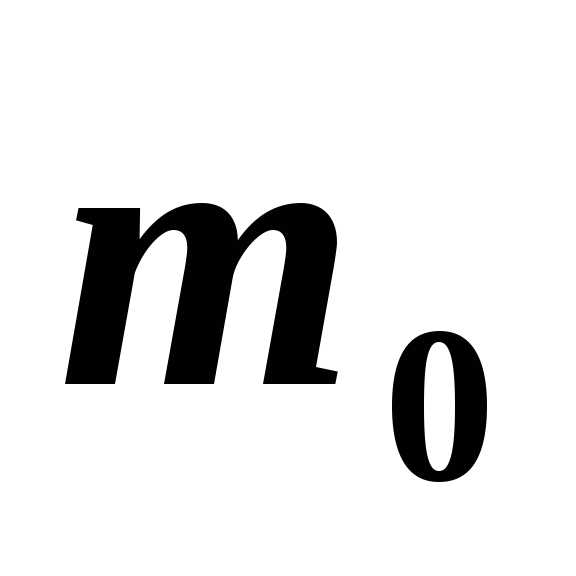– масса одной молекулы, – средняя квадратичная скорость одной молекулы, – плотность газа,–абсолютная температура, – постоянная Больцмана.

.

1) – изотермический:

2) – изобарный: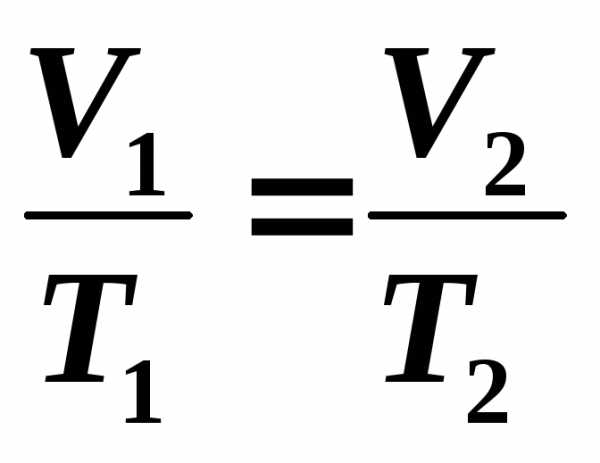

3) – изохорный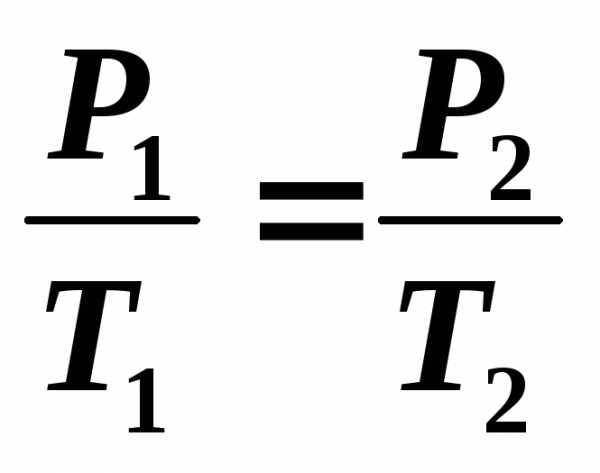

,

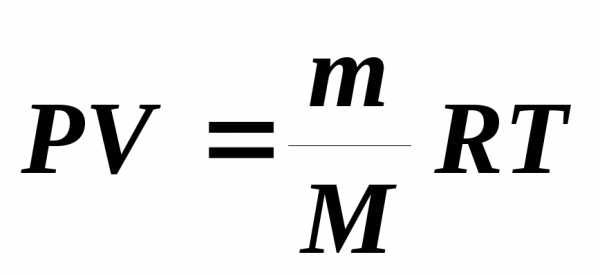где – объём газа,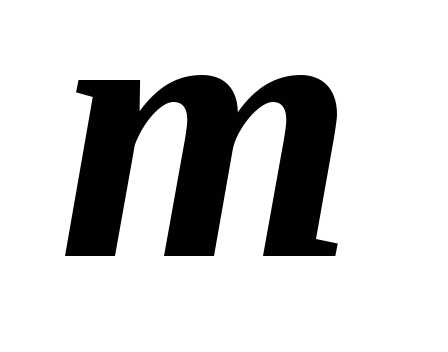– масса газа,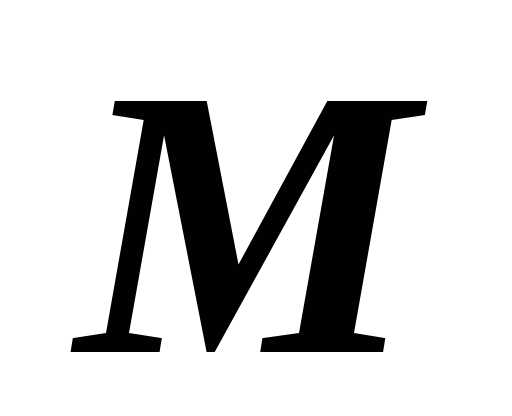– молярная масса,)- универсальная газовая постоянная.

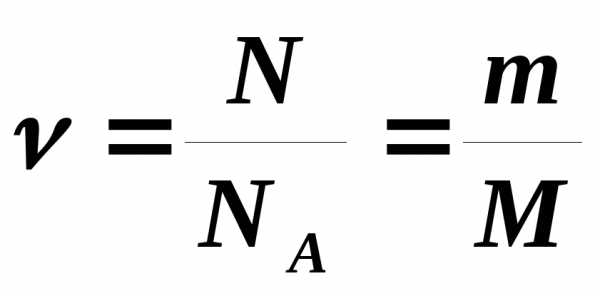
где 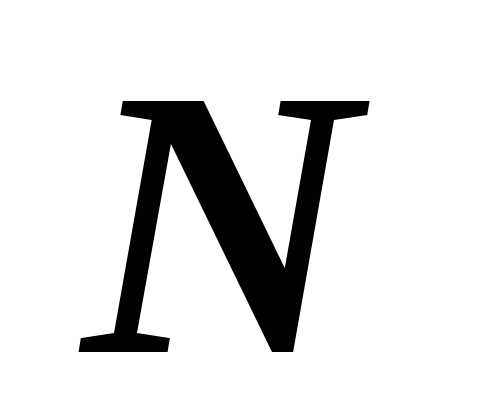– общее число молекул,- постоянная Авогадро.

– средняя квадратичная,

– средняя арифметическая,

– наиболее вероятная.

-объём одного моля газа.

.

.

Задания

5.1. В сосуде объёмом находится газ при нормальных условиях. Определите число молекул газа в сосуде и концентрацию молекул. []

5.2. Газ находится в цилиндре под поршнем при нормальных условиях. Во сколько раз изменится концентрация молекул газа при увеличении объёма газа в 5 раз при прежней температуре?

[уменьшится в 5 раз ]

5.3. Газ находится в цилиндре под поршнем при нормальных условиях. Во сколько раз изменится концентрация молекул газа при увеличении температуры газа до при прежнем давлении? [уменьшится в 1,37 раза]

5.4. В баллоне находилось 10 кг газа при давлении 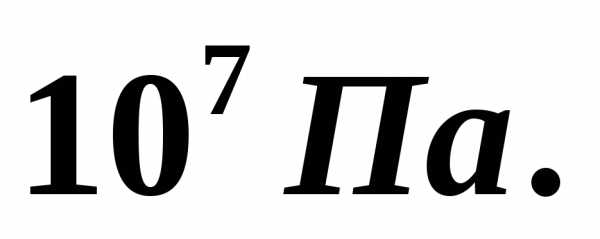Найти, какое количество газа взяли из баллона, если окончательное давление стало равноТемпературу газа считать постоянной. [7,5 кг]

5.5. 12 г газа занимают объём при температуре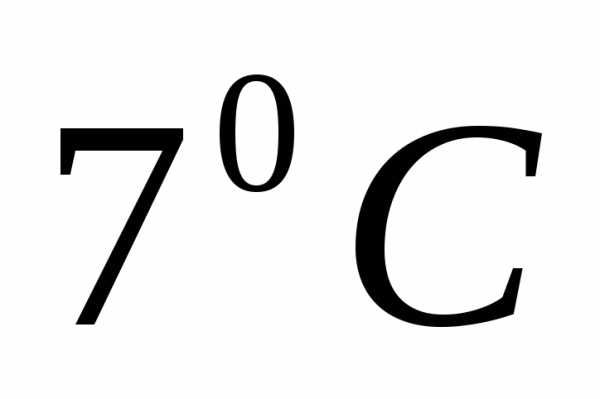. После нагревания газа при постоянном давлении его плотность стала равнаДо какой температуры нагрели газ? [1400 К]

5.5. В баллоне объёмом 10 л находится гелий () под давлением 1 МПа и при температуре 300 К. После того как из баллона было взято 10 г гелия, температура в баллоне понизилась до 290 К. Определите давление гелия, оставшегося в баллоне. [0,364 МПа]

5.6. В сосуде объёмом находится 0,02 кг азота (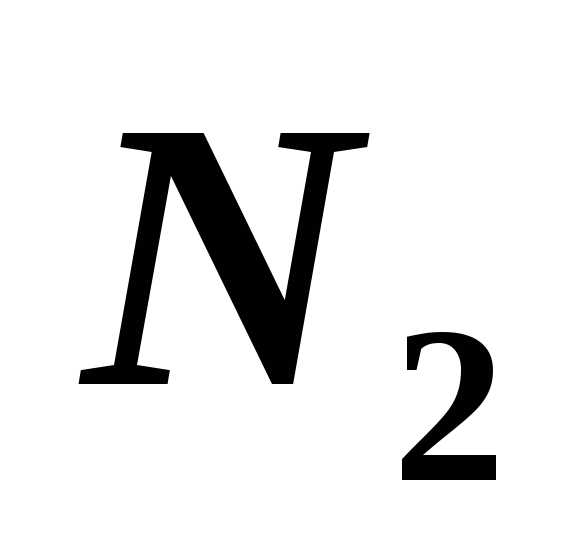)под давлением. Определите среднюю квадратичную скорость молекул газа; число молекул, находящихся в сосуде; плотность газа. []

5.7. Плотность некоторого газа , а средняя квадратичная скорость молекул этого газа равна 600 м/с. Определите давление, которое оказывает газ на стенки сосуда.

[600 Па]

5.8. Определите среднюю квадратичную скорость молекул некоторого газа, плотность которого при давлении равнаКакова масса одного моля этого газа, если значение плотности дано при температуре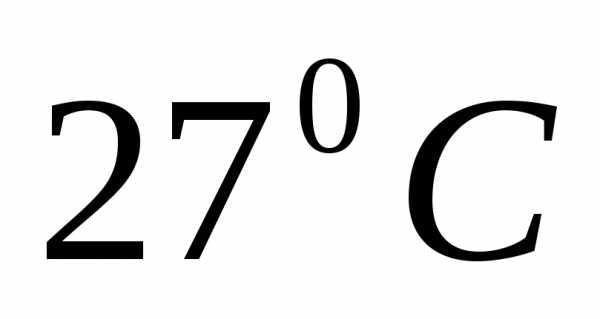? [1172,6 м/с; 0,005 кг/моль]

5.9. 6 г углекислого газа (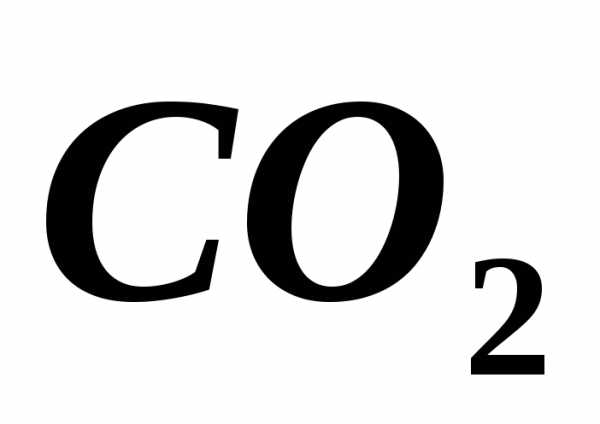) и 5 г закиси азота () заполняют сосуд объёмом. Найти общее давление в сосуде при температуре 400 К. []

5.10. Определите молярную массу смеси кислород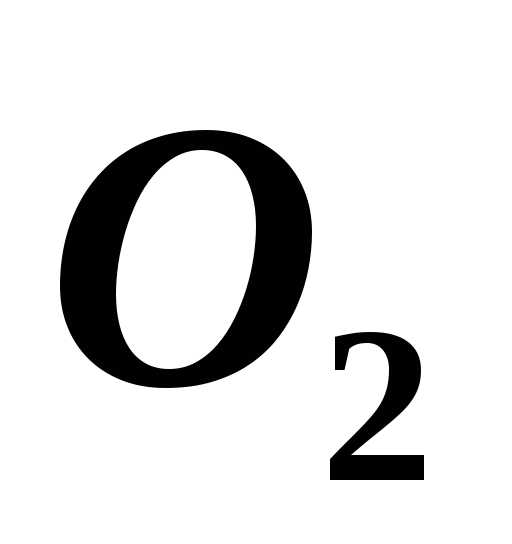а () массой 25 г и азота (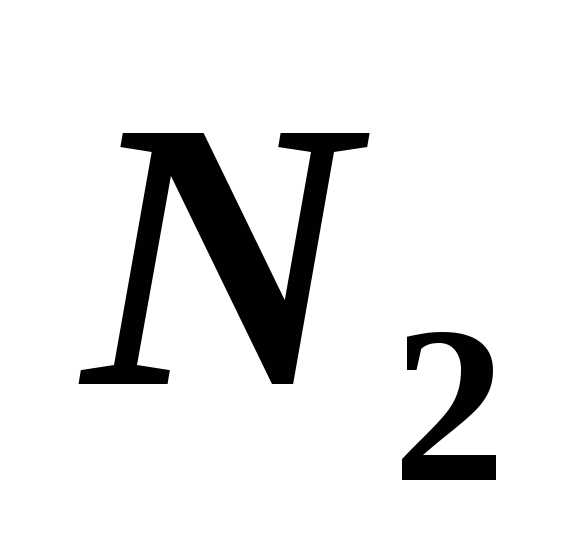) массой 75 г. []

5.11. Определите плотность смеси газов водорода ()массой 8 г и кислорода (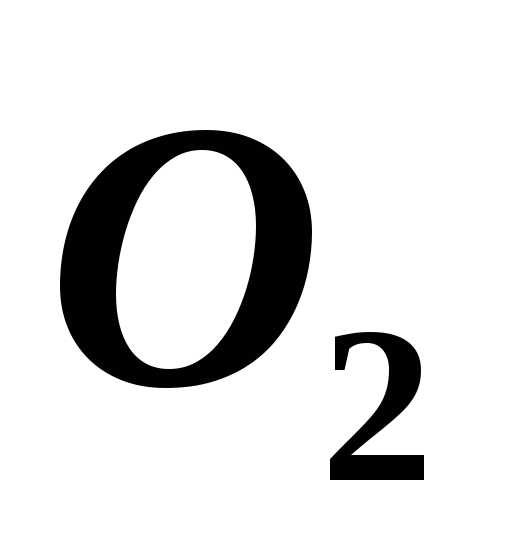) массой 64 г при температуре 290 К и при давлении 0,1 МПа. Газ считать идеальным. []

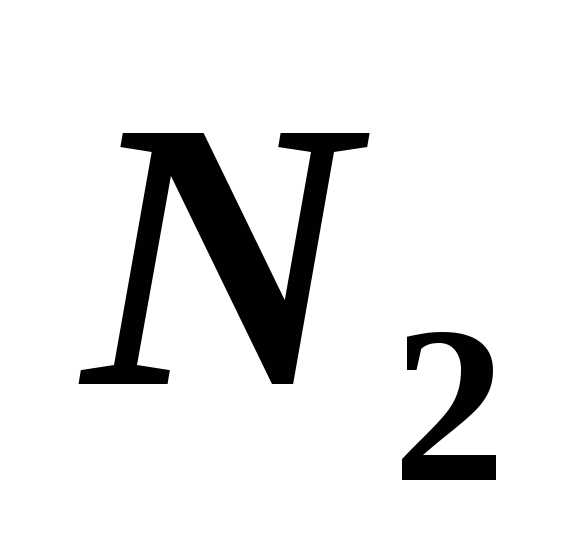5.12. Баллон вместимостью 20 л содержит смесь водорода () и азота () при температуре 290 К и давлении 1 МПа. Определите массу водорода, если масса смеси равна 150 г. [ 6,3 г]

5.13. В закрытом сосуде вместимостью 20 л находятся водород () массой 6 г и гелий ()массой 12 г. Определите давление и молярную массу газовой смеси в сосуде, если температура смеси 300 К. [0,75 МПа; 3.10-3 кг/моль]

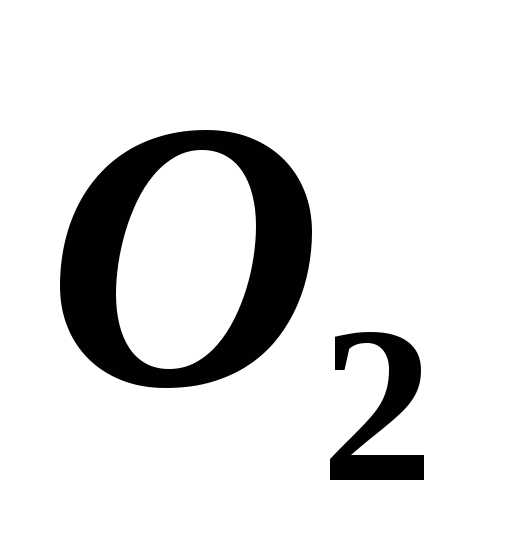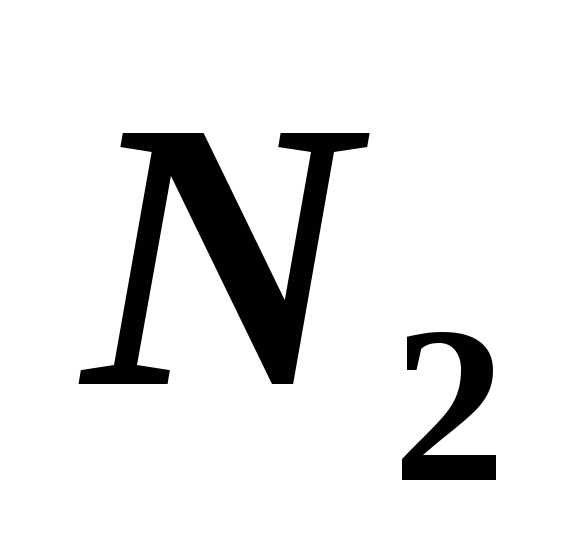5.14. Смесь кислорода () и азота () при температуре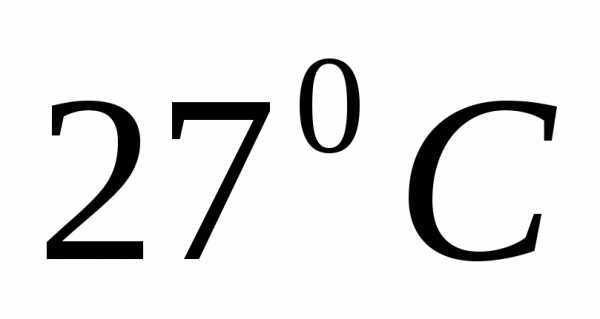находится под давлением 230 Па. Масса кислорода составляет 75% от общей массы смеси. Определите концентрацию молекул каждого из газов. []

5.15. В сосуде вместимостью 0,3 л при температуре 290 К находится некоторый газ. На сколько понизится давление газа в сосуде, если из-за утечки выйдет 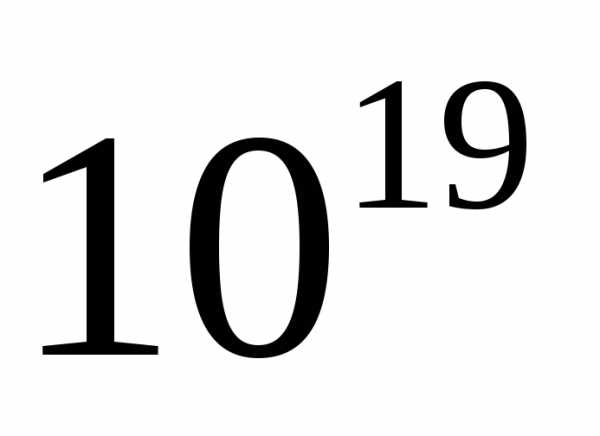молекул? [133 Па]

5.16. Два сосуда одинакового объёма содержат кислород (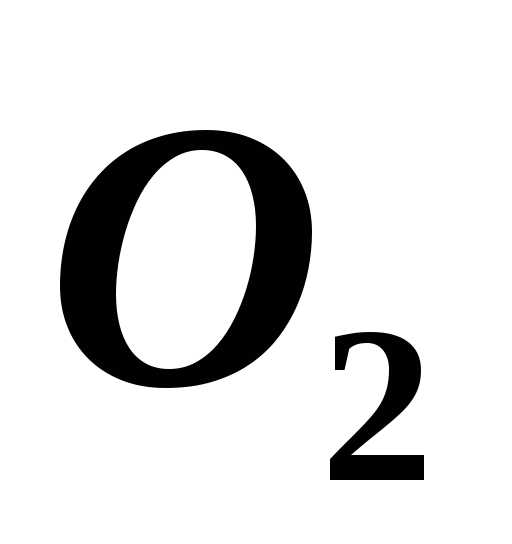). В одном сосуде давление 2 МПа и температура 800 К, в другом давление 2,5 МПа, а температура 200 К. Сосуды соединили трубкой и охладили находящийся в них кислород до 200 К. Определите установившееся в сосудах давление. [1,5 МПа]

5.17. Определите среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа при давлении 0,5 кПа, если концентрация молекул газа равна . []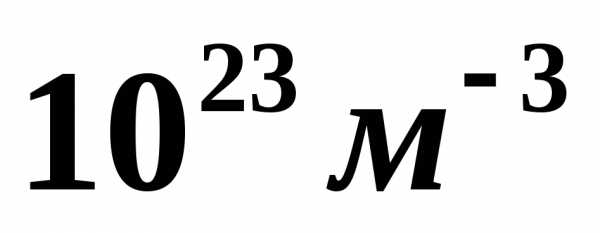

5.18. Во сколько раз средняя квадратичная скорость пылинки, взвешенной в воздухе, меньше средней квадратичной скорости молекул воздуха? Масса пылинки 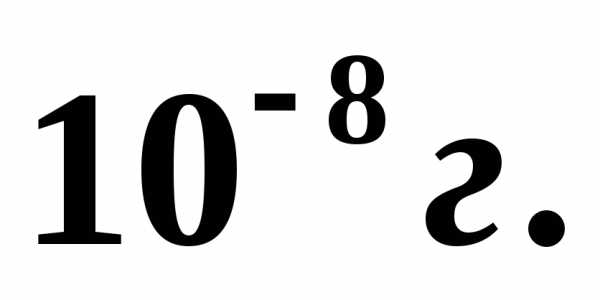Воздух считать однородным газом, молярная масса которого равна 0,029 кг/моль.

[в 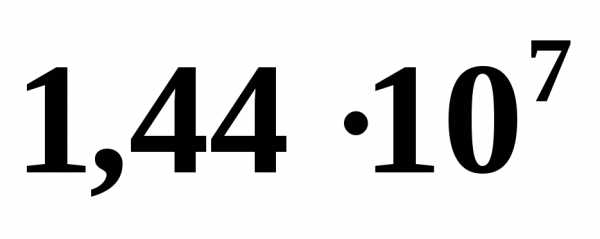раз]

5.19. Определите среднюю квадратичную скорость молекулы газа, заключённого в сосуд вместимостью 2 л под давлением 2 кПа. Масса газа 3 г. [4 км/с]

5.20. Определите наиболее вероятную скорость молекул газа, плотность которого при давлении 40 кПа составляет .

[478 м/с]

5.21. Определите наиболее вероятную, среднюю арифметическую и среднюю квадратичную скорости молекул азота (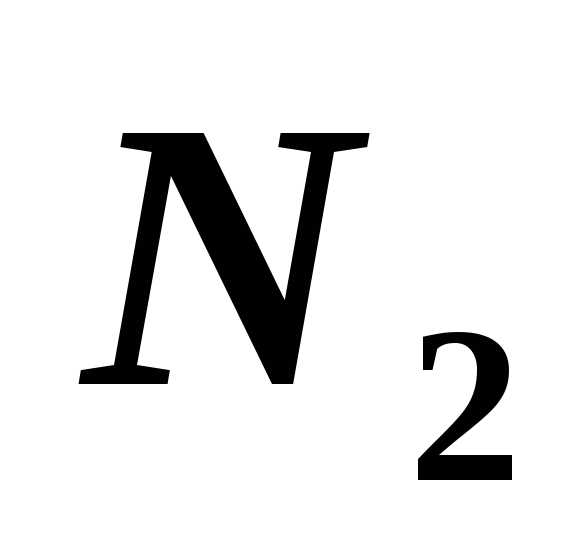) при 300 К. [422 м/с; 476 м/с; 517 м/с]

5.22. При какой температуре средняя квадратичная скорость молекул кислорода (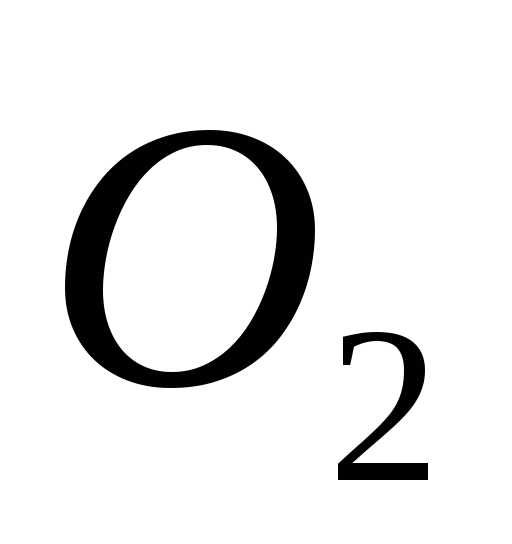) больше их наиболее вероятной скорости на 100 м/с. [381 К]

5.23. Определите среднюю арифметическую скорость молекул газа, если известно, что их средняя квадратичная скорость 1 км/с.

[920 м/с]

5.24. Смесь гелия () и аргона (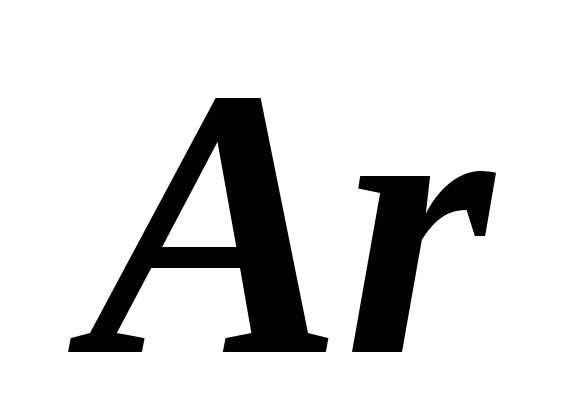) находится при температуре 1200 К. Определите среднюю квадратичную скорость и среднюю кинетическую энергию поступательного движения атомов гелия и аргона. [гелий: 2730 м/с;; аргон: 864 м/с;)]

5.25. Используя закон распределения молекул идеального газа по скоростям, найти формулу наиболее вероятной скорости. []

5.26. Используя закон распределения молекул идеального газа по скоростям, найти среднюю арифметическую скорость молекул. []

5.27. Используя закон распределения молекул идеального газа по скоростям, найти среднюю квадратичную скорость. []

5.28. Используя функцию распределения молекул идеального газа по энергиям, найти среднюю кинетическую энергию молекул. [3/2 ]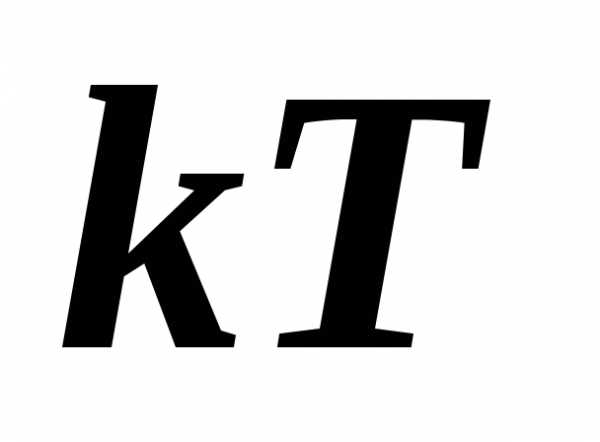

studfiles.net

Related Posts

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *