25.01.202006.01.2019

Дифференциальные уравнения это – .

• by alexxlab
• Комментариев к записи Дифференциальные уравнения это – . нет
• Советы абитуриенту

Дифференциальные уравнения, общие понятия – Доктор Лом. Первая помощь при ремонте

В общем случае определение дифференциального уравнения может выглядеть так:

Дифференциальным уравнением называется равенство между функцией и ее производной или дифференциалом.

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного аргумента. Например:

у’ = f(x) (539.1)

Напомню, функциональное уравнение может иметь следующий вид:

у = f(x) (538.1)

Дифференциальное уравнение называется уравнением в частных производных, если искомая функция зависит от нескольких аргументов. Например:

у’ = f(x₁,x₂) или у’ = f(x,u) (539.2)

где х₁, х₂ или х, u – возможные обозначения для различных аргументов функции.

Порядком дифференциального уравнения считается порядок наивысшей производной, входящей в уравнение. Например уравнение (539.1) является уравнением первого порядка. Уравнение второго порядка может иметь вид:

y” = f(x) (539.3)

Решением дифференциального уравнения является функция, подставление которой вместо неизвестной функции обращает уравнение в тождество. Другими словами уравнение становится равенством.

А теперь эти общие математические понятия (кстати тут приведены далеко не все основные понятия) попробуем описать простым человеческим языком, но начать придется издалека.

Производная функции

Мы живем в несовершенном, постоянно изменяющемся мире. Все течет, все изменяется, как подметил еще Гераклит. Однако в древности были и другие мыслители, которые в отличие от Гераклита пытались этот мир как-то понять и оценить. Так далеко в историю мы заглядывать не будем, хотя предпосылки к дифференциальному исчислению следует искать именно там, а ограничимся простыми и наглядными примерами:

Пример 1

Мы вышли из пункта А в пункт Б и находились в пути 4 часа, каждый час мы проходили по 2 километра. Вопрос: какое расстояние между пунктами А и Б?

Вообще это задачка для 3-4 класса начальной школы и решить ее вроде бы не сложно (потому я ее и выбрал): достаточно сложить все расстояния, пройденные за каждый час, а так как эти расстояния одинаковые, то можно еще больше упростить задачу, умножив на 4 расстояние, пройденное за один промежуток времени. Таким образом расстояние между пунктами А и Б составляет:

2 км · 4 = 8 км (539.4)

А между тем условия задачи можно рассматривать и по другому, т.е. как зависимость пройденного расстояния от времени. В этом случае у нас время -независимая переменная t или аргумент функции, а пройденное расстояние – значение функции в тот или иной момент времени или переменная s. Тогда условия задачи соответствуют следующему функциональному уравнению:

s = f(t) = 2t (539.5)

а также графику этой функции:

Рисунок 539.1. График функции f(t) = 2t.

 

Так если по оси t откладывать промежутки времени Δt (ч), которое мы были в пути, а по оси s – преодоленное за эти промежутки времени расстояние Δs (км), то график указанной функции будет иметь такой вид, как показано на рисунке 539.1. В общем случае используются более привычные оси х и у, соответственно рассматриваются функции вида y = f(x), но сути дела это никак не меняет.

Решая уравнение (539.5) мы можем определить не только общее расстояние, преодоленное за 4 часа пути, но и в любой интересующий нас момент времени. Например, нас интересует, какое расстояние мы прошли за 1.5 часа. Согласно уравнению (539.5) это расстояние составит 2·1.5 = 3 километра.

А если нас интересует не расстояние, преодоленное к тому или иному моменту времени, а скорость движения? Можем ли мы определить эту скорость на основе имеющихся данных?

Оказывается можем, потому что скорость – это тоже функция, которая в свою очередь также зависит от времени.

Так как каждый час мы преодолевали по 2 км, то отсюда можно сделать вывод, что скорость нашего движения была постоянной, тогда по давно известному нам уравнению, описывающему движение с постоянной скоростью:

v = s/t = 8/4 = 2 км/ч (539.6)

В данном случае, так как скорость постоянная, не имеет значения, на каком временном промежутке мы эту скорость определяем. Тем не менее рассмотрим данную ситуацию с точки зрения математики.

Временные промежутки, когда засекалось пройденное расстояние, мы обозначим как Δt = 1, соответственно t = ΣΔt = 1 + 1 + 1 + 1 = 4. Расстояния, пройденные за эти промежутки времени обозначим как Δs = 2. На графике функции это будет выглядеть так:

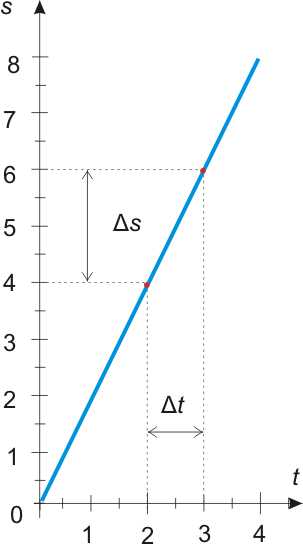
Рисунок 539.2

С точки зрения математики временные промежутки Δt – это приращение аргумента функции:

Δt = t – t₀ (539.7)

Соответственно расстояния, пройденные за рассматриваемый промежуток времени – это приращение функции:

Δs = Δf(t) = f(t) – f(t₀) (539.8)

А так как использовать греческую литеру Δ не всегда удобно (в частности мне для этого приходится заходить в отдельный редактор текста, а наборщикам в типографиях вставить эту литеру было еще сложнее), то часто приращение значения искомой функции и приращение аргумента функции обозначают как ds и dt.

Тогда формулу определения скорости можно записать так:

v = ds/dt (539.9)

Таким образом мы с одной стороны вроде бы просто разделили расстояние на время – задача для 3-4 класса, а с другой стороны мы определили производную функции s = f(t), соответствующим образом ее продифференцировав, а это уже задача курса алгебры, а то и высшей математики.

Возможно и не стоило это так подробно расписывать, но на мой взгляд это очень важно, чтобы показать, что в дифференциальном исчислении нет ничего трудного, если рассматривать его на соответствующих примерах.

Итак скорость v является производной функции s = f(t) = 2t. Дифференциальное уравнение в этом случае будет выглядеть так:

v = s’ = f'(t) (539.10.1)

v = (2t)’ = 2 (539.10.2)

Но и это еще не все, на основании имеющихся данных: времени в пути и расстояний, преодоленных за 1 час, мы можем определить ускорение нашего движения.

Так как скорость нашего движения оставалась постоянной, соответственно dv = 0, то само собой и ускорения никакого не было, ни положительного ни отрицательного. Другими словами ускорение нашего движения составляло а = 0 км/ч².

На языке математики это будет выглядеть так:

а = v’ = dv/dt = s” = d²s/dt² (539.11.1)

a = 0/1 = (2t)” = (2)’ = 0

(539.11.2)

Т.е. в данном случае для определения ускорения нужно определить первую производную функции скорости (уравнения, выражающего зависимость скорости от времени) или вторую производную функции расстояния (уравнения, выражающего зависимость пройденного расстояния от времени).

На основании вышеизложенного мы можем дать следующее предварительное определение производной:

Производная – это скорость изменения функции

В рассмотренном выше примере скорость движения – это скорость изменения функции расстояния, а ускорение – это скорость изменения функции скорости. Если бы мы все 4 часа сидели на месте, то и расстояние, пройденное нами, было бы равно нулю, и скорость и ускорение, но даже для такого случая можно записать соответствующие дифференциальные уравнения:

s = f(t) = 0

v = s’ = 0

a = v’ = s” = 0

Однако в жизни гораздо чаще встречаются функции, даже третьи производные которых не равны нулю.

Рассмотрим другой пример все с тем же движением, на этот раз чуть более сложный.

Пример 2

По ровной наклонной поверхности скатывается шар. Начальная скорость движения равна v_o = 0. Определить пройденное шаром за 4 секунды расстояние, скорость после 1, 2, 3 и 4 секунд движения и постоянное ускорение движения, если за первую секунду шар преодолел расстояние 3 м, за вторую – 9 м, за третью – 15 м, за четвертую – 21 м.

С определением пройденного расстояния по прежнему проблем нет: достаточно сложить расстояния, которые преодолел шар за каждую секунду s = ΣΔs = 3 + 9 + 15 + 21 = 48 метров. А вот скорость и ускорение в данном случае определить не так просто. Тем не менее попробуем.

Если воспользоваться полученными раннее знаниями, то вроде бы в первый промежуток времени скорость должна быть равна:

v₁ = ds₁/dt₁ = 3/1 = 3 м/с (539.12)

Вот только в данном случае у нас скорость – изменяющаяся величина, зависящая от времени, поэтому результат полученный при решении уравнения (539.12) можно рассматривать лишь как среднюю скорость движения на первом участке. Тогда более правильно уравнение скорости на первом участке записать так:

v_1ср = ds₁/dt₁ = 3/1 = 3 м/с (539.12.2)

Подобным образом мы достаточно легко можем определить среднюю скорость на всех участках пути, и она составит v_2ср = 9 м/с, v_3ср = 15 м/с, v_4ср = 21 м/с, но в данном случае нас интересует не среднее значение функции скорости на рассматриваемом участке, а значение функции скорости во вполне определенной точке, т.е. после 1, 2, 3 и 4 секунд движения. Как это сделать?

По условиям задачи ускорение – производная от скорости – является постоянной величиной, т.е. скорость изменения скорости будет постоянной. В этом случае значение средней скорости является средним арифметическим от начальной и конечной скорости на рассматриваемом участке:

v_1ср = (v_o + v₁)/2 = 3 м/с (539.13.1)

тогда при v_o = 0

v₁ = 3·2 = 6 м/с (539.13.2)

Соответствующим образом мы можем определить значения скорости и в остальных точках, например (6 + v₂)/2 = 9, v₂ = 9·2 – 6 = 12 м/с; (12 + v₃)/2 = 15, v₃ = 15·2 – 12 = 18 и так далее, а теперь переведем полученные данные на язык высшей математики. Мы видим, что v₁ = 6·1, v₂ = 6·2 = 12, v₃ = 6·3 = 18, т.е. значение скорости явно зависит от времени, соответственно уравнение скорости мы можем записать следующим образом:

v = s’ = 6t (539.14)

Соответственно ускорение движения шара составит:

a = v’ = (6t)’ = 6 м/с² (539.15)

Между тем, если бы нам были заданы меньшие значения временных промежутков и соответственно меньшие значения пройденных расстояний за эти промежутки времени, например при dt

1 = 1 секунда, ds₁ = 3 м, dt₂ = 0.1 секунды и ds₂ = 0.63 м, то средняя скорость на рассматриваемом втором участке составила бы v_2ср = ds/dt = 0.63/0.1 = 6.3 м/с, а скорость в  в точке t₂: v_2сp = (6 + v₂)/2 = 6.3, v₂ = 12.6 – 6 = 6.6 м/с. Т.е. закономерность изменения значения скорости никуда не девается, тем не менее, чем меньше рассматриваемый временной промежуток dt, тем меньше разница между значением средней скорости изменения функции и скоростью изменения функции в рассматриваемой точке. Из этого можно сделать еще один очень важный вывод:

Скорость изменения функции может быть разная. Чем меньше приращение аргумента функции dt, тем ближе значение среднего изменения скорости к изменению скорости функции в рассматриваемой точке.

На основании этого можно сформулировать более полное определение производной функции:

Производная функции в точке – это скорость изменения функции в рассматриваемой точке при стремлении приращения аргумента функции к нулю (Δt → 0)

Поэтому иногда производную называют мгновенной скоростью изменения функции. В нашем случае уравнение производной будет выглядеть так:

 (539.16)

На данном этапе вид формулы (539.16) нас уже не пугает (во всяком случае мне так кажется). Совсем другое дело, когда подобная формула приводится в начале темы, посвященной рассмотрению производных функции.

Дифференциал (первообразная) функции

С задачей определения скорости и ускорения в примере 2 мы вроде бы справились и даже составили соответствующие уравнения (539.14) и (539.15). Но иногда требуется решить и обратную задачу – например определить исходное уравнение, описывающее зависимость перемещения от времени.

Если скорость является производной функции расстояния v = s’, то расстояние при этом является первообразной (дифференциалом) функции скорости s = ∫v. Процесс нахождения первообразной функции называется интегрированием. Так, чтобы получить уравнение зависимости пройденного расстояния от времени, нам нужно проинтегрировать уравнение скорости. При этом уравнение расстояния более правильно записывать так

s = ∫vdt (539.17)

В общем случае интегрирование может быть более сложной задачей, чем дифференцирование, потому что функции бывают не только степенными, как в данном примере, но и тригонометрическими, обратными тригонометрическими  и т.п., но пока нас интересует, как проинтегрировать простую степенную функцию вида f(t) = 6t.

Вообще-то мы могли сразу построить график, отражающий зависимость пройденного расстояния от времени по данным примера 2, тем не менее сделаем это сейчас, а заодно построим график для уравнений скорости и ускорения и расположим их в такой последовательности:

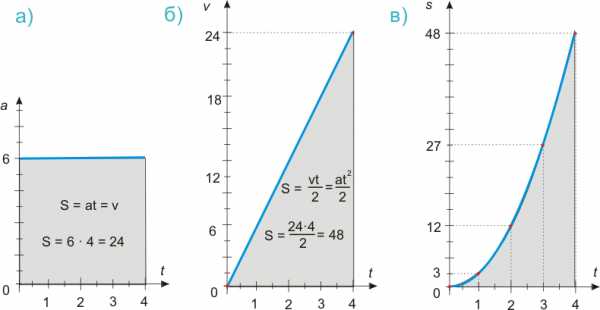
Рисунок 539.3. Графики степенных функции а) а= 6, б) v = at, в) s = at²/2.

Как видим, график, отражающий зависимость ускорения от времени, у нас самый простой. Ускорение постоянное, а = 6 м/с² и от времени никак не зависит. Тем не менее, зная ускорение, мы можем определить скорость движения в любой точке времени. Так из уравнений (539.14) и (539.15) следует, что:

v = 6t = at (539.14.2)

Соответственно решая это уравнение, мы можем определить скорость в любой момент времени.

Но если рассматривать это действие с точки зрения геометрии, то мы, умножая ускорение на время, определяем площадь прямоугольника со сторонами а = 6 и t. При t = 4 площадь прямоугольника составит 6·4 = 24, точнее 24 м/с так как мы все-таки определяем скорость.

Если мы построим график, отражающий зависимость изменения скорости от времени, то увидим, что на этом графике значения скорости в той или иной момент времени соответствуют площадям прямоугольника со сторонами а = 6 и t.

Получается, что если определить площадь треугольника со сторонами v и t, то это и будет расстояние, преодоленное к тому или иному промежутку времени:

s = vt/2 = at²/2 = 6t²/2 = 3t² (539.18)

Уравнение (539.18) можно записать как дифференциальное:

s = ∫6tdt = 3t² (539.18.2)

Если график, показанный на рисунке 539.3.в) также является графиком для производной некоторой функции, то для определения первообразной этой функции нам также следовало бы найти площадь фигуры, ограниченной квадратной параболой.

Сделать это в принципе не сложно, так как площадь фигуры, очерченной квадратной параболой таким образом, как показано на рисунке 539.3.в) в 3 раза меньше площади прямоугольника со сторонами s и t, соответственно S = st/3 = 3t²t/3 = t³ и эту процедуру можно повторять до бесконечности.

Почему площадь фигуры, ограниченной квадратной параболой именно в 3 раза меньше, чем площадь прямоугольника, а площадь фигуры ограниченной кубической параболой в 4 раза меньше площади прямоугольника, я здесь объяснять не буду, тем не менее такая закономерность существует и в математическом выражении выглядит так:

∫aхⁿdx = axⁿ⁺¹/n + C (539.19)

В данном случае С – это некоторая постоянная величина. Как мы выяснили, при дифференцировании постоянные величины обращаются в нуль, как пример – уравнение (539.11.2), соответственно решая обратную задачу, т.е. интегрируя функцию, мы допускаем, что некая постоянная величина в первообразной функции была.

Например в общем случае уравнение скорости (539.14.2) должно выглядеть так:

v = v_o + at (539.14.3)

где v_o – это и есть некая постоянная величина. В нашем случае по условиям задачи v_o = 0, поэтому мы использовали сокращенную форму записи.

Определенный интеграл

В общем случае график функции может выглядеть как угодно, например так:

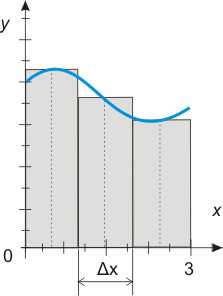
Рисунок 539.4

В этом случае сразу определить площадь фигуры, ограниченной графиком функции, не получится. Но мы можем разбить эту фигуру на участки шириной Δх и определить среднее значение у для каждого участка. Теперь определить площади трех прямоугольников большого труда не составит, вот только суммарная площадь прямоугольников не будет равна площади фигуры, ограниченной графиком функции:

S ≈ ∑y_iΔx (539.20)

Но чем больше будет у нас прямоугольников с шириной Δх, т.е, чем меньше будет значение Δх, тем точнее будет значение у, а значит и суммарная площадь прямоугольников будет ближе к площади фигуры, ограниченной графиком функции.

При интегрировании, как и при дифференцировании для получения более точного результата приращение аргумента функции должно стремиться к нулю (maxΔx → 0).

Из этого можно сделать следующий вывод:

Если существует предел суммы, определяемой по формуле (539.20) вне зависимости от количества прямоугольников и при стремлении ширины прямоугольников к нулю, то такой предел называется определенным интегралом, а суммы, определяемые по формуле (539.20) – интегральными суммами.

Так как на рисунке 539.4 показан график непрерывной функции, то такая функция является интегрируемой и для определения дифференциала функции используется определенный интеграл. При этом 0 и 3 – это пределы интегрирования.

doctorlom.com

Дифференциальные уравнения – это… Что такое Дифференциальные уравнения?

Дифференциа́льное уравне́ние — в математике это уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, не является дифференциальным уравнением.

Тео́рия дифференциа́льных уравне́ний — раздел математики, в котором изучаются дифференциальные уравнения и связанные с ними задачи. Её результаты применяются во многих естественных науках, особенно широко — в физике.

Решением (интегралом) дифференциального уравнения называется функция, при подстановке которой, уравнение становится тождеством. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида

,

где  — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени , штрих означает дифференцирование по . Число называется порядком дифференциального уравнения.

Дифференциальные уравнения в частных производных

Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:

,

где  — независимые переменные, а  — функция этих переменных.

Примеры

y” + 9y = 0 — обыкновенное дифференциальное уравнение второго порядка. Решением является семейство функций y = C₁cos(3x) + C₂sin(3x), где C₁ и C₂ — произвольные константы.

Второй закон Ньютона можно записать в форме дифференциального уравнения , где m — масса тела, x — его координата, F(x,t) — сила, действующее на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.

Колебание струны задается уравнением , где u = u(x,t) — отклонение струны в точке с координатой x в момент времени t, параметр a задает свойства струны. Это так называемое волновое уравнение.

Ссылки

Литература

Учебники

• В. И. Арнольд. Обыкновенные дифференциальные уравнения. М.: Наука, 1966.
• Л. Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.
• А. Н. Тихонов, А. А. Самарский. Уравнения математической физики. М.: Наука, 1972.
• А. Д. Полянин, В. Ф. Зайцев, А. И. Журов. Методы решения нелинейных уравнений математической физики и механики. М.: Физматлит, 2005.
• Чарльз Генри Эдвардс , Дэвид Э. Пенни Дифференциальные уравнения и проблема собственных значений: моделирование и вычисление с помощью Mathematica, Maple и MATLAB = Differential Equations and Boundary Value Problems: Computing and Modeling. — 3-е изд. — М.: «Вильямс», 2007. — ISBN 978-5-8459-1166-7
• Х. Р. Латипов. Качественные исследование характеристик одного класса дифференциальных уравнений в целом. Т.: ФАН, 1993
• А. Ф. Филиппов Введение в теорию дифференциальных уравнений. — Изд. 2-е. — 2007. — 240 с. — ISBN 5354004160
• А. Ф. Филиппов Сборник задач по дифференциальным уравнениям. — ЛКИ, 2008. — 240 с. — ISBN 9785382004556

Справочники

• Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976.
• В. Ф. Зайцев, А. Д. Полянин. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001.
• Э. Камке. Справочник по дифференциальным уравнениям в частных производных первого порядка. М.: Наука, 1966.
• В. Ф. Зайцев, А. Д. Полянин. Справочник по дифференциальным уравнениям с частными производными первого порядка. М.: Физматлит, 2003.
• А. Д. Полянин. Справочник по линейным уравнениям математической физики. М.: Физматлит, 2001.
• А. Д. Полянин, В. Ф. Зайцев. Справочник по нелинейным уравнениям математической физики: Точные решения. М.: Физматлит, 2002 .
• Н. М. Матвеев «Методы интегрирования обыкновенных дифференциальных уравнений», «Лань», 2003

Wikimedia Foundation. 2010.

dic.academic.ru

Обыкновенные дифференциальные уравнения – это… Что такое Обыкновенные дифференциальные уравнения?

Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида , где — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени , штрих означает дифференцирование по . Число называется порядком дифференциального уравнения.

Решением дифференциального уравнения называется n раз дифференцируемая функция , удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение.

Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.

Примеры

• Одно из простейших применений дифференциальных уравнений — решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения. Например, в соответствии со вторым законом Ньютона, ускорение тела пропорционально сумме действующих сил; соответствующее дифференциальное уравнение имеет вид . Зная действующие силы (правая часть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки.
• Дифференциальное уравнение y‘ = y, вместе с начальным условием y(0) = 1, задаёт экспоненту: y(x) = e^x. Если x обозначает время, то эта функция описывает рост популяции в условиях неограниченности ресурсов.
• Решением дифференциального уравнения y‘ = f(x), правая часть которого не зависит от неизвестной функции, является неопределённый интеграл: , где C — произвольная константа.

Дифференциальные уравнения первого порядка

Уравнения с разделяющимися переменными

Дифференциальное уравнение называется уравнением с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде f(x,y) = f₁(x)f₂(y). Тогда, в случае , общим решением уравнения является .

Примеры физических задач, приводящих к уравнениям с разделяющимися переменными

Охлаждение тела

Пусть T — температура тела, T₀ — температура окружающей среды (T > T₀). Пусть Q — количество теплоты, c — удельная теплоёмкость. Тогда количество теплоты передаваемое окружающей среде до выравнивания температур выражается формулой Q = mc(T − T₀), или, в дифференциальной форме, . С другой стороны скорость отдачи тепла можно выразить в виде , где k — некий коэффициент пропорциональности. Исключая из этих двух уравнений dQ получаем уравнение с разделяющимися переменными:

.

Общим решением этого уравнения является семейство функций .

Однородные уравнения

Дифференциальное уравнение называется однородным, если — однородная функция нулевой степени. Функция называется однородной степени , если для любого выполняется равенство .

Замена приводит при однородное уравнение к уравнению с разделяющимися переменными:

Подставив в исходное уравнение, получаем:

,

что является уравнением с разделяющимися переменными.

Квазиоднородные уравнения

Дифференциальное уравнение называется квазиоднородным, если для любого выполняется соотношение .

Данное уравнение решается заменой :

В силу квазиоднородности, положив , получаем:

,

что, очевидно, является однородным уравнением.

Линейные уравнения

Дифференциальное уравнение называется линейным и может быть решено двумя методами: методом интегрирующего множителя или методом вариации постоянной.

Метод интегрирующего множителя

Пусть задана функция – интегрирующий множитель, в виде:

Умножим обе части исходного уравнения на , получим:

Легко заметить, что левая часть является производной функции по . Поэтому уравнение можно переписать:

Проинтегрируем:

Таким образом, решение линейного уравнения будет:

Метод вариации постоянной (метод Лагранжа)

Рассмотрим однородное уравнение . Очевидно, это уравнение с разделяющимися переменными, его решение:

Решения исходного уравнения будем искать в виде:

Подставив полученное решение в исходное уравнение:

,

получаем:

,

где c₁ — произвольная константа.

Таким образом, решение исходного уравнения можно получить путем подстановки в решение однородного уравнения:

Уравнение Бернулли

Дифференциальное уравнение называется уравнением Бернулли, если n — действительное число, отличающееся от 0 и 1, так как при n = 0 и n = 1 уравнение обращается в линейное. Данное уравнение решается двумя способами:

Первый способ

Заменой

.

уравнение приводится к линейному

и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя.

Второй способ

Заменим

y = uv.

Тогда

.

Подберем так, чтобы было

для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка.
После этого для определения получаем уравнение  — уравнение с разделяющимися переменными.

См. также

Литература

• Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. С. 176. ISBN 5-93972-008-0

Wikimedia Foundation. 2010.

dic.academic.ru

Дифференциальные уравнения — Юнциклопедия

Математический анализ как анализ переменных величин с момента своего появления развивался в тесной связи с естествознанием, и в частности с физикой и механикой. Потребности развития физических наук, необходимость количественного изучения движения и меняющихся процессов привели к возникновению и формированию основных понятий дифференциального исчисления и интегрального исчисления. Понятие дифференциального уравнения — одно из основных. Чтобы разъяснить это понятие, рассмотрим, из чего складывается изучение какого-либо физического процесса. Это — создание физической гипотезы, основанной на эксперименте, математическая форма записи физической гипотезы, математическое решение этой задачи и физическое толкование выводов из её решения. Такой подход к изучению явлений природы впервые был предложен итальянским ученым Г. Галилеем (1564–1642). Впервые его блестяще применил один из создателей математического анализа — И. Ньютон. Математически сформулировать физические законы оказалось возможным лишь с появлением математического анализа и на его языке.

В очень большом числе случаев физические законы описывают некоторые соотношения между величинами, характеризующими изучаемый процесс, и скоростью изменения этих величин. Другими словами, эти законы выражаются равенствами, в которых участвуют неизвестные функции и их производные. Такие равенства называются дифференциальными уравнениями. Они появляются как математическая форма записи ряда физических законов. Изучение процессов, описываемых этими законами, сводится к изучению свойств решений дифференциальных уравнений. Поясним это на примерах.

Пусть тело (например, металлическая пластина), нагретое до температуры y₀, в момент времени t = 0 погружается в очень большой сосуд с воздухом нулевой температуры. Очевидно, тело начнет охлаждаться, и его температура будет функцией времени t. Обозначим её y(t).

Согласно закону охлаждения Ньютона, скорость изменения температуры тела, т. е. производная dy/dt пропорциональна разности температур тела и окружающей среды, в данном случае пропорциональна y(t). Таким образом получаем, что в каждый момент времени справедливо соотношение

$\frac{dy}{dt}=-ky$

(1)

(k — положительный коэффициент, зависящий от материала тела, знак «минус» потому, что температура убывает).

Это соотношение (1) в виде дифференциального уравнения является математической записью закона охлаждения, которое выражает зависимость между функцией (температурой) и её производной в один и тот же момент времени. Его также называют математической моделью рассматриваемого процесса.

Решить дифференциальное уравнение — значит найти все функции y(t), которые обращают уравнение в тождество. Все решения приведенного выше дифференциального уравнения даются формулой

$y=C{{e}^{-kt}}$

(где C — произвольная постоянная), которая представляет собой его общее решение. Нахождение решения дифференциального уравнения всегда связано с операцией интегрирования, поэтому вместо слова «решить» часто употребляется глагол «проинтегрировать» (дифференциальное уравнение).

В процессе охлаждения тела, который мы рассматриваем, нас интересует лишь то решение, которое в момент времени t = 0 принимает значение y₀. Подставляя в приведенную выше формулу t = 0, находим: C = y₀. Значит, закон охлаждения окончательно можно выразить так:

$y(t)={{y}_{0}}{{e}^{-kt}}.$

Как видим, температура тела с течением времени понижается по показательному (экспоненциальному) закону и стремится к температуре окружающей среды (рис. 1).

Условие $y(0)={{y}_{0}}$ принято называть начальным, оно позволяет из бесконечного множества решений выбрать единственное.

Рассмотренное дифференциальное уравнение (1) выражает тот факт, что скорость изменения функции пропорциональна (с коэффициентом −k) самой функции. Такая зависимость наблюдается и в других явлениях природы, например падение атмосферного давления в зависимости от высоты над уровнем моря пропорционально величине давления. Еще пример — радиоактивный распад: скорость уменьшения массы радиоактивного вещества пропорциональна количеству этого вещества. Следовательно, атмосферное давление у как функция высоты t над уровнем моря и масса радиоактивного вещества y как функция времени t удовлетворяют уравнению (1). Как видим, одно и то же дифференциальное уравнение может служить математической моделью совершенно разных явлений.

Рассмотрим небольшой шарик массой m, к которому прикреплена горизонтально расположенная пружина. Другой её конец закреплен (рис. 2). Направим ось O_x вдоль оси пружины, за начало координат примем положение равновесия шарика. Если немного сместить шарик вдоль оси, то возникнет упругая сила F, стремящаяся вернуть его в положение равновесия. По закону Гука, эта сила пропорциональна смещению x, т. е. F = −kx (k — положительная константа, характеризующая упругие свойства пружины, знак «минус» ставится потому, что сила восстанавливающая). Согласно второму закону Ньютона, сила, действующая на тело массой m, равна произведению массы на ускорение a:

$F=ma.$

Если же x(t) — положение шарика в момент времени t, то его ускорение выражается второй производной x″(t). Таким образом, движение шарика под действием упругих сил можно выразить дифференциальным уравнением

$m{x}”(t)=-kx(t),$

которое чаще записывается в виде

${x}”(t)+{{\omega }^{2}}x(t)=0,$ где ${{\omega }^{2}}=k/m.$

Это уравнение называется дифференциальным уравнением гармонических колебаний. Можно доказать, что любое его решение может быть записано в виде

$x(t)=A\cos (\omega t+\varphi ),$

здесь А и φ — произвольные постоянные. Движения, характеризуемые таким уравнением, называются гармоническими колебаниями. Они представляют собой периодическое движение (рис. 3) с периодом T = 2π/ω; величина А называется амплитудой колебания.

Очевидно, что дифференциальное уравнение ${x}”(t)+{{\omega }^{2}}x(t)=0$ не вполне определяет движение шарика. Оно зависит от того, на какую величину x₀ шарик был смещен в момент времени t = 0 и с какой скоростью $v={x}'(0)$ он отпущен, т. е. зависит от начальных данных. Если, например, скорость была нулевой, то движение шарика будет подчиняться закону

$x(t)={{x}_{0}}\cos \omega t.$

Полученное нами выше дифференциальное уравнение есть математическая форма записи (математическая модель) закона движения под действием только силы упругости. Если рассмотреть движение шарика в среде, оказывающей сопротивление, и предположить, что кроме сил упругости на шарик действует сила сопротивления, пропорциональная скорости движения, то дифференциальное уравнение такого движения будет иметь вид:

$m{x}”(t)+c{x}'(t)+kx(t)=0.$

Решения этого уравнения уже не являются периодическими функциями, а представляют собой колебания с изменяющейся амплитудой, так называемые затухающие колебания (рис. 4).

Если неизвестная функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным; таковы рассмотренные выше уравнения. Порядком дифференциального уравнения называется порядок старшей производной, входящей в него. Как видим, уравнение $dy/dt=-ky$ первого порядка, уравнение ${x}”(t)+{{\omega }^{2}}x(t)=0$ — второго.

Если неизвестная функция зависит от нескольких переменных, то дифференциальное уравнение содержит её частные производные и называется дифференциальным уравнением с частными производными. Такие уравнения описывают, например, колебание мембраны, распространение тепла в некоторой среде, движение спутника.

Дифференциальные уравнения — важный математический аппарат в естествознании. Они применяются в физике и астрономии, аэродинамике и теории упругости, химии и экономике, биологии и медицине.

Дифференциальное уравнение первого порядка вида $dx/dt=f(x,t)$ допускает простую геометрическую интерпретацию. Если $x=\varphi (t)$ — его решение, то это уравнение в каждой точке кривой $x=\varphi (t)$ задает значение производной $dx/dt$, т. е. значение тангенса угла наклона касательной. Таким образом, в каждой точке области определения функции $f(x,t)$ задается угловой коэффициент касательной к решению, как говорят, задается поле направлений. Геометрически поле направлений обычно изображается единичными векторами. На рис. 5 представлено поле направлений дифференциального уравнения $dx/dt={{t}^{2}}+{{x}^{2}}$.

Решение дифференциального уравнения есть кривая, которая в каждой точке касается поля направлений, её называют интегральной кривой. Рис. 5 позволяет довольно ясно представить, как должны выглядеть интегральные кривые этого уравнения.

В XVIII в. теория дифференциальных уравнений выделилась из математического анализа в самостоятельную математическую дисциплину. Её успехи связаны с именами швейцарского ученого И. Бернулли, французского математика Ж. Лагранжа и особенно Л. Эйлера. Первый период развития дифференциальных уравнений был связан с успешным решением некоторых важных прикладных задач, приводящих к дифференциальным уравнениям, разработкой методов интегрирования различных видов дифференциальных уравнений и поиском классов интегрируемых уравнений, т. е. таких, решение которых может быть найдено в квадратурах (в виде элементарных функций или их первообразных). Однако очень скоро выяснилось, что интегрируемых уравнений совсем не много. Даже уравнение первого порядка очень простого вида может не интегрироваться в квадратурах. Например, уравнение, для которого на рис. 5 было изображено поле направлений, имеет бесконечно много решений, но они не выражаются в квадратурах.

Установление таких фактов привело к развитию собственно теории дифференциальных уравнений, которая занимается разработкой методов, позволяющих по свойствам дифференциального уравнения определять свойства и характер его решения.

yunc.org

Дифференциальные уравнения – это… Что такое Дифференциальные уравнения?

Дифференциа́льное уравне́ние — в математике это уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, не является дифференциальным уравнением.

Тео́рия дифференциа́льных уравне́ний — раздел математики, в котором изучаются дифференциальные уравнения и связанные с ними задачи. Её результаты применяются во многих естественных науках, особенно широко — в физике.

Решением (интегралом) дифференциального уравнения называется функция, при подстановке которой, уравнение становится тождеством. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида

,

где  — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени , штрих означает дифференцирование по . Число называется порядком дифференциального уравнения.

Дифференциальные уравнения в частных производных

Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:

,

где  — независимые переменные, а  — функция этих переменных.

Примеры

y” + 9y = 0 — обыкновенное дифференциальное уравнение второго порядка. Решением является семейство функций y = C₁cos(3x) + C₂sin(3x), где C₁ и C₂ — произвольные константы.

Второй закон Ньютона можно записать в форме дифференциального уравнения , где m — масса тела, x — его координата, F(x,t) — сила, действующее на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.

Колебание струны задается уравнением , где u = u(x,t) — отклонение струны в точке с координатой x в момент времени t, параметр a задает свойства струны. Это так называемое волновое уравнение.

Ссылки

Литература

Учебники

• В. И. Арнольд. Обыкновенные дифференциальные уравнения. М.: Наука, 1966.
• Л. Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.
• А. Н. Тихонов, А. А. Самарский. Уравнения математической физики. М.: Наука, 1972.
• А. Д. Полянин, В. Ф. Зайцев, А. И. Журов. Методы решения нелинейных уравнений математической физики и механики. М.: Физматлит, 2005.
• Чарльз Генри Эдвардс , Дэвид Э. Пенни Дифференциальные уравнения и проблема собственных значений: моделирование и вычисление с помощью Mathematica, Maple и MATLAB = Differential Equations and Boundary Value Problems: Computing and Modeling. — 3-е изд. — М.: «Вильямс», 2007. — ISBN 978-5-8459-1166-7
• Х. Р. Латипов. Качественные исследование характеристик одного класса дифференциальных уравнений в целом. Т.: ФАН, 1993
• А. Ф. Филиппов Введение в теорию дифференциальных уравнений. — Изд. 2-е. — 2007. — 240 с. — ISBN 5354004160
• А. Ф. Филиппов Сборник задач по дифференциальным уравнениям. — ЛКИ, 2008. — 240 с. — ISBN 9785382004556

Справочники

• Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976.
• В. Ф. Зайцев, А. Д. Полянин. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001.
• Э. Камке. Справочник по дифференциальным уравнениям в частных производных первого порядка. М.: Наука, 1966.
• В. Ф. Зайцев, А. Д. Полянин. Справочник по дифференциальным уравнениям с частными производными первого порядка. М.: Физматлит, 2003.
• А. Д. Полянин. Справочник по линейным уравнениям математической физики. М.: Физматлит, 2001.
• А. Д. Полянин, В. Ф. Зайцев. Справочник по нелинейным уравнениям математической физики: Точные решения. М.: Физматлит, 2002 .
• Н. М. Матвеев «Методы интегрирования обыкновенных дифференциальных уравнений», «Лань», 2003

Wikimedia Foundation. 2010.

med.academic.ru

Дифференциальные уравнения – это… Что такое Дифференциальные уравнения?

Дифференциальные уравнения [differential equations] — уравнения, предназначенные для выражения соотношений не только между отдельно взятыми величинами, но и между их изменениями. Это уравнения, в той или иной форме связывающие независимые переменные (см. Аргумент функции), искомые функции и их производные. Решение (интегрирование) Д.у. заключается в отыскании функции, которая удовлетворяет этому уравнению для всех значений независимой переменной (или переменных) в определенном конечном или бесконечном интервале. Такое решение может быть проверено подстановкой.

Если неизвестная функция зависит от одной независимой переменной, то Д.у. называется обыкновенным; если рассматривается функция многих переменных и в уравнении содержатся частные производные — уравнением в частных производных (с частными производными). Порядком Д.у. называется высший из порядков производных или дифференциалов, входящих в уравнение.

Общий вид обыкновенного Д.у. n-го порядка:

F(x, y, y′, …, y⁽ⁿ⁾) = 0.

Общий вид решения обыкновенного Д.у. n-го порядка можно записать так:

y = f (x, c₁, c₂, …, c_n).

Здесь c₁, c₂ и т.д. — произвольные постоянные (постоянные интегрирования), каждый частный набор которых дает частное решение.

Таким образом, Д.у. сами по себе, без наложенных дополнительных ограничений, описывают целые классы функций. Если речь идет об обыкновенном уравнении n-го порядка (т.е. об уравнении, содержащем производную n-го порядка), то решение содержит ровно n произвольных постоянных. Для того чтобы выделить из этого класса единственное решение, обычно необходимо задать n дополнительных ограничений на функцию. Например, Д.у. позволяют определять поведение решения всюду, где оно существует, если заданы начальные условия, т.е. значения функции и ее производных в начальной точке. В огромном числе случаев законы природы и общества, управляющие теми или иными процессами, могут быть выражены в форме Д.у., а расчет течения этих процессов сводится к решению таких уравнений.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

economic_mathematics.academic.ru

Обыкновенное дифференциальное уравнение – это… Что такое Обыкновенное дифференциальное уравнение?

Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида

где  — неизвестная функция (возможно, вектор-функция, тогда , как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной , штрих означает дифференцирование по . Число (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1).

Независимая переменная часто интерпретируется (особенно в дифференциальных уравнениях, возникающих в физических и других естественно-научных задачах) как время, поэтому её часто обозначают буквой . Переменная  — некоторая величина (или совокупность величин, если является вектор-функцией), изменяющихся со временем. Например, может означать набор координат точки в пространстве; в этом случае уравнение (1) описывает движение точки в пространстве, то есть изменение её координат с течением времени. Независимая переменная обычно принимает вещественные значения, однако рассматриваются и дифференциальные уравнения, в которых переменная комплексная (так называемые уравнения с комплексным временем).

Наиболее часто встречаются дифференциальные уравнения вида

в которых старшая производная выражается в виде функции от переменных и производных порядков меньше Такие дифференциальные уравнения называются нормальными или разрешёнными относительно производной.

В противоположность уравнениям вида (2), дифференциальные уравнения вида (1) называются уравнениями, не разрешёнными относительно производной или неявными дифференциальными уравнениями.

Классическим решением дифференциального уравнения (2) называется раз дифференцируемая функция , удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительное условие. Начальным условием для уравнения (2) называется условие

где  — некоторое фиксированное значение независимой переменной (фиксированный момент времени), а и  — соответственно, фиксированные значения функции и всех её производных до порядка включительно. Дифференциальное уравнение (2) вместе с начальным условием (3) называется начальной задачей или задачей Коши:

При достаточно общих ограничениях на функцию , стоящую в правой части уравнения (2), задача Коши для этого уравнения имеет единственное решение, определенное на некотором интервале оси времени , содержащем начальное значение (этот интервал, вообще говоря, может не совпадать со всей осью).

Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.

История

Простейшие дифференциальные уравнения встречались уже в работах И. Ньютона и Г. Лейбница; термин «дифференциальные уравнения» принадлежит Лейбницу. Ньютон при создании исчисления «флюксий» и «флюент» ставил две задачи: по данному соотношению между флюентами определить соотношение между флюксиями; по данному уравнению, содержащему флюксии, найти соотношение между флюентами. С современной точки зрения, первая из этих задач (вычисление по функциям их производных) относится к дифференциальному исчислению, а вторая составляет содержание теории обыкновенных дифференциальных уравнений. Задачу нахождения неопределённого интеграла F(x) функции f(x) Ньютон рассматривал просто как частный случай его второй задачи. Такой подход был для Ньютона как создателя основ математического естествознания вполне оправданным: в очень большом числе случаев законы природы, управляющие теми или иными процессами, выражаются в форме дифференциальных уравнений, а расчёт течения этих процессов сводится к решению дифференциального уравнения.^[1]

Основное открытие Ньютона, то, которое он счел нужным засекретить и опубликовал лишь в виде анаграммы, состоит в следующем: «Data aequatione quotcunque fluentes quantitae involvente fluxiones invenire et vice versa». В переводе на современный математический язык это означает: «Полезно решать дифференциальные уравнения». В настоящее время теория дифференциальных уравнений представляет собой трудно обозримый конгломерат большого количества разнообразных идей и методов, в высшей степени полезный для всевозможных приложений и постоянно стимулирующий теоретические исследования во всех отделах математики.^[2][3]

Примеры

• Одно из простейших применений дифференциальных уравнений — решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения. Например, в соответствии со вторым законом Ньютона, ускорение тела пропорционально сумме действующих сил; соответствующее дифференциальное уравнение имеет вид . Зная действующие силы (правая часть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки.
• Дифференциальное уравнение , вместе с начальным условием , задаёт экспоненту: . Если обозначает время, то эта функция описывает рост популяции в условиях неограниченности ресурсов и многое другое.
• Решением дифференциального уравнения , правая часть которого не зависит от неизвестной функции, является неопределённый интеграл: , где  — произвольная константа.

Дифференциальные уравнения первого порядка

Уравнения с разделяющимися переменными

Дифференциальное уравнение называется уравнением с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде . Тогда, в случае , общим решением уравнения является .

Примеры физических задач, приводящих к уравнениям с разделяющимися переменными

Охлаждение тела

Пусть  — температура тела,  — температура окружающей среды (). Пусть  — количество теплоты,  — удельная теплоёмкость. Тогда количество теплоты передаваемое окружающей среде до выравнивания температур выражается формулой , или, в дифференциальной форме, . С другой стороны скорость отдачи тепла можно выразить в виде , где  — некий коэффициент пропорциональности. Исключая из этих двух уравнений получаем уравнение с разделяющимися переменными:

.

Общим решением этого уравнения является семейство функций .

Однородные уравнения

Дифференциальное уравнение называется однородным, если  — однородная функция нулевой степени. Функция называется однородной степени , если для любого выполняется равенство .

Замена приводит при однородное уравнение к уравнению с разделяющимися переменными:

Подставив в исходное уравнение, получаем:

,

что является уравнением с разделяющимися переменными.

Квазиоднородные уравнения

Дифференциальное уравнение называется квазиоднородным, если для любого выполняется соотношение .

Данное уравнение решается заменой :

В силу квазиоднородности, положив , получаем:

,

что, очевидно, является однородным уравнением.

Линейные уравнения

Дифференциальное уравнение называется линейным и может быть решено двумя методами: методом интегрирующего множителя или методом вариации постоянной.

Метод интегрирующего множителя

Пусть задана функция  — интегрирующий множитель, в виде:

Умножим обе части исходного уравнения на , получим:

Легко заметить, что левая часть является производной функции по . Поэтому уравнение можно переписать:

Проинтегрируем:

Таким образом, решение линейного уравнения будет:

Метод вариации постоянной (метод Лагранжа)

Рассмотрим однородное уравнение . Очевидно, это уравнение с разделяющимися переменными, его решение:

Решения исходного уравнения будем искать в виде:

Подставив полученное решение в исходное уравнение:

,

получаем:

,

где  — произвольная константа.

Таким образом, решение исходного уравнения можно получить путем подстановки в решение однородного уравнения:

Уравнение Бернулли

Дифференциальное уравнение называется уравнением Бернулли (при или получаем неоднородное или однородное линейное уравнение). При является частным случаем уравнения Риккати. Названо в честь Якоба Бернулли, опубликовавшего это уравнение в 1695 году. Метод решения с помощью замены, сводящей это уравнение к линейному, нашёл его брат Иоганн Бернулли в 1697 году.

Биномиальное дифференциальное уравнение

Уравнение вида

где — натуральное число, а — многочлен от двух переменных.

См. также

Литература

Учебники

• Арнольд В. И. Обыкновенные дифференциальные уравнения, — Любое издание.
• Арнольд В. И. Дополнительные главы теории обыкновенных дифференциальных уравнений, — Любое

издание.

• Арнольд В. И. Геометрические методы в теории обыкновенных дифференциальных уравнений, — Любое издание.
• Арнольд В. И., Ильяшенко Ю. С. Обыкновенные дифференциальные уравнения, — Итоги науки и техн. Сер. Совр. пробл. мат. Фундам. направ., 1985, том 1.
• Петровский И. Г. Лекции по теории обыкновенных дифференциальных уравнений, — Любое издание.
• Понтрягин Л. С. Обыкновенные дифференциальные уравнения, — Любое издание.
• Степанов В. В. Курс дифференциальных уравнений, — Любое издание.
• Трикоми Ф. Дифференциальные уравнения, — Любое издание.
• Филиппов А. Ф. Введение в теорию дифференциальных уравнений, — Любое издание.
• Филипс Г. Дифференциальные уравнения, — Любое издание.
• Хартман Ф. Обыкновенные дифференциальные уравнения, — Любое издание.
• Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление, — Любое издание.

Задачники

• Филиппов А. Ф. Сборник задач по дифференциальным уравнениям, — Любое издание.

Справочники

• Камке Э. Справочник по обыкновенным дифференциальным уравнениям, — Любое издание.
• Зайцев В. Ф., Полянин А. Д. Справочник по обыкновенным дифференциальным уравнениям, — Любое издание.

Примечания

dic.academic.ru

---