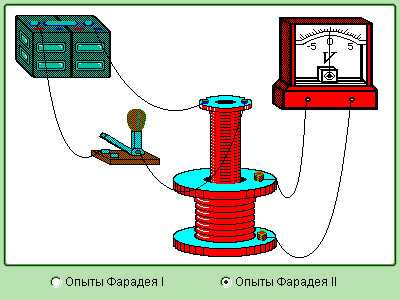
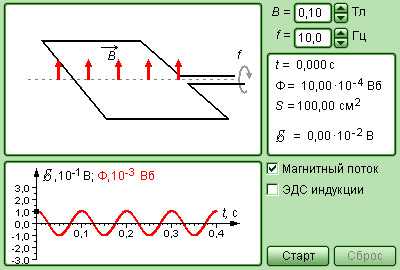
Эдс индукции возникает когда – Проводник, движущийся в магнитном поле. Электромагнитная индукция. Само- и взаимоиндукция. Виды ЭДС. Вихревые токи.
- Комментариев к записи Эдс индукции возникает когда – Проводник, движущийся в магнитном поле. Электромагнитная индукция. Само- и взаимоиндукция. Виды ЭДС. Вихревые токи. нет
- Советы абитуриенту
- что это такое, основные формулы, в чем измеряется, от чего зависит.
- Индукционным током. Явление индуктирования эдс
- ЭДС индукции в движущихся проводниках
- Природа возникновения ЭДС индукции — МегаЛекции
- Механизм возникновения ЭДС индукции
- ЭДС индукции в движущихся проводниках формула
- Проводник, движущийся в магнитном поле. Электромагнитная индукция. Само- и взаимоиндукция. Виды ЭДС. Вихревые токи.
что это такое, основные формулы, в чем измеряется, от чего зависит.
В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.
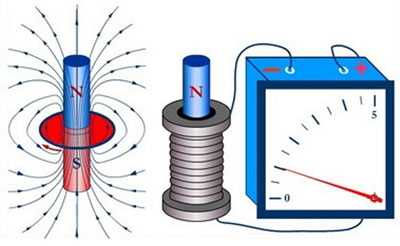
Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.
Магнитный поток
Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.
При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.
ЭДС индукции
Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.
Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.
Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.
Законы Фарадея и Ленца
Законы Фарадея и Ленца отображают закономерности возникновения электромагнитной индукции.
Фарадей выявил, что магнитные эффекты появляются в результате изменения магнитного потока во времени. В момент пересечения проводника переменным магнитным током, в нем возникает электродвижущая сила, которая приводит к возникновению электрического тока. Генерировать ток может как постоянный магнит, так и электромагнит.
Ученый определил, что интенсивность тока возрастает при быстром изменении количества силовых линий, которые пересекают контур. То есть ЭДС электромагнитной индукции пребывает в прямой зависимости от скорости магнитного потока.
Согласно закону Фарадея, формулы ЭДС индукции определяются следующим образом:
Е = — dФ/dt.
Знак «минус» указывает на взаимосвязь между полярностью индуцированной ЭДС, направлением потока и изменяющейся скоростью.
Согласно закону Ленца, можно охарактеризовать электродвижущую силу в зависимости от ее направленности. Любое изменение магнитного потока в катушке приводит к появлению ЭДС индукции, причем при быстром изменении наблюдается возрастающая ЭДС.
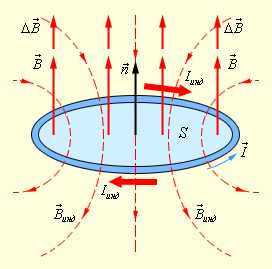
Если катушка, где есть ЭДС индукции, имеет замыкание на внешнюю цепь, тогда по ней течет индукционный ток, вследствие чего вокруг проводника появляется магнитное поле и катушка приобретает свойства соленоида. В результате вокруг катушки формируется свое магнитное поле.
Э.Х. Ленц установил закономерность, согласно которой определяется направление индукционного тока в катушке и ЭДС индукции. Закон гласит, что ЭДС индукции в катушке при изменении магнитного потока формирует в катушке ток направления, при котором данный магнитный поток катушки дает возможность избежать изменения постороннего магнитного потока.
Закон Ленца применяется для всех ситуаций индуктирования электротока в проводниках, вне зависимости от их конфигурации и метода изменения внешнего магнитного поля.
Движение провода в магнитном поле
Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.
Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.
Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.
Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.
Вращающаяся катушка
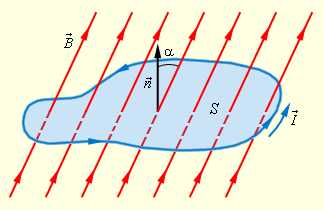
Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).
Согласно формуле, на Ф воздействуют изменения в ситуациях:
- при изменении магнитного потока меняется вектор направления;
- изменяется площадь, заключенная в контур;
- меняется угол.
Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.
На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.
ЭДС самоиндукции
При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.
В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:
Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Взаимоиндукция
При расположении двух катушек рядом в них наблюдается ЭДС взаимоиндукции, которая определяется конфигурацией двух схем и их взаимной ориентацией. При возрастании разделения цепей значение взаимоиндуктивности уменьшается, поскольку наблюдается уменьшение общего для двух катушек магнитного потока.
Рассмотрим детально процесс возникновения взаимоиндукции. Есть две катушки, по проводу одной с N1 витков течет ток I1, которым создается магнитный поток и идет через вторую катушку с N2 числом витков.
Значение взаимоиндуктивности второй катушки в отношении первой:
М21 = (N2 x F21)/I1.
Значение магнитного потока:
Ф21 = (М21/N2) x I1.
Индуцированная ЭДС вычисляется по формуле:
Е2 = — N2 x dФ21/dt = — M21x dI1/dt.
В первой катушке значение индуцируемой ЭДС:
Е1 = — M12 x dI2/dt.
Важно отметить, что электродвижущая сила, спровоцированная взаимоиндукцией в одной из катушек, в любом случае прямо пропорциональна изменению электрического тока в другой катушке.
Тогда взаимоиндуктивность считается равной:
М12 = М21 = М.
Вследствие этого , E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К является коэффициентом связи между двумя значениями инжуктивности.
Взаимоиндукция широко используется в трансформаторах, которые дают возможность менять значения переменного электротока. Прибор представляет собой пару катушек, которые намотаны на общий сердечник. Ток в первой катушке формирует изменяющийся магнитный поток в магнитопроводе и ток во второй катушке. При меньшем числе витков в первой катушке, чем во второй, возрастает напряжение, и соответственно при большем количестве витков в первой обмотке напряжение снижается.
Помимо генерирования и трансформации электрической энергии, явление магнитной индукции используется в прочих приборах. К примеру, в магнитных левитационных поездах, движущихся без непосредственного контакта с током в рельсах, а на пару сантиметров выше по причине электромагнитного отталкивания.
Похожие статьи
odinelectric.ru
Индукционным током. Явление индуктирования эдс
Возникновение в проводнике ЭДС индукции
Если поместить в магнитное поле проводник и перемещать его так, чтобы он при своем движении пересекал силовые линии поля, то в проводнике возникнет электродвижущая сила, называемая ЭДС индукции.
ЭДС индукции возникнет в проводнике и в том случае, если сам проводник останется неподвижным, а перемещаться будет магнитное поле, пересекая проводник своими силовыми линиями.
Если проводник, в котором наводится ЭДС индукции, замкнуть на какую-либо внешнюю цепь, то под действием этой ЭДС по цепи потечет ток, называемый индукционным током.
Явление индуктирования ЭДС в проводнике при пересечении его силовыми линиями магнитного поля называется
Электромагнитная индукция — это обратный процесс, т. е. превращение механической энергии в электрическую.
Явление электромагнитной индукции нашло широчайшее применение в электротехнике. На использовании его основано устройство различных электрических машин.

Величина и направление ЭДС индукции
Рассмотрим теперь, каковы будут величина и направление индуктированной в проводнике ЭДС.
Величина ЭДС индукции зависит от количества силовых линий поля, пересекающих проводник в единицу времени, т. е. от скорости движения проводника в поле.
Величина индуктированной ЭДС находится в прямой зависимости от скорости движения проводника в магнитном поле.
Величина индуктированной ЭДС зависит также и от длины той части проводника, которая пересекается силовыми линиями поля. Чем большая часть проводника пересекается силовыми линиями поля, тем большая ЭДС индуктируется в проводнике. И, наконец, чем сильнее магнитное поле, т. е. чем больше его индукция, тем большая ЭДС возникает в проводнике, пересекающем это поле.
Итак, величина ЭДС индукции, возникающей в проводнике при его движении в магнитном поле, прямо пропорциональна индукции магнитного поля, длине проводника и скорости его перемещения.
Зависимость эта выражается формулой Е = Blv,
где Е — ЭДС индукции; В — магнитная индукция; I — длина проводника; v — скорость движения проводника.
Следует твердо помнить, что в проводнике, перемещающемся в магнитном поле, ЭДС индукции возникает только в том случае, если этот проводник пересекается магнитными силовыми линиями поля. Если же проводник перемещается вдоль силовых линий поля, т. е. не пересекает, а как бы скользит по ним, то никакой ЭДС в нем не индуктируется. Поэтому приведенная выше формула справедлива только в том случае, когда проводник перемещается перпендикулярно магнитным силовым линиям поля.
Направление индуктированной ЭДС (а также и тока в проводнике) зависит от того, в какую сторону движется проводник. Для определения направления индуктированной ЭДС существует правило правой руки.
Если держать ладонь правой руки так, чтобы в нее входили магнитные силовые линии поля, а отогнутый большой палец указывал бы направление движения проводника, то вытянутые четыре пальца укажут направление действия индуктированной ЭДС и направление тока в проводнике
ЭДС индукции в катушке
Мы уже говорили, что для создания в проводнике ЭДС индукции необходимо перемещать в магнитном поле или сам проводник, или магнитное поле. В том и другом случае проводник должен пересекаться магнитными силовыми линиями поля, иначе ЭДС индуктироваться не будет. Индуктированную ЭДС, а следовательно, и индукционный ток можно получить не только в прямолинейном проводнике, но и в проводнике, свитом в катушку.
При движении внутри катушки постоянного магнита в ней индуктируется ЭДС за счет того, что магнитный поток магнита пересекает витки катушки, т. е. точно так же, как это было при движении прямолинейного проводника в поле магнита.
Если магнит опускать в катушку медленно, то возникающая в ней ЭДС будет настолько мала, что стрелка прибора может даже не отклониться. Если же, наоборот, магнит быстро ввести в катушку, то отклонение стрелки будет большим. Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от скорости движения магнита, т. е. от того, насколько быстро силовые линии поля пересекают витки катушки. Если теперь поочередно вводить в катушку с одинаковой скоростью сначала сильный магнит, а затем слабый, то можно заметить, что при сильном магните стрелка прибора будет отклоняться на больший угол. Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от величины магнитного потока магнита.
И, наконец, если вводить с одинаковой скоростью один и тот же магнит сначала в катушку с большим числом витков, а затем со значительно меньшим, то в первом случае стрелка прибора отклонится на больший угол, чем во втором. Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от числа ее витков. Те же результаты можно получить, если вместо постоянного магнита применять электромагнит.
Направление ЭДС индукции в катушке зависит от направления перемещения магнита. О том, как определять направление ЭДС индукции, говорит закон, установленный Э. X. Ленцем.
Закон Ленца для электромагнитной индукции
Всякое изменение магнитного потока внутри катушки сопровождается возникновением в ней ЭДС индукции, причем чем быстрее изменяется магнитный поток, пронизывающий катушку, тем большая ЭДС в ней индуктируется.
Если катушка, в которой создана ЭДС индукции, замкнута на внешнюю цепь, то по виткам ее идет индукционный ток, создающий вокруг проводника магнитное поле, в силу чего катушка превращается в соленоид. Получается таким образом, что изменяющееся внешнее магнитное поле вызывает в катушке индукционный ток, которой, в свою очередь, создает вокруг катушки свое магнитное поле — поле тока.
Изучая это явление, Э. X. Ленц установил закон, определяющий направление индукционного тока в катушке, а следовательно, и направление ЭДС индукции. ЭДС индукции, возникающая в катушке при изменении в ней магнитного потока, создает в катушке ток такого направления, при котором магнитный поток катушки, созданный этим током, препятствует изменению постороннего магнитного потока.
Закон Ленца справедлив для всех случаев индуктирования тока в проводниках, независимо от формы проводников и от того, каким способом достигается изменение внешнего магнитного поля.
1.20. Электромагнитная индукция. Правило Ленца
Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.
Магнитным потоком Φ через площадь S контура называют величину
|
где B – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура (рис. 1.20.1).
|
Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали и выбранное положительное направление обхода контура связаны правилом правого буравчика |
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
1 Вб = 1 Тл · 1 м2. |
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Эта формула носит название закона Фарадея.
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.
Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.
|
Рисунок 1.20.2. Иллюстрация правила Ленца. В этом примере а инд Iинд течет навстречу выбранному положительному направлению обхода контура |
Правило Ленца отражает тот экспериментальный факт, что инд и всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.
1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
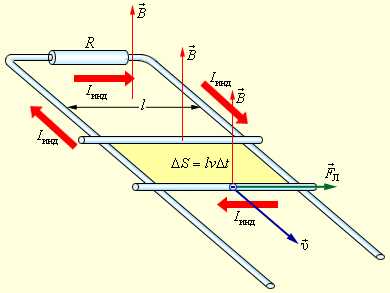
Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью по двум другим сторонам (рис. 1.20.3).
|
Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон |
На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен
Работа силы FЛ на пути l равна
По определению ЭДС
В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
Для того, чтобы установить знак в формуле, связывающей инд и нужно выбрать согласованные между собой по правилу правого буравчика направление нормали и положительное направление обхода контура как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный Iинд = инд/R. За время Δt на сопротивлении R выделится джоулево тепло
Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 г.
Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
|
Модель. Электромагнитная индукция |
|
Модель. Опыты Фарадея |
|
Модель. Генератор переменного тока |
gigabaza.ru
ЭДС индукции в движущихся проводниках
ЭДС – это аббревиатура трех слов: электродвижущая сила. ЭДС индукции () появляется в проводящем теле, которое находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции.
Закон Фарадея для электромагнитной индукции
Основным законом, который используют при расчетах, связанных с электромагнитной индукцией является закон Фарадея. Он говорит о том, что электродвижущая сила электромагнитной индукции в контуре равна по величине и противоположна по знаку скорости изменения магнитного потока () сквозь поверхность, которую ограничивает рассматриваемый контур:
Закон Фарадея (1) записан для системы СИ. Надо учитывать, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки. Если изменение потока происходит равномерно, то ЭДС индукции находят как:
Магнитный поток, который охватывает проводящий контур, может изменяться в связи с разными причинами. Это может быть и изменяющееся во времени магнитное поле и деформация самого контура, и перемещение контура в поле. Полная производная от магнитного потока по времени учитывает действие всех причин.
ЭДС индукции в движущемся проводнике
Допустим, что проводящий контур перемещается в постоянном магнитном поле. ЭДС индукции возникает во всех частях контура, которые пересекают силовые линии магнитного поля. При этом, результирующая ЭДС, появляющаяся в контуре будет равна алгебраической сумме ЭДС каждого участка. Возникновение ЭДС в рассматриваемом случае объясняют тем, что на любой свободный заряд, который движется вместе с проводником в магнитном поле, будет действовать сила Лоренца. При воздействии сил Лоренца заряды движутся и образуют в замкнутом проводнике ток индукции.
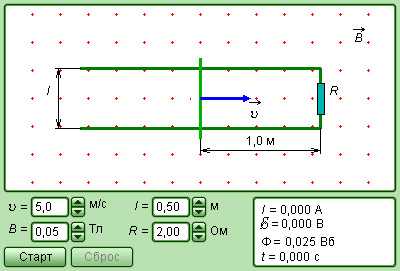
Рассмотри случай, когда в однородном магнитном поле находится прямоугольная проводящая рамка (рис.1). Одна сторона рамки может двигаться. Длина этой стороны равна l. Это и будет наш движущийся проводник. Определим, как можно вычислить ЭДС индукции, в нашем проводнике, если он перемещается со скоростью v. Величина индукции магнитного поля равна B. Плоскость рамки перпендикулярна вектору магнитной индукции. Выполняется условие .
ЭДС индукции в рассматриваемом нами контуре будет равна ЭДС, которая возникает только в подвижной его части. В стационарных частях контура в постоянном магнитном поле индукции нет.
Для нахождения ЭДС индукции в рамке воспользуемся основным законом (1). Но для начала определимся с магнитным потоком. По определению поток магнитной индукции равен:
где , так как по условию плоскость рамки перпендикулярна направлению вектора индукции поля, следовательно, нормаль к рамке и вектор индукции параллельны. Площадь, которую ограничивает рамка, выразим следующим образом:
где – расстояние, на которое перемещается движущийся проводник. Подставим выражение (2), с учетом (3) в закон Фарадея, получим:
где v – скорость движения подвижной стороны рамки по оси X.
Если угол между направлением вектора магнитной индукции () и вектором скорости движения проводника () составляет угол , то модуль ЭДС в проводнике можно вычислить при помощи формулы:
Примеры решения задач
ru.solverbook.com
Природа возникновения ЭДС индукции — МегаЛекции
Рассмотрим ситуацию, когда ЭДС индукции возникает в контуре, показанном на рисунке при перемещении подвижной стороны контура с некоторой скоро-
стью . Вместе с перемычкой с той же скоростью движутся все электроны внутри нее, и на каждый в магнитном поле действует сила Лоренца, направленная вдоль перемычки:
Действие этой силы эквивалентно действию силы со стороны электрического поля с напряженностью
. (20.1)
Это поле не имеет электростатической природы, и циркуляция вектора напряженности по контуру дает величину ЭДС, действующей в контуре:
. (20.2)
При вычислении интеграла в (20.2) примем за положительное направление обхода контура направление по часовой стрелке. Тогда положительная нормаль к контуру будет направлена так же, как вектор индукции магнитного поля. Элементы в подвижной рамке, в которых собственно действует поле, создающее ЭДС в сумме дают вектор . Векторное произведение является постоянной величиной в пределах подвижной части контура. Поэтому
. (20.3)
В смешанном произведении векторов в соотношении (20.3) можно провести циклическую перестановку векторов:
. (20.4)
Умножим и разделим это выражение на . Тогда для ЭДС индукции получим:
. (20.5)
Вектор по модулю равен площади, описанной подвижной частью за время , однако направлен «к нам». Вектор направлен по направлению нормали к контуру. Поэтому
. (20.6)
Соотношение (20.7)
. (20.7)
называют обычно законом Фарадея или законом ЭМИ.
Таким образом, в рассматриваемом случае, т.е. при движении проводника в магнитном поле, возникновение ЭДС индукции объясняется действием силы Лоренца на носители заряда в проводнике. В этом объяснении имеется существенный недостаток: индукционный ток проходя по проводникам совершает некоторую работу, а сила Лоренца работы совершать не может.
Это противоречие является кажущимся. Электроны под действием силы Лоренца приходят в движение со скоростью , направленной по вектору . Это движение вызывает появление второй составляющей силы Лоренца , направленной навстречу скорости движения подвижной части контура. Для поддержания движения со скоростью к подвижной стороне необходимо будет прикладывать силу. Эта сила и совершает ту работу, которая выделяется в проводах контура при протекании по нему индукционного тока.
Сила совершает отрицательную работу, равную положительной работе составляющей силы Лоренца . Действительно, за время полная работа силы Лоренца
. (20.8)
Часто бывает так, что контур образован не одним витком, а несколькими. По сути дела именно такая ситуация реализуется, например, во всех трансформаторах. Витки соединяются последовательно, и ЭДС в таком контуре равна сумме ЭДС в каждом из витков:
. (20.8)
Величина
(20.9)
называется потокосцеплением.
Токи Фуко
Индукционные токи могут возникать не только в контурах, но и в сплошных массивных проводниках. Действительно, всякий сплошной проводник можно представить состоящим из большого количества замкнутых контуров. В этом случае индукционные токи называют вихревыми или токами Фуко.
По правилу Ленца вихревые токи направлены так, чтобы противодействовать причине их вызывающей. Поэтому движущиеся в магнитном поле сплошные проводники испытывают сильное торможение, величина которого зависит от скорости движения. Это используют, например, для торможения подвижных частей стрелочных приборов. При этом торможение уменьшается по мере приближения стрелки к положению равновесия.
В индукционных печах вихревые токи обеспечивают разогрев металлов до плавления.
Однако в трансформаторах индукционные токи приводят к дополнительным потерям энергии на разогрев сердечника, и с ними борются, набирая сердичники из изолированных пластин.
При протекании по проводам тока создается магнитное поле, и носители заряда движутся в этом поле. Если ток переменный, то возникающие токи Токи Фуко увеличивают его вблизи поверхности провода и уменьшают в центре. В результате большая часть переменного тока протекает по поверхности проводника. Это явление называют поверхностным, или скин-эффектом.
Явление самоиндукции
Явление самоиндукции является частным случаем явления электромагнитной индукции. Если в некотором контуре протекает электрический ток, то он создает магнитное поле и магнитный поток через поверхность контура. При изменениях тока изменяется магнитный поток, и возникает ЭДС индукции противодействующая этому изменению по правилу Ленца. Ее и называют ЭДС индукции .
Величина индукции магнитного поля, а значит и магнитный поток через его поверхность, пропорциональны протекающему току:
. (20.10)
Коэффициент пропорциональности в формуле (20.10) называется индуктивностью контура. Единицей индуктивности является 1 генри (Гн).
Индуктивность определяется геометрическими параметрами контура и магнитными свойствами окружающей среды. Для того, чтобы более конкретно представить влияние на величину индуктивности этих факторов вычислим индуктивность соленоида, близкого к идеальному, т.е. с длиной , большой по сравнению с геометрическими размерами сечения, имеющего площадь ( ). Индукция магнитного поля соленоида при силе тока в нем
(20.11)
где – количество витков на единицу длины соленоида;
– магнитная проницаемость среды внутри соленоида.
Количество витков в соленоиде , и через каждый из них магнитное поле создает поток
. (20.12)
Потокосцепление (полный поток)
. (20.13)
Очевидно, что индуктивность соленоида выражается соотношением
, (20.14)
где есть объем соленоида.
Если в области действия магнитного поля ферромагнетики отсутствуют, то магнитная проницаемость остается постоянной и ЭДС индукции
. (20.15)
20.5. Токи при замыкании и размыкании цепи с индуктивностью
Влияние самоиндукции на протекание тока в цепи очень наглядно демонстрируется характером изменения тока в цепи, содержащей индуктивность и активное сопротивление при ее подключении и отключении от источника тока. В положении переключателя, показанном на рисунке, в цепи идет ток
. (20.16)
Предположим, что в некоторый момент времени переключатель мгновенно отключает источник тока и замыкает индуктивность на резистор. В отсутствие источника сила тока в цепи начнет убывать, но возникнет ЭДС самоиндукции, которая будет ее поддерживать. Падение напряжения на резисторе должно быть равно ЭДС самоиндукции :
. (20.17)
Разделим на :
(20.18)
Разделим в (20.17) переменные:
(20.19)
После интегрирования получаем:
. (20.20)
Потенцирование этого соотношения дает зависимость тока от времени:
. (20.21)
При ток равен начальному значению , поэтому и константа равна этому току:
. (20.22)
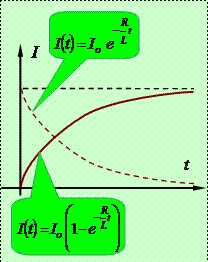 Графически эта зависимость выглядит так, как это показано на рисунке. Решение аналогичного уравнения для нарастания тока в цепи приводит к соотношению
Графически эта зависимость выглядит так, как это показано на рисунке. Решение аналогичного уравнения для нарастания тока в цепи приводит к соотношению
. (20.23)
Явление взаимной индукции
 Как и самоиндукция, явление взаимной индукции является частным случаем явления электромагнитной индукции. Заключается оно в том, что если один контур создает в пространстве магнитное поле, в котором находится другой контур, то при изменениях тока в первом контуре во втором возникает ЭДС индукции (ЭДС взаимоиндукции) , которая противодействует изменению магнитного потока в первом контуре.
Как и самоиндукция, явление взаимной индукции является частным случаем явления электромагнитной индукции. Заключается оно в том, что если один контур создает в пространстве магнитное поле, в котором находится другой контур, то при изменениях тока в первом контуре во втором возникает ЭДС индукции (ЭДС взаимоиндукции) , которая противодействует изменению магнитного потока в первом контуре.
Допустим, что имеются два контура, расположенные недалеко друг от друга, так что магнитные поля, создаваемые каждым из них, создают через витки другого контура ощутимый магнитный поток. Обозначим магнитный поток, создаваемый первым контуром с током через поверхности витков второго контура равен . Этот поток, очевидно пропорционален силе тока в первом контуре:
. (20.24)
Аналогичным образом ток второго контура создает через витки первого поток
. (20.25)
Контуры в этом в этом случае называют связанными. При изменениях тока в одном из контуров в другом индуцируется ЭДС взаимной индукции соответственно
и . (20.26)
Коэффициенты и называют коэффициентами взаимной индукции или взаимными индуктивностями.Их величина определяется формой, размерами, взаимным расположением контуров и магнитными свойствами окружающей среды. В отсутствие ферромагнетиков эти коэффициенты одинаковы.
Энергия магнитного поля
В цепи, показанной на рисунке, в исходном состоянии течет ток по индуктивности и резистору . При отключении источника тока магнитный поток в индуктивности должен упасть до нуля, но ЭДС самоиндукции некоторое время поддерживает ток, препятствуя его прекращению. При этом в резисторе продолжает выделяться энергия. В схеме и окружающих телах никаких изменений, кроме уменьшения индукции магнитного поля в катушке индуктивности не происходит. Остается предположить, что выделяющаяся в резисторе энергия была связана с существованием магнитного поля в катушке.
В процессе уменьшения тока за время ЭДС самоиндукции совершает работу
. (20.27)
Если индуктивность катушки остается постоянной, то и
. (20.28)
Ток в индуктивности спадает от некоторого значения I до нуля, поэтому вся работа за время исчезновения тока
. (20.29)
Именно такой энергией обладает магнитное поле катушки при прохождении по ней тока:
. (20.30)
Для идеального соленоида (катушки) , произведение дает напряженность поля соленоида, поэтому
. (20.31)
Поле идеального соленоида сосредоточено внутри соленоида, поэтому можно утверждать, что с магнитным полем связана энергия, распределенная в пространстве с плотностью
. (20.32)
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Механизм возникновения ЭДС индукции
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒
Наличие в контуре ЭДС означает, что на носители заряда в контуре действуют сторонние силы. В проводнике, движущемся в магнитном поле, это сила Лоренца.
Пусть проводник конечной длины l движется со скоростью в направлении, перпендикулярном к проводнику и к вектору (рис. 50). Сила Лоренца разделяет разноименные заряды, смещая их к противоположным концам проводника. В проводнике возникает электростатическое поле. Разделение зарядов продолжается до тех пор, пока лоренцева сила и сила электростатического поля не уравновесятся (Fстор = Fэл).
В процессе разделения зарядов сторонние силы совершают работу. Но сила Лоренца, работы не совершает. В рассмотренном случае сила, создающая ЭДС, является не полной силой Лоренца, а только ее составляющей.
Действительно, в процессе разделения заряды перемещаются не только вместе с проводником со скоростью, но и вдоль проводника (рис. 51).
Полная сила Лоренца перпендикулярна к результирующей скорости. Разложим эту силу на две составляющие:, перпендикулярную к проводнику и обусловленную скоростью. Составляющая играет роль сторонней силы, составляющая тормозит движение проводника.
ЭДС индукции возникает и в неподвижных проводниках, находящихся в переменном магнитном поле. Силой Лоренца механизм возникновения ЭДС в этом случае объяснить нельзя. О возникающей в этом случае ЭДС мы можем судить косвенно либо по наличию тока, когда в переменном магнитном поле находится замкнутый через гальванометр проводник, либо по возникающим токам Фуко, когда в переменном магнитном поле находится массивный проводник. Опытным путем можно убедиться, что вихревые токи циркулируют в плоскостях, перпендикулярныхменяющемуся магнитному полю. То есть индуцируемая ЭДС действует в замкнутом контуре. Это равносильно утверждению, что в каждом элементе длины контура создается поле.
Вращая в магнитном поле катушку постоянного сечения, мы получаем изменение потока в зависимости от ориентации катушки (рис. 53).
Таков принцип получения переменной ЭДС в электромагнитных генераторах.
Если равномерно вращать катушку в однородном магнитном поле, то в ней возникает индуцированный ток, периодически изменяющий свое направление. Более сложные генераторы являются улучшенными вариантами такого устройства.
23. Индуктивность длинного соленоида. Энергия контура с током. Энергия магнитного поля. Плотность энергии магнитного поля, явление взаимоиндукции.
Индуктивность соленоида выражается следующим образом:
(СИ)
Без использования магнитного материала плотность магнитного потока B в пределах катушки является фактически постоянной и равна
B = μ0Ni / l
где μ0 − магнитная проницаемость вакуума, N − число витков, i − ток и l − длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B, умноженному на площадь поперечного сечения S и число витков N:
Отсюда следует формула для индуктивности соленоида
эквивалентная предыдущим двум формулам.
Таким образом, энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции
Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить:
где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле.
Объемная плотность энергии магнитного поля соленоида:
24. Самоиндукция. Индуктивность. Цепь с активным сопротивлением и индуктивностью
Самоиндукция – явление возникновения ЭДС индукции в проводящем контуре при изменении тока в нем.
При изменении тока в контуре меняется магнитный поток через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. По направлению противоположно изменению тока.
Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L:
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время.
Индуктивность (L) — коэффициент пропорциональности между магнптным потоком (создаваемым током какого-либо витка при отсутствии намагничивающих сред, например, в воздухе) и величной этого тока. где – магнитный поток через виток
Индуктивность всегда положительна и зависит ТОЛЬКО от геометрических свойств контура.
25. Гармонические колебания. Амплитуда, круговая частота, фаза колебаний. График гармонического колебательного движения. Уравнение и решение гармонического колебательного движения.
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.
Уравнение: или ,где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая(круговая) частота колебаний, — полная фаза колебаний, — начальная фаза колебаний.
Амплитудой колебаний называют наибольшее отклонение колеблющегося тела от его первоначального (спокойного) положения. Чем больше амплитуда колебания, тем громче звук.
Круговая частота (синонимы: радиальная частота, циклическая частота, угловая частота) — скалярная величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, круговая частота равна модулю вектора угловой скорости. Угловая частота является производной по времени от фазы колебания:
Фазаобычно выражается в угловых единицах (радианах, градусах) или в циклах (долях периода): 1 цикл = радиан = 360°
26. Метод векторных диаграмм. Сложение одинаково направленных колебаний одной частоты.
Метод векторных диаграмм заключается в том, что колебание можно изобразить в виде вращения вектора
где – угол, совпадающий с начальной фазой. – скорость вращения вектора, равная частоте колебаний
длина вектора равна амплитуде колебаний (A).
Сложение одинаково направленных колебаний: S мысленно меняем на A
:
:
если
если
27.Сложение взаимно перпендикулярных колебаний одной частоты о_О ^_^ *сука_блять_няшный_смайл_нах*
Наиболее простой вид имеет уравнение движения, если тело участвует в двух взаимно перпендикулярных колебательных движениях с одинаковыми частотами . Тогда уравнения горизонтальных и вертикальных колебаний примут вид:
Воспользовавшись тригонометрическими тождествами, приведем уравнения колебаний к виду
Из первого уравнения следует, что
Подставляя полученные выражения во второе уравнение, и возводя его в квадрат, не трудно получить уравнение траектории в виде
Уравнение траектории описывается уравнением эллипса. То есть траектория результирующего колебания имеет форму эллипса. Такие колебания называются эллиптически поляризованными. Ориентация осей эллипса и его размеры зависят от амплитуд складываемых колебаний и разности фаз .
Например, когда разность фаз кратна , эллипс вырождается в отрезок прямой для нечетных m или (табл.1: ωx :ωy = 1:1, ϕ = 0, ±π). Результирующее колебание является гармоническим – тело совершает гармонические колебания вдоль прямой с амплитудой . Такие колебания называются линейно поляризованными.
В случае, когда разность фаз кратна траектория принимает форму эллипса, приведенного к осям координат (оси эллипса совпадают с осями координат). Когда амплитуды вертикальных и горизонтальных колебаний равны , эллипс вырождается в окружность. Такие колебания называются поляризованными по кругу.
28. Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Время релаксации. Логарифмический декремент затухания.
Дифференциальное уравнение принимает вид
Сделав замену x = eλt, получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
;
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Апериодичность
Если , то имеется два действительных корня, и решение дифференциального уравнения принимает вид: В этом случае колебания с самого начала экспоненциально затухают.
Граница апериодичности
Если , два действительных корня совпадают , и решением уравнения является: В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Слабое затухание
Если , то решением характеристического уравнения являются два комплексно сопряжённых корня
Тогда решением исходного дифференциального уравнения является
Где — собственная частота затухающих колебаний.
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
Релаксация — многоступенчатый процесс, т. к. не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и др.) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, т. е. производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации.
Логарифмический декремент затухания – безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.
29. Вынужденные колебания. Резонанс
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при стремлении частоты собственных колебаний к вынужденным.
Рекомендуемые страницы:
lektsia.com
ЭДС индукции в движущихся проводниках формула
ЭДС индукции и сила Лоренца
Появление электродвижущей силы (ЭДС) в телах, перемещающихся в магнитном поле легко объяснить, если вспомнить о существовании силы Лоренца. Пусть стержень движется в однородном магнитном поле с индукцией рис.1. Пусть направление скорости движения стержня () и перпендикулярны друг другу.
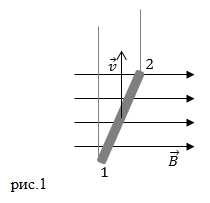
Между точками 1 и 2 стержня индуцируется ЭДС, которая направлена от точки 1 к точке 2. Движение стержня – это перемещение положительных и отрицательных зарядов, которые входят в состав молекул этого тела. Заряды вместе с телом перемещаются в сторону движения стержня. Магнитное поле оказывает воздействие на заряды при помощи силы Лоренца, пытаясь переместить положительные заряды в сторону точки 2, а отрицательные заряды к противоположному концу стержня. Так, действие силы Лоренца порождает ЭДС индукции.
Если в магнитном поле движется металлический стержень, то положительные ионы, находясь в узлах кристаллической решетки, не могут двигаться вдоль стержня. При этом подвижные электроны скапливаются в избытке на конце стержня около точки 1. Противоположный конец стержня будет испытывать недостаток электронов. Появившееся напряжение определяет собой ЭДС индукции.
В том случае, если движущийся стержень сделан из диэлектрика, разделение зарядов при воздействии силы Лоренца, приводит к его поляризации.
ЭДС индукции будет равна нулю, если проводник перемещается параллельно направлению вектора (то есть угол между и равен нулю).
ЭДС индукции в прямом проводнике, движущемся в магнитном поле
Получим формулу для вычисления ЭДС индукции, которая возникает в прямолинейном проводнике, имеющем длину l, движущемся параллельно самому себе в магнитном поле (рис.2). Пусть v – мгновенная скорость проводника, тогда за время он опишет площадь равную:
При этом проводник пересечет все линии магнитной индукции, которые проходят через площадку . Получим, что изменение магнитного потока () сквозь контур в который входит перемещающийся проводник:
где – составляющая магнитной индукции, перпендикулярная к площадке . Подставим выражение для (2) в основной закон электромагнитной индукции:
получим:
При этом направление тока индукции определено законом Ленца. То есть индукционный ток имеет такое направление, что механическая сила, которая действует на проводник, замедляет перемещение проводника.
ЭДС индукции в плоском витке, вращающемся в магнитном поле
Если плоский виток вращается в однородном магнитном поле, угловая скорость его вращения равна , ось вращения находится в плоскости витка и , тогда ЭДС индукции можно найти как:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; – угловая скорость; () – угол поворота контура. Необходимо заметить, что выражение (5) справедливо, тогда, когда ось вращения составляет прямой угол с направлением вектора внешнего поля .
Если вращающаяся рамка имеет N витков и ее самоиндукцией можно пренебречь, то:
Примеры решения задач
ru.solverbook.com
Проводник, движущийся в магнитном поле. Электромагнитная индукция. Само- и взаимоиндукция. Виды ЭДС. Вихревые токи.
В металлическом проводнике большое количество свободных электронов, которые хаотично движутся. Если двигать проводник в магнитном поле перпендикулярно силовым линиям, то поле будет отклонять движущиеся вместе с проводником электроны, и они начнут двигаться, то есть возникнет электродвижущая сила (ЭДС). Это называется электромагнитной индукцией (индуцировать – наводить).
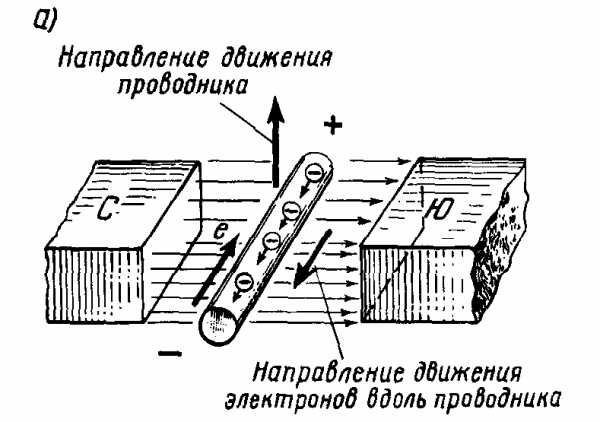 Под действием ЭДС электроны будут двигаться и скапливаться на одном конце проводника, а на другом будет недостаток электронов, то есть положительный заряд и возникнет разность потенциалов, илиэлектрическое напряжение.
Под действием ЭДС электроны будут двигаться и скапливаться на одном конце проводника, а на другом будет недостаток электронов, то есть положительный заряд и возникнет разность потенциалов, илиэлектрическое напряжение.
Если соединить такой проводник с внешней цепью (замкнуть путь), то под влиянием разности потенциалов будет протекать ток.
Если проводник двигать вдоль силовых линий, то поле на заряды действовать не будет, ЭДС, напряжение не возникнет, ток протекать не будет.
Такая ЭДС называется ЭДС индукции. Она определяется по закону Фарадея:
· ЭДС индукцииравна произведению скорости перемещения проводника V, магнитной индукции В и активной длины проводника L
E=VBL
Направление ее определяется по правилу правой руки:
· 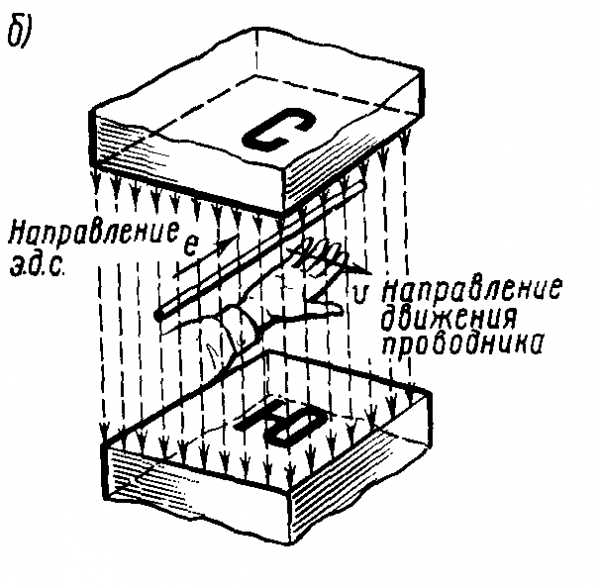 Если правую руку расположить в магнитном поле так, что силовые линии будут входить в ладонь, а отогнутый большой палец покажет направление движения проводника, то четыре вытянутых пальца покажут направление ЭДС.
Если правую руку расположить в магнитном поле так, что силовые линии будут входить в ладонь, а отогнутый большой палец покажет направление движения проводника, то четыре вытянутых пальца покажут направление ЭДС.
ЭДС будет наводиться при любом пересечении проводника и магнитного поля. То есть можно двигать проводник, можно поле, а можно магнитное поле изменять.
Тогда ЭДС определяется по Максвеллу:
ЭДС, наведенная в контуре в результате пересечения его изменяющимся магнитным потоком, равна скорости изменения этого потока.
е= – ΔФ/Δt
Где ΔФ=Ф1– Ф2 изменение магнитного потока, Вб
Δt – время, за которое изменился магнитный поток, сек.
Правило Ленца: индуцированная ЭДС имеет такое направление, что созданный ею ток противодействует изменению магнитного потока.
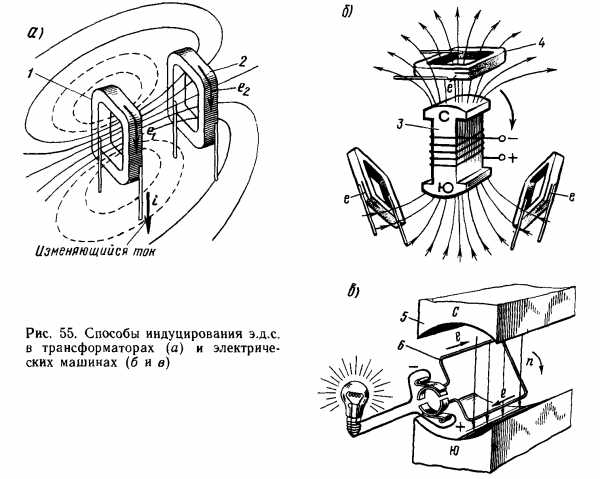 | Таким образом, способы наведения ЭДС за счет магнитного поля: 1. Изменяем ток, а значит, магнитный поток в одной катушке и пересекаем им другую катушку (трансформатор) 2. Вращаем катушку в постоянном магнитном поле (генератор постоянного тока) 3. Вращаем постоянное поле электромагнита, или постоянного магнита относительно неподвижных катушек (генератор переменного тока) |
ЭДС самоиндукции.
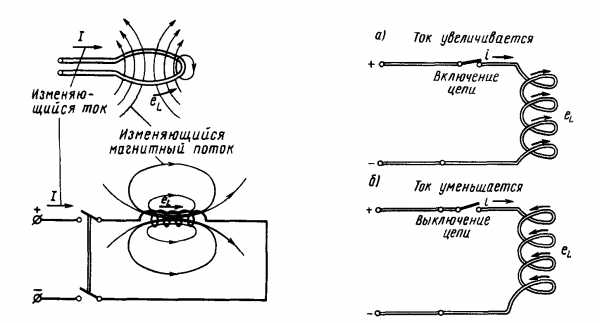 Если в проводнике изменяется ток, изменяется и магнитный поток им созданный. Распространяясь в пространстве, этот магнитный поток пересекает не только соседние проводники, но и свой собственный, а значит, в собственном проводнике наводится ЭДС. Она называется ЭДС самоиндукции.
Если в проводнике изменяется ток, изменяется и магнитный поток им созданный. Распространяясь в пространстве, этот магнитный поток пересекает не только соседние проводники, но и свой собственный, а значит, в собственном проводнике наводится ЭДС. Она называется ЭДС самоиндукции.
ЭДС самоиндукции – это ЭДС, возникающая в проводнике, при изменении собственного тока и магнитного потока.
Она возникает при всяком изменении тока и направлена так, чтобы не дать ему измениться. При уменьшении тока она направлена вместе с ним и поддерживает ток, при увеличении тока, направлена против, и ослабляет его.
Способность проводника (катушки) создавать ЭДС самоиндукции, называется индуктивностью L.
Она зависит от:
· Квадрата числа витков катушки w
· магнитной проницаемости µ
· сечения катушки S
· длины катушки l
L=(w2μS)/l , Гн(Генри)
ЭДС самоиндукции:
eL=-Δi/Δt , В
Где Δi/Δt – скорость изменения тока.
Эта ЭДС, препятствуя изменению тока мешает ему протекать, а значит создает сопротивление переменному току.
Коммутационные перенапряжения.
Это перенапряжения в цепях с большой индуктивностью при коммутации. В результате может возникнуть электрическая дуга, или искра, оплавляются контакты. Поэтому применяются меры дугогашения.
Взаимоиндукция.
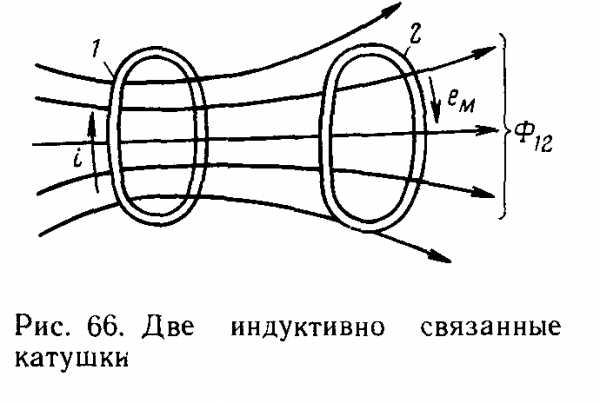 ЭДС взаимоиндукции – это ЭДС, возникающая, в катушке при пересечении ее изменяющимся магнитным потоком другой катушки.
ЭДС взаимоиндукции – это ЭДС, возникающая, в катушке при пересечении ее изменяющимся магнитным потоком другой катушки.
На этом принципе работает трансформатор.
Наведенное напряжение –это напряжение, возникающее в металлических конструкциях в результате пересечения их с переменным магнитным полем, созданным переменным током.
Таким образом, за счет магнитного поля возникают три вида ЭДС:
1. ЭДС индукции. Возникает при движении проводника в постоянном магнитном поле, или при движении поля относительно проводника.
2. ЭДС самоиндукции. Возникает из-за пересечения проводника собственным изменяющимся магнитным полем.
3. ЭДС взаимоиндукции. Возникает при пересечении проводника чужим изменяющимся магнитным полем.
Вихревые токи.
По другому: токи Фуко, индукционные токи.
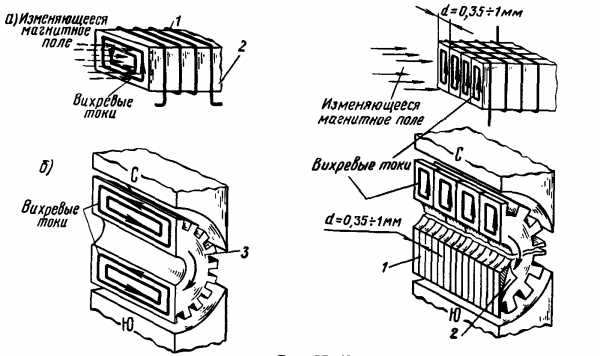 Это токи, возникающие в массивных стальных частях электроустановок (сердечниках, корпусах), из-за пересечения их изменяющимся магнитным потоком и наведения ЭДС. В результате малого сопротивления, возникшие короткозамкнутые токи сильно нагревают машины.
Это токи, возникающие в массивных стальных частях электроустановок (сердечниках, корпусах), из-за пересечения их изменяющимся магнитным потоком и наведения ЭДС. В результате малого сопротивления, возникшие короткозамкнутые токи сильно нагревают машины.
Потери на вихревые токи – это потери мощности, идущие на нагрев.
Для снижения потерь уменьшают вихревые токи следующим образом:
1. Сердечники электромашин выполняют шихтованными, то есть набирают из листов электротехнической стали, изолированных лаком. Тем самым уменьшают сечение, а значит, увеличивают сопротивление току.
2. В сталь добавляют кремний, обладающий большим сопротивлением.
Похожие статьи:
poznayka.org