Электромагнетизм физика формулы – Электромагнетизм. Основные формулы. - Центр социальной реабилитации инвалидов и детей-инвалидов Фрунзенского района Санкт-Петербурга

25.06.202017.12.2018

Электромагнетизм физика формулы – Электромагнетизм. Основные формулы.

Содержание

Электромагнетизм основные формулы

РАЗДЕЛIV. ЭЛЕКТРОМАГНЕТИЗМ

Основные формулы

Связь магнитной индукции B с напряженностьюH магнитного поля

B = µµ0 H,

где µ – магнитная проницаемость изотропной среды;µ0 – магнитная постоянная. В вакууме µ = 1, и тогда магнитная индукция в вакууме

					B = µ0 H.
Закон Био—Савара—Лапласа
d B =	µµ	0	[dlr]	I	или d B =	µµ0 I sinα		dl ,
d B =	4π		[dlr]	r3	или d B =	4π	r 2	dl ,

где d B – магнитная индукция поля, создаваемого элементом провода длинойdl

с током I;r -радиус-вектор,направленный от элемента проводника к точке, в которой определяется магнитная индукция;α – угол междурадиусом-вектороми направлением тока в элементе провода.

Магнитная индукция в центре кругового тока

B = µµ2R0 I ,

где R – радиус кругового витка.

Магнитная индукция на оси кругового тока

B =	µµ	0 2πR2 I	,

	4π (R2+ h3)3 / 2
	4π (R2+ h3)3 / 2

где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока

B = µµ0 I /(2πr0) ,

где r0 – расстояние от оси провода до точки, в которой определяется магнитная индукция.

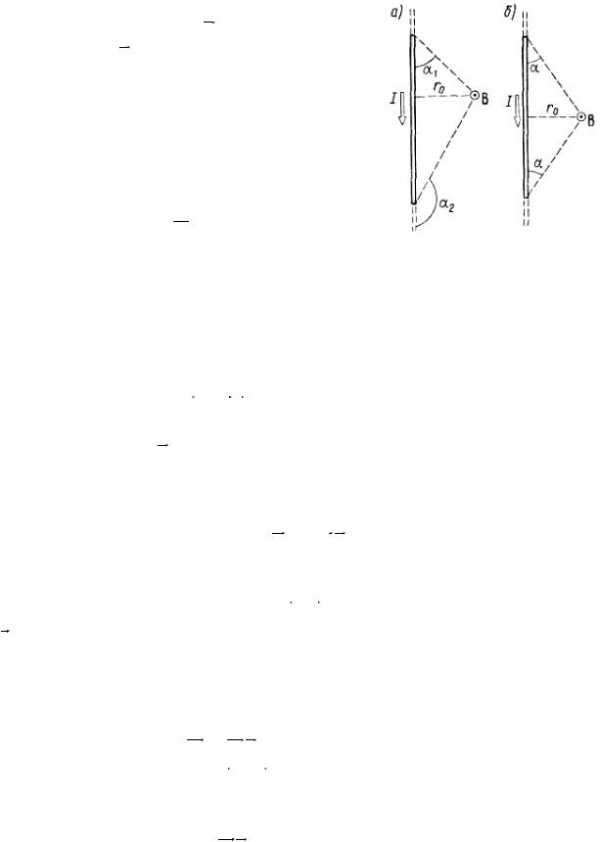
Магнитная индукция поля, создаваемого отрезком провода с током

(см. рис. 4.1,а),

B = µµ0 I (cosα1 −cosα2) . 4πr0

Обозначения ясны из рисунка. Направление вектора магнитной индукции B обозначено точкой –

это значит, что B направлен перпендикулярно плоскости чертежа к нам.

При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рисунок. 4.1,б), -cosα2 = cosα1 = cosα, тогда

B = µµ0 I cosα . 2π r0

Магнитная индукция поля соленоида	Рисунок 4.1
B = µµ0nI,

где п – отношение числа витков соленоида к его длине.

Сила, действующая на провод с током в магнитном поле (закон Ампера),

F = I[l B], или F= IBlsinα ,

где l – длина провода;α – угол между направлением тока в проводе и вектором

магнитной индукции B . Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности:

d F = I[dl B].

Магнитный момент плоского контура с током pm = nIS ,

где n – единичный вектор нормали (положительной) к плоскости контура;I – сила тока, протекающего по контуру;S – площадь контура.

Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,

M =[pm B],	или	M = pmBsinα ,
где α – угол между векторами pm иB .
Потенциальная энергия (механическая)*			контура с током в
магнитном поле
Пмех= −pmB ,	или	Пмех	= −pmB cosα .

_____________________________________________________________________

* Часть полной потенциальной энергии, которая обусловлена существованием механического (вращательного) момента.

Отношение магнитного момента рт к механическомуL (моменту импульса) заряженной частицы, движущейся по крутой орбите,

pLm = 12 Qm,

где Q – заряд частицы;т — масса частицы. Сила Лоренца*

F =Q[νB], илиF =QνB sinα ,

где ν – скорость заряженной частицы; α – угол между векторами

ν иB .

Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхности

Ф = BScosα или Ф=BnS,

где S – площадь контура;α – угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности

Ф = ∫S BndS

(интегрирование ведется по всей поверхности). Потокосцепление (полный поток)

Ψ = NФ.

Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

Работа по перемещению замкнутого контура в магнитном поле

A = I∆Ф.

ЭДС индукции

εi = −ddtΨ .

Разность потенциалов на концах провода, движущегося со скоростью ν в магнитном поле,

U = Blν sinα ,

где l – длина провода; α – угол между векторамиν иB .

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур,

Q = ∆Ф/ R, или Q= N∆Ф/ R= ∆Ψ/ R,

где R – сопротивление контура. Индуктивность контура

L=Ф/I.

ЭДС самоиндукции

εs = −L dIdt .

____________________________________________________________________

* Если частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение F = QE +Q[υ B ].

Индуктивность соленоида

L=µµ0n2V,

где п – отношение числа витков соленоида к его длине;V – объем соленоида. Мгновенное значение силы тока в цепи, обладающей сопротивлениемR

и индуктивностью L:

а) I =	ε	(1 −e−Rt / L ) (при замыкании цепи), гдеε – ЭДС источника тока;t –
	R

время, прошедшее после замыкания цепи;

б) I = Ioe−Rt / L (при размыкании цепи), гдеI0 — сила

тока в цепи при t = 0; t – время, прошедшее с момента размыкания цепи. Энергия магнитного поля

W = LI2 2 .

Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему)

ω = BH / 2, илиω = B2 /(2µµ0) , илиω = µµ0 H 2 / 2 ,

где В – магнитная индукция;H – напряженность магнитного поля.

studfiles.net

Основные формулы электромагнетизма

Электромагнетизм

Закон Кулона

Электростатическое поле

Диполь

Некоторые поля, вычисленные по теор. Гаусса

Бесконечная заряженная плоскость:

Поле между двумя заряж. плоскостями:

Поле вне заряженной сферы, вне заряженного шара:

Поле внутри заряженного шара:

Поляризуемость, поляризация

Дипольный момент молекулы:

Поляризуемость молекулы:

Поляризованность диэлектрика:

Связь поляризованности и напряженности поля для изотропных диэлектриков (через диэлектрическую восприимчивость):

При включении поля через замкнутую поверхность выходит наружу (входит внутрь) заряд:

При включении поля на поверхность выходит связанный заряд:

Вектор электрического смещения:

Внутри диэлектрика закон Кулона приобретает вид:

Условия на границе двух диэлектриков

Электроемкость и конденсаторы

Электроемкость:

Емкость конденсатора:

Емкость плоского конденсатора:

Емкость сферического конденсатора:

unnx.github.io

3 Магнетизм. Основные формулы и определения

Транскрипт

1 3 Магнетизм Основные формулы и определения Вокруг проводника с током существует магнитное поле, направление которого определяется правилом правого винта (или буравчика). Согласно этому правилу, нужно мысленно закручивать буравчик по направлению тока, тогда рукоятка буравчика будет вращаться, описывая окружность, по касательной к которой направлен вектор магнитной индукции. Модуль вектора магнитной индукции В, созданного прямым бесконечно длинным проводником с током, прямо пропорционален силе тока в проводнике I и обратно пропорционален расстоянию от проводника до точки наблюдения r. Для вакуума: В = μ 0 I /(2π r), где μ 0 магнитная постоянная. На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, Л = q [ ], где q заряд частицы, скорость частицы, – вектор магнитной индукции. Квадратные скобки означают векторное произведение двух векторов. Модуль силы Лоренца равен: F Л = q v В sin ( ^ ). Направление силы Лоренца, если движется положительный заряд, определяется по правилу левой руки. Согласно этому правилу, вектор магнитной индукции должен входить в ладонь, четыре вытянутых пальца левой руки должны показывать направление скорости, тогда отогнутый большой палец покажет направление силы Лоренца. Сила Ампера, т.е. сила, действующая на прямой проводник с током в магнитном поле, равна: А= I [ ], где I – сила тока, l длина проводника, вектор магнитной индукции. Направление силы Ампера определяется по правилу левой руки, согласно которому вектор магнитной индукции должен входить в ладонь, четыре вытянутых пальца левой руки показывать направление тока, тогда отогнутый большой палец покажет направление силы Ампера. При изменении магнитного потока в замкнутом контуре возникает индукционный ток, который, согласно закону Фарадея Ленца, создает магнитное поле, препятствующее изменению магнитного потока. Среднее значение ЭДС самоиндукции равно: ε i = – L (ΔI/Δt), где L- индуктивность, ΔI изменение силы тока, произошедшее за промежуток времени Δt. 67
2 Тест 3 1 На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем I 1 =2I 2. Индукция результирующего магнитного поля равна нулю в некоторой точке интервала… 1) d; 2) c; 3) a; 4) b. Решение Направление вектора магнитной индукции находится по правилу правого винта (или буравчика): если поступательное движение винта происходит в направлении тока, то головка винта вращается по окружности, по касательной к которой направлен вектор магнитной индукции. На рисунке, приведённом в решении, показаны линии магнитной индукции, которые представляют собой окружности, охватывающие проводники с током. Как видно из этого рисунка, ток I 1 течет на нас, буравчик выкручивается и его рукоятка вращается против часовой стрелки. Поэтому вектор магнитной индукции 1, созданный током I 1, в интервале a будет направлен вниз, а в интервалах b, c, d направлен вверх. В проводнике с током I 2 ток течет за чертеж, буравчик закручивается и вектор магнитной индукции 2 в интервалах a, b, c направлен вверх, а в интервале d вниз. Результат находится по принципу суперпозиции полей: = Понятно, что индукция результирующего магнитного поля может быть равна нулю в тех точках интервала, где вектора 1 и 2 противоположно направлены, т.е. в интервалах a и d. Модуль вектора магнитной индукции, созданного прямым бесконечно длинным проводником с током, для вакуума равен: В = μ 0 I /(2π r), где μ 0 магнитная постоянная. В интервале a индукция В 1 > В 2, т.к. токи I 1 > I 2, а соответствующие расстояния r 1< r 2. Поэтому индукция магнитного поля может быть равна нулю только в некоторой точке интервала d. Ответ: вариант 1. 68
3 Задание С3-1 для самостоятельного решения. В условиях данной задачи укажите интервал, в некоторой точке которого магнитная индукция равна нулю, если ток I 1 также как и ток I 2, направлен за чертеж. Варианты ответов те же, что в тесте 3 1. Тест 3 2 Магнитное поле создано двумя параллельными длинными проводниками с токами I 1 и I 2, расположенными перпендикулярно плоскости чертежа. Если I 1 = 2 I 2, то вектор индукции результирующего поля в точке А направлен… 1) вправо; 2) вниз; Решение 3) вверх; 4) влево. Модуль вектора магнитной индукции, созданного прямым бесконечно длинным проводником с током, прямо пропорционален силе тока в проводнике и обратно пропорционален расстоянию от проводника до точки наблюдения. Так как расстояние от обоих проводников до точки наблюдения А одинаково, а сила тока в первом проводнике в 2 раза больше, чем во втором, то В 1 = 2 В 2. Направление векторов 1 и 2 можно найти по правилу правого винта. Для этого нужно мысленно, если ток течет к нам, выкручивать буравчик. Тогда рукоятка буравчика будет вращаться против часовой стрелки, описывая окружность, по касательной к которой направлен вектор магнитной индукции. Следовательно, вектор 1 в точке А будет направлен вверх, вектор 2 вниз, результирующий вектор найдём по принципу суперпозиции. В скалярной форме: В = В 1 – В 2, т.е. В будет направлен вверх, в сторону большего вектора. Задание С3-2 для самостоятельного решения. 69 Ответ: вариант 3. В условиях данной задачи определите в точке А направление результирующего вектора магнитной индукции, если направление тока I 1 изменится на обратное, т.е. ток будет направлен от нас за чертёж. Варианты ответов те же, что в тесте 3 2.
4 Тест 3 3 На рисунке показан длинный проводник с током, около которого находится небольшая проводящая рамка. При выключении в проводнике тока заданного направления, в рамке… 1) индукционного тока не возникнет; 2) возникнет индукционный ток в направлении ; 3) возникнет индукционный ток в направлении Решение Вокруг проводника с током существует магнитное поле, направление которого определяется правилом правого винта (или буравчика). Согласно этому правилу, нужно мысленно закручивать буравчик по направлению тока, тогда рукоятка буравчика будет вращаться, описывая окружность, по касательной к которой направлен вектор магнитной индукции. В нашем примере вектор магнитной индукции, пронизывающий рамку, направлен за чертёж. При выключении тока в проводнике в замкнутом контуре возникает индукционный ток, который, согласно закону Фарадея Ленца, создает магнитное поле, препятствующее изменению магнитного потока. Поэтому магнитное поле индукционного тока тоже должно быть направлено за чертёж, чтобы препятствовать уменьшению тока. Направление индукционного тока также можно определить по правилу правого винта (буравчика), т.е. поступательное движение буравчика должно совпадать с направлением вектора магнитной индукции, созданной индукционным током. Тогда рукоятка буравчика будет двигаться в направлении индукционного тока в рамке. Поэтому в нашем примере индукционный ток возникнет в направлении Ответ: вариант 2. Задание С3-3 для самостоятельного решения. Определите направление индукционного тока в проводящей рамке, если не выключать, а включать ток в проводнике? Варианты ответов те же, что в тесте
5 Тест 3 4 На рисунке показан длинный проводник с током, около которого находится небольшая проводящая рамка. При движении рамки к проводнику со скоростью, в рамке… 1) возникнет индукционный ток в направлении ; 2) индукционного тока не возникнет; 3) возникнет индукционный ток Решение в направлении Вокруг проводника с током существует магнитное поле, направление которого определяется правилом правого винта (или буравчика). Согласно этому правилу, нужно мысленно завинчивать буравчик по направлению тока, тогда рукоятка буравчика будет вращаться, описывая окружность, по касательной к которой направлен вектор магнитной индукции. В нашем примере вектор магнитной индукции, пронизывающий рамку, направлен к нам перпендикулярно чертёжу. При движении рамки к проводнику магнитное поле усиливается, и в рамке, представляющей собой замкнутый проводящий контур, возникает индукционный ток, который, согласно закону Фарадея Ленца, создает магнитное поле, препятствующее изменению магнитного потока. Поэтому магнитное поле индукционного тока должно быть направлено за чертёж, чтобы препятствовать его изменению. Направление индукционного тока тоже можно определить по правилу правого винта (буравчика). Поступательное движение буравчика должно совпадать с направлением вектора магнитной индукции, созданной индукционным током, тогда рукоятка буравчика будет двигаться в направлении индукционного тока. Поэтому в нашем примере индукционный ток возникнет в направлении Ответ: вариант 3. Задание С3-4 для самостоятельного решения. Определите направление индукционного тока, если рамку удалять от проводника с током? Варианты ответов те же, что в тесте
6 Тест 3 5 Полная система уравнений Максвелла для электромагнитного поля имеет вид: Следующая система уравнений справедлива для… 1) в отсутствие заряженных тел; 2) в отсутствие заряженных тел и токов проводимости; 3) в отсутствие токов проводимости; 4) при наличии заряженных тел и токов проводимости. Решение. В полной системе уравнений Максвелла величина тока проводимости, обозначает плотность – плотность тока электрического смещения, а величина ρ плотность электрических зарядов. В исследуемой системе уравнений нет величин и ρ. Следовательно, система уравнений справедлива в отсутствие заряженных тел и токов проводимости. Ответ: вариант 2. 72
7 Тест 3 6 Полная система уравнений приведена в тесте 3-5. Следующая система уравнений справедлива для… 1) стационарного электромагнитного поля в отсутствие заряженных тел; 2) стационарного электромагнитного поля в отсутствие токов проводимости; 3) переменного электромагнитного поля при наличии заряженных тел и токов проводимости; 4) стационарных электрических и магнитных полей. Решение. Уравнения Максвелла являются обобщением основных законов электрических и магнитных явлений. В них приняты следующие обозначения: – напряженность электрического поля, – напряженность магнитного поля, – вектор электрического смещения, – вектор магнитной индукции. Величина обозначает плотность тока проводимости, величина D / t – плотность тока электрического смещения, а ρ плотность электрических зарядов. Первое уравнение Максвелла показывает, что переменное магнитное поле показывает, B / t порождает электрическое поле. Второе уравнение Максвелла что электрический ток и переменное электрическое поле D / t порождает магнитное поле. Для стационарных полей = const и = const. Так как в исследуемой системе уравнений отсутствуют производные D / t и B / t, то исследуемая система уравнений справедлива для стационарных электрических и магнитных полей. Ответ: вариант 4. 73

8 Задание С3-5 для самостоятельного решения. Полная система уравнений приведена в тесте 3-5. Следующая система уравнений справедлива для… 1) стационарного магнитного поля; 2) стационарного электрического поля; 3) стационарных электрических и магнитных полей; 4) стационарного электромагнитного поля в отсутствие токов проводимости. Задание С3-6 для самостоятельного решения. Полная система уравнений приведена в тесте 3-5. Следующая система уравнений справедлива для… 1) стационарного магнитного поля; 2) стационарного электрического поля; 3) стационарных электрических и магнитных полей; 4) стационарного электромагнитного поля в отсутствие заряженных тел. 74

9 Тест 3 7 Пучок однократно ионизированных изотопов магния 24 Mg и 25 Mg, движущихся с одинаковой скоростью, влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. Радиусы окружностей, по которым движутся ионы, связаны соотношением: 1) R 1 = R 2 ; 2) R 1 = R 2 ; 3) R 1 = R 2 ; 4) R 1 = R 2. Решение. На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. Направление силы Лоренца, если движется положительный заряд, определяется по правилу левой руки. Согласно этому правилу, линии магнитной индукции должны входить в ладонь, четыре вытянутых пальца левой руки должны показывать направление скорости, тогда отогнутый большой палец покажет направление силы Лоренца. Если частица влетает в магнитное поле перпендикулярно линиям магнитной индукции с постоянной по величине скоростью, то она движется по окружности (см.рис.).следовательно, сила Лоренца является центростремительной силой. Согласно второму закону Ньютона, получим: mv 2 /R = qvb. Отсюда найдём радиус траектории: R = mv/(qb). Поскольку q, v, B постоянные величины, то отношение радиусов окружностей равно отношению их масс: R 1 /R 2 = m 1 /m 2. Массы частиц в атомных единицах массы (а.е.м) указаны перед обозначениями химических элементов. Следовательно, m 1 = 24 а.е.м. и m 2,= 25 а.е.м. После численной подстановки получим R 1 = (24/25) R 2. Ответ: вариант 4. 75

10 Задание С3-7 для самостоятельного решения. Ионы, имеющие одинаковые скорости, но разные удельные заряды, влетают в однородное магнитное поле. Их траектория приведена на рисунке. Величина наименьшего удельного заряда соответствует траектории 1) 1; 2) 2; 3) 3. Примечание: удельным зарядом называется отношение заряда частицы к её массе. Значение удельного заряда можно найти из равенства силы Лоренца и центростремительной силы. Тест 3 8 На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. При этом для частицы ) q = 0; 2) q < 0; 3) q > 0. Решение На заряд, движущийся в магнитном поле, действует сила Лоренца, направление которой, если движется положительный заряд, определяется по правилу левой руки. Согласно этому правилу, вектор магнитной индукции должен входить в ладонь, четыре вытянутых пальца левой руки должны показывать направление скорости, тогда отогнутый большой палец покажет направление силы Лоренца. Следовательно, под действием силы Лоренца положительно заряженные частицы при данном направлении вектора магнитной индукции будут отклоняться вправо, отрицательно заряженные частицы – влево, а частицы, которые не имеют заряда, не будут отклоняться. Частица 1, как показывает рисунок, отклоняется влево. Следовательно, для частицы 1 q < 0. Ответ: вариант 2. 76
11 Задание С3-8 для самостоятельного решения. По рисунку в тесте 3 8 определите, какая из отклоненных частиц имеет наибольшую массу m, если скорости и заряд отклоненных частиц одинаковы. Примечание: Если скорость перпендикулярна вектору магнитной индукции, то сила Лоренца F Л = q v В равна центростремительной силе F Ц.С. = m v 2 /R. 1) 1; 2) 3; 3) 4.. Тест 3 9 В постоянном однородном магнитном поле, созданном электромагнитом с дискообразными полюсами, на некотором расстоянии от оси полюсов закреплена положительно заряженная частица. Частица выстреливается перпендикулярно силовым линиям магнитного поля по касательной к окружности, плоскость которой перпендикулярна полю, а центр лежит на оси полюсов. Скорость выстреливания такова, что частица движется именно по этой окружности. В некоторый момент ток в обмотках электромагнита начинает увеличиваться. Правильное сочетание направлений скорости и ускорения частицы в этот момент представлено на рисунке ) 1 ) 3) 4) 2 Решение. 77
12 Если частица влетает в однородное постоянное магнитное поле перпендикулярно линиям магнитной индукции с постоянной по величине скоростью, то под действием силы Лоренца она движется по окружности. Следовательно, сила Лоренца является центростремительной силой, которая создаёт нормальное ускорение n, направленное к центру окружности перпендикулярно скорости. При увеличении тока в обмотках электромагнита появляется переменное магнитное поле. Согласно теории Максвелла переменное магнитное поле порождает вихревое электрическое поле (см. первое уравнение в тесте 3 5): Вихревое электрическое поле создаёт индукционный ток. Линии индукционного тока и линии напряженности электрического поля представляют собой окружности. Направление индукционного тока и силовых линий можно определить с помощью правила Ленца, согласно которому, индукционный ток, создаёт магнитное поле, препятствующее изменению магнитного потока, вызвавшего этот ток. При этом, если ток в обмотке электромагнита увеличивается, то вектор магнитной индукции, созданный индукционным током. i, будет направлен в сторону, противоположную первоначальному направлению. Применительно к нашей задаче это означает, что вектор магнитной индукции, созданный индукционным током, будет направлен за чертёж, индукционный ток и линии напряженности электрического поля будут направлены по окружности по часовой стрелке, а вектор напряженности вихревого электрического поля будет направлен по касательной к окружности. Так как электрическое поле создаёт электрическую силу, направленную так же, как, то тангенциальное ускорение τ будет направлено по касательной к окружности. Полное ускорение равно векторной сумме: = n + τ и находится по правилу параллелограмма (см. рис. в решении). Таким образом, правильное сочетание направлений скорости и ускорения частицы в момент, когда скорость в обмотках электромагнита начинает увеличиваться, представлено на рисунке 3. Ответ: вариант 3. 78
13 Задание С3-9 для самостоятельного решения. В рамках задания теста 3 9 указать правильное сочетание направлений скорости и ускорения частицы в тот момент, когда ток в обмотках электромагнита стал уменьшаться. Варианты ответов те же, что в тесте 3 9. Тест 3 10 На рисунке показана зависимость силы тока от времени в электрической цепи с индуктивностью 1 мгн. Модуль среднего значения ЭДС самоиндукции на интервале от 0 до 5 с (в мкв) равен… 1) 0; 2) 6; 3) 15; 4) 30. Решение. В соответствии с законом Фарадея Ленца, среднее значение ЭДС самоиндукции равно: ε i = – L (ΔI/Δt), где L индуктивность, ΔI изменение силы тока, произошедшее за промежуток времени Δt. Вычислим модуль среднего значения ЭДС за промежуток времени Δt = 5 0 = 5 с. Из рисунка найдём изменение силы тока на этом промежутке времени: ΔI=30 0=30 ма. Тогда среднее значение ε i = 1 30/5= 6 мкв. Ответ: вариант 2. Задание С3-10 для самостоятельного решения. На рисунке теста 3 10 показана зависимость силы тока от времени в электрической цепи с индуктивностью 1 мгн. Определить среднее значение ЭДС самоиндукции (в мкв) на интервалах времени от 10с до 15с и от 15с до 20с 1) – 2 и 0; 2) 0 и 4; 3) 0 и 2; 4) -2 и -4. Тест
14 Рамка с током с магнитным дипольным моментом m, направление которого указано на рисунке, находится в однородном магнитном поле с индукцией. Момент сил, действующий на рамку с током, направлен… 1) от нас; 2) к нам; 3) вдоль вектора магнитной индукции; 4) против вектора магнитной индукции. Решение. Момент сил, действующий на рамку с током в магнитном поле, равен векторному произведению магнитного дипольного момента рамки m на – вектор магнитной индукции: =[ m ]. Направление вектора момента сил определяется в соответствии с правилом векторного произведения двух векторов: вектор должен быть перпендикулярен плоскости, в которой лежат перемножаемые вектора, (т.е.к нам или от нас).направление векторного произведения определяется по правилу правого винта: если первый вектор поворачивать ко второму, то поступательное движение винта покажет направление векторного произведения. В нашем случае вектор направлен за чертёж, т.е. от нас. Ответ: вариант 1. Задание С3-11 для самостоятельного решения. Рамка с током с магнитным дипольным моментом m, направление которого указано на рисунке, находится в однородном магнитном поле с индукцией. Момент сил, действующий на рамку с током, направлен… Варианты ответов те же, что в тесте Задание С3-12 для самостоятельного решения. 80
15 Рамка с током с магнитным дипольным моментом m, направление которого указано на рисунке, находится в однородном магнитном поле с индукцией. Момент сил, действующий на рамку с током, направлен… Варианты ответов те же, что в тесте Тест 3 12 На рисунке изображен проводник массой m, подвешенный на проводящих нитях, через которые подведен ток. Укажите правильную комбинацию направления вектора магнитной индукции и направления тока в проводнике, чтобы сила натяжения нитей стала равной нулю. 1) Ток в направлении L-M; вектор магнитной индукции вниз. 2) Ток в направлении M-L; вектор магнитной индукции вверх. 3) Ток в направлении L-M; вектор магнитной индукции от нас. 4) Ток в направлении M-L; вектор магнитной индукции от нас. Решение Для того, чтобы сила натяжения нитей стала равной нулю, нужно чтобы сила Ампера, т.е. сила, действующая на проводник с током в магнитном поле, была направлена против силы тяжести. Поскольку сила тяжести направлена вниз, то сила Ампера должна быть направлена вверх. Направление силы Ампера определяется по правилу левой руки, согласно которому линии магнитной индукции должны входить в ладонь, четыре вытянутых пальца левой руки показывать направление тока, тогда отогнутый большой палец покажет направление силы Ампера. Правильная комбинация направления вектора магнитной индукции и направления тока в проводнике будет соответствовать варианту 3: ток в направлении M L; вектор магнитной индукции нас. Тест 3 13 от Ответ: вариант 4. 81
16 На рисунке представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре не возникает на интервале.. 1) интервал С; 2) интервал D; 3) интервал А; 4) интервал Е; 5) интервал В. Решение Согласно закону Фарадея Ленца, ЭДС в замкнутом контуре появляется при изменении магнитного потока: ε i = — ΔФ / Δt. Поскольку на интервале В магнитный поток не изменяется, то на этом интервале в контуре ЭДС не возникает. Ответ: вариант 5. Задание С3-13 для самостоятельного решения. На рисунке теста 3 13 представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре положительна и по величине максимальна на интервале… Варианты ответов те же, что в тесте Задание С3-14 для самостоятельного решения. На рисунке теста 3 13 представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре положительна и по величине минимальна на интервале… Варианты ответов те же, что в тесте Задание С3-15 для самостоятельного решения. 82
17 На рисунке теста 3 13 представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре по модулю максимальна на интервале… Варианты ответов те же, что в тесте Тест 3 14 При помещении диамагнетика в стационарное магнитное поле… 1) у атомов индуцируются магнитные моменты; вектор намагниченности образца направлен против направления внешнего поля; 2) у атомов индуцируются магнитные моменты; вектор намагниченности образца направлен по направлению внешнего поля; 3) происходит ориентирование имевшихся магнитных моментов атомов; вектор намагниченности образца направлен по направлению внешнего поля; 4) происходит ориентирование имевшихся магнитных моментов атомов; вектор намагниченности образца направлен против направления внешнего поля. Решение. Если поместить диамагнетик в стационарное магнитное поле, то у атомов, согласно правилу Ленца, индуцируются магнитные моменты, направленные против внешнего магнитного поля. Вектор намагниченности, представляет собой векторную сумму магнитных моментов отдельных атомов, делённую на объём, поэтому у диамагнетиков он направлен против внешнего магнитного поля. Ответ: вариант 1. Задание С3-16 для самостоятельного решения. Выберите вариант ответа из теста 3-14 для парамагнетика, помещенного в стационарное магнитное поле. 83
18 Тест 3 15 На рисунке представлены графики, отражающие характер зависимости величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н. Укажите зависимость, соответствующую диамагнетикам. Решение. 1) График 1; 2) График 2; 3) График 3; 4) График 4. Вектор намагниченности, представляет собой векторную сумму магнитных моментов отдельных атомов, делённую на объём. Как показывает опыт, зависимость величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н имеет вид: I = χ Н, где χ магнитная восприимчивость. У диамагнетиков χ величина отрицательная, малая по абсолютному значению и является константой. У парамагнетиков χ тоже невелика, но положительна и в сильных магнитных полях наблюдается отступление от пропорциональности между намагниченностью парамагнетика I и напряженностью Н. У ферромагнетиков χ положительная величина, которая является функцией напряженности магнитного поля и может принимать очень большие значения. При больших значениях Н намагниченность ферромагнетика I достигает насыщения. Ответ: вариант 4. Задание С3-17 для самостоятельного решения. На рисунке теста 3 15 представлены графики, отражающие характер зависимости величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н.Укажите зависимость, соответствующую парамагнетикам. Варианты ответов те же, что в тесте Задание С3-18 для самостоятельного решения. 84
19 На рисунке теста 3-15 представлены графики, отражающие характер зависимости величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н. Укажите зависимость, соответствующую ферромагнетикам. Варианты ответов те же, что в тесте
docplayer.ru
Шпора – формулы (электричество и электромагнетизм) [DOC]
Ответы для сдачи физики (1-2 семестр) Составлено в удобной для использования при сдаче экзамена форме на 3 страницах. Содержание: Что такое материальная точка? Что такое траектория, скорость и путь? Что такое ускорение, нормальное ускорение, τангенциальное ускорение? 1-ый Закон Ньютона 2-ой Закон Ньютона 3-ий Закон Ньютона Типы фундаментальных взаимодействий Закон Гука…
49,65 КБ

дата добавления неизвестна

изменен 20.12.2010 12:09

С формулами и решениями задач. Содержание: теория Гаусса, сила Лоренца, магнитное поле тока, принцип суперпозиции, закон Био-Савара-Лапласа, виды поляризации, закон Ампера, магнетики, индуктивность, закон Ома, Фарадея, взаимоиндукция, вихревое электрическое поле, токи смещения, излучение диполя, вектор Пойнтинга и другие.
2,45 МБ

дата добавления неизвестна

изменен 11.12.2008 13:13

Поток векторного поля через поверхность. Потенциал, единицы измерения. Связь потенциала и напряженности электрического поля. Потенциал точечного заряда, шара, сферы. Электрический диполь. Электрический момент диполя. Особенности электрического поля в проводнике. Общая задача электростатики. Теорема о единственности. Метод изображений. Емкость. Емкость плоского…
131,31 КБ

дата добавления неизвестна

изменен 22.02.2010 15:45

УГАТУ, электромагнетизм. Сделано в Word 2003, в архиве представлены шпоры шрифтом 6, и шрифтом 14. Даны ответы почти на все темы такие, как: Электрический заряд. Опыты Милликена. Закон сохранения заряда. Закон Кулона. Электростатическое поле. Напряженность электростатического поля. Принцип суперпозиции. Графическое изображение электростатического поля. Поток вектора…
2,05 МБ

дата добавления неизвестна

изменен 26.01.2010 17:17

УГАТУ 2 семестр Теория по электромагнетизму по физике. Два вида электричества. Электрический заряд. Свойства электрического заряда. Закон взаимодействия двух точечных зарядов Электростатическое поле. Напряженность электростатического поля. Принцип суперпозиции. Силовые линии поля. Поток вектора через поверхность. Теорема Гаусса – одна из важнейших теорем векторного анализа….
1,25 МБ

дата добавления неизвестна

изменен 09.03.2009 23:29

Шпоры по физике по теме электричество и магнетизм, шпаргалки сделаны в столбик, готовы к распечатыванию, вопросы рассмотрены следующие: Электрические свойства тел. Элементарный заряд. Закон Кулона. Электрическое поле. Напряженность поля. Поле точечного заряда. Принцип суперпозиции полей. Силовые линии электростатического поля. Поток вектора напряженности. Теорема Гаусса для…
341,22 КБ

дата добавления неизвестна

изменен 27.10.2018 04:15

www.twirpx.com

Электромагнетизм физика формулы – Электромагнетизм. Основные формулы.

Электромагнетизм основные формулы