Физика энергия формула – формула, определение. Как найти кинетическую энергию молекулы, поступательного движения, пружины, тела, молекулы газа?
- Комментариев к записи Физика энергия формула – формула, определение. Как найти кинетическую энергию молекулы, поступательного движения, пружины, тела, молекулы газа? нет
- Советы абитуриенту
Формула кинетической энергии | Все формулы
Кинетическая энергия — энергия, которой обладает тело вследствие своего движения.
– кинетическая энергия движущегося тела, – его масса, – скорость его движения.
Условное обозначение —
Единица измерения энергии — Дж (джоуль).
Кинетическая энергия характеризует движение тела. Это векторная физическая величина. Она равна нулю, когда тело неподвижно. Кинетическую энергию подразделяют на энергию поступательного и вращательного движения. Указанная формула имеет смысл только для поступательного движения.
Примеры решения задач по теме «Кинетическая энергия»
ПРИМЕР 1
| Задание | Тело массой 1 кг движется поступательно со скоростью 50 км/ч. Найти его кинетическую энергию. |
| Решение | Переведём скорость тела в единицы СИ: Подставим исходные данные в формулу: |
| Ответ | Кинетическая энергия тела приблизительно равна Дж |
Формула потенциальной энергии | Все формулы
Потенциальная энергия — это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.
– потенциальная энергия тела, – его масса, – ускорение свободного падения, – высота тела над некоторым нулевым уровнем.
Условное обозначение —
Единица измерения энергии — Дж (джоуль).
Потенциальная энергия характеризует энергию тела в некотором поле тяготения. Это скалярная физическая величина. Чаще всего рассматривается поле тяготения, связанное с землёй, в нём м/с. Для других объектов величина различается.
Примеры решения задач по теме «Потенциальная энергия»
ПРИМЕР 1
| Задание | Тело массой 12 кг находится на высоте 5 км над землёй. Найти его потенциальную энергию. |
| Решение | Подставим исходные данные в формулу. Не забываем, что км = м. Дж |
| Ответ | Потенциальная энергия тела относительно земли равна Дж. |
xn--b1agsdjmeuf9e.xn--p1ai
Кинетическая энергия | Все формулы
Кинетическая энергия — скалярная физическая величина, равная половине произведения массы тела на квадрат его скорости.
Что бы понять, что же такое кинетическая энергия тела, рассмотрим случай, когда тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v1 до v2.
Как мы знаем, работа постоянной силы вычисляют по формуле . Так как в рассматриваемом нами случае направление силы F и перемещения s совпадают, то , и тогда у нас получается, что работа силы равна А=Fs. По второму закону Ньютона найдем силу F=ma. Для прямолинейного равноускоренного движения справедлива формула:
Из это формулы мы выражаем перемещение тела:
Подставляем найденные значения F и S в формулу работы, и получаем:
Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины . А механическая работа это и есть мера изменения энергии. Следовательно, в правой части формулы стоит разность двух значений энергии данного тела. Это значит, что величина представляет собой энергию, обусловленную движением тела. Эту энергию называют кинетической. Она обозначается Wк.
Если взять выведенную нами формулу работы, то у нас получится
Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела
Так же есть :
Потенциальная энергия :
В формуле мы использовали :
— Кинетическая энергия
— Масса тела
— Скорость движения тела
— Начальная скорость тела
— Конечная скорость тела
— Работа тела
— Ускорение тела
— Сила, действующая на тело
— Перемещение тела
xn--b1agsdjmeuf9e.xn--p1ai
Энергия | Физика
Термин «энергия» был введен в 1807 г. английским ученым Т. Юнгом. В переводе с греческого это слово означает «действие, деятельность».
Современная наука немыслима без этого понятия. Оно присутствует во всех разделах физики. Это и электрическая энергия, магнитная энергия, атомная энергия и т. д.
Энергия, изучаемая в механике, называется механической. Именно с нее мы и начнем знакомство с этим важнейшим понятием.
Механическая энергия обозначается буквой Е и измеряется в тех же единицах, что и работа, т. е. в джоулях (Дж).
Поскольку в механике изучают движение тел и их взаимодействие друг с другом, то принято различать два вида механической энергии — энергию, обусловленную движением тел, и энергию, обусловленную их взаимодействием. Первая из них обозначается Eк и называется кинетической энергией, вторая обозначается Eп и называется потенциальной энергией
.Для расчета и той и другой энергии существует общее правило. Чтобы определить энергию, которой обладает тело, надо найти работу, необходимую для перевода этого тела из нулевого состояния в данное (нулевое состояние — это то, в котором соответствующая энергия тела считается равной нулю). Чем больше эта работа, тем большей энергией обладает тело в данном состоянии.
Воспользуемся этим правилом для расчета каждой из энергий.
1. Кинетическая энергия. Найдем кинетическую энергию тела массой т, движущегося со скоростью, равной и. Кинетическая энергия — это энергия, обусловленная движением. Поэтому нулевым состоянием для нее является то, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем и его кинетическую энергию.
Воспользовавшись определением работы (A = Fs), вторым законом Ньютона (F = ma), а также формулами (2.1) и (4.2), получаем (рис. 25)
Последнее из написанных здесь выражений и является кинетической энергий тела:
Итак, кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.
2. Потенциальная энергия. Найдем потенциальную энергию тела, взаимодействующего с Землей. Нулевым будем считать положение тела на поверхности Земли. Тогда потенциальная энергия тела, находящегося на некоторой высоте h, будет равна работе, необходимой для перемещения этого тела с поверхности Земли на заданную высоту. При равномерном подъеме, когда прикладываемая к телу сила совпадает по величине с силой тяжести (рис. 26), эта работа может быть найдена следующим образом:
A = Fs = Fтh = mgh.
Это и есть потенциальная энергия тела на высоте h:
Eп = mgh. (14.2)
Итак, потенциальная энергия тела, взаимодействующего с Землей, равна произведению массы этого тела, ускорению свободного падения и высоты, на которой находится тело.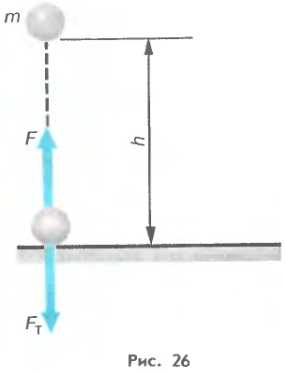
За нулевое положение тела при расчете его потенциальной энергии необязательно выбирать то, которое расположено на поверхности Земли. Это может быть и уровень пола в помещении, и поверхность стола и т. д. Нулевое положение, от которого отсчитывается высота тела h, выбирают произвольно, руководствуясь обычно лишь соображениями удобства и простоты.
По формуле (14.2) находится потенциальная энергия тела, взаимодействующего с Землей. Потенциальная энергия других взаимодействий находится по другим формулам.
От энергии, которой обладает тело, зависит работа, которую оно может совершить. Чем больше энергия тела, тем большая работа будет совершена при переходе тела из данного состояния в нулевое. Проиллюстрируем это простыми опытами.
Возьмем составной желоб, имеющий наклонную и горизонтальную части, и поместим на его сгибе алюминиевый цилиндр (рис. 27). Пуская по наклонной части желоба шарики разной массы с одинаковой высоты и шарики одинаковой массы с разных высот, можно заметить, что, чем большей потенциальной энергией наверху желоба и кинетической энергией внизу обладал шарик, тем на большее расстояние он передвинет металлический цилиндр.
1. Чем обусловлена кинетическая энергия? 2. Чему равна кинетическая энергия тела? 3. Чем обусловлена потенциальная энергия? 4. Чему равна потенциальная энергия тела, взаимодействующего с Землей? 5. Как называется единица энергии? 6. В каком случае кинетическая энергия тела равна нулю? 7. Какой энергией — кинетической, потенциальной или обеими вместе — обладает летящий в небе самолет? 8. Какой энергией обладает вода, удерживаемая плотиной, и какой энергией обладает вода, падающая с плотины? 9. Как изменяются потенциальная и кинетическая энергии мяча, брошенного вертикально вверх, в процессе его полета?
phscs.ru
Формула потенциальной энергии
ОПРЕДЕЛЕНИЕПотенциальная энергия
— это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.
– потенциальная энергия тела, – его масса, – ускорение свободного падения, – высота тела над некоторым нулевым уровнем.
Условное обозначение —
Единица измерения энергии — Дж (джоуль).
Потенциальная энергия характеризует энергию тела в некотором поле тяготения. Это скалярная физическая величина. Чаще всего рассматривается поле тяготения, связанное с землёй, в нём м/с. Для других объектов величина различается.
Примеры решения задач по теме «Потенциальная энергия»
ПРИМЕР 1| Задание | Тело массой 12 кг находится на высоте 5 км над землёй. Найти его потенциальную энергию. |
| Решение | Подставим исходные данные в формулу. Не забываем, что км = м.
Дж |
| Ответ | Потенциальная энергия тела относительно земли равна Дж. |
| Задание | Астероид массой тонн вращается вокруг Солнца на расстоянии м. Известно, что м/с. Найти потенциальную энергию астероида относительно Солнца. |
| Решение | Помня, что т = кг подставим исходные данные в формулу:
Дж |
| Ответ | Потенциальная энергия астероида приблизительно равна Дж. |
Все формулы по физике
Формула момента силы
Формула мощности
Формула силы тока
Формула массы тела
Формула давления
Формула силы выталкивания
ru.solverbook.com
Работа, энергия, мощность – ДИНАМИКА – МЕХАНИКА – ФИЗИКА
ФИЗИКА
МЕХАНИКА
ДИНАМИКА
Работа, энергия, мощность
Работа
А — механическая работа постоянной силы, [Н · м], [Дж];
F — сила, [Н];
S — перемещение, [м];
α — угол между направлениями векторов силы и перемещения
Кинетическая энергия
Ек – кинетическая энергия, [Дж];
m – масса тела, [кг];
υ – скорость тела, [м/с].
Теорема об кинетическую энергию
А — работа, [Дж];
ΔEк — изменение кинетической энергии, [Дж].
Потенциальная энергия тела, поднятого над Землей
Ег — потенциальная энергия, [Дж];
m – масса тела, [кг];
g — ускорение свободного падения, g = 9,8 м/с2;
h — высота тела над Землей, [м].
Потенциальная энергия упруго деформированного тела
х = 0 — нулевой уровень
х — величина деформации , [м];
k — коэффициент жесткости пружины [Н/м];
li —длина недеформованої пружины (х = 0), [м].
Потенциальная энергия гравитационного взаимодействия
m1.2 — массы материальных точек, [кг];
R — расстояние между точками, [м];
G — гравитационная постоянная,
Закон сохранения механической энергии
Е — полная механическая энергия [Дж];
Ек — кинетическая энергия, [Дж];
Ег — потенциальная энергия, [Дж].
Мощность
N — мощность, [Дж/c], [Вт];
t — время, [с].
КПД
η — коэффициент полезного действия
Ак полезная работа, [Дж];
Аиз — затрачена работа, [Дж].
schooled.ru
Потенциальная энергия | Все формулы
Потенциальная энергия — Чтобы увеличить расстояние тела от центра Земли (поднять тело), над ним следует совершить работу. Эта работа против силы тяжести запасается в виде потенциальной энергии тела.
Для того, чтоб понять что же такое потенциальная энергия тела найдем работу, совершаемую силой тяжести при перемещении тела массой m вертикально вниз с высоты над поверхностью Земли до высоты .
Если разность пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяготения во время движения тела можно считать постоянной и равной mg.
Так как перемещение совпадает по направлению с вектором силы тяжести то получается, что , работа силы тяжести равна
Из последней формулы видно, что работа силы тяжести при переносе материальной точки массой m в поле тяготения Земли равна разности двух значений некоторой величины mgh. Поскольку работа есть мера изменения энергии, то в правой части формулы стоит разность двух значений энергии этого тела. Это значит, что величина mgh представляет собой энергию, обусловленную положением тела в поле тяготения Земли.
Энергию, обусловленную взаимным расположением взаимодействующих между собой тел (или частей одного тела), называют потенциальной и обозначают Wp. Следовательно, для тела, находящегося в поле тяготения Земли,
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях
Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, то есть высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.
При таком выборе нулевого уровня потенциальная энергия тела, находящегося на высоте h над поверхностью Земли, равна произведению массы тела на Модуль ускорения свободного падения и расстояние его от поверхности Земли:
Из всего выше сказанного, можем сделать вывод: потенциальная энергия тела зависит всего от двух величин, а именно: от массы самого тела и высоты, на которую поднято это тело. Траектория движения тела никак не влияет на потенциальную энергию.
Потенциальная энергия упруго деформированного тела. Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Так же есть:
Кинетическая энергия
В формуле мы использовали :
— Потенциальная энергия
— Масса тела
— Ускорение свободного падения
— Высота на которую поднято тело
— Работа силы тяжести
— Сила тяжести
— Перемещение тела
— Жесткость пружины
— Деформация пружины
— Угол между направлением тела и силой тяжести
xn--b1agsdjmeuf9e.xn--p1ai



