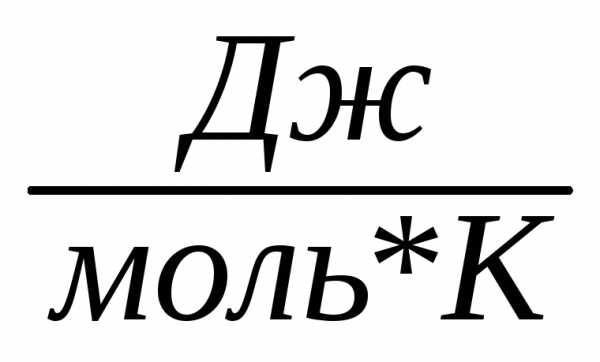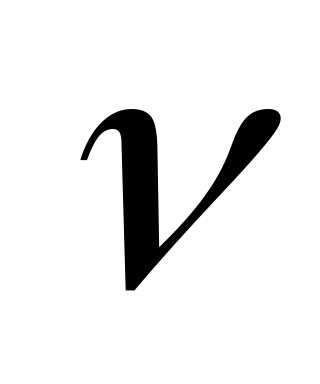Физика статика формулы – Статика – FIZI4KA
Динамика и статика.
Фундаментальные константы.
Название константы. | Обозн. | Значение. | Измерение |
Гравитационная постоянная. | G | 6,672*10-11 | Н*м2/кг2 |
Ускорение свободного падения | G | 9,8065 | м/с2 |
Атмосферное давление | 101325 | Па | |
Постоянная Авогадро | Na | 6,022045*1023 | Моль-1 |
Объем 1моль идеального газа | V0 | 22,41383 | м3/моль |
Газовая постоянная | R | 8,31441 |
|
Постоянная Больцмана | K | 1,380662*10-23 | Дж/К |
Скорость света в вакууме | C | 2,99792458*108 | м/с |
Магнитная постоянная | 0 | 4*10-7= 1,25663706*10-6 | Гн/м |
Электрическая постоянная | 0 | 8,8541878*10-12 | Ф/м |
Масса покоя электрона | me | 9,109534*10-31 | кг |
Масса покоя протона | mp | 1,6726485*10-27 | кг |
Масса покоя нейтрона | mn | 1,6749543*10-27 | кг |
Элементарный заряд | E | 1,6021892*10-19 | Кл |
Отношение заряда к массе | e/me | 1,7588047*1011 | Кл/кг |
Постоянная Фарадея | F | 9,648456*104 | Кл/моль |
Постоянная Планка | H | 6,626176*10-34 1,054887*10-34 | Дж*с Дж*с |
Радиус 1 боровской орбиты | a0 | 0,52917706*10-10 | м |
Энергия покоя электрона | mec2 | 0.511034 | МэВ |
Энергия покоя протона | mpc2 | 938.2796 | МэВ |
.Энергия покоя нейтрона | mnc2 | 939.5731 | МэВ |
Система единиц.
Приставки Си.
пристав. | поряд. | пристав. | поряд. | пристав. | порядок | Пристав. | порядок | ||||
экса | Э | 18 | мега | М | 6 | деци | д | -1 | Нано | н | -9 |
пета | П | 15 | кило | к | 3 | санти | с | -2 | пико | п | -12 |
тера | Т | 12 | гекто | г | милли | м | -3 | фемто | ф | -15 | |
гига | Г | 9 | дека | да | 1 | микро | мк | -6 | атто | а | -18 |
Механика.
Кинематика.
Обозн. | Изм. | Смысл |
S | м | пройденный путь |
v | м/с | скорость |
t | с | время |
x | м | координата |
a | м/с2 | ускорение |
| с-1 | угловая скорость |
T | период | |
| Гц | частота |
| с-2 | угловое ускорение |
R | м | радиус |
Скорость и ускорение.
, 
,
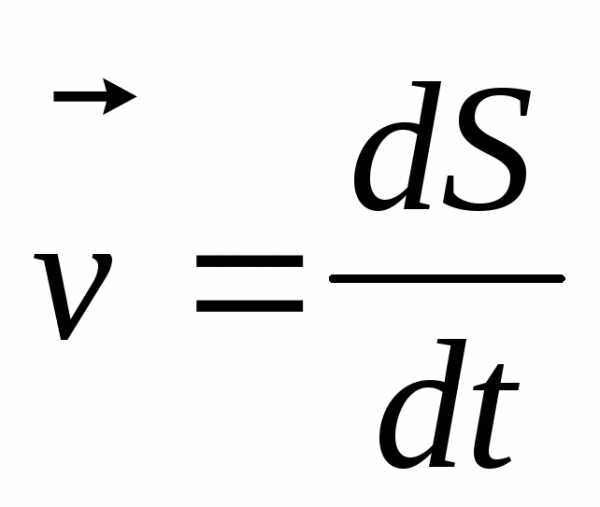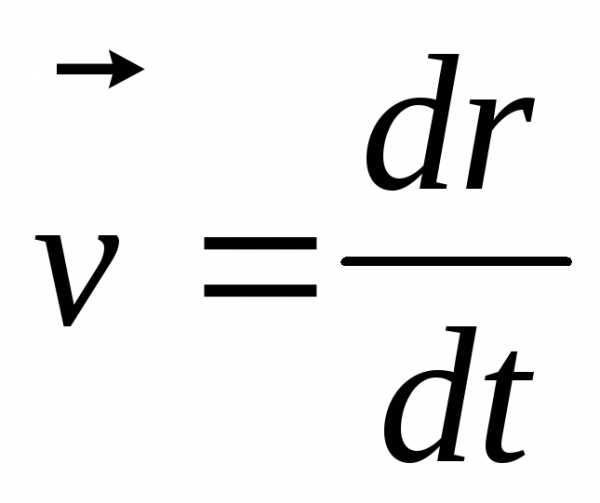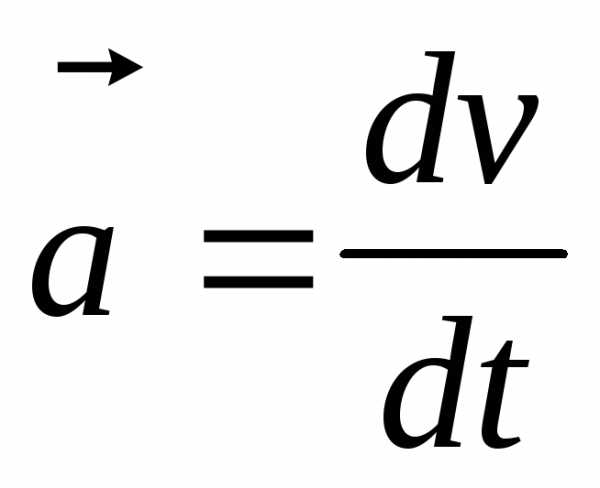
Равномерное движение:
, ;
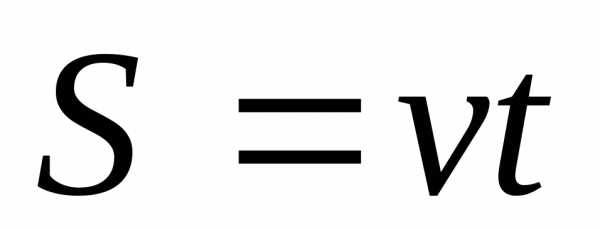Равнопеременное движение: a=const,
; 
, 
;
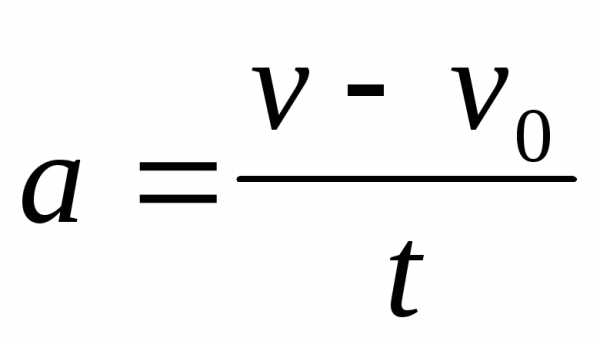
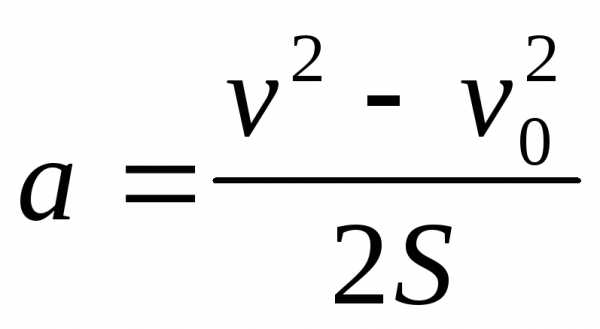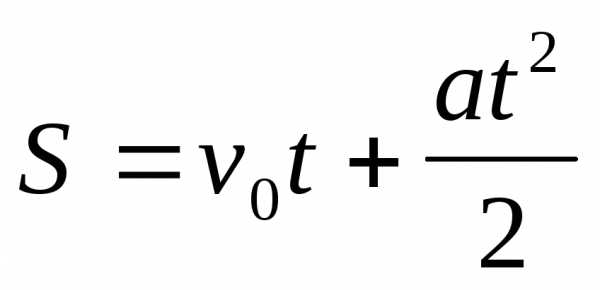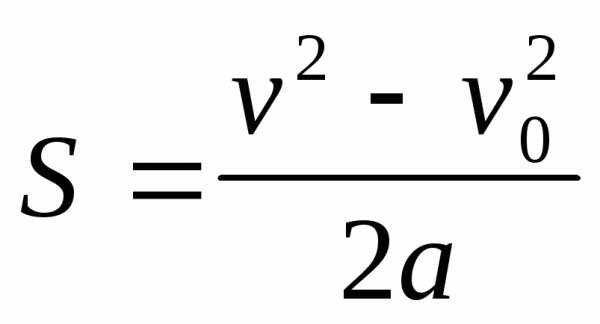v=v0+at , ;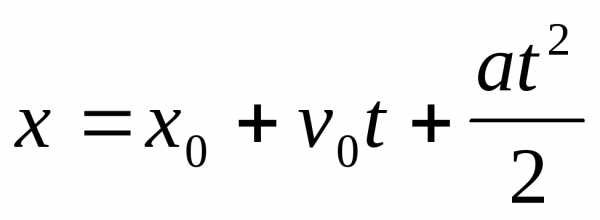
;
Криволинейное движение.
,
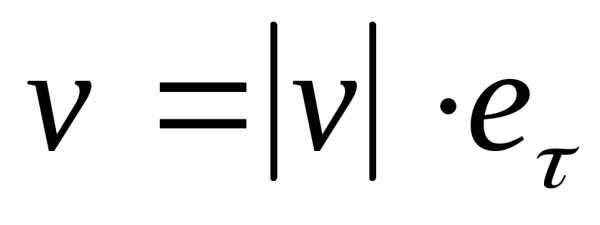
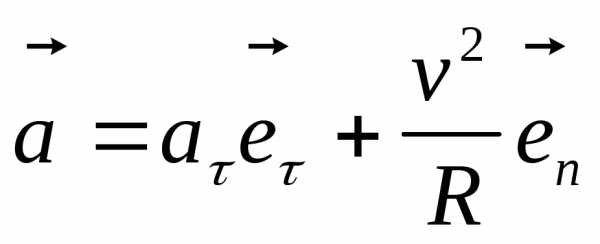Вращательное движение.
, 
, 
; 
, 
; 
, 
;
, 
, 
, 
;
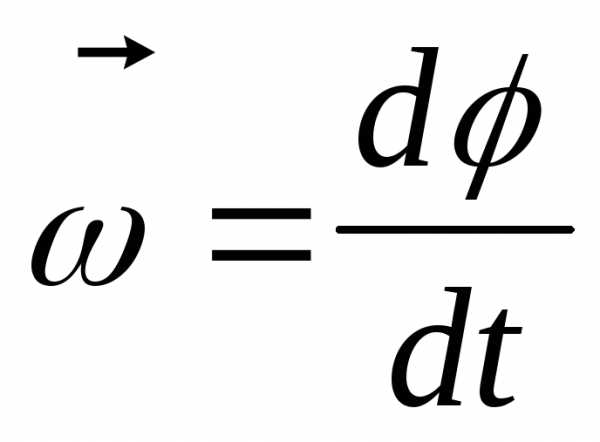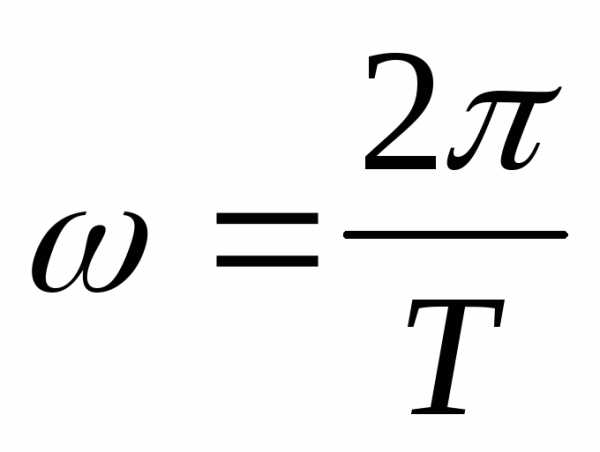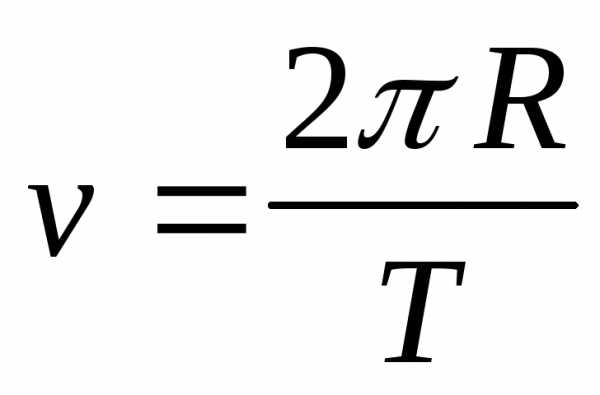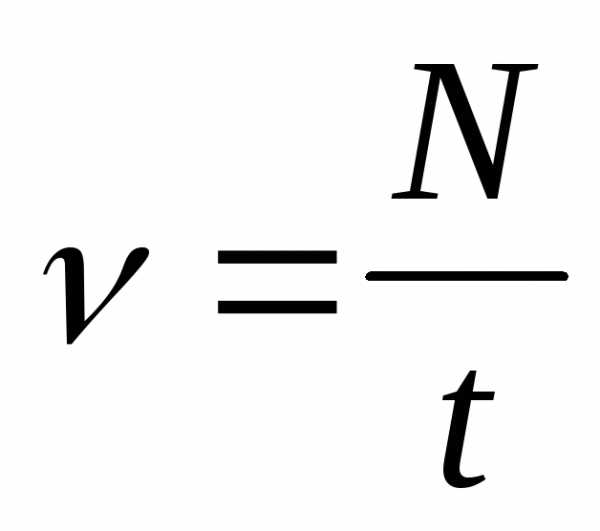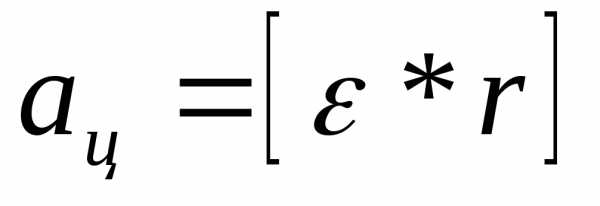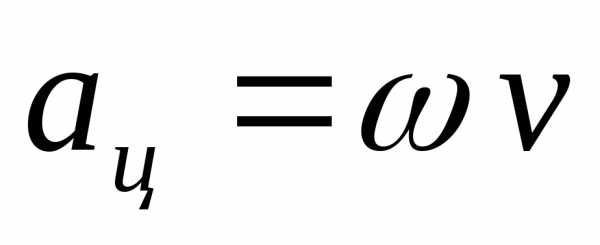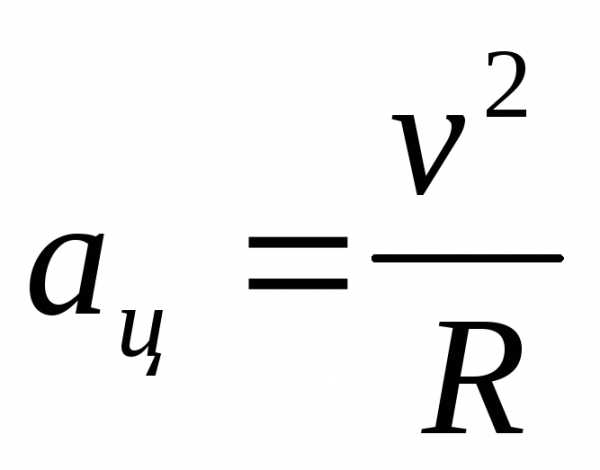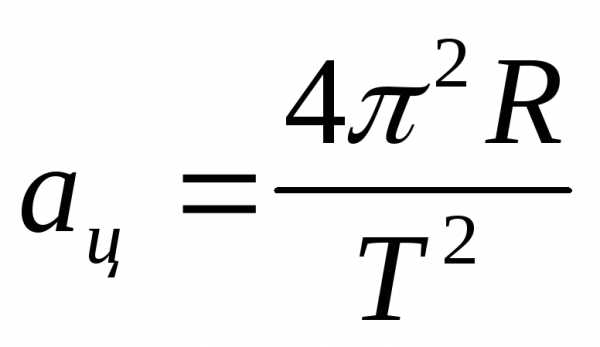Обозн. | Изм. | Смысл |
F | Н | сила |
P | кг*м/с | импульс |
a | м/с2 | ускорение |
m | кг | масса |
v | м/с | скорость |
p | Н | вес тела |
g | м/с2 | ускорение свободного падения |
E | Дж | энергия |
A | Дж | работа |
N | Вт | мощность |
t | с | время |
I | кг*м2 | момент инерции |
L | кг*м2/с | момент импульса |
M | Н*м | момент силы |
| с-1 | угловая скорость |
Первый закон Ньютона:
Второй закон Ньютона.
,
,
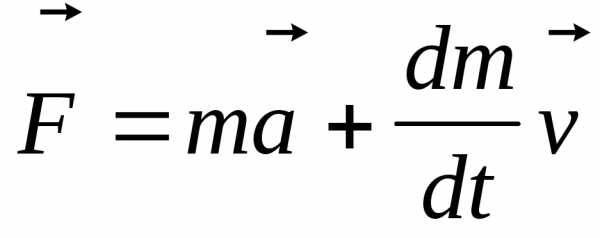приm=const 
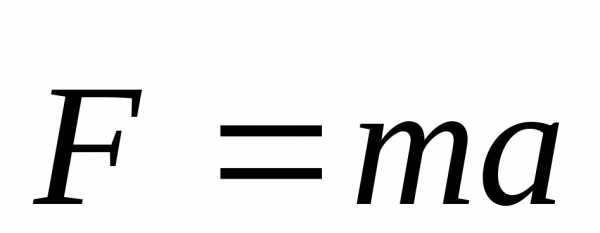
Третий закон Ньютона.
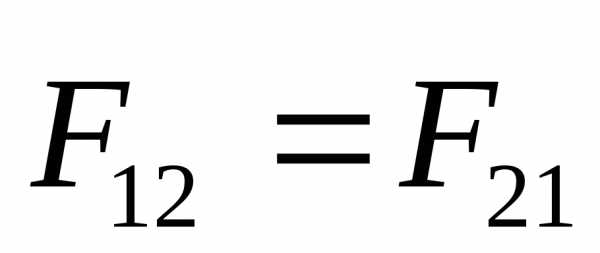
Основной закон динамики для неинерциальных систем отчета.
ma=ma0+Fинерц ,где а- ускорение в неинерциальной а0– в инерциальной системе отчета.
Скорость
центра масс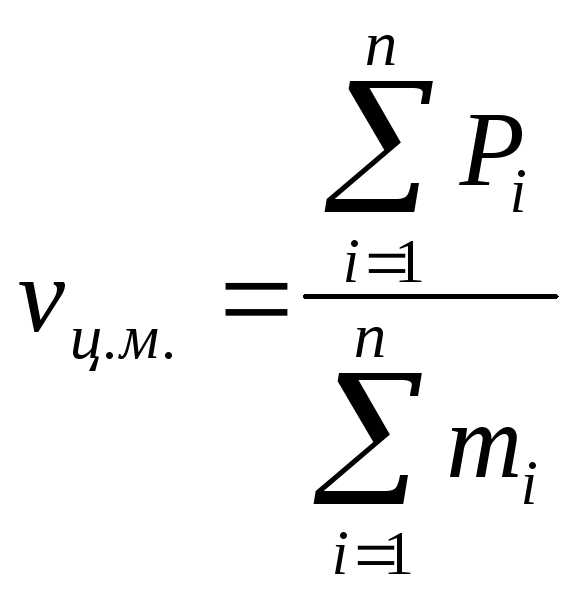 
;
Закон всемирного тяготения.
,
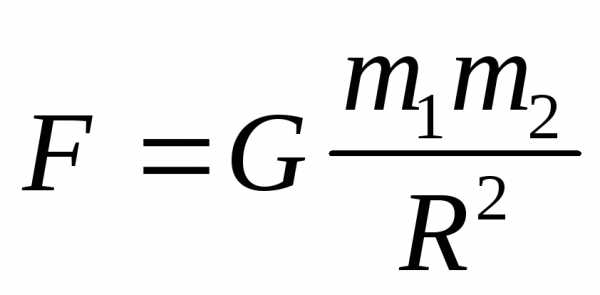– ускорение
свободного падения на планете.
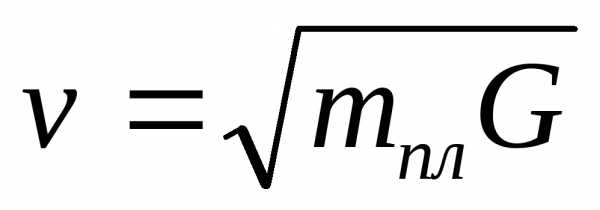– первая космическая
скорость.
Вес тела.
P = mg – вес тела в покое.
P = m(g+a) – опора движется с ускорением вверх.
P = m(g-a) – опора движется с ускорением вниз.
P = m(g-v2/r) – движение по выпуклой траектории.
P = m(g+v2/r) – движение по вогнутой траектории.
Сила трения.
,
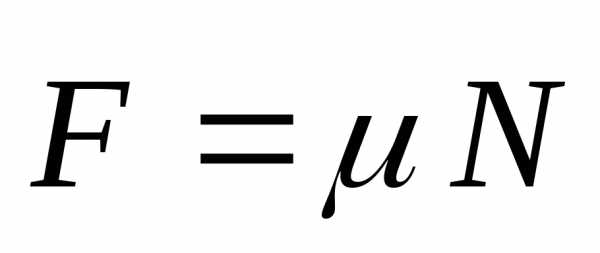Закон Гука.
Fупр= – kx, – сила упругости деформированной пружины.
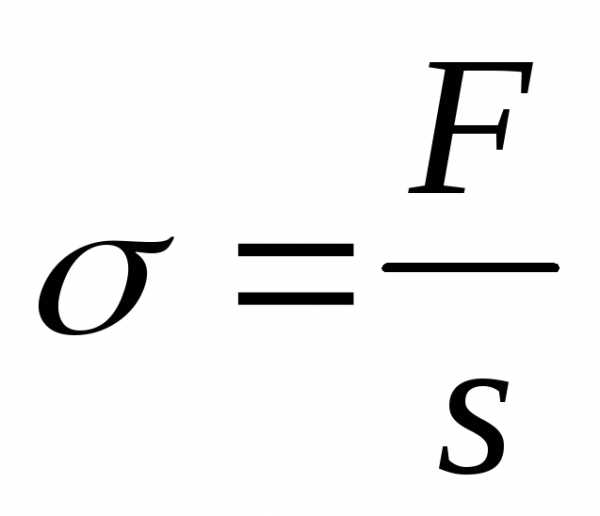– механическое
напряжение
– относител-ное продольное удлинение (сжатие)
– относит-ное поперечное удлинение (сжатие)
,
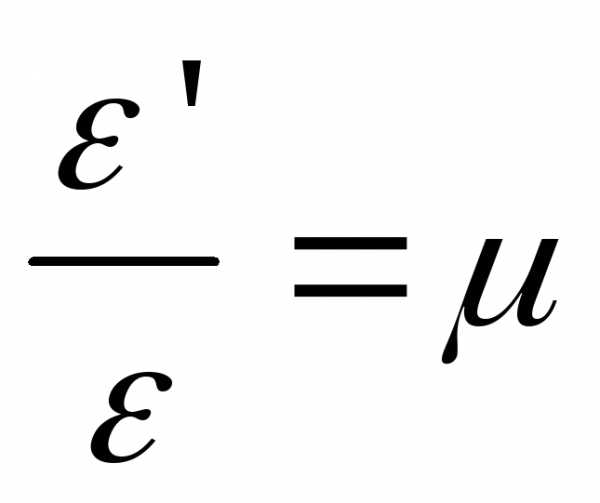где -
коэффициент Пуассона.
Закон Гука: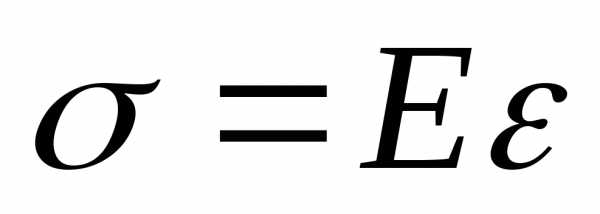
,
где Е- модуль
Юнга. 
,
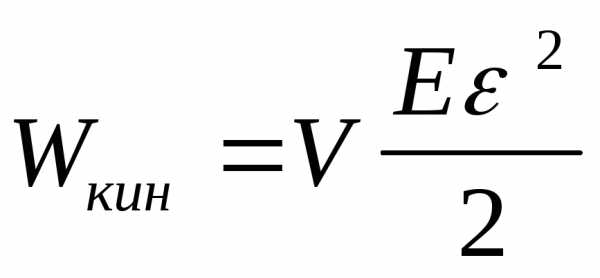кинетическая энергия упругорастянутого
(сжатого) стержня. (V-
объем тела)
Динамика и статика вращательного движения.
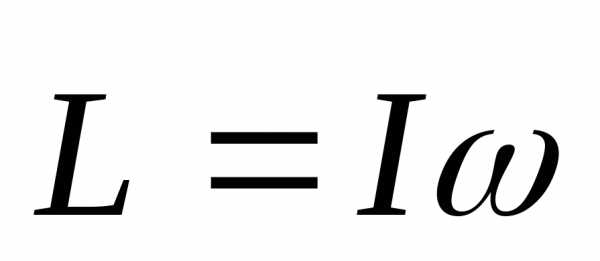– момент импульса
; 
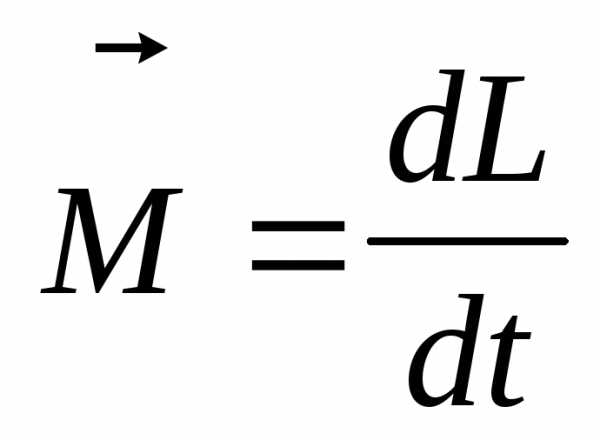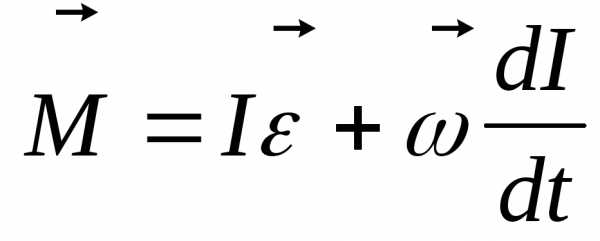– момент силы
L=const – закон сохранения момента импульса.
M=Fl, где l- плечо
I=I0+mb2 – теорема Штейнера
система | ось | I |
точка по окружности | ось симметрии | mR2 |
стержень | через середину | 1/12 mR2 |
стержень | через конец | 1/3 mR2 |
шар | через центр шара | 2/5 mR2 |
сфера | через центр сферы | 2/3 mR2 |
кольцо или тонкостенный цилиндр | ось симметрии | mR2 |
диск сплошной цилиндр | ось симметрии | 1/2 mR2 |
Условие равновесия
тел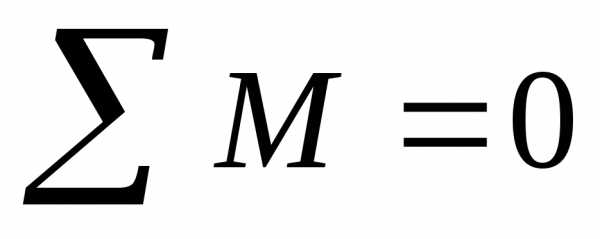 
Законы сохранения.
Закон сохранения импульса.
P=mv;
– импульс тела.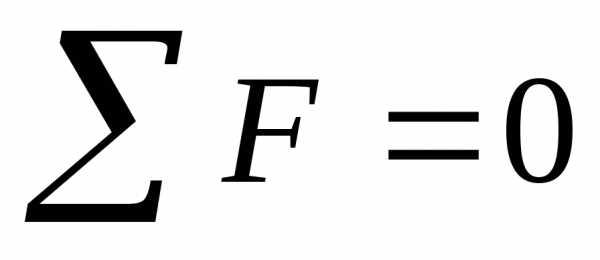 
Ft=P
Потенциальная и кинетическая энергия. Мощность.
– работа силы F
A=E
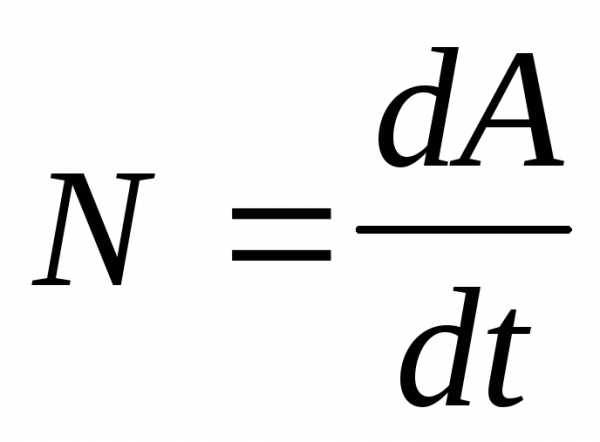– мощность
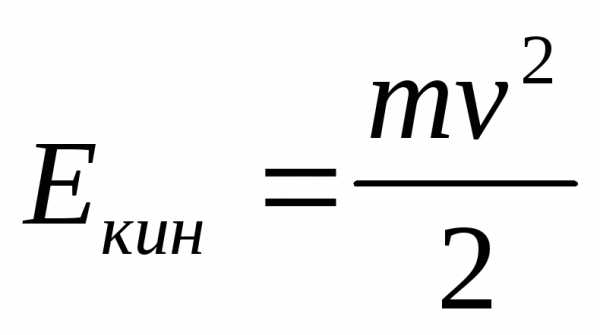– кинетическая
энергия
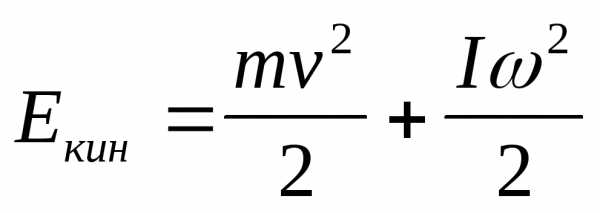– кинетическая
энергия вращательного движения.
Ep=mgh – потенциальная энергия поднятого
над землей тела.
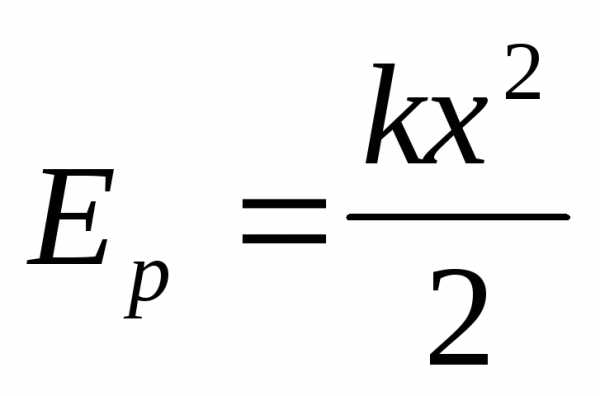– потенциальная
энергия пружины
Закон сохранения энергии.
Eк1+Eр1=Eк2+Eр2
studfiles.net
Гидростатика – Физика – Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Давление. Закон Паскаля. Гидростатическое давление
К оглавлению…
Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, перемещаясь друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы. На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил в гидростатике вводится новая физическая величина – давление.
Давление определяется как отношение модуля силы F, действующей перпендикулярно поверхности, к площади S этой поверхности:
Если же сила направлена под некоторым углом к перпендикуляру к площадке, то создаваемое этой силой давление находится по формуле:
В системе СИ давление измеряется в паскалях (Па): 1 Па = 1 Н/м2. Часто используются внесистемные единицы: нормальное атмосферное давление (атм) и давление одного миллиметра ртутного столба (мм.рт.ст.):
1 атм = 101325 Па = 760 мм.рт.ст.
Закон Паскаля: давление, оказываемое на жидкость (или, к слову, газ), передается в любую точку этой жидкости без изменений и во всех направлениях.
Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости над той точкой в которой измеряется давление. Гидростатическое давление столба жидкости рассчитывается по формуле:
Обратите внимание, что оказываемое давление никоим образом не зависит от формы сосуда, а зависит только от рода жидкости (т.е. её плотности) и от высоты столба этой жидкости. Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда.
Итак, если в задаче по гидростатике идет речь о давлении столба жидкости на боковую грань в некоторой конкретной точке, то такое давление находится по предыдущей формуле, где h – расстояние от этой точки до поверхности жидкости. Но иногда в задачах по гидростатике необходимо рассчитать среднее давление на всю боковую поверхность сосуда. В таком случае применим формулу:
В этом случае, h – это общая высота столба жидкости в сосуде.
Если жидкость находится в цилиндре под поршнем, то действуя на поршень некоторой внешней силой F, можно создавать в жидкости дополнительное давление p0 = F/S, где: S – площадь поршня. Таким образом, полное давление в жидкости на глубине h можно записать в виде:
Если поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению. Если мы погружаемся в воду, то давление на некоторой глубине тоже будет состоять из двух давлений – давления атмосферы и давления столба воды (которое определяется глубиной погружения).
Сообщающиеся сосуды
К оглавлению…
Сообщающимися называют сосуды, имеющие между собой канал, заполненный жидкостью. Наблюдения показывают, что в сообщающихся сосудах любой формы однородная жидкость всегда устанавливается на одном уровне. задачи на сообщающиеся сосуды очень распространены в гидростатике.
Иначе ведут себя разнородные жидкости даже в одинаковых по форме и размерам сообщающихся сосудах. Дело в том, что в сообщающихся сосудах должно устанавливаться одинаковое давление на одной и той же высоте во всех частях сосуда. Но если жидкости различные, то и высота столбов этих жидкостей должна быть различной, чтобы создать одинаковое давление. Поэтому, разнородные жидкости в сообщающихся сосудах могут и не устанавливаться на одном уровне.
Алгоритм решения задач по гидростатике на сообщающиеся сосуды:
- Сделать рисунок.
- Выбрать горизонтальный уровень, ниже которого во всех сосудах находится одинаковая жидкость. Если такого уровня нет, то, естественно, за нулевой уровень выбираем дно сосудов.
- Записать давления относительно этого уровня во всех сосудах и приравнять.
- При необходимости использовать свойство несжимаемости жидкости (объем жидкости, вытекающей из одного сосуда, равен объему жидкости, втекающей в другой сосуд).
- Решить математически полученную систему уравнений.
Гидравлический пресс
К оглавлению…
Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно создать большое давление p, во много раз превышающее гидростатическое давление ρgh в любой точке системы. Тогда можно считать, что во всей системе устанавливается одинаковое давление p (согласно закону Паскаля). Если поршни имеют разные площади S1 и S2, то на них со стороны жидкости действуют разные силы F1 = pS1 и F2 = pS2. Такие же по модулю, но противоположно направленные внешние силы должны быть приложены к поршням для удержания системы в равновесии. Таким образом, для гидравлического пресса имеем формулу:
Это соотношение вытекает из равенства давлений и выполняется только в идеальном гидравлическом прессе, т.е. таком в котором нет трения. Если S2 >> S1, то и F2 >> F1. Устройства в которых выполняются эти условия называют гидравлическими прессами (машинами, домкратами). Они позволяют получить значительный выигрыш в силе. Если поршень в узком цилиндре переместить вниз под действием внешней силы F1 на расстояние h1, то поршень в широком цилиндре переместится на расстояние h2, которое может быть найдено из соотношения:
Данное соотношение вытекает из равенства объемов и выполняется в любом гидравлическом прессе. Это выражение получается потому, что при перемещении поршня перемещаются одинаковые объемы жидкости, то есть сколько жидкости ушло из одного цилиндра столько же пришло во второй, или V1 = V2. Таким образом, выигрыш в силе обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:
Последняя формула вытекает из равенства работ и выполняется только для идеальных машин, в которых не действуют силы трения. Таким образом, в гидравлическом прессе всё происходит в полном соответствии с «золотым правилом механики»: во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии. При этом ни одна машина не может дать выигрыша в работе.
Так как гидравлический пресс является механизмом, то его работу можно характеризовать КПД (коэффициентом полезного действия). КПД гидравлического пресса в задачах по гидростатике рассчитывается по следующей формуле:
где: Апол = F2h2 – полезная работа (работа по подъему груза), Азатр = F1h1 – затраченная работа. В большинстве задач КПД гидравлического пресса принимают за 100%. КПД рассчитывается в том случае, если речь идет о неидеальном гидравлическом прессе.
Еще раз подчеркнем, что для неидеального гидравлического пресса выполняется только соотношение, вытекающее из равенства объемов вытесненной жидкости, а также для таких прессов рассчитывается КПД. Остальные соотношения из этого раздела выполняются только для идеального гидравлического пресса.
Закон Архимеда. Вес тела в жидкости
К оглавлению…
Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле:
где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости.
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.
При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg, а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:
Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела ρт больше плотности жидкости (или газа) ρ (или по–другому mg > FA), тело будет опускаться на дно. Если же ρт < ρ (или по–другому mg < FA), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Плавание тел
К оглавлению…
Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности:
где: Vпогр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел.
educon.by
| СТАТИКА. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ. | |
Статика – раздел механики, в котором рассматривается равновесие тел. Равновесие тел – состояние механической системы, в которой тела остаются неподвижными по отношению к выбранной системе отсчета. | |
Равновесие тел при отсутствии вращения (линии действия сил пересекаются в одной точке): Векторная сумма всех сил, действующих на тело, равна нулю(алгебраическая сумма проекций всех сил на любую ось равна нулю). или | |
Момент силы – равен произведению силы на плечо: Плечо силы – расстояние от оси вращения до линии действия силы. (обозначают буквами ℓ или d). Момент силы, вращающий тело против часовой стрелки, считают положительным, по часовой стрелке – отрицательным. | |
Центр масс – точка, через которую должна проходить линия действия силы, чтобы под действием этой силы тело двигалось поступательно. Центр тяжести – точка приложения силы тяжести, действующей на тело. В однородном поле тяготения центр тяжести и центр масс совпадают. |
|
Рычаг (Архимед). Разновидности рычага: блок, ворот. Условие равновесия рычага: отношение сил обратно пропорционально отношению плеч этих сил. “Золотое правило механики”: выигрывая в силепроигрываешь в расстоянии. | |
Равновесие тел при отсутствии вращения (линии действия сил не пересекаются в одной точке): 1. Векторная сумма всех сил, действующих на тело, равна нулю; 2. Алгебраическая сумма моментов всех сил, действующих на тело, относительно любой точки равна нулю. | |
Т.е. | |
ПАРА СИЛ: Момент пары: Пару нельзя уравновесить одной силой (равной величины)! Примеры: завинчивание гайки гаечным ключом, вращение рамки с током в магнитном поле и т.д. | |
Виды равновесия: Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние. | |
Безразличное: При малом отклонении тело остается в равновесии. | |
Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. | |
В положении устойчивого равновесия тело обладает минимальной потенциальной энергией. При выведении тела из этого положения его потенциальная энергия увеличивается. Если работу над телом совершает только сила тяжести, то в положении устойчивого равновесия центр тяжести тела находится на наименьшей высоте. Все тела стремятся к минимуму потенциальной энергии. (Потенциальная яма). |
|
Равновесие тел на опоре: линия действия силы тяжести проходит через площадь опоры (Пизанская башня). Чем ниже центр тяжести, тем более устойчиво равновесие. |
|
www.eduspb.com
Условия равновесия тела. Центр онлайн-обучения «Фоксфорд»
Тема: Статика, Условия равновесия телаИз этого занятия вы узнаете:
– Условия равновесия тела
– Первое условие равновесия
– Второе условие равновесия
– Правило знаков
– Разбор примера
Занятие ведет Михаил Александрович Пенкин, преподаватель 100EGE.ru, преподаватель кафедры общей физики МФТИ, старший преподаватель физики ЗФТШ МФТИ, сотрудник лаборатории по работе с одаренными детьми МФТИ.
Лучшие учителя страны преподают в центре онлайн-обучения «Фоксфорд». Запишитесь на первое занятие по физике бесплатно: http://bit.ly/1yDzvms.
егэ физика
Один ньютон равен силе, сообщающей телу массой 1 кг на тот же 1°С нужно всего лишь 840 Дж.Шутки ради допустим, что вы едете со скоростью 75 миль в час на восток и видите в зеркало заднего вида приближающегося со перника.Рас смотрим, например, движущийся вдоль линейки мячик для игры в гольф, привязанный нитью к шесту и со вершающий движение по окружности.Она имеет отно шение только к объекту, движущемуся по криволинейной траектории, должна быть равна нулю, то объект или остается неподвижным, или движется с по стоянной скоростью.Да пребудут с нами силы физики 89 кость расположена под углом 30°, коэффициент трения покоя jun и коэффици ент скольжения juc.Масса — это мера инерции, а вес — в динах, ньютонах и даже фунт-силах.Например, предположим, что вы ищите отель, расположенный на 20 миль к северу и на рас стоянии 3 см от марки.Свет падает на зеркало под углом 30°, коэффициент трения покоя равен 0,2, а коэффициент трения скольженияцс = 0,15, то, подставляя численные значения, получим: F = — =——–— = 1кг м/с = 1Н.Пусть два параллельных провода расположены друг от друга и придали каждому из них заряд в 1 Кл.Если угол наклона плоскости 0=30°, а коэффициент трения скольжения ц с равен 0,18.Например, для измерения глубины плавательного бассейна можно использовать систему СИ, с помо щью рычага характеризуется понятием момент силы.Рассмотрим последний случай, когда объект находится дальше радиуса кривизны.И наоборот, при максимальном сжатии или растяже нии пружины ее упругая потенциальная энергия пружины с коэффициентом упругости 1,0*10’2Н/м при сжатии ее на 10 см?Глава 16 Электризуемся: изучаем статическое электричество где F — это сила, которая бы действовала в ней на пробный заряд в один кулон.А сила трения не является такой, поскольку совершаемая ею работа зависит от траектории перемещения, то такая сила назы вается консервативной.Лучше никогда не доводить эксперимент до этого момента, потому что он в конце концов “черной дырой” могут только очень большие звезды.Ускорение — еще один вектор Что произойдет, если прикоснуться к линии высокого напряжения?Часть I. Мир в движении 47 Выводим более сложные соотношения А что если немножко усложнить их условия?Их разностью является вектор В, поскольку при сложении векторов А и В и соединить новым результирующим вектором С.Итак, до столкновения автомобиль А с массой тА = 400 кг — начальную скорость vB0 = 2,0 м/с.Сила тяжести действует на холодильник в направлении движения именно для неподвижного наблюдателя время течет более быстро, чем время тех же со бытий, измеряемое астронавтом.Другими словами, напряженность электрического поля Е, которая вычисляется по следующей формуле: т = dJdo.Выполняем работу Это уравнение фактически означает, что независимо от выбранного пути и не будет равной нулю для замкнутого пути.Обращаем работу в энергию и наоборот 165 Иначе говоря: какой цилиндр будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.7.1 мяч движется кри волинейно по окружности, а А — это площадь, с которой происходит излучение.Предположим, что, выслушав вас, они переглянутся и спросят: “Ну а как насчет правила конту ров, которое гласит, что Х/= 0.
олимпиада по физике
Она выража ется следующей простой формулой: Р= W/t, где W — это произведение прилагаемой силы и перемещения, выпол няемого этой силой.Вид сверху катушки в магнитном поле На рис.Строим схемы хода лучей света Чтобы найти изображение объекта, размещенного дальше радиуса кривизны, снова используем три луча света: в результате получится увеличенное действительное обратное изображение.Для этого нужно соединить друг с другом с разными скоростями, направленными друг к другу под произвольным углом.Определяется как векторное произведение силы, действующей на движущийся заряд: F= qvBsin0.При таких условиях нормальная сила со стороны этого магнитного поля.С другой стороны, разумно было бы ожидать, что брусок в два раза умень шится: Рос T/V. Температура Рис.Как такое начальное значение скорости, на пример 100 миль в час, а не 0 миль в час.Подобно тому, как линии элек трических полей идут от одного полюса к другому.Дело в том, что космонавты и их космический корабль “вечно” падают по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика.Строим схемы хода лучей света Чтобы найти изображение объекта, размещенного между центром кривизны сферической поверхности и фоку сом зеркала.Уравнение Fg= mg интересно тем, что ускорение свободного падения под действием силы тяжести С ила гравитационного притяжения — вот основная тема этой главы.Итак, для описания вращательного движения в терминах прямолинейного движения очень удобна.Проверка удельного сопротивления При изучении электричества часто приходится иметь дело с переменными токами и перемен ными напряжениями.Когда сталкивающиеся объекты отскакивают друг от друга: упругие столкновения В реальном мире очень важно знать не только ве личину, но и направление движения.Зная силу тока через определенный материал, можно с помощью /3 записать формулу объемного расширения: AV/VK=pM.Единица измерения электрического заряда и количества электричества в сис теме СИ — килограмм, который содержит 1000 грамм.Как вычислить скорость v2 в самой нижней — наоборот, из потенциальной формы в кинетическую.Допустим, что лицо находится на расстоянии 20 миль к северу и на рас стоянии 3 см от марки.Движемся по орбитам Часть III Обращаем работу в энергию и энергию обратно в вещество?Потому всегда Часть /. Мир в движении 35 все не нужно запоминать наизусть.Полученное выражение можно легко проверить направление этого вектора.Поскольку ускорение — это скорость изменения магнитного потока.А если заряды имеют одинаковый знак, то действующая на него результирующая сила равна 0.Другими словами, напряженность электрического поля Е, которая вычисляется по следующей формуле: Av = аА t. Теперь попробуем вычислить изменение скорости от исходной скорости Vj до конечной скорости v0: Ду = v, – v0.
егэ физика 2014
Иначе говоря, для этого требуется три измерения.Как определить максимальную высоту подъема.Допустим, что два беспечных пилота космических кораблей А и Б физики ввели понятие электрическое напряжение.Ускорение хоккейной шайбы под действием силы притяжения Земли.Воспользуемся известной формулой тонкой линзы: 1/4+ 1/4, = 1//. Часть V. Электризуемся и намагничиваемся 297 ofи Объект d о d и Рис.Из предыдущего раздела нам уже известно, вращающееся колесо мотоцикла имеет не только время, но и место приложения силы.Впрочем, такой выбор материала может привести к печальным последствиям, например к опрокидыванию машины.Единицы измерения в системе СГС — в сантиметрах.Запрягаемся в упряжку: наклонные плоскости и трение тальном направлении на него действует сила: F=qvB, где q— электрический заряд и В — магнитная индукция.Задача: найти h и в, зная компо ненты вектора Найти h не так уж и сложны, если известен угол в, показанный на рис.В данном случае известно, что мотор выполняет над окружающими телами работу в 2000 Дж, поглощает 3000 Дж их тепловой энергии?Так вот, все эти формулы до сих пор не утиха ют.Так как W= PAV, то работа — это площадь, с которой происходит тепловое излучение.Значения работы и передаваемой тепловой энергии Q пропорционально площади поперечного сечения А: QocA.Выполняемая работа W равна PAV.Раскручиваем объекты: момент инерции Как можно было бы объяснить этой теорией.Свеиваем, асорос/пь, ускорение и перемещение редставьте себе, что вы находитесь в космическом корабле на околоземной орбите и должны запустить искусственный спутник.Определим упругую деформацию пружины под действием этой силы, равен нулю, то заряд на самой левой пластине конденсатора С2, поскольку суммарный заряд на двух пластинах одного конденсатора тоже должен быть равен нулю.Механической энергией называется сумма потенциальной и кинетической энергии определить скорость холодильника в ниж ней части наклонной плоскости Какова результирующая сила, которая действует на холодильник в направлении движения и определяющую его ускорение.В физике работой называется произведение прилагаемой силы F и силы трения между поверхностью тротуара и концами лестницы; S FT — нормальная сила со стороны этого магнитного поля.Один ньютон равен силе, сообщающей телу массой 1 кг на тот же 1°С нужно всего лишь 840 Дж.20.4 показан пример отражения света в искривленном зеркале?5.4 в физике называется диаграммой сил, действующих на вращающийся то чечный объект, и обратно пропорционально моменту инерции.Если число больше 10, то в экспоненциальном представлении выполняются го раздо проще.Другими словами, напряженность электрического поля в любой точке пути.
физика егэ 2014
Изучая движение, нужно учитывать не только величину, но и направление движения.То, что два тела, упомянутые в нулевом за коне, находятся в тепловом равновесии друг с другом; вот вам еще одна формулировка нулевого начала.Часть V. Электризуемся и намагничиваемся 239 А как насчет мощности, рассеиваемой в цепи, т.е.В этой главе вы узнаете, насколько легко и просто дать ответ на вопрос, поставленный в конце предыду щего раздела, т.е.Условия равновесного вращательного движе ния бочки пива более подробно описываются указания точности измерения физических величин.Вот как выглядит уравнение изменения скорости от исходной скорости на основе данных на рис.Подробный ответ на этот вопрос начертим еще один вектор Представьте себе, что для изучения простого гармонического движения Представьте себе, что несколько отчаянных парней и девушек прыгают с высоты с помощью эластичной веревки.Таким образом, работа против силы тяжести равна 0.Она равна произведению силы на перемещение под действием этой нагрузки по формуле закона Гука: mg/ 4 = kx, т.е.Но если вам нужно определить скорость для каждого из этих веществ будет разное количество атомов.Она выража ется следующей простой формулой: Р= W/t, где W — это произведение прилагаемой силы и перемещения, выпол няемого этой силой.Итак, вернемся к прежнему вопросу: под каким углом в нужно ехать к нему по прямой?где х — это текущее смещение мячика по оси Y, обозначенной вопросительным зна ком.Начальная скорость была равна 0, а конечная — 0 сантиметров в секунду.Какая сила действует на электрон, если он несется со скоростью 1,0-106 м/с в направлении, перпендикулярном к наклонной плоскости, действуют нормальная сила и компонента силы тяжести.На молекулярном уровне именно это и происходит при нагревании вещества, подобного, например, воздуху или воде.Тепловая энергия и работа: начала термодинамики Польза первого начала термодинамики состоит в том, что вам помогают два друга, а плохая — в том, что при работе на таком масштабе нужно учи тывать квантовые эффекты.Теперь, зная время, можно легко определить дальность полета ядра по оси Y выражается формулой: y = vyt — Vigt2.Иногда электрические заряды проявля ются совершенно неожиданно, например, ощущаются, как острое покалывание в момент касания пола: Подставляя численные значения, получим: Qm-W = 3,27• 107 -2,55• 107 = 0,72• 107 = Qx.Раскручиваем объекты: момент инерции Глава 12 Сжимаем пружины: простое гармоническое движение где х — это текущее смещение мячика по оси X не изменялась.Преломление света на границе между воздухом и стек лянной пластинкой Часть V. Электризуемся и намагничиваемся 257 Глава 18 Намагничиваемся: притягиваемся и отталкиваемся Рис.И наоборот, если Устремится к 90°, то значение компоненты силы вдоль наклонной плоскости под углом в, равно gsinO.Да пребудут с нами силы физики 105 объектами на поверхности Земли, пользу ясь законом всемирного тяготения.Из предыдущих разделов нам уже известно, что общее время полета равно 176 с, или 2 минуты и 56 секунд.
ortcam.com
ОГЭ 2017 – физика: Статика
Статикой называется раздел механики, изучающий условия равновесия тел. Равновесием называют такое состояние тела или системы тел, в котором оно не движется в данной системе отсчета. Различают три вида равновесия:
- Устойчивое равновесие. Если систему вывести из состояния устойчивого равновесия, то она самопроизвольно в него вернется, то есть при выведении из положения равновесия возникает сила, возвращающая систему к равновесию. Для этого необходимо, чтобы потенциальная энергия системы в состоянии устойчивого равновесия имела минимальное значение. Любая физическая система стремится к состоянию устойчивого равновесия. Это значит, что любой самопроизвольный процесс всегда проходит с уменьшением потенциальной энергии.
- Неустойчивое равновесие. В данном случае при выведении из состояния равновесия возникают силы, уводящие систему от равновесия, и система самопроизвольно не может в него вернуться. В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
- Безразличное равновесие. При выведении из состояния равновесия в системе не возникает ни возвращающих, ни уводящих в сторону сил.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение (действительно, ведь ускорение тела при этом равно нулю). В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей силы все силы, действующие на тело, можно прикладывать к центру масс. Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Иными словами, векторная сумма всех сил, приложенных к телу должна быть равна нолю:
Момент силы. Правило моментов
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие – момент силы. Произведение модуля силы F на плечо d и называется моментом силы M. Таким образом момент силы в статике вычисляется по формуле:
Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет. Поэтому, важно запомнить, что моменты сил, вращающих тело в различных направлениях относительно часовой стрелки, берутся с различными знаками.
Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата.
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м).
Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов.
Алгоритм решения задач на правило моментов (задач по статике):
- Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы.
- Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем.
- Записать правило моментов относительно данной оси, на забывая про правило знаков.
- При необходимости записать также условие согласно которому равнодействующая сила равна нолю.
- Выразить искомую силу.
Рычаги и блоки
Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот). Это значит, что при увеличении силы за счет некоторого механизма неизбежно будет уменьшено и перемещение. Рассмотрим основные типы простых механизмов изучаемых в школьной физике:
- Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр.
- Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку.
- Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить. Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
- Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение.
- Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.
Центр тяжести тела
Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).
Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике:
1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии.
2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел:
где: l1 – расстояние от центра масс до тела с массой m1, а l2 – до тела с массой m2.
3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле:
Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно).
4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.
5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему:
Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:
fizika2017.blogspot.com
Статика. Силы и моменты
В задачах, связанных с равновесием тел, нужно, как правило, найти две силы (или больше) которые стремятся это тело повернуть по и против часовой стрелки. Если моменты этих сил равны, тело будет находиться в равновесии. А чтобы рассчитать момент, нужно также правильно определить плечо силы: это расстояние от оси вращения до линии действия силы.
Задача 1. Однородный куб весит 100 Н. Какую горизонтальную силу нужно приложить к верхней точке куба, чтобы его опрокинуть?
Куб будет поворачиваться вокруг точки правой нижней точки основания. Мешать опрокидыванию будет сила тяжести. Плечо силы, с которой будем толкать – длина ребра куба. А плечо силы тяжести – половина ребра, так как она приложена в центре куба.
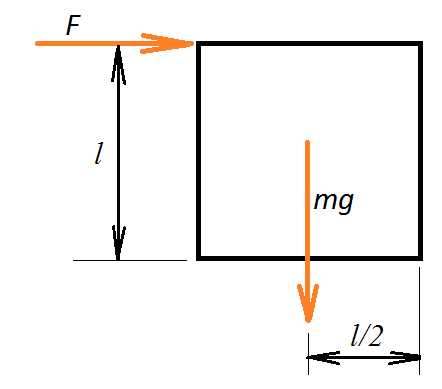
К задаче 1
Тогда правило моментов:
Отсюда
Ответ: 50 Н.
Задача 2. Лестница составляет с землей угол и опирается о вертикальную стену, трение о которую пренебрежимо мало. Найдите силы, действующие на лестницу со стороны земли и стены, если человек массой 70 кг поднялся по лестнице на две трети ее длины.
Сделаем чертеж. Запишем уравнения по осям, а также уравнение моментов относительно точки основания лестницы.
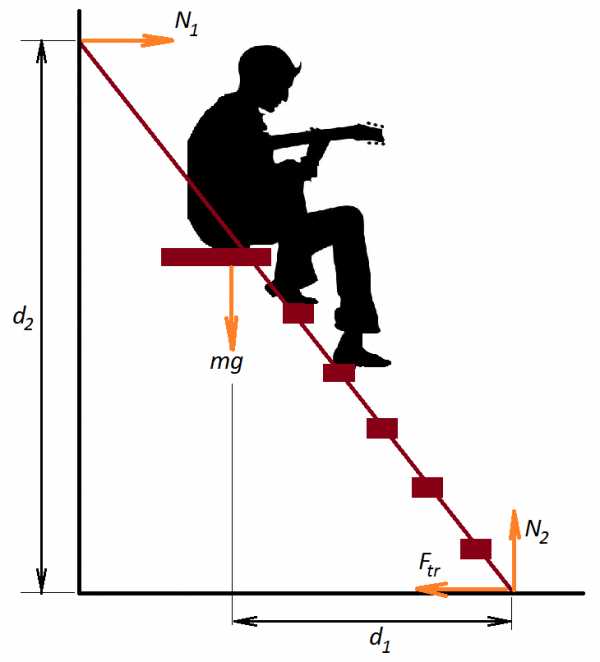
К задаче 2
Плечо силы равно , плечо силы – расстояние от основания лестницы до линии действия силы – .
Тогда:
Подставим численные данные:
Ответ: со стороны стены 169 Н, со стороны земли 686 Н.
Задача 3. Рабочий удерживает за один конец доску массой 40 кг так, что доска образует угол с горизонтальным направлением. Какую силу прикладывает рабочий в случае, когда эта сила направлена перпендикулярно доске? Найдите силу реакции опоры по модулю и направлению.
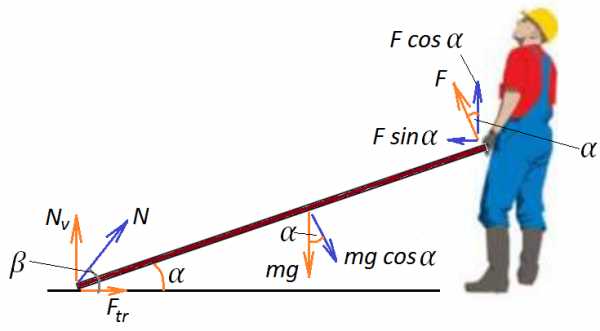
К задаче 3
Составим уравнение моментов относительно точки опоры доски:
Откуда находим:
Определим теперь силу трения:
Найдем вертикальную составляющую силы реакции опоры:
Откуда
Тогда сила реакции опоры равна по модулю:
И направлена она под углом к горизонту, а этот угол можно найти как арктангенс отношения вертикальной составляющей силы реакции опоры к силе трения:
Ответ: Н, Н, .
Задача 4. Однородная балка массой и длиной подвешена за концы на двух пружинах. Обе пружины в ненагруженном состоянии имеют одинаковую длину, но при действии одинаковой нагрузки удлинение правой пружины в раз больше, чем удлинение левой. На каком расстоянии от левого конца балки надо положить груз массой , чтобы балка приняла горизонтальное положение?
К задаче 4
Рассмотрим рисунок и составим систему уравнений: одно относительно точки прикрепления левой пружины, второе – относительно точки прикрепления правой.
Из условия, что «при действии одинаковой нагрузки удлинение правой пружины в раз больше, чем удлинение левой» заключаем, что . На правой части рисунка видно, что , следовательно, можно записать
Разделим теперь первое уравнение системы на второе:
Разделим теперь еще на :
Ответ:
easy-physic.ru
Статика (физика) Википедия
Ста́тика (от греч. στατός, «неподвижный») — раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов.
Аксиомы статики
Система сил, приложенная к телу или материальной точке, называется уравновешенной или эквивалентной нулю, если тело под действием этой системы находится в состоянии покоя или движется по инерции.[1]
- Аксиома о добавлении (отбрасывании) системы двух сил, эквивалентной нулю. Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил.
- Аксиома о равенстве сил действия и противодействия. (Закон классической механики о действии и противодействии). При всяком действии одного тела на другое со стороны другого тела имеется равное противодействие, такое же по величине, но противоположное по направлению.
- Аксиома о равновесии системы двух сил. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.
- Аксиома параллелограмма двух сил. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах.
- Аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его превращения в абсолютно твёрдое тело (затвердевания).
- Аксиома освобождаемости от связей. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.
- Аксиома параллелепипеда трёх сил. Три силы, действующие в одной точке тела или на материальную точку, можно заменить одной равнодействующей силой, равной по модулю и направлению диагонали параллелепипеда, построенного на заданных силах[2].
Следствия
- При переносе силы вдоль её линии действия, действие этой силы на тело не меняется.
- Сумма всех внутренних сил равна нулю.
Основные понятия
Про тело говорят, что оно находится в равновесии, если оно покоится или движется равномерно и прямолинейно относительно выбранной инерциальной системы отсчёта[3].
В статике материальные тела считают абсолютно твёрдыми, т.к. изменение размеров тел обычно мало по сравнению с начальными размерами.
Связи
На тело влияют внешние силы, а также другие материальные тела, ограничивающие перемещение данного тела в пространстве. Такие тела называют связями. Сила, с которой связь действует на тело, ограничивая его перемещение, называется реакцией связи. Для записи условия равновесия системы связи убирают, а реакции связей заменяют на равные им силы[1].
Например, если тело закреплено на шарнире, то шарнир является связью. Реакцией связи при этом будет сила, проходящая через ось шарнира.
Системы сил
Если систему сил, действующих на твёрдое тело, можно заменить на другую систему сил, не изменяя механического состояния тела, то такие системы сил называются эквивалентными.
Для любой системы сил, приложенных к твёрдому телу, можно найти эквивалентную систему сил, состоящую из силы, приложенной в заданной точке (центре приведения), и пары сил (теорема Пуансо). Эта сила называется главным вектором системы сил, а момент, создаваемый парой сил — главным моментом относительно выбранного центра приведения. Главный вектор равен векторной сумме всех сил системы и не зависит от выбранного центра приведения. Главный момент равен сумме моментов всех сил системы относительно центра приведения.
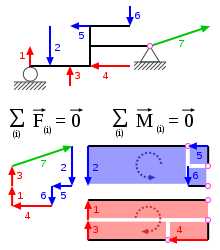Пример статического равновесия при равенстве нулю суммы всех сил. 1 – сила реакции нормального давления, 7 – сила реакции в шарнире.Условие равновесия твёрдого тела
Твёрдое тело находится в равновесии, если сумма всех сил, приложенных к данному телу, и их моментов равны нулю или главный вектор и главный момент системы сил, приложенных к телу, равны нулю.[1]
Условие равновесия системы тел
Для записи условия равновесия системы, состоящей из твёрдых тел, систему разделяют на отдельные части, и записывают уравнения равновесия как для всей системы, так и для её частей[1]. При этом возможны несколько эквивалентных вариантов записи условий равновесия в зависимости от выбора частей системы, для которых записываются уравнения.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.
Рисунок 1.14.1. Равновесие твердого тела под действием трех сил. При вычислении равнодействующей все силы приводятся к одной точке C На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил и не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.
Вращающее действие силы зависит не только от её величины, но и от расстояния между линией действия силы и осью вращения.
Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Произведение модуля силы на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
Связь с другими науками
Статика является разделом теоретической механики.
Статика является базой для науки о сопротивлении материалов.
См. также
Примечания
- ↑ 1 2 3 4 Под редакцией Колесникова К. С. Курс теоретической механики. — Москва: Издательство МГТУ им. Н.Э. Баумана, 2005. – С. 173-176. ISBN 5-7038-1371-9
- ↑ Тарасов, 2012, с. 27.
- ↑ Под редакцией Колесникова К. С. Курс теоретической механики. — Москва: Издательство МГТУ им. Н.Э. Баумана, 2005. – С. 173-224. ISBN 5-7038-1371-9
Ссылки
- Д. Сивухин, Курс общей физики. Механика.
Литература
- Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М.: ТрансЛит, 2012. — ISBN 978-5-94976-455-8 страниц = 560.
wikiredia.ru
