Физика траектория определение – Равномерное движение, траектория, путь и перемещение. Определение, формулы, тесты
- Комментариев к записи Физика траектория определение – Равномерное движение, траектория, путь и перемещение. Определение, формулы, тесты нет
- Советы абитуриенту
- Траектория – это… Что такое Траектория?
- “Перемещение. Траектория. Путь” (9-й класс)
- III. Траектория, путь и перемещение
- Траектория, путь и перемещение
- Kvant. Траектория, путь — PhysBook
- Траектория Википедия
- ТРАЕКТОРИЯ – это… Что такое ТРАЕКТОРИЯ?
Траектория – это… Что такое Траектория?
Рис.1 Траектории трёх объектов (угол запуска — 70°, Distance — расстояние, Height — высота), разное лобовое сопротивлениеТраекто́рия материа́льной то́чки — линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве.[1]. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.
Кроме того, и при наличии движущегося по ней объекта, траектория, изображаемая в наперёд заданной системе пространственных координат, сама по себе не может ничего определённого сказать в отношении причин его движения, пока не проведён анализ конфигурации поля действующих на него сил в той же координатной системе.[2]
Не менее существенно, что форма траектории неотрывно связана и зависит от конкретной системы отсчёта, в которой описывается движение.[3]
Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, звёздное небо считается хорошей моделью инерциальной и неподвижной системы отсчёта
Возможен и случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.
Траектория свободной материальной точки
В соответствии с Первым законом Ньютона, иногда называемым законом инерции должна существовать такая система, в которой свободное тело сохраняет (как вектор) свою скорость. Такая система отсчёта называется инерциальной. Траекторией такого движения является прямая линия, а само движение называется равномерным и прямолинейным.
Описание траектории
Рис.2 Прямолинейное равномерно ускоряющееся движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.Разложение действующей силы на составляющие произведено формально правильно и обсуждается в тексте Принято описывать траекторию материальной точки в наперёд заданной системе координат при помощи радиус-вектора, направление, длина и начальная точка которого зависят от времени. При этом кривая, описываемая концом радиус-вектора в пространстве может быть представлена в виде сопряжённых дуг различной кривизны, находящихся в общем случае в пересекающихся плоскостях. При этом кривизна каждой дуги определяется её радиусом кривизны, направленном к дуге из мгновенного центра поворота, находящегося в той же плоскости, что и сама дуга. При том прямая линия рассматривается как предельный случай кривой, радиус кривизны которой может считаться равным бесконечности. И потому траектория в общем случае может быть представлена как совокупность сопряжённых дуг.Существенно, что форма траектории зависит от системы отсчёта, избранной для описания движения материальной точки. Так прямолинейное равномерно ускоряющееся движение в инерциальной системе в общем случае будет параболическим (до тех пор, пока набираемая скорость тела сравнима по величине со скоростью относительного движения равномерно двигающейся инерциальной системе отсчёта. См. Рисунок 2).
Связь со скоростью и нормальным ускорением
 Рис.3 Суточное движение светил в системе отсчёта, связанной с фотоаппаратом в проекции на плоскость рисунка
Рис.3 Суточное движение светил в системе отсчёта, связанной с фотоаппаратом в проекции на плоскость рисункаСкорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории точки. При этом существует связь между величиной скорости , нормальным ускорением и радиусом кривизны траектории в данной точке:
Однако, не всякое движение с известной скоростью по кривой известного радиуса и найденное по приведённой выше формуле нормальное (центростремительное) ускорение
связано с проявлением силы, направленной по нормали к траектории (центростремительной силы). Так, найденное по данным фотографии суточного движения светил ускорение любой из звёзд отнюдь не говорит о существовании вызывающей это ускорение силы, притягивающей её к Полярной звезде, как центру вращения.Связь с уравнениями динамики
Представление траектории как следа, оставляемого движением материальной точки, связывает чисто кинематическое понятие о траектории, как геометрической проблеме, с динамикой движения материальной точки, то есть проблемой определения причин её движения. Фактически, решение уравнений Ньютона (при наличии полного набора исходных данных) даёт траекторию материальной точки.
В соответствии с принципом относительности Галилея, существует бесконечное множество равноправных инерциальных систем (ИСО), движение которых одна относительно другой не может быть установлено никаким образом путём наблюдения любых процессов и явлений, происходящих только в этих системах. Прямая траектория равномерного движения объекта в одной системе будет выглядеть также прямой в любой другой инерциальной системе, хотя величина и направление скорости будут зависеть от выбора системы, то есть от величины и направления их относительной скорости.
Вместе с тем Принцип Галилея не утверждает, что одно и то же явление, наблюдаемое из двух разных ИСО, будут выглядеть одинаково. Поэтому Рис.2 предупреждает о двух типичных ошибках, связанных с забвением того, что:
1. Истинно, что любой вектор (в том числе вектор силы) может быть разложен по крайней мере на две составляющие. Но это разложение совершенно произвольно и не значит, что такие компоненты существуют в действительности. Для подтверждения их реальности должна привлекаться дополнительная информация, в любом случае не взятая из анализа формы траектории. Например, по рисунку 2 невозможно определить природу силы F, так же как невозможно утверждать, что она сама является или не является суммой сил разной природы. Можно лишь утверждать, что на изображённом участке она постоянна, и что для формирования наблюдаемой в данной СО криволинейности траектории служит вполне определённая в данной СО центростремительная часть этой силы. Зная лишь траекторию материальной точки в какой-либо инерциальной системе отсчёта и её скорость в каждый момент времени, нельзя определить природу сил, действовавших на неё.
2. Даже в случае наблюдения из ИСО, форма траектории ускоренно движущегося тела будет определяться не только действующими на него силами, но и выбором этой ИСО, никак на эти силы не влияющим. Центростремительная сила, показанная на рисунке 2, получена формально, и её величина непосредственно зависит от выбора ИСО.
Движение под действием внешних сил в инерциальной системе отсчёта
Если в заведомо инерциальной системе скорость движения объекта (для неподвижного в данной системе наблюдателя) с массой меняется по направлению, даже оставаясь прежней по величине, то есть тело производит поворот и движется по дуге с радиусом кривизны , то значит, это тело испытывает нормальное ускорение . Причиной, вызывающей это ускорение, является центростремительная сила, прямо пропорциональная этому ускорению. В этом состоит суть Второго закона Ньютона:
- (1)
Где есть векторная сумма сил, действующих на тело, его ускорение, а — инерционная масса.[4]
В общем случае тело не бывает свободно в своём движении, и на его положение, а в некоторых случаях и на скорость, налагаются ограничения — связи. Если связи накладывают ограничения только на координаты тела, то такие связи называются геометрическими. Если же они распространяются и на скорости, то они называются кинематическими. Если уравнение связи может быть проинтегрировано во времени, то такая связь называется голономной.
Действие связей на систему движущихся тел описывается силами, называемыми реакциями связей. В таком случае сила, входящая в левую часть уравнения (1), есть векторная сумма активных (внешних) сил и реакции связей.
Существенно, что в случае голономных связей становится возможным описать движение механических систем в обобщённых координатах, входящих в уравнения Лагранжа. Число этих уравнений зависит лишь от числа степеней свободы системы и не зависит от количества входящих в систему тел, положение которых необходимо определять для полного описания движения.
Если же связи, действующие в системе идеальны, то есть в них не происходит переход энергии движения в другие виды энергии, то при решении уравнений Лагранжа автоматически исключаются все неизвестные реакции связей.
Наконец, если действующие силы принадлежат к классу потенциальных, то при соответствующем обобщении понятий становится возможным использования уравнений Лагранжа не только в механике, но и других областях физики.[5]
Действующие на материальную точку силы в этом понимании однозначно определяют форму траектории её движения (при известных начальных условиях). Обратное утверждение в общем случае не справедливо, поскольку одна и та же траектория может иметь место при различных комбинациях активных сил и реакций связи.
Движение под действием внешних сил в неинерциальной системе отсчёта
Если система отсчёта неинерциальна (то есть движется с неким ускорением относительно инерциальной системы отсчёта), то в ней также возможно использование выражения (1), однако в левой части необходимо учесть так называемые силы инерции (в том числе, центробежную силу и силу Кориолиса, связанные с вращением неинерциальной системы отсчёта)[4].
Иллюстрация
Траектории одного и того же движения в неподвижной и вращающейся системах отсчёта. Вверху в инерциальной системе видно, что тело двигается по прямой. Внизу в неинерциальной видно, что тело повернуло в сторону от наблюдателя по кривой.Как пример, рассмотрим работника театра, передвигающегося в колосниковом пространстве над сценой по отношению к зданию театра равномерно и прямолинейно и несущего над вращающейся сценой дырявое ведро с краской. Он будет оставлять на ней след от падающей краски в форме раскручивающейся спирали (если движется от центра вращения сцены) и закручивающейся — в противоположном случае. В это время его коллега, отвечающий за чистоту вращающейся сцены и на ней находящийся, будет поэтому вынужден нести под первым недырявое ведро, постоянно находясь под первым. И его движение по отношению к зданию также будет равномерным и прямолинейным, хотя по отношению к сцене, которая является неинерциальной системой, его движение будет искривлённым и неравномерным . Более того, для того, чтобы противодействовать сносу в направлении вращения, он должен мышечным усилием преодолевать действие силы Кориолиса, которое не испытывает его верхний коллега над сценой, хотя траектории обоих в инерциальной системе здания театра будут представлять прямые линии.
Но можно себе представить, что задачей рассматривающихся здесь коллег является именно нанесение
Более того, равномерное движение тела в одной системе, может быть неравномерным в другой. Так, две капли краски, упавшие в разные моменты времени из дырявого ведра, как в собственной системе отсчёта, так и в системе неподвижного по отношению к зданию нижнего коллеги (на уже прекратившей вращение сцене), будут двигаться по прямой (к центру Земли). Различие будет заключаться в том, что для нижнего наблюдателя это движение будет ускоренным, а для верхнего его коллеги, если он, оступившись, будет падать, двигаясь вместе с любой из капель, расстояние между каплями будет увеличиваться пропорционально первой степени времени, то есть взаимное движение капель и их наблюдателя в его ускоренной системе координат будет равномерным со скоростью , определяемой задержкой между моментами падения капель:
- .
Где — ускорение свободного падения.
Поэтому форма траектории и скорость движения по ней тела, рассматриваемая в некоторой системе отсчёта, о которой заранее ничего не известно, не даёт однозначного представления о силах, действующих на тело. Решить вопрос о том, является ли эта система в достаточной степени инерциальной, можно лишь на основе анализа причин возникновения действующих сил.
Таким образом, в неинерциальной системе:
- Кривизна траектории и/или непостоянство скорости являются недостаточным аргументом в пользу утверждения о том, что на движущееся по ней тело действуют внешние силы, которые в конечном случае могут быть объяснены гравитационными или электромагнитными полями.
- Прямолинейность траектории является недостаточным аргументом в пользу утверждения о том, что на движущееся по ней тело не действуют никакие силы.
Примечания
- ↑ Понятие траектории достаточно наглядно может быть проиллюстрировано трассой бобслея. (Если по условиям задачи можно пренебречь её шириной). И именно трассой, а не самим бобом.
- ↑ Так улица, в начале которой висит знак «кирпич» останется в принципе траекторией движения по ней. А поезда разной массы, движущиеся под различными тяговыми усилиями на сцепных крюках локомотивов и потому с разной скоростью, будут двигаться по одной и той же траектории, определяемой формой рельсового пути, налагающего на движение несвободного тела (поезда) конкретные связи, интенсивность которых будет в каждом случае различной
- ↑ Так, Луна обращается вокруг Земли только в системе отсчёта, связанной с их общим центром гравитации (находится внутри Земного шар). В системе же отсчёта, началом которой является Солнце, Луна обращается вокруг него по той же эллиптической орбите, что и Земля, но с периодическими отклонениями от неё на величину расстояния от Луны до Земли. Никакого взаимного обращения этих небесных тел в этом случае просто нет. Наличие земного притяжения для объяснения формы траектории Луны в системе координат, связанной с Солнцем, вообще не обязательно. Так, исчезни Земля, Луна могла бы продолжать двигаться, как самостоятельное небесное тело, по той же самой старой траектории, а её периодические возмущения можно было бы тогда в качестве гипотезы объяснить изменением силы тяготения, скажем, за счёт вариации массы Солнца по причине пульсации его светимости (что, кстати, и наблюдается в определённых пределах в действительности). И обе упомянутые формы траектории истинны и оба объяснения их формы на основании правильно проведённого анализа действующих сил справедливы. Но они исключают друг друга, как исключается возможность одновременного рассмотрения при выборе той или иной системы координат.
- ↑ 1 2 С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
- ↑ Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. М.: Сов.энциклопедия, 1983. — 323 с.,ил, 2 л.цв.ил. страница 282.
В физике есть ещё одна формула измерения траектории (пути): s=4Atv, где A – амплитуда, t – время, v – частота колебаний
Литература
- Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
- Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. М.: ГИТТЛ, 1957
Ссылки
dvc.academic.ru
“Перемещение. Траектория. Путь” (9-й класс)
Разделы: Физика
Цели урока:
- Образовательная:
– ввести понятия “перемещение”, “путь”, “траектория”. - Развивающая:
– развивать логическое мышление, правильную физическую речь, использовать соответствующую терминологию. - Воспитательная:
– достигать высокой активности класса, внимания, сосредоточенности учащихся.
Оборудование:
- пластмассовая бутылка вместимостью 0,33 л с водой и со шкалой;
- медицинский флакончик вместимостью 10 мл (или малая пробирка) со шкалой.
Демонстрации: Определение перемещения и пройденного пути.
Ход урока
1. Актуализация знаний.
– Здравствуйте, ребята! Садитесь! Сегодня мы с вами продолжим изучать тему “Законы взаимодействия и движения тел” и на уроке познакомимся с тремя новыми понятиями (терминами), касающихся этой темы. А пока проверим выполнение вами домашнего задания у данному уроку.
2. Проверка домашнего задания.
Перед уроком один учащийся выписывает на доске решение следующего домашнего задания:
Двум учащимся раздаются карточки с индивидуальными заданиями, которые выполняются во время устной проверки упр. 1 стр. 9 учебника. [1]
Карточка 1: (Приложение 1)
1. Какую систему координат(одномерную, двухмерную, трехмерную) следует выбрать для определения положения тел:
а) трактор в поле;
б) вертолет в небе;
в) поезд
г) шахматная фигура на доске.
2. Дано выражение: S = υ0 · t + (а · t2) / 2, выразите: а, υ0
Карточка 2: (Приложение 2)
1. Какую систему координат (одномерную, двухмерную, трехмерную) следует выбрать для определения положения таких тел:
а) люстра в комнате;
б) лифт;
в) подводная лодка;
г) самолет на взлетной полосе.
2. Дано выражение: S = (υ2 – υ02 ) / 2 · а, выразите: υ2 , υ02.
3. Изучение нового теоретического материала.
С изменениями координат тела связана величина, вводимая для описания движения, – ПЕРЕМЕЩЕНИЕ.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Перемещение принято обозначать буквой . В СИ перемещение измеряется в метрах (м).
[ ] – [ м ] – метр.
Перемещение – величина векторная, т.е. кроме числового значения имеет еще и направление. Векторную величину изображают в виде отрезка, который начинается в некоторой точке и заканчивается острием, указывающим направление. Такой отрезок-стрелка называется вектором.
– вектор, проведенный из точки М в М1Знать вектор перемещения – значит, знать его направление и модуль. Модуль вектора – это скаляр, т.е. численное значение. Зная начальное положение и вектор перемещения тела, можно определить, где находится тело.
В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка “описывает” в пространстве какую-то линию. Иногда эта линия видна, – например, высоко летящий самолет может оставлять за собой след в небе. Более знакомый пример – след куска мела на доске.
Воображаемая линия в пространстве, по которой движется тело называется ТРАЕКТОРИЕЙ движения тела.
Траектория движения тела – это непрерывная линия, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Движение, при котором все точки тела движутся по одинаковым траекториям, называется поступательным.
Очень часто траектория – невидимая линия. Траектория движущейся точки может быть прямой или кривой линией. Соответственно форме траектории движение бывает прямолинейным и криволинейным.
Длина траектории – это ПУТЬ. Путь является скалярной величиной и обозначается буквой l. Путь увеличивается, если тело движется. И остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.
Модуль перемещения и путь могут совпадать по значению, только в том случае, если тело движется вдоль прямой в одном направлении.
Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия: (Приложение 3) (раздаются в виде карточек каждому ученику)
- Путь – скалярная величина и характеризуется только числовым значением.
- Перемещение – векторная величина и характеризуется как числовым значением (модулем), так и направлением.
- При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
- Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.
| Путь | Перемещение | |
| Определение | Длина траектории, описываемой телом за определенное время | Вектор, соединяющий начальное положение тела с его последующим положением |
| Обозначение | l [ м ] | S [м ] |
| Характер физических величин | Скалярная, т.е. определяется только числовым значением | Векторная, т.е. определяется числовым значением (модулем) и направлением |
| Необходимость введения | Зная начальное положение тела и путь l, пройденный за промежуток времени t, нельзя определить положение тела в заданный момент времени t | Зная начальное положение тела и S за промежуток времени t, однозначно определяется положение тела в заданный момент времени t |
| l = S в случае прямолинейного движения без возвратов | ||
4. Демонстрация опыта (учащиеся выполняют самостоятельно на своих местах за партами, учитель вместе с учащимися выполняет демонстрацию этого опыта)
- Заполните водой до горловины пластмассовую бутылку со шкалой.
- Флакончик со шкалой заполните водой на 1/5 его объема.
- Наклоните бутылку так, чтобы вода подошла к горловине, но не вытекала из бутылки.
- Быстро опустите флакончик с водой в бутылку (не закрывая его пробкой) так, чтобы горловина флакончика вошла в воду бутылки. Флакончик плавает на поверхности воды в бутылке. Часть воды при этом из бутылки выльется
- Завинтите крышку бутылки.
- Сжимая боковые стенки бутылки, опустите поплавок на дно бутылки.
- Ослабляя давление на стенки бутылки, добейтесь всплытия поплавка. Определите путь и перемещение поплавка:________________________________________________________
- Опустите поплавок на дно бутылки. Определите путь и перемещение поплавка:______________________________________________________________________________
- Заставьте поплавок всплыть и утонуть. Каков путь и перемещение поплавка в этом случае?_______________________________________________________________________________________
5. Упражнения и вопросы для повторения.
- Путь или перемещение мы оплачиваем при поездке в такси? (Путь)
- Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. найти путь и перемещение мяча. (Путь – 4 м, перемещение – 2 м.)
6. Итог урока.
Повторение понятий урока:
– перемещение;
– траектория;
– путь.
7. Домашнее задание.
§ 2 учебника [1], вопросы после параграфа, упражнение 2 (стр.12) учебника [1], повторить выполнение опыта урока дома.
Список литературы
1. Перышкин А.В., Гутник Е.М. Физика. 9 кл.: учеб.для общеобразоват.учреждений – 9-е изд., стереотип. – М.: Дрофа, 2005.
xn--i1abbnckbmcl9fb.xn--p1ai
III. Траектория, путь и перемещение
Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета – совокупность системы координат и часов, связанных с телом отсчета.
В декартовой системе координат положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами x, y и z или радиусом-вектором r – вектор, проведенный из начала системы координат в данную точку. При движении материальной точки ее координаты с течением времени изменяются. r=r(t) или x=x(t), y=y(t), z=z(t) – кинематические уравнения материальной точки.
Основная задача механики – зная состояние системы в некоторый начальный момент времени t0, а также законы, управляющие движением, определить состояния системы во все последующие моменты времени t.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве. В зависимости от формы траектории различают прямолинейное и криволинейное движение точки. Если траектория точки – плоская кривая, т.е. целиком лежит в одной плоскости, то движение точки называют плоским.
Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути Δs и является скалярной функцией времени: Δs=Δs(t). Единица измерения – метр (м)– длина пути, проходимого светом в вакууме за 1/299792458 с.
IV. Векторный способ задания движения
Радиус-вектор r – вектор,
проведенный из начала системы координат
в данную точку. Вектор Δr=r–r0,
проведенный из начального положения
движущейся точки в положение ее в данный
момент времени называется перемещением (приращение радиуса-вектора точки за
рассматриваемый промежуток времени).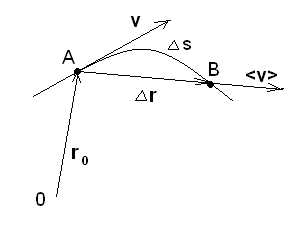
Вектором средней скорости <v> называется отношение приращения Δr радиуса-вектора точки к промежутку времени Δt: (1). Направление средней скорости совпадает с направлением Δr.При неограниченном уменьшении Δt средняя скорость стремиться к предельному значению, которое называется мгновенной скоростью v. Мгновенная скорость это скорость тела в данный момент времени и в данной точке траектории: (2). Мгновенная скоростьv есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени.
Для характеристики быстроты изменения скорости v точки в механике вводится векторная физическая величина, называемая ускорением.
Средним ускорением неравномерного движения в интервале от t до t+Δt называется векторная величина, равная отношению изменения скорости Δv к интервалу времени Δt:
(3).
Мгновенным ускорением а материальной точки в момент времени t будет предел среднего ускорения:(4). Ускорениеа есть векторная величина, равная первой производной скорости по времени.
V. Координатный способ задания движения
Положение точки М можно характеризовать радиус – вектором r или тремя координатами x, y и z: М(x,y,z). Радиус – вектор можно представить в виде суммы трех векторов, направленных вдоль осей координат: (5).
Из определения скорости (6). Сравнивая (5) и (6) имеем:(7). Учитывая (7) формулу (6) можно записать(8). Модуль скорости можно найти:(9).
Аналогично для вектора ускорения:
(10),
(11),
(12),
(13).
Естественный способ задания движения (описание движения с помощью параметров траектории)
Движение
описывается формулой s=s(t).
Каждая точка траектории характеризуется
своим значением s.
Радиус – вектор является функцией от
s
и траектория может быть задана уравнением r=r(s).
Тогда r=r(t)
можно представить как сложную функцию r[s(t)].
Продифференцируем
(14). Величина Δs
– расстояние между двумя точками вдоль
траектории, |Δr|
– расстояние
между ними по прямой линии. По мере
сближения точек разница уменьшается.
,
гдеτ –
единичный вектор, касательный к
траектории.
,
тогда (13) имеет видv=τv
(15). Следовательно скорость направлена
по касательной к траектории.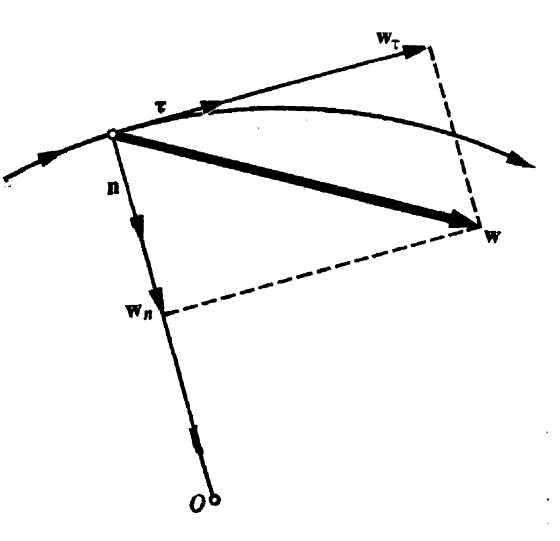
Ускорение может быть направлено под любым углом к касательной к траектории движения. Из определению ускорения (16). Еслиτ – касательный к траектории, то – вектор перпендикулярный этой касательной, т.е. направлен по нормали. Единичный вектор, в направлении нормали обозначаетсяn. Значение вектора равно 1/R, где R – радиус кривизны траектории.
Точка, отстоящая от траектории на расстоянии и R в направлении нормали n, называется центром кривизны траектории. Тогда (17). Учитывая вышеизложенное формулу (16) можно записать:(18).
Полное ускорение состоит из двух взаимно перпендикулярных векторов: , направленного вдоль траектории движения и называемого тангенциальным, и ускорения, направленного перпендикулярно траектории по нормали, т.е. к центру кривизны траектории и называемого нормальным.
Абсолютное значение полного ускорения найдем: (19).
Лекция 2 Движение материальной точки по окружности. Угловое перемещение, угловая скорость, угловое ускорение. Связь между линейными и угловыми кинематическими величинами. Векторы угловой скорости и ускорения.
План лекции
Кинематика вращательного движения
Частные случаи вращательного движения
Кинематика вращательного движения
При
вращательном движении мерой перемещения
всего тела за малый промежуток времени
dt
служит вектор dφ элементарного поворота тела. Элементарные
повороты (обозначаются
или)
можно рассматривать какпсевдовекторы
(как бы).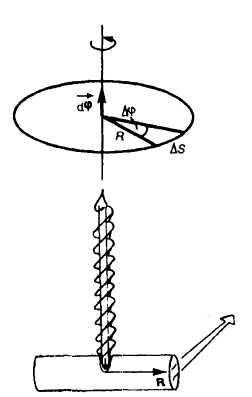
Угловое перемещение — векторная величина, модуль которой равен углу поворота, а направление совпадает с направлением поступательного движения правого винта (направленный вдоль оси вращения так, что если смотреть с его конца, то вращение тела кажется происходящим против часовой стрелки). Единица углового перемещения – рад.
Быстроту изменения углового перемещения с течением времени характеризует угловая скорость ω. Угловая скорость твердого тела – векторная физическая величина, характеризующая быстроту изменения углового перемещения тела с течением времени и равная угловому перемещению, совершаемому телом за единицу времени:
(1).
Направлен вектор ω вдоль оси вращения в ту же сторону, что и dφ (по правилу правого винта). Единица угловой скорости— рад/с
Быстроту изменения угловой скорости с течением времени характеризует угловое ускорение ε
(2).
Направлен вектор ε вдоль оси вращения в ту же сторону, что и dω, т.е. при ускоренном вращении , при замедленном.
Единица углового ускорения – рад/с2.
За время dt произвольная точка твердого тела А переместиться на dr, пройдя путь ds. Из рисунка видно, что dr равно векторному произведению углового перемещения dφ на радиус – вектор точки r: dr=[dφ·r] (3).
Линейная скорость точки связана с угловой скоростью и радиусом траектории соотношением:
В векторном виде формулу для линейной скорости можно написать как векторное произведение: (4)
По определению векторного произведения его модуль равен , где— угол между векторами и, а направление совпадает с направлением поступательного движения правого винта при его вращении отк .
Продифференцируем (4) по времени:
. (5)
Учитывая, что – линейное ускорение,- угловое ускорение, а- линейная скорость, получим:
(6).
Первый вектор в правой части направлен по касательной к траектории точки. Он характеризует изменение модуля линейной скорости. Следовательно, этот вектор – касательное ускорение точки: aτ=[ε·r] (7). Модуль касательного ускорения равен aτ=ε·r. Второй вектор в (6) направлен к центру окружности и характеризует изменение направления линейной скорости. Этот вектор – нормальное ускорение точки: an=[ω·v] (8). Модуль его равен an=ω·v или учитывая, что v = ω·r, an= ω2·r = v2/r (9).
Частные случаи вращательного движения
При равномерном вращении: , следовательно .
Равномерное вращение можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот,
(10)
Частота вращения — число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени: (11)
. (12)
Единица частоты вращения — герц (Гц).
При равноускоренном вращательном движении :
(13), (14)(15).
Лекция 3 Первый закон Ньютона. Сила. Принцип независимости действующих сил. Результирующая сила. Масса. Второй закон ньютона. Импульс. Закон сохранения импульса. Третий закон Ньютона. Момент импульса материальной точки, момент силы, момент инерции.
План лекции
Первый закон Ньютона
Второй закон Ньютона
Третий закон Ньютона
Момент импульса материальной точки, момент силы, момент инерции
Первый закон Ньютона. Масса. Сила
Первый закон Ньютона: Существуют такие системы отсчета, относительно которых тела движутся прямолинейно и равномерно или покоятся, если на них не действуют силы или действие сил скомпенсировано.
Первый закон Ньютона выполняется только в инерциальной системе отсчёта и утверждает существование инерциальной системе отсчёта.
Инерция – это свойство тел стремиться сохранять скорость неизменной.
Инертностью называют свойство тел препятствовать изменению скорости под действием приложенной силы.
Масса тела – это физическая величина являющаяся количественной мерой инертности, это скалярная аддитивная величина. Аддитивность массы состоит в том, что масса системы тел всегда равна сумме масс каждого тела в отдельности. Масса – основная единица системы «СИ».
Одной из форм взаимодействия является механическое взаимодействие. Механическое взаимодействие вызывает деформацию тел, а также изменение их скорости.
Сила – это векторная величина являющаяся мерой механического воздействия на тело со стороны других тел, или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры (деформируется). Сила характеризуется модулем, направлением действия, точкой приложения к телу.
studfiles.net
Траектория, путь и перемещение
Чтобы разобраться с такими понятиями как траектория, путь и перемещение рассмотрим пример.
Представим человечка, который гуляет по лабиринту. Он может ходить по этому лабиринту хоть целый день и пройти десятки километров: поворачивать то направо, то налево, то возвращаться и проходить по одним и тем же дорожкам снова и снова, пока не найдет выход.
Мы же, как самые хитрые, наблюдаем за его попытками выйти из лабиринта сверху, и нам он кажется маленькой точкой в лабиринте.
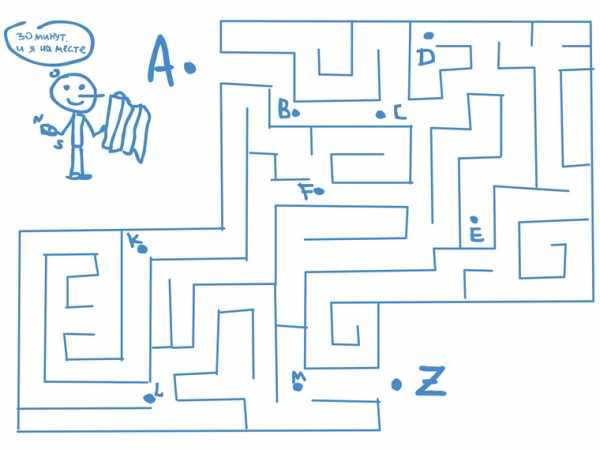
Синие точки – это положение нашего человечка в лабиринте в разное время.
Если бы человечек чертил за собой линию, то мы могли бы увидеть весь его маршрут за день – получилась бы сложная линия с изгибами и петлями. По-умному эта линия называется траекторией.

Человечек не захотел чертить за собой линию и поручил это дело помощнику.
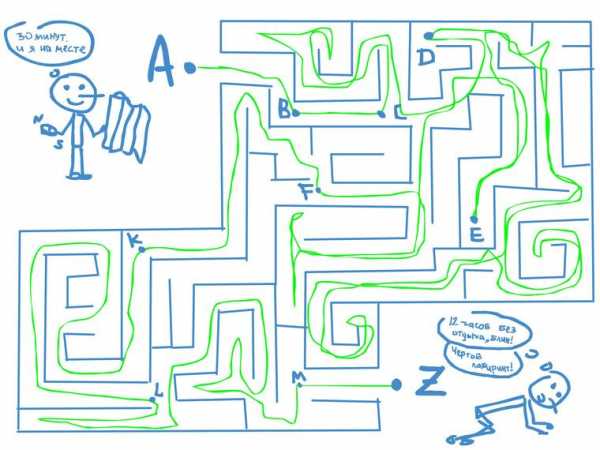
На рисунке зеленой линией указана траектория движения человечка
Траектория — это линия, которую описывает тело при своем движении.
Траектория бывает двух видов: в виде прямой линии (прямолинейной) и в виде кривой линии (криволинейной).
На рисунке траектория на участках BC и MZ прямолинейная, а на участках AB, CD, DE, EF, FK, KL, LM – криволинейная.
Если мы измерим длину всей зеленой линии ABCDEFKLMZ (траектории), то получим путь. Путь – длина траектории.
Вроде все просто, если бы не одно НО. Кроме пути физики еще придумали такое понятие как перемещение. Чем же путь отличается от перемещения? Разве это не одно и то же?!
Оказывается, нет.
Перемещение – это, если мы не будем следить за траекторией движения человечка весь день, а просто отметим точку на карте в начале его движения (Точка А) и затем в конце дня отметим точку, где он закончил свое движение (Точка Z), и потом просто соединим эти две точки прямой линией. Длина этой прямой линии и будет перемещение человечка за день.
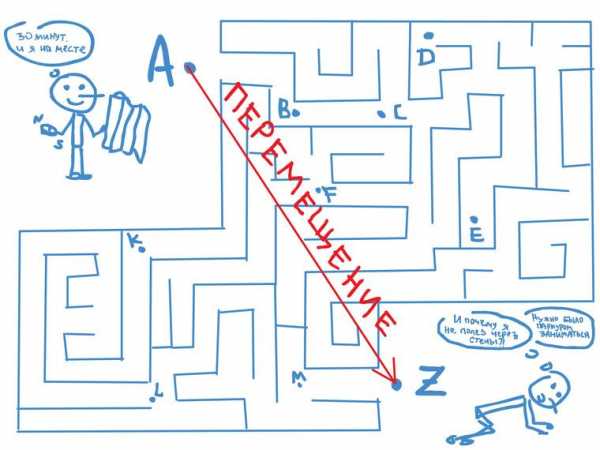
Перемещение человечка – направленный красный отрезок AZ
Соединять начальную и конечную точку принято стрелочкой, которая указывает направление, в котором переместилось тело. Таким образом, перемещение – это длина прямой стрелочки (направленного отрезка), соединяющей начальное и конечное положение тела.
ВЫВОДЫ:
Траектория – воображаемая линия, по которой движется тело.
Путь – длина траектории.
Перемещение – направленный отрезок, соединяющий начальное и конечное положения тела.
P.S. Путь и перемещение равны, если тело двигается всегда по прямой. Перемещение тела может быть равно нулю, а путь одновременно равен десяткам и тысячам километров (если тело вернется в ту же точку, откуда и начало двигаться).
Как видите путь и перемещение – это разные вещи.
virtuallab.by
Kvant. Траектория, путь — PhysBook
Кикоин А.К. Траектория, путь, перемещение //Квант. — 1984. — № 9. — С. 19-20.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Три слова в заглавии этой заметки связаны с движением тел (материальных точек). Первые два широко употребляются в житейском обиходе, третьим пользуются, главным образом, в науке о движении тел — механике.
Траектория — это непрерывная линия, которую описывает движущаяся точка. Она может быть прямой линией. Отеле (точке), движущемся по такой траектории, говорят, что оно совершает прямолинейное движение. Траектория может представлять собой и кривую линию любой формы. Тело, движущееся по такой траектории, совершает криволинейное движение. Например, траектория свободно падающего тела по отношению к Земле (если пренебречь ее вращением) — вертикальная прямая, а траектория искусственного спутника Земли — кривая (окружность или эллипс).
Если траектория известна заранее, то задачей механики может быть, скажем, определение точки на траектории, где находится движущееся тело в тот или иной момент времени. Траектория может быть и неизвестной, тогда задача состоит в том, чтобы найти вид траектории. Законы движения позволяют решать и ту, и другую задачи.
Путь, пройденный телом (точкой),— это длина его траектории (измеренная в метрах, километрах и т. д.). Его можно определить, например, по счетчику километров в автомобиле.
Для решения задач механики знать пройденный путь обычно недостаточно и вот почему. Явление движения тела состоит в том, что с течением времени изменяются координаты тела. Путь же с изменением координат связан не всегда. Может даже случиться и так, что пройденный путь не равен нулю, а изменение координат равно нулю (тело прошло по замкнутой траектории). Вот поэтому путь, как правило, в уравнения механики не входит.
Для описания движения тела (точки) в механике (точнее — в кинематике) используется другая физическая величина — перемещение. Напомним, что перемещение — это направленный отрезок прямой (вектор), соединяющий некоторое начальное положение движущейся точки с каким-то последующим ее положением («Физика 8», §3). Важность для механики именно этой величины вытекает из того, что проекции вектора перемещения на оси координат равны изменениям соответствующих координат («Физика 8», §5). А это значит, что, если известен вектор перемещения, можно найти и координаты тела. Правда, для этого нужно знать еще начальные координаты.
Рис. 1
Возникает вопрос: не равны ли друг другу модуль вектора перемещения и пройденный путь (и то и другое — скаляры)? Оказывается, что в общем случае — нет, не равны. Например, если тело из точки А пришло в точку В по траектории, представляющей собой половину окружности радиуса R, то пройденный телом путь l = πR, а модуль перемещения \(~|\vec s| = 2R\) (рис. 1). Если бы тело прошло не половину окружности, а сделало полный оборот (вторая половина траектории показана на рисунке 1 штриховой линией), то путь был бы равен 2πR, а модуль перемещения — нулю. Только в одном случае, когда траектория движения тела — прямая линия и тело движется по такой траектории в одном направлении, модуль перемещения и пройденный путь равны друг другу.
Рис. 2
Существует простая связь между величинами перемещения и пройденного пути. Поясним ее на уже рассмотренном примере движения тела по полуокружности. Разобьем эту траекторию на малые участки 1, 2, 3 и т. д. (рис. 2). На участке 1 путь тела — это длина дуги Аа, а перемещение \(~\vec s_1\) по модулю равно длине хорды Аа. На участке 2 путь тела — это длина дуги ab, а модуль перемещения \(~\vec s_2\) — длина хорды ab и т. д. Можно сделать участки, на которые мы разбили траекторию, такими малыми, чтобы дуга участка мало отличалась от хорды. Тогда, как это видно из рисунка 2, вектор полного перемещения \(~\vec s\) равен сумме векторов элементарных перемещений \(~\vec s_1\), \(~\vec s_2\), \(~\vec s_3\) и т. д.:
\(~\vec s = \vec s_1 + \vec s_2 + \vec s_3 + \ldots + \vec s_n\) ,а длина пути l равна алгебраической сумме модулей \(~|\vec s_1|\), \(~|\vec s_2|\), \(~|\vec s_3|\) и т. д. элементарных перемещений:
\(~l = |\vec s_1| + |\vec s_2| + |\vec s_3| + \ldots + |\vec s_n|\) .www.physbook.ru
Траектория Википедия
 Рис. 1. Траектории трёх объектов (угол запуска — 70°, Distance — расстояние, Height — высота), разное лобовое сопротивление
Рис. 1. Траектории трёх объектов (угол запуска — 70°, Distance — расстояние, Height — высота), разное лобовое сопротивлениеТраекто́рия материа́льной то́чки — линия в пространстве, по которой движется тело, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта.[1] Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.
Кроме того, и при наличии движущегося по ней объекта, траектория, изображаемая в наперёд заданной системе пространственных координат, сама по себе не может ничего определённого сказать в отношении причин его движения, пока не проведён анализ конфигурации поля действующих на него сил в той же координатной системе.[2]
Не менее существенно, что форма траектории неотрывно связана и зависит от конкретной системы отсчёта, в которой описывается движение.[3]
Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, звёздное небо может послужить хорошей моделью инерциальной и неподвижной системы отсчёта. Однако при длительной экспозиции эти звёзды представляются движущимися по круговым траекториям (Рис. 3)
Возможен и случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.
Траектория свободной материальной точки[ | ]
В соответствии с Первым законом Ньютона, иногда называемым законом инерции, должна существовать такая система, в которой свободное тело сохраняет (как вектор) свою скорость. Такая система отсчёта называется инерциальной. Траекторией такого движения является прямая линия, а само движение называется равномерным и прямолинейным.
Описание траектории[ | ]
Рис. 2. Прямолинейное равномерно ускоряющееся движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.Принято описывать траекторию материальной точки в наперёд заданной системе координат при помощи радиус-вектора, направление, длина и начальная точка которого зависят от вре
ru-wiki.ru
ТРАЕКТОРИЯ – это… Что такое ТРАЕКТОРИЯ?
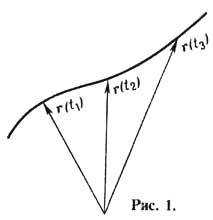
– кривая, к-рую описывает радиус-вектор r(t )координат тела с течением времени (рис. 1). Понятие “Т.” тесно связано с понятиями “материальная точка” и “уравнения движения”. Говорить о траектории имеет смысл лишь в том случае, когда размеры тела малы по сравнению с расстоянием, к-рое оно проходит.
Для определения ф-ции r(t) (а следовательно, и Т.) необходимо решить дифференц. ур-ние 2-го порядка, вытекающее из 2-го закона Ньютона:
где т – масса тела, F– действующая на него сила.
Ур-ние (1) при заданной F определяет целое семейство траекторий. Выбор к.-л. одной из них осуществляется фиксацией нач. условий, роль к-рых обычно выполняют нач. координаты и скорость тела, Напр., подставляя в качестве силы F в ф-лу (1) силу всемирного тяготения,
где G – гравитационная постоянная, -масса Солнца, т – масса его спутника, n – единичный вектор, направленный от спутника к Солнцу, r– расстояние между ними, и, решая ур-ние (1), можно доказать [И. Ньютон (I. Newton, 1684)], что Т. движения спутника в зависимости от нач. условий является эллипсом, параболой или гиперболой.
В классич. механике, если известны координаты и скорость тела в к.-л. момент времени, то Т. движения [ф-ция r(t)]однозначно определяется законом движения (1).
Представление о Т. движения тела как о нек-рой гладкой кривой, к-рую можно найти, решив ур-ние (1), является чисто макроскопическим. Для микроскопич. тел это не так. Из основных постулатов термодинамики следует, что независимо от природы действующих на тело сил среднеквадратичная флуктуация скорости тела, находящегося в термодинамическом равновесии с внеш. средой, описывается ф-лой
где k- постоянная Больцмана, т – масса тела, Т- абс. темп-pa среды, в к-рую тело помещено.
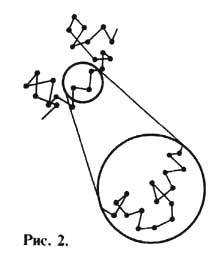
Величина при комнатной темп-ре пренебрежимо мала для макроскопич. тел, но для отд. молекул она составляет уже неск. сотен м в секунду. Поэтому Т. движения микроскопич. тела будет представлять собой хаотическую ломаную линию, подобную изображённой на рис. 2. Это почти везде непрерывная и почти нигде недифференцируемая кривая. Она называется б р о у н о вс к о й т р а е к т о р и е й (см. Броуновское движение )и обладает тем свойством, что если увеличить любой её фрагмент, то мы увидим такую же кривую. Т., изображённая на рис. 2, является случайной, и имеет смысл говорить лишь о статистич. ансамбле таких Т. Полностью определёнными являются только средние по ансамблю величины. Напр., квадрат ср. смещения частицы <x2> как ф-ция времени t есть [А. Эйнштейн (A. Einstein), 1905]:
где D – коэф. диффузии.
Броуновское движение является заданным, если известна ф-ция
к-рая имеет смысл вероятности того, что частица, находящаяся в точке r1 в момент времени t1 в момент t2 окажется в точке r2.
В простейшем случае одномерного броуновского движения ф-ция (5) имеет вид
Т. о., для микроскопии, тел Т. является статистич. понятием.
Для квантовых частиц понятие “Т.” утрачивает смысл. Количеств. критерием квантового движения является условие
здесь 2p/h – постоянная Планка, т – масса частицы (напр., электрона), u-характерная скорость, L – характерный размер области движения частицы.
“Увидеть” Т. движения квантовой частицы (напр., электрона в атоме) непосредственно при помощи микроскопа или попытаться “поймать” Т. к.-л. способом невозможно. С формальной точки зрения причина состоит в том, что в квантовой частице неприменимо понятие материальной точки, можно говорить лишь об амплитуде вероятности обнаружить частицу в том или ином состоянии. Как показал-Кйзенберг (1927), физ. причина такого положения вещей заключается в том, что, пытаясь измерить положение частицы, мы неизбежно воздействуем на неё, причём это воздействие не может быть меньше постоянной Планка. Следовательно, в квантовом случае [когда выполнено условие (7)] представление о Т. как о геом. месте точек, в каждой из к-рых частицы имеют определ. скорость, физически бессмысленно.
Несмотря на это, в 1947 Т. “вернулась” в квантовую механику благодаря остроумному формализму интегрирования по траекториям, разработанному Р. Фейнманом (R. P. Feynman), и, т. о., легла в основу его интерпретации квантовой механики (см. Фейнмана представление в квантовой механике).
Оказывается, амплитуда перехода квантовой частицы из точки r1,t1 в точку r2,t2 можно записать в виде
Здесь S[x(t)] –действие классической частицы, движущейся по Т. х(t), символ означает, что необходимо просуммировать величину по всем Т., соединяющим точки r1,t1 и r2,t2. При этом величина имеет смысл амплитуды вероятности того, что частица попадёт из точки r1,t1 в точку r2,t2, двигаясь по Т. x(t). Т. хода G квантовой частицы (рис. 3).
Ур-ние (1) определяет экстремальную Т. в интеграле (8), к-рую называют классич. Т.
В классич. механике, к-рая описывает поведение мак-роскопич. тел, Т. движения является непосредственно измеряемой величиной. Для микроскопич. тел имеет смысл говорить лишь о статистическом ансамбле траекторий, поскольку для таких тел существенную роль играют термодинамич. флуктуации. И, наконец, в квантовой области представление о Т. как .о наблюдаемой физ. величине не имеет смысла. И всё же Т., уже как матсм. абстракция, образует основу очень красивого и плодотворного описания природы на квантовом уровне.
Лит.: Винер Н., Нелинейные задачи в теории случайных процессов, пер. с англ., М., 1961; Фейнман Р. Ф., Хибс А. Р., Квантовая механика и интегралы по траекториям, пер. с англ., М., 1968; Сивухин Д. В., Общий курс физики, 3 изд., т. 1. Механика, М., 1989. М. А. Савров.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
dic.academic.ru



