04.02.202013.11.2018

Формула закон термодинамики – Второй закон термодинамики (№1) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

• by alexxlab
• Комментариев к записи Формула закон термодинамики – Второй закон термодинамики (№1) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко нет
• Советы абитуриенту

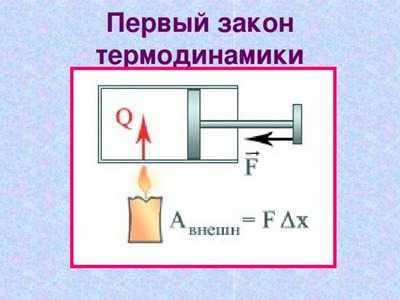
Первый закон термодинамики простыми словами

Содержание:

Определение первого закона термодинамики

Формула первого закона термодинамики

Процессы первого закона термодинамики

Первый закон термодинамики для изохорного процесса

Первый закон термодинамики для изобарного процесса

Применение первого закона термодинамики

Первый закон термодинамики, видео

Определение первого закона термодинамики

Простая формулировка первого закона термодинамики может звучать примерно так: изменение внутренней энергии той или иной системы возможно исключительно при внешнем воздействии. То есть другими словами, чтобы в системе произошли какие-то изменения необходимо приложить определенные усилия извне. В народной мудрости своеобразным выражением первого закона термодинамики могут служить пословицы – «под лежачий камень вода не течет», «без труда не вытащишь рыбку из пруда» и прочая. То есть на примере пословицы про рыбку и труд, можно представить, что рыбка и есть наша условно закрытая система, в ней не произойдет никаких изменений (рыбка сама себя не вытащит из пруда) без нашего внешнего воздействия и участия (труда).

Интересный факт: именно первый закон термодинамики устанавливает, почему потерпели неудачу все многочисленные попытки ученых, исследователей, изобретателей изобрести «вечный двигатель», ведь его существование является абсолютно невозможным согласно этому самому закону, почему, смотрите абзац выше.

В начале нашей статьи было максимального простое определение первого закона термодинамики, в действительности в академической науке существует целых четыре формулировки сути данного закона:

• Энергия ни откуда не появляется и ни куда не пропадает, она лишь переходит из одного вида в другой (закон сохранения энергии).
• Количество теплоты, полученной системой, идет на совершение ее работы против внешних сил и изменение внутренней энергии.
• Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданной системе, и не зависит от способа, которым осуществляется этот переход.
• Изменение внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты, переданной системе, и работой, совершенной системой над внешними силами.

Формула первого закона термодинамики

Формулу первого закона термодинамики можно записать таким образом:

Q = ΔU + A

Количество теплоты Q, передаваемое системе равно суме изменения ее внутренней энергии ΔU и работы A.

Процессы первого закона термодинамики

Также первый закон термодинамики имеет свои нюансы в зависимости от проходящих термодинамических процессов, которые могут быть изохронными и изобарными, и ниже мы детально опишем о каждом из них.

Первый закон термодинамики для изохорного процесса

Изохорным процессом в термодинамике называют процесс, происходящий при постоянном объеме. То есть, если будь-то в газе или жидкости нагреть вещество в сосуде, произойдет изохорный процесс, так как объем вещества останется неизменным. Это условие имеет влияние и на первый закон термодинамики, проходящий при изохорном процессе.

В изохорном процессе объем V является константой, следовательно, газ работы не совершает A = 0

Из этого выходит следующая формула:

Q = ΔU = U (T2) – U (T1).

Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

Первый закон термодинамики для изобарного процесса

Аналогично изобарным процессом называется термодинамический процесс, происходящий в системе при постоянном давлении и массе газа. Следовательно, в изобарном процессе (p = const) работа, совершаемая газом, выражается следующим уравнением первого закона термодинамики:

A = p (V2 – V1) = p ΔV.

Изобарный первый закон термодинамики дает:

Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV. При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.

Применение первого закона термодинамики

Первый закон термодинамике имеет практическое применение к различным процессам в физике, например, позволяет вычислить идеальные параметры газа при разнообразных тепловых и механических процессах. Помимо сугубо практичного применение можно этому закону найти применение и философское ведь что ни говорите, но первый закон термодинамики является выражением одного из самых общих законов природы – закона сохранения энергии. Еще Еклезиаст писал, что ничто ни откуда не появляется и никуда не уходит, все пребывает вечно, постоянно трансформируясь, в этом и кроется вся суть первого закона термодинамики.

Первый закон термодинамики, видео

И в завершение нашей статьи вашему вниманию образовательное видео о первом законе термодинамике и внутренней энергии.

www.poznavayka.org

Формула первого закона термодинамики

Основные законы, которые являются основой термодинамики, называют началами. В основании термодинамики лежат три начала. Первое начало термодинамики является законом сохранения энергии для термодинамических процессов. В интегральном виде формула первого начала термодинамики выглядит как:

   

что означает: количество теплоты, подводимое к термодинамической системе, идет на совершение данной системой работы и изменение ее внутренней энергии. Условлено считать, что если теплота к системе подводится, то она больше нуля () и если работу выполняет сама термодинамическая система, то она положительна ().

Первое начало термодинамики можно представить в дифференциальном виде, тогда формула для него будет:

   

где – бесконечно малое количество теплоты, подводимое к системе; – элементарная работа системы; – малое изменение внутренней энергии системы.

Если исследуемой термодинамической системой является идеальный газ, то работа выполняемая им связана с изменением объема (), в таком случае формулой первого начала термодинамики (в дифференциальном виде) можно считать выражение:

   

Следует напомнить, что первое начало термодинамики не указывает направление, в котором происходит термодинамический процесс. Формула первого начала отображает только изменение параметров системы, если процесс происходит. В термодинамике за указание на направление процесса отвечает второе начало.

Формулы первого начала термодинамики для процессов

Будем считать, что все далее рассматриваемые процессы происходят в идеальном газе.

Для процесса, происходящего в некоторой массе газа при постоянной температуре (изотермический процесс), формула первого начала термодинамики преобразуется к виду:

   

Из выражения (4) следует, что вся теплота, которую получает термодинамическая система, расходуется на совершение этой системой работы.

Формулой первого начала термодинамики для изохорного процесса служит выражение:

   

При изохорном процессе, все тепло, полученное системой, идет на увеличение ее внутренней энергии.

В изобарном процессе формула первого закона термодинамики остается без изменения (3).

Адиабатный процесс отличается тем, что он происходит без обмена теплотой с окружающей средой. В формуле для первого начала термодинамики это отражается так:

   

В адиабатическом процессе газ совершает работу за счет своей внутренней энергии.

Примеры решения задач по теме «Первый закон термодинамики»

ru.solverbook.com

Законы термодинамики и их описание :: SYL.ru

Законы термодинамики называют также ее началами. На самом деле начало термодинамики представляет собой не что иное, как совокупность тех или иных постулатов, которые лежат в основе соответствующего раздела молекулярной физики. Данные положения устанавливали в течение научных исследований. В то же время они были доказаны экспериментальным путем. Почему же законы термодинамики принимают за постулаты? Все дело в том, что таким образом термодинамику можно строить аксиоматическим путем.

Основные законы термодинамики

Немного о структуризации. Законы термодинамики разделяются на четыре группы, каждая из которых имеет определенный смысл. Итак, что могут поведать нам начала термодинамики?

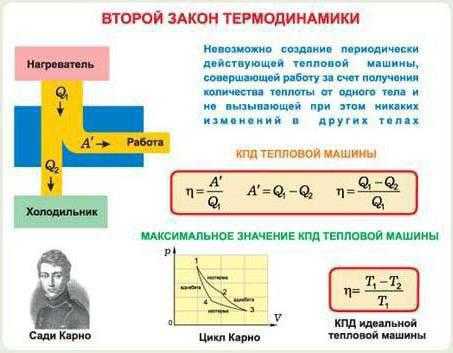
Первое и второе

Первое начало расскажет о том, как применяется закон сохранения энергии по отношению к той или иной термодинамической системе. Второе начало выдвигает некоторые ограничения, которые применяются к направлениям термодинамических процессов. Более конкретно, они запрещают самопроизвольную передачу тепла, совершаемую от менее нагретого к более нагретому телу. Есть у второго закона термодинамики и альтернативное название: закон возрастания энтропии.

Третье и четвертое

Третий закон описывает поведение энтропии вблизи абсолютного температурного нуля. Есть еще одно начало, последнее. Оно носит название “нулевой закон термодинамики”. Смысл его заключается в том, что любая замкнутая система придет к состоянию термодинамического равновесия и из него выйти уже самостоятельно не сможет. При этом ее начальное состояние может быть любым.

Зачем нужны начала термодинамики?

Законы термодинамики были изучены для того, чтобы описывать макроскопические параметры тех или иных систем. При этом конкретные предложения, имеющие связь с микроскопическим устройством, не выдвигаются. Этот вопрос изучается отдельно, но уже другим ответвлением науки – статистической физикой. Законы термодинамики независимы друг от друга. Что это может означать? Это нужно понимать так, что ни одно начало термодинамики из другого вывести невозможно.

Первое начало термодинамики

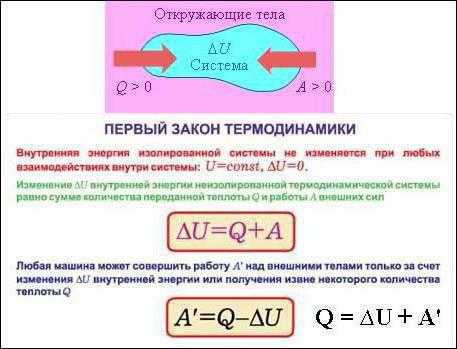
Как известно, термодинамическая система характеризуется несколькими параметрами, в числе которых есть и внутренняя энергия (обозначается буквой U). Последняя формируется из кинетической энергии, которую имеют все частицы. Это может быть энергия поступательного, а также колебательного и вращательного движения. На этом моменте вспомним о том, что энергия может быть не только кинетической, но и потенциальной. Так вот, в случае идеальных газов потенциальной энергией пренебрегают. Именно поэтому внутренняя энергия U будет складываться исключительно из кинетической энергии движения молекул и зависеть от температуры.

Эта величина – внутренняя энергия – называется иными словами функцией состояния, поскольку она определяется состоянием термодинамической системы. В нашем случае она определяется температурой газа. Следует отметить, что внутренняя энергия не зависит от того, каким был переход в состояние. Допустим, что термодинамическая система совершает круговой процесс (цикл, как его называют в молекулярной физике). Иными словами, система, выйдя из начального состояния, подвергается определенным процессам, но в результате возвращается в первичное состояние. Тогда нетрудно догадаться, что изменение внутренней энергии будет равно 0.

Как изменяется внутренняя энергия?

Изменить внутреннюю энергию идеального газа можно двумя способами. Первый вариант – совершить работу. Второй – сообщить системе то или иное количество теплоты. Логично, что второй способ подразумевает не только сообщение теплоты, но и ее отнятие.

Формулировка первого начала термодинамики

Их (формулировок) может быть несколько, так как все любят говорить по-разному. Но на самом деле суть остается той же. Она сводится к тому, что количество теплоты, которое было подведено к термодинамической системе, расходуется на совершение идеальным газом механической работы и изменение внутренней энергии. Если говорить о формуле или математической записи первого начала термодинамики, то она выглядит следующим образом: dQ = dU + dA.

– Все величины, которые входят в состав формулы, могут иметь разные знаки. Ничто не запрещает им быть отрицательными. Допустим, что к системе подводится количество теплоты Q. Тогда газ будет нагреваться. Возрастает температура, а значит, увеличивается и внутренняя энергия газа. То есть и Q, и U будут иметь положительные значения. Но если внутренняя энергия газа увеличивается, он начинает вести себя активнее, расширяться. Следовательно, работа также будет положительной. Можно сказать, что работу совершает сама система, газ.

– В случае если у системы забирают определенное количество теплоты, внутренняя энергия уменьшается, а газ сжимается. В таком случае можно говорить уже о том, что работу совершают над системой, а не она сама. Предположим опять, что некоторая термодинамическая система совершает цикл. В таком случае (как уже было сказано ранее) изменение внутренней энергии будет равно 0. Значит, работа, совершаемая газом или над ним, будет численно равна подведенной или отведенной к системе теплоте.

– Математическую запись этого следствия называют еще одной формулировкой первого начала термодинамики. Примерно она звучит следующим образом: “В природе невозможно существование двигателя первого рода, то есть, двигателя, который совершал бы работу, превосходящую полученную извне теплоту”.

Второе начало термодинамики

Нетрудно догадаться, что термодинамическое равновесие характерно для системы, в которой макроскопические величины остаются неизменными во времени. Это, конечно же, давление, объем и температура газа. Их неизменность может быть построена на нескольких условиях: на отсутствии теплопроводности, химических реакций, диффузии и других процессов. Если под действием внешних факторов система была выведена из термодинамического равновесия, она к нему со временем вернется. Но если эти факторы будут отсутствовать. Причем произойдет это самопроизвольно.

Мы пойдем немного другим путем, отличным от того, что рекомендуют многие учебники. Для начала ознакомимся со вторым началом термодинамики, а уже потом разберемся, что за величины в него входят, и что они обозначают. Итак, в замкнутой системе при наличии любых протекающих в ней процессов энтропия не убывает. Записывается второе начало термодинамики следующим образом: dS >(=) 0. Здесь знак > будет связан с необратимым процессом, а знак = – с обратимым.

Что же называется в термодинамике обратимым процессом? А это такой процесс, при котором система возвращается (спустя череду каких-то процессов) к своему первоначальному состоянию. Причем в этом случае ни в системе, ни в окружающей среде никаких изменений не остается. Иными словами, обратимый процесс – это такой процесс, для которого возможно возвращение в начальное состояние через промежуточные состояния, идентичные прямому процессу. В молекулярной физике таких процессов очень мало. Например, переход количества теплоты от более нагретого тела к менее нагретому будет необратимым. Аналогично и в случае диффузии двух веществ, а также распространения газа на весь объем.

Энтропия

Энтропия, имеющая место во втором законе термодинамики, равна изменению количества теплоты, деленному на температуру. Формула: dS = dQ/T. Она имеет определенные свойства.

www.syl.ru

1.2. Законы термодинамики

Основу термодинамики составляют фундаментальные законы природы, сформулированые на основании обобщения результатов множества опытных исследований и открытий. Из этих законов, принимаемых за аксиомы; логическим путем получены все главнейшие следствия, касающиеся различных термодинамических систем, которые именуются н а ч а л а м и или з а к о- н а м и термодинамики.

1.2.1. Первый закон термодинамики

Абсолютный по своему существу, один из наиболее общих законов природы – закон сохранения и превращения энергии. Согласно этому закону, энергия закрытой системы при любых процессах, происходящих в системе, остается неизменной. При этом энергия может только превращаться из одной формы в другую.

Первый закон термодинамики является частным случаем этого всеобщего закона и представляет собой его приложение к процессам в термодинамических системах. Он устанавливает возможность превращения различных форм энергии друг в друга и определяет, в каких количественных соотношениях эти взаимные превращения осуществляются.

Изменение энергии произвольной неизолированной системы может происходить в общем случае только за счет двух форм энергообмена – теплоты и работы:

∆E = Q –L , (1.12)

где ∆ E – изменение энергии системы;

Q – теплота, подведенная к системе;

L – работа, совершенная над системой.

Согласно уравнению (1.12), изменение энергии термодинамической системы возможно за счет подведенной к системе теплоты и совершенной над системой работой.

Уравнение (1.12) представляет собой общее аналитическое выражение первого закона термодинамики. Выразим его через параметры состояния системы. Изменение энергии ∆E получим из выражения (1.7):

∆E = ∆I + m ().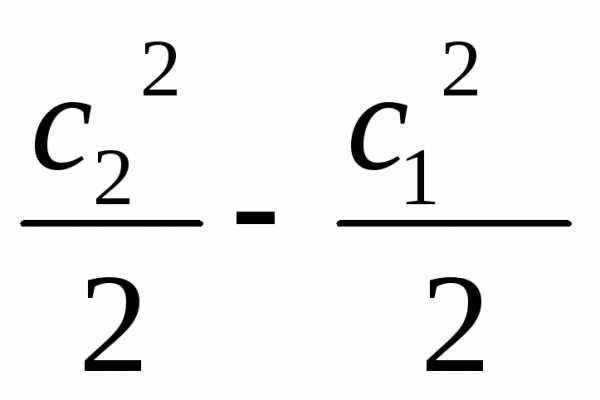

Для термодинамической системы, в которой разностью кинетической энергии можно пренебречь, изменение энергии системы будет равно изменению энтальпии, т.е. ∆E = ∆I. Тогда с учетом выражений (1.11) и (1.12) получим уравнение первого закона термодинамики в виде:

Q = ∆I + L

_тех (1.13)

Теплота, подведенная к системе, идет на изменение энтальпии системы и совершение системой технической работы.

Заменим в уравнении (1.13) изменение энтальпии ∆I изменением внутренней энергии DU и, используя выражение (1. 6), получим:

Q = ∆U + L _расш. (1.14)

Уравнения (1.13) и (1.14) представляют собой интегральную форму записи первого закона термодинамики.

Из выражения (1.13) следует, что техническая работа может быть совершена термодинамической системой за счет уменьшения энтальпии и подведенной теплоты. Если процесс круговой, то ∆I = 0, следовательно, в постоянно действующих машинах (в них процессы изменения состояния круговые) для получения технической работы необходимым условием является подведение теплоты.

Аналогичное рассуждение можно провести и по уравнению (1.14).

Термодинамическая система может совершить работу расширения только за счет уменьшения своей внутренней энергии или за счет подведенной теплоты. Если в результате процесса внутренняя энергия системы не изменяется (например, в системе не изменяется температура), то вся теплота, полученная системой от окружающей среды, идет на совершение работы:

Q = L _расш.

Это выражение позволяет дать следующие формулировки первого закона термодинамики.

При неизменной внутренней энергии системы теплота и работа эквивалентны.

Вечный двигатель первого рода невозможен.

Предполагалось, что вечный двигатель первого рода должен только совершать работу над окружающей средой, ничего не получая от нее.

До сих пор рассматривались системы произвольной массы. Для анализа удобнее пользоваться величинами, приведенными к единице массы вещества. Запишем уравнения (1.13) и (1.14) для 1 кг массы:

q = ∆i + l_тех ; (1.15)

q = ∆u + l_{рас .} (1.16)

Используя выражения (1.9) и (1.11), запишем полученные уравнения в дифференциальной форме:

dq = di – vdp (1.17)

dq= du + pdv (1.18)

Уравнения (1.17) и (1.18) представляют собой разновидность математической записи первого закона термодинамики в дифференциальной форме..

Значение первого закона:

во-первых, он формирует принцип устройства теплоэнергетических установок и систем;

во-вторых, он объясняет физическую сущность процессов, происходящих в тепловых машинах;

в-третьих, он используется при расчетах термодинамических процессов и позволяет оценить энергетический баланс тепловых машин.

1.2.2. Второй закон термодинамики

Первый закон термодинамики, являясь частным случаем закона сохранения и превращения энергии, рассматривает только его количественную сторону, заключающуюся в том, что при известном изменении энергии системы соотношение между теплотой и работой строго определенно. Этот закон не устанавливает направлений и полноты передачи энергии между телами, не определяет условий, при которых возможно преобразование теплоты в работу, не делает различий между их прямыми и обратными превращениями. Если исходить лишь из первого закона термодинамики, то правомерно считать, что любой мыслимый процесс, который не противоречит закону сохранения энергии, принципиально возможен и мог бы иметь место в природе. Ответ на поставленные вопросы дает второй закон термодинамики, который представляет собой совокупность положений, обобщающих опытные данные о качественной стороне закона сохранения и превращения энергии.

Многообразие особенностей взаимного превращения теплоты и работы, а также различные аспекты, в которых эти превращения рассматриваются, объясняют наличие нескольких, по сути эквивалентных, формулировок второго закона термодинамики.

Основные положения этого закона были высказаны французским инженером С. Карно (1824 г.). Карно пришел к выводу, что для преобразования теплоты в работу необходимы два источника теплоты с разной температурой. Само же название “Второй закон термодинамики” и исторически первая его формулировка (1850 г.) принадлежат немецкому физику Р. Клаузиусу:

“Теплота может переходить сама собой только от горячего тела к холодному; для обратного перехода надо затратить работу”,

Из этого утверждения следует, что для перехода теплоты от тела с меньшей температурой к телу с большей температурой обязательно необходим подвод энергии от внешнего источника в какой-либо форме, например, в форме работы. В противоположность этому теплота от тела с большей температурой самопроизвольно, без затрат каких-либо видов энергии, переходит к телам с меньшей температурой. Это означает, в частности, что теплообмен при конечной разности температур представляет собой строго односторонний, необратимый процесс, и направлен он в сторону тел с меньшей температурой.

Второй закон термодинамики лежит в основе теории тепловых двигателей. Тепловой двигатель представляет собой непрерывно действующее устройство, результатом действия которого является превращение теплоты в работу. Так, чтобы создать тепловой двигатель, непрерывно производящий работу, необходимо, прежде всего, иметь тело, являющееся поставщиком энергии в форме теплоты. Назовем его и с т о ч н и к о м т е п л о т ы.

Обязательно наличие и другого тела, которое воспринимает от первого

э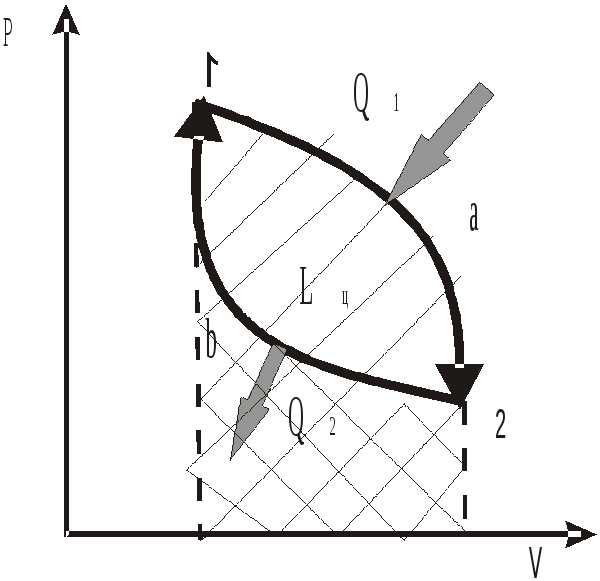нергию в форме теплоты, а отдает ее в форме работы. Это так называемое р а б о ч е е т е л о. Его роль выполняет какая-либо упругая среда (газ, пар). Подвод тепла и преобразование его в работу сопровождается изменением состояния рабочего тела. На рис. 1.6 покажем это изменение условно кривой процесса 1-а-2. Здесь изменяются параметры состояния и, прежде всего, объем рабочего тела, что приводит к совершению работы расширения. Для получения непрерывной работы требуется рабочее тело вернуть в первоначальное состояние по процессу 2-б-1. Таким образом

Рис. 1.6 для непрерывного преобразования теплоты в работу надо постоянно осуществлять этот замкнутый к р у г о в о й п р о ц е с с или ц и к л.

Круговым процессом, или циклом, называют совокупность термодинамических процессов, в результате осуществления которых рабочее тело возвращается в свое первоначальное состояние.

Чтобы замкнуть цикл, требуется затратить некоторое количество энергии, в данном случае в форме работы сжатия. Эта работа сжатия должна быть компенсирована путем отвода от рабочего тела эквивалентного ей количества теплоты. Следовательно, необходимо третье тело, которое воспринимает эту компенсацию. Назовем его т е п л о п р и е м н и к о м. Чтобы теплоприемник воспринял некоторое количество теплоты, его температура должна быть ниже температуры теплоисточника.

В результате выполненного таким способом цикла 1-а-2-б-1, изображенного на рис. 1.6, только часть теплоты Q₁, полученной рабочим телом от теплоисточника, преобразовывается в работу, другая же часть этой теплоты Q₂ обязательно отдается теплоприемнику.

Начало формы

В рассмотренной схеме непрерывно действующего теплового двигателя одно и то же рабочее тело постоянно участвует в круговом процессе. В циклах реальных двигателей рабочее вещество периодически обновляется, т.е. заменяет равным количеством “свежего” вещества. С термодинамической точки зрения замена рабочего вещества может рассматриваться как возращение рабочего тела в исходное состояние.

Конец формы

Таким образом, для непрерывного преобразования теплоты в работу нужны: источник теплоты; рабочее тело и теплоприемник, имеющий более низкую температуру, чем теплоисточник. Отвод некоторой части теплоты в теплоприемник является обязательным условием функционирования тепловых двигателей. Это условие изложено в следующих формулировках второго закона термодинамики:

“Невозможно построить периодически действующую машину, кото- рая не производит ничего другого, кроме работы и охлаждения источника теплоты” (В. Томсон).

“ Все естественные процессы являются переходом от менее вероятных к более вероятным состояниям” (Л. Больцман).

“Осуществление вечного двигателя второго рода невозможно”

(В. Освальд).

Под “вечным” двигателем второго рода подразумевается такой тепловой двигатель, который мог бы совершать непрерывную работу, имеятолько один источник теплоты. Из второго закона термодинамики следует, что какой бы по величине тепловой энергией ни обладала система, при равенстве температур тел системы эту энергию нельзя преобразовать в работу. По этой причине оказались бесплодными попытки тысяч изобретателей “вечных” двигателей к совершению работы расширения.

Распределение энергии, полученной от теплоисточника, в тепловых двигателях схематично показано на рис. 1.7. Полезная работа, совершаемая 1 кг массы рабочего тела за цикл, равна разности работ расширения l _расш и сжатия l _сж , т.е.

l _ц = l _расш – l _сж. (1.19)

Количественную связь между теплотой и работой для 1 кг рабочего тела в процессах расширения 1-а-2 и сжатия 2-б-1

(см. рис. 1.6) на основании первого закона термодинамики запишем уравнениями:

q₁ = ∆ u _{1-a 2} + l _расш и q₂ = ∆u _2-б-1 + l _{cж ,}

где q₁ – количество теплоты, подведенного к 1 кг рабочего тела от теплоисточника;

q₂ – количество теплоты, отведенного от

1 кг рабочего тела к теплоприемнику;

∆u_1-а-2 и ∆u_2-б-1 – изменение внутрен-

ней энергии 1 кг рабочего тела в процессахРис. 1.7

1-а-2 и 2-б-1, соответственно.

Вычтем второе уравнение из первого и получим:

q₁ – q₂ = ∆u _1-а-2-б-1 + (l _расш – l _сж).

Так как рабочее тело возвращается в исходное состояние, то изменение внутренней энергии за цикл будет равно нулю, т.е. ∆u_1-а-2-б-1= 0. В итоге с учетом выражения (1.19) получим:

l _ц = q₁ – q₂ (1.20)

Из (1.20) следует, что, во-первых, работа цикла совершается только за счет теплоты и, во-вторых, работа цикла равна теплоте, подведенной от теплоисточника, за вычетом теплоты, отведенной к теплоприемнику.

Долю полезно используемой теплоты оценивают т е р м и ч е с к и м

КПД цикла, который обозначают η _t .

Под термическим КПД понимают отношение теплоты, преобразо-

ванной в полезную работу цикла, ко всей подведенной теплоте:

η _t = 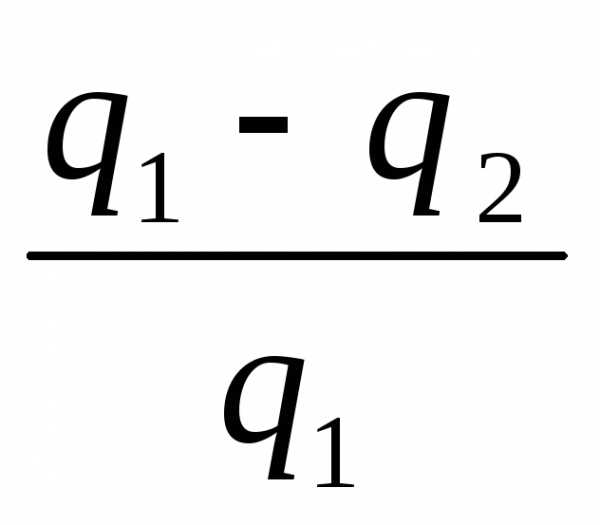или η_t = 1 – 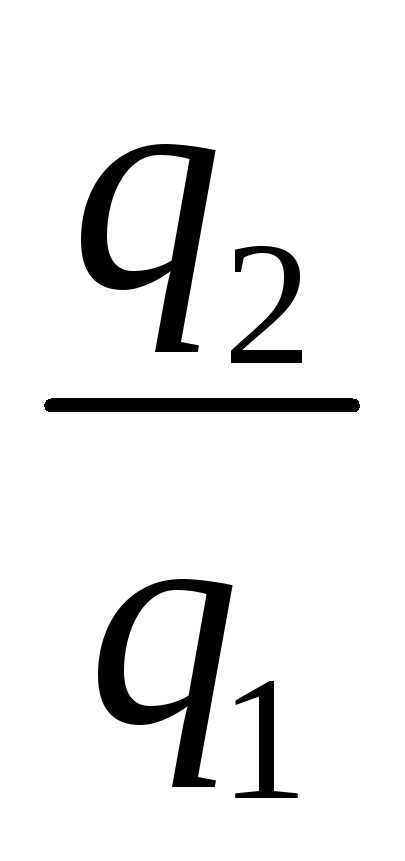. (1.21)

Из данных выражений следует, что чем меньше теплоы передается теплоприемнику, тем больше значение η_t. Это означает, что происходит более полное преобразование теплоты в работу.

Ввиду необходимости передавать часть энергии в форме теплоты теплоприемнику термический КПД любого цикла не может быть равен единице.

Таким образом, второй закон термодинамики устанавливает полноту преобразования теплоты в работу.

Кроме того, он указывает на качественное различие между теплотой и работой. Если работа может вся без остатка преобразовываться в теплоту, то теплота никогда полностью не может быть преобразована в работу.

Уникальным научным достижением явилось выражение этого качественного различия количественной величиной – э н т р о п и е й.

1.2.3. Энтропия. Математическое выражение второго закона

термодинамики.

“Энтропия” в переводе с греческого означает “поворот” или “превращение”. Сначала понятие энтропии было введено в науку формально. Р.Клаузиус (1854г.) показал, что для термодинамической системы существует некая функция S , приращение которой определяется выражением

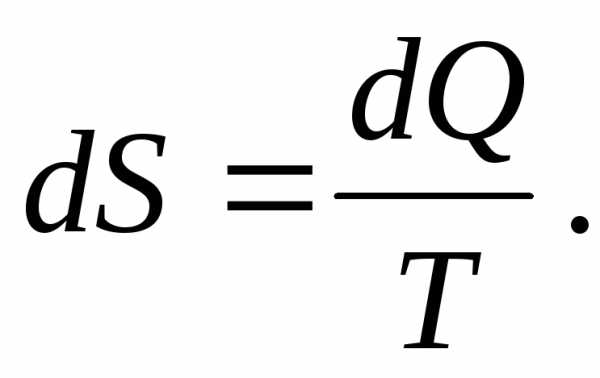(1.22)

Он назвал эту функцию энтропией. Позже, при рассмотрении большого числа задач, было выявлено физическое содержание энтропии.

Так как энтропия не поддается простому интуитивному представлению, попытаемся уточнить ее смысл путем сравнения с аналогичными величинами, более доступными для нашего понимания. Запишем выражение работы расширения в дифференциальной форме:

dL_расш = p dV.

Здесь давление p является величиной необходимой, но не достаточной для совершения работы. Изменение же объема приведет к работе расширения. Объем в приведенном уравнении выполняет свойство достаточного параметра. Таким образом , судить о том, что совершена работа расширения или сжатия можно лишь по изменению объема.

Теперь запишем выражение (1.22) в виде:

dQ = T dS.

Здесь температура является величиной необходимой, но еще не достаточной для того, что бы говорить о том, подводится тепло к системе или отводится от неё. Так, в адиабатном процессе система не обменивается теплотой с окружающей средой, а температура изменяется существенно. Остается один параметр, который должен обладать свойством достаточности, и этот параметр – энтропия. Только по изменению энтропии можно судить о теплообмене системы с окружающей средой. Отсюда

Энтропия есть калорический параметр состояния термодинамичес-

кой системы, характеризующий направление протекания процесса

теплообмена между системой и внешней средой.

Можно сказать, что энтропия – это единственная физическая величина, изменение которой в процессе однозначно указывает на наличие энергообмена в форме теплоты.

Выражение (1.22) устанавливает как качественную, так и количественную связь между теплотой и энтропией: если изменяется энтропия тела или системы, то в том и другом случае подводится энергия в форме теплоты; если энтропия неизменна, то процесс протекает без энергообмена в форме теплоты. Равенство (1.22) является аналитическим выражением второго закона термодинамики для элементарного равновесного процесса.

.Выражение (1.22) дает возможность установить единицу энтропии, которая равна Дж/К.

Абсолютное значение энтропии определяется с точностью до некоторой постоянной S₀. Численное значение постоянной S₀ на основе только первого и второго законов термодинамики не может быть определено. Однако это не накладывает ограничений на использование энтропии в расчетах. В практике, как правило, интерес представляет не абсолютная величина энтропии, а ее изменение, для которого численное значение постоянной S₀ особой роли не играет. Поэтому часто величине придают произвольное значение для условно принятого, так называемого с т а н д а р т н о г о состояния тела. Если это стандартное состояние считать исходным и приписать ему значение энтропии S₀, то для вычисления энтропии в состоянии а будет выражение:

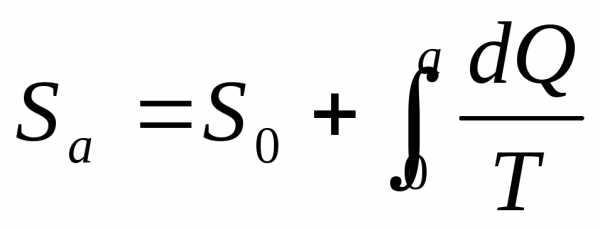
Приведенное значение энтропии обозначают через s = S / m c единицей измерения Дж/(кг×К).

Выражение (1.22), записанное через приведенные значения, будет иметь вид:

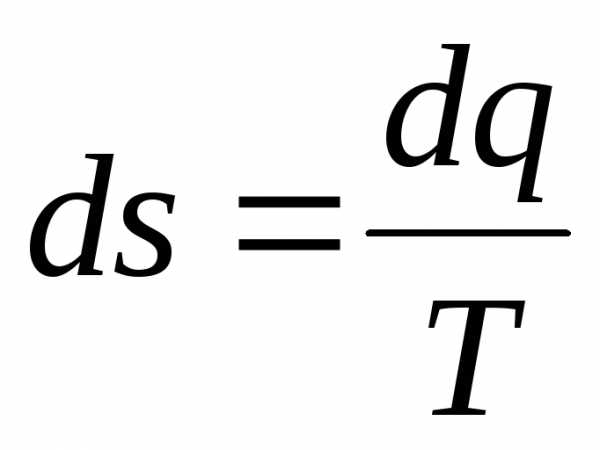. (1.23)

Энтропия, являясь калорическим параметром, обладает рядом свойств.

1. Энтропия является однозначной функцией состояния системы.

2. Энтропия, подобно внутренней энергии, является аддитивной величиной.

.

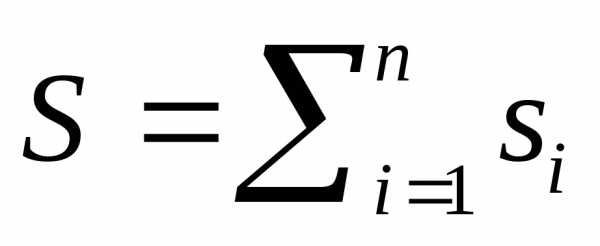3.Для обратимых и необратимых процессов в термодинамической сис

теме изменение энтропии определяется уравнением:

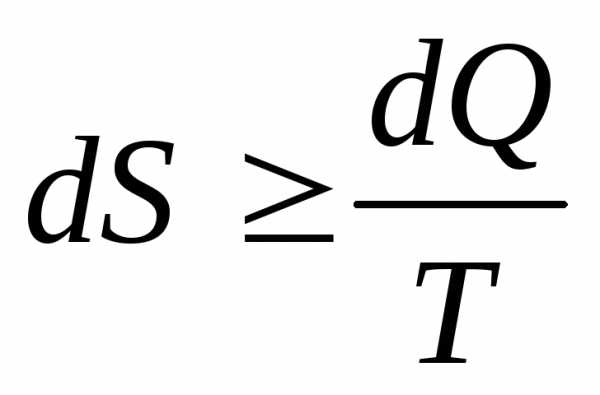, (1.24)

в котором знак равенства относится к обратимым процессам, знак ²больше² – к необратимым.

. Из выражений (1.24) следует, что энтропия изолированной системы может оставаться без изменения или возрастать, но не уменьшаться.

1.2.4. Эксергия

Введение понятия ‘энтропия’ дает возможность количественно оценить качественное различие между теплотой и работой. Для системы массой 1 кг получим уравнения, объединяющие аналитические выражения первого и второго законов термодинамики. Так, из выражений (1.23) и (1.19) следует:

ds = 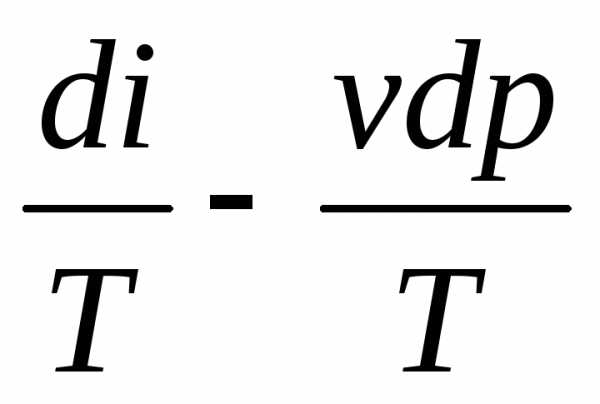. (1.25)

Из равенств (1.23) и (1.18) получим:

ds = 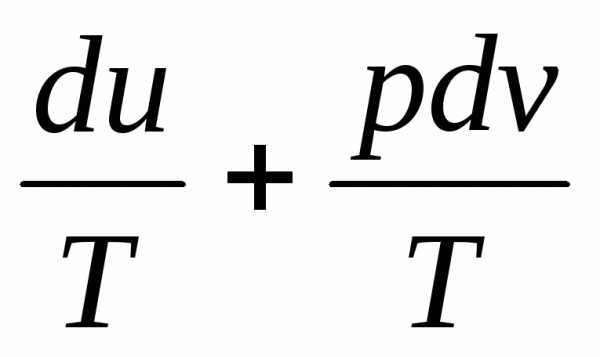. (1.26)

Уравнения в виде (1.25) и (1.26) именуют т е р м о д и н а м и ч е с к и- м и т о ж д е с т в а м и. С их помощью в термодинамике устанавливается ряд особенностей систем, полнее раскрываются связи между физическими величинами в процессах.

Используя уравнение (1.25), установим максимально возможное количество технической работы, которую может совершить данная термодинамическая система, находящаяся в заданном начальном состоянии, если все совершаемые системой процессы обратимы и осуществляются до конечного состояния, равновесного с окружающей средой.

В термодинамике максимально возможную техническую работу системы называют э к с е р г и е й.

Обозначают эксэргию системы через E_x. За единицу эксэргии в СИ принят джоуль. Ее приведенное значение (e_x = Е_x/m) имеет единицу измерения Дж/кг.

В закрытой термодинамической системе при преобразовании теплоты в работу по циклу Карно можно принять e_x = l _ц . Тогда, при отводе тепла от источника с температурой T₁ в окружающую среду с температурой T₀ вправе записать e_x = q·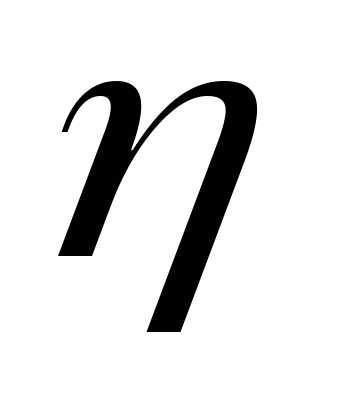_t = q (1 – 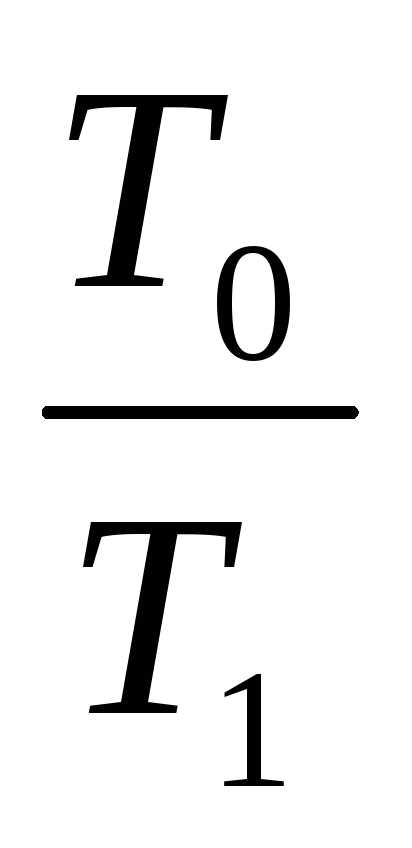). Определим условия, при которых эти преобразования дадут максимально возможную работу в других циклах.

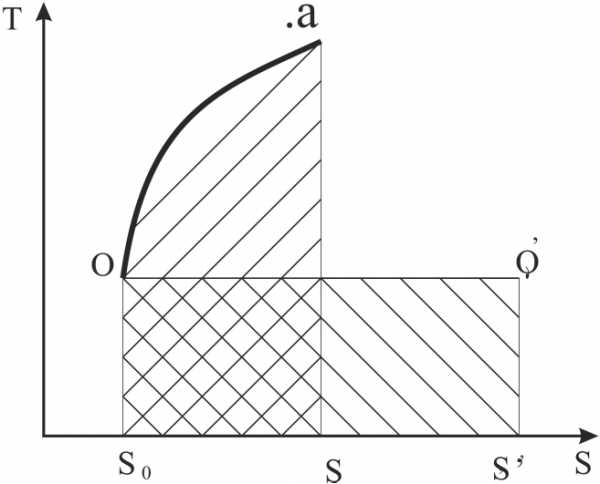Пусть начальное состояние системы характеризуется точкой а, рис.1.8. При взаимо-действии с окружающей средой состояние с истемы стремится к равновесному, обозначенному точкойо. Процесс а-о не что иное, как переход системы из начального в равновесное состояние. Будем иметь в виду, что температура окружающей среды, несмотря н

а

а ее взаимодействие с системой, остается постоянной и равнойT₀. Используя уравнение первого закона термодинамики вида (1.15) и Рис. 1.8

и заменяя техническую работу эксэргией, получим:

e_x = q_a–o+( i₀ – i_а). (1.27)

Изменение энтальпии не зависит от характера процесса. Поэтому, если известны начальное и конечное состояние системы, всегда можно определить разность энтальпий. Количество тепла является функцией процесс а-о. Для определения q_a–o воспользуемся вторым законом термодинамики. Очевидно, что количество тепла, полученное окружающей средой q_ср, равно количеству тепла, переданному системой среде, q_а-о, т.е.

q_ср = – q_a–o (1.28)

Количество тепла q_a–o пропорционально площади под кривой процесса (рис.1.8, пл.s_o–o–a–s_a). Окружающая среда воспринимает теплоту в изотермическом процессе при T = T_o. Начальное состояние этого процесса характеризуется точкой о, а конечное (точка о^′) должно быть таким, чтобы пл. s_o–o–o^‘–s_o/ , согласно (1.28), была равна пл. s_o–o–a–s_a.

Так как по второму закону термодинамики

dq_ср = T_o ds_ср,

то после интегрирования этого выражения от состояния о до состояния а будет иметь:

q_cp = T₀(s_0′ -s_a) = T₀( s_a –s₀) + T₀ (s_0′ – s_a). (1.29)

Тогда с учетом (1.28) выражение (1.27) запишется:

e_x = ( i_a – i_o ) – T_o( s_a – s_o ) – T_o (s_o/ – s_a ). (1.30)

Из уравнения (1.30) следует ряд важных выводов:

1. В системе при обратимых процессах эксэргия больше, чем в той-же системе с необратимыми процессами, т.к. T₀ (s_0/ –s_a ) ≥ 0.

2. Чем больше значение начальной энтропии системы s_a, тем меньшую работу может она совершить при неизменной разности энтальпий (i_a – i₀). Следовательно, энтропия характеризует энергию системы.

– пределяет условия, необходимые для взаимного преобразования таких форм энергообмена, как теплота и работа;

– устанавливает полноту преобразования теплоты в работу.

1.2.5 Понятие о третьем законе термодинамики

При изучении свойств различных веществ в условиях низких температур, близких к абсолютному нулю (Т = 0), обнаруживается важная закономерность в поведении реальных тел: в области абсолютного нуля энтропия тела в любом равновесном состоянии не зависит от температуры, объема и других параметров, характеризующих состояние тела.

Этот результат, являющийся обобщением ряда опытных данных и не вытекающий непосредственно из первого или второго законов термодинамики, составляет содержание тепловой теоремы Нернста.

Из теоремы следует, что в каком бы состоянии – жидком или твердом, в виде чистого вещества или химического соединения – ни существовало вещество, его энтропия при Т→ 0 имеет одно и то же значение. Постоянство энтропии при Т→ 0 означает, что в области абсолютного нуля dq всегда равно нулю. Следовательно, нельзя достигнуть абсолютного нуля с помощью отвода теплоты от тела, поскольку при T→ 0 каждое из тел при любом процессе изменения состояния сохраняет неизменное значение энтропии, т.е. перестает отдавать теплоту окружающей среде.

В. Нернст, используя квантовую теорию М. Планка, пришел к выводу, что lim ∆s_{T→ 0} = 0. (1.31)

Отсюда и формулировка третьего закона термодинамики.

При температуре абсолютного нуля энтропия всех веществ в состоянии равновесия независимо от давления, плотности и фазы обращается в нуль.

Аналитическим выражением третьего закона термодинамики является равенство (1.31).

studfiles.net

Первый закон термодинамики, теория и примеры

Существует две формы передачи энергии от одних тел к другим — это совершение работы одних тел над другими и передача теплоты. Энергия механического движения может переходить в энергию теплового движения и наоборот. В таких переходах энергии выполняется закон сохранения энергии. В применении к процессам, рассматриваемым в термодинамике, закон сохранения энергии именуется первым законом (или первым началом) термодинамики. Этот закон является обобщением эмпирических данных.

Формулировка первого закона термодинамики

Первый закон термодинамики формулируют следующим образом:

Количество теплоты, которое подводится к системе, расходуется на совершение данной системой работы (против внешних сил) и изменение ее внутренней энергии. В математическом виде первый закон термодинамики можно записать в интегральном виде:

   

где – количество теплоты, которое получает термодинамическая система; – изменение внутренней энергии рассматриваемой системы; A – работа, которую выполняет система над внешними телами (против внешних сил).

В дифференциальном виде первый закон термодинамики записывают как:

   

где – элемент количества теплоты, который получает система; – бесконечно малая работа, которую выполняет термодинамическая система; – элементарное изменение внутренней энергии, рассматриваемой системы. Следует обратить внимание на то, что в формуле (2) – элементарное изменение внутренней энергии является полным дифференциалом, в отличие от и .

Количество теплоты считают положительным, если система тепло получает и отрицательным, если тепло отводится от термодинамической системы. Работа будет больше нуля, если ее совершает система, и работа будет считаться отрицательной, если она совершается над системой внешними силами.

В то случае, если система вернулась в первоначальное состояние, то изменение ее внутренней энергии будет равно нулю:

   

В таком случае в соответствии с первым законом термодинамики мы имеем:

   

Выражение (4) означает, что невозможен вечный двигатель первого рода. То есть, принципиально нельзя создать периодически действующую систему (тепловой двигатель), совершающую работу, которая была бы больше, чем количество теплоты, полученное системой извне. Положение о невозможности вечного двигателя первого рода, также является одним из вариантов формулировки первого закона термодинамики.

Примеры решения задач

ru.solverbook.com

Первый и второй законы термодинамики.

Первый закон термодинамики



Первый закон термодинамики представляет собой закон сохранения энергии применительно к термодинамическим процессам: энергия не исчезает в никуда и не возникает из ничего, а лишь переходит из одного вида в другой в эквивалентных количествах. Примером может послужить переход теплоты (тепловой энергии) в механическую энергию, и наоборот.

Если к М кг газа, занимающего объем V (м³) при температуре Т подвести при постоянном давлении некоторое количество теплоты dQ, то в результате этого температура газа повысится на dT, а объем – на dV. Повышение температуры связано с увеличением кинетической энергии движения молекул dK.
Увеличение объема сопровождается увеличением расстояния между молекулами и, как следствие, уменьшением потенциальной энергии dH взаимодействия между ними. Кроме того, увеличив объем, газ совершает работу dA по преодолению внешних сил.
Если, кроме указанных, никаких иных процессов в рабочем теле не происходит, то на основании закона сохранения энергии можно записать:

dQ = dK + dH + dA.

Сумма dK + dH представляет собой изменение внутренней энергии dU молекул системы в результате подвода теплоты.
Тогда формулу сохранения энергии для термодинамического процесса можно записать в виде:

dQ = dU + dA    или    dQ = dU + pdV.

Это уравнение представляет собой математическое выражение первого закона термодинамики: количество теплоты dQ, подводимое к системе газа, затрачивается на изменение ее внутренней энергии dU и совершение внешней работы dA.

Условно считают, что при dQ > 0 теплота сообщается рабочему телу, а при dQ < 0 теплота отнимается от тела. При dA > 0 система совершает работу (газ расширяется), а при dA < 0 работа совершается над системой (газ сжимается).

Для идеального газа, между молекулами которого нет взаимодействия, изменение внутренней энергии dU полностью определяется изменением кинетической энергии движения (т. е. увеличением скорости молекул), а изменение объема характеризует работу газа по преодолению внешних сил.

Первый закон термодинамики имеет еще одну формулировку: энергия изолированной термодинамической системы остается неизменной независимо от того, какие процессы в ней протекают.
Невозможно построить вечный двигатель первого рода, т. е. периодически действующую машину, которая совершала бы работу без затраты энергии.

***



Второй закон термодинамики

Первый закон термодинамики описывает количественные соотношения между параметрами термодинамической системы, имеющими место в процессах преобразования тепловой энергии в механическую и наоборот, но не устанавливает условия, при которых эти процессы возможны. Эти условия, необходимые для преобразования одного вида энергии в другой, раскрывает второй закон термодинамики.

Существует несколько формулировок этого закона, и каждая из них имеет одинаковое смысловое содержание. Здесь приведены наиболее часто упоминающиеся формулировки второго закона термодинамики.

1. Для превращения теплоты в механическую работу необходимо иметь источник теплоты и холодильник, температура которого ниже температуры источника, т. е. необходим температурный перепад.

2. Нельзя осуществить тепловой двигатель, единственным результатом действия которого было бы превращение теплоты какого-либо тела в работу без того, чтобы часть теплоты не передавалась другим телам.
Из этой формулировки можно сделать вывод, что невозможно построить вечный двигатель, совершающий работу благодаря лишь одному источнику теплоты, поскольку любой, даже самый колоссальный источник теплоты в виде материального тела не способен отдать тепловой энергии больше, чем ему позволяет энтальпия (часть полной энергии тела, которую можно превратить в теплоту, охладив тело до температуры абсолютного нуля).

3. Теплота не может сама по себе переходить от менее нагретого тела к более нагретому без затраты внешней работы.

Как видите, второй закон термодинамики не имеет в своей основе формулярнго содержания, а лишь описывает условия, при которых возможны те или иные термодинамические явления и процессы, подтверждая, по сути, общий закон сохранения энергии.

***

Что такое удельная теплоемкость?

Скачать теоретические вопросы к экзаменационным билетам
по учебной дисциплине “Основы гидравлики и теплотехники”
(в формате Word, размер файла 68 кБ)

Скачать рабочую программу
по учебной дисциплине “Основы гидравлики и теплотехники” (в формате Word):

Скачать календарно-тематический план
по учебной дисциплине “Основы гидравлики и теплотехники” (в формате Word):



k-a-t.ru

Второй закон термодинамики, теория и примеры

Как известно, первое начало термодинамики отображает закон сохранения энергии в термодинамических процессах, однако оно не дает представление о направлении протекания процессов. Помимо этого можно придумать множество термодинамических процессов, которые не будут противоречить первому началу, но в реальной действительности таких процессов не существует. Существование второго закона (начала) термодинамики вызвано необходимостью установить возможность того или иного процесса. Этот закон определяет направление течения термодинамических процессов. При формулировке второго начала термодинамики используют понятия энтропии и неравенство Клаузиуса. В таком случае второй закон термодинамики формулируется как закон роста энтропии замкнутой системы, если процесс является необратимым.

Формулировки второго закона термодинамики

Если в замкнутой системе происходит процесс, то энтропия этой системы не убывает. В виде формулы второй закон термодинамики записывают как:

   

где S – энтропия; L – путь по которому система переходит из одного состояния в другое.

В данной формулировке второго начала термодинамики следует обратить внимание на то, что рассматриваемая система должна быть замкнутой. В незамкнутой системе энтропия может вести себя как угодно (и убывать, и возрастать, и оставаться постоянной). Заметим, что энтропия не изменяется в замкнутой системе при обратимых процессах.

Рост энтропии в замкнутой системе при необратимых процессах — это переход термодинамической системы из состояний с меньшей вероятностью в состояния с большей вероятностью. Известная формула Больцмана дает статистическое толкование второго закона термодинамики:

   

где k – постоянная Больцмана; w – термодинамическая вероятность (количество способов при помощи которых, может реализовываться рассматриваемое макросостояние системы). Так, второй закон термодинамики является статистическим законом, который связан с описанием закономерностей теплового (хаотического) движения молекул, которые составляют термодинамическую систему.

Другие формулировки второго закона термодинамики

Существует ряд других формулировок второго закона термодинамики:

1) Формулировка Кельвина: Невозможно создать круговой процесс, результатом которого станет исключительно превращение теплоты, которое получено от нагревателя, в работу. Из данной формулировки второго закона термодинамики делают вывод о невозможности создания вечного двигателя второго рода. Это означает, что периодически действующая тепловая машина должна иметь нагреватель, рабочее тело и холодильник. При этом КПД идеальной тепловой машины не может быть больше, чем КПД цикла Карно:

   

где – температура нагревателя; — температура холодильника; ().

2) Формулировка Клаузиуса: Невозможно создать круговой процесс в результате которого будет происходить исключительно передача тепла от тела с меньшей температурой к телу с большей температурой.

Второй закон термодинамики отмечает существенное различие между двумя формами передачи энергии (работой и теплотой). Из этого закона следует, переход упорядоченного перемещение тела, как единого целого в хаотическое движение молекул тела и внешней среды – является необратимым процессом. При этом упорядоченное движение может переходить в хаотическое без дополнительных (компенсационных) процессов. Тогда как переход неупорядоченного движения в упорядоченное должен сопровождаться компенсирующим процессом.

Примеры решения задач

ru.solverbook.com

---