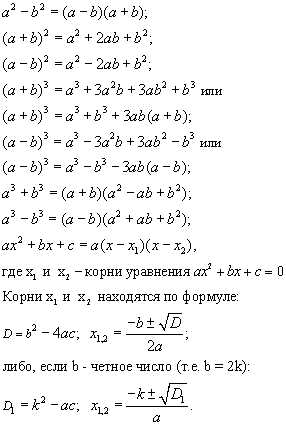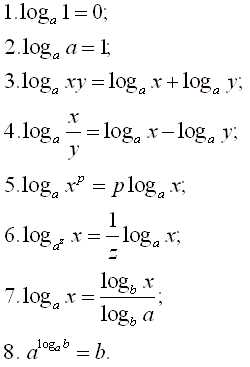Формулы со – Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике – Алгебра – Формулы сокращенного умножения
- Комментариев к записи Формулы со – Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике – Алгебра – Формулы сокращенного умножения нет
- Советы абитуриенту
- Формулы сокращенного умножения
- Формулы сокращенного умножения. Примеры.
- Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике – Алгебра – Формулы сокращенного умножения
- Все формулы по математике
- Формулы Арифметики:
- Формулы Алгебры:
- Геометрические Формулы:
- Арифметические формулы:
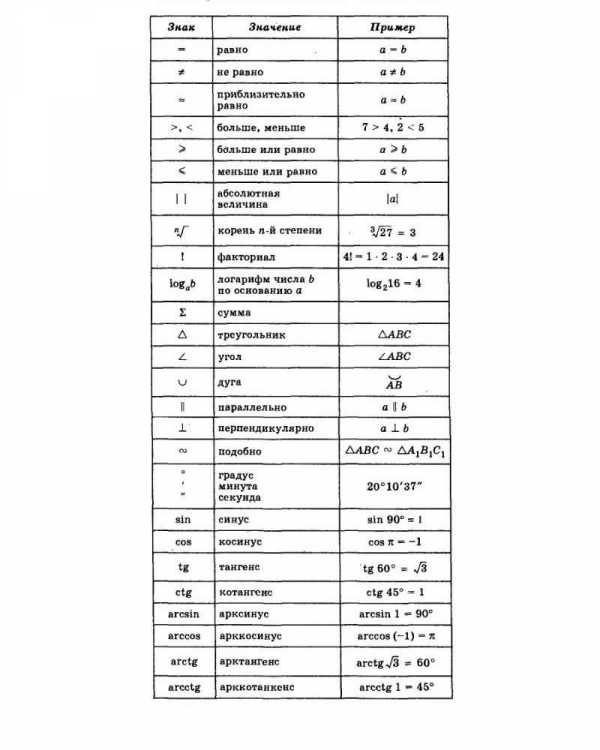
- Некоторые математические обозначения и сокращения:
- Признаки делимости
- Признаки делимости на «2»
- Абсолютная величина — формулы (модуль)
- Формулы Действия с дробями
- Пропорции
- Средние величины
- Некоторые конечные числовые ряды
- Тождественные преобразования алгебраических и тригонометрических выражений
- Многочлены
- Свойства числовых неравенств
- Соотношения между тригонометрическими функциями одного и того же аргумента
- Формулы Прогрессии:
- Основные правила дифференцирования:
- Работа в Excel с формулами и таблицами для чайников
- Формулы со ссылками на другие листы
- Стоковые векторные изображения Формула со2
Формулы сокращенного умножения
Формулы сокращенного умножения.
Цели:
– Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.
– Применение формул сокращенного умножения при решении примеров.
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть.
Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b)2 = a2 + 2ab + b2
2. Квадрат разности двух выражений равен
(a – b)2 = a2 – 2ab + b2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.a2 – b2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a – b)3 = a3 – 3a2b + 3ab2 – b3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
a3 + b3 = (a + b) (a2 – ab + b2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
a3 – b3 = (a – b) (a2 + ab + b2)
Применение формул сокращенного умножения при решении примеров.
Пример 1.
Вычислить
а) (40+1)2
б) 982
Решение:
а) Используя формулу квадрата суммы двух выражений, имеем
б) Используя формулу квадрата разности двух выражений, получим
982 = (100 – 2)2 = 1002 – 2 · 100 · 2 + 22 = 10000 – 400 + 4 = 9604
Пример 2.
Вычислить
Решение
Используя формулу разности квадратов двух выражений, получим
Пример 3.
Упростить выражение
(х – у)2 + (х + у)2
Решение
Воспользуемся формулами квадрата суммы и квадрата разности двух выражений
(х – у)2 + (х + у)2 = х2 – 2ху + у2 + х2 + 2ху + у2 = 2х2 + 2у2
Формулы сокращенного умножения в одной таблице:
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
a2 – b2 = (a – b) (a+b)
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a – b)3 = a3 – 3a2b + 3ab2 – b3
a3 + b3 = (a + b) (a2 – ab + b2)
a3 – b3 = (a – b) (a2 + ab + b2)
mirurokov.ru
Формулы сокращенного умножения. Примеры.
data-ad-client=”ca-pub-8602906481123293″
data-ad-slot=”2890988705″>
1) Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a+b)2 = a2+2ab+b2
a) (x + 2y)2 = x2 + 2 ·x·2y + (2y)2 = x2 + 4xy + 4y2
б) (2k + 3n)2 = (2k)2 + 2·2k·3n + (3n)2 = 4k2 + 12kn + 9n2
2) Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)2 = a2-2ab+b2
а) (2a – c)2
= (2a)2-2·2a·c + c2 = 4a2 – 4ac + c2б) (3a – 5b)2 = (3a)2-2·3a·5b + (5b)2 = 9a2 – 30ab + 25b2
3) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
a2–b2 = (a–b)(a+b)
a) 9x2 – 16y2 = (3x)2 – (4y)2 = (3x – 4y)(3x + 4y)
б) (6k – 5n)( 6k + 5n) = (6k)2 – (5n)2 = 36k2 – 25n2
4) Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a+b)3 = a3+3a2b+3ab2+b3
a) (m + 2n)3 = m3 + 3·m2·2n + 3·m·(2n)
б) (3x + 2y)3 = (3x)3 + 3·(3x)2·2y + 3·3x·(2y)2 + (2y)3 = 27x3 + 54x2y + 36xy2 + 8y3
5) Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a-b)3 = a3-3a2b+3ab2-b3
а) (2x – y)3 = (2x)3-3·(2x)2·y + 3·2x·y2 – y3 = 8x3 – 12x2y + 6xy2 – y3
б) (x – 3n)3 = x3-3·x2·3n + 3·x·(3n)2 – (3n)3 = x3 – 9x2n + 27xn2 – 27n3
6) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.a3+b3 = (a+b)(a2–ab+b2)
a) 125 + 8x3 = 53 + (2x)3 = (5 + 2x)(52 — 5·2x + (2x)2) = (5 + 2x)(25 – 10x + 4x2)
б) (1 + 3m)(1 – 3m + 9m2) = 13 + (3m)3 = 1 + 27m3
7) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
a3-b3 = (a-b)(a2+ab+b2)
а) 64с3 – 8 = (4с)3 – 23 = (4с – 2)((4с)2 + 4с·2 + 22) = (4с – 2)(16с2 + 8с + 4)
б) (3a – 5b)(9a2 + 15ab + 25b2) = (3a)3 – (5b)3 = 27a3 – 125b3
Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.Запись имеет метки: Правила и формулы сокращенного умножения
www.mathematics-repetition.com
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике – Алгебра – Формулы сокращенного умножения
Формулы сокращенного умножения включают в себя следующие группы формул:
Степень суммы
Группа формул «Степень суммы» составляет Таблицу 1. Эти формулы можно получить, выполняя вычисления в следующем порядке:
| (x + y)2 = (x + y)(x + y) , (x + y)3 = (x + y)2(x + y) , (x + y)4 = (x + y)3(x + y) |
и т.д.
Группу формул «Степень суммы» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.
Таблица 1. – Степень суммы
| Название формулы | Формула |
| Квадрат (вторая степень) суммы | (x + y)2 = x2 + 2xy + y2 |
| Куб (третья степень) суммы | (x + y)3 = x3 + 3x2y + 3xy2 + y3 |
| Четвертая степень суммы | (x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4 |
| Пятая степень суммы | (x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5 |
| Шестая степень суммы | (x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6 |
| … | … |
Квадрат (вторая степень) суммы (x + y)2 = x2 + 2xy + y2 |
Куб (третья степень) суммы (x + y)3 = |
Четвертая степень суммы (x + y)4 = x4 + 4x3y + |
Пятая степень суммы (x + y)5 = x5 + 5x4y + |
Шестая степень суммы (x + y)6 = x6 + 6x5y + |
| … |
Общая формула для вычисления суммы
(x + y)n
с произвольным натуральным значением n рассматривается в разделе «Бином Ньютона» нашего справочника.
Степень разности
Если в формулах из Таблицы 1 заменить y на – y , то мы получим группу формул «Степень разности» (Таблица 2.):
Таблица 2. – Степень разности
| Название формулы | Формула |
| Квадрат (вторая степень) разности | (x – y)2 = x2 – 2xy + y2 |
| Куб (третья степень) разности | (x – y)3 = x3 – 3x2y + 3xy2 – y3 |
| Четвертая степень разности | (x – y)4 = x4 – 4x3y + 6x2y2 – 4xy3 + y4 |
| Пятая степень разности | (x – y)5 = x5 – 5x4y + 10x3y2 – 10x2y3 + 5xy4– y5 |
| Шестая степень разности | (x – y)6 = x6 – 6x5y + 15x4y2 – 20x3y3 + 15x2y4 – 6xy5 + y6 |
| … | … |
Квадрат (вторая степень) разности (x – y)2 = x2 – 2xy + y2 |
Куб (третья степень) разности (x – y)3 = |
Четвертая степень разности (x – y)4 = x4 – 4x3y + |
Пятая степень разности (x – y)5 = x5 – 5x4y + |
Шестая степень разности (x – y)6 = x6 – 6x5y + |
| … |
Квадрат многочлена
Следующая формула применяется достаточно часто и называется «Квадрат многочлена»:
Словами эту формулу можно выразить так: – «Квадрат многочлена равен сумме квадратов всех его членов плюс сумма всевозможных удвоенных произведений его членов».
Куб трехчлена
Следующая формула называется «Куб трехчлена»:
(x + y + z)3 =
= x3 + y3 + z3 + 3x2y +
+ 3x2z + 3xy2 +
+ 3xz2 +
+ 3y2z + 3yz2 + 6xyz .
Другие формулы сокращенного умножения приведены в разделе «Формулы сокращенного умножения: сумма степеней, разность степеней» нашего справочника.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Все формулы по математике
На этой странице собраны все формулы, необходимые для сдачи контрольных и самостоятельных работ, экзаменов по по алгебре, геометрии, тригонометрии, стереометрии и другим разделам математики.
Здесь вы можете скачать или посмотреть онлайн все основные тригонометрические формулы, формулу площади круга, формулы сокращенного умножения, формула длины окружности, формулы приведения и многие другие.
Можно так же распечатать необходимые сборники математических формул.
Успехов в учебе!
Формулы Арифметики:
Формулы Алгебры:
Геометрические Формулы:
Арифметические формулы:
Законы действий над числамиПереместительный закон сложения: a + b = b + a.
Сочетательный закон сложения: (a + b) + с = a + (b + c).
Переместительный закон умножения: ab = ba.
Сочетательный закон умножения: (ab)с = a(bc).
Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.
Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.
Некоторые математические обозначения и сокращения:
Признаки делимости
Признаки делимости на «2»
- Число, делящееся на «2» без остатка называется чётным, не делящееся – нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, 8) или ноль
Признаки делимости на «4»
- Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»
Признаки делимости на «8»
- Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и.т.д.)
Признаки делимости на «3» и на «9»
- Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»
Признаки делимости на «5»
- Без остатка на «5» делятся числа, последняя цифра которых «0» или «5»
Признаки делимости на «25»
- Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т.е. числа, оканчивающиеся на «00», «25», «50», «75»
Признаки делимости на «10», «100» и на «1 000»
- Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули
Признаки делимости на «11»
- Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»
Абсолютная величина — формулы (модуль)
|a| ? 0, причём |a| = 0 только если a = 0; |-a|=|a| |a2|=|a|2=a2 |ab|=|a|*|b| |a/b|=|a|/|b|, причём b ? 0; |a+b|?|a|+|b| |a-b|?|a|-|b|Формулы Действия с дробями
Формула обращения конечной десятичной дроби в рациональную дробь:
Пропорции
<span «>Два равных отношения образуют пропорцию:
Основное свойство пропорцииad = bc
Нахождение членов пропорции
Пропорции, равносильные пропорции : Производная пропорция — следствие данной пропорции в видеСредние величины
Некоторые конечные числовые ряды
Алгебра:
Тождественные преобразования алгебраических и тригонометрических выражений
Свойства степеней
- Для любых x, y и положительных a и b верны равенства:
Свойства арифметических корней
Для любых натуральных n и k, больших 1, и любых неотрицательных a и b верны равенства:Многочлены
Для любых a, b и c верны равенства:
Свойства числовых неравенств
1) Если a < b, то при любом c: a + с < b + с.
2) Если a < b и c > 0, то aс < bс.
3) Если a < b и c < 0, то aс > bс.
4) Если a < b, a и b одного знака, то 1/a > 1/b.
5) Если a < b и c < d, то a + с < b + d, a — d < b — c.
6) Если a < b, c < d, a > 0, b > 0, c > 0, d > 0, то ac < bd.
7) Если a < b, a > 0, b > 0, то
8) Если , то
Соотношения между тригонометрическими функциями одного и того же аргумента
(здесь и в дальнейшем запись n є Z означает, что n – любое целое число)Формулы сложения:
Формулы двойного аргумента:
Формулы тройного аргумента:
Формулы Прогрессии:
Арифметическая прогрессия
(a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n первых членов):
Геометрическая прогрессия
(b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn – сумма n первых членов, S – сумма бесконечной геом. прогрессии):
Производная
Основные правила дифференцирования:
- Логарифмы:

- Координаты и векторы
1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:
2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:
3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:
y = kx + q.
Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.
4. Общее уравнение прямой имеет вид: ax + by + c = 0.5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:
ax + by + c = 0.6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид:
7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:
8. Уравнение:представляет собой уравнение параболы с вершиной в точке, абсцисса которой
- Прямоугольная декартова система координат в пространстве
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:
2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:
3. Модуль вектора заданного своими координатами, находится по формуле:
4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы:
5. Единичный вектор сонаправленный с вектором находится по формуле:
6. Скалярным произведением векторов называется число:
где — угол между векторами.
7. Скалярное произведение векторов
8. Косинус угла между векторами и находится по формуле:
9. Необходимое и достаточное условие перпендикулярности векторов и имеет вид:10. Общее уравнение плоскости, перпендикулярной вектору имеет вид:
ax + by + cz + d = 0.11. Уравнение плоскости, перпендикулярной вектору и проходящей через точку (xo;yo;zo), имеет вид:
a(x — xo) + b(y — yo) + c(z — zo) = 0.12. Уравнение сферы с центром O(0;0;0) записывается в виде:
- Комбинаторика и бином Ньютона
1) Число перестановок из n элементов находится по формуле:
2) Число размещений из n элементов по m находится по формуле:
3) Число сочетаний из n элементов по m находится по формуле:
4) Справедливы следующие свойства сочетаний:
5) Формула бинома Ньютона имеет вид:
Сумма показателей чисел a и b равна n.
6) (k+1)-й член находится по формуле:
7) Число сочетаний также можно найти по треугольнику Паскаля.
Треугольник Паскаля (до n=7):
8) Сумма биномиальных коэффициентов равна 2n.
9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.
- Пределы
- Теоремы о пределах
- Замечательные пределы
- Неопределенные интегралы


















Геометрия
advice-me.ru
Работа в Excel с формулами и таблицами для чайников
Формула предписывает программе Excel порядок действий с числами, значениями в ячейке или группе ячеек. Без формул электронные таблицы не нужны в принципе.
Конструкция формулы включает в себя: константы, операторы, ссылки, функции, имена диапазонов, круглые скобки содержащие аргументы и другие формулы. На примере разберем практическое применение формул для начинающих пользователей.
Формулы в Excel для чайников
Чтобы задать формулу для ячейки, необходимо активизировать ее (поставить курсор) и ввести равно (=). Так же можно вводить знак равенства в строку формул. После введения формулы нажать Enter. В ячейке появится результат вычислений.
В Excel применяются стандартные математические операторы:
| Оператор | Операция | Пример |
| + (плюс) | Сложение | =В4+7 |
| – (минус) | Вычитание | =А9-100 |
| * (звездочка) | Умножение | =А3*2 |
| / (наклонная черта) | Деление | =А7/А8 |
| ^ (циркумфлекс) | Степень | =6^2 |
| = (знак равенства) | Равно | |
| Меньше | ||
| > | Больше | |
| Меньше или равно | ||
| >= | Больше или равно | |
| Не равно |
Символ «*» используется обязательно при умножении. Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.
Программу Excel можно использовать как калькулятор. То есть вводить в формулу числа и операторы математических вычислений и сразу получать результат.
Но чаще вводятся адреса ячеек. То есть пользователь вводит ссылку на ячейку, со значением которой будет оперировать формула.
При изменении значений в ячейках формула автоматически пересчитывает результат.
Ссылки можно комбинировать в рамках одной формулы с простыми числами.
Оператор умножил значение ячейки В2 на 0,5. Чтобы ввести в формулу ссылку на ячейку, достаточно щелкнуть по этой ячейке.
В нашем примере:
- Поставили курсор в ячейку В3 и ввели =.
- Щелкнули по ячейке В2 – Excel «обозначил» ее (имя ячейки появилось в формуле, вокруг ячейки образовался «мелькающий» прямоугольник).
- Ввели знак *, значение 0,5 с клавиатуры и нажали ВВОД.
Если в одной формуле применяется несколько операторов, то программа обработает их в следующей последовательности:
Поменять последовательность можно посредством круглых скобок: Excel в первую очередь вычисляет значение выражения в скобках.
Как в формуле Excel обозначить постоянную ячейку
Различают два вида ссылок на ячейки: относительные и абсолютные. При копировании формулы эти ссылки ведут себя по-разному: относительные изменяются, абсолютные остаются постоянными.
Все ссылки на ячейки программа считает относительными, если пользователем не задано другое условие. С помощью относительных ссылок можно размножить одну и ту же формулу на несколько строк или столбцов.
- Вручную заполним первые графы учебной таблицы. У нас – такой вариант:
- Вспомним из математики: чтобы найти стоимость нескольких единиц товара, нужно цену за 1 единицу умножить на количество. Для вычисления стоимости введем формулу в ячейку D2: = цена за единицу * количество. Константы формулы – ссылки на ячейки с соответствующими значениями.
- Нажимаем ВВОД – программа отображает значение умножения. Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь.
Находим в правом нижнем углу первой ячейки столбца маркер автозаполнения. Нажимаем на эту точку левой кнопкой мыши, держим ее и «тащим» вниз по столбцу.
Отпускаем кнопку мыши – формула скопируется в выбранные ячейки с относительными ссылками. То есть в каждой ячейке будет своя формула со своими аргументами.
Ссылки в ячейке соотнесены со строкой.
Формула с абсолютной ссылкой ссылается на одну и ту же ячейку. То есть при автозаполнении или копировании константа остается неизменной (или постоянной).
Чтобы указать Excel на абсолютную ссылку, пользователю необходимо поставить знак доллара ($). Проще всего это сделать с помощью клавиши F4.
- Создадим строку «Итого». Найдем общую стоимость всех товаров. Выделяем числовые значения столбца «Стоимость» плюс еще одну ячейку. Это диапазон D2:D9
- Воспользуемся функцией автозаполнения. Кнопка находится на вкладке «Главная» в группе инструментов «Редактирование».
- После нажатия на значок «Сумма» (или комбинации клавиш ALT+«=») слаживаются выделенные числа и отображается результат в пустой ячейке.
Сделаем еще один столбец, где рассчитаем долю каждого товара в общей стоимости. Для этого нужно:
- Разделить стоимость одного товара на стоимость всех товаров и результат умножить на 100. Ссылка на ячейку со значением общей стоимости должна быть абсолютной, чтобы при копировании она оставалась неизменной.
- Чтобы получить проценты в Excel, не обязательно умножать частное на 100. Выделяем ячейку с результатом и нажимаем «Процентный формат». Или нажимаем комбинацию горячих клавиш: CTRL+SHIFT+5
- Копируем формулу на весь столбец: меняется только первое значение в формуле (относительная ссылка). Второе (абсолютная ссылка) остается прежним. Проверим правильность вычислений – найдем итог. 100%. Все правильно.
При создании формул используются следующие форматы абсолютных ссылок:
- $В$2 – при копировании остаются постоянными столбец и строка;
- B$2 – при копировании неизменна строка;
- $B2 – столбец не изменяется.
Как составить таблицу в Excel с формулами
Чтобы сэкономить время при введении однотипных формул в ячейки таблицы, применяются маркеры автозаполнения. Если нужно закрепить ссылку, делаем ее абсолютной. Для изменения значений при копировании относительной ссылки.
Простейшие формулы заполнения таблиц в Excel:
- Перед наименованиями товаров вставим еще один столбец. Выделяем любую ячейку в первой графе, щелкаем правой кнопкой мыши. Нажимаем «Вставить». Или жмем сначала комбинацию клавиш: CTRL+ПРОБЕЛ, чтобы выделить весь столбец листа. А потом комбинация: CTRL+SHIFT+”=”, чтобы вставить столбец.
- Назовем новую графу «№ п/п». Вводим в первую ячейку «1», во вторую – «2». Выделяем первые две ячейки – «цепляем» левой кнопкой мыши маркер автозаполнения – тянем вниз.
- По такому же принципу можно заполнить, например, даты. Если промежутки между ними одинаковые – день, месяц, год. Введем в первую ячейку «окт.15», во вторую – «ноя.15». Выделим первые две ячейки и «протянем» за маркер вниз.
- Найдем среднюю цену товаров. Выделяем столбец с ценами + еще одну ячейку. Открываем меню кнопки «Сумма» – выбираем формулу для автоматического расчета среднего значения.
Чтобы проверить правильность вставленной формулы, дважды щелкните по ячейке с результатом.
exceltable.com
Формулы со ссылками на другие листы
Формула на любом листе рабочей книги может содержать ссылки на ячейки других листов. В этом случае адресу ячейки в формуле должно предшествовать имя листа с восклицательным знаком.
Например:
=Лист1!$А$2*Лист2!В5
Для этого по ходу ввода формулы следует щелкать на ярлыках нужных листов и выбирать в них ячейку или диапазон, на которые должна быть ссылка.
Диаграммы и Графика в Excel
В программе Excel термин диаграмма используется для обозначения всех видов графического представления числовых данных. Основными типами диаграмм являются: график, гистограмма,круговая диаграмма. Построение графического изображения производится на основе ряда данных. Так называют диапазон ячеек с числовыми значениями в пределах отдельной строки или столбца. На одной диаграмме можно отображать несколько рядов данных. К построенной диаграмме автоматически добавляется легенда – расшифровка рядов данных.
Диаграмма является объектом, вставленным на один из листов рабочей книги. Она может располагаться на том же листе, на котором находятся данные или на отдельном листе. Диаграмма сохраняет связь с данными, на основе которых она построена, и при обновлении этих данных немедленно изменяет свой вид.
Для построения диаграммы предназначен Мастер диаграмм.
Как правило, диапазон данных, которые будут отображаться на диаграмме, выделяют заранее, но указать данные можно и в ходе работы Мастера диаграмм.
6.1. Построение диаграмм
Выделить ряды данных вместе с подписями столбцов (тогда они будут отображены в легенде). Для графиков и гистограмм можно выделять несколько рядов данных. В этом случае несколько графиков или столбцов гистограммы будут расположены в одной области построения. Для круговой диаграммы выделяется один ряд данных. Если нужны подписи по оси Х (или подписи секторов круговой диаграммы), то следует выделить и столбец с текстовыми данными. Если в качестве подписей должен использоваться ряд с числовыми значениями, то на этом этапе его не нужно выделять.
Запустить Мастер диаграмм кнопкой в панели инструментов или командой меню ВставкаДиаграмма
Далее работа выполняется с последовательными окнами Мастера диаграмм. Переход к очередному окну выполняется щелчком на кнопке Далее.
Первый шаг Мастера – окно Тип диаграммы (рисунок 6.1). Здесь выбирается тип и вид диаграммы.
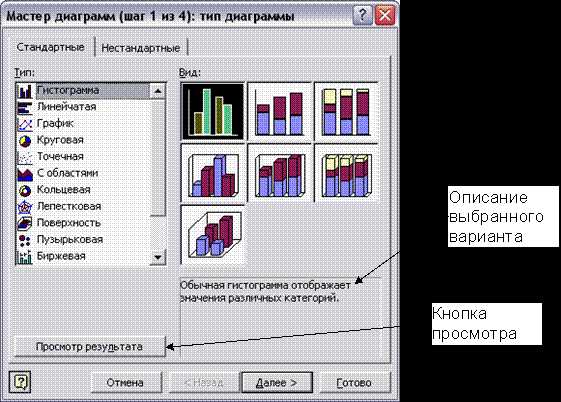
Рис. 6.1
На вкладке Стандартные перечислены различные типы диаграмм и варианты представления каждого типа. Ниже приводится краткое описание выбранного варианта. Удерживая мышью кнопку Просмотр результата, можно увидеть будущую диаграмму, если диапазон данных был заранее выделен.
На вкладке Нестандартные отображается набор разных типов диаграмм с готовым форматированием. На этой вкладке можно выбрать построение смешанной диаграммы, например, гистограммы и графика по разным рядам данных в одной области построения.
Второй шаг Мастера – окно Источник данных диаграммы.
На вкладке Диапазон данных(рисунок 6.2) указан выделенный диапазон. Если данные не были выделены заранее или потребовалось включить другие ряды данных, следует щелкнуть в поле Диапазон и выделить данные в таблице.
Переключатель ряда данных (в строках или столбцах) устанавливается автоматически – по логике выбранных данных.
Вкладка Ряд (рисунок 6.3) используется для корректировки рядов данных, по которым строится диаграмма, и подписей по оси Х.
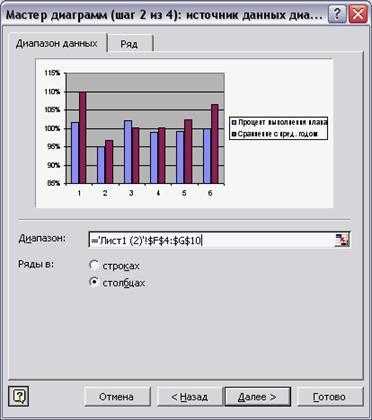
Рис. 6.2
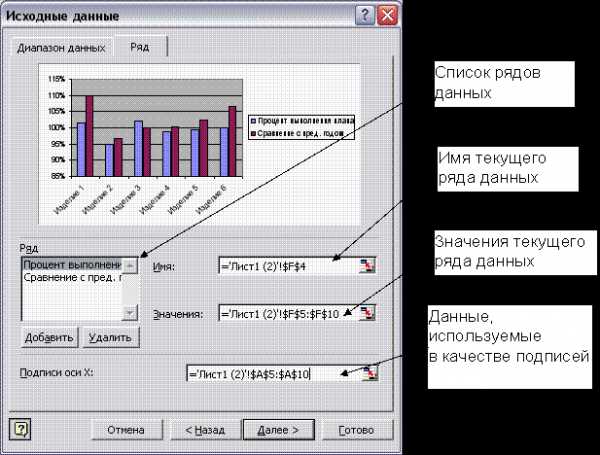
Рис. 6.3
Поле Ряд содержит список всех выбранных рядов с числовыми данными. Если данные выделялись с подписями, то список рядов содержит эти названия и в поле имени отображается адрес ячейки, содержащей подпись. Если подписи рядов не были выделены, то рядам присваиваются стандартные имена (Ряд1, Ряд2…).
Ряд данных можно исключить из списка представления, щелкнув на кнопке Удалить. Для подключения ряда данных нужно щелкнуть на кнопке Добавить и выделить данные в таблице.
Если данные, предназначенные в качестве подписей по оси Х, не были выделены заранее, их можно выбрать, щелкнув в поле Подписи по оси Х (подписи категорий).
Третий шаг Мастера – окно Параметры диаграммы.
Это окно содержит несколько вкладок, количество и поля которых зависят от типа диаграммы (рисунок 6.4).
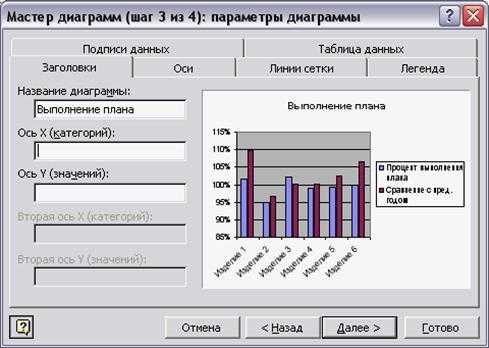
Рис. 6.4
Установка каждого параметра сразу отображается в области просмотра.
На вкладке Заголовки можно ввести название диаграммы и подписи осей (для круговых диаграмм – только название).
На вкладке Оси устанавливают отображение и маркировку осей координат.
На вкладке Легенда можно указать отображение или отсутствие легенды и выбрать место ее размещения.
На вкладке Линии сетки устанавливается отображение основных и промежуточных линий сетки в области построения диаграммы.
На вкладке Подписи данных можно выбрать отображение подписей элементов данных на диаграмме:
На вкладке Таблица данных можно добавить к диаграмме таблицу рядов данных, использованных в диаграмме.
Четвертый шаг Мастера – окно Размещение диаграммы.
На последнем шаге работы Мастера запрашивается, где следует поместить диаграмму – на отдельном листе или на одном из имеющихся. При выборе первого варианта в рабочей книге появится новый лист со стандартным именем – Диаграмма.
studfiles.net
Стоковые векторные изображения Формула со2
- Фотографии
- Векторы
- Эдиториал
- Видео
- Живой чат
- Для бизнеса
- Наши планы и цены
- Все изображения
- Фотографии
- Векторы
- Видео
- Применить
- Зарегистрироваться
- Войти
Лучший выбор
- Лучший выбор
- Популярные
- Новые
- Неизведанное
- Закрыть
- Лучший выбор
- Популярные
- Новые
- Неизведанное
1
1-100 из 45,554
 Бесшовный фон математические
Бесшовный фон математическиеgoldenshrimp
8000 x 8000
 Фон математики
Фон математикиvtorous
4098 x 3465
 Физика
Физикаetiamos
2000 x 2000
 Математические формулы
Математические формулыWillypd
5007 x 3540
 Молекула
МолекулаRazvodovska
5000 x 3732
 Гонки фоне горизонтали
Гонки фоне горизонталиecelop
5000 x 3533
 Фон химии – модели молекулы и формулы
Фон химии – модели молекулы и формулыkytalpa
5000 x 3750
 Рука рисовать химии на фоне
Рука рисовать химии на фонеSonneOn
4747 x 5000
 Бесшовный фон математические
Бесшовный фон математическиеgoldenshrimp
8000 x 8000
 Физические формулы, графики и научные вычисления на доске. Старинные ручной обращается иллюстрации Лаборатория бесшовный фон
Физические формулы, графики и научные вычисления на доске. Старинные ручной обращается иллюстрации Лаборатория бесшовный фонkateja
5208 x 5208
 Клетчатый угловой красный
Клетчатый угловой красныйNicemonkey
5030 x 3578
 Гран-при Монако f1 плакат
Гран-при Монако f1 плакатupstudio
3508 x 2480
 Рисование бизнес формул: мышь
Рисование бизнес формул: мышьPalau83
4724 x 4724
 Молекула Векторный икона set
Молекула Векторный икона setnatis76
3976 x 4374
 Формула 1
Формула 1suricoma
5000 x 3571
 Гонки фон, вектор
Гонки фон, векторnatis76
3189 x 2244
 Фон математики
Фон математикиvtorous
4678 x 3306
 Научные исследования и образование
Научные исследования и образованиеroyalty
5000 x 5000
 Формула 1 икона набор, спортивные значки и наклейки
Формула 1 икона набор, спортивные значки и наклейкиerryan
5000 x 5000
 Формула один икона set
Формула один икона setshemoto
5000 x 5000
 Формула автомобиль и объекты
Формула автомобиль и объектыbogalo
3429 x 3429
 F1 гоночный автомобиль
F1 гоночный автомобильh5nk
6300 x 4455
 Атом
Атомpavelmidi
4130 x 3459
 Гонки квадратных фон
Гонки квадратных фонecelop
5000 x 5000
 Формула 1
Формула 1suricoma
5000 x 4167
 Горение разнообразившего мчащегося флага
Горение разнообразившего мчащегося флагаdvargg
5000 x 5000
 Формула 1 икона набор, спортивные значки и наклейки – 2
Формула 1 икона набор, спортивные значки и наклейки – 2erryan
5000 x 5000
 Вектор, мчащийся флаги
Вектор, мчащийся флагиdmstudio
5450 x 3275
 Гонки знак 06
Гонки знак 06ecelop
5000 x 5000
 Фон математики
Фон математикиvtorous
3852 x 3308
 Математические каракулей бесшовный фон
Математические каракулей бесшовный фонkytalpa
5000 x 5000
 Научные символы
Научные символыSeamartini
5700 x 4000
 Гоночный автомобиль
Гоночный автомобильPuchalt
4200 x 4200
 Математика дерево для вашего дизайна
Математика дерево для вашего дизайнаKudryashka
5014 x 5014
 Гоночный автомобиль плакат
Гоночный автомобиль плакатsnegok13
4000 x 2606
 Клетчатый флаг, Векторный фон
Клетчатый флаг, Векторный фонnatis76
3071 x 2244
 Формула 1 икона набор, спортивные значки и наклейки – 3
Формула 1 икона набор, спортивные значки и наклейки – 3erryan
5000 x 5000
 Рисованной химии формул
Рисованной химии формулundrey
4167 x 4167
 Векторный фон с формулами, химия
Векторный фон с формулами, химияfrenta
5162 x 3651
 Зеленый молекула
Зеленый молекулаnatis76
3740 x 4488
 Химия бесшовный фон
Химия бесшовный фонAlenaPohu
4000 x 4000
 Пропуск гонки 07
Пропуск гонки 07ecelop
5000 x 5000
 Гонки фона горизонтальной, 10eps
Гонки фона горизонтальной, 10epsnatis76
3189 x 2126
 Гонки фон, вертикальные
Гонки фон, вертикальныеecelop
3533 x 5000
 Школа
Школаetiamos
4000 x 4000
 Молекулярная структура с шарами. 3D векторные иллюстрации
Молекулярная структура с шарами. 3D векторные иллюстрацииstudiom1
4000 x 4000
 Инструменты рисования. Образование
Инструменты рисования. Образованиеthreecvet.gmail.com
5000 x 5000
 Шаблон бесшовные векторные уравнения
Шаблон бесшовные векторные уравненияLeonardi
2362 x 2362
 Гоночный автомобиль формулы
Гоночный автомобиль формулыbogalo
3425 x 3425
 Алгебра бесшовные
Алгебра бесшовныеSeamartini
5005 x 5005
 Математические формулы
Математические формулыa2bb5s
5262 x 3721
 Гонка визитная карточка водителя – вторые
Гонка визитная карточка водителя – вторыеecelop
5000 x 4958
 Бесшовные математической модели
Бесшовные математической моделиihor_seamless
5000 x 5000
 Гоночный автомобиль
Гоночный автомобильPuchalt
4200 x 4200
Формула 1suricoma
4629 x 1363
 Автомобиль гоночный баннер. Шины дрейф на финише гонки цепи
Автомобиль гоночный баннер. Шины дрейф на финише гонки цепиMatriyoshka
5000 x 2500
 Бесшовный фон математические
Бесшовный фон математическиеru.depositphotos.com