Геометрический смысл уравнения бернулли – Геометрических смысл уравнения Бернулли. Энергетический смысл уравнения Бернулли. Полный напор. Напорная и пьезометрическая линии.
- Комментариев к записи Геометрический смысл уравнения бернулли – Геометрических смысл уравнения Бернулли. Энергетический смысл уравнения Бернулли. Полный напор. Напорная и пьезометрическая линии. нет
- Советы абитуриенту
- 2.4. Геометрический и энергетический смысл уравнения д.Бернулли
- 30. Геометрический смысл уравнения Бернулли. Гидравлика
- 7.Физический смысл уравнения Бернулли .
- 7. Уравнение Бернелли для идеальной и реальной жидкостей.
- Геометрических смысл уравнения Бернулли. Энергетический смысл уравнения Бернулли. Полный напор. Напорная и пьезометрическая линии.
- Геометрический смысл – уравнение – Большая Энциклопедия Нефти и Газа, статья, страница 2
- 17. Геометрический, энергетический смысл уравнения Бернулли.
2.4. Геометрический и энергетический смысл уравнения д.Бернулли
Все члены, входящие в уравнение Д.Бернулли, имеют линейную размерность, поэтому их принято называть высотами. Соответственно общеприняты следующие названия для этих членов:
 – геометрическая
или геодезическая высота;
– геометрическая
или геодезическая высота;
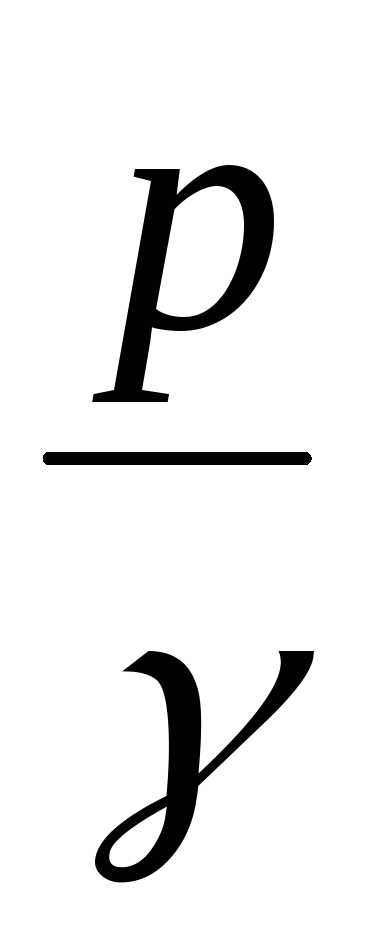 – пьезометрическая
высота или высота давления;
– пьезометрическая
высота или высота давления;
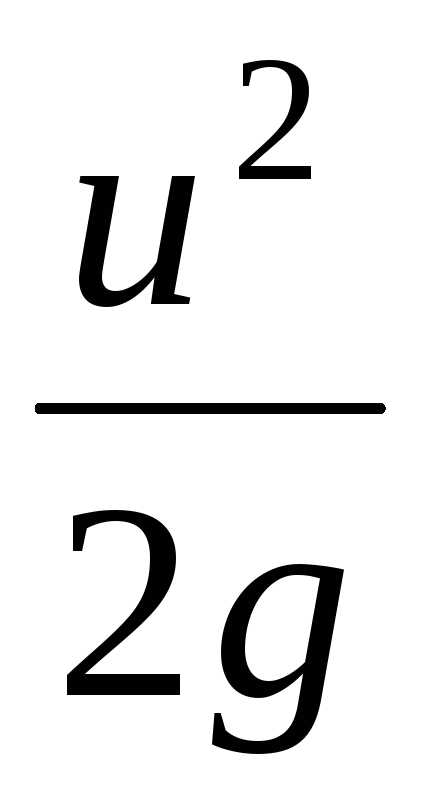 – скоростная высота
или скоростной напор.
– скоростная высота
или скоростной напор.
Легко усмотреть следующий геометрический смысл уравнения Д.Бернулли, который заключается в том, что при установившемся движении идеальной жидкости сумма трех высот (геометрической, пьезометрической и скоростной) не меняется вдоль данной элементарной струйки. Это положение наглядно иллюстрируется II.01.
Можно трактовать
смысл отдельных членов уравнения
Бернулли иначе. Выше было показано, что
сумма 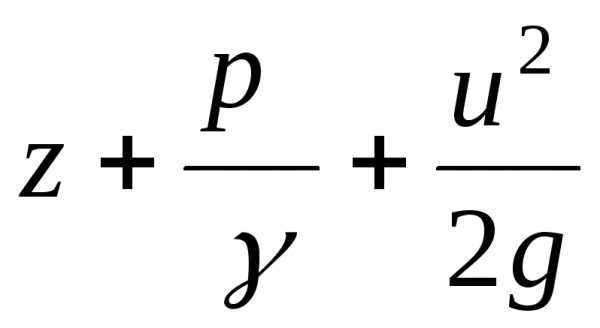 представляет собой
удельную энергию жидкости. В соответствии
с этим можно считать, что:
представляет собой
удельную энергию жидкости. В соответствии
с этим можно считать, что:
 – есть удельная
энергия положения;
– есть удельная
энергия положения;
– есть удельная энергия давления;
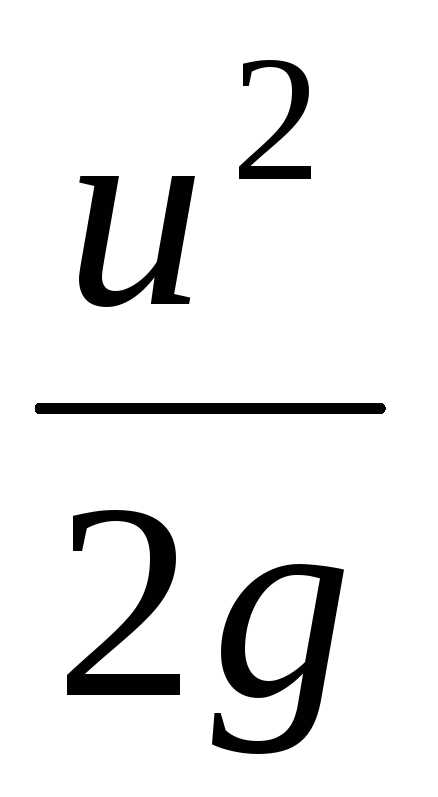 – есть удельная
кинетическая энергия.
– есть удельная
кинетическая энергия.
Энергетический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма удельных энергий положения, давления и кинетической не меняется вдоль данной элементарной струйки.
Очевидно, двучлен 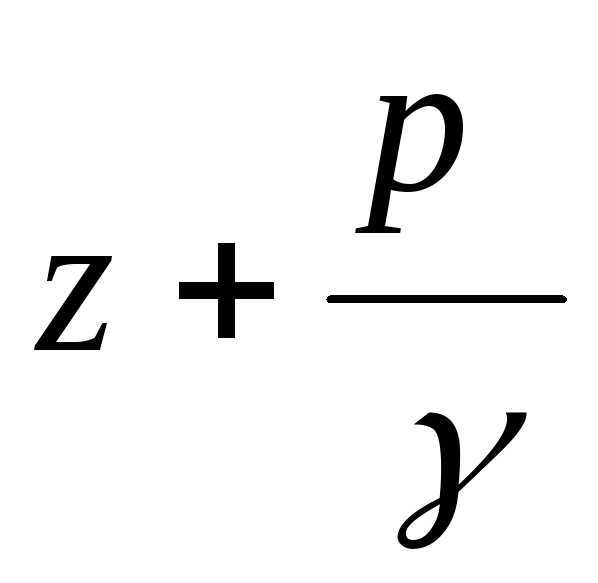
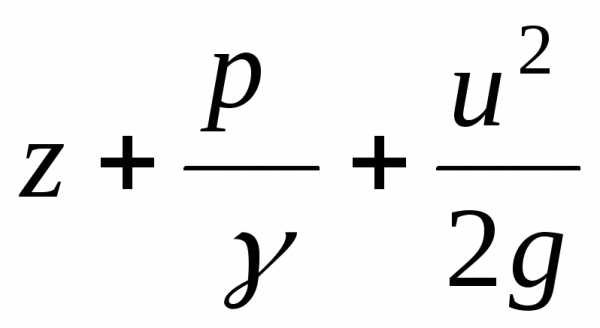 называется гидродинамическим напором
и обозначается
называется гидродинамическим напором
и обозначается 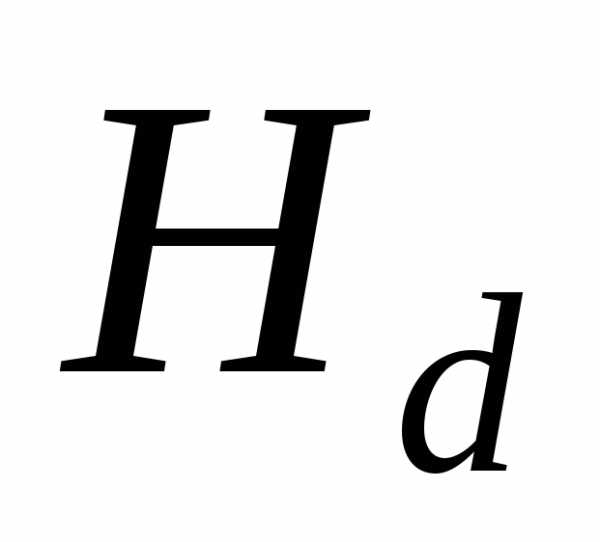 .
Таким образом, уравнение Бернулли
показывает, что при установившемся
движении идеальной жидкости для данной
струйки гидродинамический напор есть
величина постоянная.
.
Таким образом, уравнение Бернулли
показывает, что при установившемся
движении идеальной жидкости для данной
струйки гидродинамический напор есть
величина постоянная. 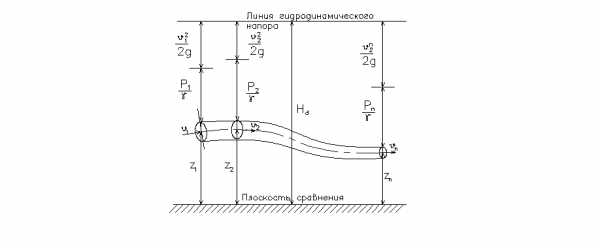
Рис. II.01
На графике линия гидродинамического напора изображается горизонтальной линией.
2.5. Уравнение д.Бернулли для элементарной струйки реальной жидкости. Пьезометрический и гидравлический уклоны
При движении
реальной жидкости между соседними
струйками возникают силы трения, на
преодоление которых затрачивается
часть энергии жидкости. Поэтому удельная
энергия жидкости в сечении элементарной
струйки 2-2 будет мене удельной энергии
жидкости в сечении 1-1 на некоторую
величину 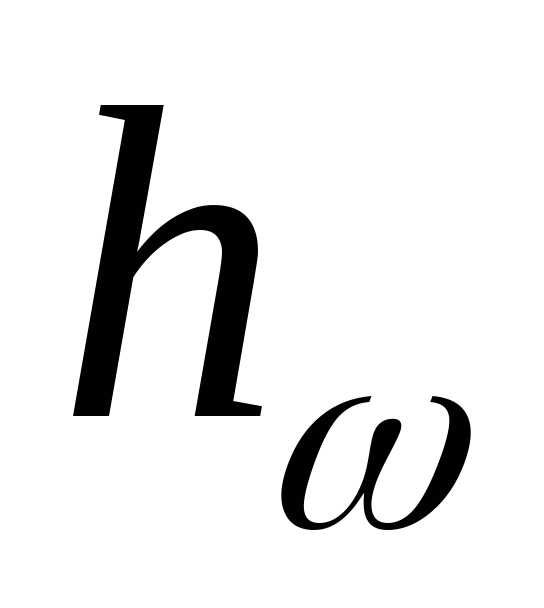
(11.14)
Следовательно, при установившемся движении реальной жидкости сумма четырех высот (геометрической, пьезометрической, скоростной и потерянной) или, что то же самое, сумма четырех удельных энергий 9положения, давления, кинетической и потерянной) не изменяется вдоль данной элементарной струйки.
Легко изобразить
уравнение Бернулли для рассматриваемого
случая графически. Для этого следует,
выбрав произвольную горизонтальную
плоскость сравнения, отложить на ней в
каждом сечении высоты 
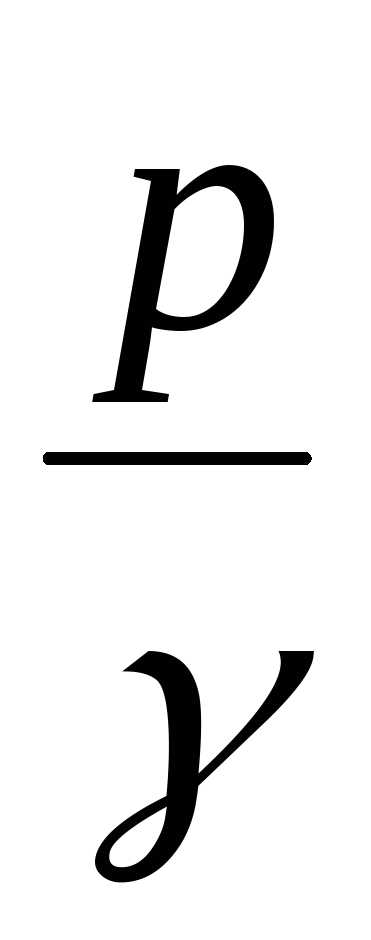 ;
;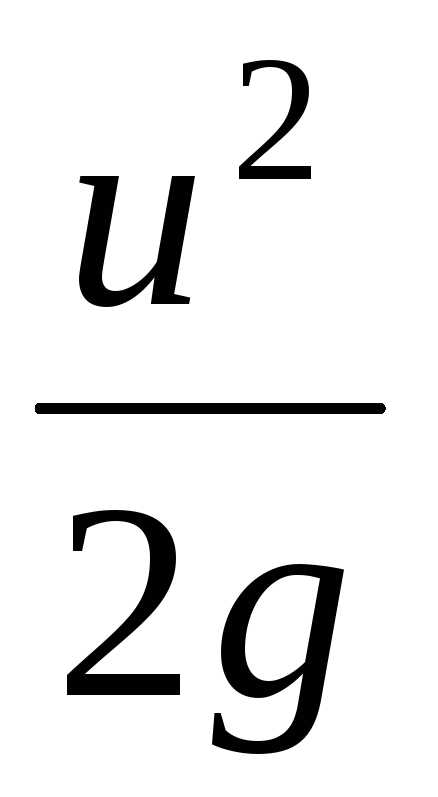 и
и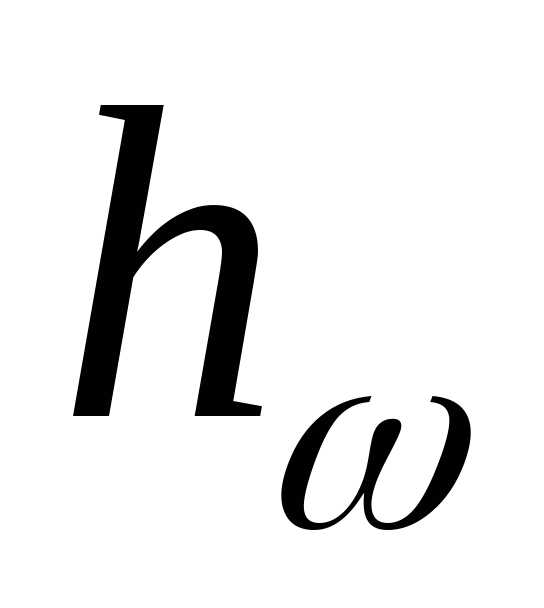 .
Концы отрезков
.
Концы отрезков ,
соединенные плавной кривой, покажут
положение оси струйки. Соединяя концы
отрезков
,
соединенные плавной кривой, покажут
положение оси струйки. Соединяя концы
отрезков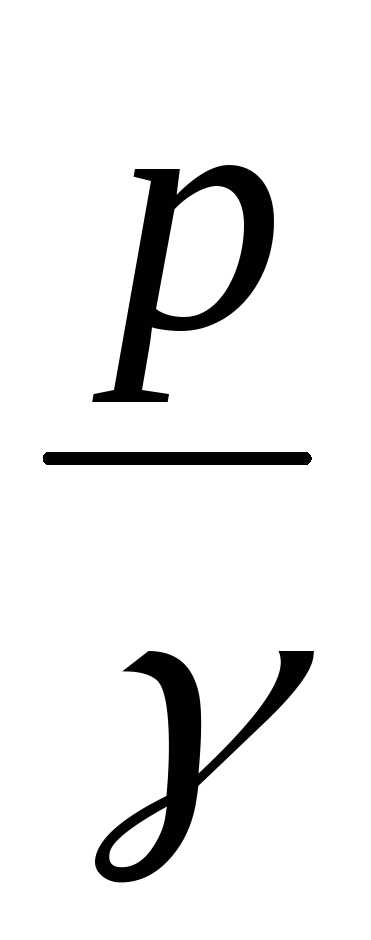 плавной кривой, получим так называемую
пьезометрическую линию. Отложив в каждом
сечении вверх от пьезометрической линии
отрезки, равные скоростным напорам
плавной кривой, получим так называемую
пьезометрическую линию. Отложив в каждом
сечении вверх от пьезометрической линии
отрезки, равные скоростным напорам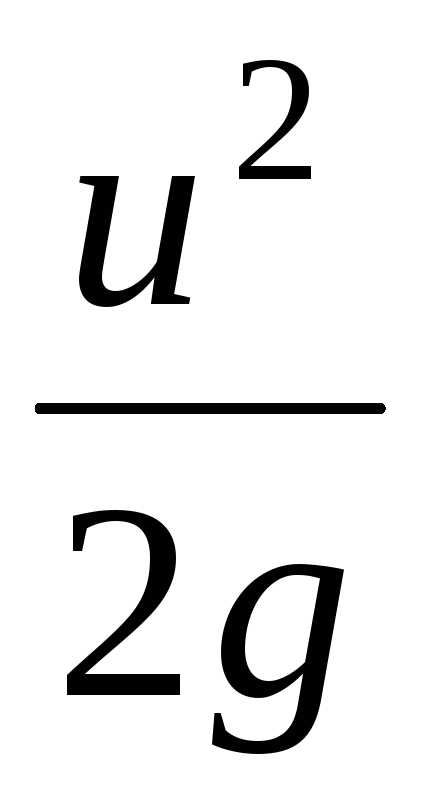 ,
и соединив их концы плавной кривой,
получим линию гидродинамического напора
или, как ее часто называют, гидравлическую
линию (рис.II.02).
Отрезки, равные расстояниям по вертикали
от гидравлической линии, проходящей
над плоскостью сравнения на высоте,
равной начальной удельной энергии на
гидравлические сопротивления на участке
от начального до рассматриваемого
сечения.
,
и соединив их концы плавной кривой,
получим линию гидродинамического напора
или, как ее часто называют, гидравлическую
линию (рис.II.02).
Отрезки, равные расстояниям по вертикали
от гидравлической линии, проходящей
над плоскостью сравнения на высоте,
равной начальной удельной энергии на
гидравлические сопротивления на участке
от начального до рассматриваемого
сечения. 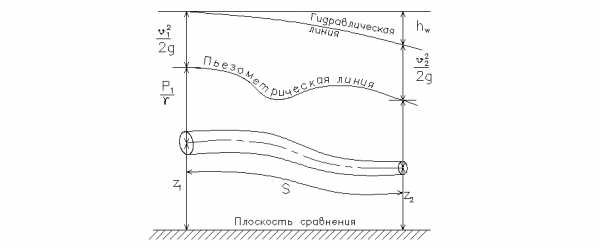
Рис. II.02
Проделаем теперь
следующее построение: разверзнем
криволинейную ось струйки s
в горизонтальную прямую линию и в каждой
ее точке отложим по вертикали значения
удельных энергий  ;
;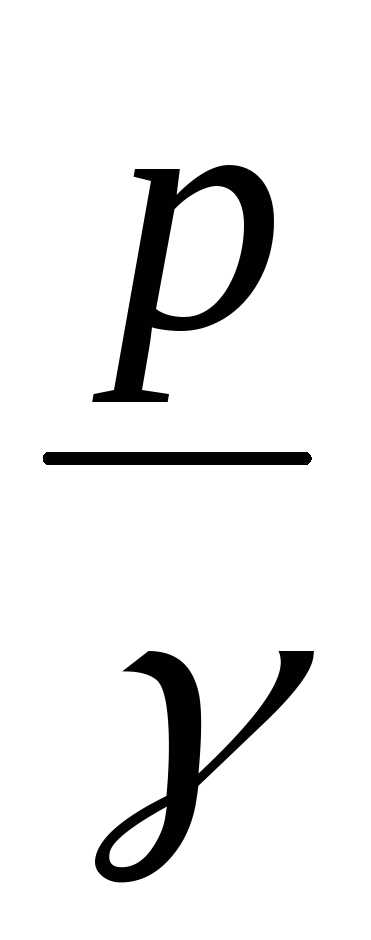 и
и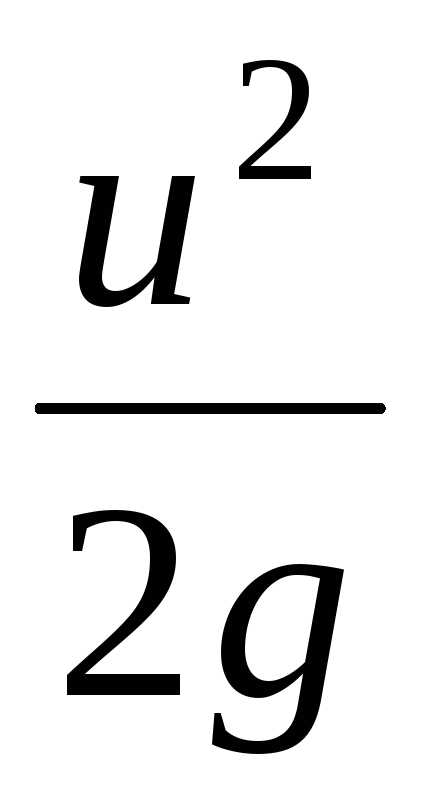 .
Соединяя концы отрезков
.
Соединяя концы отрезков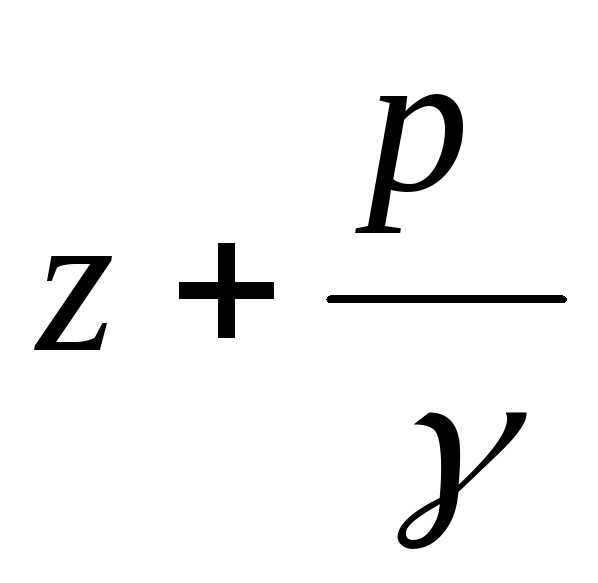 и
и 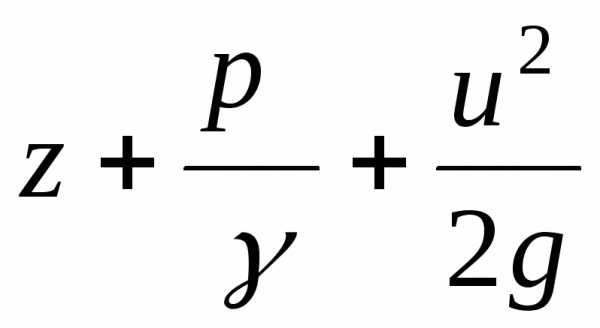 ,
получим изображение пьезометрической
и гидравлической линий. Падение
пьезометрической линии на единицу длины
элементарной струйки назовем
пьезометрическим уклоном
,
получим изображение пьезометрической
и гидравлической линий. Падение
пьезометрической линии на единицу длины
элементарной струйки назовем
пьезометрическим уклоном
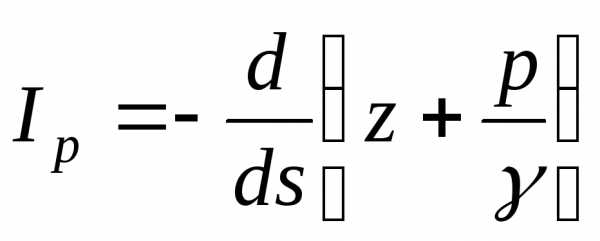 . (11.15)
. (11.15)
Соответственно падение гидравлической линии на единицу длины элементарной струйки назовем гидравлическим уклоном I:
(11.16)
На графике (рис.
II.03)
пьезометрический уклон представляется
тангенсом угла наклона касательной к
пьезометрической линии, а гидравлический
уклон – тангенсом угла наклона касательной
к гидравлической линии. Значение
пьезометрического уклона может быть
положительным или отрицательным в
зависимости от того, увеличивается или
уменьшается величина удельной
потенциальной энергии 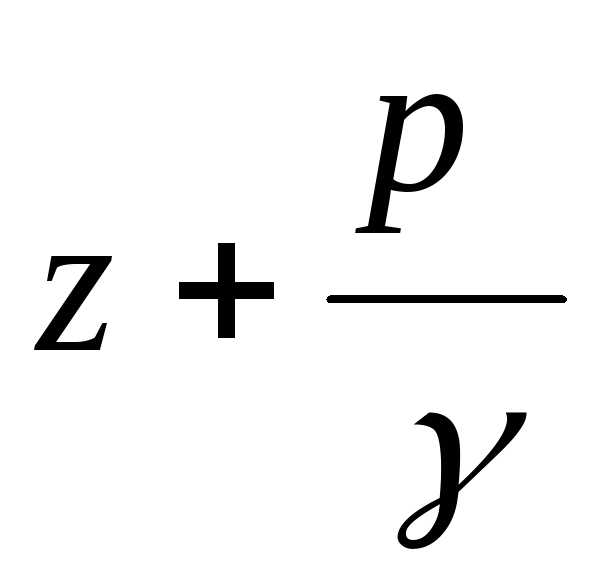
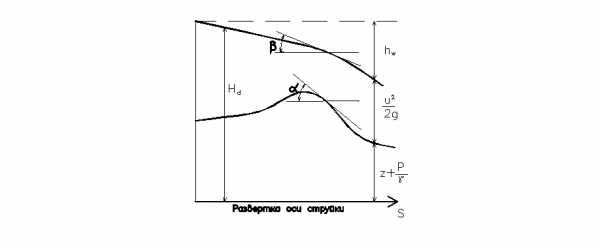
Рис. II.03
Гидравлиеческий уклон есть всегда величина положительная, так как полная удельная энергия движущейся части жидкости постепенно уменьшается по мере ее продвижения вдоль элементарной струйки, затрачиваясь на преодоление сил трения, превращаясь в тепловую энергию и рассеиваясь.
studfiles.net
30. Геометрический смысл уравнения Бернулли. Гидравлика
30. Геометрический смысл уравнения Бернулли
Основу теоретической части такой интерпретации составляет гидравлическое понятие напор, которое принято обозначать буквой Н, где
Гидродинамический напор Н состоит из следующих разновидностей напоров, которые входят в формулу (198) как слагаемые:
1) пьезометрический напор, если в (198) p = pизг, или гидростатический, если p ? pизг;
2) U2/2g – скоростной напор.
Все слагаемые имеют линейную размерность, их можно считать высотами. Назовем эти высоты:
1) z – геометрическая высота, или высота по положению;
2) p/?g – высота, соответствующая давлению p;
3) U2/2g – скоростная высота, соответствующая скорости.
Геометрическое место концов высоты Н соответствует некоторой горизонтальной линии, которую принято называть напорной линией или линией удельной энергии.
Точно так же (по аналогии) геометрические места концов пьезометрического напора принято называть пьезометрической линией. Напорная и пьезометрическая линии расположены друг от друга на расстоянии (высоте) pатм/?g, поскольку p = pизг + pат, т. е.
Отметим, что горизонтальная плоскость, содержащая напорную линию и находящаяся над плоскостью сравнения, называется напорной плоскостью. Характеристику плоскости при разных движениях называют пьезометрическим уклоном J
Пьезометрический уклон считается положительным, если он по течению струйки (или потока) уменьшается, отсюда и знак минус в формуле (3) перед дифференциалом. Чтобы Jп остался положительным, должно выполняться условие
Поделитесь на страничке Следующая глава >tech.wikireading.ru
7.Физический смысл уравнения Бернулли .
Уравнение Бернулли дает связь между давлением (P) , средней скоростью (v) ,
И геометрической высотой в различных сечениях (z) , является основным уравнением для практических расчетов в гидродинамике. Оно записывается для двух сечений потока 1-1 и 2-2 :
Где H – полная высота или полный напор.
 Геометрическая
высота , характеризует потенциальную
энергию положения.
Геометрическая
высота , характеризует потенциальную
энергию положения.
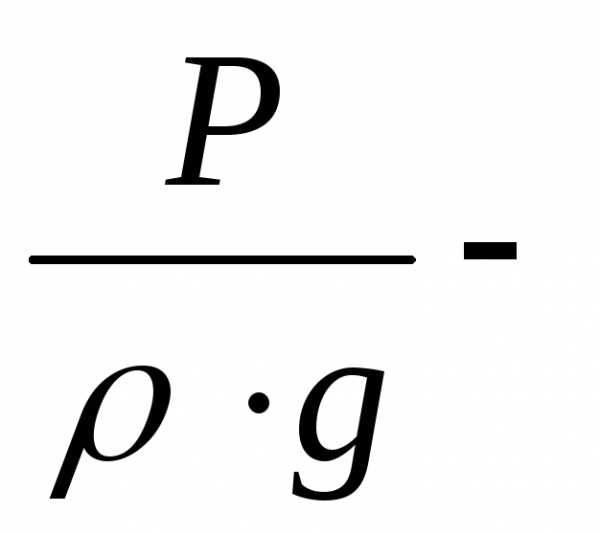 пьезометрическая
высота , характеризует потенциальную
энергию давления .
пьезометрическая
высота , характеризует потенциальную
энергию давления .
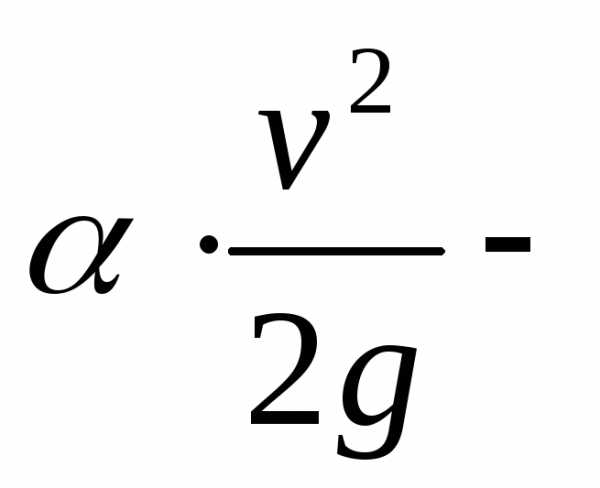 скоростная
высота характеризует кинетическую
энергию жидкости .
скоростная
высота характеризует кинетическую
энергию жидкости .
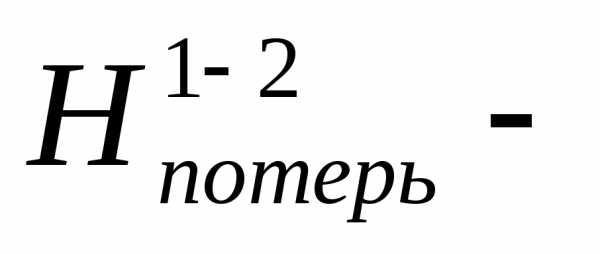 потерянная
высота.
потерянная
высота.
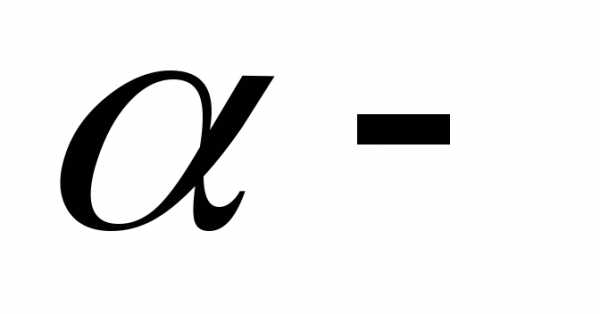 коэффициент
неравномерности скорости по потоку .
коэффициент
неравномерности скорости по потоку .
Геометрический смысл :
При установившемся движении жидкости сумма четырёх высот в каждом живом сечении есть величина постоянная и равна полной высоте (H) (полному напору )
Физический смысл:
При установившемся движении жидкости сумма четырех удельных энергий неизменна вдоль потока и равна общему запасу удельной энергии .
8.Уравнение Бернулли для потока вязкой жидкости.
Вязкая жидкость –это жидкость в которой при движении возникают касательные напряжения .
Уравнение Бернулли выражает закон сохранения механической энергии .
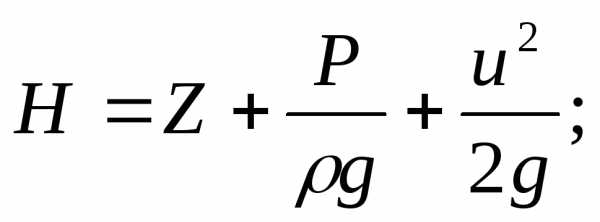 H
– полный напор –это удельная механическая
энергия .
H
– полный напор –это удельная механическая
энергия .
Z- геометрический напор(удельная потенциальная энергия положения ) .
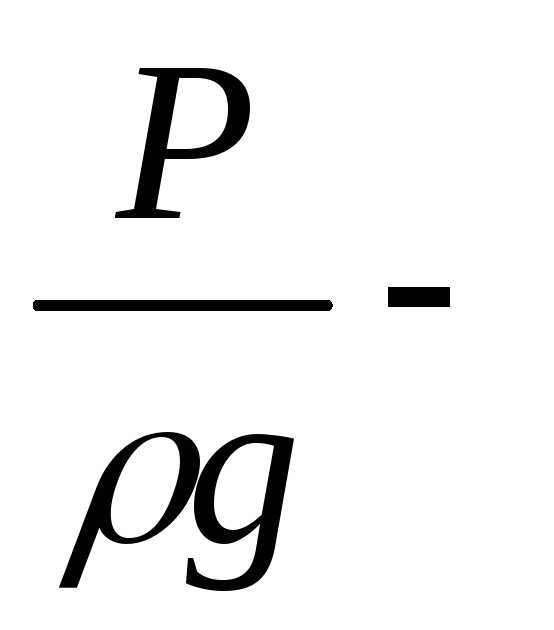 пьезометрический
напор (удельная потенциальная энергия
давления).
пьезометрический
напор (удельная потенциальная энергия
давления).
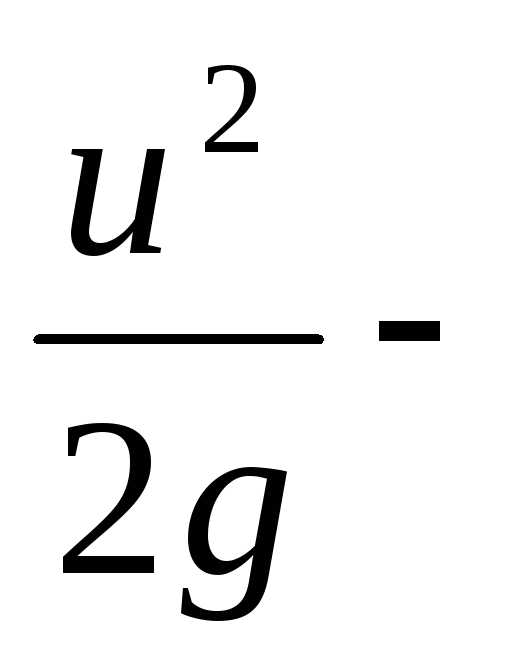 скоростной
напор (удельная кинетическая энергия
).
скоростной
напор (удельная кинетическая энергия
).
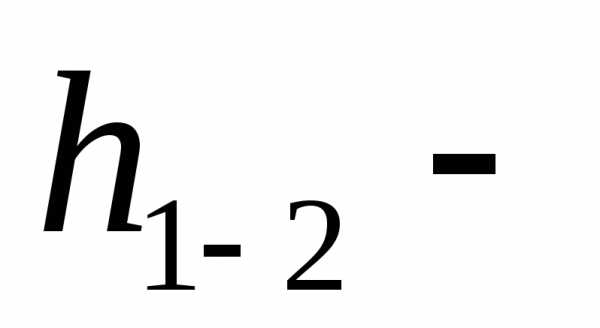 потери
напора (для идеальной жидкости равно
0-ю).
потери
напора (для идеальной жидкости равно
0-ю).
Для вязкой несжимаемой жидкости :
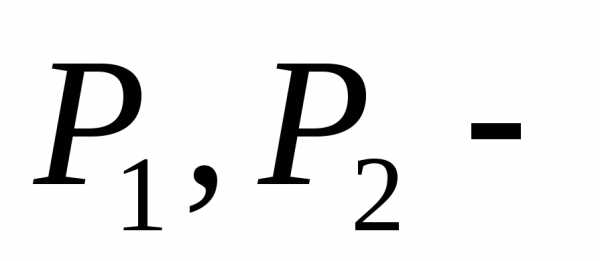 давление
в сечениях 1-1 и2-2.
давление
в сечениях 1-1 и2-2.
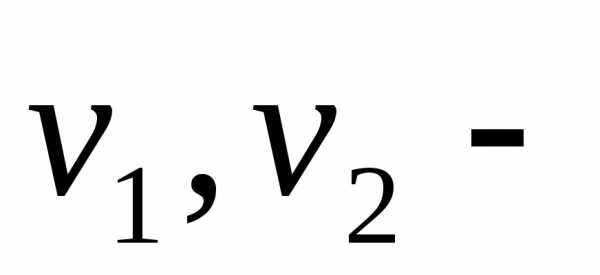 средние
скорости.
средние
скорости.
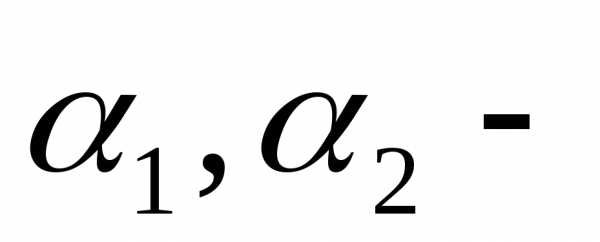 коэффициенты
учитывающие неоднородность распределения
скоростей.
коэффициенты
учитывающие неоднородность распределения
скоростей.
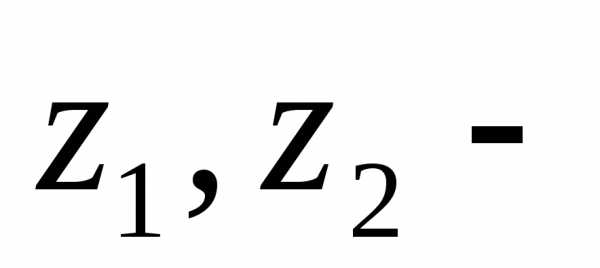 координаты
сечений.
координаты
сечений.
9.Применение уравнения Бернулли при решении технических задач.
Мощность насоса.
Уравнение Бернулли –это основное уравнение гидродинамики , с помощью которого производят расчеты течения жидкости в трубопроводах , насосах , турбинах , приборах.
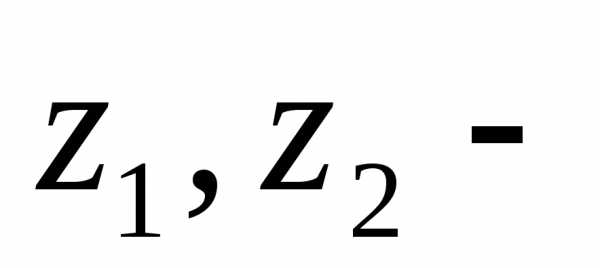 Геометрическая
высота , характеризует потенциальную
энергию положения.
Геометрическая
высота , характеризует потенциальную
энергию положения.
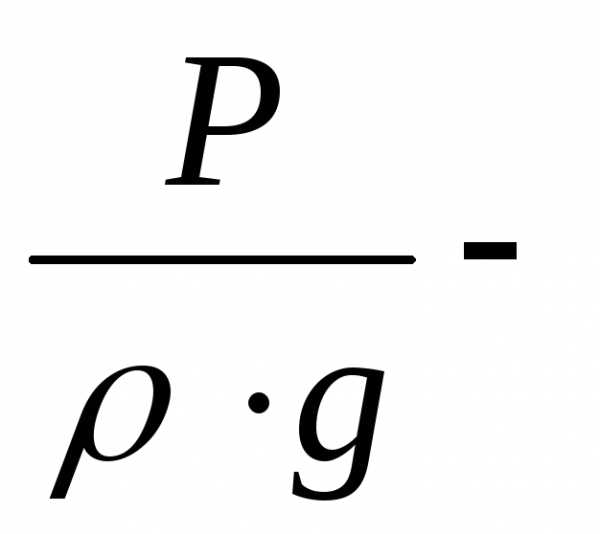 пьезометрическая
высота , характеризует потенциальную
энергию давления .
пьезометрическая
высота , характеризует потенциальную
энергию давления .
H- полный напор.
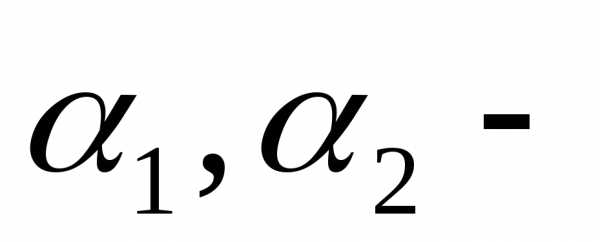 коэффициенты
учитывающие неоднородность распределения
скоростей.
коэффициенты
учитывающие неоднородность распределения
скоростей.
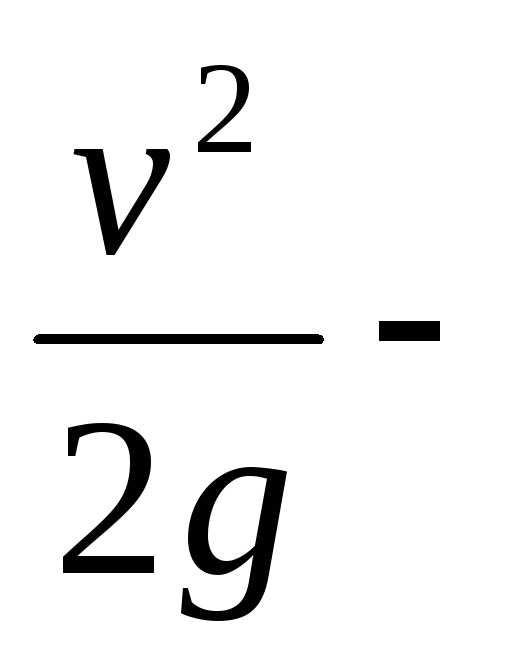 скоростная
высота характеризует кинетическую
энергию жидкости .
скоростная
высота характеризует кинетическую
энергию жидкости .
Пример.
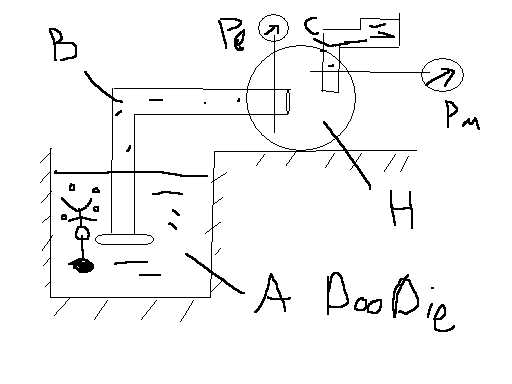
Продолжение 9
Жидкость
поступает из А по В (всасывающей трубке)
в насос (Н) где энергия от двигателя
передается жидкости , поступающей в
нагнетательную линию (С).В сечении 1-1
установлен вакуумметр (P )
.За насосом установлен манометр (P
)
.За насосом установлен манометр (P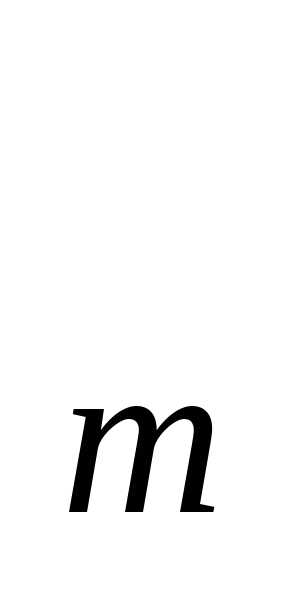 ).
).
Удельная энергия в сечении 1-1 и 2-2 :
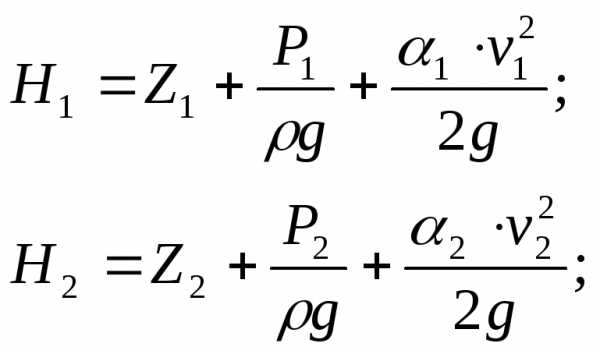
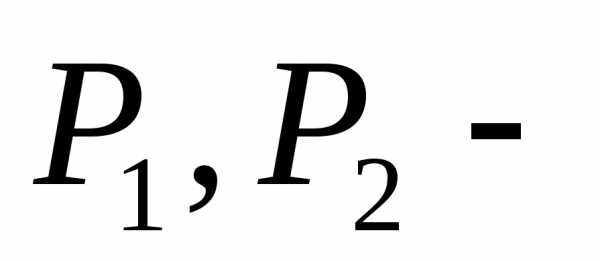 абсолютное
давление.
абсолютное
давление.
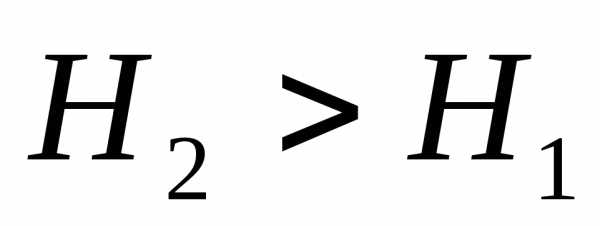 т.к.
жидкость приобретает дополнительную
энергию .
т.к.
жидкость приобретает дополнительную
энергию .
Тогда :
Мощность насоса равна N :
т.е.N = расходу (Q) умноженному на разность давлений .
10.Расходометр Вентури .
Р.В.служит для измерения расхода жидкости (Q) в трубопроводах. Р.в. состоит из 2х участков : широкого и узкого . Этот расходометр с горизонтальной осью. Проведем сечение 1-1 в широкой части и2-2 в узкой . Запишем уравнение неразрывности:
(Расход)
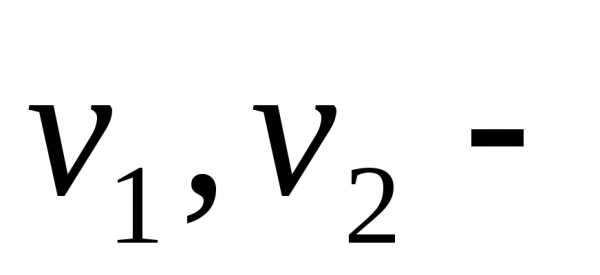 скорости.
скорости.
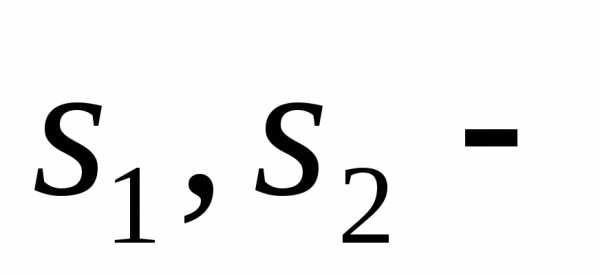 площадь
сечений .
площадь
сечений .
Уравнение Бернулли будет :
т.к. труба горизонтальная то пренебрегаем.
Примем (коэффициент неравномерности скоростей).
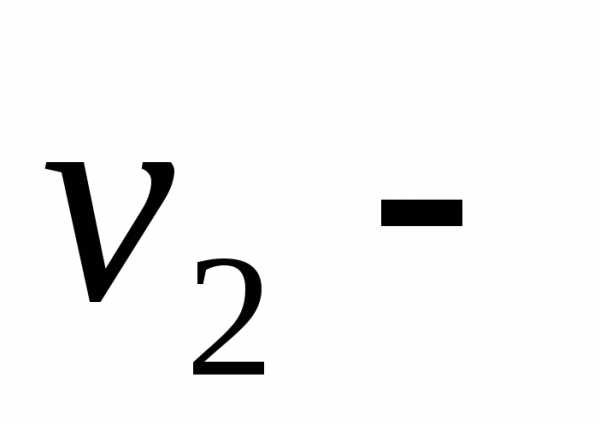 исключаем
из уравнения т.к. очень узкий проход 2,
получаем :
исключаем
из уравнения т.к. очень узкий проход 2,
получаем :
находим 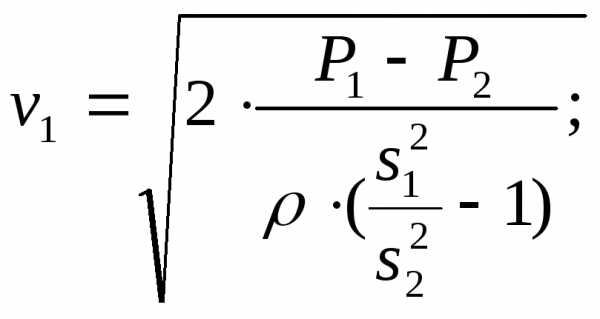 измеряем
манометрами
измеряем
манометрами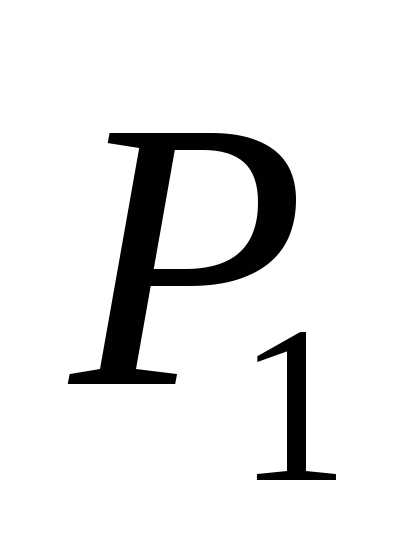 и
и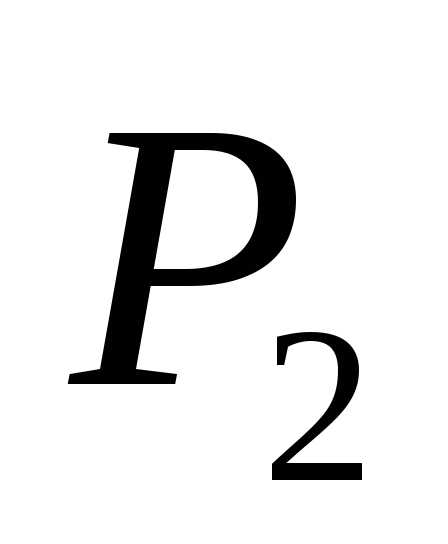 ,
,
 плотность ртути
. Расход
плотность ртути
. Расход 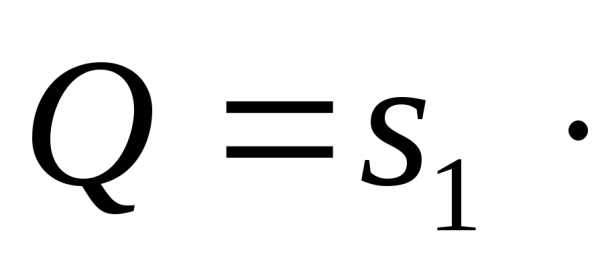
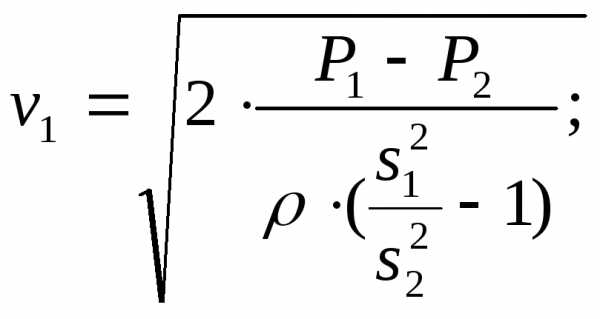
studfiles.net
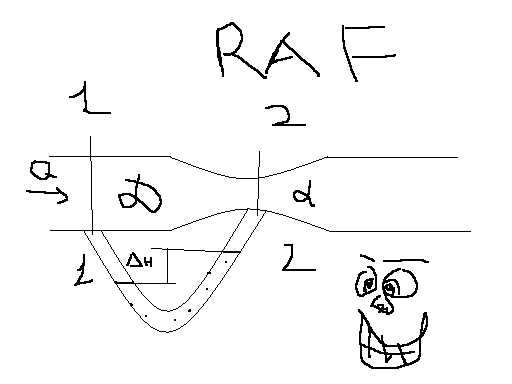
7. Уравнение Бернелли для идеальной и реальной жидкостей.
Уравнение Бернулли для струйки идеальной жидкости. движение жидкости в трубопроводах и каналах осуществляется за счет энергии самой жидкости . чаще всего необходимо энергии для перемещения передавай передается жидкости с помощью насосов.
Механическая энергия жидкости состоит из трех видов энергии: энергии положение, давления и кинетической энергии . В гидравлике под напором понимает энергию жидкости относительно единица веса. в этом случае напор измеряется в метрах что используется при его графическом представлении. Полный гидродинамический напор действующей жидкости равен сумме3 напоров геометрического напора( Удельная потенциальная энергия положения) , пьезометрического напора (Удельная потенциальная энергия давления) и скоростного напора Удельная кинетическая энергия).
Уравнение Бернулли для потока идеальной жидкости
В потоке идеальной жидкости, движущийся по трубопроводам и каналам, вследствие отсутствия потери энергии при движении, полный гидродинамический напор жидкости остается постоянным. это условие является частным случаем законы сохранения энергии и записывается для двух сечений потока жидкости равенство полное гидростатический напор от называют уравнением Бернулли или
в процессе движения идеальной жидкости один вид энергии может превращаться в другой , Однако полная энергия при этом остается без изменений.
Уравнение Бернулли для реальной жидкости
При движении реальной вязкой жидкости вследствие влияния сил молекулярного сцепления между стенкой и жидкостью происходит торможение потока приводящее к скольжению слоев жидкости друг относительно друга на вене и возникновению напряжений трения между слоями. Кроме того движения вязкой жидкости часто сопровождается вращением частиц , вихреобразованием и перемешиванием . Все это требует затрат энергии жидкости, поэтому энергия реальной жидкости не остается постоянной, как случается идеальной жидкостью, а постоянно расходуется на Преодоление сопротивлений и , следовательно уменьшается вдоль потока . Из-за неравномерного распределения скоростей потока реальной жидкости приходится вводить в рассмотрение среднюю скорость , а также средние значения Удельной энергии жидкости в данном сечении . при этом предполагается, что гидростатический напор в пределах сечения , есть величина одинакова для всех точек данного сечения.
В Результате полная Удельная энергия жидкости в течении 3-3 будет больше полной удельной энергии в сечении 4-4 на величину потерянной Удельной энергии . Потерянная удельная энергия или потерянный напор обозначаетсяи имеют также линейную размерность. уравнение Бернулли для реальной жидкости, таким образом представляет собой баланс энергии в потоке с учетом потерь.
8. Геометрический и физический смысл уравнения Бернулли.
Физический смысл
геометрический напор(z) характеризует запас удельной потенциальной энергии положения пьезометрический напор() характеризует запас энергии жидкости обусловленный ее давлением относительно давления сравнения (часто атмосферного давления . Удельная потенциальная энергия давления) геометрический и пьезометрический напоры присущи жидкости находящейся в покое, поэтому их сумму называют гидростатическим напором. скоростной напор( ) характеризует запас энергии обусловленный скоростью ее движения. (Удельная кинетическая энергия)
сумма трех наборов называется полный гидродинамический напор.
Геометрический смысл
геометрический напор равен расстоянию от плоскости сравнения до рассматриваемой точке жидкости (для потока жидкости до точки совпадающий с центром тяжести рассматриваем его сечения) пьезометрический напор это расстояние в пьезометрической трубке (To есть расстояние до рассматриваемой точки от плоскости).
studfiles.net
Геометрических смысл уравнения Бернулли. Энергетический смысл уравнения Бернулли. Полный напор. Напорная и пьезометрическая линии.
Геометрический смысл уравнения Бернулли
Основу теоретической части такой интерпретации составляет гидравлическое понятие напор, которое принято обозначать буквой Н, где
Гидродинамический напор Н состоит из следующих разновидностей напоров, которые входят в формулу (198) как слагаемые:
1) пьезометрический напор, если в (198) p = pизг, или гидростатический, если p ? pизг;
2) U2/2g – скоростной напор.
Все слагаемые имеют линейную размерность, их можно считать высотами. Назовем эти высоты:
1) z – геометрическая высота, или высота по положению;
2) p/?g – высота, соответствующая давлению p;
3) U2/2g – скоростная высота, соответствующая скорости.
Геометрическое место концов высоты Н соответствует некоторой горизонтальной линии, которую принято называть напорной линией или линией удельной энергии.
Точно так же (по аналогии) геометрические места концов пьезометрического напора принято называть пьезометрической линией. Напорная и пьезометрическая линии расположены друг от друга на расстоянии (высоте) pатм/?g, поскольку p = pизг + pат, т. е.
Отметим, что горизонтальная плоскость, содержащая напорную линию и находящаяся над плоскостью сравнения, называется напорной плоскостью. Характеристику плоскости при разных движениях называют пьезометрическим уклоном Jп, который показывает, как изменяется на единице длины пьезометрический напор (или пьезометрическая линия):
Пьезометрический уклон считается положительным, если он по течению струйки (или потока) уменьшается, отсюда и знак минус в формуле (3) перед дифференциалом. Чтобы Jп остался положительным, должно выполняться условие
Энергетический смысл уравнения Бернулли
Пусть теперь имеем установившееся движение жидкости, которая невязкая, несжимаемая.
И пусть она находится под воздействием сил тяжести и давления, тогда уравнение Бернулли имеет вид:
Теперь требуется идентифицировать каждое из слагаемых. Потенциальная энергия положения Z – это высота элементарной струйки над горизонтальной плоскостью сравнения. Жидкость с массой М на высоте Z от плоскости сравнения имеет некоторую потенциальную энергию MgZ. Тогда
Это та же потенциальная энергия, отнесенная к единичной массе. Поэтому Z называют удельной потенциальной энергией положения.
Движущаяся частица с массой Ми скоростью u имеет вес MG и кинематическую энергию U2/2g. Если соотнести кинематическую энергию с единичной массой, то
Полученное выражение есть не что иное, как последнее, третье слагаемое в уравнении Бернулли. Следовательно, U2/ 2 – это удельная кинетическая энергия струйки. Таким образом, общий энергетический смысл уравнения Бернулли таков: уравнение Бернулли представляет собой сумму, содержащую в себе полную удельную энергию сечения жидкости в потоке:
1) если полная энергия соотнесена с единичной массой, то она есть сумма gz + p/? + U2/ 2;
2) если полная энергия соотнесена с единичным объемом, то ?gz + p + pU2/ 2;
3) если полная энергия соотнесена единичному весу, то полная энергия есть сумма z + p/?g + U2/ 2g. Не следует забывать, что удельная энергия определяется относительно плоскости сравнения: эта плоскость выбирается произвольно и горизонтально. Для любой пары точек, произвольно выбранной из потока, в котором установившееся движение и который движется потенциальноовихрево, а жидкость невязко-несжимаемая, суммарная и удельная энергия одинаковы, то есть распределены по потоку равномерно.
НАПОР ПОЛНЫЙ В ПОТОКЕ
— энергия массы жидкости, протекающей в единицу времени через избранное живое сечение потока, отнесенное к единице веса, определяемая относительно условной горизонтальной плоскости.
Напорная линия (см. рис. 12) графически изображает напоры вдоль потока. Отметки этой линии могут быть определены с помощью трубок Питó или расчётом. По ходу движения она всегда падает с уклоном, так как потери напора не обратимы.
Пьезометрическая линия (линия давлений) графически отражает напоры вдоль потока без скоростного напора hV , поэтому она располагается всегда ниже напорной линии. Отметки этой линии могут быть зарегистрированы непосредственно пьезометрами или, с пересчётом, манометрами. В отличие от напорной линии, пьезометрическая — может понижаться или повышаться вдоль потока (рис. 13).

infopedia.su
Геометрический смысл – уравнение – Большая Энциклопедия Нефти и Газа, статья, страница 2
Геометрический смысл – уравнение
Cтраница 2
Следовательно, геометрический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма трех высот ( напоров) – геометрической, пьезометрической и обусловленной скоростным напором – есть величина постоянная вдоль потока. [17]
Следовательно, геометрический смысл уравнения Бернулли можно сформулировать так: при установившемся движении идеальной жидкости сумма трех высот ( пьезометрической; высоты, соответствующей скоростному напору, и высоты положения) вдоль потока остается неизменной. [19]
Следовательно, геометрический смысл уравнения Бернулли может быть сформулирован так: при установившемся движении жид – кости сумма четырех высот ( высоты положения, пьезометрической вы-сс ты, высоты, соответствующей скоростному напору, и высоты, со – ornsemcmeyioiui u потерям напора) остается неизменной вдоль потока. [21]
Если мы вспомним геометрический смысл уравнения ( 9), то увидим: при преобразованиях группы О16 ( действительные, собственные) прямые каждого отдельного слоя таким образом преобразуются друг в друга, что ортогональное пересечение прямых различных слоев сохраняется. [22]
Все изложенное отражает геометрический смысл уравнения Бернулли. [23]
Данный вывод поясняет геометрический смысл уравнения Бернулли для элементарной струйки вязкой жидкости. Согласно рис. 80, потеря энергии или потеря напора h m представляет собой разность между высотой горизонтальной линии О – О, проведенной через уровень жидкости в трубке Пито в начальном сечении, и высотой уровня жидкости в трубке Пито в рассматриваемом сечении относительно плоскости сравнения О – О. [24]
Все изложенное и заключает в себе геометрический смысл уравнения Бернулли. [25]
Данный вывод является одновременно и пояснением геометрического смысла уравнения Бернулли для элементарной струйки вязкой жидкости. [26]
Гамильтоновы структуры на группах Ли, биалгебры Ли и геометрический смысл уравнения Янга – Бакстера. [27]
Гамилътоновы структуры на группах Ли, биалгеб-ры Ли и геометрический смысл уравнений Янга Бакстера. [28]
В – 3L Вставляя полученные значения коэффициентов в уравнение искомой прямой, получим Ч х – ЗХу О, или 2х – Зу 0, Так как геометрический смысл уравнения не меняется от умножения ( или деления) всех его членов на одно и то же число, то при составлении уравнения прямой, параллельной данной, можно брать коэффициенты при координатах не только пропорциональными, но равными соответствующим коэффициентам данного уравнения. [29]
Не все уравнения первой степени с двумя неизвестными являются Уравнениями прямых. Например, уравнению 0 – л: 0 – г / 0 соответствует вся плоскость, а уравнение 0 – х – – 0-у не соответствует ничему. Это следует иметь в виду, когда мы говорим о геометрическом смысле уравнений первой степени: из того, что все решения одного уравнения удовлетворяют другому уравнению, отнюдь не следует, что и всякое решение второго уравнения есть в же время решение первого уравнения. [30]
Страницы: 1 2 3
www.ngpedia.ru
17. Геометрический, энергетический смысл уравнения Бернулли.
Все члены уравнения Бернулли (2.66) имеют линейную размерность, и каждый из них может называться высотой, например: z – геометрическая высота, gV22 – высота скоростного напора.
Сформулируем геометрический смысл уравнения Бернулли.
При установившемся движении жидкости элементарной струйки сумма трех высот есть величина постоянная вдоль элементарной струйки.
Уравнение Бернулли (2.68) выражает один из случаев закона сохранения энергии в любом сечении элементарной струйки.
Таким образом, энергетический смысл уравнения Бернулли заключается в следующем: при установившемся движении жидкости элементарной струйки сумма трех удельных энергий (энергии положения, энергии давления и кинетической энергии) остается неизменной вдоль элементарной струйки. В уравнении Бернулли (2.66) можно слагаемые рассматривать как удельные энергии, но уже по отношению к единице веса жидкости.
18. Дифференциальные уравнения движения реальной жидкости (уравнения Навье-Стокса).
Уравнения Навье —Стокса —система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости.
В случае несжимаемой жидкости система состоит из двух уравнений:
-Уравнения движения
-Уравнения неразрывности
В векторном виде для несжимаемой жидкости они записываются следующим образом:
где — оператор набла,— векторный оператор Лапласа,— время,— коэффициент кинематической вязкости,— плотность,— давление,— векторное поле скоростей,— векторное поле массовых сил. Неизвестныеиявляются функциями времени.
19. Уравнения д. Бернулли для потока реальной жидкости.
В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора” h составят:
,
где h2-1– напор в первом сечении потока жидкости,
h3-2– напор во втором сечении потока,
h – потерянный напор – энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.
С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть
20. Коэффициент «альфа» в уравнении д. Бернулли и его физический смысл.
Коэффициент Кориолиса. Для применения уравнения Бернулли необходимо знать величину удельной энергии.
Коэффициент Кориолиса при турбулентном режиме течения меняется в пределах от 1,11 до 1,15.
Коэффициент Кориолиса а является определенной величиной и характеризует степень неравномерности распределения скоростей по живому сечению потока. Установлено, что а> I и обычно его значение заключено в пределах а =1,03-=- 1,1. В инженерной практике чаще всего принимают а=1.
Обычно коэффициент Кориолиса определяется опытным путем. Он зависит от степени неравномерности распределения скоростей в поперечном сечении потока и всегда больше единицы; для так называемого ламинарного режима в цилиндрической трубе а = 2, а для так называемого турбулентного режима а = = 1,0454-1,10.
studfiles.net



