История архимеда – Архимед — великий учёный и изобретатель древности — История изобретений
- Комментариев к записи История архимеда – Архимед — великий учёный и изобретатель древности — История изобретений нет
- Советы абитуриенту
- Архимед | Человек и история
- История закона Архимеда | sebulfin.com
- Сказка об учёном Архимеде, который стоил целой армии
- Архимед
- XPOHOC
- ВВЕДЕНИЕ В ПРОЕКТ
- БИБЛИОТЕКА ХРОНОСА
- ИСТОРИЧЕСКИЕ ИСТОЧНИКИ
- БИОГРАФИЧЕСКИЙ УКАЗАТЕЛЬ
- ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
- ГЕНЕАЛОГИЧЕСКИЕ ТАБЛИЦЫ
- СТРАНЫ И ГОСУДАРСТВА
- ЭТНОНИМЫ
- РЕЛИГИИ МИРА
- СТАТЬИ НА ИСТОРИЧЕСКИЕ ТЕМЫ
- МЕТОДИКА ПРЕПОДАВАНИЯ
- КАРТА САЙТА
- АВТОРЫ ХРОНОСА
- ХРОНОС:
- В Фейсбуке
- ВКонтакте
- В ЖЖ
- Форум
- Личный блог
- Родственные проекты:
- РУМЯНЦЕВСКИЙ МУЗЕЙ
- ДОКУМЕНТЫ XX ВЕКА
- ИСТОРИЧЕСКАЯ ГЕОГРАФИЯ
- ПРАВИТЕЛИ МИРА
- ВОЙНА 1812 ГОДА
- ПЕРВАЯ МИРОВАЯ
- СЛАВЯНСТВО
- ЭТНОЦИКЛОПЕДИЯ
- АПСУАРА
- РУССКОЕ ПОЛЕ
- Архимед
- История открытия закона Архимеда – Задача
- История открытия закона Архимеда
- Архимед, один из величайших ученых Древней Греции, блестящий математик и механик, жил в Сиракузах в III веке до н. э. В то время в Сиракузах правил царь Гиерон. Однажды Гиерон, получив от мастеров заказанную им золотую корону, усомнился в их честности; ему показалось, что они утаили часть золота, выданного на ее изготовление, и заменили его серебром. Но как уличить ювелиров в подделке? Вызвал Гиерон Архимеда, к тому времени уже прославившегося остроумными решениями многих проблем, и поручил ему определить, есть ли в золотой короне примесь серебра. Сейчас такая задача по плечу даже школьнику. Удельный вес каждого из металлов есть в любом справочнике, определить удельный вес сплава совсем не трудно: взял образец, взвесил его, потом опустил в воду и определил объем вытесненной им жидкости, поделил первое число на второе и по соотношению удельных весов нашел долю каждого металла. Вот и вся премудрость. Но 2200 лет назад Архимед, выйдя после царской аудиенции, даже не знал, что такое удельный вес. Задача перед ним стояла в самом общем виде, и никаких конкретных путей ее решения он найти не мог. Но искал их. Искал постоянно, не переставая думать об этом, когда занимался другими делами. Иначе, если бы выкидывал ее из головы всякий раз, как прекращал работу, не могло бы произойти то прямо-таки сказочное событие, которое и легло в основу легенды. Случилось оно, как говорят, в бане. Бани в то время представляли собой место не только для мытья, но и для светских встреч, развлечений, спортивных игр. Поначалу Архимед, наверное, поупражнялся гирями, потом зашел в парильню, там его помассировали, потом он поговорил с друзьями, может быть рассказал им о своем последнем посещении царя Гиерона – прием у царя всегда событие, – не исключено, что поведал о его задаче и посетовал на трудность решения. А потом он, как и полагается, намылился золой и полез в ванну. И вот тут-то и случилось главное. Собственно, ничего нового не случилось, произошло то, что бывает всякий раз, когда любой человек, даже не ученый, садится в любую, даже не мраморную ванну – вода в ней поднимается. Но то, на что обычно Архимед не обращал никакого внимания, вдруг заинтересовало его. Он привстал – уровень воды опустился, он снова сел – вода поднялась; причем поднималась она по мере погружения тела. И вот в этот миг Архимеда осенило. Он усмотрел в десятке раз проведенном опыте намек на то, как объем тела связан с его весом. И понял, что задача царя Гиерона разрешима. И так обрадовался своей случайной находке, что как был – голый, с остатками золы на теле – побежал домой через город, оглашая улицу криками: «Эврика! Эврика!» Вот так Архимед, если верить легенде, нашел решение задачи Гиерона. Архимед не вынашивал долгое время свою гипотезу. Если, разумеется, не предположить, что ходил он в баню раз в несколько лет или что озарило его на сотом или тысячном посещении. Скорее всего, оба предположения одинаково маловероятны. Первое – по причинам, связанным с обликом ученого, второе – второе потому, что ассоциация, возникшая в голове ученого, должна была либо появиться сразу же, либо не появиться никогда, она достаточно наглядна, если поставленную задачу держать все время перед глазами. А повеление царя не пустяк. И хотя Архимед был слишком крупный ученый и слишком известный гражданин Сиракузов, чтобы можно было предположить, будто он, дрожа от подобострастия, сломя голову побежал выполнять волю Гиерона, но все же в те времена, когда благополучие ученого целиком зависело от милости его покровителя, к просьбам монарха легкомысленно не относились. И потом, думаю, Архимеда, как истинного ученого, увлекла сама задача, он размышлял не о конечной цели заказанной ему работы – уличить ювелиров, а о ее сути – о возможности как-то отличать металлы в сплаве. Поэтому, когда ученый, целиком поглощенный обдумыванием различных возможностей, получил неожиданно внешний толчок, мысль мгновенно устремилась от собственного тела, вытесняющего воду, к короне, и мелькнувшее решение показалось столь неожиданно простым, что Архимед не удержался и… И вот в том, что он сделал дальше, я сильно сомневаюсь. Все, что было до этого, представляется весьма вероятным, во всяком случае против этого нет никаких логических возражений, даже против места, где было сделано открытие, потому что оно хоть и самое неподходящее для научной работы, но в данном случае единственно возможное. А вот бег из бани голым по городу как-то не вяжется с обликом Архимеда, человека, быть может, и рассеянного и углубленного в себя, но, право же, слишком известного и уважаемого в Сиракузах, чтобы не подумать о своей репутации. Но простим эту маленькую деталь авторам легенды, она, безусловно, очень эффектна, очень театральна и несомненно украшает историю об ученом, случайно натолкнувшемся на истинное решение. Но случайно ли от этого само открытие? Если бы Архимед на том и успокоился, то есть определил, взвешивая корону в воде, есть ли в ней серебро, доложил бы об этом Гиерону и, довольный сам собой, своей работой и царской милостью, отправился заниматься другими делами, а этот случай выкинул из головы, то тогда нам пришлось бы согласиться: да, это решение случайно, как и сама работа. Но Архимед поступил иначе, как и должен был поступить настоящий ученый. Решение частной задачи о сплаве натолкнуло его на мысль о законе, который относится ко всем телам и который не случайно носит имя его автора (на всякое тело, погруженное в жидкость, действует со стороны этой жидкости подъемная сила, направленная вверх и равная весу вытесненной телом жидкости). Когда мы опускаемся в ванну, мы чувствуем на себе действие этого закона – как и почувствовал его Архимед; но мы уже знаем, в чем здесь дело, а он не знал, он должен был понять это первым из людей. И он понял, и не узко, не только применительно к сплавам, и поэтому, кроме доклада царю, содержащему, по-видимому, расчеты, связанные с короной, появилось позже еще одно сочинение, где ничего не говорится о короне, но зато говорится о плавающих телах. Причем обоснование закона дано здесь не только эмпирически: Архимед приводит геометрическое доказательство, и мало этого – он рассматривает не горизонтальную поверхность жидкости, а сферическую, как и следует из предположения о шарообразности Земли. Этот штрих сразу показывает тот всеобщий характер, какой придавал своему закону Архимед. И когда читаешь простое и ясное доказательство Архимеда, то понимаешь, сколь прав был древнегреческий философ и писатель Плутарх, с почтением писавший о своем великом соотечественнике: «Если бы кто-либо попробовал сам разрешить эти задачи, он ни к чему не пришел бы, но если бы он познакомился с решением Архимеда, у него тотчас бы получилось такое впечатление, что это решение он смог бы найти и сам, – столь прямым и кратким путем ведет нас к цели Архимед». Первое сочинение – расчет состава царской короны — до нас не дошло, и поэтому мы не знаем точно ни обстоятельств, связанных с решением задачи Гиерона, ни судьбы мастеров, изготовивших корону. Второе же сочинение – трактат «О плавающих телах» – нам известно и дает полное право утверждать: открытие закона Архимеда не случайно. Ведь не были же случайны все его другие открытия: аксиома Архимеда, на которой построен в современной арифметике и геометрии процесс последовательного деления; архимедов винт – устройство, изобретенное для перекачки жидкостей и применяемое до сих пор во многих машинах; закон рычага, позволяющий с помощью сравнительно небольшого усилия поднимать большие грузы; прибор для измерения видимого диаметра Солнца; небесный глобус, на котором можно видеть движение планет, солнечное и лунное затмение, и еще многие-многие математические исследования и инженерные находки, которых бы вполне хватило на успешную деятельность нескольких людей. Даже античные историки, нередко склонные к приукрашиванию подвигов своих героев – а Архимед был героической фигурой, – нигде не намекают более на случайность его творчества. Так правомерно ли тогда говорить о случайности открытия удельного веса и закона о плавающих телах? Человек, столь тонко разбирающийся в математике, механике, астрономии, уже не раз показавший, на что способен его проницательный ум, разве не решил бы он задачу царя Гиерона, даже если бы не помог ему случай с ванной? Все равно бы решил – пусть чуть позже, пусть путем каких-то иных ассоциаций, может быть наблюдая различную осадку по-разному нагруженных галер. Приди Архимед к такому же решению не в бане, а дома, вспомнив одно из своих прежних купаний, и никто не решился бы утверждать, что ученый случайно натолкнулся на открытие. Наоборот, сказали бы, что не случайно правильное решение нашел именно Архимед – человек, способный использовать разрозненные наблюдения для обобщений, имеющих универсальный, всеобъемлющий характер. Ведь в сближении вроде бы далеких явлений и заключается один из мощнейших методов научного мышления. С этой точки зрения, использование наблюдений над погружением в воду собственного тела – вполне правомерный прием и вовсе даже не случайный, а обязательный. Значит, все дело в несколько случайном месте и кажущемся случайным поводе.textarchive.ruАрхимед — Википедия Архиме́д (Ἀρχιμήδης; 287 до н. э. (-287) — 212 до н. э.) — древнегреческий математик, физик и инженер из Сиракуз. Сделал множество открытий в области геометрии. Заложил основы механики, гидростатики, был автором ряда важных изобретений. Биография
- Видео по теме
- Научная деятельность
- Сочинения
- Память
- См. также
- Примечания
- Литература
- Ссылки
- Архимед — биография | Великие исторические личности
Архимед | Человек и история
 Архимед – один из крупнейших ученых античности, его исследовательская деятельность коснулась не только математики, но и физики, механики, астрономии. Он изобретал изделия, применявшиеся в самых разных сферах человеческой деятельности — от сельского хозяйства до военного дела.
Архимед – один из крупнейших ученых античности, его исследовательская деятельность коснулась не только математики, но и физики, механики, астрономии. Он изобретал изделия, применявшиеся в самых разных сферах человеческой деятельности — от сельского хозяйства до военного дела.
Винтообразный насос, открытый при изучении спиралей, использовался для орошения земель в долине Нила еще в древности. «Архимедов винт» широко применялся для откачки воды из шахт, а ныне составляет рабочий элемент во многих приборах, например, в мясорубках и бетономешалках.
Архимед экспериментировал с вогнутыми зеркалами и на этой основе создал ряд работ по изучению свойств парабол.
Используя принцип интегрирования, Архимед открыл число π (Pi).
Архимед является одной из знаковых фигур мировой культуры.
Годы жизни: 287 – 212 годы до н. э.
Родители:
Отец – Фидий, родственник царя Гиерона II, видный астроном-астролог.
Мать – нет сведений.
Краткая хронология:
270 год до н. э. – Гиерон II захватывает власть в Сиракузах. Путешествие Архимеда в Александрию.
260-250 годы до н. э. – Открытие числа л. Исчисление песчинок: зная размер Вселенной и размер песчинки, Архимед вычислил количество песчинок, способных заполнить всю Вселенную. Полученное им число было немногим меньше 1063. «Задача о быках».
250-240 годы до н. э. – Принцип рычага. Создание формулы расчета объема и площади поверхности сфер. Открытие «Архимедовой силы».
212 год до н.э. – Гибель Архимеда в Сиракузах.
75 год до н. э. – Цицерон находит могилу Архимеда.
Архимед (287 до н. э. — 212 до н. э.) — древнегреческий математик, механик и инженер из Сиракуз (о.Сицилия).
Дата рождения Архимеда (287 до н.э.) определяется исходя из свидетельства византийского историка XII века Иоанна Цеца, согласно которому он «прожил семьдесят пять лет».
Отец его был математик и астроном Фидий, состоявший в близком родстве с Гиероном, тираном Сиракуз. Отец привил сыну с детства любовь к математике, механике и астрономии.
Покинув Александрию, Архимед вернулся в Сицилию. В Сиракузах он был окружён вниманием и не нуждался в средствах. Из-за давности лет жизнь Архимеда тесно переплелась с легендами о нём.
Архимед был замечательным механиком-практиком и теоретиком, но основным делом его жизни была математика. По словам Плутарха, Архимед был просто одержим ею. Он забывал о пище, совершенно не заботился о себе.
Остались отрывки работы Архимеда, в которой он развивает математическую теорию популярной в Греции игры (так называемой стомахии), предвосхищая, таким образом, более чем на 2 тыс. лет создание математической теории игр.
Но главное его внимание было сосредоточено на трёх типах проблем:

Архимед
Картина Доменико Фетти, 1620г.
1. Определение площадей криволинейных фигур или соответственно, объёмов тел. Мы уже знаем, как определять площади прямолинейных фигур, площадь круга, объём призмы, пирамиды, цилиндра и конуса. Все это умели делать греки и до Архимеда.
Но только он нашёл общий метод, позволяющий найти любую площадь или объём. Трудно переоценить значение этого метода, без которого была бы немыслима ни физика, ни астрономия. Идеи Архимеда легли в основу интегрального исчисления.
Сам Архимед определил с помощью своего метода площади и объёмы почти всех тел, которые рассматривались в античной математике. Лучшим своим достижением он считал определение поверхности и объёма шара. Он просил выбить на своей могиле шар, вписанный в цилиндр.
2. Пусть дана некоторая кривая линия. Как определить касательную в любой её точке? Или, если переложить эту проблему на язык физики, пусть нам известен путь некоторого тела в каждый момент времени. Как определить скорость его в любой точке?
В школе учат, как проводить касательную к окружности. Древние греки умели, кроме того, находить касательные к эллипсу, гиперболе и параболе. Первый общий метод решения и этой задачи был найден Архимедом. Этот метод впоследствии лёг в основу дифференциального исчисления.
3. В математике, физике и астрономии очень важно уметь находить наибольшие и наименьшие значения изменяющихся величин — их экстремумы. Например, как среди цилиндров, вписанных в шар, найти цилиндр, имеющий наибольший объём?
Все такие задачи в настоящее время могут быть решены с помощью дифференциального исчисления. Архимед первым увидел связь этих задач с проблемами определения касательных и показал, как с можно решать задачи на экстремумы. Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру.
 Архимед прославился многими механическими конструкциями. Изобретённый им бесконечный, или архимедов, винт для вычерпывания воды до сих пор применяется в Египте.
Архимед прославился многими механическими конструкциями. Изобретённый им бесконечный, или архимедов, винт для вычерпывания воды до сих пор применяется в Египте.
Архимед построил планетарий или «небесную сферу», при движении которой можно было наблюдать движение пяти планет, восход Солнца и Луны, фазы и затмения Луны, исчезновение обоих тел за линией горизонта.
Идеи Архимеда почти на два тысячелетия опередили своё время. Только в XVII в. учёные смогли продолжить и развить труды великого греческого математика. Только тогда было раскрыто их подлинное значение.
Уже при жизни Архимеда вокруг его имени создавались легенды, поводом для которых служили его поразительные изобретения, производившие ошеломляющее действие на современников. Известен рассказ о том как Архимед сумел определить, сделана ли корона царя Гиерона из чистого золота или ювелир подмешал туда значительное количество серебра.
Удельный вес золота был известен, но трудность состояла в том, чтобы точно определить объём короны: ведь она имела неправильную форму!
Архимед всё время размышлял над этой задачей. Как-то он принимал ванну, и тут ему пришла в голову блестящая идея: погружая корону в воду, можно определить её объём, измерив, объём вытесненной ею воды.
Согласно легенде, Архимед выскочил голый на улицу с криком «Эврика!», т. е, «Нашёл!». В этот момент был открыт основной закон гидростатики.
Другая легенда рассказывает, что построенный Гиероном в подарок египетскому царю Птолемею роскошный корабль «Сирокосия» никак не удавалось спустить на воду. Архимед соорудил систему блоков (полиспаст), с помощью которой он смог проделать эту работу одним движением руки. Этот случай или размышления Архимеда над принципом рычага послужили поводом для его крылатых слов: «Дайте мне точку опоры, и я сдвину Землю».
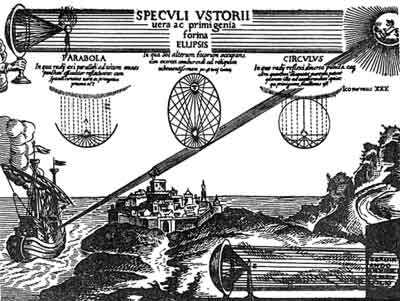
Рисунок из книги немецкого
математика Афанасия Кирхера
“Великое искусство света и тени”
(1647 г.), предложившего
систему из параболических зеркал, способных
зажигать дерево на любом расстоянии
Инженерный гений Архимеда с особой силой проявился во время осады Сиракуз римлянами в 212 до н. э. А ведь в это время ему было уже 75 лет!
Построенные Архимедом мощные метательные машины забрасывали римские войска тяжёлыми камнями. Думая, что они будут в безопасности у самых стен города, римляне кинулись туда, но в это время лёгкие метательные машины близкого действия забросали их градом ядер. Мощные краны захватывали железными крюками корабли, приподнимали их кверху, а затем бросали вниз, так что корабли переворачивались и тонули.
Знаменитый историк древности Полибий писал: «Такова чудесная сила одного человека, одного дарования, умело направленного на какое-либо дело… римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузян одного старца».
Но даже во время осады Архимед не давал покоя римлянам. По легенде, во время осады римский флот был сожжён защитниками города, которые при помощи зеркал и отполированных до блеска щитов сфокусировали на них солнечные лучи по приказу Архимеда.
Этот день 212 года до н. э. уцелевшим римлянам запомнился на всю жизнь. Почти полтысячи маленьких солнц вдруг загорелись на крепостной стене.
Сначала они просто ослепили, но через некоторое время произошло нечто фантастическое: передовые римские корабли, подошедшие к Сиракузам, один за другим вдруг начали вспыхивать, как факелы. Бегство римлян было паническим…
Вообще говоря, о необычном архимедовом оружии вспомнили мы не ради исторических изысканий. Нас интересуют уникальные свойства вогнутых зеркал. Да-да, вогнутых зеркал.
Ведь Архимедом, по существу, было изобретено «распределенное» вогнутое зеркало. Составленное из множества обычных зеркал, отражения от которых направлены в одну точку, оно способно концентрировать в своем фокусе огромную энергию. В случае с римскими кораблями это – световая и тепловая энергии.

Смерть Архимеда. Римская мозаика.
Легенда была дважды опровергнута в телепередаче «Разрушители легенд» (в 46-м и 16-м выпусках). Существует мнение, что корабли поджигались метко брошенными зажигательными снарядами, а сфокусированные лучи служили лишь прицельной меткой для баллист.
Справедливости ради надо сказать и о следующих попытках восстановления репутации Архимеда.
По команде Сакаса, помощники несколько раз поднимали зеркала, пытаясь сфокусировать солнечные зайчики на лодке, груженной смолой.
Наконец, когда лучи удалось совместить в одной точке, лодка в этом месте задымилась и через три минуты вспыхнула!
Аналогичный опыт, правда, на суше, 30 сентября 2005 года провели студенты и профессора Массачусетского технологического института. Дело пошло не так гладко, как у греков: студенты никак не могли навести в одну точку все 129 квадратных зеркал, закупленных для эксперимента. Вскоре небо затянули облака и продолжение экслеримента стало невозможным.
Вторая попытка увенчалась полным успехом: на этот раз профессора решили обойтись без студентов и сделали все сами.
С помощью зеркала, дающего крестообразный «зайчик» – мишень на макет римского корабля, они поочередно навели в одно место все 129 зеркал, предварительно задрапированных тканью, чтобы свет одного зеркала не мешал наводить другое.
Наконец, когда все было сфокусировано, ученые скинули покрывала. Через несколько минут от макета из красного дуба повалил густой дым, а затем на месте фокусировки вспыхнуло пламя. Полюбовавшись на дело рук своих и затушив огонь, ученые обнаружили, что их гигантскии «солнечный заяц» прожег доску толщиной 2,54 сантиметра насквозь (!..)
В общем и целом, проведенные в разные времена опыты убедительно доказали: Архимед вполне мог для поджога римских квинкирем использовать систему зеркал собственной конструкции.
Только вследствие измены Сиракузы были взяты римлянами осенью 212 до н. э. При этом Архимед был убит. Плутарх сохранил нам яркий рассказ о его смерти: «К Архимеду подошёл солдат и объявил, что его зовёт Марцелл. Но Архимед настойчиво просил его подождать одну минуту, чтобы задача, которой он занимался, не осталась нерешённой. Солдат, которому не было дела до его доказательства, рассердился и пронзил его своим мечом».
Источники информации:
1. Де Агостини «100 человек, которые изменили ход истории. Архимед»
2. Википедия
historical-persons.ru
История закона Архимеда | sebulfin.com
Слово “Эврика!“, в переводе с греческого языка, означает “Я нашёл !“. Именно этим высказыванием ознаменовалось открытие великим математиком древности Архимедом Сиракузским ( ок.287-212 гг.до н.э) основного закона гидростатики. Этот закон в наше время носит имя Архимеда и формулируется так: «Закон статики жидкостей и газов. На всякое тело погружённое в жидкость или газ, действует со стороны этой жидкости или газа поддерживающая сила, равная весу вытесненной телом жидкости (газа),направленная вверх и приложенная к центру тяжести вытесненного объёма. Оставим физикам научные рассуждения об этом законе и перейдём к лирике, расскажем о том, как Архимед сделал своё открытие.
На основании повествования римского инженера и зодчего Витрувия ( I в.до н.э), сделанного им в 9-й книге трактата” Об архитектуре”, история закона Архимеда выглядит так.
Однажды, сиракузский царь Гиерон II поручил своему ювелиру изготовить золотую корону. После изготовления сего абсолютно необходимого для царей предмета, в голову Гиерону закралась естественная для большого руководителя мысль: ” А не обманул ли меня мой ювелир? Не подмешал ли он в корону значительную часть серебра вместо золота и не прибрал ли ювелир золотишко к рукам?”
Проверить это было поручено Архимеду. Нужно было выяснить, содержит ли корона серебро вместо золота, не разрушая при этом
Легенда гласит, что Архимед пришёл в полный восторг от этого открытия и голый с криком “Эврика!” побежал из купальни, чтобы проверить свою теорию.
Великий математик пришел к Гиерону II и попросил предоставить ему слиток золота и слиток серебра точно такого же веса, что и корона. Потом он наполнил доверху сосуд и положил в него слиток серебра. Вполне понятно, что каков был объём серебряного слитка, такое количество воды и вытекло.
Затем,вынув слиток, он долил в этот сосуд точное количество вытесненной воды, измеряя этот объём секстарием. Таким образом, Архимед определил, какой вес серебра соответствует какому количеству воды.
Затем, он опустил золотой слиток в сосуд и тем же способом, при помощи секстариев, великий математик выяснил, насколько меньший объём занимает слиток золота по сравнению с со слитком серебра аналогичного веса.
После чего, опять наполнив сосуд и опустив в него корону, Архимед определил, что при погружении короны вытекло больше воды, чем при погружении в сосуд золотой массы того же веса.
Заключение “криминалистической экспертизы” Архимеда было следующим. Так как короной вытеснялось большее количество воды, чем золотым слитком, то в золоте, из которого изготовлена корона, содержится примесь серебра.
Что стало с ювелиром история умалчивает, а Архимед своими изысканиями произвёл первое в истории применение физического измерительного метода к контролю и анализу химического состава изделия, без нарушения его целостности.
Открытый Архимедом физический принцип лёг в основу закона гидростатики, по праву носящего имя великого математика.
Вконтакте
Одноклассники
Мой мир
LiveJournal
Google+
sebulfin.com
Сказка об учёном Архимеде, который стоил целой армии
Другие научные сказки Ник. Горькавого печатались в журнале «Наука и жизнь» в 2010—2013 годах.Доменико Фетти. Архимед размышляет. 1620 год. Картина из Галереи старых мастеров, Дрезден.
Эдуард Вимон. Смерть Архимеда. 1820-е годы.
Гробница Архимеда в Сиракузах. Фото: Codas2.
Остров Ортигия, исторический центр Сиракуз, родного города Архимеда. У этих берегов Архимед сжёг и потопил римские галеры. Фото: Marcos90.
Греческий театр в Сиракузах. Фото: Victoria|photographer_location_London, UK.
Архимед переворачивает Землю с помощью рычага. Старинная гравюра. 1824 год.
Шар, вписанный в цилиндр. Автор иллюстрации Андре Карвас.
Изображение Архимеда на золотой медали Филдса — высшей награде среди математиков. Надпись на латыни: «Transire suum pectus mundoque potiri» — «Превзойти свою человеческую ограниченность и покорить Вселенную». Фото Стефана Захова.
‹
›
Каждая новая сказка писателя и астрофизика, доктора физико-математических наук Николая Николаевича Горькавого (Ник. Горькавого) — это рассказ о том, как совершались важные открытия в той или иной области науки. И неслучайно героями его научно-популярных романов и сказок стали принцесса Дзинтара и её дети — Галатея и Андрей, ведь они из породы тех, кто стремится «всё знать». Истории, рассказанные Дзинтарой детям, вошли в сборник «Звёздный витамин». Он оказался таким интересным, что читатели потребовали продолжения. Предлагаем вам ознакомиться с некоторыми сказками из будущего сборника «Создатели времён». Перед вами — первая публикация.
Величайший учёный античного мира древнегреческий математик, физик и инженер Архимед (287—212 годы до н.э.) был родом из Сиракуз — греческой колонии на самом большом острове Средиземноморья — Сицилии. Древние греки, создатели европейской культуры, поселились там почти три тысячи лет назад — в VIII веке до нашей эры, и к моменту рождения Архимеда Сиракузы были процветающим культурным городом, где жили свои философы и учёные, поэты и ораторы.
Каменные дома горожан обступали дворец царя Сиракуз Гиерона II, высокие стены защищали город от врагов. Жители любили собираться на стадионах, где состязались бегуны и метатели диска, и в банях, где не просто мылись, а отдыхали и обменивались новостями.
В тот день в банях на главной площади города было шумно — смех, крики, плеск воды. Молодёжь плавала в большом бассейне, а люди почтенного возраста, держа в руках серебряные кубки с вином, вели неспешную беседу на удобных ложах. Солнце заглядывало во внутренний дворик бань, освещая проём двери, ведущей в отдельную комнату. В ней, в небольшом бассейне, похожем на ванну, сидел в одиночестве человек, который вёл себя совсем не так, как другие. Архимед — а это был именно он — прикрыл глаза, но по каким-то неуловимым признакам было видно, что человек этот не спит, а напряжённо думает. В последние недели учёный настолько углубился в свои мысли, что часто забывал даже про еду и домашним приходилось следить, чтобы он не остался голодным.
Началось с того, что царь Гиерон II пригласил Архимеда к себе во дворец, налил ему лучшего вина, спросил про здоровье, а потом показал золотую корону, изготовленную для правителя придворным ювелиром.
— Я не разбираюсь в ювелирном деле, но разбираюсь в людях, — сказал Гиерон. — И думаю, что ювелир меня обманывает.
Царь взял со стола слиток золота.
— Я дал ему точно такой же слиток, и он сделал из него корону. Вес у короны и слитка одинаковый, мой слуга проверил это. Но меня не оставляют сомнения, не подмешано ли в корону серебро? Ты, Архимед, самый великий учёный Сиракуз, и я прошу тебя это проверить, ведь, если царь наденет фальшивую корону, над ним будут смеяться даже уличные мальчишки…
Правитель протянул корону и слиток Архимеду со словами:
— Если ты ответишь на мой вопрос, то оставишь золото себе, но я всё равно буду твоим должником.
Архимед взял корону и слиток золота, вышел из царского дворца и с тех пор потерял покой и сон. Уж если он не сможет решить эту задачу, то и никто не сможет. Действительно, Архимед был самым известным учёным Сиракуз, учился в Александрии, дружил с главой Александрийской библиотеки, математиком, астрономом и географом Эратосфеном и другими великими мыслителями Греции. Архимед прославился множеством открытий в математике и геометрии, заложил основы механики, на его счету несколько выдающихся изобретений.
Озадаченный учёный пришёл домой, положил корону и слиток на чаши весов, поднял их за середину и убедился, что вес у обоих предметов одинаковый: чаши покачивались на одном уровне. Плотность чистого золота была Архимеду известна, предстояло узнать плотность короны (вес, делённый на объём). Если в короне есть серебро, её плотность должна быть меньше плотности золота. А раз веса` короны и слитка совпадают, то объём фальшивой короны должен быть больше объёма золотого слитка. Объём слитка измерить можно, но как определить объём короны, в которой столько сложных по форме зубцов и лепестков? Вот эта проблема и мучила учёного. Он был прекрасным геометром, например, решил сложную задачу — определение площади и объёма шара и описанного вокруг него цилиндра, но как найти объём тела сложной формы? Нужно принципиально новое решение.
В баню Архимед пришёл, чтобы смыть с себя пыль жаркого дня и освежить уставшую от размышлений голову. Обычные люди, купаясь в бане, могли болтать и жевать инжир, а Архимеда мысли о нерешённой задаче не оставляли ни днём, ни ночью. Его мозг искал решение, цепляясь за любую подсказку.
Архимед снял хитон, положил его на лавку и подошёл к маленькому бассейну. Вода плескалась в нём на три пальца ниже края. Когда учёный погрузился в воду, её уровень заметно поднялся, и первая волна даже выплеснулась на мрамор пола. Учёный прикрыл глаза, наслаждаясь приятной прохладой. Мысли об объёме короны привычно кружились в голове.
Вдруг Архимед почувствовал, что случилось что-то важное, но не мог понять — что. Он с досадой открыл глаза. Со стороны большого бассейна доносились голоса и чей-то горячий спор — кажется, о последнем законе правителя Сиракуз. Архимед замер, пытаясь осознать, что же всё-таки произошло? Он осмотрелся вокруг: вода в бассейне не доставала до края всего на один палец, а ведь когда он входил в воду, уровень её был ниже.
Архимед встал и вышел из бассейна. Когда вода успокоилась, она вновь оказалась на три пальца ниже края. Учёный снова забрался в бассейн — вода послушно поднялась. Архимед быстро оценил размер бассейна, вычислил его площадь, потом умножил на изменение уровня воды. Получилось, что объём воды, вытесненной его телом, равен объёму тела, если принять, что плотности воды и человеческого тела почти одинаковы и каждый кубический дециметр, или кубик воды со стороной в десять сантиметров, можно приравнять к килограмму веса самого учёного. Но при погружении тело Архимеда потеряло в весе и плавало в воде. Каким-то таинственным образом вода, вытесненная телом, отобрала у него вес…
Архимед понял, что он на верном пути, — и вдохновение понесло его на своих могучих крыльях. Можно ли применить найденный закон об объёме вытесненной жидкости к короне? Конечно! Надо опустить корону в воду, измерить увеличение объёма жидкости, а потом сравнить с объёмом воды, вытесняемой золотым слитком. Задача решена!
Согласно легенде, Архимед с победным криком «Эврика!», что значит по-гречески «Нашёл!», выскочил из бассейна и, забыв надеть хитон, помчался домой. Надо было срочно проверить своё решение! Он бежал по городу, а жители Сиракуз приветственно махали ему руками. Всё-таки не каждый день открывается важнейший закон гидростатики и не каждый день можно увидеть голого человека, бегущего по центральной площади Сиракуз.
На следующий день царю доложили о приходе Архимеда.
— Я решил задачу, — сказал учёный. — В короне действительно много серебра.
— Как ты это узнал? — поинтересовался правитель.
— Вчера, в банях, я догадался, что тело, которое погружается в бассейн с водой, вытесняет объём жидкости, равный объёму самого тела, и теряет при этом в весе. Вернувшись домой, я провёл множество опытов с чашами весов, погружёнными в воду, и доказал, что тело в воде теряет в весе ровно столько, сколько весит вытесненная им жидкость. Поэтому человек может плавать, а золотой слиток — нет, но всё равно в воде он весит меньше.
— И как же это доказывает наличие серебра в моей короне? — спросил царь.
— Вели принести чан с водой, — попросил Архимед и достал весы. Пока слуги тащили чан в царские покои, Архимед положил на весы корону и слиток. Они уравновесили друг друга.
— Если в короне есть серебро, то объём короны больше, чем объём слитка. Значит, при погружении в воду корона потеряет в весе больше и весы изменят своё положение, — сказал Архимед и осторожно погрузил обе чаши весов в воду. Чаша с короной немедленно поднялась вверх.
— Ты поистине великий учёный! — воскликнул царь. — Теперь я смогу заказать себе новую корону и проверить — настоящая она или нет.
Архимед спрятал в бороде усмешку: он понимал, что закон, открытый им накануне, гораздо ценнее тысячи золотых корон.
Закон Архимеда остался в истории навсегда, им пользуются при проектировании любых кораблей. Сотни тысяч судов бороздят океаны, моря и реки, и каждое из них держится на поверхности воды благодаря силе, открытой Архимедом.
Когда Архимед состарился, его размеренные занятия наукой неожиданно закончились, впрочем как и спокойная жизнь горожан, — быстро растущая Римская империя решила завоевать плодородный остров Сицилию.
В 212 году до н.э. огромный флот галер, набитых римскими воинами, подошёл к острову. Преимущество в силе римлян было очевидным, и командующий флотом нисколько не сомневался, что Сиракузы будут захвачены очень быстро. Но не тут-то было: стоило галерам подойти к городу, как со стен ударили мощные катапульты. Они бросали тяжёлые камни так точно, что галеры захватчиков разлетались в щепки.
Римский полководец не растерялся и скомандовал капитанам своего флота:
— Подойдите к самым стенам города! На близком расстоянии катапульты будут нам не страшны, а лучники смогут прицельно стрелять.
Когда флот с потерями прорвался к городским стенам и приготовился его штурмовать, римлян ждал новый сюрприз: теперь уже лёгкие метательные машины забросали их градом ядер. Спускаемые крюки мощных подъёмных кранов цепляли римские галеры за носы и поднимали их в воздух. Галеры переворачивались, падали вниз и тонули.
Знаменитый историк древности Полибий писал о штурме Сиракуз: «Римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузцев одного старца». Этим старцем был Архимед, который сконструировал метательные машины и мощные подъёмные краны для защиты города.
Быстрый захват Сиракуз не получился, и римский полководец дал команду отступить. Сильно поредевший флот отошёл на безопасное расстояние. Город стойко держался благодаря инженерному гению Архимеда и мужеству горожан. Лазутчики донесли римскому полководцу имя учёного, который создал столь неприступную оборону. Полководец решил, что после победы нужно заполучить Архимеда как самый ценный военный трофей, ведь он один стоил целой армии!
День за днём, месяц за месяцем мужчины дежурили на стенах, стреляли из луков и заряжали катапульты тяжёлыми камнями, которые, увы, не достигали цели. Мальчишки подносили солдатам воду и еду, но воевать им не давали — малы ещё!
Архимед был стар, он, как и дети, не мог стрелять из лука так далеко, как молодые и сильные мужчины, но у него был могучий мозг. Архимед собрал мальчишек и спросил их, показывая на вражеские галеры:
— Хотите уничтожить римский флот?
— Мы готовы, говори, что делать!
Мудрый старец объяснил, что придётся серьёзно поработать. Он велел каждому мальчишке взять большой медный лист из уже приготовленной стопы и положить его на ровные каменные плиты.
— Каждый из вас должен отполировать лист так, чтобы он сиял на солнце, как золотой. И тогда завтра я покажу вам, как потопить римские галеры. Работайте, друзья! Чем лучше вы сегодня отполируете медь, тем легче нам будет завтра воевать.
— А мы сами будем воевать? — спросил маленький кудрявый мальчуган.
— Да, — твёрдо сказал Архимед, — завтра вы все будете на поле боя наравне с воинами. Каждый из вас сможет совершить подвиг, и тогда о вас будут складывать легенды и песни.
Трудно описать энтузиазм, который охватил мальчишек после речи Архимеда, и они энергично взялись надраивать свои медные листы.
Назавтра, в полдень, солнце обжигающе пылало в небе, а римский флот неподвижно стоял на якорях на внешнем рейде. Деревянные борта вражеских галер разогрелись на солнце и сочились смолой, которую использовали для защиты кораблей от протечек.
На крепостных стенах Сиракуз, там, куда не доставали вражеские стрелы, собрались десятки подростков. Перед каждым из них стоял деревянный щит с отполированным медным листом. Опоры щита были сделаны так, что лист меди можно было легко поворачивать и наклонять.
— Вот сейчас мы и проверим, как хорошо вы отполировали медь, — обратился к ним Архимед. — Надеюсь, все умеют пускать солнечные зайчики?
Архимед подошёл к маленькому кудрявому мальчику и сказал:
— Поймай своим зеркалом солнце и направь солнечный зайчик в середину борта большой чёрной галеры, как раз под мачтой.
Мальчишка бросился выполнять указание, а воины, столпившиеся на стенах, удивлённо переглянулись: что ещё затеял хитрец Архимед?
Учёный остался доволен результатом — на боку чёрной галеры появилось световое пятно. Тогда он обратился к остальным подросткам:
— Наведите свои зеркала в то же место!
Заскрипели деревянные опоры, загремели медные листы — стая солнечных зайчиков сбежалась к чёрной галере, и её бок стал наливаться ярким светом. На палубы галер высыпали римляне — что происходит? Вышел главнокомандующий и тоже уставился на сверкающие зеркала на стенах осаждённого города. Боги Олимпа, что ещё придумали эти упрямые сиракузцы?
Архимед инструктировал своё воинство:
— Не спускайте глаз с солнечных зайчиков — пусть они всё время будут направлены в одно место.
Не прошло и минуты, как от сияющего пятна на борту чёрной галеры повалил дым.
— Воды, воды! — закричали римляне. Кто-то бросился черпать забортную воду, но дым быстро сменился пламенем. Сухое просмолённое дерево прекрасно горело!
— Переведите зеркала на соседнюю галеру справа! — скомандовал Архимед.
Считаные минуты — и соседняя галера тоже занялась огнём. Римский флотоводец вышел из оцепенения и приказал сниматься с якоря, чтобы отойти подальше от стен проклятого города с его главным защитником Архимедом.
Сняться с якорей, посадить гребцов на вёсла, развернуть огромные корабли и отвести их в море на безопасное расстояние — дело не быстрое. Пока римляне суматошно бегали по палубам, задыхаясь от удушливого дыма, юные сиракузцы переводили зеркала на новые корабли. В суматохе галеры подходили друг к другу так близко, что огонь перекидывался с одного судна на другое. Спеша отплыть, некоторые корабли развернули паруса, которые, как оказалось, горели ничуть не хуже смоляных бортов.
Вскоре сражение было окончено. На рейде догорало множество римских кораблей, а остатки флота отступили от стен города. Среди юного воинства Архимеда потерь не было.
— Слава великому Архимеду! — кричали восхищённые жители Сиракуз и благодарили и обнимали своих детей. Могучий воин в блестящих доспехах крепко пожал руку кудрявому мальчику. Его маленькая ладонь была покрыта кровавыми мозолями и ссадинами от полировки медного листа, но он даже не поморщился при рукопожатии.
— Молодец! — уважительно сказал воин. — Этот день сиракузцы запомнят надолго.
Прошло два тысячелетия, а этот день остался в истории, и запомнили его не только сиракузцы. Жители разных стран знают удивительную историю о сожжении Архимедом римских галер, но он один ничего бы не сделал без своих юных помощников. Кстати, совсем недавно, уже в ХХ веке нашей эры, учёные провели эксперименты, которые подтвердили полную работоспособность древнего «сверхоружия», изобретённого Архимедом для защиты Сиракуз от захватчиков. Хотя есть историки, считающие это легендой…
— Эх, жаль, меня там не было! — воскликнула Галатея, внимательно слушавшая вместе с братом вечернюю сказку, которую рассказывала им мать — принцесса Дзинтара. Та продолжила читать книгу:
— Потеряв надежду захватить город с помощью оружия, римский полководец прибег к старому испытанному способу — подкупу. Он нашёл в городе предателей, и Сиракузы пали. Римляне ворвались в город.
— Найдите мне Архимеда! — приказал командующий. Но солдаты, опьянённые победой, плохо понимали, чего он от них хочет. Они врывались в дома, грабили и убивали. Один из воинов выбежал на площадь, где работал Архимед, рисуя на песке сложную геометрическую фигуру. Солдатские башмаки затоптали хрупкий рисунок.
— Не тронь моих чертежей! — грозно сказал Архимед.
Римлянин не узнал учёного и в гневе ударил его мечом. Так погиб этот великий человек.
Известность Архимеда была столь велика, что книги его часто переписывали, благодаря чему ряд трудов сохранился до нашего времени, несмотря на пожары и войны двух тысячелетий. История дошедших до нас книг Архимеда нередко была драматической. Известно, что в XIII веке какой-то невежественный монах взял книгу Архимеда, написанную на прочном пергаменте, и смыл формулы великого учёного, чтобы получить чистые страницы для записи молитв. Прошли века, и этот молитвенник попал в руки других учёных. Они с помощью сильной лупы исследовали его страницы и различили следы стёртого драгоценного текста Архимеда. Книга гениального учёного была восстановлена и напечатана большим тиражом. Теперь она уже никогда не исчезнет.
Архимед был настоящим гением, сделавшим множество открытий и изобретений. Он опередил своих со-временников даже не на века — на тысячелетия.
В книге «Псаммит, или Исчисление песчинок» Архимед пересказал смелую теорию Аристарха Самосского, согласно которой в центре мира расположено большое Солнце. Архимед писал: «Аристарх Самосский … полагает, что неподвижные звёзды и Солнце не меняют своего места в пространстве, что Земля движется по окружности около Солнца, находящегося в его центре…» Архимед считал гелиоцентрическую теорию Самосского убедительной и использовал её, чтобы оценить размеры сферы неподвижных звёзд. Учёный даже построил планетарий, или «небесную сферу», где можно было наблюдать движение пяти планет, восход солнца и луны, её фазы и затмения.
Правило рычага, которое открыл Архимед, стало основой всей механики. И хотя рычаг был известен до Архимеда, он изложил его полную теорию и успешно применил её на практике. В Сиракузах он в одиночку спустил на воду новый многопалубный корабль царя Сиракуз, используя хитроумную систему блоков и рычагов. Именно тогда, оценив всю мощь своего изобретения, Архимед воскликнул: «Дайте мне точку опоры, и я переверну мир».
Неоценимы достижения Архимеда в области математики, которой, по словам Плутарха, он был просто одержим. Его главные математические открытия относятся к математическому анализу, где идеи учёного легли в основу интегрального и дифференциального исчисления. Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру. Архимед дал приближение для числа π (Архимедова числа):
Своим наивысшим достижением учёный считал работы в области геометрии и, прежде всего, расчёт шара, вписанного в цилиндр.
— Что за цилиндр и шар? — спросила Галатея. — Почему он так ими гордился?
— Архимед сумел показать, что площадь и объём сферы относятся к площади и объёму описанного цилиндра как 2:3.
Дзинтара поднялась и сняла с полки модель земного шара, который был впаян внутрь прозрачного цилиндра так, что соприкасался с ним на полюсах и на экваторе.
— Я с детства люблю эту геометрическую игрушку. Посмотрите, площадь шара равна площади четырёх кругов такого же радиуса или площади боковой стороны прозрачного цилиндра. Если добавить площади основания и верха цилиндра, то получится, что площадь цилиндра в полтора раза больше площади шара внутри него. То же самое соотношение выполняется для объёмов цилиндра и шара.
Архимед был восхищён полученным результатом. Он умел ценить красоту геометрических фигур и математических формул — именно поэтому не катапульта и не горящая галера украшают его могилу, а изображение шара, вписанного в цилиндр. Таково было желание великого учёного.
www.nkj.ru
XPOHOCВВЕДЕНИЕ В ПРОЕКТБИБЛИОТЕКА ХРОНОСАИСТОРИЧЕСКИЕ ИСТОЧНИКИБИОГРАФИЧЕСКИЙ УКАЗАТЕЛЬПРЕДМЕТНЫЙ УКАЗАТЕЛЬГЕНЕАЛОГИЧЕСКИЕ ТАБЛИЦЫСТРАНЫ И ГОСУДАРСТВАЭТНОНИМЫРЕЛИГИИ МИРАСТАТЬИ НА ИСТОРИЧЕСКИЕ ТЕМЫМЕТОДИКА ПРЕПОДАВАНИЯКАРТА САЙТААВТОРЫ ХРОНОСАХРОНОС:В ФейсбукеВКонтактеВ ЖЖФорумЛичный блогРодственные проекты:РУМЯНЦЕВСКИЙ МУЗЕЙДОКУМЕНТЫ XX ВЕКАИСТОРИЧЕСКАЯ ГЕОГРАФИЯПРАВИТЕЛИ МИРАВОЙНА 1812 ГОДАПЕРВАЯ МИРОВАЯСЛАВЯНСТВОЭТНОЦИКЛОПЕДИЯАПСУАРАРУССКОЕ ПОЛЕ | Архимед
Архимед Архимед (ок. 287-212 до н. э.), древнегреческий ученый. Родом из Сиракуз (Сицилия). Разработал предвосхитившие интегральное исчисление методы нахождения площадей, поверхностей и объемов различных фигур и тел. В основополагающих трудах по статике и гидростатике (закон Архимеда) дал образцы применения математики в естествознании и технике. Автор многих изобретений (архимедов винт, определение состава сплавов взвешиванием в воде, системы для поднятия больших тяжестей, военные метательные машины и др.). Организатор инженерной обороны Сиракуз против римлян. + + +Архимед (Arkhimedes) (287—212 гг. до н.э.). Родился в Сиракузах, сын астронома Фидия. Был одним из величайших греческих математиков, а также изобретателем, физиком и астрономом. Возможно, учился в Александрии, а затем жил при дворе Гиерона II Сиракузского. Был убит римским солдатом во время осады Сиракуз. До нашего времени дошел ряд его математических трактатов (в основном — на греческом языке, два — на арабском) на различные темы — например о круге, сфере и цилиндре. Среди этих трактатов следует назвать «О сфере и цилиндре», «О плавающих телах» (изобретенная им наука гидростатики), «О спиралях», «Метод механических теорем» и «Число песчинок» (средство выражения больших чисел словами). Открыв способ определения пропорций золота и серебра в короне, сделанной для Гиерона, издал знаменитый возглас «Эврика!» (eureka-«Нашел!»). Адкинс Л., Адкинс Р. Древняя Греция. Энциклопедический справочник. М., 2008, с. 446. Архимед (ок. 287 – 212 гг. до н. э.) — знаменитый древнегреческий математик и физик. Родом из Сиракуз (Сицилия). При обороне города от римлян опробовал работу военных машин. Погиб при взятии города. В своем сочинении «Парабола квадратуры» он определил площадь (квадратуру) сегмента. Как физик Архимед обосновал закон рычага и закон гидростатики (закон Архимеда). Автор многочисленных изобретений (архимедов винт, определение состава сплавов взвешиванием в воде, системы для поднятия больших тяжестей, военные метательные машины, др.). Его труды оказали большое влияние на развитие высшей математики в XIV–XVII вв. Грейдина Н.Л., Мельничук А.А. Античность от А до Я. Словарь-справочник. М., 2007. Архимед (ок. 287-212 до н.э.). Греческий механик, физик, математик, инженер. Родился и провел большую часть жизни в Сиракузах (Сицилия). Учился в Александрии (Египет). Был советником царя Сицилии Гиерона II. По легенде, он с помощью системы зеркал, отражающих солнечные лучи, сжег римский флот, осадивший Александрию (эта история отражает его успехи в оптике). Считается изобретателем катапульты. Установил правило рычага, в связи с чем ему приписывают изречение: «Дайте мне точку опоры, и я сдвину Землю». Архимед блестяще сочетал таланты инженера-изобретателя и ученого-теоретика. Кроме военных машин сконструировал планетарий и винт для подъема воды, который до сих пор используют. Написал трактаты: «О спиралях», «О шаре и цилиндре» (эти фигуры изображены на его могильной плите), «О коноидах и сфероидах», «О рычагах», «О плавающих телах» и др. Вычислил объем сферы и значение числа «пи». Подсчитал число песчинок в объеме земного шара (трактат «О песчинках»). Однажды царь Гиерон II предложил Архимеду определить, не подмешали ли ювелиры серебра к золоту, когда делали его корону. Для этого надо было узнать не только вес, но и объем изделия. Архимед решил непростую задачу изящно: опустил корону в воду и определил объем вытесненной жидкости. Говорят, мысль об этом пришла к нему тогда, когда он принимал ванну. Радостный, он выскочил на улицу в чем был (то есть без ничего) с криком: «Эврика!» (нашел, открыл). С именем Архимеда связано немало легенд, подлинность которых вряд ли можно подтвердить. Безусловно, он не мог с помощью зеркал сжечь вражеские корабли. А вот история с царской короной вполне правдоподобна (но была ли ванна?). Рассказывают, что Гиерон предложил ему поднять большую часть малой силой. Ученый изобрел механизм (или полиспаст, сложный блок), с помощью которого вытащил на берег тяжелогруженную триеру. Один из историков науки высказал предположение, что Архимед применил свой винт в соединении с системой зубчатых колес. Правда, скорее всего данная история выдумана для того, чтобы ярче представить инженерный гений Архимеда. Греческие моряки, по-видимому, умели вытаскивать на берег даже крупные суда с помощью рычагов и блоков, а вот способен ли был один Архимед справиться с такой задачей? Вряд ли. Более достоверными считаются слухи о созданном им планетарии. В центре находилась Земля, Солнце, Луна и несколько планет вращались вокруг нее, приводимые в движение каким-то механизмом (возможно, водяным двигателем). Об этом сооружении с восторгом упомянул Цицерон, не оставив подробного описания Предполагается, что по образцу архимедова планетария в Средние века создавали аналогичные Однако если в памяти поколений имя Архимеда связано с изумительными изобретениями, то историки науки выделяют прежде всего его математические открытия. В сочинении об измерении окружности он вычислил число «пи», использовав остроумный метод «подчерпывания», сближения периметров вписанного в круг и описанного вокруг него многоугольников Изучая плоские фигуры, он вышел за пределы элементарной математики, учил определять площадь параболы и эллипса, открыл свойства кривых высшего порядка, например спиралей Поразили современников его работы о шаре и цилиндре вычисление их поверхностей, отношение объемов цилиндра и шара, вписанного в него (как 3×2) и т д По преданию, римский полководец Марцелл, войско которого осаждало Сиракузы, очень высоко ценил гений Архимеда, несмотря на то что изобретенные ученым метательные орудия причиняли большой урон нападавшим В отличие от других сицилийских городов, Сиракузы держались долго, несколько месяцев Многопудовые камни, выброшенные из архимедовых катапульт, сметали десятки римлян, крушили их осадные сооружения. Корабли нападавших сожгли, по-видимому, «огненные снаряды» (сосуды с горючей смесью), которые метали те же катапульты, что, кстати, могло послужить поводом для фантазий о «зажигательных зеркалах» Архимеда Когда Сиракузы пали под натиском римлян, разъяренные захватчики устроили страшную резню, жертвой которой стал и Архимед. Рассказывали, будто он во время штурма был занят решением геометрической задачи. По одной версии, когда римский солдат занес над ним свой короткий меч, ученый сказал «Не трогай моих чертежей», а по другой версии «Подожди, сейчас я решу задачу». Узнав о его кончине, Марцелл якобы очень огорчился и велел на могиле мыслителя поставить камень, на котором высечен шар, вписанный в цилиндр (таково было завещание Архимеда). Так ли все это было, сказать трудно. Однако Цицерон, посетивший через полтора столетия Сиракузы, рассказал, что на заброшенном участке кладбища он увидел маленькую колонну, едва возвышавшуюся над кустарником, а на ней изображение шара с цилиндром. Знаменитого оратора сопровождали знатные сиракузцы, по приказу которых был откопан весь памятник, уже наполовину погрузившийся в землю. И тогда открылась стихотворная эпитафия, посвященная Архимеду (она была известна по литературному источнику). С гордостью Цицерон завершил свое повествование «Таким образом виднейший и некогда столь образованный город Великой Греции не имел бы понятия о могиле своего величайшего мыслителя, если бы иноземец не показал ее его гражданам» Надо ли напоминать, что убийца Архимеда был, как и Цицерон, гражданином Рима. Баландин Р.К. Сто великих гениев / Р.К. Баландин. – М.: Вече, 2012. Из энциклопедии:Архимед – величайший из математиков древности; родился в Сиракузах, в 287 г. до Р. Х., был родственником царя Гиерона II. Математика обязана этому знаменитому ученому своими драгоценнейшими открытиями и важнейшими истинами, образующими блестящую эру прогресса в древности. Биографы А. не оставили нам сведений, под чьим руководством он занимался в детстве; но кто бы ни были его учителя, он их превзошел. Известно лишь, что А. был знаком с элементарными принципами Евклида. Все отрасли математики одинаково входили в предмет изучений в исследований А., но геометрия и механика принадлежат к числу тех, которыми он занимался с большим успехом и превосходством: он предавался им с таким усердием и самопожертвованием, что забывал ради них про существенные жизненные потребности, и не раз его рабы обязаны были принуждать его воспользоваться их услугами. К великому несчастию для человечества, многие его открытия из области геометрии не дошли до нас, но и того, что составляет наше достояние, совершенно достаточно, чтобы предать его память заслуженному бессмертию. Арифметику А. обогатил своим трактатом, под названием “Псамит” (пер. на русском языке Ф. Петрушевским, 1824), в котором он указывает способ для вычисления количества песчинок, могущих заключиться в объеме земного шара. В области геометрии А. сделал открытие, которое поныне выражается в законе: “сегмент, шар и цилиндр с одинаковыми основаниями и при равных высотах относятся между собою, как 1, 2, 3”, или, что “шар равен 2/3 описанного около него цилиндра”. Это открытие доставило А. так много радостей, что он изъявил желание иметь эпитафией на своем гробу шар, вписанный в цилиндр, найденный закон об отношении шара к цилиндру составляет предмет прекрасного трактата А. “О шаре и цилиндре”. В другом трактате: “Об измерении длины окружности” А. впервые доказывает истину, что площадь круга равна площади треугольника, высота которого равна радиусу, а основание – периферии. Отношение длины окружности к диаметру круга (что ныне известно под видом p) А. пытался выразить при помощи вписанных и описанных правильных многоугольников и нашел это отношение в пределах 22/7, и 223/71, что весьма близко подходить к величине ныне общепринятого p. Из других дошедших до нас сочинений А. по геометрии особенно замечательно “Исследование коноидов и сфероидов” (2 т.), при чем он последние сравнивает с цилиндром и шаром с одинаковыми высотами и равными диаметрами и выводить их взаимные отношения. К этим важным открытиям А. по геометрии надо прибавить еще другие, которые не менее способствовали славе сиракузского ученого, а именно, квадратуру параболы и исследование свойств спиралей, одна из которых получила даже названо “Архимедовой спирали”. Мы не упомянем еще о некоторых сочинениях А. по чистой математике, из которых дошла до нас только малая часть, а перейдем к другой отрасли работ А. Важные открытия сделанные А. в механике, дают ему право считаться творцом этой ветви математических наук. Все познания, которыми обладали до него по этому предмету, включая сюда и трактаты Аристотеля, не выходили из категории первоначальных понятий и неопределенных гипотез, характеризовавших зародышевое состояние этой науки. А. же быстро превзошел своих предшественников и первый установил верные принципы статики и особенно – гидростатики. Статика А. основана на идее центра тяжести, впервые им высказанной и при том так уверенно, что он мог сказать однажды: “Дайте мне точку опоры, и я подниму земной шар”. Что касается открытий А. по гидростатике, то передают следующие обстоятельства, вызвавшие бессмертный принцип А. : “Всякое тело при погружении в жидкость теряет в своем весе столько, сколько весит вытесненная им жидкость”. Гиерон, царь сиракузский, подозревая своего ювелира в обмане при выделки золотой короны, поручил своему родственнику А. открыть обман и доказать, что в корону примешано серебра больше, чем следовало. Долго безуспешно трудился А. над решением предложенной задачи, пока наконец случайно во время купания открыл основной гидростатический закон и пришел от своего открытия в такой восторг, что голый с криками “eurhka” (я нашел !) побежал из купальни домой, чтобы испробовать свою теорию, которая так прекрасно впоследствии подтвердилась. В древности Архимеду приписывали до 40 открытий в области практической механики, но не все они описаны его биографами и комментаторами, так что некоторые известны лишь по названию, как то: архимедов рычаг, полиспаст и др. Архимедов винт применил он, будучи в Египте, к осушке залитых Нилом местностей. Укажем также на изобретенный А. планетарий – прибор, который с наглядностью показывал движение небесных тел. Не менее замечательно, что А. знал про силу водяных паров и пытался применить ее к орудиям своего века, так наз. метательным снарядам. Римляне, под предводительством консула Марцелла, осаждали во время второй Пунической войны (212 г. до Р. Х.) родину А. – Сиракузы. Посвятив себя защите Сиракуз, А. стал душой самого упорного и вместе с тем самого искусного сопротивления, о котором говорит история. Он построил метательные снаряды, причинившие много вреда римскому войску. Историки Полибий, Ливий и Плутарх, описавшие эту редкую по выдержанности осаду, повествуют, что А. построил также громадные “зажигательные ст„кла” (двояковыпуклые чечевицы), посредством которых сжег римский флот. Тем не менее, А. не мог спасти свою родину от печальной участи: римляне вторглись в город. Солдаты, предававшиеся грабежу, не пропустили и дома Архимеда; который в это время сидел на полу, посыпанном песком, на котором чертил свои геометрические фигуры. А. встретил победителей классическими словами: “Не трогай моих фигур!” (Noli turbare circulos meos!), но варвар не пощадил старца и умертвил его на месте. Так кончил свою плодотворную деятельность А. на 75 году жизни, окруженный двойным ореолом славы, приобретенной наукой и редким патриотизмом. На его могилу поставили цилиндр, с включенным (вписанным) в него шаром, чтобы этим увековечить его открытие взаимного отношения шара и цилиндра, которому он придавал особое значение. Цицерон, будучи квестором Сицилии, отыскал этот памятник, скрытый в кусте. Оставшиеся после него сочинения собрал Торелли (Оксфорд, 1792 г.), Гейберг (Лейпциг, 1680 г.). Они были переведены и объяснены Ницце (Штральзунд, 1824). Отдельные сочинения его переведены Гаубером (Тюбинген, 1798 г.), Гофманом (Ашафенб., 1817 г.), Крюгером (Кведлинб. и Лейпциг, 1820 г.) и Гутенекером (Вюрцбург, 1828 г.). Ср. Гейберг, “Quaestiones Archimedeae” (Копенгаген, 1879 г.). Закон АрхимедаАрхимеда закон – так наз. открытый Архимедом важный гидростатический закон, согласно которому каждое тело, погруженное в жидкость, теряет столько своего веса, сколько весит вытесненная им жидкость. Этот закон основан на гидростатическом давлении, вследствие которого тело, погруженное в жидкость. поднимается с действующей отвесно вверх силой, равной весу вытесненной им жидкости. Для доказательства Архимедова закона на опыте служат гидростатические весы, т.е. совершенно равноплечие весы, которые дают возможность взвешивать тела, погруженные в воду или в любую жидкость. На этих весах одна чашка повешена короче другой, но вес обеих чашек с подвесками одинаков; к более короткой чашке подвешивают два металлических цилиндра: один полый, а другой под ним массивный (последний такой величины, что он совершенно плотно входит в полый). Приведя тарированием весы в равновесие, погружают массивный цилиндр в воду. Чашка весов, к которой подвешены цилиндры, поднимается, но стоит только налить в пустой цилиндр до верху воды, весы возвращаются опять в равновесие. Этим доказывается истинность Архимедова закона, который применяется для объяснения пассивного плавания, равно как действия воздушного шара; на основании этого закона производится также определение плотности (удельного веса тела) с помощью гидростатических весов и ареометра. Ф.А. Брокгауз, И.А. Ефрон Энциклопедический словарь. Смерть Архимеда. Римская мозаика. Архимед справедлив для любого кругаАрхимед родился в 287 году до нашей эры в греческом городе Сиракузы, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали самую большую в мире библиотеку. После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики. В сочинении “Параболы квадратуры” Архимед обосновал метод расчета площади параболического сегмента, причем сделал это за две тысячи лет до открытия интегрального исчисления. В труде “Об измерении круга” Архимед впервые вычислил число “пи” – отношение длины окружности к диаметру – и доказал, что оно одинаково для любого круга. Математический метод Архимеда, связанный с математическими работами пифагорейцев и с завершившей их работой Эвклида, а также с открытиями современников Архимеда, подводил к познанию материального пространства, к познанию теоретической формы предметов, находящихся в этом пространстве, формы совершенной, геометрической формы, к которой предметы более или менее приближаются и законы которой необходимо знать, чтобы воздействовать на материальный мир. Архимед изучал силы, которые двигают предметы или приводят в равновесие, изобретая новую отрасль математики, в которой материальные тела, приведенные к их геометрической форме, сохраняют в то же время свою тяжесть. Эта геометрия веса и есть рациональная механика, это статика, а также гидростатика, первый закон которой открыл Архимед (закон, носящий его имя), согласно которому на тело, погруженное в жидкость, действует сила, равная весу вытесненной им жидкости. Знаменитое “Эврика!” было произнесено не в связи с открытием закона Архимеда, но по поводу закона удельного веса металлов – открытия, которое также принадлежит сиракузскому ученому. Согласно преданию, однажды к Архимеду обратился правитель Сиракуз. Он приказал проверить, соответствует ли вес золотой короны весу отпущенного на нее золота. Для этого Архимед сделал два слитка: один из золота, другой из серебра, каждый такого же веса, что и корона. Затем поочередно положил их в сосуд с водой, отметил, на сколько поднялся ее уровень. Опустив в сосуд корону, Архимед установил, что ее объем превышает объем слитка. Архимед проверяет и создает теорию пяти механизмов, известных в его время и именуемых “простые механизмы”. Это – рычаг (“Дайте мне точку опоры, – говорил Архимед, – и я сдвину Землю”), клин, блок, бесконечный винт и лебедка.. Изобретение бесконечного винта привело его к изобретению болта, сконструированного из винта и гайки. В 212 году до нашей эры при обороне Сиракуз от римлян во время второй Пунической войны Архимед сконструировал несколько боевых машин, которые позволили горожанам отражать атаки превосходящих в силе римлян в течение почти трех лет. Одной из них стала система зеркал, с помощью которой египтяне смогли сжечь флот римлян. Архимед погиб во время осады Сиракуз: его убил римский воин в тот момент, когда ученый был поглощен поисками решения поставленной перед собой проблемы. Завоевав Сиракузы, римляне так и не стали обладателями трудов Архимеда. Только через много веков они были обнаружены европейскими учеными. Плутарх пишет, что Архимед умер в глубокой старости. На его могиле была установлена плита с изображением шара и цилиндра. Использованы материалы сайта http://100top.ru/encyclopedia/ Далее читайте:Исторические лица Греции (биографический справочник). Греция, Эллада, южная часть Балканского полуострова, одна из наиболее важных исторических стран древности. Философы, любители мудрости (биографический справочник).
|
www.hrono.info
История открытия закона Архимеда – Задача
История открытия закона Архимеда
Архимед, один из величайших ученых Древней Греции, блестящий математик и механик, жил в Сиракузах в III веке до н. э. В то время в Сиракузах правил царь Гиерон. Однажды Гиерон, получив от мастеров заказанную им золотую корону, усомнился в их честности; ему показалось, что они утаили часть золота, выданного на ее изготовление, и заменили его серебром. Но как уличить ювелиров в подделке? Вызвал Гиерон Архимеда, к тому времени уже прославившегося остроумными решениями многих проблем, и поручил ему определить, есть ли в золотой короне примесь серебра. Сейчас такая задача по плечу даже школьнику. Удельный вес каждого из металлов есть в любом справочнике, определить удельный вес сплава совсем не трудно: взял образец, взвесил его, потом опустил в воду и определил объем вытесненной им жидкости, поделил первое число на второе и по соотношению удельных весов нашел долю каждого металла. Вот и вся премудрость. Но 2200 лет назад Архимед, выйдя после царской аудиенции, даже не знал, что такое удельный вес. Задача перед ним стояла в самом общем виде, и никаких конкретных путей ее решения он найти не мог. Но искал их. Искал постоянно, не переставая думать об этом, когда занимался другими делами. Иначе, если бы выкидывал ее из головы всякий раз, как прекращал работу, не могло бы произойти то прямо-таки сказочное событие, которое и легло в основу легенды.
Случилось оно, как говорят, в бане. Бани в то время представляли собой место не только для мытья, но и для светских встреч, развлечений, спортивных игр. Поначалу Архимед, наверное, поупражнялся гирями, потом зашел в парильню, там его помассировали, потом он поговорил с друзьями, может быть рассказал им о своем последнем посещении царя Гиерона – прием у царя всегда событие, – не исключено, что поведал о его задаче и посетовал на трудность решения. А потом он, как и полагается, намылился золой и полез в ванну. И вот тут-то и случилось главное. Собственно, ничего нового не случилось, произошло то, что бывает всякий раз, когда любой человек, даже не ученый, садится в любую, даже не мраморную ванну – вода в ней поднимается. Но то, на что обычно Архимед не обращал никакого внимания, вдруг заинтересовало его. Он привстал – уровень воды опустился, он снова сел – вода поднялась; причем поднималась она по мере погружения тела. И вот в этот миг Архимеда осенило. Он усмотрел в десятке раз проведенном опыте намек на то, как объем тела связан с его весом. И понял, что задача царя Гиерона разрешима. И так обрадовался своей случайной находке, что как был – голый, с остатками золы на теле – побежал домой через город, оглашая улицу криками: «Эврика! Эврика!»
Вот так Архимед, если верить легенде, нашел решение задачи Гиерона. Архимед не вынашивал долгое время свою гипотезу. Если, разумеется, не предположить, что ходил он в баню раз в несколько лет или что озарило его на сотом или тысячном посещении. Скорее всего, оба предположения одинаково маловероятны. Первое – по причинам, связанным с обликом ученого, второе – второе потому, что ассоциация, возникшая в голове ученого, должна была либо появиться сразу же, либо не появиться никогда, она достаточно наглядна, если поставленную задачу держать все время перед глазами. А повеление царя не пустяк. И хотя Архимед был слишком крупный ученый и слишком известный гражданин Сиракузов, чтобы можно было предположить, будто он, дрожа от подобострастия, сломя голову побежал выполнять волю Гиерона, но все же в те времена, когда благополучие ученого целиком зависело от милости его покровителя, к просьбам монарха легкомысленно не относились. И потом, думаю, Архимеда, как истинного ученого, увлекла сама задача, он размышлял не о конечной цели заказанной ему работы – уличить ювелиров, а о ее сути – о возможности как-то отличать металлы в сплаве. Поэтому, когда ученый, целиком поглощенный обдумыванием различных возможностей, получил неожиданно внешний толчок, мысль мгновенно устремилась от собственного тела, вытесняющего воду, к короне, и мелькнувшее решение показалось столь неожиданно простым, что Архимед не удержался и… И вот в том, что он сделал дальше, я сильно сомневаюсь. Все, что было до этого, представляется весьма вероятным, во всяком случае против этого нет никаких логических возражений, даже против места, где было сделано открытие, потому что оно хоть и самое неподходящее для научной работы, но в данном случае единственно возможное. А вот бег из бани голым по городу как-то не вяжется с обликом Архимеда, человека, быть может, и рассеянного и углубленного в себя, но, право же, слишком известного и уважаемого в Сиракузах, чтобы не подумать о своей репутации. Но простим эту маленькую деталь авторам легенды, она, безусловно, очень эффектна, очень театральна и несомненно украшает историю об ученом, случайно натолкнувшемся на истинное решение. Но случайно ли от этого само открытие? Если бы Архимед на том и успокоился, то есть определил, взвешивая корону в воде, есть ли в ней серебро, доложил бы об этом Гиерону и, довольный сам собой, своей работой и царской милостью, отправился заниматься другими делами, а этот случай выкинул из головы, то тогда нам пришлось бы согласиться: да, это решение случайно, как и сама работа. Но Архимед поступил иначе, как и должен был поступить настоящий
ученый. Решение частной задачи о сплаве натолкнуло его на мысль о законе, который относится ко всем телам и который не случайно носит имя его автора (на всякое тело, погруженное в жидкость, действует со стороны этой жидкости подъемная сила, направленная вверх и равная весу вытесненной телом жидкости). Когда мы опускаемся в ванну, мы чувствуем на себе действие этого закона – как и почувствовал его Архимед; но мы уже знаем, в чем здесь дело, а он не знал, он должен был понять это первым из людей. И он понял, и не узко, не только применительно к сплавам, и поэтому, кроме доклада царю, содержащему, по-видимому, расчеты, связанные с короной, появилось позже еще одно сочинение, где ничего не говорится о короне, но зато говорится о плавающих телах. Причем обоснование закона дано здесь не только эмпирически: Архимед приводит геометрическое доказательство, и мало этого – он рассматривает не горизонтальную поверхность жидкости, а сферическую, как и следует из предположения о шарообразности Земли. Этот штрих сразу показывает тот всеобщий характер, какой придавал своему закону Архимед. И когда читаешь простое и ясное доказательство Архимеда, то понимаешь, сколь прав был древнегреческий философ и писатель Плутарх, с почтением писавший о своем великом соотечественнике: «Если бы кто-либо попробовал сам разрешить эти задачи, он ни к чему не пришел бы, но если бы он познакомился с решением Архимеда, у него тотчас бы получилось такое впечатление, что это решение он смог бы найти и сам, – столь прямым и кратким путем ведет нас к цели Архимед».
Первое сочинение – расчет состава царской короны — до нас не дошло, и поэтому мы не знаем точно ни обстоятельств, связанных с решением задачи Гиерона, ни судьбы мастеров, изготовивших корону. Второе же сочинение – трактат «О плавающих телах» – нам известно и дает полное право утверждать: открытие закона Архимеда не случайно.
Ведь не были же случайны все его другие открытия: аксиома Архимеда, на которой построен в современной арифметике и геометрии процесс последовательного деления; архимедов винт – устройство, изобретенное для перекачки жидкостей и применяемое до сих пор во многих машинах; закон рычага, позволяющий с помощью сравнительно небольшого усилия поднимать большие грузы; прибор для измерения видимого диаметра Солнца; небесный глобус, на котором можно видеть движение планет, солнечное и лунное затмение, и еще многие-многие математические исследования и инженерные находки, которых бы вполне хватило на успешную деятельность нескольких людей.
Даже античные историки, нередко склонные к приукрашиванию подвигов своих героев – а Архимед был героической фигурой, – нигде не намекают более на случайность его творчества. Так правомерно ли тогда говорить о случайности открытия удельного веса и закона о плавающих телах? Человек, столь тонко разбирающийся в математике, механике, астрономии, уже не раз показавший, на что способен его проницательный ум, разве не решил бы он задачу царя Гиерона, даже если бы не помог ему случай с ванной? Все равно бы решил – пусть чуть позже, пусть путем каких-то иных ассоциаций, может быть наблюдая различную осадку по-разному нагруженных галер.
Приди Архимед к такому же решению не в бане, а дома, вспомнив одно из своих прежних купаний, и никто не решился бы утверждать, что ученый случайно натолкнулся на открытие. Наоборот, сказали бы, что не случайно правильное решение нашел именно Архимед – человек, способный использовать разрозненные наблюдения для обобщений, имеющих универсальный, всеобъемлющий характер. Ведь в сближении вроде бы далеких явлений и заключается один из мощнейших методов научного мышления. С этой точки зрения, использование наблюдений над погружением в воду собственного тела – вполне правомерный прием и вовсе даже не случайный, а обязательный. Значит, все дело в несколько случайном месте и кажущемся случайным поводе.
textarchive.ru
Архимед — Википедия
Архиме́д (Ἀρχιμήδης; 287 до н. э. (-287) — 212 до н. э.) — древнегреческий математик, физик и инженер из Сиракуз. Сделал множество открытий в области геометрии. Заложил основы механики, гидростатики, был автором ряда важных изобретений.
Биография
Сведения о жизни Архимеда оставили нам Полибий, Тит Ливий, Цицерон, Плутарх, Витрувий, Диодор Сицилийский и другие. Почти все они жили на много лет позже описываемых событий, и достоверность этих сведений оценить трудно.
Архимед родился в Сиракузах — греческой колонии на острове Сицилия. Отцом Архимеда, возможно, был математик и астроном Фидий. По утверждению Плутарха, Архимед состоял в близком родстве с Гиероном II, тираном Сиракуз. Для обучения Архимед отправился в Александрию Египетскую — научный и культурный центр того времени.
Александрия
В Александрии Архимед познакомился и подружился со знаменитыми учёными: астрономом Кононом, разносторонним учёным Эратосфеном из Кирены, с которыми потом переписывался до конца жизни. В то время Александрия славилась своей библиотекой, в которой было собрано более 700 тыс. рукописей. Он называл Конона своим другом, в то время как две его работы «Метод механических теорем»[en] и «Задача о быках»[en] имеют введения, адресованные Эратосфену. По-видимому, именно здесь Архимед познакомился с трудами Демокрита, Евдокса и других замечательных греческих геометров, о которых он упоминал и в своих сочинениях.
По окончании обучения Архимед вернулся на Сицилию. В Сиракузах он был окружён вниманием и не нуждался в средствах. Из-за давности лет жизнь Архимеда тесно переплелась с легендами о нём.
Легенды
Архимед переворачивает планету Земля.Уже при жизни Архимеда вокруг его имени создавались легенды, поводом для которых служили его поразительные изобретения, производившие ошеломляющее действие на современников. Известен рассказ о том, как Архимед сумел определить, сделана ли корона царя Гиерона из чистого золота, или ювелир подмешал туда значительное количество серебра. Удельный вес золота был известен, но трудность состояла в том, чтобы точно определить объём короны: ведь она имела неправильную форму! Архимед всё время размышлял над этой задачей. Как-то он принимал ванну и заметил, что из неё вытекает такое количество воды, каков объём его тела, погружённого в ванну, и тут ему пришла в голову блестящая идея: погружая корону в воду, можно определить её объём, измерив объём вытесненной ею воды. Согласно легенде[1], Архимед выскочил голый на улицу с криком «Эврика!» (др.-греч. εὕρηκα), то есть «Нашёл!». В этот момент был открыт основной закон гидростатики — закон Архимеда.
Другая легенда, приведенная Паппом Александрийским, рассказывает, что построенный Гиероном в подарок египетскому царю Птолемею тяжёлый многопалубный корабль «Сиракузия» никак не удавалось спустить на воду. Архимед соорудил систему блоков (полиспаст), с помощью которой он смог проделать эту работу одним движением руки. По легенде, Архимед заявил при этом: «Будь в моём распоряжении другая Земля, на которую можно было бы встать, я сдвинул бы с места нашу» (в другом варианте: «Дайте мне точку опоры, и я переверну мир»).
Осада Сиракуз
Осада Сиракуз, гравюра XVIII векаИнженерный гений Архимеда с особой силой проявился во время осады Сиракуз римлянами в 212 году до н. э. в ходе Второй Пунической войны. Сиракузами с 215 года до н. э. правил Гиероним Сиракузский, внук Гиерона II. Гиероним поддержал в войне Карфаген, и римские войска двинулись на Сиракузы. В этот момент Архимеду было уже 75 лет. Подробное описание осады Сиракуз римским полководцем Марцеллом и участия Архимеда в обороне содержится в сочинениях Плутарха и Тита Ливия.
Построенные Архимедом мощные метательные машины забрасывали римские войска тяжёлыми камнями. Думая, что они будут в безопасности у самых стен города, римляне кинулись туда, но в это время лёгкие метательные машины близкого действия забросали их градом ядер. Мощные краны захватывали железными крюками корабли, приподнимали их кверху, а затем бросали вниз, так что корабли переворачивались и тонули (см. коготь Архимеда). В 2005 году были проведены несколько экспериментов с целью проверить правдивость описания этого «сверхоружия древности»; построенная конструкция показала свою полную работоспособность[2].
Римляне вынуждены были отказаться от мысли взять город штурмом и перешли к осаде. Знаменитый историк древности Полибий писал: «Такова чудесная сила одного человека, одного дарования, умело направленного на какое-либо дело… римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузян одного старца».
По одной из легенд, во время осады римский флот был сожжён защитниками города, которые при помощи зеркал и отполированных до блеска щитов сфокусировали на них солнечные лучи по приказу Архимеда. Существует мнение, что корабли поджигались метко брошенными зажигательными снарядами, а сфокусированные лучи служили лишь прицельной меткой для баллист. Однако в эксперименте греческого учёного Иоанниса Саккаса (1973 год) удалось поджечь фанерную модель римского корабля с расстояния 50 м, используя 70 медных зеркал[3]. Тем не менее достоверность легенды сомнительна; ни Плутарх, ни другие античные историки при описании оборонительных изобретений Архимеда о зеркалах не упоминают, впервые этот эпизод обнаружен в трактате Анфимия Траллийского (VI век), одного из архитекторов собора Святой Софии в Константинополе (трактат был посвящён выпуклым и вогнутым зеркалам). В XII веке легенда получила популярность после публикации Иоанном Зонара́ обширной хроники мировой истории.
Осенью 212 года до н. э. Сиракузы были взяты римлянами (по словам Плутарха, благодаря изменнику). При этом Архимед был убит.
Смерть
Эдуар Вимон (1846—1930). Смерть АрхимедаРассказ о смерти Архимеда от рук римлян существует в нескольких версиях[4]:
- Рассказ Иоанна Цеца (Chiliad, книга II): в разгар боя 75-летний Архимед сидел на пороге своего дома, углублённо размышляя над чертежами, сделанными им прямо на дорожном песке. В это время пробегавший мимо римский воин наступил на чертёж, и возмущённый учёный бросился на римлянина с криком: «Не тронь моих чертежей!» Солдат остановился и хладнокровно зарубил старика мечом.
- Рассказ Плутарха: «К Архимеду подошёл солдат и объявил, что его зовёт Марцелл. Но Архимед настойчиво просил его подождать одну минуту, чтобы задача, которой он занимался, не осталась нерешённой. Солдат, которому не было дела до его доказательства, рассердился и пронзил его своим мечом». Плутарх утверждает, что консул Марцелл был разгневан гибелью Архимеда, которого он якобы приказал не трогать.
- Архимед сам отправился к Марцеллу, чтобы отнести ему свои приборы для измерения величины Солнца. По дороге его ноша привлекла внимание римских солдат. Они решили, что учёный несёт в ларце золото или драгоценности, и, недолго думая, перерезали ему горло.
- Рассказ Диодора Сицилийского: «Делая набросок механической диаграммы, он склонился над ним. И когда римский солдат подошёл и стал тащить его в качестве пленника, он, целиком поглощённый своей диаграммой, не видя, кто перед ним, сказал: „Прочь с моей диаграммы!“ Затем, когда человек продолжил тащить его, он, повернувшись и узнав в нём римлянина, воскликнул: „Быстро, кто-нибудь, подайте одну из моих машин!“ Римлянин, испугавшись, убил слабого старика, того, чьи достижения являли собой чудо. Как только Марцелл узнал об этом, он сильно огорчился и совместно с благородными гражданами и римлянами устроил великолепные похороны среди могил его предков. Что касается убийцы, то он, кажется, был обезглавлен».
- «Римская история от основания города» Тита Ливия (Книга XXV, 31): «Передают, что когда при той сильной суматохе, какую только могла вызвать распространившаяся во взятом городе паника, воины разбежались, производя грабёж, то много было явлено отвратительных примеров злобы и алчности; между прочим, один воин убил Архимеда, занятого черчением на песке геометрических фигур, не зная, кто он. Марцелл, говорят, был этим огорчён, озаботился погребением убитого, разыскал даже родственников Архимеда, и имя его и память о нём доставили последним уважение и безопасность».
 Римская гробница, построенная не менее чем через 2 века после гибели Архимеда в Сиракузах и которую принято называть «Гробницей Архимеда» (итал. Tomba di Archimede)[5].
Римская гробница, построенная не менее чем через 2 века после гибели Архимеда в Сиракузах и которую принято называть «Гробницей Архимеда» (итал. Tomba di Archimede)[5].Цицерон, бывший квестором на Сицилии в 75 году до н. э., пишет в «Тускуланских беседах» (книга V)[6], что ему в 75 году до н. э., спустя 137 лет после этих событий, удалось обнаружить полуразрушенную могилу Архимеда; на ней, как и завещал Архимед, было изображение шара, вписанного в цилиндр.
Видео по теме
Научная деятельность
Математика
По словам Плутарха, Архимед был просто одержим математикой. Он забывал о пище, совершенно не заботился о себе. Идеи Архимеда почти на два тысячелетия опередили своё время. Только в XVII веке учёные смогли продолжить и развить труды великого греческого математика.
Математический анализ
Работы Архимеда относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так, он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида x2(a±x)=b{\displaystyle x^{2}(a\pm x)=b}, корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.
Однако главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призмы и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского. В своей работе «Послание к Эратосфену о методе» (иногда называемой «Метод механических теорем») он использовал бесконечно малые для вычисления объёмов. Идеи Архимеда легли впоследствии в основу интегрального исчисления.
В сочинении Квадратура параболы Архимед доказал, что площадь сегмента параболы, отсекаемого от неё прямой, составляет 4/3 от площади вписанного в этот сегмент треугольника (см. рисунок). Для доказательства Архимед подсчитал сумму бесконечного ряда:
- ∑n=0∞14n=1+141+142+143+⋯=43{\displaystyle \sum _{n=0}^{\infty }{\frac {1}{4^{n}}}=1+{\frac {1}{4^{1}}}+{\frac {1}{4^{2}}}+{\frac {1}{4^{3}}}+\cdots ={4 \over 3}}
Каждое слагаемое ряда — это общая площадь треугольников, вписанных в неохваченную предыдущими членами ряда часть сегмента параболы.
В математике, естественных науках и технике очень важно уметь находить наибольшие и наименьшие значения изменяющихся величин — их экстремумы. Например, как среди цилиндров, вписанных в шар, найти цилиндр, имеющий наибольший объём? Все такие задачи в настоящее время могут быть решены с помощью дифференциального исчисления. Архимед первым увидел связь этих задач с проблемами определения касательных и показал, как решать задачи на экстремумы.
Геометрия
Архимед сумел установить, что объёмы конуса и шара, вписанных в цилиндр, и самого цилиндра соотносятся как 1:2:3.
Лучшим своим достижением он считал определение поверхности и объёма шара — задача, которую до него никто решить не мог. Архимед просил выбить на своей могиле шар, вписанный в цилиндр.
 Шар, вписанный в цилиндр
Шар, вписанный в цилиндрПомимо перечисленного, Архимед вычислил площадь поверхности для сегмента шара и витка открытой им «спирали Архимеда», определил объёмы сегментов шара, эллипсоида, параболоида и двуполостного гиперболоида вращения.
Следующая задача относится к геометрии кривых. Пусть дана некоторая кривая линия. Как определить касательную в любой её точке? Или, если переложить эту проблему на язык физики, пусть нам известен путь некоторого тела в каждый момент времени. Как определить скорость его в любой точке? В школе учат, как проводить касательную к окружности. Древние греки умели, кроме того, находить касательные к эллипсу, гиперболе и параболе. Первый общий метод решения и этой задачи был найден Архимедом. Этот метод впоследствии лёг в основу дифференциального исчисления.
Схема архимедова метода вычисления числа π{\displaystyle \pi }Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру. В работе «Об измерении круга» Архимед дал своё знаменитое приближение для числа π{\displaystyle \pi }: «архимедово число» 317{\displaystyle 3{\frac {1}{7}}}. Более того, он сумел оценить точность этого приближения: 31071<π<317{\displaystyle 3{\frac {10}{71}}<\pi <3{\frac {1}{7}}}. Для доказательства он построил для круга вписанный и описанный 96-угольники и вычислил длины их сторон.
Он также доказал, что площадь круга равна π{\displaystyle \pi } (числу пи), умноженному на квадрат радиуса круга (πr2{\displaystyle \pi r^{2}}).
Аксиома Архимеда
В работе «О шаре и цилиндре» Архимед постулирует, что любая величина при её добавлении к себе достаточное число раз превысит любую заданную величину. Это свойство — аксиома Архимеда, включаемая сейчас в аксиоматику вещественных чисел. Она утверждает следующее:
Если имеются две величины, a{\displaystyle a} и b{\displaystyle b}, и a{\displaystyle a} меньше b{\displaystyle b}, то, взяв a{\displaystyle a} слагаемым достаточное количество раз, можно превзойти b{\displaystyle b}:
a+a+…+a⏟n>b{\displaystyle \underbrace {a+a+\ldots +a} _{n}>b}Механика
Архимед прославился многими механическими конструкциями. Рычаг был известен и до него , но лишь Архимед изложил его полную теорию и успешно её применял на практике. Плутарх сообщает, что Архимед построил в порту Сиракуз немало блочно-рычажных механизмов для облегчения подъёма и транспортировки тяжёлых грузов. Изобретённый им архимедов винт (шнек) для вычерпывания воды до сих пор[когда?] применяется в Египте.
Архимед является и первым теоретиком механики. Он начинает свою книгу «О равновесии плоских фигур» с доказательства закона рычага. В основе этого доказательства лежит аксиома о том, что равные тела на равных плечах по необходимости должны уравновешиваться. Точно также и книга «О плавании тел» начинается с доказательства закона Архимеда. Эти доказательства Архимеда представляют собой первые мысленные эксперименты в истории механики.
Архимед рассмотрел вопрос о центре тяжести параллелограмма, треугольника, трапеции и параболического сегмента. В сочинении «О плавающих телах» Архимед доказал закон гидростатики, носящий его имя[7].
Астрономия
Архимед построил планетарий или «небесную сферу», при движении которой можно было наблюдать движение пяти планет, восход Солнца и Луны, фазы и затмения Луны, исчезновение обоих тел за линией горизонта. Занимался проблемой определения расстояний до планет; предположительно в основе его вычислений лежала система мира с центром в Земле, но планетами Меркурием, Венерой и Марсом, обращающимися вокруг Солнца и вместе с ним — вокруг Земли[8]. В своем сочинении «Псаммит» донёс информацию о гелиоцентрической системе мира Аристарха Самосского[9].
Сочинения
До наших дней сохранились:
- Квадратура параболы / τετραγωνισμὸς παραβολῆς — определяется площадь сегмента параболы.
- О шаре и цилиндре / περὶ σφαίρας καὶ κυλίνδρου — доказывается, что объём шара равен 2/3 от объёма описанного около него цилиндра, а площадь поверхности шара равна площади боковой поверхности этого цилиндра.
- О спиралях[en] / περὶ ἑλίκων — выводятся свойства спирали Архимеда.
- О коноидах и сфероидах / περὶ κωνοειδέων καὶ σφαιροειδέων — определяются объёмы сегментов параболоидов, гиперболоидов и эллипсоидов вращения.
- О равновесии плоских фигур / περὶ ἰσορροπιῶν — выводится закон равновесия рычага; доказывается, что центр тяжести плоского треугольника находится в точке пересечения его медиан; находятся центры тяжести параллелограмма, трапеции и параболического сегмента.
- Послании к Эратосфену о механическом методе[en] / πρὸς Ἐρατοσθένην ἔφοδος — обнаружено в 1906 году, по тематике частично дублирует работу «О шаре и цилиндре», но здесь используется механический метод доказательства математических теорем.
- О плавающих телах / περὶ τῶν ὀχουμένων — выводится закон плавания тел; рассматривается задача о равновесии сечения параболоида, моделирующего корабельный корпус.
- Измерение круга / κύκλου μέτρησις — до нас дошёл только отрывок из этого сочинения. Именно в нём Архимед вычисляет приближение для числа π{\displaystyle \pi }.
- Псаммит / ψαμμίτης (О счислении песчинок) — вводится способ записи очень больших чисел. В этом трактате Архимед показывает, что при помощи этой записи можно оценить сверху число песчинок, которые поместятся внутри Вселенной. Эта книга упоминает гелиоцентрическую теорию Солнечной системы, предложенную Аристархом Самосским, а также современные представления о размерах Земли и расстояние между различными небесными телами. С помощью системы чисел, использующих степени с основанием мириада (десять тысяч), Архимед приходит к выводу, что количество песчинок, необходимых для заполнения Вселенной составляет не более чем 1063{\displaystyle 10^{63}} в современной нотации. В первой части говорится, что отец Архимеда был астрономом по имени Фидий. Псаммит — единственное сохранившееся произведение, в котором Архимед обсуждает свои взгляды на астрономию[10].
- Стомахион / στομάχιον — дано описание популярной головоломки-мозаики, состоящей в составлении квадрата из многоугольников, на которые он был вначале разрезан. Более простым вариантом такой головоломки является китайская головоломка танграм. Задача состоит в сборке квадрата из 14 его частей, среди которых 1 пятиугольник, 2 четырёхугольника и 11 треугольников.
- Задача о быках[en] / πρόβλημα βοικόν) — ставится задача, приводимая к уравнению Пелля. Эта работа была обнаружена Готхольдом Эфраимом Лессингом в греческой рукописи, состоящей из стихотворения из 44 строк, в библиотеке герцога Августа в Вольфенбюттеле в Германии в 1773 году. Она адресована Эратосфену и математикам Александрии. Архимед ставит им задачу подсчитать количество голов скота в стаде Солнца, решая ряд совместных диофантовых уравнений.
Ряд работ Архимеда сохранившихся только в арабском переводе:
- Трактат о построении около шара телесной фигуры с четырнадцатью основаниями;
- Книга лемм;
- Книга о построении круга, разделённого на семь равных частей;
- Книга о касающихся кругах
Память

В честь Архимеда названы:
Лейбниц писал: «Внимательно читая сочинения Архимеда, перестаёшь удивляться всем новым открытиям геометров»[15].
В честь Архимеда также названы улицы в Донецке[16], Днепре[17], Нижнем Новгороде[18], Амстердаме[19], а также площадь в Сиракузе[20].
- В художественной литературе
- Житомирский С. В. Учёный из Сиракуз: Архимед. Историческая повесть. М.: Молодая гвардия, 1982. — Серия «Пионер — значит первый» — 191 с.
- Карел Чапек. Смерть Архимеда.
Весьма неканонические версии гибели Архимеда даны в двух рассказах современных русских писателей Озара Ворона «Война и геометр» и А. Башкуева «Убить Архимеда». Рассказы исторически непротиворечивы, но при этом написаны с точки зрения римского легионера — убийцы великого учёного, но вовсе не «безграмотного варвара, не понимавшего, кого убивает».
- В мультипликации
- В кино
См. также
Примечания
- ↑ Легенда приведена у Витрувия, «Об архитектуре», книга IX, глава 3.
- ↑ BBC Secrets of the Ancients: The Claw
- ↑ Science: Archimedes’ Weapon (англ.). Архивировано 2 февраля 2012 года.
- ↑ См. впечатляющую галерею картин на эту тему.
- ↑ Tomb of Archimedes
- ↑ …С трудом разыскав могилу, горько заключил: «Один из самых славных городов Греции, некогда породивший на свет столько учёных, не знал уже даже, где находится гробница самого гениального из его граждан».
- ↑ Зубов В. П. Физические идеи древности // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 54-55;
- ↑ Житомирский, 2001.
- ↑ Christianidis et al., 2002.
- ↑ English translation of The Sand Reckoner. University of Waterloo. Проверено 23 июля 2007. Архивировано 11 августа 2007 года.
- ↑ Oblique view of Archimedes crater on the Moon. NASA. Проверено 5 февраля 2010. Архивировано 21 августа 2011 года.
- ↑ 20091109 Archimedes Crater and Montes Archimedes. Проверено 5 февраля 2010. Архивировано 21 августа 2011 года.
- ↑ Циркуляры малых планет за 4 июня 1993 года — в документе надо выполнить поиск Циркуляра № 22245 (M.P.C. 22245)
- ↑ 3600 Archimedes (1978 SL7). НАСА. Проверено 5 февраля 2010. Архивировано 21 августа 2011 года.
- ↑ История математики / Под ред. А. П. Юшкевича, в 3-х т. — М.: Наука, 1970. — Т. I. — С. 129.
- ↑ Архивированная копия (недоступная ссылка — история). Проверено 3 февраля 2010. Архивировано 4 февраля 2012 года. Пункт 10
- ↑ http://gorod.dp.ua/history/article_ru.php?article=205 Раздел «Кто „обидел“ Паганини?»
- ↑ http://maps.google.ru/maps?hl=ru&q=улица+архимеда+нижний+новгород&lr=&um=1&ie=UTF-8&hq=&hnear=Нижегородская+область,+город+Нижний+Новгород,+ул.+Архимеда&gl=ru&ei=OTZpS9SGG8WpsQaro9HADA&sa=X&oi=geocode_result&ct=title&resnum=1&ved=0CA0Q8gEwAA Карта города
- ↑ http://www.px-pict.com/7/3/1/1/1/1.html Ван дер Варден о Пифагоре
- ↑ Сиракузы (Сиракуза): родина Архимеда.
Литература
Тексты и переводы
- На русском языке
- Архимедовы теоремы, Андреем Таккветом, езуитом, выбранные и Георгием Петром Домкиио сокрашенные… / Пер. с лат. И. Сатарова. СПб., 1745. С. 287—457.
- Архимеда Две книги о шаре и цилиндре, измерение круга и леммы. / Пер. Ф. Петрушевского. СПб., 1823. 240 стр.
- Архимеда Псаммит, или Изчисление песку в пространстве равном шару неподвижных звезд. / Пер. Ф. Петрушевского. СПб., 1824. 95 стр.
- Новое сочинение Архимеда. Послание Архимеда к Эратосфену о некоторых теоремах механики. / Пер. с нем. Одесса, 1909. XVI, 28 стр.
- О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). / Пер. с нем. под ред. С. Н. Бернштейна. (Серия «Библиотека классиков точного знания», 3). Одесса, 1911. 156 стр.
- 3-е изд. (Серия «Классики естествознания»). М.-Л.: ОНТИ. 1936. 235 стр. 5000 экз.
- Архимед. Исчисление песчинок (Псаммит). / Пер. и прим. Г. Н. Попова. (Серия «Классики естествознания»). М.-Л., Гос. техн.-теор. изд. 1932. 102 стр.
- Архимед. Сочинения. / Перевод, вступительная статья и комментарии И. Н. Веселовского. Перевод арабских текстов Б. А. Розенфельда. М.: Гос. изд-во физ.-мат. лит-ры (Физматгиз), 1962. 640 стр. 4000 экз.
- На французском языке
- Издание в серии «Collection Budé»: Archiméde. Oeuvres.
- T. I: De la sphère et du cylindre. — La Mesure du cercle. — Sur les conoïdes et les sphéroïdes. Texte établi et traduit par Ch. Mugler. 2e tirage 2003. XXX, 488 p.
- T. II: Des spirales. — De l’équilibre des figures planes. — L’Arénaire. — La Quadrature de la parabole. Texte établi et traduit par Ch. Mugler. 2e tirage 2002. 371 p.
- T. III: Des corps flottants. — Stomachion. — La Méthode. — Le livre des lemmes. — Le Problème des boeufs. Texte établi et traduit par Ch. Mugler. 2e tirage 2002. 324 p.
- T. IV: Commentaires d’Eutocius. — Fragments. Texte établi et traduit par Ch. Mugler. 2e tirage 2002. 417 p.
Исследования
- Башмакова И. Г. Дифференциальные методы у Архимеда // Историко-математические исследования. — М.: ГИТТЛ, 1953. — № 6. — С. 609—658.
- Башмакова И. Г. Трактат Архимеда «О плавающих телах» // Историко-математические исследования. — М.: ГИТТЛ, 1956. — № 9. — С. 759—788.
- Башмакова И. Г. Лекции по истории математики в Древней Греции // Историко-математические исследования. — М.: Физматгиз, 1958. — № 11. — С. 363—406.
- Бондаренко С.Б. Философские взгляды Архимеда (к 2300-летию со дня рождения) // Философия науки. — Новосибирск: Институт философии и права СО РАН, 2013. — № 2. — С. 176—185.
- Бондаренко С.Б. Жизнь и смерть Архимеда Сиракузского // Вопросы культурологии. — М.: ИД ПАНОРАМА, 2014. — № 10. — С. 38—42.
- Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. Перевод с голландского. М.: Физматгиз, 1959.
- Веселовский И. Н. Архимед. М.: Учпедгиз, 1957. 111 стр. 30000 экз.
- Житомирский С. В. Астрономические работы Архимеда. Историко-астрономические исследования, 11, 1977, с. 319—397.
- Житомирский С. В. Архимед: Пособие для учащихся. М.: Просвещение, 1981. 112 стр. 100000 экз.
- Житомирский С. В. Античная астрономия и орфизм. М.: Янус-К, 2001.
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука. Том I. С древнейших времен до начала Нового времени. (1970)
- Каган В. Ф. Архимед, краткий очерк о жизни и творчестве. М.-Л.: Гостехиздат, 1949. 52 стр. 20000 экз.
- Лурье С. Я. Архимед. М.-Л.: Изд-во АН СССР, 1945.
- Чвалина А. Архимед. М.-Л.: ОНТИ, 1934.
- Щетников А. И. Архимед, корабль Гиерона и «золотое правило механики // Сибирский физический журнал. — 1995. — № 4. — С. 74—76.
- Щетников А. И. Задача Архимеда о быках, алгоритм Евклида и уравнение Пелля // Математика в высшем образовании. — 2004. — № 2. — С. 27—40.
- Aaaboe A., Berggern J. L. Didactical and other remarks on some theorems of Archimedes and infinitesimals. Centaurus, 38, 1996, p. 295—316.
- Berggern J. L. A lacuna in Book I of Archimedes’ Sphere and Cylinder. Historia mathematica, 4, 1977, p. 1-5.
- Berggern J. L. Spurious theorems in Archimedes’ Equilibria of Planes. Archive for History of Exact Sciences, 16, 1977, p. 87-103.
- Christianidis J. et al. Having a Knack for the Non-intuitive: Aristarchus’s Heliocentrism through Archimedes’s Geocentrism, History of Science, V. 40, Part 2, No. 128, June 2002, 147—168. Статья на сайте журнала
- Dijksterhuis E. J. Archimedes. Copenhagen, 1956.
- Drachmann A. G. Fragments from Archimedes in Heron’s Mechanics. Centaurus, 8, 1963, p. 91-146.
- Heath T. L. The works of Archimedes. (Repr. NY: Dover, 2002)
- Netz R., Saito K., Tschernetska N. A new reading of Method Proposition 14: Preliminary evidence from the Archimedes palimpsest. SCIAMVS, 2, 2001, p. 9-29; 3, 2002, p. 109—127.
- Кузнецов О. Планиметрические задачи Архимеда. Статья в газете Математика . — 2002 — № 4.- С.27-31.
Ссылки
wiki2.red
Архимед — биография | Великие исторические личности
Апр 23, 2012 Опубликовано Апр 23, 2012 в Новости
Архимед родился в 287 году до н.э. в Сиракузах на острове Сицилия. Отец Архимеда — астроном и математик Фидий. Фидий дал сыну хорошее образование. Находясь в Александрии, Архимед познакомился со знаменитым астрономом Кононом, астрономом и математиком Эратосфеном, с которыми он поддерживал в дальнейшем научную переписку. Здесь он усиленно работал в богатейшей библиотеке, изучал труды Демокрита, Евдокса и других ученых.
Архимед вернулся в Сицилию зрелым математиком, однако первые его труды были посвящены механике. Принцип рычага, учение о центре тяжести и закон Архимеда являются важнейшими достижениями Архимеда в области механики. Архимед был не только математиком и механиком, но и одним из крупнейших инженеров и конструкторов своего времени. Машина для поливки полей «Улитка», водоподъемный винт (винт Архимеда), разнообразные военные машины для метания копий и дротиков, для поднятия и потопления кораблей увековечили славу Архимеда, способствовали обрастанию фактов из его жизни вымыслами и легендами. Под руководством Архимеда сиракузяне построили множество машин разного назначения. Когда римляне высадили в Сицилии сухопутное войско, а под стенами Сиракуз появился римский флот под командованием Марцелла, то наступила очередь Архимеда. Предоставим слово греческому историку Плутарху, написавшему биографию Марцелла: «При двойной атаке римлян (с суши и с моря) сиракузцы онемели, пораженные ужасом. Что они могли противостоять таким силам, такой могущественной рати? Архимед пустил в ход свои машины. Сухопутная армия была поражена градом метательных снарядов и громадных камней, бросаемых с великой стремительностью. Ничто не могло противостоять их делу, они все низвергали пред собой и вносили смятение в ряды. Что касается флота — то вдруг с высоты стен бревна опускались, вследствие своего веса и природной скорости, на суда и топили их.
Остановимся на результатах исследований Архимеда в области физики. Основные научные проблемы, выдвинутые развитием техники древнего мира, были в первую очередь проблемами статики. Строительная и военная техника была тесно связана с вопросами равновесия и подводила к выработке понятия центра тяжести. В основе этой техники лежал рычаг и другие простые механизмы. Машины, построенные с использованием этих механизмов, и в первую очередь рычага, помогли человеку «перехитрить» природу. Отсюда и пошло название «механика». Греческое слово «механе» означало орудие, приспособление, осадную или театральную машину, а также уловку, ухищрение.
В течение многих веков механика рассматривалась как наука о простых статических машинах. Ее основой были теория рычага, изложенная Архимедом в сочинении «О равновесии плоских фигур». В этой книге также содержатся определения центров тяжести треугольника, параллелограмма, трапеции, параболического сегмента, трапеции, боковые стороны которой являются дугами парабол. Не подлежит сомнению, что все законы, постулаты и другие результаты, данные в этой книге, получены Архимедом в результате длительного практического опыта, обобщением которого и явилась механика Архимеда.
……Рассмотрим теперь знаменитый закон Архимеда, изложенный в его сочинении «О плавающих телах». На тело, погруженное в жидкость, действует сила, равная весу жидкости в объеме этого тела. Существует легенда, что Архимед пришел к своему закону, решая задачу: содержит ли золотая корона, заказанная Героном мастеру, посторонние примеси или нет. Однако, вероятно, мотивы работы Архимеда были все же более глубокими. Ведь Сиракузы были портовым и судостроительным городом. Вопросы плавания тел здесь решались ежедневно практически, и поэтому перед Архимедом стояла задача выяснения научной основы этих вопросов. В своей книге он разбирает не только условия плавания тел, но и вопрос об устойчивости равновесия плавающих тел различной геометрической формы. Научный гений Архимеда в этом сочинении, оставшемся, по-видимому, незаконченным, проявился с исключительной силой.
……Кроме математики и механики, Архимед занимался оптикой и астрономией. Сохранилась легенда о том, что Архимед использовал в борьбе с римским флотом вогнутые зеркала, поджигая корабли противника сфокусированными солнечными лучами. Имеются сведения о том, что Архимедом было написано не дошедшее до нас сочинение по оптике «Катоптрика». Из дошедших до нас отрывков, цитируемых авторами, видно, что Архимед хорошо знал зажигательные свойства вогнутых зеркал, проводил опыты по преломлению света, знал свойства изображений в плоских, выпуклых и вогнутых зеркалах.
……О занятиях Архимеда астрономией свидетельствуют рассказы о построенной им астрономической сфере, захваченной Марцеллом как военный трофей, и сочинение «Псаммит», в котором Архимед подсчитывает число песчинок во Вселенной. Сама постановка задачи представляет большой исторический интерес: точное естествознание впервые приступило к подсчетам космического масштаба, пользуясь неудобной системой чисел. Результат, полученный Архимедом, выражается в современных обозначениях числом 10х63. Кроме того, в сочинении Архимеда впервые в истории науки сопоставляются две системы мира: геоцентрическая и гелиоцентрическая (в центре Земля или Солнце). Архимед указывает, что «большинство астрономов называют миром шар, заключающийся между центрами Солнца и Земли».
Архимед сообщает далее, что Аристарх Самосский предполагает мир гораздо большим. «Действительно, он предполагает, что неподвижные звезды и Солнце находятся в покое, а Земля обращается вокруг Солнца по окружности круга, расположенного посередине между Солнцем и неподвижными звездами…». Архимед интерпретирует мысль Аристарха как равенство отношения размеров мира к размерам Земли, отношению радиуса сферы неподвижных звезд к радиусу земной орбиты. Таким образом, Архимед принимает мир, хотя и очень большим, но конечным, что позволяет ему довести свой расчет до конца.
Хочется привести слова Плутарха: «Архимед был настолько горд наукой, что именно о тех своих открытиях, благодаря которым он приобрел славу …, он не оставил ни одного сочинения». Хотя это и не совсем точно, но многих работ Архимеда мы действительно не знаем. Мы не знаем, например, конструкций его боевых машин, нам не известно, как он мог вычислять квадратные корни из больших чисел, и многое другое. «Поэтому нет оснований не верить написанному об Архимеде, что он жил как бы околдованный какою-то домашнею сиреною, постоянной его спутницей, заставляющей его забывать пищу, питье, всякие заботы о своем теле. Иногда, приведенный в баню, он чертил пальцем на золе очага геометрические фигуры, или проводил линии на умащенном маслом своем теле. Автор прекрасных открытий, он просил своих родственников поставить на его могиле цилиндр, включающий в себя конус и шар, и подписать отношение их объемов (3:2:1)», — так характеризовал Архимеда Плутарх. И в память об этом гении древности потомки Архимеда через века пронесут его радостный возглас, боевой клич науки: «Эврика!» — «Я нашел!».
После учебы в Александрии вернулся в Сиракузы, где конструировал боевые машины для защиты города от римлян во время 2-й Пунической войны. Благодаря изобретениям Архимеда, Сиракузы долгое время успешно выдерживали осаду римских воинов. Архимед погиб во время одного из боев. Существует четыре версии его гибели.
По первой, в разгар боя он сидел на пороге своего дома, углубленно размышляя над чертежами, сделанными им прямо на дорожном песке. В это время пробегавший мимо римский воин наступил на чертеж, и возмущенный ученый бросился на римлянина с криком:

Не тронь моих чертежей!
Эта фраза стоила Архимеду жизни. Солдат остановился и хладнокровно зарубил старика мечом.
Вторая версия гласит, что полководец римлян Марцелл специально послал воина на поиски Архимеда. Воин разыскал ученого и сказал:
Иди со мной, тебя зовет Марцелл.Какой еще Марцелл?! Я должен решить задачу!
Разгневанный римлянин выхватил меч и убил Архимеда.
По третьей версии, воин ворвался в дом Архимеда для грабежа, занес меч на хозяина, а тот только и успел крикнуть:
Остановись, подожди хотя бы немного. Я хочу закончить решение задачи, а потом делай что хочешь!

Наконец, четвертая версия такова: Архимед сам отправился к Марцеллу, чтобы отнести ему свои приборы для измерения величины Солнца. По дороге его ноша привлекла внимание римских солдат. Они решили, что ученый несет в ларце золото или драгоценности, и, недолго думая, перерезали ему горло.
Таковы легенды. Однако многие историки полагают, что Архимед был убит не случайно — ведь его ум стоил в те времена целой армии.
Источник: http://www.aska-life.com.ua
Похожие записи:
history-persons.ru



