Кинематика определение в физике – Основные понятия и определения кинематики — Теоретическая механика. Кинематика
- Комментариев к записи Кинематика определение в физике – Основные понятия и определения кинематики — Теоретическая механика. Кинематика нет
- Советы абитуриенту
- Кинематика (физика) – это… Что такое Кинематика (физика)?
- Что такое кинематика? Определение и понятие :: SYL.ru
- Кинематика материальной точки: основные понятия, элементы
- Т. Понятия кинематики — PhysBook
- Определение кинематики
- Кинематика (физика)
- Кинематика — WiKi
Кинематика (физика) – это… Что такое Кинематика (физика)?
У этого термина существуют и другие значения, см. Кинематика.Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.
Различают классическую кинематику, в которой пространственные (длины отрезков) и временные (промежутки времени) характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Относительной становится также одновременность. В релятивистской механике вместо отдельных понятий пространство и время вводится понятие пространства-времени, в котором инвариантным относительно преобразований Лоренца является величина, называемая интервалом.
История кинематики
Долгое время понятия о кинематике были основаны на работах Аристотеля, в которых утверждалось, что скорость падения пропорциональна весу тела, а движение в отсутствие сил невозможно. Только в конце XVI века этим вопросом подробно занялся Галилео Галилей. Изучая свободное падение (знаменитые опыты на Пизанской башне) и инерцию тел, он доказал неправильность идей Аристотеля. Итоги своей работы по данной теме он изложил в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению»[1].
Рождением современной кинематики можно считать выступление Пьера Вариньона перед Французской Академией наук 20 января 1700 года. Тогда впервые были даны понятия скорости и ускорения в дифференциальном виде.
В XVIII веке Ампер первый использовал вариационное исчисление в кинематике.
После создания СТО, показывающей, что время и пространство не абсолютны и скорость имеет принципиальное ограничение, кинематика вошла в новый этап развития в рамках релятивистской механики (см. Релятивистская кинематика).
Основные понятия кинематики
Задачи кинематики
Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движение рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).
Положение точки (или тела) относительно заданной системы отсчёта определяется некоторым количеством взаимно независимых функций координат:
- ,
где определяется количеством степеней свободы. Так как точка не может быть в нескольких местах одновременно, все функции должны быть однозначными. Также в классической механике выдвигается требование их дифференцируемости на промежутках. Производные этих функций определяют скорость тела[2].
Скорость движения определяется как производная координат по времени:
- ,
где — единичные векторы, направленные вдоль соответствующих координат.
Ускорение определяется как производная скорости по времени:
Следовательно, характер движения можно определить, зная зависимость скорости и ускорения от времени. А если кроме этого известны ещё и значения скорости/координат в определённый момент времени, то движение полностью задано.
Деление кинематики по типам объекта исследования
В зависимости от свойств изучаемого объекта, кинематика делится на кинематику точки, кинематику твёрдого тела, кинематику деформируемого тела, кинематику газа, кинематику жидкости и т. д.
Кинематика точки
Основная статья: Кинематика точки
Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.
Частные случаи движения в кинематике точки:
- Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).
- ,
где — длина пути траектории за промежуток времени от до , — проекции на соответствующие оси координат.
- Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении;
- ,
где — длина пути траектории за промежуток времени от до , — проекции на соответствующие оси координат, — проекции на соответствующие оси координат.
- Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.
- ,
где — радиус окружности, по которой движется тело.
Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.
Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:
- ,
где и — проекции на соответствующие оси.
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.
- В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:
Кинематика твёрдого тела
Кинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).
Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).
Связь скорости двух точек твердого тела выражается через формулу Эйлера:
- ,
где — вектор угловой скорости тела.
Кинематика деформируемого тела, Кинематика жидкости
Основные статьи: Кинематика деформируемого тела, Кинематика жидкости
Кинематика деформируемого тела и кинематика жидкости относятся к кинематике непрерывной среды.
Кинематика газа
Основная статья: Кинематика газа
Кинематика газа изучает деление газа на скопления при движении и описывает движение этих скоплений. В рамках кинематики газа описываются не только основные параметры движения, но и типы движения газа.
Примечания
Литература
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. — М.: Изд-во Физического факультета МГУ, 1997.
- Матвеев. А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Павленко Ю. Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392 с.
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Стрелков С. П. Механика. — М.: Наука, 1975.
- Яворский Б. М., Детлаф А. А.
dic.academic.ru
Что такое кинематика? Определение и понятие :: SYL.ru
Описание перемещения тела — это способ определить его положение в пространстве в любое время. Что такое кинематика? В ней рассматривается движение тела с геометрической стороны, не учитывая причины, то есть силы, производящих его.

Достаточно длительное время вся кинематика основывалась на работах небезызвестного Аристотеля. Ученый утверждал, что скорость падения любого тела прямо пропорциональна его весу, и двигаться оно не может в отсутствии сил. Главная задача кинематики — математическое определение характеристик движения тел и их положения во времени. Для изложения она не требует новых начал и обращается к аксиомам геометрии.
Определение того, что такое кинематика, звучит следующим образом: “Это подраздел механики, который изучает механическое движение тела, но при этом не рассматривает причины, которые его вызывают”.

Идеализирование как метод исследования
Так все-таки, что такое кинематика? Это звено, которое соединяет механику и геометрию. Свойства физических тел, жидких, твердых и газообразных в механике, частью которой и является кинематика, идеализируются. Твердое тело рассматривается кинематикой как абсолютно твердое тело. Т.е. расстояние между двумя частицами его не может изменяться. Капельная жидкость рассматривается как абсолютно несжимаемое и т.д. Такой способ идеализировать предметы изучения и есть способ научного исследования.
В природе все движется, и то, что мы можем наблюдать, относительно, но его всегда можно абсолютизировать. Передвижение всего тела определено, если нам известно передвижение каждой его точки. Поэтому, прежде чем рассматривать перемещение тела, рассматривается перемещение точек. В природе свободное падение — это естественное, равноускоренное движение.
Траектория падающего свободно тела зависит от вектора начальной скорости. Если оно было брошено строго вертикально вниз, то она — это прямой вертикальный отрезок, а движение его равнопеременное.
Введение понятия точки облегчает исследования. Изучением относительного перемещения тела и занимается кинематика. Физика движения по окружности, например, говорит, что скорость человека, который идет по краю вращающейся карусели, равняется векторной сумме скорости движения самого человека и скорости вращения карусели. Это так называемый закон сложения скоростей.
Закон движения
Положение так называемой материальной точки определяют три координаты. Ее перемещение — это последовательное и непрерывное прохождение через точки пространства, которые совершаются с течением времени и сопровождаемое изменением координат. Ее траектория — это путь, по которому она движется.

Кинематика движения материальной точки
Кроме идеализированных тел, эта наука ввела понятие о материальной точке как об объекте, который имеет исчезающе малые размеры и бесконечно малый вес. Кинематика материальной точки исследует объекты, размерами которых можно легко пренебречь.
Так как в первую очередь изучаются составные движения, то есть ход в двух системах отсчета, взаимно перемещающихся относительно друг друга, кинематика точки полагает равными координаты всех точек, ускорение и саму скорость. А сама система координат, которая связана с точкой отсчета, и часы, которые отсчитывают время, являются системой отсчета, которая определяет положение движущегося объекта в момент времени.
Кинематика точки учитывает пройденный путь, скорость, ускорение и перемещение. Путь — длина траектории, описываемой точкой в заданный промежуток времени. Перемещение — это вектор, который соединяет начальное положение точки с конечным. Направление скорости будет оставаться неизменным, а ее величина, при неравномерном движении, может изменяться. Прямолинейное движение именуется равнопеременным в том случае, когда скорость объекта в любые временные промежутки изменяется одинаково.
В случае с бесконечно малой массой точка есть результат разделения объекта на бесконечное число бесконечно малых частиц. В случае с конечной массой точка есть результат беспредельного сжатия объекта. Представьте шарик заполненный материей, радиус которого уменьшается до бесконечно малого размера, а масса при этом сохраняется.
Какие бывают скорости?
Абсолютная скорость — это та, которая наблюдается относительно неподвижных осей. Относительная — это скорость, которую имеет точка, если рассматривать подвижные оси, как неподвижные. И переносная — это скорость, которую имеет точка, если рассматривать ее неподвижной, а оси — подвижными.
Определение движения
Под движением понимается непрерывное изменение положения тела во времени. Движение точки известно, если возможно для каждого произвольного мгновения указать ее положение в пространстве.
Аналитическая геометрия дает различные способы для определения положения точки в пространстве при помощи особых геометрических величин, называемых координатами. Значит, само движение точки может рассматриваться, как непрерывное изменение во времени ее координат.
Прямое и прямолинейное движение

Самое простое из всех движений есть то, в котором расстояние s точки от начала по прямой изменяется пропорционально времени t. Обозначая через s0 расстояние точки в начальный момент времени от начала расстояния, получаем уравнение равномерного движения в его общем виде:
s = s0 +/- vt,
где v – коэффициент пропорциональности. Он называется скоростью равномерного движения и имеет физический смысл, как мера изменения пути со временем.
Поступательное движение
Кинематика системы своим развитием обязана инженеру-геометру Шалю из Франции. Поступательное движение у него – прямая линия, взятая в теле, которая движется параллельно себе самой. Поступательное движение не стоит путать с прямолинейным. Тело может двигаться поступательно и криволинейно. Прямолинейное движение – это только частный случай поступательного. Например, ось земли, которая описывает эллипс, движется поступательно.
Любое движение, которое не удовлетворяет условию равномерности, называется переменным. Однако любое переменное движение в его бесконечно малых величинах можно рассматривать как равномерное. Скорость переменного движения есть скорость равномерных, на которые движение в своих элементах распадается.
Кинематика: формулы
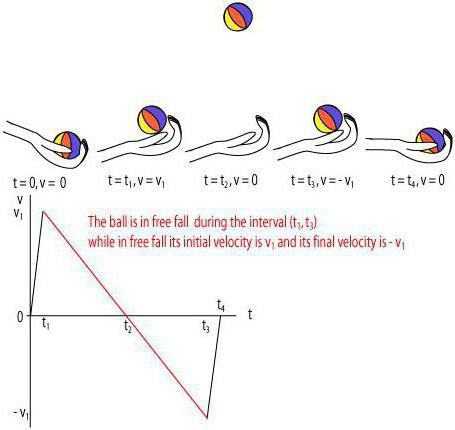
Существует целый ряд физических формул этой науки. Они объясняют, что такое кинематика и позволяют узнать путь, скорость, ускорение, высоту тела, которое было брошено вертикально вниз или вверх и т.д. Например, уравнение равномерного прямолинейного движения точки, когда начальное расстояние равно нулю выглядит так:
s = vt
где s – это путь, v – скорость, а t – время.
Скорость свободно падающего тела:
v = gt
где v — скорость, g – ускорение свободного падения, а t – время.
История кинематики
Галилео Галилей проводил многочисленные опыты на известной Пизанской башне. Он изучал свободное падение объектов и их инерцию. Его исследования как раз и доказали ошибочность идей Аристотеля.
Выводы он изложил в своей рукописи: “Беседа и математические доказательства, касающихся двух новых отраслей науки, относящихся к механике и местному движению”.
Речь Пьера Вариньона на выступлении перед знаменитой Французской академией наук, которую он произнес в январе 1700 года, принято считать рождением кинематики в том виде, в котором мы ее знаем. Тогда же были определены понятия скорости и ускорения в дифференциальном виде.
В 18 веке Ампер впервые использовал вариационное исчисление и заложил самостоятельное развитие кинематики.
После того как была разработана СТО (самостоятельная теория относительности), которая показала, что пространство и время не абсолютные величины, а скорость имеет принципиальное ограничение, кинематика получила новый виток развития в рамках релятивистской механики. Она рассматривает законы движения частиц и тел при скоростях, которые сравнимы со скоростью света.
Таким образом, мы разобрались, что за наука кинематика и какие методы исследований она использует.
www.syl.ru
Кинематика материальной точки: основные понятия, элементы
Темой нашей сегодняшней статьи станет кинематика материальной точки. Что это вообще такое? Какие понятия фигурируют в ней и какое определение необходимо дать этому термину? На эти и многие другие вопросы мы сегодня и постараемся ответить.
Определение и понятие
Кинематика материальной точки представляет собой не что иное, как подраздел физики под названием «механика». Она, в свою очередь, изучает закономерности движения тех или иных тел. Кинематика материальной точки занимается также этой задачей, однако делает это не в общем виде. На самом деле этот подраздел изучает методы, которые позволяют описать движение тел. При этом для исследования подходят только так называемые идеализированные тела. К таковым относятся: материальная точка, абсолютно твердое тело и идеальный газ. Рассмотрим понятия подробнее. Все мы со школьной скамьи знаем, что материальной точкой принято называть тело, размерами которого в той или иной ситуации можно пренебречь. К слову, кинематика поступательного движения материальной точки впервые начинает фигурировать в учебниках седьмого класса по физике. Это наиболее простая отрасль, поэтому начинать знакомство с наукой при ее помощи наиболее удобно. Отдельным вопросом является то, какие имеются элементы кинематики материальной точки. Их достаточно много, причем условно их можно разбить на несколько уровней, имеющих различную сложность для понимания. Если говорить, например, о радиус-векторе, то, в принципе, в его определении нет ничего запредельно сложного. Однако согласитесь с тем, что гораздо проще его понять будет студенту, нежели ученику средней или старшей школы. Да и если честно говорить, нет никакой необходимости объяснять особенности этого термина старшеклассникам.
Краткая история создания кинематики
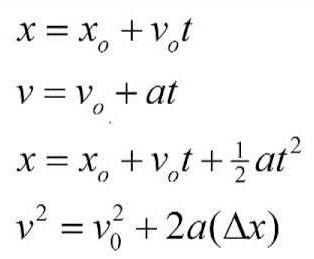
Еще много-много лет назад великий ученный Аристотель посвятил львиную долю своего свободного времени изучению и описанию физики как отдельной науки. В том числе он работал и над кинематикой, пытаясь представить ее основные тезисы и понятия, так или иначе применяемые при попытках решения практических и даже обыденных задач. Аристотель дал первоначальные представления о том, что представляют собой элементы кинематики материальной точки. Его работы и труды очень ценны для всего человечества. Тем не менее в своих выводах он сделал немалое количество ошибок, и виной тому были определенные заблуждения и просчеты. Работами Аристотеля в свое время заинтересовался другой ученный – Галилео Галилей. Один из основополагающих тезисов, выдвинутых Аристотелем, гласил о том, что движение тела происходит только в том случае, если на него действует какая-то сила, определенная по интенсивности и направлению. Галилей доказал, что это ошибка. Сила будет оказывать влияние на параметр скорости движения, но не более. Итальянец показал, что сила есть причина ускорения, и оно может возникнуть только обоюдно с ней. Также Галилео Галилей уделил немалое внимание изучению процесса свободного падения, выводя соответствующие закономерности. Наверное, все помнят о его знаменитых опытах, которые он проводил на Пизанской башне. В своих работах основы кинематических решений использовал и физик Ампер.
Исходные понятия
Как говорилось ранее, кинематика изучает способы описания движения идеализированных объектов. При этом на практике могут применяться основы математического анализа, обыкновенной алгебры и геометрии. Но какие же понятия (именно понятия, а не определения и на параметрические величины) лежат в основе этого подраздела физики? Во-первых, все должны четко усвоить, что кинематика поступательного движения материальной точки рассматривает движение без учета силовых показателей. То есть для решения соответствующих задач нам не понадобятся формулы, связанные с силой. Она кинематикой не учитывается, сколько бы их ни было – одна, две, три, хоть несколько сотен тысяч. Тем не менее существование ускорения все же предусматривается. В целом ряде задач кинематика движения материальной точки предписывает определить величину ускорения. Однако причины возникновения этого явления (то есть силы и их природа) не рассматриваются, а опускаются.
Классификация
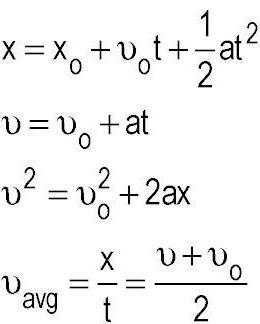
Мы выяснили, что кинематика исследует и применяет методы описания движения тел без оглядки на воздействующие на них силы. Кстати говоря, такой задачей занимается уже другой подраздел механики, который называют динамикой. Вот уже там применяются законы Ньютона, которые позволяют на практике определить достаточно многие параметры при малом количестве известных первоначальных данных. Основные понятия кинематики материальной точки – это пространство и время. А в связи с развитием науки как в целом, так и в данной области, возник вопрос о целесообразности использования подобной комбинации.
С самого начала существовала классическая кинематика. Можно говорить о том, что ей свойственно не просто наличие как временных, так и пространственных промежутков, но и их независимость от выбора той или иной системы отсчета. Кстати, об этом мы поговорим несколько позже. Сейчас же просто объясним, о чем идет речь. Пространственным промежутком в данном случае будет считаться отрезок, временным – интервал времени. Вроде бы все должно быть понятно. Так вот, эти промежутки будет в классической кинематике считаться абсолютными, инвариантными, иными словами не зависящими от перехода из одной системы отсчета в другую. То ли дело релятивистская кинематика. В ней промежутки при переходе между системами отсчета могут изменяться. Правильнее даже будет сказать, что не могут, а должны, наверное. В силу этого одновременность двух случайных событий также становится относительной и подлежит особому рассмотрению. Именно поэтому в релятивистской кинематике два понятия – пространство и время – объединяются в одно.
Кинематика материальной точки: скорость, ускорение и другие величины
Чтобы хотя бы немного понимать данный подраздел физики, необходимо ориентироваться в наиболее главных понятиях, знать определения и представлять, что собой представляет в общем плане та или иная величина. Ничего сложно в этом нет на самом деле, все очень легко и просто. Рассмотрим, пожалуй, для начала основные понятия, применяемые в задачах по кинематике.
Движение
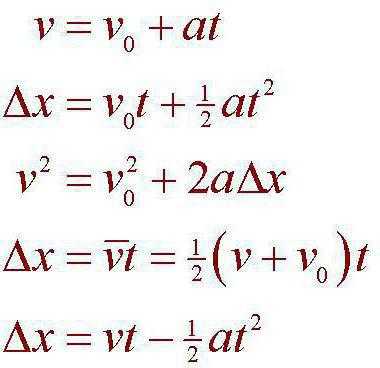
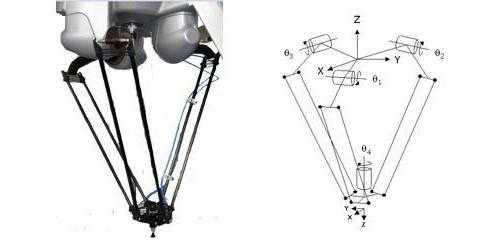
Механическим движением мы будем считать процесс, в ходе которого тот или иной идеализированный объект изменяет свое положение в пространстве. При этом можно говорить о том, что изменение происходит относительно других тел. Необходимо учитывать и тот факт, что одновременно происходит и установление определенного временного промежутка между двумя событиями. Например, можно будет выделить определенный интервал, образовавшийся за время, прошедшее между тем, как тело прибыло из одной позиции в другую. Отметим также, что тела при этом могут и будут взаимодействовать между собой, согласно общим законам механики. Это как раз то, чем чаще всего оперирует кинематика материальной точки. Система отсчета – следующее понятие, которое неразрывно связано с ней.
Координаты
Их можно назвать обыкновенным данными, которые позволяют определить положение тела в тот или иной момент времени. Координаты неразрывно связаны с понятием системы отсчета, а также координатной сеткой. Чаще всего представляют собой комбинацию букв и цифр.
Радиус-вектор
Из названия уже должно быть понятно, что он представляет собой. Тем не менее все же поговорим об этом подробнее. Если точка движется по некоторой траектории, а мы точно знаем начало той или иной системы отсчета, то можно в любой момент времени провести радиус-вектор. Он будет соединять первоначальное положение точки с мгновенным или конечным.
Траектория
Ею будет называться непрерывная линия, которая прокладывается в результате движения материальной точки в той или иной системе отсчета.
Скорость (как линейная, так и угловая)
Это величина, которая может рассказать о том, как быстро тело проходит тот или иной промежуток дистанции.
Ускорение (и угловое, и линейное)
Показывает, по какому закону и как интенсивно изменяется скоростной параметр тела.
Пожалуй, вот они – основные элементы кинематики материальной точки. Следует отметить, что и скорость, и ускорение являются векторными величинами. А это означает то, что они не просто имеют некоторое показательное значение, но и определенное направление. К слову, они могут быть направлены как в одну сторону, так и в противоположные. В первом случае тело будет ускоряться, во втором – тормозить.
Простейшие задачи
Кинематика материальной точки (скорость, ускорение и расстояние в которой являются практически фундаментальными понятиями) насчитывает даже не то что огромное количество задач, а много их различных категорий. Давайте попробуем решить достаточно простенькую задачку по определению пройденного телом расстояния.
Предположим, условия, которые мы имеем на руках, следующие. Автомобиль гонщика стоит на стартовой черте. Оператор подает отмашку флагом, и машина резко срывается с места. Определить, сможет ли она поставить новый рекорд в состязании гонщиков, если дистанцию, равную одной сотне метров, очередной лидер прошел за 7,8 секунд. Ускорение автомобиля принять равным 3 метра, деленным на секунду в квадрате.
Итак, как же решить подобную задачу? Она достаточно интересная, поскольку от нас требуется не «сухое» определение тех или иных параметров. Она скрашена оборотами и определенной ситуацией, что разнообразит процесс решения и поиска показателей. Но чем же мы должны руководствоваться перед тем, как подступиться к заданию?
1. Кинематика материальной точки предусматривает использование в данном случае ускорения.
2. Предполагается решение при помощи формулы расстояния, поскольку его численное значение фигурирует в условиях.
Решается задача вообще-то просто. Для этого берем формулу расстояния: S = VoT + (-) AT^2/2. В чем заключается смысл? Нам нужно узнать, за какое время гонщик пройдет обозначенную дистанцию, а затем сравнить показатель с рекордом, чтобы узнать, побьет он его или же нет. Для этого выделим время, получим формулу для него: AT^2 + 2VoT – 2S. Это есть не что иное, как квадратное уравнение. Но автомобиль срывается с места, значит, начальная скорость будет равна 0. При решении уравнения дискриминант окажется равным 2400. Для поиска времени необходимо извлечь корень. Сделаем до второго знака после запятой: 48,98. Найдем корень уравнения: 48,98/6 = 8,16 секунд. Получается, что гонщик не сможет побить существующий рекорд.
fb.ru
Т. Понятия кинематики — PhysBook
Основные понятия кинематики
Кинематика — раздел механики, изучающий движение тел без учета причин, вызвавших это движение.
Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.
Механическое движение — это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.
Для описания механического движения надо выбрать систему отсчета.
Тело отсчета — тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.
Система отсчета — это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).
Рис. 1
Положение тела можно определить с помощью радиуса-вектора \(~\vec r\) или с помощью координат.
Радиус-вектор \(~\vec r\) точки Μ — направленный отрезок прямой, соединяющий начало отсчета О с точкой Μ (рис. 2).
Рис. 2
Координата x точки Μ — это проекция конца радиуса-вектора точки Μ на ось Ох. Обычно пользуются прямоугольной системой ко ординат. В этом случае положение точки Μ на линии, плоскости и в пространстве определяют соответственно одним (x), двумя (х, у) и тремя (х, у, z) числами — координатами (рис. 3).
Рис. 3
В элементарном курсе физики изучают кинематику движения материальной точки.
Материальная точка — тело, размерами которого в данных условиях можно пренебречь.
Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.
Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.
В дальнейшем под словом “тело” будем понимать “материальная точка”.
Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (y = f(x) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.
В зависимости от вида траектории различают прямолинейное и криволинейное движение.
Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s > 0.
Перемещение \(~\Delta \vec r\) тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка M0) и конечное (точка М) положение тела (см. рис. 2):
\(~\Delta \vec r = \vec r – \vec r_0,\)где \(~\vec r\) и \(~\vec r_0\) — радиусы-векторы тела в эти моменты времени.
Проекция перемещения на ось Ox\[~\Delta r_x = \Delta x = x – x_0\], где x0 и x — координаты тела в начальный и конечный моменты времени.
Модуль перемещения не может быть больше пути\[~|\Delta \vec r| \le s\].
Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.
Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
\(~\vec r = \vec r_0 + \Delta \vec r;\) \(~\left\{ \begin{matrix} x = x_0 + \Delta r_x ; \\ y = y_0 + \Delta r_y . \end{matrix} \right.\)Скорость — мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.
Средняя скорость \(~\mathcal h \vec \upsilon \mathcal i\) — векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения (рис. 4):
\(~\mathcal h \vec \upsilon \mathcal i = \frac{\Delta \vec r}{\Delta t}; \qquad \mathcal h \vec \upsilon \mathcal i \upuparrows \Delta \vec r .\)Рис. 4
В СИ единицей скорости является метр в секунду (м/с).
Средняя скорость, найденная по этой формуле, характеризует движение только на том участке траектории, для которого она определена. На другом участке траектории она может быть другой.
Иногда пользуются средней скоростью пути\[~\mathcal h \upsilon \mathcal i = \frac{s}{\Delta t}\], где s — путь, пройденный за промежуток времени Δt. Средняя скорость пути — это скалярная величина.
Мгновенная скорость \(~\vec \upsilon\) тела — скорость тела в данный момент времени (или в данной точке траектории). Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени \(~\vec \upsilon = \lim_{\Delta t \to 0} \frac{\Delta \vec r}{\Delta t} = \vec r \ ‘\). Здесь \(~\vec r \ ‘\) — производная от радиуса-вектора по времени.
В проекции на ось Ох:
\(~\upsilon_x = \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} = x’.\)Мгновенная скорость тела направлена по касательной к траектории в каждой ее точке в сторону движения (см. рис. 4).
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.
Среднее ускорение — физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло:
\(~\mathcal h \vec a \mathcal i = \frac{\Delta \vec \upsilon}{\Delta t} = \frac{\vec \upsilon – \vec \upsilon_0}{\Delta t} .\)Вектор \(~\mathcal h \vec a \mathcal i\) направлен параллельно вектору изменения скорости \(~\Delta \vec \upsilon\) (\(~\mathcal h \vec a \mathcal i \upuparrows \Delta \vec \upsilon\)) в сторону вогнутости траектории (рис. 5).
Рис. 5
Мгновенное ускорение:
\(~\vec a = \lim_{\Delta t \to 0} \frac{\Delta \vec \upsilon}{\Delta t} = \vec \upsilon \ ‘ .\)В СИ единицей ускорения является метр на секунду в квадрате (м/с2).
В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.
При прямолинейном движении с возрастающей по модулю скоростью (рис. 6, а) векторы \(~\vec a\) и \(~\vec \upsilon_0\) сонаправлены (\(~\vec a \upuparrows \vec \upsilon_0\)) и проекция ускорения на направление движения положительна.
При прямолинейном движении с убывающей по модулю скоростью (рис. 6, б) направления векторов \(~\vec a\) и \(~\vec \upsilon_0\) противоположны (\(~\vec a \uparrow \downarrow \vec \upsilon_0\)) и проекция ускорения на направление движения отрицательна.
Рис. 6
Вектор \(~\vec a\) при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости \(~\vec a_{\tau}\) и перпендикулярно скорости \(~\vec a_n\) (рис. 1.7), \(~\vec a_{\tau}\) — тангенциальное ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении, \(~\vec a_n\) — нормальное ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении Модуль ускорения \(~a = \sqrt{a^2_{\tau} + a^2_n}\).
Рис. 7
Литература
- Аксенович Л.А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л.А. Аксенович, Н.Н.Ракина, К.С. Фарино; Под ред. К.С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.5-8.
www.physbook.ru
Определение кинематики
Физика > Определение кинематики
Кинематика – изучение перемещения точек, объектов и групп объектов без учета причин движения.
Задача обучения
Определение понятия «кинематика».
Основные пункты
- Чтобы описать движение, кинематика исследует траектории точек, линий и прочих геометрических объектов.
- Изучение кинематики можно свести к математическому выражению.
- Кинематические уравнения применяют для вычисления разнообразных аспектов движения, вроде скорости, смещения, ускорения и время.
Термин
Кинематика – раздел механики, изучающий движение объектов, но игнорирующий связанные с этим силы.
Кинематика выступает разделом классической механики, описывающей перемещение точек, объектов и целых групп, но не учитывающей силы, влияющие на весь процесс. Очень часто кинематику именуют «геометрией движения».
Оглянитесь и вы заметите, что объекты вокруг вас пребывают в движении. Более того, пока вы спите, ваша кровь продолжает циркулировать по венам. Даже неодушевленные предметы остаются активными, так как атомы и молекулы движутся. Умение разбираться в движении не только отвечает на интересные вопросы, но и помогает понять остальные понятия в физике. Например, изучить силу не получится без понимания процесса ускорения.
Чтобы описать движение в кинематике, следует подружиться с траекториями точек, линий и прочих геометрических объектов, а также их дифференциальными свойствами (ускорение и скорость). Кинематику используют в астрофизике, чтобы описать перемещение небесных тел и систем. Она активно задействована в машиностроении, робототехнике и биомеханике.
Если говорить формально, то само изучение физики начинается с основ кинематики. Это слово имеет греческие корни («кинезис»), обозначающие движение. Кинематический анализ – вычисление кинематических величин, которые используют для описания движения. Кинематику можно упростить до математического выражения и использовать при расчетах различных аспектов движения, вроде скорости, времени, ускорения, траектории и смещения.
v-kosmose.com
Кинематика (физика)
Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.
Содержание
- 1 История кинематики
- 2 Основные понятия кинематики
- 3 Задачи кинематики
- 4 Деление кинематики по типам объекта исследования
- 4.1 Кинематика точки
- 4.2 Кинематика твёрдого тела
- 4.3 Кинематика деформируемого тела, Кинематика жидкости
- 4.4 Кинематика газа
- 5 Примечания
- 6 Литература
История кинематики
Долгое время понятия о кинематике были основаны на работах Аристотеля, в которых утверждалось, что скорость падения пропорциональна весу тела, а движение в отсутствие сил невозможно. Только в конце XVI века этим вопросом подробно занялся Галилео Галилей. Изучая свободное падение (знаменитые опыты на Пизанской башне) и инерцию тел, он доказал неправильность идей Аристотеля. Итоги своей работы по данной теме он изложил в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению».
Рождением современной кинематики можно считать выступление Пьера Вариньона перед Французской Академией наук 20 января 1700 года. Тогда впервые были даны понятия скорости и ускорения в дифференциальном виде.
В XVIII веке Ампер первый использовал вариационное исчисление в кинематике.
После создания СТО, показывающей, что время и пространство не абсолютны и скорость имеет принципиальное ограничение, кинематика вошла в новый этап развития в рамках релятивистской механики (см. Релятивистская кинематика).
Основные понятия кинематики
- Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.
- Система отсчёта — сопоставленная с континуумом реальных или воображаемых тел отсчёта система координат и прибор (ы) для измерения времени (часы). Используется для описания движения.
- Координаты — способ определения положения точки или тела с помощью чисел или других символов.
- Радиус-вектор используется для задания положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
- Траектория — непрерывная линия, которую описывает точка при своём движении.
- Скорость — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.
- Ускорение — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени.
- Угловая скорость — векторная величина, характеризующая скорость вращения тела.
- Угловое ускорение — величина, характеризующая быстроту изменения угловой скорости.
Задачи кинематики
Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движение рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).
Положение точки (или тела) относительно заданной системы отсчёта определяется некоторым количеством взаимно независимых функций координат:
,где определяется количеством степеней свободы. Так как точка не может быть в нескольких местах одновременно, все функции должны быть однозначными. Также в классической механике выдвигается требование их дифференцируемости на промежутках. Производные этих функций определяют скорость тела.
Скорость движения определяется как производная координат по времени:
,где — единичные векторы, направленные вдоль соответствующих координат.
Ускорение определяется как производная скорости по времени:
Следовательно, характер движения можно определить, зная зависимость скорости и ускорения от времени. А если кроме этого известны ещё и значения скорости/координат в определённый момент времени, то движение полностью задано.
Деление кинематики по типам объекта исследования
В зависимости от свойств изучаемого объекта, кинематика делится на кинематику точки, кинематику твёрдого тела, кинематику деформируемого тела, кинематику газа, кинематику жидкости и т. д.
Кинематика точки
Основная статья: Кинематика точки
Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.
Частные случаи движения в кинематике точки:
- Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).
где — длина пути траектории за промежуток времени от до , — проекции на соответствующие оси координат.
- Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении; равнозамедленное — если в разные).
где — длина пути траектории за промежуток времени от до , — проекции на соответствующие оси координат, — проекции на соответствующие оси координат.
- Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.
где — радиус окружности, по которой движется тело.
Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.
Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:
,где и — проекции на соответствующие оси.
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.
- В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:
Кинематика твёрдого тела
Основная статья: Кинематика твёрдого телаКинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).
Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).
Связь скорости двух точек твердого тела выражается через формулу Эйлера:
,где — вектор угловой скорости тела.
Кинематика деформируемого тела, Кинематика жидкости
Основные статьи: Кинематика деформируемого тела, Кинематика жидкости
Кинематика деформируемого тела и кинематика жидкости относятся к кинематике непрерывной среды.
Кинематика газа
Основная статья: Кинематика газаКинематика газа изучает деление газа на скопления при движении и описывает движение этих скоплений. В рамках кинематики газа описываются не только основные параметры движения, но и типы движения газа.
Примечания
- ↑ Научная биография Галилео Галилея
- ↑ Кинематика — статья из Физической энциклопедии
Литература
- Алешкевич В. А., Деденко, Л. Г., Караваев В. А. Механика твердого тела. Лекции. — М.: Изд-во Физического факультета МГУ, 1997.
- Матвеев. А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Павленко Ю. Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392 с.
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Стрелков С. П. Механика. — М.: Наука, 1975.
- Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов (4-е изд.). — М.: Наука, 1968.
Кинематика (физика) Информацию О

Кинематика (физика) Комментарии
Кинематика (физика)
Кинематика (физика)
Кинематика (физика) Вы просматриваете субъект
Кинематика (физика) что, Кинематика (физика) кто, Кинематика (физика) описание
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
Кинематика — WiKi
Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.
Различают классическую кинематику, в которой пространственные (длины отрезков) и временные (промежутки времени) характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Относительной становится также одновременность. В релятивистской механике вместо отдельных понятий пространство и время вводится понятие пространства-времени, в котором инвариантным относительно преобразований Лоренца является величина, называемая интервалом.
В зависимости от свойств изучаемого объекта, кинематика делится на кинематику точки, кинематику твёрдого тела, кинематику деформируемого тела, кинематику газа, кинематику жидкости и т. д.
Кинематика точки
Основная статья: Кинематика точки
Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.
Частные случаи движения в кинематике точки:
- Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).
- a→=0{\displaystyle {\vec {a}}=0}
- v→=const{\displaystyle {\vec {v}}=\mathrm {c} onst}
- p1(t)=p1(0)+v1t{\displaystyle p_{1}(t)=p_{1}(0)+v_{1}t}
- p2(t)=p2(0)+v2t{\displaystyle p_{2}(t)=p_{2}(0)+v_{2}t}
- …{\displaystyle \dots }
- pn(t)=pn(0)+vnt{\displaystyle p_{n}(t)=p_{n}(0)+v_{n}t}
- s=∣v→∣(t1−t2){\displaystyle s=\mid {\vec {v}}\mid (t_{1}-t_{2})} ,
где s{\displaystyle s} — длина пути траектории за промежуток времени от t2{\displaystyle t_{2}} до t1{\displaystyle t_{1}} , v1,v2,…,vn{\displaystyle v_{1},v_{2},\dots ,v_{n}} — проекции v→{\displaystyle {\vec {v}}} на соответствующие оси координат.
- Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении; равнозамедленное — если в разные).
- a→=const{\displaystyle {\vec {a}}=\mathrm {c} onst}
- v→(t)=v→(0)+a→t{\displaystyle {\vec {v}}(t)={\vec {v}}(0)+{\vec {a}}t}
- p1(t)=p1(0)+v1(0)t+a1t22{\displaystyle p_{1}(t)=p_{1}(0)+v_{1}(0)t+{\frac {a_{1}t^{2}}{2}}}
- p2(t)=p2(0)+v2(0)t+a2t22{\displaystyle p_{2}(t)=p_{2}(0)+v_{2}(0)t+{\frac {a_{2}t^{2}}{2}}}
- …{\displaystyle \dots }
- pn(t)=pn(0)+vn(0)t+ant22{\displaystyle p_{n}(t)=p_{n}(0)+v_{n}(0)t+{\frac {a_{n}t^{2}}{2}}}
- s=∫t1t2∣v→(t)∣dt{\displaystyle s=\int \limits _{t_{1}}^{t_{2}}\mid {\vec {v}}(t)\mid dt} ,
где s{\displaystyle s} — длина пути траектории за промежуток времени от t2{\displaystyle t_{2}} до t1{\displaystyle t_{1}} , v1,v2,…,vn{\displaystyle v_{1},v_{2},\dots ,v_{n}} — проекции v→{\displaystyle {\vec {v}}} на соответствующие оси координат, a1,a2,…,an{\displaystyle a_{1},a_{2},\dots ,a_{n}} — проекции a→{\displaystyle {\vec {a}}} на соответствующие оси координат.
- Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.
- a→⊥v→{\displaystyle {\vec {a}}\perp {\vec {v}}}
- ∣a→∣=∣v→∣2R{\displaystyle \mid {\vec {a}}\mid ={\frac {{\mid {\vec {v}}\mid }^{2}}{R}}}
- s=∣v→∣(t1−t2){\displaystyle s=\mid {\vec {v}}\mid (t_{1}-t_{2})} ,
где R{\displaystyle R} — радиус окружности, по которой движется тело.
Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:
- y=Rsin(∣v→∣Rt+arcsin(y(0)R)){\displaystyle y=R\sin {\Bigg (}{\frac {\mid {\vec {v}}\mid }{R}}t+\arcsin {\Big (}{\frac {y(0)}{R}}{\Big )}{\Bigg )}}
- x=Rcos(∣v→∣Rt+arccos(x(0)R)){\displaystyle x=R\cos {\Bigg (}{\frac {\mid {\vec {v}}\mid }{R}}t+\arccos {\Big (}{\frac {x(0)}{R}}{\Big )}{\Bigg )}}
- z=0{\displaystyle z=0}
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.
- a→=const{\displaystyle {\vec {a}}=\mathrm {c} onst}
- v→(t)=v→(0)+a→t{\displaystyle {\vec {v}}(t)={\vec {v}}(0)+{\vec {a}}t}
- s=∫t1t2∣v→(t)∣dt{\displaystyle s=\int \limits _{t_{1}}^{t_{2}}\mid {\vec {v}}(t)\mid dt}
Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:
- y(t)=y(0)+vy(0)t+∣a→∣t22{\displaystyle y(t)=y(0)+v_{y}(0)t+{\frac {\mid {\vec {a}}\mid t^{2}}{2}}}
- x(t)=x(0)+vx(0)t{\displaystyle x(t)=x(0)+v_{x}(0)t}
- z=0{\displaystyle z=0} ,
где vy{\displaystyle v_{y}} и vx{\displaystyle v_{x}} — проекции v→{\displaystyle {\vec {v}}} на соответствующие оси.
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.
- В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:
- s=∫t1t2∣v→(t)∣dt{\displaystyle s=\int \limits _{t_{1}}^{t_{2}}\mid {\vec {v}}(t)\mid dt}
Кинематика твёрдого тела
Кинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).
Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).
Связь скорости двух точек твердого тела выражается через формулу Эйлера:
- v→B=v→A+ω→×AB→{\displaystyle {\vec {v}}_{B}={\vec {v}}_{A}+{\vec {\omega }}\times {\vec {AB}}} ,
где ω→{\displaystyle {\vec {\omega }}} — вектор угловой скорости тела.
Кинематика деформируемого тела, Кинематика жидкости
Основные статьи: Кинематика деформируемого тела, Кинематика жидкости
Кинематика деформируемого тела и кинематика жидкости относятся к кинематике непрерывной среды.
Кинематика газа
Основная статья: Кинематика газа
Кинематика газа изучает деление газа на скопления при движении и описывает движение этих скоплений. В рамках кинематики газа описываются не только основные параметры движения, но и типы движения газа.
ru-wiki.org



