Контрольная кинематика материальной точки – Контрольная работа по теме «Кинематика материальной точки» – ВВЕДЕНИЕ. ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ – Поурочные разработки по физике к учебнику Г. Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского – Физика – Поурочные планы к учебникам Г. Я. Мякишева, С. В. Громова и В. Л. Касьянова 10 класс – разработки уроков – авторские уроки
- Комментариев к записи Контрольная кинематика материальной точки – Контрольная работа по теме «Кинематика материальной точки» – ВВЕДЕНИЕ. ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ – Поурочные разработки по физике к учебнику Г. Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского – Физика – Поурочные планы к учебникам Г. Я. Мякишева, С. В. Громова и В. Л. Касьянова 10 класс – разработки уроков – авторские уроки нет
- Советы абитуриенту
Контрольная работа по теме «Кинематика материальной точки» (1)
II. 4. За время торможения, равное 5 с, скорость автомобиля уменьшилась с 72 км/ч до 36 км/ч. Определите ускорение автомобиля при торможении и длину тормозного пути.
6.По графику проекции скорости, изображенному на рисунке, определите ускорение, с которым двигалось тело, и перемещение, совершенное им за время
10 с.
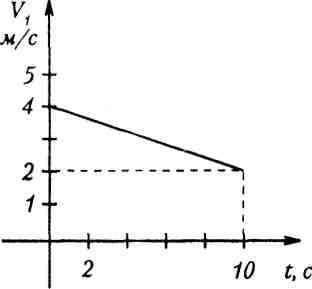
Рис.
III. 7. Два велосипедиста едут навстречу друг другу. Первый, имея скорость 27км/ч, поднимается в гору с ускорением 0,15 м/с2, а второй, имея скорость 9 км/ч, спускается с горы с ускорением 0,25 м/с2. Через какой промежуток времени они встретятся, если известно, что встреча произойдет на середине пути?
8. Автобус,
отходя от остановки, движется
равноускоренно и проходит за
9. Уравнения
движения двух тел имеют следующий
вид:
x1 = 10t + 0,4t2 и х2=-6t + 2t2.
Найдите место и время их встречи. Каким будет расстояние между ними через.5 с?
Контрольная работа по теме
«Динамика материальной точки»
1. Масса космонавта 60 кг. Какова его масса на Луне, где гравитационное притяжение тел в шесть раз слабее, чем на Зе
2. При отправлении поезда груз, подвешенный к потолку вагона, отклонился на восток. В каком направлении начал двигаться п
3. В ящик массой 15 кг, скользящий по полу, садится ребенок массой 30 кг. Как при этом изменится сила трения ящика о пол?
4. Два бруска, связанные невесомой нерастяжимой нить, тянут с силой F=2 Н вправо по столу. Массы брусков т1 = 0,2 кг и т2 = 0,3 кг. Коэффициент трения скольжения бруска по столу м = 0,2. С каким ускорением сдвинутся бруски (рис.)?
5. Шайба скользит с ледяной горки высотой Н =5 м, наклонной к горизонту под углом а» 45″. Коэффициент трения шайбы о лед м – 0,2. Горка плавно переходит в горизонтальную ледяную поверхность. Какой путь пройдет шайба до остановки по горизонтальной поверхности?
Контрольная работа по теме «Закон сохранения»
1. Шарик массой m , движущийся вправо со скоростью V0 в направлении стенки, абсолютно упруго отражается от нее. Каково изменение импульса шарика?
A. mV0(направлено
влево). Б. 2mV
B. mV0 (направлено вправо). Г. 2mV0 (направлено вправо). Д. О
2. По условию задачи 1 определите изменение кинетической энергии шарика.
А. т V02; Б. (т V02 )/2; В. 0; Г. (-т V02 )/2; Д. -т V02;
3. Два мяча, движущихся друг другу со скоростями 2 м/с и 4 м/с. Массы мячей равны 150 г и 50 г соответственно (рис.). V1=2 м/с, V2 = 4 м/с.
После столкновения меньший мяч стал двигаться вправо со скоростью 5 м/с. С какой скоростью и в каком направлении будет двигаться больший мяч?
А. 1 м/с, влево; Б. 1 м/с, вправо; В. 2 м/с, влево; Г. 2 м/с, вправо; Д. 3 м/с, влево
4. Шарик из пластилина массой m, висящий на нити, отклоняют от положения равновесия на высоту Н и отпускают. Он сталкивается с другим шариком массой 2m,висящим на нити равной длины (рис.).
На какую высоту поднимутся шарики после абсолютно неупругого столкновения?
А Н/16; Б. Н/9; В. Н/8; Г. Н/4; Д. Н/2
5. На столе высотой 1 м лежат рядом пять словарей, толщиной по 10 см и массой по 2 кг каждый. Какую работу требуется совершить, чтобы уложить их друг на друга?
А. 29,4 Дж; Б. 24,5 Дж; В. 19,6 Дж; Г. 9,8 Дж;
Д. Среди ответов А-Г нет правильного.
gigabaza.ru
Контрольная работа по теме «Кинематика материальной точки» – ВВЕДЕНИЕ. ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ – Поурочные разработки по физике к учебнику Г. Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского – Физика – Поурочные планы к учебникам Г. Я. Мякишева, С. В. Громова и В. Л. Касьянова 10 класс – разработки уроков – авторские уроки
РАЗДЕЛ II. Поурочные разработки по физике к учебнику Г. Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского
ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ
Урок 21. Контрольная работа по теме «Кинематика материальной точки»
Вариант 1
1. На рис. 48 представлен график зависимости ускорения тела от времени t. Какой из графиков зависимости скорости V от времени t, приведенных ниже на рисунке, может соответствовать этому графику?
A. I.
Б. II.
В. I и III.
Г. II и III.
Д. I, II и III.
2. По графику зависимости модуля скорости велосипедиста V от времени t определите модуль его ускорения а в течение первых трех секунд движения (рис. 49).
A. 3 м/с2.
Б. 4 м/с2.
B. 4 м/с2.
Г. 6 м/с2.
Д. 12 м/с2.
3. По графику зависимости скорости от времени (рис. задачи 2) определите среднюю скорость велосипедиста за время t = 6 с.
А. 2 м/с.
Б. 4 м/с.
В. 6 м/с.
Г. 7 м/с.
Д. 8 м/с.
4. Теннисный мяч, брошенный горизонтально с высоты 4,9 м, упал на землю на расстоянии 30 м от точки бросания. Какова начальная скорость мяча и время его полета?
A. 30 м/с, 1 с.
Б. 26 м/с, 1,5 с.
B. 20 м/с, 1 с.
Г. 15 м/с, 1 с.
Д. 10 м/с, 3 с.
5. Тело свободно падает с высоты 24,8 м. Какой путь оно проходит за 0,5 с до падения на землю?
А. 12,4 м.
Б. 10,2 м.
B. 9,8 м.
Г. 9 м.
Д. 8,2 м.
Вариант 2
1. Наездник, проходит первую половину дистанции со скоростью 30 км/ч, а вторую – со скоростью 20 км/ч. Какова средняя скорость наездника на дистанции?
A. 22 км/ч.
Б. 24 км/ч.
B. 25 км/ч.
Г. 26 км/ч.
Д. 28 км/ч.
2. На рисунке представлен график зависимости скорости тела V от времени t. Какой из графиков ниже на рисунке может соответствовать этой зависимости?
А. I.
Б. II.
В. I и III.
Г. II и III.
Д. I, II и III.
3. Какой из графиков зависимости ускорения тела а от времени t соответствует зависимости скорости от времени?
А. I.
Б. II.
В. III.
Г. I и II.
Д. I, II и III.
4. Какой путь проходит свободно падающая (без начальной скорости) капля за третью секунду от момента отрыва?
A. 24,5 м.
Б. 27,4 м.
B. 30,2 м.
Г. 32,6 м.
Д. 33,1 м.
5. Упругий шар падает вертикально на наклонную плоскость со скоростью 5 м/с. На каком расстоянии шар второй раз ударится об эту плоскость? Угол наклона плоскости к горизонту равен 30°.
A. 6,1 м.
Б. 5,9 м.
B. 5,5 м.
Г. 5,3 м.
Д. 5,1 м.
Ответы к контрольной работе
Номер вопроса и ответ | |||||
| 1 | 2 | 3 | 4 | 5 | |
Вариант 1 | Г | В | Г | А | В |
Вариант 2 | Б | В | Б | А | д |
Вариант урока 21. Контрольная работа по теме «Кинематика материальной точки»
Вариант 1
I. 1. Лыжник спускается с горы с начальной скоростью 6 м/с и ускорением 0,5 м/с2. Какова длина горы, если спуск с нее продолжался 12 с?
2. Автобус движется со скоростью 54 км/ч. На каком расстоянии от
compendium.su
Контрольная работа по теме Кинематика материальной точки. Базовый уровень
Контрольные работы. 10класс
Контрольная работа по теме «Кинематика материальной точки».
Базовый уровень
Вариант 1
А1. Траектория движущейся материальной точки за конечное время это
отрезок линии
часть плоскости
конечный набор точек
среди ответов 1,2,3 нет правильного
А2. Стул передвинули сначала на 6 м, а затем еще на 8 м. Чему равен модуль полного перемещения?
1) 2 м 2) 6 м 3) 10м 4) нельзя определить
А3. Пловец плывёт против течения реки. Скорость течения реки 0,5 м/с, скорость пловца относительно воды 1,5 м/с. Модуль скорости пловца относительно берега равен
1) 2 м/с 2) 1,5 м/с 3) 1м/с 4) 0,5 м/с
А4. Двигаясь прямолинейно, одно тело за каждую секунду проходит путь 5 м. Другое тело, двигаясь по прямой в одном направлении, за каждую секунду проходит путь 10м. Движения этих тел
равномерные
неравномерные
первого – неравномерное, второго – равномерное
нельзя сказать о характере движения тел
А5. На графике изображена зависимость координаты X тела, движущегося вдоль оси ОХ, от времени. Какова начальная координата тела?
1) 1 м 2) Ом
3) -1 м 4) – 2 м
А6. Какая функция v(t) описывает зависимость модуля скорости от времени при равномерном прямолинейном движении? (длина измеряется в метрах, время – в секундах)
1) v = 5t 2) v = 5/t 3) v = 5 4) v = -5
А7. Модуль скорости тела за некоторое время увеличился в 2 раза. Какое утверждение будет правильным?
ускорение тела возросло в 2 раза
ускорение уменьшилось в 2 раза
ускорение не изменилось
тело движется с ускорением
А8. Тело, двигаясь прямолинейно и равноускоренно, увеличило свою скорость от 2 до 8 м/с за 6с. Каково ускорение тела?
1) 1м/с2 2) 1,2м/с2 3) 2,0м/с2 4) 2,4м/с2
А9. При свободном падении тела его скорость (принять g=10м/с2)
за первую секунду увеличивается на 5м/с, за вторую – на 10м/с;
за первую секунду увеличивается на 10м/с, за вторую – на 20м/с;
за первую секунду увеличивается на 10м/с, за вторую – на 10м/с;
за первую секунду увеличивается на 10м/с, а за вторую – на 0м/с.
А10. Скорость обращения тела по окружности увеличилась в 2 раза. Центростремительное ускорение тела
1) увеличилось в 2 раза 2) увеличилось в 4 раза
3) уменьшилось в 2 раза 4) уменьшилось в 4 раза
Вариант 2
А1. Решаются две задачи:
а. рассчитывается маневр стыковки двух космических кораблей;
б. рассчитывается период обращения космических кораблей
вокруг Земли.
В каком случае космические корабли можно рассматривать как материальные точки?
только в первом случае
только во втором случае
в обоих случаях
ни в первом, ни во втором случае
А2. Автомобиль дважды объехал Москву по кольцевой дороге, длина которой 109 км. Путь, пройденный автомобилем, равен
1) 0 км 2) 109 км 3) 218 км 4) 436 км
А3. Когда говорят, что смена дня и ночи на Земле объясняется восходом и заходом Солнца, то имеют в виду систему отсчёта связанную
1) с Солнцем 2) с Землёй
3) с центром галактики 4) с любым телом
А4. При измерении характеристик прямолинейных движений двух материальных точек зафиксированы значения координаты первой точки и скорости второй точки в моменты времени, указанные соответственно в таблицах 1 и 2:
Что можно сказать о характере этих движений, предполагая, что он не изменялся в промежутках времени между моментами измерений?
1)оба равномерные
2)первое – неравномерное, второе – равномерное
3)первое – равномерное, второе неравномерное
4)оба неравномерные
А5. По графику зависимости пройденного пути от времени определите скорость
велосипедиста в момент времени t = 2 с.
1) 2 м/с 2) 3 м/с
3) 6 м/с 4) 18 м/с
А6. На рисунке представлены графики зависимости пройденного в одном направлении пути от времени для трех тел. Какое из тел двигалось с большей скоростью?
1) 1 2) 2 3) 3 4) скорости всех тел одинаковы
А7. Скорость тела, движущегося прямолинейно и равноускоренно, изменилась при перемещении из точки 1 в точку 2 так, как показано на рисунке. Какое направление имеет вектор ускорения на этом участке?
4) направление может быть любым
А8. По графику зависимости модуля скорости от времени, представленному на рисунке, определите ускорение прямолинейно движущегося тела в момент времени t=2с.
1) 2 м/с2 2) 3 м/с2 3) 9 м/с2 4) 27м/с2
А9. В трубке, из которой откачан воздух, с одной и той же высоты одновременно сбрасываются дробинка, пробка и птичье перо. Какое из тел быстрее достигнет дна трубки?
1) дробинка 2) пробка 3) птичье перо 4) все три тела одновременно.
А10. Автомобиль на повороте движется по круговой траектории радиусом 50м с постоянной по модулю скоростью 10 м/с. Каково ускорение автомобиля?
1) 1 м/с2 2) 2 м/с2 3) 5 м/с2 4) 0 м/с2
Ответы.
| Номер задания | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 |
| Вариант1 | 3 | 4 | 3 | 1 | 3 | 3 | 4 | 1 | 3 | 2 |
| Вариант2 | 2 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 4 | 2 |
Профильный уровень
Вариант 1
А1. Тело, брошенное вертикально вверх, достигло наибольшей высоты 10 м и упало на землю. Модуль перемещения при этом равен
1) 20м 2) 10м 3) 5м 4) 0м
А2. Тело, брошенное вертикально вверх, достигло наибольшей высоты 5 м и упало на землю. Путь, пройденный телом равен
1) 2,5м 2) 10м 3) 5м 4) 0м
А3. Два автомобиля движутся по прямому шоссе: первый – со скоростью V , второй – со скоростью 4 V . Чему равна скорость первого автомобиля относительно второго?
1) 5V 2) 3V 3) -3V 4) -5V
А4. От самолета, летящего горизонтально со скоростью V , в точке А оторвался небольшой предмет. Какая линия является траекторией движения этого предмета в системе отсчета, связанной с самолетом, если пренебречь сопротивлением воздуха?
А5. Две материальные точки движутся по оси ОХ по законам:
х1 = 5 + 5t, х2 = 5 – 5t (х – в метрах, t – в секундах). Чему равно расстояние между ними через 2 с?
1) 5м 2) 10м 3) 15м 4) 20м
А6. Зависимость координаты X от времени при равноускоренном движении по оси ОХ, дается выражением: X(t)= -5 + 15t2 (X измеряется в метрах, время – в секундах). Модуль начальной скорости равен
1)0м/с 2) 5 м/с 3) 7,5 м/с 4) 15 м/с
А7. Две материальные точки движутся по окружностям радиусами R, = R и R2 = 2R с одинаковыми скоростями. Сравните их центростремительные ускорения.
1) а1= а2 2)a1=2a2 3)a 1 =a 2 /2 4)a1=4a2
Часть 2.
В1. На графике представлена зависимость скорости движения от времени. Чему равна средняя скорость движения за первые пять секунд?
В2. Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, достиг максимальной высоты 4,05м. Сколько времени прошло от броска до того момента, когда его скорость стала направлена горизонтально?
Часть 3.
С1. Координаты движущегося тела изменяются по закону X=3t+2, Y=-3+7t2. Найдите скорость тела через 0,5с после начала движения.
Вариант 2
А1. Мяч, брошенный вертикально вниз с высоты 3 м, отскочил от пола вертикально и поднялся на высоту 3 м. Путь мяча равен
1) -6м 2) 0м 3) 3м 4) 6м
А2. Камень, брошенный из окна второго этажа с высоты 4 м, падает на землю на расстоянии 3 м от стены дома. Чему равен модуль перемещения камня?
1) 3м 2) 4м 3) 5м 4) 7м
А3. Плот равномерно плывет по реке со скоростью 6 км/ч. Человек движется поперек плота со скоростью 8 км/ч. Чему равна скорость человека в системе отсчета, связанной с берегом?
1) 2 км/ч 2) 7 км/ч 3) 10 км/ч 4) 14 км/ч
А4. Вертолет равномерно поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с корпусом вертолета?
1) окружность 2) прямая
3) точка 4) винтовая линия
А5. Материальная точка движется в плоскости равномерно и прямолинейно по закону: X = 4 + 3t, Y = 3 – 4t, где X,Y -координаты тела, м; t – время, с. Каково значение скорости тела?
1) 1м/с 2) 3 м/с 3) 5 м/с 4) 7 м/с
А6. Зависимость координаты X от времени при равноускоренном движении по оси ОХ, дается выражением: X(t)= -5t+ 15t2 (X измеряется в метрах, время – в секундах).
Модуль начальной скорости равен
1)0м/с 2) 5 м/с 3) 7,5 м/с 4) 15 м/с
А7. Период равномерного движения материальной точки по окружности равен 2 с. Через какое минимальное время направление скорости изменится на противоположное?
1) 0,5 с 2) 1 с 3) 1,5 с 4) 2 с
Часть 2.
В1. На графике представлена зависимость скорости V тела от времени t, описывающая движение тела вдоль оси ОХ. Определить модуль средней скорости движения за 2 секунды.
В2. Небольшой камень бросили с ровной горизонтальной поверхности земли под углом к горизонту. Какова дальность полета камня, если через 2с после броска его скорость была направлена горизонтально и равна 5м/с?
Часть 3.
С1. Тело, вышедшее из некоторой точки, двигалось с постоянным по модулю и направлению ускорением. Скорость его в конце четвертой секунды была 1,2м/с, в конце 7с тело остановилось. Найдите путь, пройденный телом.
Ответы.
| Номер задания | А1 | А2 | А3 | А4 | А5 | А6 | А7 | В1 | В2 | С1 |
| Вариант1 | 4 | 2 | 3 | 3 | 4 | 1 | 2 | 1,6 | 0,9 | 7,6 |
| Вариант2 | 4 | 3 | 3 | 1 | 3 | 2 | 2 | 0,75 | 20 | 4,2 |
Контрольная работа по теме «Законы Ньютона. Силы в механике».
Базовый уровень
Вариант 1
А1. Какое равенство правильно выражает закон Гука для упругой пружины?
1) F=kx 2) Fx=kx 3) Fx=-kx 4) Fx=k | x |
А2. С каким, из перечисленных ниже тел связаны системы отсчета, которые нельзя считать инерциальными?
А. Парашютист, опускающийся с установившейся скоростью.
Б. Камень, брошенный вертикально вверх.
В. Спутник, движущийся по орбите с постоянной по модулю скоростью.
1) А 2) Б 3) В 4) Б и В
А3. Вес имеет размерность
1) массы 2) ускорения 3) силы 4) скорости
А4. Тело вблизи поверхности Земли находится в состоянии невесомости, если оно движется с ускорением, равным ускорению свободного падения и направленным
1) вертикально вниз 2) вертикально вверх
3) горизонтально 4) под острым углом к горизонту.
А5. Как изменится сила трения скольжения при движении бруска по горизонтальной плоскости, если силу нормального давления увеличить в 2 раза?
1) не изменится 2) увеличиться в 2 раза
3) уменьшится в 2 раза 4) увеличиться в 4 раза.
А6. Какое соотношение между силой трения покоя, силой трения скольжения и силой трения качения справедливо?
1) Fтр.п=Fтр>Fтр.к 2) Fтр.п>Fтр>Fтр.к 3) Fтр.птр>Fтр.к 4) Fтр.п>Fтр=Fтр.к
А7. Парашютист пускается равномерно со скоростью 6м/с. Сила тяжести, действующая на него, равна 800Н. Какова масса парашютиста?
1) 0 2) 60 кг 3) 80 кг 4) 140 кг.
А8. Что является мерой взаимодействия тел?
1) Ускорение 2) Масса 3) Импульс. 4) Сила.
А9. Как связаны между собой изменение скорости и инертность тела?
А. Если тело более инертно, то изменение скорости больше.
Б. Если тело более инертно, то изменение скорости меньше.
В. Менее инертно то тело, которое быстрее изменяет свою скорость.
Г. Более инертно то тело, которое быстрее изменяет свою скорость.
1) А и В 2) Б и Г 3) А и Г 4) Б и В.
Вариант 2
А1. Какая из приведенных ниже формул выражает закон всемирного тяготения?
1) F=ma 2) F=μN 3) Fx=-kx 4) F=Gm1m2/R2
А2. При столкновении двух вагонов буферные пружины жесткостью 105 Н/м сжались на 10 см. Чему равна максимальная сила упругости, с которой пружины воздействовали на вагон?
1) 104Н 2) 2*104Н 3) 106Н4) 2*106Н
А3. Тело массой 100 г лежит на горизонтальной неподвижной поверхности. Вес тела приблизительно равен
1) 0Н 2) 1Н 3) 100Н 4) 1000 Н.
А4. Что такое инерция?
1) свойство тел сохранить скорость
2) явление сохранения скорости тела при отсутствии действия на него других тел
3) изменение скорости под действием других тел
4) движение без остановки.
А5. Какую размерность имеет коэффициент трения?
1) Н/кг 2) кг/Н 3) нет размерности 4) Н/с
А6. По какой формуле рассчитать силу трения скольжения?
1) F=μN 2) F=kv 3) F=mg 4) F=μmg
А7. Ученик подпрыгнул на некоторую высоту и опустился на землю. На каком участке траектории он испытал состояние невесомости?
1) при движении вверх 2) при движении вниз
3) только в момент достижения верхней точки 4) во время всего полета.
А8. Какими характеристиками определяется сила?
А. Модуль.
Б. Направление.
В. Точка приложения.
Г. Масса.
1) А, В, Г 2) Б и Г 3) Б, В, Г 4) А, Б, В.
А9. Какие из величин (скорость, сила, ускорение, перемещение) при механическом движении всегда совпадают по направлению?
1) сила и ускорение 2) сила и скорость
3) сила и перемещение 4) ускорение и перемещение.
Ответы.
| Номер задания | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 |
| Вариант1 | 3 | 4 | 3 | 1 | 2 | 2 | 3 | 4 | 4 |
| Вариант2 | 4 | 1 | 2 | 2 | 3 | 1 | 4 | 4 | 1 |
Профильный уровень
Вариант 1
А1. Какие силы в механике сохраняют свое значение при переходе из одной инерциальной системы в другую?
1) силы тяготения, трения, упругости.
2) только сила тяготения
3) только сила трения
4) только сила упругости.
А2. Как изменится максимальная сила трения покоя, если силу нормального давления бруска на поверхность увеличить в 2 раза?
1) Не изменится. 2) Уменьшится в 2 раза.
3) Увеличится в 2 раза. 4) Увеличится в 4 раза.
А3. Брусок массой 200г скользит по льду. Определите силу трения скольжения, действующую на брусок, если коэффициент трения скольжения бруска по льду равен 0,1.
1) 0,2Н. 2) 2Н. 3) 4Н. 4) 20Н
А4. Как и во сколько раз нужно изменить расстояние между телами, чтобы сила тяготения уменьшилась в 4 раза?
1) Увеличить в 2 раза. 2) Уменьшить в 2 раза.
3) Увеличить в 4 раза. 4) Уменьшить в 4 раза
А5. На полу лифта, начинающего движение вниз с ускорением g, лежит груз массой m.
Каков вес этого груза?
1) mg. 2) m (g+a). 3) m (g-a). 4) 0
А6. После выключения ракетных двигателей космический корабль движется вертикально вверх, достигает верхней точки траектории и затем опускается вниз. На каком участке траектории космонавт находится в состоянии невесомости? Сопротивлением воздуха пренебречь.
1) Только во время движения вверх. 2) Только во время движения вниз.
3) Во время всего полета с неработающим двигателем.
4) Во время всего полета с работающим двигателем.
topuch.ru
Контрольная работа №1 по теме “Кинематика материальной точки”. 10 класс
Вариант 1
1 Лыжник спускается с горы с начальной скоростью 6 м/с и ускорением 0,5 м/с2. Какова длина горы, если спуск с нее продолжался 12 с?
2. Автобус движется со скоростью 54 км/ч. На каком расстоянии от остановки водитель должен начать торможение, если для удобства пассажиров ускорение не должно превышать 1, 2 м/с2?
3. Координата движущегося тела с течением времени меняется по следующему закону: х = -1 + 3t – t2. Определите начальную координату тела, проекцию начальной скорости и проекцию ускорения. Укажите характер движения тела.
4. По графику проекции скорости, изображенному
на рисунке, определите ускорение, с которым двигалось тело,
и перемещение, совершенное им за время 8 с.5. Скорость некоторой точки на грампластинке 0,3 м/с, а центростремительное ускорение 0,9 м/с2. Найдите расстояние этой точки от оси вращения.
6. Шарик бросили горизонтально с высоты 20 м, при этом дальность полета составила 6 м. Найдите время полета и начальную скорость шарика.
Контрольная работа №1 по теме «Кинематика материальной точки» 10 класс
Вариант 2
При какой скорости самолет может приземлиться на посадочной полосе аэродрома длиной 800 м при торможении с ускорением 5 м/с2?
Через сколько секунд после отправления от станции скорость поезда метрополитена достигнет 72 км/ч, если ускорение при разгоне равно 1 м/с2?
Координата движущегося тела с течением времени меняется по следующему закону: х=10 -t- 2t
4.По графику проекции скорости, изображенному на рисунке, определите ускорение, с которым двигалось тело, и перемещение, совершенное им за время 10 с.
5. Самолет при скорости 360 км/ч делает петлю Нестерова радиусом 400 м. Определите центростремительное ускорение, с которым двигался самолет.
6. Мяч бросают горизонтально с высоты 20 м с начальной скоростью 25 м/с.
Найдите дальность полета.
infourok.ru
Тематический тест по теме “Кинематика материальной точки”
Тематический тест № 1. Кинематика материальной точки 1.
Вариант 1.
1) 280 м 2) 200 м 3) 40 м 4) 40 км | 2 | |||||||||||
1) 35 с, 10 м 2) 15 с, 20 м 3) 20 с, 15 м 4) 10 с, 35 м | 4 | |||||||||||
Автомобиль трогается с места с ускорением 10 м/с2. Чему будет равна его скорость через 5 с? | ||||||||||||
| ||||||||||||
| 7,5 м/ с 1,5 м/с2 v=7,5+1,5t sx=7,5t+ +0,75t2 Равно ускорен | |||||||||||
| 62,5 м | |||||||||||
| t = 10 c h = 500 м | |||||||||||
Тематический тест № 1. Кинематика материальной точки 1.
Вариант 2.
1) 2 км 2) 2,8 км 3) 4,8 км 4) 0,4 км | 1 | ||||||||||||
1) 35 с, 40 м 2) 20 с, 80 м 3) 25 с, 15 м 4) 40 с, 35 м | 2 | ||||||||||||
Ракета стартует с космодрома и в течении 10 с развивает скорость 1000 м/с. Определить ее ускорение. | 100 | ||||||||||||
| |||||||||||||
| 15 м/ с 1,25 м/с2 v=15- -1,25t sx=15t- -0,625t2 Равно замедл | ||||||||||||
| 75 м | ||||||||||||
| v= 50м/с h =125 м | ||||||||||||
Тематический тест № 1. Кинематика материальной точки 1.
Вариант 3.
1) 360 м 2) 280 м 3) 200 м 4) 190 м | 2 | ||||||||||||
1) 2 с, 14 м 2) 5 с, 12 м 3) 2 с, 25 м 4) 10 с, 30 м | 1 | ||||||||||||
Автомобиль трогается с места и в течение 10 с развивает скорость 36 км/ч. Определить его ускорение. | |||||||||||||
| |||||||||||||
| -1 м/ с -0,5 м/с2 v= -1- -0,5t sx= -t- -0,25t2 Равно замедл | ||||||||||||
| 50 м | ||||||||||||
| h = 125 м | ||||||||||||
Тематический тест № 1. Кинематика материальной точки 1.
Вариант 4.
1) 140 км 2) 100 км 3) 190 км 4) 20 км | 1 | ||||||||||||
1) 3,5 с, 10 м 2) 1,5 с, 12 м 3) 2 с, 1,5 м 4) 10 с, 15 м | 2 | ||||||||||||
Автобус, двигаясь со скоростью 36 км/ч тормозит у остановки в течении 5 с. Определить его ускорение. | – 2 | ||||||||||||
| |||||||||||||
| -3 м/ с 0,5 м/с2 v= -3+ +0,5t sx= -3t+ +0,25t2 Равно ускор | ||||||||||||
| 40 м | ||||||||||||
| t = 15 с h =1125 м | ||||||||||||
Тематический тест № 1. Кинематика материальной точки 1.
Вариант 5.
1) 20 км 2) 100 км 3) 190 км 4) 140 км | 4 | ||||||||||||
1) 35 с, 10 м 2) 20 с, 0 м 3) 20 с, 15 м 4) 10 с, 35 м | 2 | ||||||||||||
Мячик, подброшенный вверх достигает максимальной высоты через 5 с. Определите, с какой скоростью мячик был подброшен. | |||||||||||||
| |||||||||||||
| -6 м/ с 1,2 м/с2 v= -6+ +1,2t sx= -6t+ +0,6t2 Равно ускор | ||||||||||||
| 40 м | ||||||||||||
| v= 40м/с h =80 м | ||||||||||||
videouroki.net
Контрольная работа по физике “Кинематика материальной точки” (10 класс)
Методический комментарий: работа проводится в классе с преобладающим количеством сильных учеников. Последняя задача в каждом варианте предусматривает решение с использованием теоремы Виета. Ученики получают тексты работы на листах. Ученики слабые, неуверенные в себе, выполняют работу по другим, тоже дифференцированным, но более легким текстам.
Например:
Вариант 1
1. Шарик начинает скатываться с желоба. Какое расстояние он пройдет за 2 с?
2. С каким ускорением движется гоночный автомобиль, если его скорость за 6 с увеличилась со 144 до 216 км/ч?
3. Лыжник спускается с горы за 10 с. Начальная скорость его 18 км/ч, а ускорение 0,2 м/с2. Найти длину горы.
4. Тело движется по прямой из точки хо = 2 м с ускорением 0,5 м/с2 и начальной скоростью 5 м/с. Написать уравнение движения и формулу зависимости скорости от времени. Построить графики этих зависимостей. Определить время движения и путь, пройденный телом до полной остановки.
С целью подготовки к контрольной работе учащимся было предложено творческое задание: составить задачи по теме с использованием теоремы Виета. Вот некоторые их них.
Задача. По наклонной доске пустили катиться снизу вверх шарик с начальной скоростью vо. На расстоянии L от начала пути шарик побывал дважды: через t1 и через t2 после начала движения. Определите неизвестную величину по данным таблицы. Ускорение считать постоянным.
1
2
3
4
5
6
7
8
9
10
t1, с
2
1
1
3
1
2
2
2
t2, с
4
5
3
8
8
3
L
0,5 м
2 м
50 см
4 м
8 м
4 м
Vо, м/с
2
4
6
5
a, м/с2
0,1
0,5
1
0,5
3
0,2
Из графика зависимости v(t) найти модуль ускорения а велосипедиста в течение первых 3-х секунд движения
t, с
V, м/с
0 3 4 6 t.c
2. Теннисный мяч, брошенный горизонтально с высоты 4,9 м, упал на землю на расстоянии 30 м от точки бросания. Какова начальная скорость мяча и время его полета?
3. Тело брошено вертикально вверх с высоты 20 м с начальной скоростью 3 м/с. На какой высоте окажется тело через 2 с после начала движения?
4. Тело брошено под углом 600 к горизонту с начальной скоростью 15м/с. Найти максимальную высоту подъема, дальность полета и время полета.
12
4. Тело брошено под углом 600 к горизонту с начальной скоростью 15м/с. Найти максимальную высоту подъема, дальность полета и время полета.
5. По наклонной плоскости пустили катиться снизу вверх шарик с начальной скоростью 0,6 м/с и ускорением 0,3 м/с2. На расстоянии L от начала пути шарик побывал дважды: через t1 и t2 после начала движения. Найти t2 и L, t1 = 1c.
1 Движение 2-х мотоциклистов заданы уравнениями x1=15+t2 и x2=8t. Описать характер движения каждого. Найти время и место встречи.
2. Из окна выбросили мяч в горизонтальном направлении со скоростью 12 м/с. Он упал на землю через 2 с. С какой высоты был выброшен мяч и на каком расстоянии от здания он упал?
3. Камень брошен под углом 300 к горизонту со скоростью 10 м/с. Через какое время камень будет на высоте 1 м?
4. Тело упало с высоты 45 м. Определить время падения.
5. Тело пущено снизу вверх по наклонной плоскости с начальной скоростью 2 м/с и ускорением 0,6 м/с2. На расстоянии L от начала пути оно побывало дважды: спустя t1 и t2 после начала движения. t2 = 4 с. Найти t1 и L.
Скорость движения тела задана уравнением v =8 – 2t. Записать уравнение для перемещения.
Из пружинного пистолета выстрелили вертикально вверх шариком, который поднялся на высоту 4,9 м. С какой скоростью вылетел шарик из пистолета?
Из винтовки, находящейся на высоте 4 м над поверхностью земли, в горизонтальном направлении был произведен выстрел. Определите дальность и время полета пули, если ее горизонтальная скорость при выстреле 1000 м/с.
Тело, брошенное под углом 600 к горизонту, достигло максимальной высоты полета. Найти начальную скорость, дальность и время полета тела. Максимальная высота полета равна 40 м.
Шарик, пущенный катиться по наклонной плоскости, побывал на расстоянии 10 см от начала пути дважды: спустя 0,1 с и 2 с от начала движения. Считая ускорение постоянным, найти это ускорение и начальную скорость v0.
1. По графику, изображенному на рисунке, записать уравнение зависимости скорости и координаты от времени.
V, м/с
1
2
2222220 1 2 3 t, с
22
2. На какую максимальную высоту поднимается тело, брошенное вертикально вверх со скоростью 40 м/с?
3. Мяч был брошен под углом 300 к горизонту с начальной скоростью 20 м/с. Найти максимальную высоту и дальность полета.
4. Тело свободно падает с высоты 80 м. Найти его перемещение за последнюю секунду падения.
5. По наклонной плоскости снизу вверх пустили катиться шарик. На расстоянии 4 м от начала пути шарик побывал дважды: через t1 и t2 от начала движения. Ускорение постоянно и равно 0,2 м/с2. Найти начальную скорость v0 и t2, t1 = 2 с.
infourok.ru
Контрольные работы. 9 класс Контрольная работа по теме «Кинематика материальной точки». Вариант 1
А1. Линию, вдоль которой движется тело, называют
А. Пройденным путем Б. Перемещением В. Траекторией.
А2. Буксирный катер, двигаясь равномерно, за 3ч. прошёл путь 54км. Скорость катера равна …
А. 18м/с Б. 5м/с В. 15м/с
А3. Используя график зависимости скорости движения тела от времени, определите путь, пройденный телом за 3с.
А. 12м Б. 15м В. 18м.
А4. По графику координаты определите положение первого тела в момент t=5с.
А. 5м Б. 0 м В. 15м
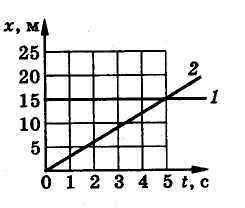А5. Решают две задачи:
А) рассчитывают выталкивающую силу, действующую на спортсмена,
плывущего дистанцию 400м,
Б) рассчитывают скорость спортсмена, бегущего дистанцию 400м.
При решении какой задачи спортсмена можно принять за материальную точку?
А. И А, и Б. Б. А. В. Б.
А6. Какой из графиков соответствует равноускоренному движению тела, при котором вектор ускорения направлен противоположно вектору скорости?
А. 1 Б. 2 В. 3
А7. Мяч, упав с высоты 2м и отскочив от Земли, был пойман на высоте 1м. В обоих направлениях мяч двигался вдоль вертикальной прямой. Определите путь мяча за всё время движения.
А. 3м Б. 1м В. 0м
Часть 2.
В1. Три человека соревновались в беге. Первый бежал 20мин. со скоростью 12км/ч, второй пробежал 5км за полчаса, третий пробежал 6км со скоростью 11км/ч. Кто бежал быстрее всех?
В2. С каким ускорением движется гоночный автомобиль, если его скорость за 5с увеличивается от 144 до 216км/ч?
Часть 3.
С1. Рассчитайте длину взлетной полосы, если скорость самолета при взлете 300км/ч, а время разгона равно 40с.
Вариант 2
А1. Расстояние, пройденное телом в течение некоторого промежутка времени, называют…
А. Траекторией движения Б. Пройденным путем В. Перемещением.
А2. Велосипедист, двигаясь равномерно, за 1,5ч проехал 27км. Скорость велосипедиста равна…
А. 18м/с Б. 5м/с В. 15м/с
А3. Используя график зависимости скорости движения тела от времени, определите путь, пройденный телом за 4с.
А. 12м Б. 24м В. 18м.
А4. По графику координаты определите положение второго тела в момент времени t=5с.
А. 15м Б. 5м В. 0 м.
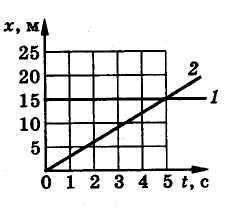А5. Решают две задачи:
А) рассчитывают время движения поезда между двумя станциями,
Б) рассчитывают время движения поезда вдоль железнодорожной
платформы.
При решении какой задачи поезд можно принять за материальную точку?
А. И А, и Б Б. А В. Б
А6. Какой из графиков соответствует равноускоренному движению тела, при котором вектор ускорения совпадает по направлению с вектором скорости?
А. 1 Б. 2 В. 3
А7. Мяч, упав с высоты 2м и отскочив от Земли, был пойман на высоте 1м. В обоих направлениях мяч двигался вдоль вертикальной прямой. Определите перемещение мяча за всё время движения.
А. 3м Б. 1м В. 0м
studfiles.net
