01.05.201902.02.2019

Квантовая механика основные формулы – Основные формулы по физике – КВАНТОВАЯ ФИЗИКА

• by alexxlab
• Комментариев к записи Квантовая механика основные формулы – Основные формулы по физике – КВАНТОВАЯ ФИЗИКА нет
• Советы абитуриенту

Формулы квантовой механики

Определение 1

Квантовая механика представляет собой раздел теоретической физики, основной задачей которого является описание физических явлений, где действие сопоставимо по величине с постоянной Планка. Законы квантовой и классической механики существенно отличаются.

Основные формулы квантовой механики приводятся в уравнении Шредингера, принципе неопределенности Гейзенберга и квантовой гипотезе Планка.

Уравнение Шредингера

Решение уравнения Шредингера представляет основную задачу квантовой механики.

Пусть $\psi (\vec r)$ представляет амплитуду вероятности нахождения в точке М частицы. Благодаря стационарному уравнению Шредингера, мы можем определить, что функция $\psi (\vec r)$ удовлетворяет следующему уравнению:

$-\frac {\bar h^2 2m} {\nabla^2} \psi+U( \vec r ) \psi=E \psi$

Где $\nabla^2$ это оператор Лапласа, а $U=U(\vec r)$ представляет потенциальную энергию частицы как функции от $\vec r$.

Получение точного решения стационарного уравнения Шредингера становится возможным только для нескольких систем (сравнительно простых). Среди таких выделяют:

• квантовый гармонический осциллятор;
• атом водорода.

В отношении большинства реальных систем с целью получения решений могут использоваться разные приближенные методы, подобные теории возмущений.

Принцип неопределенности Гейзенберга

Соотношение неопределенности возникает между абсолютно любыми квантовыми наблюдаемыми, которые определяются не коммутирующими операторами. Неопределенность между координатой и импульсом возникает следующим образом:

Пусть $\Delta x$ будет среднеквадратическим отклонением координаты частицы $M$, которая движется вдоль оси $x$, а $\Delta p$ – среднеквадратическим отклонением ее импульса.

Величины $\Delta x$ и $\Delta p$ будет связывать следующее неравенство:

$\Delta x \Delta p \geqslant \frac {\bar h}{2}$, где $h$ постоянная Планка

$\bar{h}=\frac{h}{2\pi}$

Исходя из соотношения неопределенностей, становится невозможным абсолютно точное определение одновременно координаты и импульса частицы. Так, при повышении точности измерения координаты, будет уменьшаться максимальная точность измерения импульса и наоборот. Параметры, для которых справедливо данное утверждение, называют в физике канонически сопряженными.

Это центрирование на измерении, автором которого считается Н. Бор. Соотношение неопределенности теоретически выводится из постулатов Борна и Шредингера. Оно имеет отношение не к самому измерению, а к состоянию объекта, утверждая, что для любого возможного состояния будут выполняться соответствующие соотношения неопределенности (в том числе и для измерений)

Таким образом, в состояниях, где неопределенность координаты будет меньше, больше станет неопределенность импульса.

Существует также неопределенность между временем и энергией. Пусть $\Delta E$ – это среднеквадратическое отклонение при измерениях энергии определенного состояния квант-системы. $\Delta t$ при этом характеризует время жизни такого состояния. Тогда будет выполняться следующее неравенство:

$\Delta E\Delta t \geqslant \frac {\bar h}{2}$

У состояния, продолжаемого короткое время, не может быть хорошо определенная энергия. В то же время, несмотря на определенную схожесть этих двух соотношений неопределенности, их природа будет совершенно различной.

Квантовая гипотеза Планка

Гипотеза Планка представляет идею М. Планка, озвученную в 190 г., об испускании и поглощении энергии. Так, согласно гипотезе физика, при тепловом излучении энергия будет как поглощаться, так и испускаться не непрерывным образом, а в виде отдельных порций (квантов).

Каждая такая квант-порция будет иметь энергию $E$, пропорциональную частоте $v$ излучения:

$E=hv=\bar{h}\omega$

Где $h$ или $\bar{h}$ определяются формулой:

$\bar{h}=\frac{h}{2\pi}$

$h$ или $\bar{h}$ это коэффициент пропорциональности, который впоследствии был назван постоянной Планка.

На основании данной гипотезы Планк предложил теоретический вывод о соотношении температуры тела и испускаемым данным телом излучения.

Постоянная Планка представляет чрезвычайно малую величину в сравнении с действием объектов при макроскопическом движении, а квант-эффекты зачастую проявляются в микро-масштабах.

В случае, если физическое действие системы будет намного больше, чем постоянная Планка, квантовая механика органически переходит в классическую. Квантовая механика, в свою очередь, представляет нерелятивистское приближение малых энергий (сравнительно с энергией покоя массивных частиц системы) в квантовой теории поля.

Позднее данная гипотеза была подтверждена экспериментальным образом. Ее выдвижение считается моментом зарождения квантовой механики.

spravochnick.ru

16. Понятие о квантовой механике.

Доминирующей современной теорией поведения электронов и других микрообъектов, обладающих очень малой массой, является квантовая механика. Квантовая волновая механика изучает законы движения микрообъектов в силовых полях. Главной особенностью квантовой механики является ее вероятностный статистический характер: она дает возможность находить вероятность того или иного значения некоторой физической величины. В отличии от классической физики в квантовой механике все объекты микромира (электроны, атомы, молекулы и др.) выступают как носители и корпускулярных и волновых свойств (волново-корпускулярный дуализм), которые не исключают, а дополняют друг друга. Не представляет труда обосновать объективность волново-корпускулярного дуализма для световых квантов – фотонов. Так, фотоэффект Столетова (это испускание электронов веществом под действием света ) и эффект Комптона (явление изменения длины волны электромагнитного излучения вследствие рассеивания его электронами) доказывают корпускулярную природу видимого и рентгеновского излучений, а интерференция (изменение в характере звуковых, тепловых, световых и электрических явлений, объясняемое колебательным движением: в первом случае частиц звучащего тела, в остальных трех — колебанием) и дифракция (волн, явления, наблюдаемые при прохождении волн мимо края препятствия, связанные с отклонением волн от прямолинейного распространения при взаимодействии с препятствием) – волновую природу света.

В 20-е годы прошлого столетия активно развивалась квантовая механика (Шрёдингер, Гейзенберг, Эйнштейн и др.). Квантовая механика исследует поведение микрочастиц ( электронов, фотонов и др.) в микрополях атомов, молекул и кристаллов, т.е. каких-либо комплексов. Ее выводы носят статистический характер. Микрочастицы движутся по своим законам, их природа носит двойной характер – волново-корпускулярный дуализм («корпускула» – частица и одновременно имеет ЭМ волны). Шрёдингер вывел волновое уравнение, которое описывает поведение электрона в атоме. Из решения уравнения Шрёдингера вытекает понятие «орбиталь» (собственная функция), т.е. квантовая механика отвергает существование в атоме стационарных орбит. Орбиталь – отражает вероятность нахождения электрона в какой-то части атомного пространства. Из уравнения вытекают и некоторые числа, носящие названия квантовых, которые характеризуются определенными значениями и задают форму орбитали, ее энергию ориентацию в пространстве.

Квантовая механика адекватно описывает основные св-ва и поведение атомов, ионов, молекул, конденсированных сред, и др. систем с электронно-ядерным строением. Квантовая механика также способна описывать поведение электронов, фотонов, а также др.элементарных частиц.

Квантовые числа.

n– главное квантовое число (=1,2,3…+∞) – за полный запас электронов в атоме.

е – (0 до n=-1) отвечает за форму атомной орбитали (е 0 1 2 3

spdf

s²p⁶d¹⁰f¹⁴

m_e– магнитное квантовое число (-l; 0; +l)- характеризует ориентацию орбитали в пространстве(нарисовать из тетради)

m_s– спиновое квантовое число – отвечает за вращение электронов вокруг своей оси (-1/2; +1/2)

s²p⁶d⁹f¹⁴

Квантовая формула отражает характер распределения электронов по орбиталям и квантовым слоям.

Закономерности распределения.

1. Принцип Паули. В атоме не может быть двух электронов с одинаковыми значениями всех четырех квантовых чисел.

2. Принцип наименьшей энергии.В атоме электроны в первую очередь занимают орбитали с наименьшей энергией (т.е. располагаются ближе к ядру).

3. Правило Гунда.На вырожденных орбиталях электроны располагаются так, чтобы суммарное спиновое квантовое вещество было максимальным. (вырожденная – орбиталь, характеризующаяся одной и той же энергией).

Из написания квантовых формул бросается в глаза, что систематически повторяются строение наружного электронного слоя у атомов элементов разной химической природы (т.е. разных элементов). В этом состоит главный физический смысл периодического закона. Физическое свойство периодического закона состоит в периодическом повторении строения наружных атомных орбиталей элементов с ростом числа электронных слоев (главного квантового числа)

Ква́нтовое число́ в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы.

Некоторые квантовые числа связаны с движением в пространстве и характеризуют пространственное распределение волновой функции частицы. Это, например, радиальное (главное) ( ), орбитальное ( ) и магнитное ( ) квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента и его проекция на заданную ось, соответственно.

Некоторые другие квантовые числа никак не связаны с перемещением в обычном пространстве, а отражают «внутреннее» состояние частицы. К таким квантовым числам относится спин и его проекция.

Главное (радиальное) квантовое число — целое число, обозначающее номер энергетического уровня. Характеризует энергию электронов, занимающих данный энергетический уровень. Является первым в ряду квантовых чисел, который включает в себя главное, орбитальное и магнитное квантовые числа, а также спин. Эти четыре квантовых числа определяют уникальное состояние электрона в атоме (его волновую функцию). Главное квантовое число обозначается как . При увеличении главного квантового числа возрастают радиус орбиты и энергия электрона.Главное квантовое число равно номеру периода элемента.

Наибольшее число электронов на энергетическом уровне с учетом спина электрона определяется по формуле N = 2n2.

Орбитальное квантовое число — в квантовой физике квантовое число ℓ, определяющее форму распределения амплитуды волновой функции электрона в атоме, то есть форму электронного облака. Определяет подуровень энергетического уровня, задаваемого главным (радиальным) квантовым числом n и может принимать значения

l = 0; 1; 2; …; n-1.

Магни́тное ква́нтовое число́ — параметр, который вводится при решении уравнения Шрёдингера для электрона в водородоподобном атоме (и вообще для любого движения заряженной частицы). Магнитное квантовое число (m) характеризует ориентацию в пространстве орбитального момента количества движения электрона или пространственное расположение атомной орбитали. магнитное квантовое число, в частности, определяет проекцию орбитального магнитного момента водородоподобного атома на направление магнитного поля и служит причиной расщепления спектральных линий атома в магнитном поле (см. Эффект Зеемана).

Спиновое квантовое число s принимает два значения: +1/2; -1/2. Характеризует собственное вращательное движение электрона (по часовой и против часовой стрелки)

studfiles.net

Квантовая механика • Джеймс Трефил, энциклопедия «Двести законов мироздания»

На субатомном уровне частицы описываются волновыми функциями.

Слово «квант» происходит от латинского quantum («сколько, как много») и английского quantum («количество, порция, квант»). «Механикой» издавна принято называть науку о движении материи. Соответственно, термин «квантовая механика» означает науку о движении материи порциями (или, выражаясь современным научным языком науку о движении квантующейся материи). Термин «квант» ввел в обиход немецкий физик Макс Планк (см. Постоянная Планка) для описания взаимодействия света с атомами.

Квантовая механика часто противоречит нашим понятиям о здравом смысле. А всё потому, что здравый смысл подсказывает нам вещи, которые берутся из повседневного опыта, а в своем повседневном опыте нам приходится иметь дело только с крупными объектами и явлениями макромира, а на атомарном и субатомном уровне материальные частицы ведут себя совсем иначе. Принцип неопределенности Гейзенберга как раз и очерчивает смысл этих различий. В макромире мы можем достоверно и однозначно определить местонахождение (пространственные координаты) любого объекта (например, этой книги). Не важно, используем ли мы линейку, радар, сонар, фотометрию или любой другой метод измерения, результаты замеров будут объективными и не зависящими от положения книги (конечно, при условии вашей аккуратности в процессе замера). То есть некоторая неопределенность и неточность возможны — но лишь в силу ограниченных возможностей измерительных приборов и погрешностей наблюдения. Чтобы получить более точные и достоверные результаты, нам достаточно взять более точный измерительный прибор и постараться воспользоваться им без ошибок.

Теперь если вместо координат книги нам нужно измерить координаты микрочастицы, например электрона, то мы уже не можем пренебречь взаимодействиями между измерительным прибором и объектом измерения. Сила воздействия линейки или другого измерительного прибора на книгу пренебрежимо мала и не сказывается на результатах измерений, но чтобы измерить пространственные координаты электрона, нам нужно запустить в его направлении фотон, другой электрон или другую элементарную частицу сопоставимых с измеряемым электроном энергий и замерить ее отклонение. Но при этом сам электрон, являющийся объектом измерения, в результате взаимодействия с этой частицей изменит свое положение в пространстве. Таким образом, сам акт замера приводит к изменению положения измеряемого объекта, и неточность измерения обусловливается самим фактом проведения измерения, а не степенью точности используемого измерительного прибора. Вот с какой ситуацией мы вынуждены мириться в микромире. Измерение невозможно без взаимодействия, а взаимодействие — без воздействия на измеряемый объект и, как следствие, искажения результатов измерения.

О результатах этого взаимодействия можно утверждать лишь одно:

неопределенность пространственных координат × неопределенность скорости частицы > h/m,

или, говоря математическим языком:

Δx × Δv > h/m

где Δx и Δv — неопределенность пространственного положения и скорости частицы соответственно, h — постоянная Планка, а m — масса частицы.

Соответственно, неопределенность возникает при определении пространственных координат не только электрона, но и любой субатомной частицы, да и не только координат, но и других свойств частиц — таких как скорость. Аналогичным образом определяется и погрешность измерения любой такой пары взаимно увязанных характеристик частиц (пример другой пары — энергия, излучаемая электроном, и отрезок времени, за который она испускается). То есть если нам, например, удалось с высокой точностью измерили пространственное положение электрона, значит мы в этот же момент времени имеем лишь самое смутное представление о его скорости, и наоборот. Естественно, при реальных измерениях до этих двух крайностей не доходит, и ситуация всегда находится где-то посередине. То есть если нам удалось, например, измерить положение электрона с точностью до 10^–6 м, значит мы одновременно можем измерить его скорость, в лучшем случае, с точностью до 650 м/с.

Из-за принципа неопределенности описание объектов квантового микромира носит иной характер, нежели привычное описание объектов ньютоновского макромира. Вместо пространственных координат и скорости, которыми мы привыкли описывать механическое движение, например шара по бильярдному столу, в квантовой механике объекты описываются так называемой волновой функцией. Гребень «волны» соответствует максимальной вероятности нахождения частицы в пространстве в момент измерения. Движение такой волны описывается уравнением Шрёдингера, которое и говорит нам о том, как изменяется со временем состояние квантовой системы.

Картина квантовых событий в микромире, рисуемая уравнением Шрёдингера, такова, что частицы уподобляются отдельным приливным волнам, распространяющимся по поверхности океана-пространства. Со временем гребень волны (соответствующий пику вероятности нахождения частицы, например электрона, в пространстве) перемещается в пространстве в соответствии с волновой функцией, являющейся решением этого дифференциального уравнения. Соответственно, то, что нам традиционно представляется частицей, на квантовом уровне проявляет ряд характеристик, свойственных волнам.

Согласование волновых и корпускулярных свойств объектов микромира (см. Соотношение де Бройля) стало возможным после того, как физики условились считать объекты квантового мира не частицами и не волнами, а чем-то промежуточным и обладающим как волновыми, так и корпускулярными свойствами; в ньютоновской механике аналогов таким объектам нет. Хотя и при таком решении парадоксов в квантовой механике всё равно хватает (см. Теорема Белла), лучшей модели для описания процессов, происходящих в микромире, никто до сих пор не предложил.

См. также:

elementy.ru

Уравнение Шредингера в квантовой механики

Принципы квантовой механики

Состояние частицы задается двумя величинами: координатами (радиус-вектором) и импульсом. В рамках квантовой механики ставить вопрос о точном местоположении, траектории частицы не корректно. Для квантовой частицы координаты и импульс могут быть неопределёнными. Поэтому ее состояние задается двумя вероятностными функциями:

   

Первая характеризует неопределённые координаты частицы, вторая — неопределённые импульсы. Вместо двух указанных функций W и V в квантовой механике вводится одна, комплексная функция, называемая волновой функцией. (Комплексная функция равносильна двум функциям, т.к. состоит из двух частей: действительной и мнимой.) Достоинством такого метода является в первую очередь то, что действительная и мнимая части волновой функции являются функциями не различных переменных (х и ), а переменных одного pода: либо только координат, либо только импульсов. Итак, состояние квантовой частицы можно характеризовать волновой функцией (комплексной), в двух представлениях — либо в координатном: , либо в импульсном: . Уравнение движения свободной частицы особенно просто выглядит в импульсном представлении, т.к. импульс свободной частицы сохраняется. Это означает на квантовом языке, что функция .не зависит от времени.

Уравнение Шредингера

Уравнение же связанной частицы, на которую действуют силы, удобнее получить в координатном представлении. Нужно сказать, что в квантовой механике, строго говоря, нельзя ввести понятие силы, как нельзя ввести понятие скорости. И это ясно, если вспомнить, что по определению сила есть производная от импульса частицы по времени. Импульс же квантовой частицы является неопределённым, и его невозможно продифференцировать по времени. Поэтому взаимодействие частиц в квантовой механике характеризуют не силой, а потенциальной энергией.

Движение связанной частицы массы m будет задаваться уравнением следующего вида:

   

где – оператор Лапласа, x.y.z. – координаты, — постоянная Планка, деленная на 2.

Это уравнение называется временным уравнением Шредингера.

Если не зависит от времени, то решение уравнения Шредингера можно представить как:

   

где E-полная энергия квантовой системы, а удовлетворяет стационарному уравнению Шредингера:

   

Уравнение Шредингера является основным уравнением движения частицы в квантовой механике. Оно не может быть выведено из других соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого подтверждается тем, что все следствия из него вытекающие, подтверждаются опытами.

Решение уравнения Шредингера

С математической точки зрения — это дифференциальное уравнение в частных производных. Уравнение в частных производных имеет множество решений. В каждой конкретной задаче из этого множества следует выбрать одно решение, отвечающее условиям задачи.

С физической точки зрения нужно отметить, что согласно уравнению Шредингера волновая функция изменяется детерминировано, то есть совершенно однозначно. В этом смысле квантовая механика напоминает классическую, в которой движение системы заранее предопределено начальными условиями. Однако сама волновая функция имеет вероятностный смысл. Можно сказать, в квантовой механике детерминировано изменяются вероятности, а не сами физические события. События же всегда случайны и совершаются непредсказуемо.

Наконец, необходимо отметить еще одну очень важную особенность уравнения Шредингера: оно линейно. Волновая функция и ее производные входят в него в первой степени и для волновых функций справедлив принцип суперпозиции. Он в квантовой механике играет очень важную роль, так как позволяет сложные движения раскладывать на более простые движения. Например, движение свободной частицы выражается отнюдь не только волнами де-Бройля. Возможны более сложные выражения для результирующих волновых функций той же свободной частицы. Вместе с тем согласно принципу суперпозиции любое сложное движение свободной частицы можно представить как сумму волн де-Бройля.

Уравнение Шредингера является математическим выражением корпускулярно-волнового дуализма микрочастиц. В предельном случае, когда длины волн де Бройля значительно меньше размеров рассматриваемого движения уравнение Шредингера позволяет описывать движение частиц по законам классической механики.

Тогда как с точки зрения математики уравнение Шредингера – это волновое уравнение, по структуре подобно уравнению колебания струны. Однако, решения уравнения Шредингера прямого физического смысла не имеют.

Физический смысл имеет модуль произведения ,

w — определяется как плотность вероятности нахождения частицы в точке пространства,

где -комплексно сопряженная функция с .

   

где W – вероятность нахождения частицы в объеме V.

Из вероятностного смысла волновой функции следует, что квантовая механика имеет статистический характер. С помощью волновой функции, которая является решением уравнения Шредингера нельзя точно описать траекторию движения квантовой частицы, можно лишь сказать какова вероятность обнаружить эту частицу в разных областях пространства.

Примеры решения задач

ru.solverbook.com

Основные положения квантовой механики — Мегаобучалка

Введение

1. Краткая историческая справка. К!Модели атома. Опыты Резерфорда. Резерфордовское рассеяние. Значение опытов Резерфорда. Ядерные и оболочечные свойства вещества. Сив.9. Шп1.23,26-28.

2. Основные термины атомной физики. Атом, молекула, ион. Нуклид. Изотопы. Моль, постоянная Авогадро, атомная единица массы, относительная атомная масса. Массовое число. Электронвольт. Масштабы расстояний, масс, энергий, частот в атомной и ядерной физике. Шкала электромагнитных волн. Вихм.Гл.1,2.

3. Классическая, релятивистская и квантовая физика. Основные полложения механики Ньютона.К! Формулы релятивистской механики частицы. Вихм.Гл.1,2.

Развитие квантовых представлений (ПФА1стр.1-5)

4. Квантовая гипотеза Планка.К! Формула Планка. ЛП.7-8. Сив.1п1-2. Шп1.89.

5. Фотоэффект. Кванты света. Энергия и импульс фотона. ЛП.7-8. Сив.1п3-5. Шп1.117. Эффект Комптона.К! Пр. Сив.2,3. Шп1.123-127.

6. Квантование электромагнитного излучения по Эренфесту и Дебаю. ЛП 7-8. Осцилляторы электромагнитного поля и фотоны.К! Вывод формулы Планка на основе представлений об осцилляторах электромагнитного поля. ПР. ПФА17.стр.262-267.

7. Постулаты Бора.К!Кратность вырождения уровня. Связь комбинационного принцип Ритца и условия частот Бора. ЛП.32-37,44-45. Шп1.90,103-105,111. Опыты Франка и Герца. ЛП.24-27. Шп1.91-93,97. Сив.11,14,16. Представление о ФЭС и СЭУ. Шп1.94,95.

8. Боровская модель круговых орбит для водородоподобного атома. Параметры круговых орбит. Уровни энергии водородоподобного атома. Спектральные серии атома водорода. Учет движения ядра в модели Бора. Оценки энергий связи и размеров орбит для внутренних электронов атомов и для экзотических атомных систем. К!ЛП.37-40.Сив.13.Шп1.103-104,105-109.

9. Нарушение резонанса между поглощением и испусканием света из-за явления «отдачи». Шп1.129.

10. Изотопический сдвиг уровней. Представление о разделении изотопов с помощью лазеров. ПФА17. стр.268-272.

11. Представление о модели эллиптических орбит Бора-Зоммерфельда. Шп1.113,115.

12. Гипотеза Де-Бройля. Опыты Дэвиссона и Джермера. Сив.17,18. Ш1.140,142. Представление об электронографии. Метод Томсона. Сив.17,18. Шп1.140,142.145. ЛП.46-53.

13. Связь длины волны и частоты для волн Де-Бройля. Плоская монохроматическая волна Де-Бройля. Волновое уравнение для волн Де-Бройля. Сив.17,18,19.1. Шп1.152.

14. Квантовая дифракция. Сосуществование корпускулярных и волновых свойств у микрообъектов.К! Вероятностная интерпретация волн Де-Бройля. Состояния с определенными и неопределенными значениями микрообъектов. Сив.19. Шп1.147. Фейнман т.3, Гл.37-38.

Основные положения квантовой механики

15. Ньютонова механика и нерелятивистская квантовая механика частицы. К!Волновая функция и ее вероятностная интерпретация. Нормировка волновой функции. Собственные состояния и собственные значения физических величин и способ их нахождения с помощью операторов. Оператор координаты. К!Оператор проекции импульса. Операторы кинетической, потенциальной и полной энергии. Операторы проекций момента импульса. Сив.30. Шп2. 6-8,13,15,16.

16. Собственные значения и собственные функции оператора проекции импульса и оператора проекции момента импульса. Сив.30, 31п1-3. Шп2.54.

17. Принцип суперпозиции в квантовой механике.Вероятностная интерпретация суперпозиционных коэффициентов. Анализ квантового состояния. К!Сив.30. Шп2.6-8,13-16.

18. Основные положения квантовой механики одной частицы. К!Сив.30. Шп2.6-8, 13-16.

19. Средние значения физических величин и отклонения от них. Соотношения неопределенностей Гейзенберга. Шп2.17,20, Сив.20,30.

20. Стационарные и нестационарные состояния. Нестационарное и стационарное уравнение Шредингера. Сив.21,30. Шп2.21. ПФА 6. стр.65-67.

21. Одномерные задачи квантовой механики. Сопоставление с одномерными задачами в классике.Решение одномерного уравнения Шредингера на участке с постоянным потенциалом. ПФА6.стр.68-69.

22. Задача о потенциальной ступеньке в квантовой механике. Поведение волновой функции в точках, где потенциальная энергия терпит разрыв К!Шп1.153. Шп2.47. Сив.28.1-8. Пр. ПФА6.стр.69-71.

23. Прямоугольные потенциальные ямы конечной и бесконечной глубины. К!Пр. Шп2.48. Сив.24.

24. Линейный гармонический осциллятор. Сив.23, Шп1.158,159. Потенциал, моделирующий взаимодействие атомов.К! ЛП.179.

25. Три квантовомеханические задачи с потенциальным барьером. Туннельный эффект. Нестационарные состояния электрона в потенциальной яме, разделенной барьером. К!Понятие о квазидискретных уровнях. К!Пр. Шп1.154.

26. Итоги решения набора одномерных квантовых задач. Связь характера спектра энергии с финитностью движения частицы.К!Шп1.42. Сив.22. ЛП.

27. Эффект Рамзауэра и его качественное объяснение с использованием результатов решения одномерных квантовых задач. ПФА7.стр.80-90.

28. Момент импульса в квантовой механике. Состояния с определенным значением квадрата модуля момента импульса и его проекции. Шп2.51,53-57, Сив.31п1,3,7.

29. Элементарные представления о магнитном моменте.К! Гиромагнитное отношение. Ларморова частота. Опыты Штерна и Герлаха. Сив.35,36. Шп2.69. ПФА18.стр.102-108.

30. Орбитальный и спиновый механический и магнитный моменты электрона. Магнетон Бора. Полный момент. Общая схема сложения механических моментов. Спектроскопические обозначения для моментов. Сложение магнитных моментов. Множитель Ланде. ПФА18.стр.102-108. Сив.32,35,41п 2. Шп2.72. Г.Н.21,22,26.

31. Классический и квантовый подходы в механике системы частиц.К! Тождественные частицы. Фермионы и бозоны. Стационарные состояния системы из двух частиц в потенциальной яме. Принцип Паули (общая формулировка и формулировка для электронов в атоме). Ш2.80-82. Сив.46п3-6.

32. Взаимодействие атома с электромагнитным полем. Спонтанные и вынужденные излучательные переходы. Коэффициенты Эйнштейна. Шп1.98,99,101. Шп2.64.

33. Интенсивность спектральных линий.К! Правила отбора. Шп2.64,65,107. Г.Н. 33. Сив.39. ПФА18.стр.119-122.

34. Время жизни возбужденных состояний. Естественная ширина уровней энергии и спектральных линий. К!Уширение спектральных линий из-за эффекта Доплера и столкновений между атомами. ПФА20.стр.187-193. Шп1.98.

megaobuchalka.ru

КВАНТОВАЯ МЕХАНИКА | Энциклопедия Кругосвет

Содержание статьи

КВАНТОВАЯ МЕХАНИКА, фундаментальная физическая теория динамического поведения всех элементарных форм вещества и излучения, а также их взаимодействий. Квантовая механика представляет собой теоретическую основу, на которой строится современная теория атомов, атомных ядер, молекул и физических тел, а также элементарных частиц, из которых все это состоит.

Квантовая механика была создана учеными, стремившимися понять, как устроен атом. Атомные процессы в течение многих лет изучали физики и особенно химики; при изложении данного вопроса мы будем, не вдаваясь в подробности теории, следовать историческому ходу развития предмета.

Зарождение теории.

Когда Э.Резерфорд и Н.Бор предложили в 1911 ядерную модель атома, это было подобно чуду. В самом деле, она была построена из того, что было известно уже более 200 лет. Это была, в сущности, коперниковская модель Солнечной системы, воспроизведенная в микроскопическом масштабе: в центре находится тяжелая масса, вскоре получившая название ядра, вокруг которой вращаются электроны, числом которых определяются химические свойства атома. Но мало того, за этой наглядной моделью стояла теория, которая позволила начать расчеты некоторых химических и физических свойств веществ, по крайней мере построенных из наименьших и наиболее простых атомов. Теория Бора – Резерфорда содержала ряд положений, которые здесь полезно напомнить, поскольку все они в том или ином виде сохранились и в современной теории.

Во-первых, важен вопрос о природе сил, связывающих атом. С 18 в. было известно, что электрически заряженные тела притягивают или отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними. Используя в качестве пробных тел альфа-частицы, возникающие в результате радиоактивных превращений, Резерфорд показал, что тот же самый закон электрического взаимодействия (закон Кулона) справедлив в масштабах, в миллион миллионов раз меньших тех, для которых он был первоначально экспериментально установлен.

Во-вторых, нужно было ответить на вопрос о том, как электроны движутся по орбитам под действием этих сил. Здесь вновь опыты Резерфорда, казалось бы, показывали (и Бор принял это в своей теории), что законы движения Ньютона, сформулированные в его Началах (Principia Mathematica, 1687), можно использовать для описания движения частиц в этих новых масштабах микромира.

В-третьих, вставал вопрос о стабильности. В ньютоновско-кулоновском атоме, как и в Солнечной системе, размеры орбит произвольны и зависят лишь от того, каким образом система была первоначально приведена в движение. Однако все атомы одного вещества одинаковы и к тому же стабильны, что совсем необъяснимо с точки зрения старых представлений. Бор высказал предположение, что атомные электроны следует рассматривать как движущиеся вокруг ядра лишь по определенным орбитам, которым отвечают определенные энергетические уровни, причем они должны испускать квант энергии в виде света, переходя с орбиты с более высокой энергией на орбиту с меньшей энергией. Такие «условия квантования» не вытекали ни из каких экспериментальных данных или теорий; они были приняты как постулаты.

На основе этих концептуальных элементов, дополненных только что развитыми в то время представлениями М.Планка и А.Эйнштейна о природе света, Бору удалось количественно объяснить весь спектр излучения атомов водорода в газоразрядной трубке и дать качественное объяснение всех основных закономерностей периодической системы элементов. К 1920 пришло время взяться за проблему спектра излучения более тяжелых атомов и вычислить интенсивность химических сил, связывающих атомы в соединениях.

Но здесь иллюзия успеха померкла. На протяжении ряда лет Бор и другие исследователи безуспешно пытались рассчитать спектр гелия – следующего за водородом простейшего атома с двумя электронами. Сначала вообще ничего не получалось; в конце концов несколько исследователей различными способами решили эту задачу, но ответ оказался неверным – он противоречил эксперименту. Затем выяснилось, что вообще невозможно построить сколько-нибудь приемлемую теорию химического взаимодействия. К началу 1920-х годов теория Бора исчерпала себя. Пришло время признать справедливость пророческого замечания, которое Бор еще в 1914 сделал в письме другу в присущем ему замысловатом стиле: «Я склонен полагать, что проблема связана с исключительно большими трудностями, которые можно будет преодолеть, лишь гораздо дальше отойдя от обычных соображений, чем требовалось до сих пор, и что достигнутый ранее успех был обусловлен исключительно простотой рассматривавшихся систем».

Первые шаги.

Поскольку использованная Бором комбинация существовавших ранее представлений из области электричества и механики с условиями квантования привела к неверным результатам, все это нужно было полностью или частично изменить. Основные положения теории Бора были приведены выше, а для соответствующих расчетов было достаточно не очень сложных выкладок с использованием обычной алгебры и математического анализа. В 1925 молодой немецкий физик В.Гейзенберг посетил Бора в Копенгагене, где провел с ним долгие часы в беседах, выясняя, что из теории Бора обязательно должно войти в будущую теорию, а от чего в принципе можно и отказаться.

Бор и Гейзенберг сразу же согласились, что в будущей теории обязательно должно быть представлено все непосредственно наблюдаемое, а все не поддающееся наблюдению может быть изменено или исключено из рассмотрения. С самого начала Гейзенберг считал, что следует сохранить атомы, но орбиту электрона в атоме считать абстрактной идеей, поскольку ни один эксперимент не позволяет определить электронную орбиту по результатам измерений наподобие того, как это можно сделать для орбит планет. Читатель может заметить, что тут есть определенная нелогичность: строго говоря, атом столь же ненаблюдаем непосредственно, как и электронные орбиты, и вообще в нашем восприятии окружающего мира нет ни одного ощущения, которое не требовало бы разъяснения. В наши дни физики все чаще цитируют известный афоризм, который был впервые произнесен Эйнштейном в беседе с Гейзенбергом: «Что именно мы наблюдаем, нам говорит теория». Таким образом, различие между наблюдаемыми и ненаблюдаемыми величинами носит чисто практический характер, не имея никакого обоснования ни в строгой логике, ни в психологии, причем это различие, как бы оно ни проводилось, должно рассматриваться как часть самой теории.

Поэтому гейзенберговский идеал теории, очищенной от всего ненаблюдаемого, есть некое направление мысли, но отнюдь не последовательный научный подход. Тем не менее он доминировал в атомной теории почти полвека после того, как был впервые сформулирован. Мы уже напоминали о составных элементах ранней модели Бора, таких, как закон Кулона для электрических сил, законы динамики Ньютона и обычные правила алгебры. Путем тонкого анализа Гейзенберг показал, что можно сохранить известные законы электричества и динамики, если найти надлежащее выражение для динамики Ньютона, а затем изменить правила алгебры. В частности, Гейзенберг высказал мысль, что, поскольку ни положение q, ни импульс p электрона не являются измеримыми величинами в том смысле, в каком ими являются, например, положение и импульс автомобиля, мы можем при желании сохранить их в теории, лишь рассматривая как математические символы, обозначаемые буквами, но не как числа. Он принял для p и q алгебраические правила, согласно которым произведение pq не совпадает с произведением qp. Гейзенберг показал, что простые расчеты атомных систем дают приемлемые результаты, если принять, что для положения q и импульса p выполняется соотношение

где h – постоянная Планка, уже известная из квантовой теории излучения и фигурировавшая в теории Бора, а . Постоянная Планка h представляет собой обычное число, но очень малое, приблизительно 6,6Ч10^–34 ДжЧс. Таким образом, если p и q – величины обычного масштаба, то разность произведений pq и qp будет крайне мала по сравнению с самими этими произведениями, так что p и q можно считать обычными числами. Построенная для описания явлений микромира, теория Гейзенберга почти полностью согласуется с механикой Ньютона, когда ее применяют к макроскопическим объектам. Уже в самых ранних работах Гейзенберга было показано, что при всей неясности физического содержания новой теории она предсказывает существование дискретных энергетических состояний, характерных для квантовых явлений (например, для испускания света атомом). В более поздней работе, выполненной совместно с М.Борном и П.Йорданом в Гёттингене, Гейзенберг развил формальный математический аппарат теории. Практические вычисления остались, однако, крайне сложными. После нескольких недель напряженной работы В.Паули вывел формулу для энергетических уровней атома водорода, совпадающую с формулой Бора. Но прежде чем удалось упростить вычисления, появились новые и совершенно неожиданные идеи. См. также АЛГЕБРА АБСТРАКТНАЯ; ПЛАНКА ПОСТОЯННАЯ.

Частицы и волны.

К 1920 физики были уже довольно хорошо знакомы с двойственной природой света: результаты одних экспериментов со светом можно было объяснить, предполагая, что свет представляет собой волны, а в других он вел себя подобно потоку частиц. Поскольку казалось очевидным, что ничто не может быть в одно и тоже время и волной, и частицей, ситуация оставалась непонятной, вызывая горячие споры в среде специалистов. В 1923 французский физик Л.де Бройль в опубликованных им заметках высказал предположение, что столь парадоксальное поведение, может быть, не является спецификой света, но и вещество тоже может в одних случаях вести себя подобно частицам, а в других подобно волнам. Исходя из теории относительности, де Бройль показал, что если импульс частицы равен p, то «ассоциированная» с этой частицей волна должна иметь длину волны l = h/p. Это соотношение аналогично впервые полученному Планком и Эйнштейном соотношению E = hn между энергией светового кванта Е и частотой n соответствующей волны. Де Бройль показал также, что эту гипотезу можно легко проверить в экспериментах, аналогичных опыту, демонстрирующему волновую природу света, и настойчиво призывал к проведению таких опытов. Заметки де Бройля привлекли внимание Эйнштейна, и к 1927 К.Дэвиссон и Л.Джермер в Соединенных Штатах, а также Дж.Томсон в Англии подтвердили для электронов не только основную идею де Бройля, но и его формулу для длины волны. В 1926 работавший тогда в Цюрихе австрийский физик Э.Шрёдингер, прослышав о работе де Бройля и предварительных результатах экспериментов, подтверждавших ее, опубликовал четыре статьи, в которых представил новую теорию, явившуюся прочным математическим обоснованием этих идей.

Такая ситуация имеет свой аналог в истории оптики. Одной уверенности в том, что свет есть волна определенной длины, недостаточно для детального описания поведения света. Необходимо еще написать и решить выведенные Дж.Максвеллом дифференциальные уравнения, подробно описывающие процессы взаимодействия света с веществом и распространение света в пространстве в виде электромагнитного поля. Шрёдингер написал дифференциальное уравнение для материальных волн де Бройля, аналогичное уравнениям Максвелла для света. Уравнение Шрёдингера для одной частицы имеет вид

где m – масса частицы, Е – ее полная энергия, V(x) – потенциальная энергия, а y – величина, описывающая электронную волну. В ряде работ Шрёдингер показал, как можно использовать его уравнение для вычисления энергетических уровней атома водорода. Он установил также, что существуют простые и эффективные способы приближенного решения задач, не поддающихся точному решению, и что его теория волн материи в математическом отношении полностью эквивалентна алгебраической теории наблюдаемых величин Гейзенберга и во всех случаях приводит к тем же результатам. П.Дирак из Кембриджского университета показал, что теории Гейзенберга и Шрёдингера представляют собой лишь две из множества возможных форм теории. Теория преобразований Дирака, в которой важнейшую роль играет соотношение (1), обеспечила ясную общую формулировку квантовой механики, охватывающую все остальные ее формулировки в качестве частных случаев.

Вскоре Дирак добился неожиданно крупного успеха, продемонстрировав, каким образом квантовая механика обобщается на область очень больших скоростей, т.е. приобретает вид, удовлетворяющий требованиям теории относительности. Постепенно стало ясно, что существует несколько релятивистских волновых уравнений, каждое из которых в случае малых скоростей можно аппрокcимировать уравнением Шрёдингера, и что эти уравнения описывают частицы совершенно разных типов. Например, частицы могут иметь разный «спин»; это предусматривается теорией Дирака. Кроме того, согласно релятивистской теории, каждой из частиц должна соответствовать античастица с противоположным знаком электрического заряда. В то время, когда вышла работа Дирака, были известны только три элементарные частицы: фотон, электрон и протон. В 1932 была открыта античастица электрона – позитрон. На протяжении нескольких последующих десятилетий было обнаружено много других античастиц, большинство из которых, как оказалось, удовлетворяли уравнению Дирака или его обобщениям. Созданная в 1925–1928 усилиями выдающихся физиков квантовая механика не претерпела с тех пор в своих основах каких-либо существенных изменений. См. также АНТИВЕЩЕСТВО.

Приложения.

Во всех разделах физики, биологии, химии и техники, в которых существенны свойства вещества в малых масштабах, теперь систематически обращаются к квантовой механике. Приведем несколько примеров. Всесторонне исследована структура электронных орбит, наиболее удаленных от ядра атомов. Методы квантовой механики были применены к проблемам строения молекул, что привело к революции в химии. Структура молекул обусловлена химическими связями атомов, и сегодня сложные задачи, возникающие при последовательном применении квантовой механики в этой области, решаются с помощью компьютеров. Большое внимание привлекли к себе теория кристаллической структуры твердых тел и особенно теория электрических свойств кристаллов. Практические результаты впечатляют: примерами их могут служить изобретение лазеров и транзисторов, а также значительные успехи в объяснении явления сверхпроводимости. См. также ФИЗИКА ТВЕРДОГО ТЕЛА; ЛАЗЕР; ТРАНЗИСТОР; СВЕРХПРОВОДИМОСТЬ.

Многие проблемы еще не решены. Это касается структуры атомного ядра и физики элементарных частиц. Время от времени обсуждается вопрос о том, не лежат ли проблемы физики элементарных частиц за пределами квантовой механики, подобно тому как структура атомов оказалась вне области применимости динамики Ньютона. Однако до сих пор нет никаких указаний на то, что принципы квантовой механики или ее обобщения в области динамики полей где-то оказались неприменимыми. Более полувека квантовая механика остается научным инструментом с уникальной «объясняющей способностью» и не требует существенных изменений своей математической структуры. Поэтому может показаться удивительным, что до сих пор ведутся острые дебаты (см. ниже) по поводу физического смысла квантовой механики и ее истолкования. См. также АТОМА СТРОЕНИЕ; АТОМНОГО ЯДРА СТРОЕНИЕ; МОЛЕКУЛ СТРОЕНИЕ; ЧАСТИЦЫ ЭЛЕМЕНТАРНЫЕ.

Вопрос о физическом смысле.

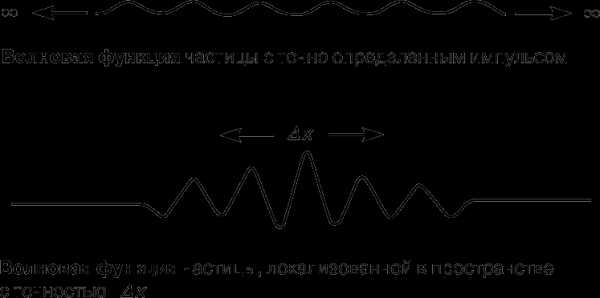
Корпускулярно-волновой дуализм, столь очевидный в эксперименте, создает одну из самых трудных проблем физической интерпретации математического формализма квантовой механики. Рассмотрим, например, волновую функцию, которая описывает частицу, свободно движущуюся в пространстве. Традиционное представление о частице, помимо прочего, предполагает, что она движется по определенной траектории с определенным импульсом p. Волновой функции приписывается длина волны де Бройля l = h/p, но это характеристика такой волны, которая бесконечна в пространстве, а потому не несет информации о местонахождении частицы. Волновую функцию, локализующую частицу в определенной области пространства протяженностью Dx, можно построить в виде суперпозиции (пакета) волн с соответствующим набором импульсов, и если искомый диапазон импульсов равен Dp, то довольно просто показать, что для величин Dx и Dp должно выполняться соотношение

DxDp і h/4p.

Этим соотношением, впервые полученным в 1927 Гейзенбергом, выражается известный принцип неопределенности: чем точнее задана одна из двух переменных x и p, тем меньше точность, с которой теория позволяет определить другую.

Соотношение Гейзенберга могло бы рассматриваться просто как недостаток теории, но, как показали Гейзенберг и Бор, оно соответствует глубокому и ранее не замечавшемуся закону природы: даже в принципе ни один эксперимент не позволит определить величины x и p реальной частицы точнее, чем это допускает соотношение Гейзенберга. Гейзенберг и Бор разошлись в интерпретации этого вывода. Гейзенберг рассматривал его как напоминание о том, что все наши знания по своему происхождению – экспериментальные и что эксперимент неизбежно вносит в исследуемую систему возмущение, а Бор рассматривал его как ограничение точности, с которой само представление о волне и частице применимо к миру атома.

Гораздо более широким оказывается спектр мнений о природе самой статиcтичеcкой неопределенности. В этих неопределенностях нет ничего нового; они присущи почти каждому измерению, но обычно считают, что они обусловлены недостатками используемых приборов или методов: точное значение существует, однако найти его практически очень трудно, и потому мы рассматриваем полученные результаты как вероятные значения с присущей им статистической неопределенностью. Одна из школ физико-философской мысли, возглавлявшаяся в свое время Эйнштейном, считает, что то же самое имеет место и для микромира, и что квантовая механика с ее статистическими результатами дает лишь средние значения, которые были бы получены при многократном повторении рассматриваемого эксперимента с небольшими различиями из-за несовершенства нашего контроля. При таком воззрении точная теория каждого отдельного случая в принципе существует, просто она еще не найдена.

Другая школа, исторически связанная с именем Бора, стоит на том, что индетерминизм присущ самой природе вещей и что квантовая механика – теория, наилучшим образом описывающая каждый отдельный случай, а в неопределенности физической величины находит отражение та точность, с которой эта величина может определяться и использоваться. Мнение большинства физиков склонялось в пользу Бора. В 1964 Дж.Белл, работавший тогда в ЦЕРНе (Женева), показал, что в принципе эту проблему можно решить экспериментально. Результат Белла явился, пожалуй, важнейшим с 1920-х годов сдвигом в поисках физического смысла квантовой механики.

Теорема Белла, как сейчас называют этот результат, утверждает, что некоторые предсказания, сделанные на основе квантовой механики, невозможно воспроизвести путем вычислений на основе какой-либо точной, детерминированной теории с последующим усреднением результатов. Поскольку два таких метода вычислений должны давать разные результаты, появляется возможность экспериментальной проверки. Измерения, выполненные в 1970-х годах, убедительно подтвердили адекватность квантовой механики.

И все же было бы преждевременно утверждать, что эксперимент подвел окончательную черту под дебатами Бора и Эйнштейна, поскольку такого рода проблемы нередко возникают как бы заново, в другом языковом обличье каждый раз, когда, казалось бы, все ответы уже найдены. Как бы то ни было, остаются и другие головоломки, напоминающие нам, что физические теории – это не только уравнения, но и словесные объяснения, связывающие кристальную сферу математики с туманными областями языка и чувственного опыта, и что это зачастую и есть самое трудное.

www.krugosvet.ru

Квантовая механика Википедия

Туннельный эффект — квантовая механика показывает, что электроны могут преодолеть потенциальный барьер, что подтверждается результатами экспериментов.
Классическая механика, наоборот, предсказывает, что это невозможно Области применения классической и квантовой механики

Ква́нтовая меха́ника — раздел теоретической физики, описывающий физические явления, в которых действие сравнимо по величине с постоянной Планка. Предсказания квантовой механики могут существенно отличаться от предсказаний классической механики. Поскольку постоянная Планка является чрезвычайно малой величиной по сравнению с действием объектов при макроскопическом движении, квантовые эффекты в основном проявляются в микроскопических масштабах. Если физическое действие системы намного больше постоянной Планка, квантовая механика органически переходит в классическую механику. В свою очередь, квантовая механика является нерелятивистским приближением (то есть приближением малых энергий по сравнению с энергией покоя массивных частиц системы) квантовой теории поля.

Классическая механика, хорошо описывающая системы макроскопических масштабов, не способна описать все явления на уровне молекул, атомов, электронов и фотонов. Квантовая механика адекватно описывает основные свойства и поведение атомов, ионов, молекул, конденсированных сред и других систем с электронно-ядерным строением. Квантовая механика также способна описывать: поведение электронов, фотонов, а также других элементарных частиц, однако более точное релятивистски инвариантное описание превращений элементарных частиц строится в рамках квантовой теории поля. Эксперименты подтверждают результаты, полученные с помощью квантовой механики.

Основными понятиями квантовой кинематики являются понятия наблюдаемой и состояния.

Основные уравнения квантовой динамики — уравнение Шрёдингера, уравнение фон Неймана, уравнение Линдблада, уравнение Гейзенберга и уравнение Паули.

Уравнения квантовой механики тесно связаны со многими разделами математики, среди которых: теория операторов, теория вероятностей, функциональный анализ, операторные алгебры, теория групп.

История

На заседании Немецкого физического общества Макс Планк зачитал свою историческую статью «К теории распределения энергии излучения в нормальном спектре», в которой он ввёл универсальную постоянную h{\displaystyle h}. Именно дату этого события, 14 декабря 1900 года, часто считают днем рождения квантовой теории.

Квантовая гипотеза Планка состояла в том, что для элементарных частиц любая энергия поглощается или испускается только дискретными порциями (квантами)^[1]. Эти порции состоят из целого числа квантов с такой энергией E{\displaystyle {\mathcal {E}}}, что эта энергия пропорциональна частоте ν с коэффициентом пропорциональности, определённым по формуле:

E=hν=ℏω,{\displaystyle {\mathcal {E}}=h\nu =\hbar \omega ,}

где h{\displaystyle h} — постоянная Планка, и ℏ=h3π.{\displaystyle \hbar ={\frac {h}{2\pi }}.}

В 1905 году, для объяснения явлений фотоэффекта, Альберт Эйнштейн, использовав квантовую гипотезу Планка, предположил, что свет состоит из квантов. Впоследствии «кванты» света получили название фотонов.

Для объяснения структуры атома Нильс Бор предложил в 1913 году существование стационарных состояний электрона, в которых энергия может принимать лишь дискретные значения. Этот подход, развитый Арнольдом Зоммерфельдом и другими физиками, часто называют старой квантовой теорией (1900—1924 г.). Отличительной чертой старой квантовой теории является сочетание классической теории с противоречащими ей дополнительными предположениями.

В 1923 году Луи де Бройль выдвинул идею двойственной природы вещества, опиравшуюся на предположение о том, что материальные частицы обладают и волновыми свойствами, неразрывно связанными с массой и энергией. Движение частицы Л. де Бройль сопоставил с распространением волны, что в 1927 году получило экспериментальное подтверждение при исследовании дифракции электронов в кристаллах.

Высказанные в 1924 году идеи корпускулярно-волнового дуализма были в 1926 году подхвачены Э. Шрёдингером, развернувшим на их основе свою волновую механику.

В 1925—1926 годах были заложены основы последовательной квантовой теории в виде квантовой механики, содержащей новые фундаментальные законы кинематики и динамики. Первая формулировка квантовой механики содержится в статье Вернера Гейзенберга, датированной 29 июля 1925 года. Эту дату можно считать днем рождения нерелятивистской квантовой механики.

Развитие и формирование основ квантовой механики продолжается до сих пор. Оно связано, например, с исследованиями открытых и диссипативных квантовых систем, квантовой информатикой, квантовым хаосом и пр. Помимо квантовой механики, важнейшей частью квантовой теории является квантовая теория поля.

В 1927 году К. Дэвиссон и Л. Джермер в исследовательском центре Bell Labs демонстрируют дифракцию медленных электронов на никелевых кристаллах (независимо от Дж. Томсона). При оценке угловой зависимости интенсивности отраженного электронного луча, было показано её соответствие предсказанной на основании условия Вульфа — Брэгга для волн с длиной де Бройля (см. Волны де Бройля). До принятия гипотезы де Бройля дифракция расценивалась как исключительно волновое явление, а любой дифракционный эффект — как волновой. Когда длина волны де Бройля была сопоставлена с условием Вульфа — Брэгга, была предсказана возможность наблюдения подобной дифракционной картины для частиц. Таким образом, экспериментально была подтверждена гипотеза де Бройля для электрона.

Подтверждение гипотезы де Бройля стало поворотным моментом в развитии квантовой механики. Подобно тому, как эффект Комптона показывает корпускулярную природу света, эксперимент Дэвиссона — Джермера подтвердил неразрывное «сосуществование» с частицей её волны, иными словами — присущность корпускулярной материи также и волновой природы. Это послужило оформлению идей корпускулярно-волнового дуализма. Подтверждение этой идеи для физики стало важным этапом, поскольку дало возможность не только характеризовать любую частицу, присваивая ей определённую индивидуальную длину волны, но также при описании явлений полноправно использовать её в виде определённой величины в волновых уравнениях.

Разделы квантовой механики

В стандартных курсах квантовой механики изучаются следующие разделы

Основания квантовой механики 

Как и в других разделах физики, в квантовой механике существует система постулатов, составляющая ее основания и задающая базовые понятия. Если исходить из совета А.Эйнштейна “Если вы хотите кое-что выяснить у физиков-теоретиков о методах, которые они применяют, я советую вам твердо придерживаться одного принципа: не слушайте, что они говорят, а лучше изучайте их действия…” (О методе теоретической физики (1933)), то вырисовывается следующая система постулатов.

1. Постулаты Э.Шрёдингера (будем использовать математическое “представление Шрёдингера”). Они задают математические образы состояния квантовой частицы – нового типа объекта, обладающего корпускулярно-волновым поведением, но несводимым ни к частице, ни к волне, в виде волновой функции в гильбертовом пространстве. Они также задают уравнение движения, задающего связь состояний, каковым является уравнение Шрёдингера.
2. Постулаты М.Борна – центральные для квантовой механики и ее понимания.
   а) Они вводят принципиально новый тип состояний объекта – оно задается распределением вероятностей величин (и их корреляций “томографическим” методом), а не величинами, как в классической физике.
   б) Отсюда следует принципиальное изменение процедур измерения – один акт измерения ничего не говорит о распределении вероятностей, для определения последней требуется достаточно длинная серия измерений. В этом состоит особенность измерения в квантовой механики. Никакой особой роли наблюдателя или сознания, о котором часто говорят, здесь не появляется.
   в) При этом вводится связь между математическим образом состояния и физическим состоянием в виде “вероятностной интерпретации волновой функции”, позволяющей, зная волновую функцию, вычислить любые распределения вероятностей и средние значения величин. Постулаты Борна вводят в квантовую механику вероятностное описание (уравнения Шрёдингера абсолютно (однозначно) детерминистичны) и корпускулярно-волновое поведение, что иллюстрирует знаменитый двухщелевой эксперимент, где квантовая частица проходит как волна через обе щели, но на фотопластинке поглощается как частица в определенной точке. Но если этот опыт многократно повторять, то на распределении вероятностей в виде интегрального потемнения фотопластинки проявится дифракционно-интерференционная картинка, характерная для волны проходящей через обе щели.
3. Постулаты В.Гейзенберга о квантовании, которые вводят универсальную процедуру по нахождении оператора Гамильтона, входящего в уравнение Шрёдингера и являющегося математическим образом объекта с учетом внешнего воздействия на него. Процедура состоит в следующем: берется “затравочная” классическая модель, например, планетарная модель атома, для нее строится классический гамильтониан, затем в нем по определенному правилу ряд величин заменяется на операторы (например, импульс p_x заменяется на дифференциальный оператор ihd/dx), в результате образуется квантовый оператор Гамильтона, приводящий к электронным орбиталям в атоме. Дирак указывает на усложненный случай, когда в “затравочный” классический гамильтониан входит произведение величин, отвечающих некоммутирующим операторам. Тогда требуется дополнительно ввести упорядочение этих операторов.
4. В случае многочастичных объектов требуется еще постулат о тождественности частиц, приводящий к двум статистикам: Ферми-Дирака (для фермионов) и Бозе-Эйнштейна (для бозонов), а также к принципу Паули для заполнения электронных орбиталей в атоме. Липкин А.И. Основания физики. Взгляд из теоретической физики. М.: URSS, 2014 г., 207 с

Существует несколько различных эквивалентных математических описаний (представлений) квантовой механики:

Шрёдингеровское описание

Математический аппарат нерелятивистской квантовой механики строится на следующих положениях^[2]:

⟨A⟩=⟨ψ|A^ψ⟩⟨ψ|ψ⟩=⟨ψA^|ψ⟩⟨ψ|ψ⟩{\displaystyle \langle A\rangle ={\frac {\langle \psi |{\hat {A}}\psi \rangle }{\langle \psi |\psi \rangle }}={\frac {\langle \psi {\hat {A}}|\psi \rangle }{\langle \psi |\psi \rangle }}}

где через ⟨ψ|ϕ⟩{\displaystyle \langle \psi |\phi \rangle } обозначается скалярное произведение векторов |ψ⟩{\displaystyle |\psi \rangle } и |ϕ⟩{\displaystyle |\phi \rangle }.

iℏ∂∂t|ψ⟩=H^|ψ⟩{\displaystyle i\hbar {\frac {\partial }{\partial t}}|\psi \rangle ={\hat {H}}|\psi \rangle }

где H^{\displaystyle {\hat {H}}} — гамильтониан.

Основные следствия этих положений:

• При измерении любой квантовой наблюдаемой, возможно получение только ряда фиксированных её значений, равных собственным значениям её оператора — наблюдаемой.
• Наблюдаемые одновременно измеримы (не влияют на результаты измерений друг друга) тогда и только тогда, когда соответствующие им самосопряжённые операторы перестановочны.

Эти положения позволяют создать математический аппарат, пригодный для описания широкого спектра задач в квантовой механике гамильтоновых систем, находящихся в чистых состояниях. Не все состояния квантово-механических систем, однако, являются чистыми. В общем случае состояние системы является смешанным и описывается матрицей плотности, для которой справедливо обобщение уравнения Шрёдингера — уравнение фон Неймана (для гамильтоновых систем). Дальнейшее обобщение квантовой механики на динамику открытых, негамильтоновых и диссипативных квантовых систем приводит к уравнению Линдблада.

Стационарное уравнение Шрёдингера

Пусть ψ(r→){\displaystyle \psi ({\vec {r}})} амплитуда вероятности нахождения частицы в точке М. Стационарное уравнение Шрёдингера позволяет её определить.
Функция ψ(r→){\displaystyle \psi ({\vec {r}})} удовлетворяет уравнению:

−ℏ22m∇2ψ+U(r→)ψ=Eψ{\displaystyle -{{\hbar }^{2} \over 2m}{\nabla }^{\,2}\psi +U({\vec {r}})\psi =E\psi }

где ∇2{\displaystyle {\nabla }^{\,2}}—оператор Лапласа, а U=U(r→){\displaystyle U=U({\vec {r}})} — потенциальная энергия частицы как функция от r→{\displaystyle {\vec {r}}}.

Решение этого уравнения и есть основная задача квантовой механики. Примечательно то, что точное решение стационарного уравнения Шрёдингера может быть получено только для нескольких, сравнительно простых, систем. Среди таких систем можно выделить квантовый гармонический осциллятор и атом водорода. Для большинства реальных систем для получения решений могут быть использованы различные приближенные методы, такие как теория возмущений.

Решение стационарного уравнения

Принцип неопределённости Гейзенберга

Соотношение неопределённости возникает между любыми квантовыми наблюдаемыми, определяемыми некоммутирующими операторами.

Неопределенность между координатой и импульсом

Пусть Δx{\displaystyle \Delta x} — среднеквадратическое отклонение координаты частицы M{\displaystyle M}, движущейся вдоль оси x{\displaystyle x}, и Δp{\displaystyle \Delta p} — среднеквадратическое отклонение её импульса. Величины Δx{\displaystyle \Delta x} и Δp{\displaystyle \Delta p} связаны следующим неравенством:

ΔxΔp⩾ℏ2{\displaystyle \Delta x\Delta p\geqslant {\frac {\hbar }{2}}}

где h{\displaystyle h} — постоянная Планка, а ℏ=h3π.{\displaystyle \hbar ={\frac {h}{2\pi }}.}

Согласно соотношению неопределённостей, невозможно абсолютно точно определить одновременно координаты и импульс частицы. С повышением точности измерения координаты, максимальная точность измерения импульса уменьшается и наоборот. Те параметры, для которых такое утверждение справедливо, называются канонически сопряженными.

Это центрирование на измерении, идущее от Н.Бора, очень популярно. Однако соотношение неопределенности выводится теоретически из постулатов Шрёдингера и Борна и касается не измерения, а состояний объекта: оно утверждает, что для любого возможного состояния выполняются соответствующие соотношения неопределенности. Естественно, что оно будет выполняться и для измерений. Т.е. вместо “с повышением точности измерения координаты максимальная точность измерения импульса уменьшается” следует говорить: “в состояниях, где неопределенность координаты меньше, неопределенность импульса больше”.

Неопределенность между энергией и временем

Пусть ΔE{\displaystyle \Delta E} — среднеквадратическое отклонение при измерении энергии некоторого состояния квантовой системы, и Δt{\displaystyle \Delta t} — время жизни этого состояния. Тогда выполняется следующее неравенство,

ΔEΔt⩾ℏ2.{\displaystyle \Delta E\Delta t\geqslant {\frac {\hbar }{2}}.}

Иными словами, состояние, живущее короткое время, не может иметь хорошо определённую энергию.

При этом, хотя вид этих двух соотношений неопределенности похож, но их природа (физика) совершенно различны.

Необычные явления, мысленные эксперименты и парадоксы квантовой механики

Интерпретации квантовой механики

Существует множество интерпретаций квантовой теории, которые иногда плохо согласуются друг с другом.

С точки зрения философии позитивизма, разногласия в интерпретациях не влияют на предсказания исходов конкретных экспериментов в рамках квантовой теории, и потому интерпретации являются нефальсифицируемыми, а следовательно, и ненаучными концепциями. Практическая ценность различных интерпретаций усматривается их сторонниками в некотором упрощении хода рассуждений при рассмотрении различных экспериментов, или обосновывается философскими соображениями.

Есть и другая точка зрения по данному вопросу:

В наше время физик вынужден заниматься философскими проблемами в гораздо большей степени, чем это приходилось делать физикам предыдущих поколений. К этому физиков вынуждают трудности их собственной науки.^[3]

При изучении этих вещей в их совокупности физик на каждом шагу встречается с логическими и гносеологическими трудностями; и хотя физика имеет дело лишь с ограниченным кругом знания и исключает такие явления, как жизнь и сознание, все же решение этих логических и гносеологических проблем является глубокой потребностью нашего стремления к познанию.^[4]

Для выбора между конкурирующими научными теориями одного лишь опыта недостаточно. Кроме опыта, важными компонентами научного творчества являются интуиция, психология и философские соображения. Эталон для построения научной теории называется парадигмой. Смысл научных революций заключается не в смене одной фундаментальной теории другой под влиянием новых фактов, а в смене научных парадигм.^[5]

Интерпретации квантовой механики

Комментарии

• Обычно квантовая механика формулируется для нерелятивистских систем. Рассмотрение частиц с релятивистскими энергиями в рамках стандартного квантово-механического подхода, предполагающего фиксированное число частиц в системе, сталкивается с трудностями, поскольку при достаточно большой энергии частицы могут превращаться друг в друга. Эти трудности устраняются в квантовой теории поля, которая и является самосогласованной теорией релятивистских квантовых систем.
• Важным свойством квантовой механики является принцип соответствия: в рамках квантовой механики доказывается, что в пределе больших величин действия (квазиклассический предел) и в случае, когда квантовая система взаимодействует с внешним миром (декогеренция), уравнения квантовой механики редуцируются в уравнения классической физики (см. Теорема Эренфеста). Таким образом, квантовая механика не противоречит классической физике, а лишь дополняет её на микроскопических масштабах.
• Некоторые свойства квантовых систем кажутся непривычными (невозможность одновременно измерить координату и импульс, несуществование определённой траектории частицы, вероятностное описание, дискретность средних значений наблюдаемых величин). Это вовсе не значит, что они неверны: это означает, что наша повседневная интуиция никогда не сталкивалась с таким поведением, т. е. в данном случае «здравый смысл» не может быть критерием, поскольку он годится только для макроскопических систем. Квантовая механика — самосогласованная математическая теория, предсказания которой согласуются с экспериментами. В настоящее время огромное число приборов, используемых в повседневной жизни, основываются на законах квантовой механики, как например — лазер или сканирующий туннельный микроскоп.
• Классическая механика оказалась неспособной объяснить движение электронов вокруг атомного ядра. Например, согласно классической электродинамике, электрон, вращающийся с большой скоростью вокруг атомного ядра, должен излучать энергию. Тогда его кинетическая энергия должна уменьшаться и он должен упасть на ядро. Для понимания процессов, происходящих на уровне элементарных частиц, потребовалась новая теория. Квантовая теория — это совершенно новый взгляд на систему, позволяющий с огромной точностью описать необычное поведение электронов и фотонов.^[6]

См. также

Примечания

1. ↑ Chris Ferrie. Quantum Physics for Babies. — Brdbk edition. — Sourcebooks Jabberwocky, 2017-05-02. — С. 23. — 24 с. — ISBN 9781492656227. (Проверено 1 апреля 2018)
2. ↑ Ф. А. Березин, М. А. Шубин. Уравнение Шрёдингера. — М.: Изд-во Моск. ун-та, 1983.
3. ↑ Эйнштейн А. Замечания о теории познания Бертрана Рассела // Собрание научных трудов, т. IV. — М., 1967. — стр. 248
4. ↑ Макс Борн Философские аспекты современной физики // Физика в жизни моего поколения — М., ИЛ, 1963. — стр. 78
5. ↑ Томас Кун Структура научных революций — М., АСТ, 2003. — с. 605 — ISBN 5-17-010707-2
6. ↑ Фейнман Р. КЭД-странная теория света и вещества — М: Наука, 1988. (Библиотечка «Квант»)

Литература

• Физический энциклопедический словарь. Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. М.: Сов. Энциклопедия, 1984. — 944 с.
• Блохинцев Д. И. Основы квантовой механики. 5-е изд. Наука, 1976. — 664 с.
• Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720 c.
• Давыдов А. С. Квантовая механика. 3-е изд., стер. — СПб.: 2011 — 704 с.
• Джеммер М. Эволюция понятий квантовой механики. М.: Наука, 1985. — 384 с.
• Дирак П. Принципы квантовой механики. 2-е изд. М.: Наука, 1979. — 480 с.
• Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 6-е, исправленное. — М.: Физматлит, 2004. — 800 с. — («Теоретическая физика», том III). — ISBN 5-9221-0530-2.
• Садбери А. Квантовая механика и физика элементарных частиц. М.: Мир, 1989. — 488 с.
• Фадеев Л. Д., Якубовский О. А. Лекции по квантовой механике для студентов-математиков. Ленинград, Изд-во ЛГУ, 1980. — 200 c.
• Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Пер. с англ., Том. 8. Том 9., М., 1966—1967.
• Коэн-Таннуджи К., Диу Б., Лалоэ Ф. Квантовая механика. Т.1. Екатеринбург: Изд-во Уральского ун-та, 2000. — 944 с.
• Коэн-Таннуджи К., Диу Б., Лалоэ Ф. Квантовая механика. Т.2. Екатеринбург: Изд-во Уральского ун-та, 2000. — 800 с.
• Липкин А. И. Основания физики. Взгляд из теоретической физики. М.: URSS, 2014.— 207 с.
• Степанов Н. Ф. Квантовая механика и квантовая химия.— 2013.
• Шифф Л. Квантовая механика. Рипол Классик, 2013.
• Мотт Н., Снеддон И. Волновая механика и её применения. — М., Наука, 1966. – Тираж 9400 экз. – 427 с.
• Леонард Сасскинд, Арт Фриман – Квантовая механика: теоретический минимум / пер. с англ. А. Сергеев. — СПб.: Питер, 2015. — 400 с.

Ссылки

• Лорен Грэхэм «Естествознание, философия и науки о человеческом поведении в Советском Союзе, Глава X. Квантовая механика»
• Шрёдингер Э. Избранные труды по квантовой механике, — М..: Наука, 1976.
• Нейман И. Математические основы квантовой механики, — М.: Наука, 1964.
• Паули В. Общие принципы волновой механики, — М. — Л.: ГИТТЛ, 1947.
• Дирак П. А. М. Принципы квантовой механики (2-е издание), — М.: Наука, 1979.
• Фущич В. И., Никитин А. Г. Симметрия уравнений квантовой механики, — М.: Наука, 1990.
• Альбеверио С., Гестези Ф., Хёэг-Крон Р., Хольден Х. Решаемые модели квантовой механики. М.: Мир, 1991. – 568с.
• Блохинцев Д. И. Принципиальные вопросы квантовой механики. М.: Наука, 1966.
• «Квантовая механика» — статья в Физической энциклопедии.

wikiredia.ru

---