Lim в математике – Как считать пределы 🚩 виды неопределенности пределов 🚩 Математика

Lim 1 — Высшая математика — 22 ответа



В разделе ВУЗы, Колледжи на вопрос Высшая математика заданный автором Анна ‘Taitou-dono’ лучший ответ это 1. Предел существует только при х -> минус бесконечность.
lim (3-x) [ ln (1-x) – ln (2-x)] ( при x-> минус бесконечность) =1.
При х -> бесконечность:
ln(1-x)-ln(2-x) определено только при х -> минус бесконечность и
ln(1-x)-ln(2-x)= ln((1-x)/(2-x))=ln(1-1/(2-x)) эквивалентно 1/(2-x) (по следствию из второго зам. пред. -а) .
Поэтому первый предел равен пределу (3-х) /(2-х) при х -> минус бесконечность, т. е. равен 1.
2.
lim (3x^2+6x-1) / ((x+2)(2x-4)) (при x-> бесконечность) =3/2.
Разделив числитель и знаменатель на x^2, получим:
(3+6/x-1/x^2)/(2-8/x^2).
При x-> бесконечность 1/x и 1/x^2 бесконечно малые, поэтому данный предел равен 3/2.
3.
lim x(ln 4x – ln(4x+3)) (при x-> + бесконечность)
При х -> +бесконечность:
ln(4x)-ln(4x+3)= ln(1-3/(4х+3)) эквивалентно -3/(4х+3) (по следствию из второго зам. пред. -а) .
Поэтому первый предел равен пределу -3х/(4х+3) при х -> +бесконечность, т. е. равен-3/4.
4.
lim (3-x)/(2x+1) – (3x^2+2)/(4x^2-1)) (при x->бесконечность) =-5/4.
Аналогично примеру 2: (3-x)/(2x+1) -> -1/2; (3x^2+2)/(4x^2-1) -> 3/4.
Поэтому lim ((3-x)/(2x+1)-(3x^2+2)/(4x^2-1))=-1/2-3/4=-5/4.
5.
lim (x^3 e^(-x/2)) (при x-> + бесконечность) =0.
x^3 e^(-x/2)= x^3 /e^(x/2).
При x-> + бесконечность получается неопределённость вида бесконечность/бесконечность, которая может быть вычислена трёхкратным применением правила Лопиталя:
lim (x^3/e^(x/2))=lim (3x^2/(e^(x/2)/2))=lim (6x/(e^(x/2)/4))=lim (6/(e^(x/2)/8))=0.
6.
lim (1/x^1/2) (tg (x/3)) (при x->0)=0.
По следствию из первого зам. пред. -а: при x->0 tg (x/3) эквивалентно х/3.
Поэтому:
lim (1/x^(1/2))(tg(x/3))=lim (1/x^(1/2))*x/3)=lim x^(1/2)/3=0.
————————————————————————————–
График функции sin(x)/x.
(Первый —вид «в целом» , по осям X и Y различный масштаб;
второй —вид вблизи нуля, масштаб по осям X и Y —одинаковый. )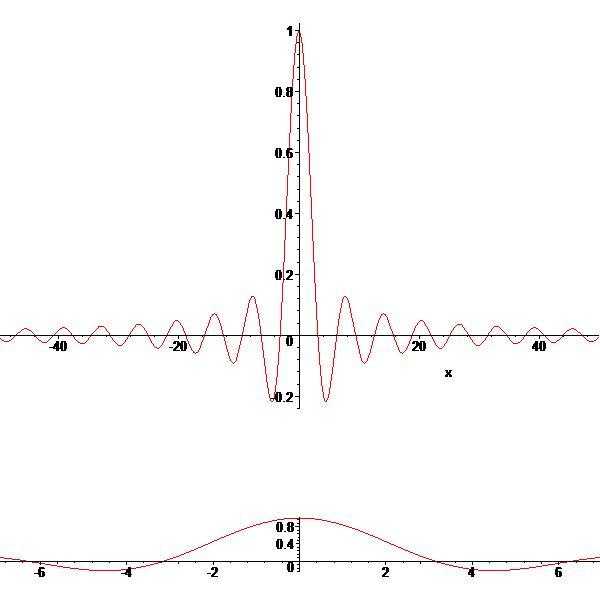

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Высшая математика

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Замечательные пределы на Википедии
Посмотрите статью на википедии про Замечательные пределы

 

Ответить на вопрос:

22oa.ru

Замечательные пределы | Математика | FANDOM powered by Wikia

    Замечательный тригонометрический предел Править

    $ \lim_{x \to 0}\frac{\sin x}{x} = 1 $ (без доказательства)

    Следствия

    $ \lim_{x \to 0}\frac{\sin \alpha x}{hx} = k $
    $ \lim_{x \to 0}\frac{\arcsin x}{x} = 1 $
    $ \lim_{x \to 0}\frac{\tan x}{x} = 1 $
    $ \lim_{x \to 0}\frac{\arctan x}{x} = 1 $

    Доказательство следствий

    $ \lim_{x \to 0}\frac{\sin kx}{x} = \lim_{x \to 0}\frac{k \sin kx}{kx} = k $
    $ \lim_{x \to 0}\frac{\tan x}{x} = \lim_{x \to 0}\frac{\sin x}{x \cos x} = \lim_{x \to 0}\frac{\sin x}{x} \cdot \lim_{x \to 0}\frac{1}{\cos x} = 1 \cdot 1 = 1 $
    $ \lim_{x \to 0}\frac{\arcsin x}{x} = \left [ \begin{matrix} u = \arcsin x \\ x = \sin u \\ u \to 0 \\ x \to 0 \end{matrix} \right ] = \lim_{u \to 0}\frac{u}{\sin u} = 1 $
    $ \lim_{x \to 0}\frac{\arctan x}{x} = \left [ \begin{matrix} u = \arctan x \\ x = \tan u \\ u \to 0 \\ x \to 0 \end{matrix} \right ] = \lim_{u \to 0}\frac{u}{\tan u} = 1 $

    Замечательный показательно-степенной предел Править

    $ \lim_{x \to \infty}(1 + \frac{1}{x})^x = e $ (без доказательства)

    Следствия

    $ \lim_{x \to \infty}(1 + \frac{k}{x})^x = e^k $

    Доказательство следствия

    $ \lim_{x \to \infty}(1 + \frac{k}{x})^x = \left [ \begin{matrix} u = \frac{k}{x} \\ x = \frac{k}{u} \\ u \to 0 \\ x \to \infty \end{matrix} \right ] = \lim_{u \to 0}(1 + u)^\frac{k}{u} = (\lim_{u \to 0}(1 + u)^\frac{1}{u})^k = e^k $

    Замечательный логарифмический предел Править

    $ \lim_{x \to 0}\frac{\ln(1 + x)}{x} = 1 $

    Доказательство предела

    • Используя замечательный показательно-степенной предел: $ \lim_{x \to 0}\frac{\ln(1 + x)}{x} = \lim_{x \to 0}\frac{1}{x}\ln(1 + x) = \lim_{x \to 0}\ln((1 + x)^\frac{1}{x}) = \ln e = 1 $
    • Используя правило Лопиталя: $ \lim_{x \to 0}\frac{\ln(1 + x)}{x} = (0/0) =\lim_{x \to 0}\frac{(\ln(1 + x))’}{x’} = \lim_{x \to 0}\frac{1}{1+x} = 1 $

    Замечательный показательный предел Править

    $ \lim_{x \to 0}\frac{e^x – 1}{x} = 1 $

    Следствия

    $ \lim_{x \to 0}\frac{a^x – 1}{x \ln a} = 1 $ для $ a > 0 \,\! $, $ a \neq 1 \,\! $

    Доказательство предела

    $ \lim_{x \to 0}\frac{e^x – 1}{x} = \left [ \begin{matrix} u = e^x – 1 \\ x = \ln(1 + u) \\ x \to 0 \\ u \to 0 \end{matrix} \right ] = \lim_{u \to 0}\frac{u}{\ln(1 + u)} = 1 $

    Доказательство следствия

    $ \lim_{x \to 0}\frac{a^x – 1}{x \ln a} = \lim_{x \to 0}\frac{e^{\ln(a^x)} – 1}{x \ln a} = \lim_{x \to 0}\frac{e^{x \ln a} – 1}{x \ln a} = \left [ \begin{matrix} u = x \ln a \\ u \to 0 \\ x \to 0 \end{matrix} \right ] = \lim_{u \to 0}\frac{e^u – 1}{u} = 1 $

    Замечательный степенной предел Править

    $ \lim_{x \to 0}\frac{(1 + x)^\alpha – 1}{x} = \alpha $ (без доказательства)

    ru.math.wikia.com

    Свойства пределов функции

    Предел функции является в математическом анализе одним из основных понятий. Функция f(x) в точке х0 предел имеет L. Если все значения х достаточно близки к х0, то близко к L и значение f(x).

    На бесконечности предел функции описывает поведение значения самой функции, когда аргумент ее становится бесконечно большим.

    Предел функции обозначается в виде f(x) → L в случае, если х→а

    К основным свойствам пределов функции относят:

    • предел постоянной величины, который равен самой постоянной величины;
    • предел суммы, который равен сумме пределов самих функций. Также по аналогии и предел разности функций равен разности пределов данных функций;
    • предел суммы множества функций равен также сумме пределов таких функций. По аналогии рассчитывает и предел нескольких функций, который равен разности пределов данных функций;
    • повышение предела произведения функции (постоянного коэффициента) на знак предела;
    • произведению пределов функций равен предел произведения двух функций;
    • расширенное свойство предела произведения, которое в том заключается, что предел произведения функций равен и произведению пределов данных функций;
    • предел частного функций равен отношению пределов данных функций, но только в том случае, если предел знаменателя нулю не равен;
    • предел функции степенной, где действительным числом является степень р;
    • предел функции показательной, при которой основание b больше 0;
    • предел функции логарифмической, в которой основание b больше 0;
    • теорема «двух милиционеров», при которой «зажатой» остается функция f(x)между другими двумя функции, которые также стремятся к пределу А.

    Все перечисленные свойства пределов позволяют исходный предел функции свести к уже известному, чтобы получить ответ.

    Определение и свойства пределов

    Число b называется пределом функции f(x) при x → a, если
    для любого ε > 0 сущестувует δ > 0 такое, что для любого x
    из δ-окрестности a (|x – a|
    Запись: ∀ ε > 0 ∃ δ > 0 : |x – a| |f(x) – f(a)|

    Обозначение

    Свойства пределов
     
    lim
    x → a    		(f(x) + g(x) – h(x)) = 
    lim
    x → a    		f(x) + 
    lim
    x → a    		g(x) – 
    lim
    x → a    		h(x)
     
    lim
    x → a    		(f(x) * g(x)) = 
    lim
    x → a    		f(x) * 
    lim
    x → a    		g(x)
     
    lim
    x → a    		(cf(x)) = c * 
    lim
    x → a    		f(x)
     
    lim
    x → a    		(f(x)
    g(x)    		) =   ( 
    lim
    x → a    		g(x) ≠ 0)

    Замечательные пределы
     
    lim
    x → ∞    		(1 + 1 
    x    		)x
         		 = 
    lim
    α → 0    		(1 + α) 1 
    α
     
         		 = e
    e = 2,718281828459045235360287471352662497757…

    Связь между десятичными и натуральными логарифмами
    lg(x) = M ln(x),
    где M = lg(e) = 0,43429448190325182765112891891666…

    mateshka.ru

    Как находить пределы?

    Существует в математике такое понятие, как предел функции. Чтобы понимать, как находить пределы, нужно помнить определение предела функции: функция f (x) имеет предел L в точке x = a, если для каждой последовательности значений х, сходящейся к точке a, последовательность значений у приближается к:

    Понятие и свойства пределов

    Что такое предел, можно понять из примера. Предположим, мы имеем функцию у=1/х. Если мы будем последовательно увеличивать значение х и смотреть, чему равен у, то получим всё уменьшающиеся значения: при х=10000 у=1/10000; при х=1000000 у=1/1000000. Т.е. чем больше х, тем меньше у. Если х=∞, у будет настолько мал, что его можно будет считать равным 0. Таким образом, предел функции у=1/х при х стремящемся к ∞ равен 0. Записывается это так:

    Предел функции имеет несколько свойств, которые нужно помнить: это существенно облегчит решение задач на нахождение пределов:

    • Предел суммы равен сумме пределов: lim(x+y)=lim x+lim y
    • Предел произведения равен произведению пределов: lim(xy)=lim x*lim y
    • Предел частного равен частному от пределов: lim(x/y)=lim x/lim y
    • Постоянный множитель выносят за знак предела: lim(Cx)=C lim x

    У функции у=1 /x, в которой x →∞, предел равен нулю, при x→0, предел равен ∞.

    В статье Как решать пределы подробно рассказывается методика решения таких задач. А мы рассмотрим несколько примеров.

    Решение примеров на пределы

    Начинать находить пределы функций надо всегда с подстановки в функцию того значения х, к которому он стремится.

    Пример 1

    • Lim (х-3) = lim (3-3) = 0
    • х→3

    Пример 2

    • Lim [х²/(1-х)]. Если подставить х=∞, получим
    • х→∞
    • ∞²/(1-∞) = ∞²/(-∞).

    Одну бесконечность в числителе и знаменателе сокращаем:

    • ∞/(-1) = -∞. Значит,
    • Lim [х²/(1-х)] = -∞.
    • х→∞

    В этих примерах всё просто. Однако обычно пределы функций ищут при таких значениях х, которые создают неопределённость типа 0/0 или ∞/∞. Такие неопределённости нужно раскрыват

    elhow.ru

Related Posts

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *