Матан идз тпу – Готовый учебная работа по теме «ИДЗ№ 2 ТПУ математика», купить по цене 250 руб
- Комментариев к записи Матан идз тпу – Готовый учебная работа по теме «ИДЗ№ 2 ТПУ математика», купить по цене 250 руб нет
- Советы абитуриенту
Краткая информацияОткрыта в 1982 году путём выделения её из состава кафедры высшей математики, основанной в 1900 году. Лекция, прочитанная 22 октября 1900 года Некрасовым В.Л. по высшей математике для студентов Томского технологического института, была началом деятельности в институте кафедры высшей математики. Именно на плечи В.Л. Некрасова, проработавшего в институте свыше 30 лет, легла почетная и нелегкая задача первой постановки учебного процесса по математике и механике в институте. Наибольший вклад в дело математической подготовки студентов института с 1900 года внесли профессора В.Л. Некрасов, Ф.Э. Молин, В.А. Малеев, В.И. Шумилов, М.Н. Иванов, С.П. Кузнецов, Е.Т. Ивлев, М.М. Никитин, которые в разное время были заведующими кафедрой. В начале двадцатых годов на кафедре работали И.М. Виноградов, впоследствии директор МИАН им. В.А. Стеклова, и Р.О. Кузьмин – автор известного задачника. Кафедра высшей математики и математической физики ТПУ обеспечивает преподавание дисциплин: аналитическая геометрия и линейная алгебра, высшая математика, математический анализ, уравнения математической физики, теория вероятностей и математическая статистика, многомерные статистические методы, функциональный анализ, информатика, математические методы в экономике, финансовая математика, планирование эксперимента в экономике, математические методы и модели исследования операций, теория случайных процессов, ценные бумаги и управление портфелем и др., на физико-техническом, электрофизическом, химико-технологическом факультетах, факультете естественных наук и математики и в электротехническом институте ТПУ.
|
|
mph.phtd.tpu.ru
ТПУ Линейная алгебра 1курс ИДЗ №1
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Национальный исследовательский Томский политехнический Университет»
Институт
дистанционного образования
линейная алгебра
Индивидуальное домашнее задание № 1
вариант №1
по дисциплине:
Линейная алгебра и аналитическая геометрия
Исполнитель: | |||||
студент группы | 18.11.2013 | ||||
Руководитель: | |||||
преподаватель | . | ||||
Томск 2013
Вариант № 1
Решение:
Решение:
Выполним вначале умножение матриц на число и упростим уравнение:
Обозначим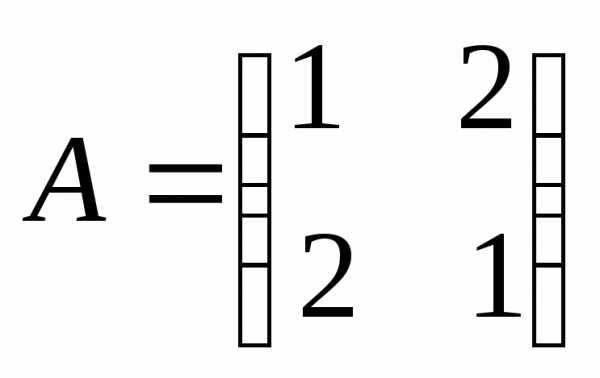 
,
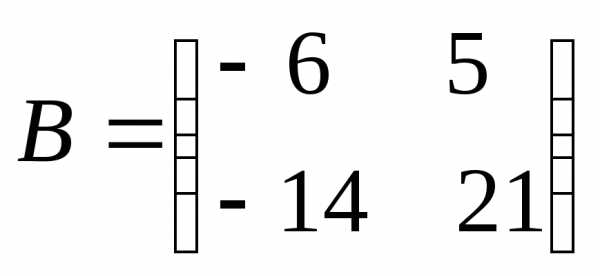
Тогда получим матричное уравнение вида , решение которого, где А-1 – это матрица, обратная матрице А.
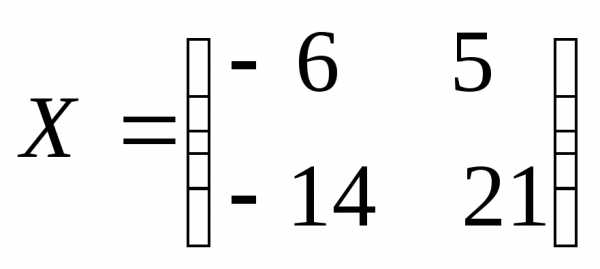
Найдем А-1 по известной схеме:
1)
2) 
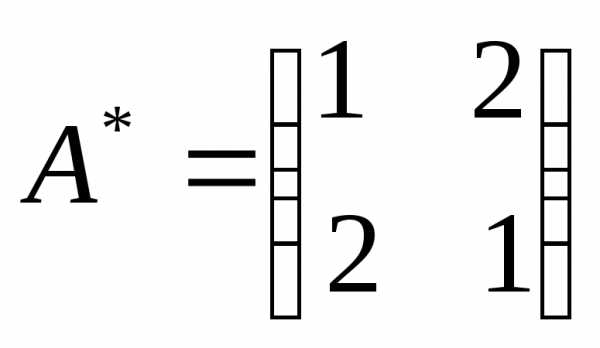
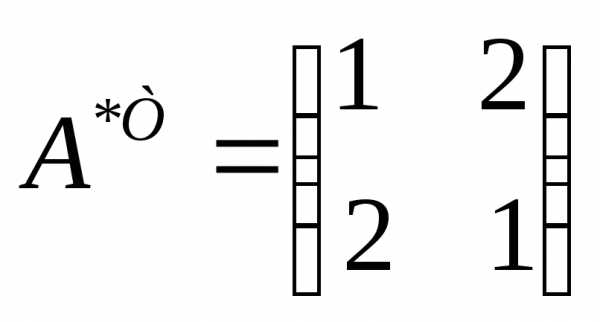
4)
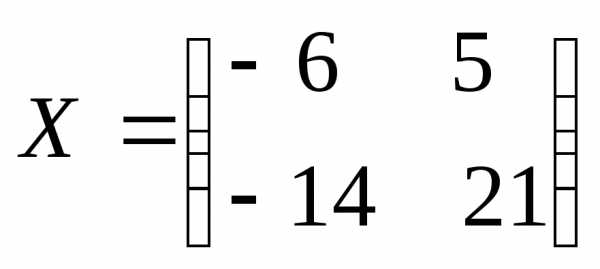
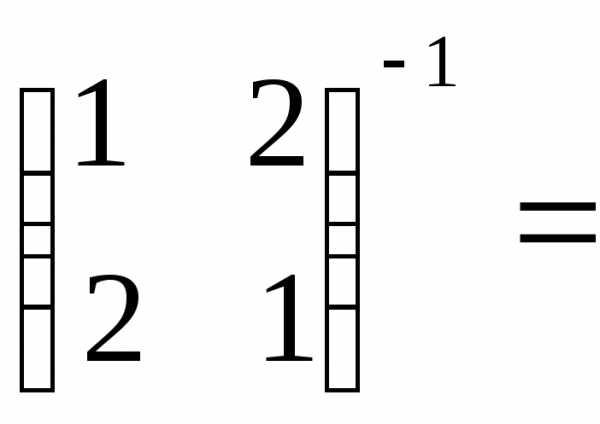
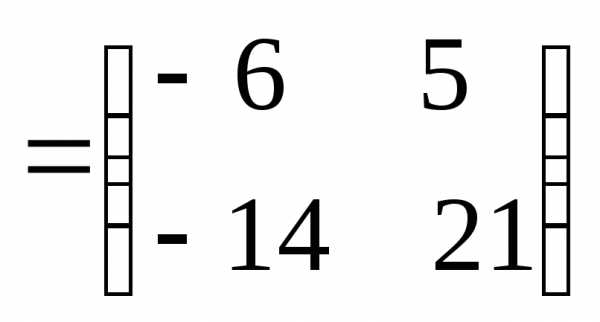
1. Метод Крамера
1)Вычислим главный определитель системы, который составляется из коэффициентов при неизвестных.
2)Вычислим побочные определители системы
Решение системы находим по формулам Крамера
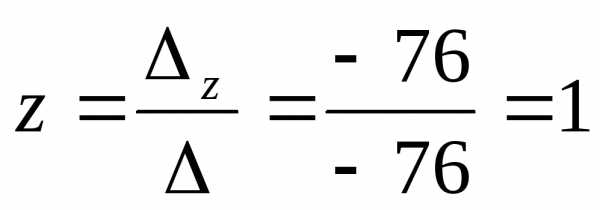
2. Матричный метод
1) обозначим матрицы
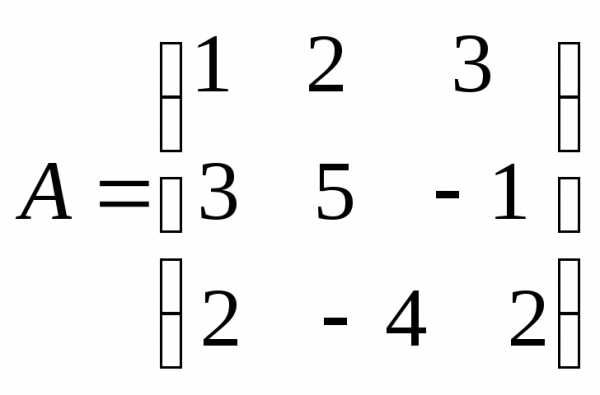
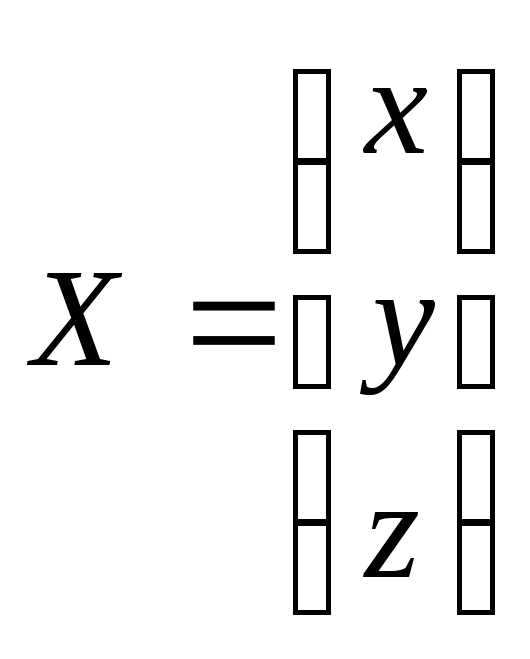
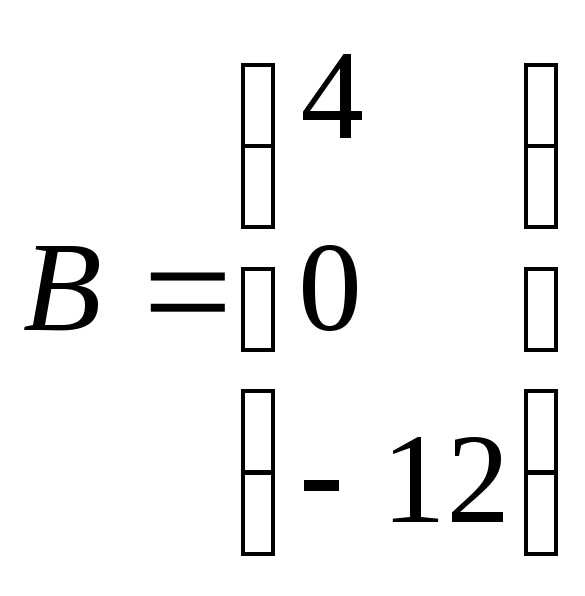
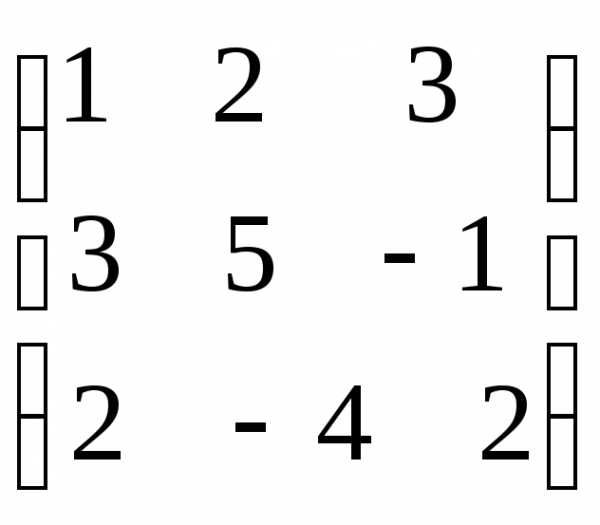
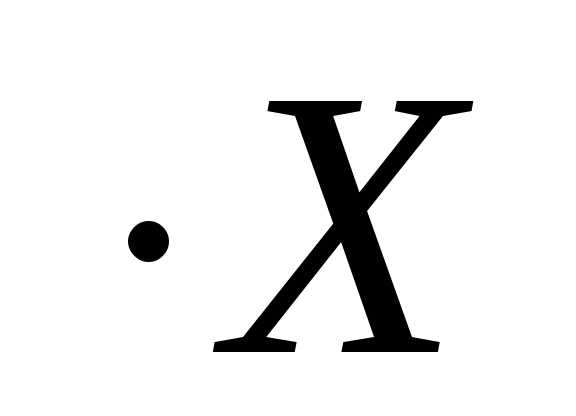
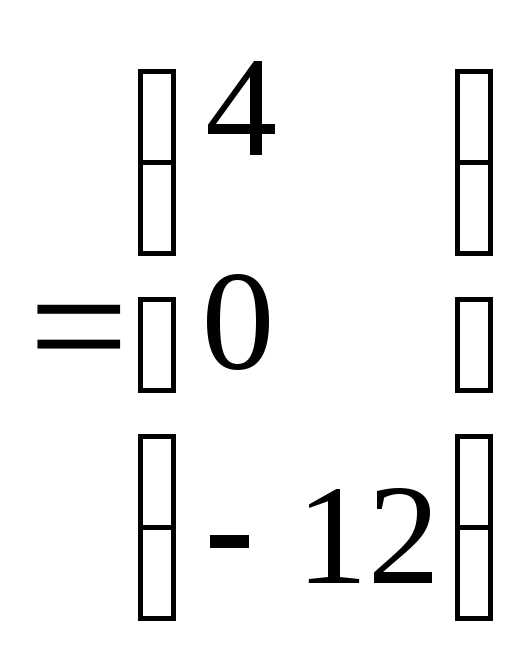
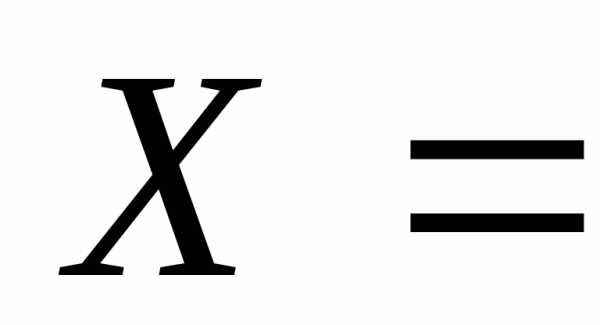
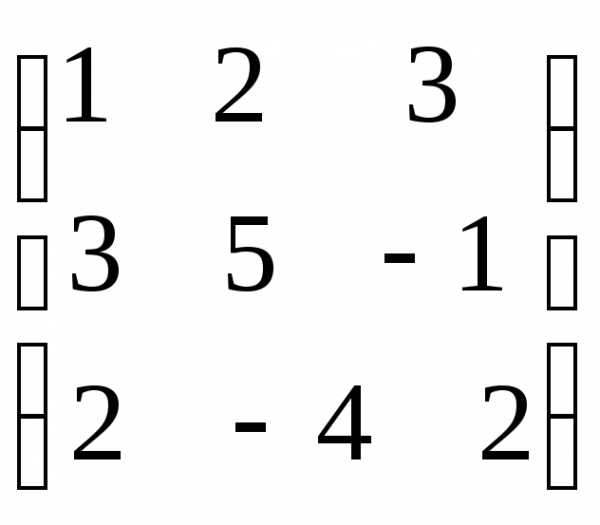
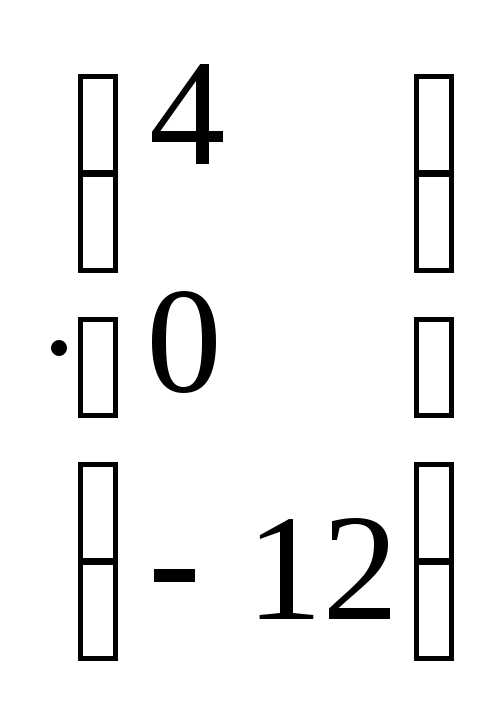
2) Находим обратную матрицу А-1 согласно схеме
Находим определитель данной матрицы
Находим алгебраические дополнения для каждого элемента матрицы А:
Вычисляем обратную матрицу А-1:
Решение системы уравнений Х=А-1В
3. Метод Гаусса
1) Выпишем расширеную матрицу системы и преобразуем её
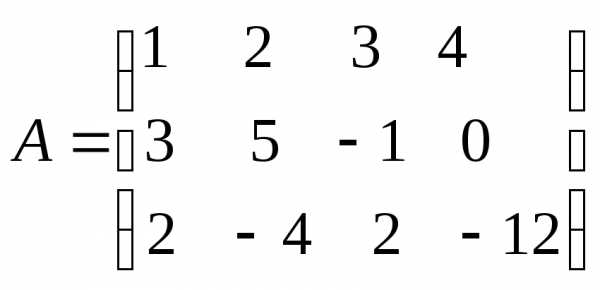
Умножаем строки 1 на (-3) и прибавляем строку 2, затем умножаем строку 1 на (-2) и прибавляем строку 3. получим.
умножаем
строку 2 на (-8) и прибавляем строку 3.
получим.
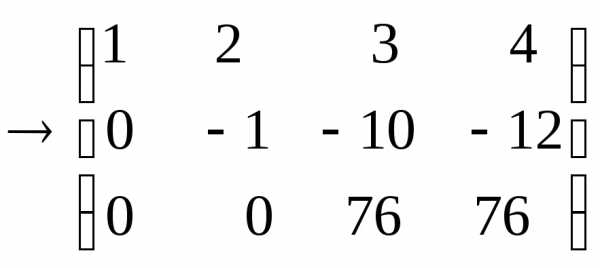
2) Выписываем эквивалентную систему и её решение
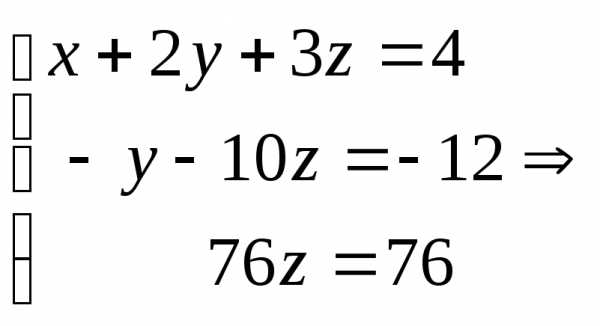
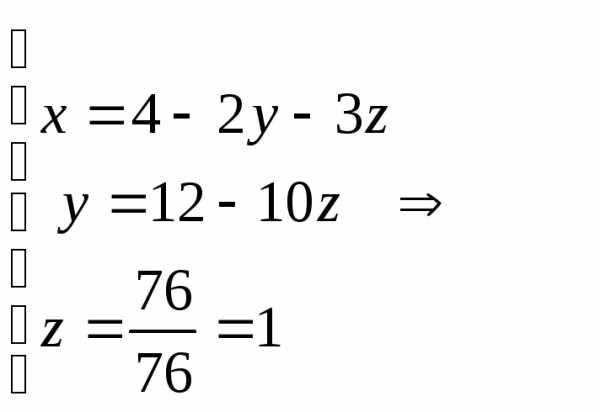
Ответ: х=-3, y=2, z=1
Список литературы по дисциплине «Линейная алгебра и аналитическая
геометрия»
1. Бугров Я.С., Никольский С.Н. Элементы линейной алгебры и аналитической геометрии.
М.: Наука, 2003г.
2. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры.- М.: Наука, 2002г.
3. Данко П.Е., Попов А.Г.Кожевникова Т.Я.Высшая математика в упражнениях и задачах.-
М.: Высшая школа, 2005г., ч.1
4. Письменный Д.Т.Конспект лекций по высшей математике: Полный курс.- М.:Айрис-
пресс,2004г.
5. Проскуряков И. В. Сборник задач по линейной алгебре.- М.: Наука, 2001.
6. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, 2005г.
7. Шнейдер В.Е. Краткий курс высшей математики. – М.: Высшая школа, 1999г. Т.1,2
8. Смирнов В.И. Курс высшей математики. – М.: Наука. 2001г.
9. Воеводин В.В. Линейная алгебра.- М.: Наука, 1980г.
10. Проскуряков И. В. Сборник задач по линейной алгебре.- М.: Наука, 1970г.
19
studfiles.net
I семестр – Тихоокеанский государственный университет
Бидерман В.И. Элементы векторной алгебры скачать (1.0 МБ)
Бидерман В.И. Введение в дифференциальное исчисление функции одной переменной скачать (399.6 КБ)
Бидерман В.И. Введение в математический анализ скачать (780.1 КБ)
Бидерман В.И. Линии и поверхности второго порядка скачать (390.4 КБ)
Бидерман В.И. Метод Гаусса скачать (436.4 КБ)
Бидерман В.И. Основные теоремы и приложения дифференциального исчисления функции одной переменной скачать (450.4 КБ)
Бидерман В.И. Элементы интегрального исчисления скачать (546.4 КБ)
Бушина Г.З., Кутний Л.А., Мун Г.В. Кривые второго порядка скачать (441.9 КБ)
Васильева Л.В., Мухранова В.В., Романчук О.А. Высшая математика. Справочное пособие скачать (640.2 КБ)
Индивидуальное домашнее задание «Дифференциальное исчисление функции одной переменной» скачать (304.0 КБ)
Индивидуальное домашнее задание «Последовательности» скачать (215.7 КБ)
Индивидуальное домашнее задание «Предел функции и непрерывность» скачать (186.7 КБ)
Индивидуальное домашнее задание «Элементы алгебры и геометрии» скачать (462.4 КБ)
Индивидуальное домашнее задание «Элементы математического анализа» скачать (145.7 КБ)
Карань Г.М., Манаков В.М., Мухранова В.В. Действия с матрицами скачать (276.0 КБ)
Ломакина Е.Н. Меженова Т.Я. Дифференцирование скачать (589.9 КБ)
Список литературы для бакалавриата и специалитета технических направлений скачать (133.0 КБ)
Список литературы для специальности «Компьютерная безопасность» скачать (140.7 КБ)
Таблица интегралов и дифференциалов скачать (173.4 КБ)
Таблица производных и дифференциалов скачать (171.8 КБ)
Чеботарев В.И. Исследование функций и построение графиков скачать (626.8 КБ)
Образцы рубежных контрольных работ
Аналитическая геометрия и линейная алгебра скачать (42.4 КБ)
Векторы скачать (45.1 КБ)
Входной контроль знаний скачать (360.5 КБ)
Выходной контроль знаний за I семестр скачать (250.4 КБ)
Вычисление пределов скачать (286.3 КБ)
Вычисление производных скачать (259.0 КБ)
Линейная алгебра и Аналитическая геометрия скачать (255.7 КБ)
Элементы математического анализа функции одной переменной скачать (53.0 КБ)
Вопросы к экзамену
Вопросы к экзамену ТЭФ-2016-17 (ГД, ЭТМ, ЭСУ) I семестр скачать (228.6 КБ)
Вопросы к экзамену ФКФН-2016-17 (КБ). I семестр, Математический анализ скачать (48.0 КБ)
pnu.edu.ru
Титульный лист
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Национальный исследовательский Томский политехнический Университет»
Институт
дистанционного образования
Электроэнергетика и электротехника
Индивидуальное домашнее задание № 1
по дисциплине:
Математический анализ 2
Исполнитель: | ||||||
студент группы | З-5А24 В№7 | Половников К Ю | 17.01.14. | |||
преподаватель | Мастеров И В | |||||
Томск 2014
studfiles.net
ТПУ Линейная алгебра 1курс ИДЗ №2
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Национальный исследовательский Томский политехнический Университет»
Институт
дистанционного образования
линейная алгебра
Индивидуальное домашнее задание № 2
вариант №1
по дисциплине:
Линейная алгебра и аналитическая геометрия
Исполнитель: | |||||
студент группы | 02.12.2013 | ||||
Руководитель: | |||||
преподаватель | |||||
Томск 2013
Вариант 1.
Задача 1. Даны три вектораa ={1;1;4},b ={0;-3;2},c ={2;1;-1}.
Требуется найти:
a) вектор
,
его модуль и направляющие косинусы,
записать орт вектора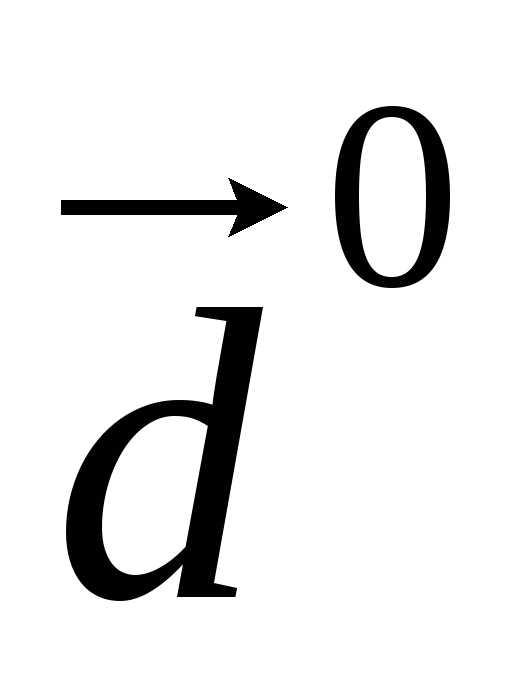
b) скалярное произведение векторов
c) векторное произведение векторов 
d) смешанное произведение векторов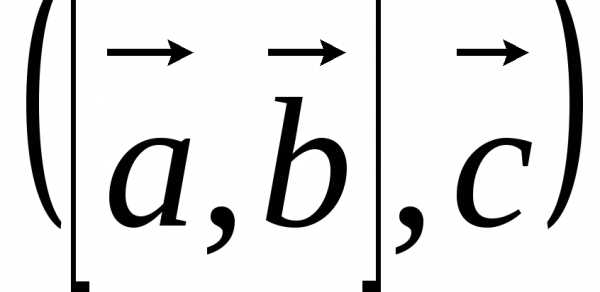 
Решение:
А) По правилам выполнения арифметических операций над векторами
Модуль вектора
Направляющие косинусы:
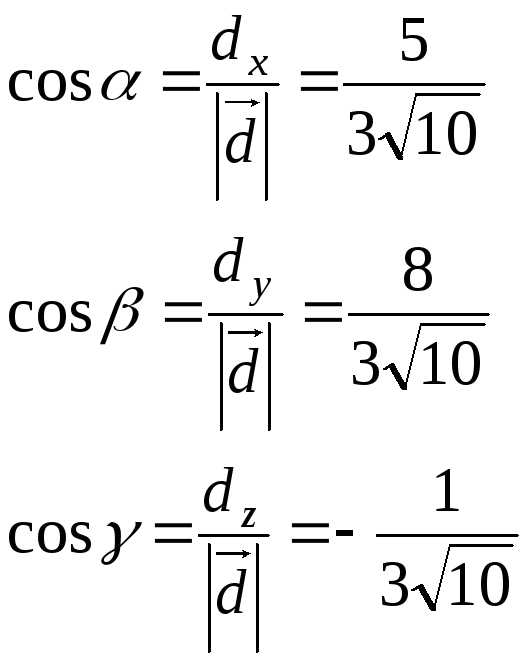
Координаты орта вектора равны отношению координат данного вектора к его модулю.
b) Сначала выполним операцию сложения векторов, а затем
скалярное умножение (сумма произведений одноименных координат)
c) векторное произведение векторов находится по правилу
d) Произведение векторов, обозначаемое
символом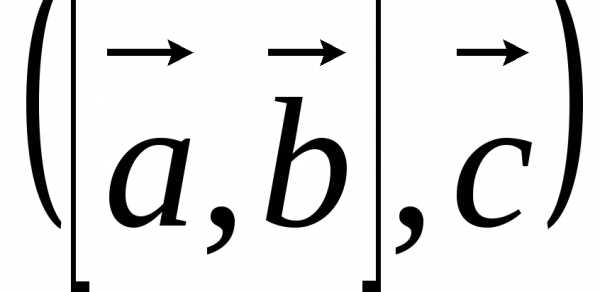 
,
есть векторно-скалярное, т.е. смешанное
произведение 3-х векторов. Оно вычисляется
по правилу
=
Задача 2. Определить координаты точкиC на отрезкеAB , если
A(2;-3;1),B(-2;2;-4) и |AC |:|CB |= 5: 2
Решение:
Обозначим координаты точки С: и составим 2 вектора
Координаты этих векторов находятся как разность соответствующих координат конечной и начальной точек. Так как все точки лежат на одной прямой, то составленные векторы являются коллинеарными и, согласно известному отношению, в котором точка делит отрезок
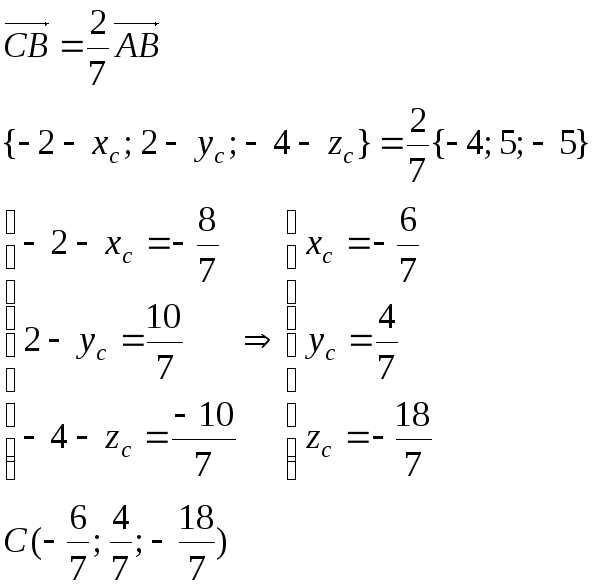
Задача 3.Найти модули векторов, если
Решение:
Так как координаты векторов не даны,
для нахождения длин воспользуемся общей
формулой длины вектора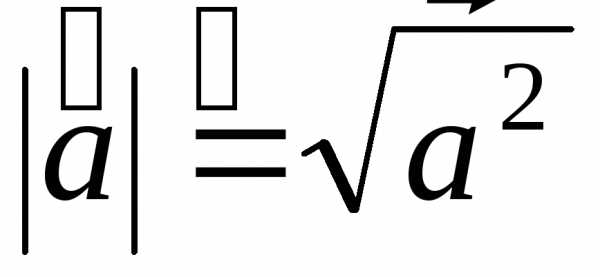 
Так как
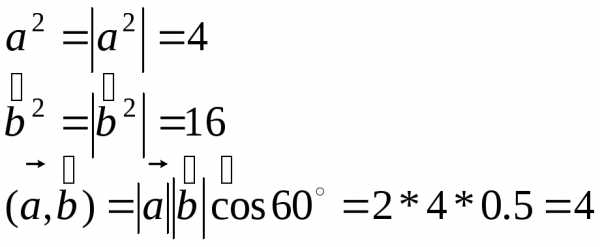
То
Задача 4. Даны три вершины параллелограммаABCD A(3;0;-3),B(-8;2;0),C(0;3;-4) . Определить:
a) координаты четвертой вершины D ,
в) длину высоты, опущенной из вершины D на сторонуAB,
с) косинус острого угла между диагоналями AC иBD .
Решение:
a) Координаты вершины Dможно найти из условия равенства векторовAD иBC . Как известно, равные векторы имеют одинаковые координаты.
Координаты вектора
Координаты вектора
Таким образом
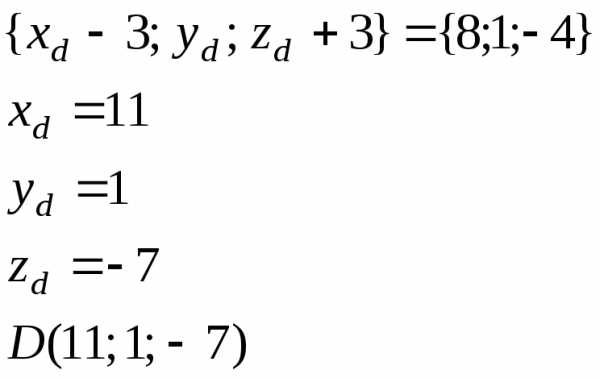
b) длину высоты найдем через площадь
параллелограмма, построенного на
векторах 
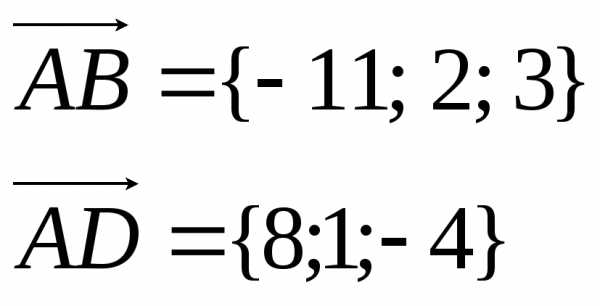
С одной стороны
С другой стороны
Таким образом
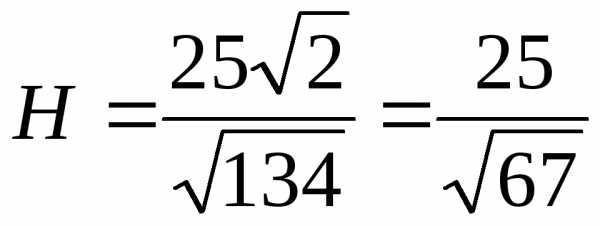
c) Для нахождения косинуса угла между
диагоналями воспользуемся формулой
косинуса угла между векторами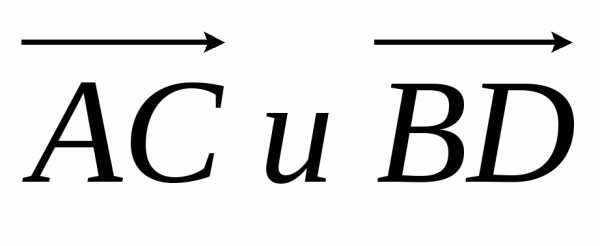 
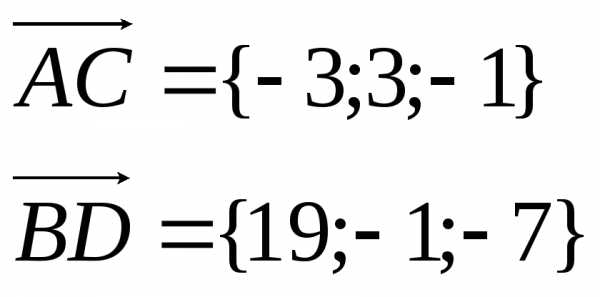
Скалярное произведение векторов диагоналей
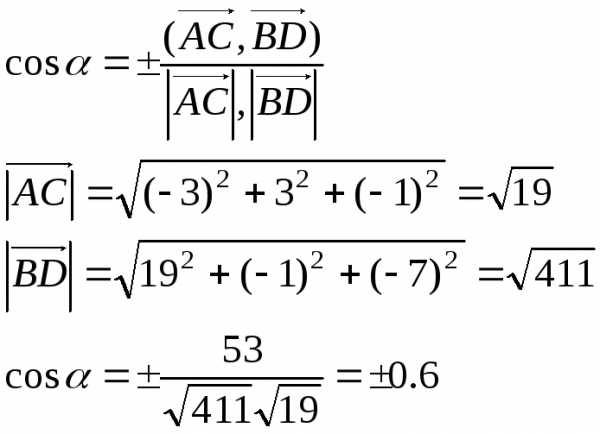
Так как требуется определить косинус острого угла (косинус острого угла больше нуля), то
Задача 5. Даны векторыa ={1;-2;3} иb ={5;0;-12}. Найти векторx, если известно, что
Решение
Из условия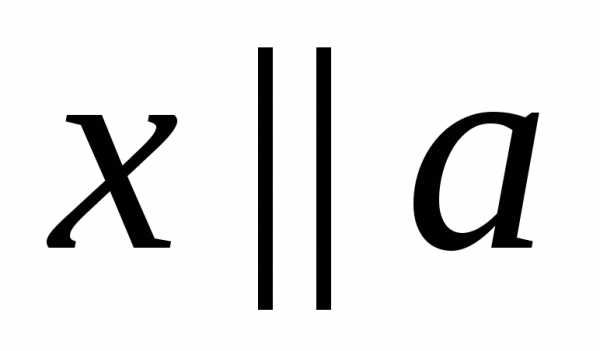 
следует, что
Из условия следует, что
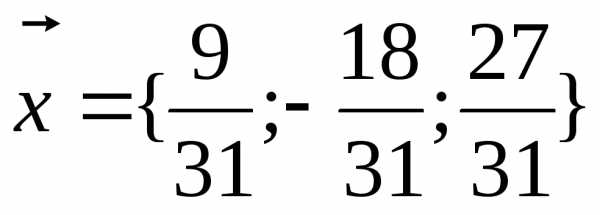
Задача 6. Найти единичный векторx, который одновременно перпендикулярен векторам
a ={-3;-5;1} иb ={-2;6;2}, если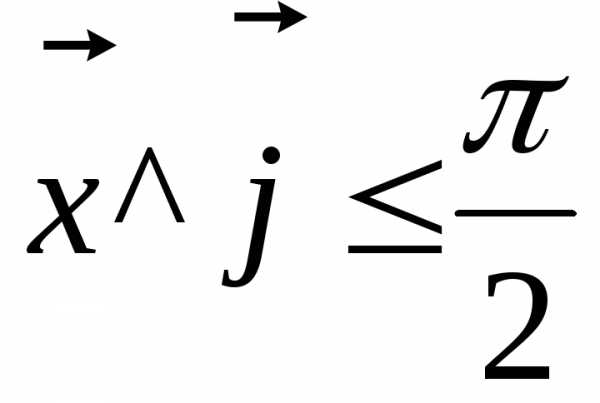
Решение
Так как вектор х перпендикулярен векторам а и b, значит, он параллелен нормали к этим векторамn
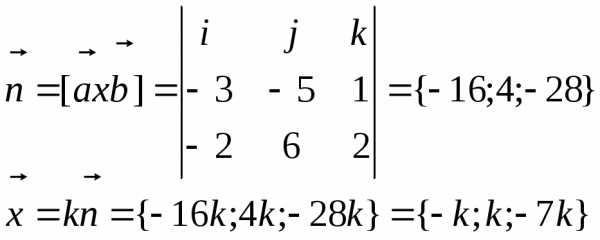
Вектор х по условию единичный, т.е.
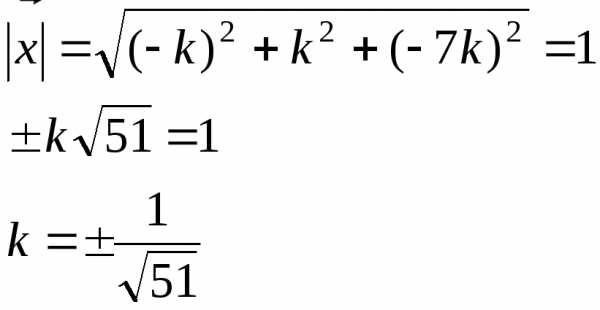
Получили 2 варианта ответа:
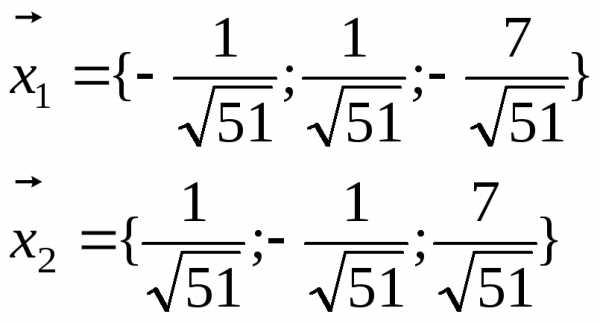
Согласно последнему условию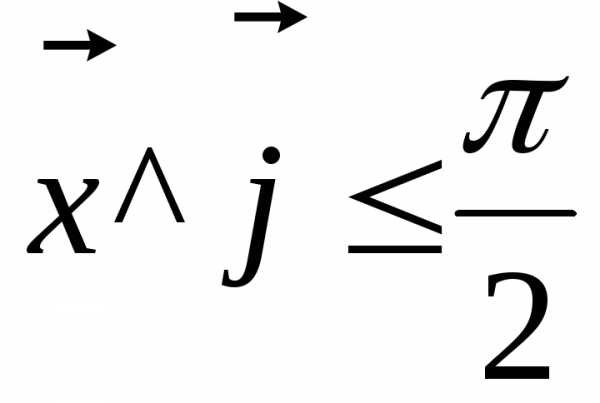 
,
которое означает, что угол между искомым
вектором и осьюOYострый, то есть
вторая координата вектора должна быть
положительной, поэтому окончательным
вариантом ответа есть вектор
Задача 7. В пирамидеABCD с вершинами в точкахA(1;1;1),B(-1;2;4),C(2;0;6),D(-2;5;1)
найти объем пирамиды и длину ее высоты, опущенной на грань ABC .
Решение:
Найдем векторы трех ребер пирамиды
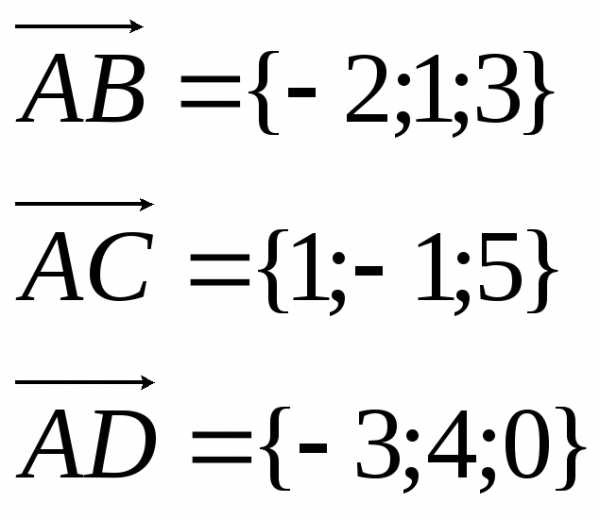
Объем пирамиды можно найти как шестая часть модуля смешанного произведения векторов ее сторон
Длину высоты пирамиды, опущенной на грань ABC, можно найти
через полученное значение объема.
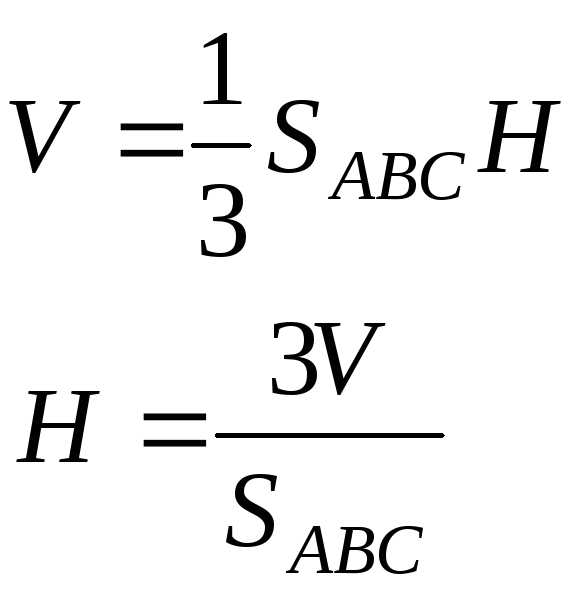
Площадь основания найдем с помощью векторного произведения
Таким образом
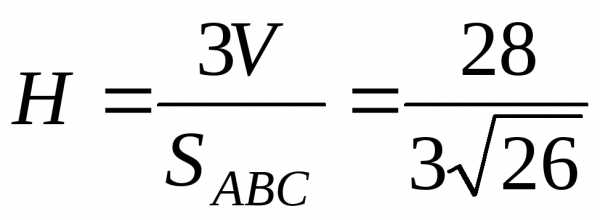
Задача 8. Доказать, что векторыa ={0;2;1},b ={0;1;-1},c ={5;-3;2} образуют базис и найти разложение вектораx ={15;-20;-1} в этом базисе.
Решение:
Для того, чтобы доказать, что три вектора в пространстве образуют базис, достаточно установить, что они некомпланарны, т.е. их смешанное произведение не равно нулю. Проверим это
Таким образом, вектор xможно разложить в этом базисе.
Уравнивая одноименные координаты векторов, получаем систему уравнений для нахождения коэффициентов разложения.
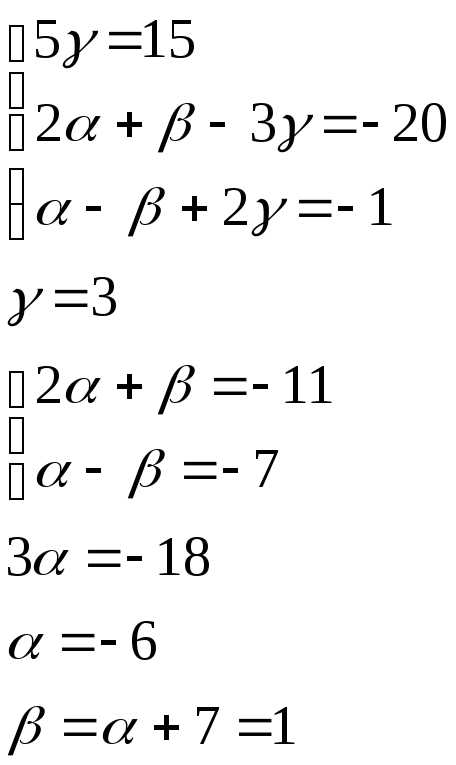
10
studfiles.net
МатАн ТПУ | Томск
Беломестных Л.А., Пестова Н.Ф., Пилипенко В.А., Заверткин C.Д.
Неопределенный интеграл: Методические указания и контрольные задания по высшей математике с элементами учебных исследований для студентов всех специальностей / Сост. Л.А. Беломестных, Н.Ф. Пестова, В.А. Пилипенко, C.Д. Заверткин. – Томск: Изд-во ТПУ, 2006. – 34 с.
Гиль Л.Б., Тищенкова А.В.
Гиль Л.Б. Сборник задач по высшей математике. Часть II. Введение в математический анализ. Дифференциальное исчисление функции одного вещественного аргумента: учебное пособие / Л.Б. Гиль, А.В. Тищенкова. – 2-е изд., испр. и допол. – Томск: Изд-во Томского политехнического университета, 2009. – 113 с.
Подскребко Э.Н., Пестова Н.Ф.
Подскребко Э.Н. Дифференциальное исчисление функций нескольких переменных: учебное пособие / Э.Н. Подскребко, Н.Ф. Пестова. – Томск: Изд-во Томского политехнического университета, 2008. – 132 с.
Гиль Л.Б., Тищенкова А.В.
Определённый интеграл: методические указания по математике для студентов всех специальностей очной формы обучения / Сост. Л.Б. Гиль, А.В. Тищенкова. – Юрга: Изд-во Юргинского технологического института (филиала) Томского политехнического университета, 2011. – 71 с.
Гиль Л.Б., Тищенкова А.В.
Двойной интеграл: методические указания по математике для студентов всех специальностей очной формы обучения / Сост. Л.Б. Гиль, А.В. Тищенкова. – Юрга: Изд-во Юргинского технологического института (филиала) Томского политехнического университета, 2011.- 37 с.
Гиль Л.Б., Тищенкова А.В.
Дифференциальное исчисление функции нескольких переменных: методические указания для студентов всех специальностей / Сост. Л.Б. Гиль, А.В. Тищенкова. – Юрга: Изд-во Юргинского технологического института (филиала) Национального исследовательского Томского политехнического университета, 2010. – 77 с.
zzapomni.com
