Математические функции matlab – Иллюстрированный самоучитель по MatLab › Специальные математические функции › Функции Эйри [страница – 208] | Самоучители по математическим пакетам
- Комментариев к записи Математические функции matlab – Иллюстрированный самоучитель по MatLab › Специальные математические функции › Функции Эйри [страница – 208] | Самоучители по математическим пакетам нет
- Советы абитуриенту
Основные математические функции MatLab
Поиск ЛекцийВ ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква d. sin(x) – аргумент в радианах, а sind(x) – аргумент в градусах.
Некоторые часто используемые математические функции:
· exp(x)–экспонента числа x;
· log(x)– натуральный логарифм;
· log10(x)– десятичный логарифм;
· sqrt(x)– квадратный корень;
· abs(x)– абсолютное значение x;
· mod(x, y)– остаток от целочисленного деления с учетом знака;
· rem(x, y)– остаток от целочисленного деления без учета знака;
· real(z)– вещественная часть комплексного числа;
· imag(z)– мнимая часть комплексного числа;
· round(x)– округление до ближайшего целого.
Более полный список основных математических функций MatLab:
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x,y) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения:
Вычислить: res=
Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. Причем открытую скобку следует сразу закрывать и продолжать набор формулы внутри скобок. В этом случае число открывающих скобок будет равно числу закрывающих, и вероятность ошибки будет минимальной.
Если в выражении многократно встречаются одинаковые фрагменты, то их целесообразно вычислять 1 раз и результат помещать в отдельные переменные. Это позволяет избежать одинаковых вычислений и тем самым оптимизирует вычисления.
x =0.5;
y =1;
res=(3*cos(x^3)^2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
res =
1.0207e+006
Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. При сохранении они автоматически получают расширение системы – m.
Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Перед запуском программы на выполнение необходимо установить нужный каталог в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна.
Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
Операторы ввода/вывода
Рекомендуемые страницы:
poisk-ru.ru
Основные элементы языка программирования Matlab
Как и большинство других языков программирования, Matlab предоставляет возможность использования математических выражений, но в отличие от многих из них, эти выражения в Matlab включают матрицы. Основные составляющие выражения:
— переменные;
— числа;
— операторы;
— функции.
Переменные. В Matlab нет необходимости в определении типа переменных или размерности. Когда Matlab встречает новое имя переменной, он автоматически создает переменную и выделяет соответствующий объем памяти. Если переменная уже существует, Matlab изменяет ее состав и если это необходимо выделяет дополнительную память. Например,
num_students = 25
создает матрицу 1×1 с именем num_students и сохраняет значение 25 в ее единственном элементе.
Имена переменных состоят из букв, цифр или символов подчеркивания. Matlab использует только первые 31 символ имени переменной. Matlab чувствителен к регистрам, он различает заглавные и строчные буквы. Поэтому A и a — не одна и та же переменная. Чтобы увидеть матрицу, связанную с переменной, просто введите название переменной.
Числа. Matlab использует принятую десятичную систему счисления, с необязательной десятичной точкой и знаками плюс-минус для чисел. Научная система счисления использует букву e для определения множителя степени десяти. Мнимые числа используют i или j как суффикс. Некоторые примеры правильных чисел приведены ниже:
3 | -99 | 0.0001 |
9.6397238 | 1.60210е-20 | 6.02252е23 |
1i | -3.14159j | 3e5i |
Все числа для хранения используют формат long, это числа с плавающей точкой обладающие ограниченной точностью — приблизительно 16 значащих цифр и ограниченным диапазоном — приблизительно от 10-308 до 10308.
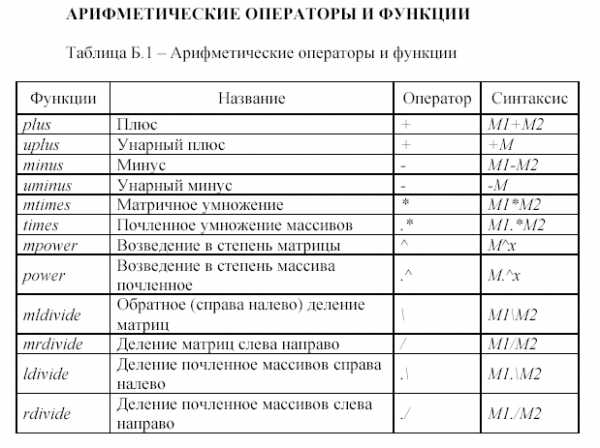
Операторы. Выражения используют обычные арифметические операции и правила старшинства (табл. 1).
Таблица 1
Арифметические операции пакета Matlab
help elfun
Чтобы посмотреть список всех функций Matlab для анализа данных:
help datafun
Если вам нужно узнать о Statistics Toolbox, введите:
help stats
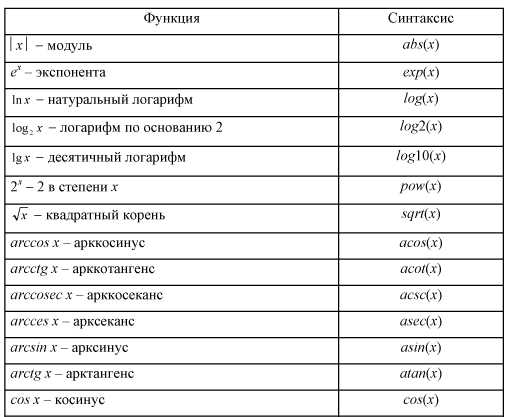
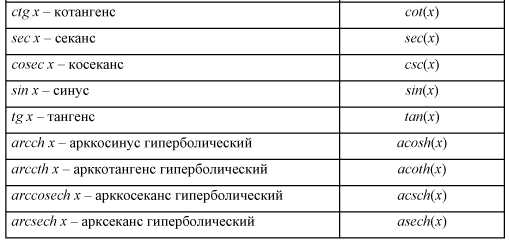
Список элементарных функций представлен в табл. 2.
Таблица 2
Элементарные функции пакета Matlab
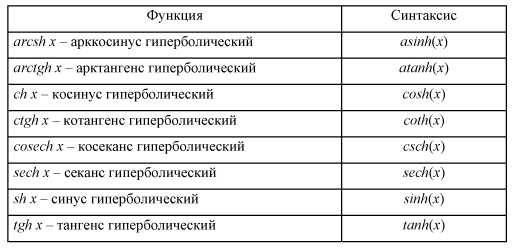
Логарифм числа по основанию:.
Для вывода более сложных математических и матричных функций, наберите:
help specfun
help elmat
соответственно.
Некоторые функции, такие как sqrt и sin, — встроенные. Они являются частью Matlab, поэтому они очень эффективны, но их вычислительные детали трудно доступны. В то время как другие функции, такие как gamma и sinh, реализованы в m-файлах. Поэтому можно увидеть их код и, в случае необходимости, даже модифицировать его.
pi | Число 3,14159265… |
i или j | Мнимая единица |
eps | Относительная точность числа с плавающей точкой |
realmin | Наименьшее число с плавающей точкой |
realmax | Наибольшее число с плавающей точкой |
Inf | Бесконечность |
| NaN | Не число (неопределенность вида 0/0 или ∞/∞) |
Бесконечность появляется при делении на ноль или при выполнении математического выражения, приводящего к переполнению, т. е. к превышению realmax. Не число (NaN) генерируется при вычислении выражений типа 0/0 или Inf/Inf, которые не имеют определенного математического значения.
Имена функций не являются зарезервированными, поэтому возможно изменять их значения на новые, например:
eps = 1.e-6
и далее использовать это значение в последующих вычислениях. Начальное значение может быть восстановлено следующим образом:
clear eps
Операторы отношения служат для сравнения двух величин, векторов или матриц, все операторы отношения имеют две сравниваемые величины и записываются, как показано в табл. 3.
Таблица 3
studfiles.net
Основные математические функции MatLab – Математика
В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква d. sin(x) – аргумент в радианах, а sind(x) – аргумент в градусах.
Некоторые часто используемые математические функции:
· exp(x)–экспонента числа x;
· log(x)– натуральный логарифм;
· log10(x)– десятичный логарифм;
· sqrt(x)– квадратный корень;
· abs(x)– абсолютное значение x;
· mod(x, y)– остаток от целочисленного деления с учетом знака;
· rem(x, y)– остаток от целочисленного деления без учета знака;
· real(z)– вещественная часть комплексного числа;
· imag(z)– мнимая часть комплексного числа;
· round(x)– округление до ближайшего целого.
Более полный список основных математических функций MatLab:
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x,y) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения:
Вычислить: res=
Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. Причем открытую скобку следует сразу закрывать и продолжать набор формулы внутри скобок. В этом случае число открывающих скобок будет равно числу закрывающих, и вероятность ошибки будет минимальной.
Если в выражении многократно встречаются одинаковые фрагменты, то их целесообразно вычислять 1 раз и результат помещать в отдельные переменные. Это позволяет избежать одинаковых вычислений и тем самым оптимизирует вычисления.
x =0.5;
y =1;
res=(3*cos(x^3)^2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
res =
1.0207e+006
Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. При сохранении они автоматически получают расширение системы – .m.
Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
Перед запуском программы на выполнение необходимо установить каталог, содержащий скрипт-файл, в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна. Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта.
Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
student2.ru
Специальные математические функции MatLab
Урок 9. Специальные математические функции
Функции Эйри
Функции Бесселя
Бета-функция и ее варианты
Эллиптические функции и интегралы
Функции ошибки
Интегральная показательная функция
Гамма-функция и ее варианты
Ортогональные полиномы Лежандра
Что нового мы узнали?
Функции Эйри
Функции Бесселя
Бета-функция и ее варианты
Эллиптические функции и интегралы
Функции ошибки
Интегральная показательная функция
Гамма-функция и ее варианты
Ортогональные
полиномы Лежандра
Специальные математические функции являются решениями дифференциальных уравнений специального вида или обозначениями некоторых видов интегралов. Довольно полный обзор специальных функций дается в книгах [55-58], так что ниже мы ограничимся только указанием функций системы MATLAB, реализующих их вычисление. Набор специальных математических функций в системе MATLAB настолько представителен, что позволяет решать практически все задачи, связанные с применением таких функций. Если и обнаруживаются недостающие специальные функции, то пользователь может сам задать их вычисления. Специфика специальных функций в MATLAB та же, что и элементарных, — их аргументами могут быть как одиночные численные значения, так и массивы чисел. В последнем случае функции возвращают массив тех же размерности и размера с преобразованием каждого элемента в соответствии с действием функции. В версии MATLAB 6 вы теперь можете получить справку с записью формул в стандартной математической форме, набрав в командной строке doc function, где function — имя специальной функции.
radiomaster.ru
Система математических расчетов MATLAB
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ
MATLAB
УЧЕБНОЕ ПОСОБИЕ
Гаспарян Олег Николаевич
Д.т.н, с.н.с
2005
СОДЕРЖАНИЕ
Система математических расчетов MATLAB 4
Рабочий стол (desktop) системы MATLAB 5
Получение справок (Getting Help) 7
Рабочее пространство системы MATLAB 13
редактора Array Editor 16
Пути доступа системы MATLAB 18
Действия над матрицами в системе MATLAB 24
Анализ данных и статистика 50
Создание Многомерных Массивов 66
Организация и хранение данных 74
Массивы структур 75
Массивы ячеек 86
Програмирование на MATLAB-е 97
Типы данных 108
Команды управления данными ( Flow Control) 114
Приложение 1. Тематические направления системы MATLAB 121
Приложение 2 . Команды общего назначения
(General purpose commands) 123
(Elementary math functions). 127
(Elementary matrices and matrix manipulation)
Приложение 6. – Матричные функции и линейная алгебра
(Matrix functions – numerical linear algebra) 129
Приложение 7. Полиномы и интерполяция
(Interpolation and polynomials) 132
Приложение 9. Функции обработки символьных строк
(Character strings) 135
Справочник по базовым функциям
системы MATLAB 137
Система математических расчетов MATLAB
Система MATLAB (сокращение от MATrix LABoratory – МАТричная Лаборатория) разработана фирмой The MathWorks, Inc. (США, г.Нейтик, шт. Массачусетс) и является интерактивной системой для выполнения инженерных и научных расчетов, которая ориентирована на работу с массивами данных. Система использует математический сопроцессор и допускает обращения к программам, написанным на языках Fortran, C и C++ .
Наиболее известные области применения системы MATLAB:
· математика и вычисления;
· разработка алгоритмов;
· вычислительный эксперимент, имитационное моделирование;
· анализ данных, исследование и визуализация результатов;
· научная и инженерная графика;
· разработка приложений, включая графический интерфейс
пользователя.
MATLAB – это интерактивная система, основным объектом которой является массив, для которого не требуется указывать размерность явно. Это позволяет решать многие вычислительные задачи, связанные с векторно-матричными формулировками, существенно сокращая время, необходимое для программирования на скалярных языках типа Fortran или C. Будучи ориентированной на работу с реальными данными, эта система выполняет все вычисления в арифметике с плавающей точкой, в отличие от систем компьютерной алгебры REDUCE, MACSYMA, DERIVE, Maple, Mathematica, Theorist, где преобладает целочисленное представление и символьная обработка данных.
Система MATLAB – это одновременно и операционная среда и язык программирования. Одна из наиболее сильных сторон системы состоит в том, что на языке MATLAB могут быть написаны программы для многократного использования. Пользователь может сам написать специализированные функции и программы, которые оформляются в виде М-файлов. По мере увеличения количества созданных программ возникают проблемы их классификации и тогда можно попытаться собрать родственные функции в специальные папки. Это приводит к концепции пакетов прикладных программ (Application Toolboxes или просто Toolboxes), которые представляют собой коллекции М-файлов для решения определенной задачи или проблемы.
В действительности Toolboxes – это нечто большое, чем просто набор полезных функ-ций; часто это результат работы многих исследователей по всему миру, которые объеди- няются в группы по самым различным интересам, начиная от нейтронных сетей, дифференциальных уравнений в частных производных, сплайн-аппроксимации, статистики и размытых множеств до проектирования робастных систем управления, теории сигналов, идентификации, а также моделирования линейных и нелинейных динамических систем с помощью исключительно эффективного пакета SIMULINK. Именно поэтому пакеты прикладных программ MATLAB Application Toolboxes, входящие в состав семейства продуктов MATLAB, позволяют находиться на уровне самых современных мировых достижений в разных областях науки и техники.
Вызов и выход из MATLAB
Вызов MATLAB-а . Для вызова системы MATLAB требуется двойное нажатие на иконку в рабочем столе Windows. При инсталляции MATLAB-а стартовой директорией по умол-чанию является $matlabroot\work, где $matlabroot есть директория, где установлены файл-ы системы MATLAB.
При вызове, система MATLAB автоматически выполняет главный М-файл (master M-file) matlabrc.m., и файл startup.m (есди последний существует). Файл matlabrc.m , которые расположен в директории local , зарезервирован фирмой The MathWorks, а в многопользова-тельских системах может быть использован также системным менеджером. Файл startup.m предназначен для задания ряда стартовых опций (возможностей) по усмотрению пользователя. Вы можете изменить исходные пути доступа (см. далее), ввести заранее определенные переменные в рабочее пространство, изменить текущую директорию и т.д. Стартовый файл startup.m следует ввести в директорию $matlabroot\toolbox\local (более подробно с данным вопросом можно ознакомиться в справочных пособиях по MATLAB-у).
Выход из MATLAB-а. Для окончания сеанса работы с MATLAB следует выбрать опцию Exit MATLAB (Выход из MATLAB) в меню File на рабочем столе MATLAB-а, или напеча-тать quit (Выход) в командном окне Command Window.
При выходе, MATLAB выполняет специальный файл finish.m , относящийся к типу сценари-ев (см. далее) , если только данный файл существует в текущей директории или где-либо на пути доступа системы MATLAB. Файл finish.m создается пользователем. Он должен содер-жать функции или операции, которые пользователь желает автоматически выполнить при выходе из системы MATLAB, например, такие как сохранение рабочего пространства или вызов диалогового окна, запрашивающего подтверждения выхода. В указанной выше дирек-тории $matlabroot\toolbox\local имеются два файла, которые пользователь может использо-вать в качества образца при создании своего файла finish.m :
•finishsav.m – Включает функцию save , что приводит к автоматическому запоминанию рабо-чего пространства при выходе из MATLAB-а.
•finishdlg.m – Выводит на экран подтверждающее диалоговое окно, которое позволяет анну-лировать выход.
Рабочий стол (desktop) системы MATLAB
Рабочий стол системы MATLAB содержит следующие инструментальные окна, часть из которых не появляется при начальном запуске:
• Command Window (Командное Окно) – Выполняет все функции и команды системы
MATLAB.
• Command History (История Команд) – Просмотр функций, введенных ранее в
Command Window , их копирование и выполнение.
• Launch Pad (Окно Запуска) – Запускает все инструменты и обеспечивает доступ ко
всем пакетам системы MATLAB .
• Current Directory Browser (Окно Просмотра Текущего Каталога) – Просмотр файлов
MATLAB, а также сопутствующих файлов, а также выполнение таких операций
над файлами, как поиск и открытие файлов.
• Help Browser (Окно Просмотра Помощи) – Поиск и просмотр документации по всем
функциям и средствам системы MATLAB.
• Workspace Browser (Окно Просмотра Рабочего Пространства) – Просмотр и изменение
содержания рабочего пространства (workspace) системы MATLAB.
• Array Editor (Редактор Массивов Данных) – Просмотр содержимого массивов данных,
записанных в виде таблицы и редактирование данных.
• Editor/Debugger (Редактор/Отладчик) – Для создания, редактирования и отладки
М-файлов, т.е. файлов, содержащих функции системы MATLAB.
Общий вид рабочего окна MATLAB представлен ниже (рис.1). Каждое из перечисленных окон может быть выведено из конфигурации рабочего стола нажатием кнопки со стрелкой
в верхнем правом углу окна (см. рис. 1). Обратная операция, то есть ввод в общую конфигурацию, осуществляется выбором опции Dock в меню View сответствующего окна. Можно также изменить конфигурацию рабочего стола путем перемещения любого откры-того окна в новое положение. Для этого нужно просто нажать левой клавишей мыши на выбранное название окна (Title Bar) и «перетащить» его в желаемое положение.Для восстановления стандартной конфигурации рабочего стола MATLAB необходимо выбрать опцию Default (По Умолчанию) в подменю Desktop Layout (План Рабочего Стола) в меню View (Вид) любого открытого окна системы. Все окна MATLAB содержат также контекстное меню (context menu), которое вызывается нажатием правой кнопки мыши и содержит наиболее часто применяемые опции (функции), связанные с данным окном.
Таким образом. в системе MATLAB имеется возможность изменения вида рабочего стола путем открытия, закрытия, перемещения или изменения размеров каждого из индивидуаль-ных окон.
Просмотр продуктов Просмотр или Кнопка для
и демонстрационных Вызов изменение текущей вывода окна из состава
роликов помощи Ввод функций директории рабочего стола Закрытие окна
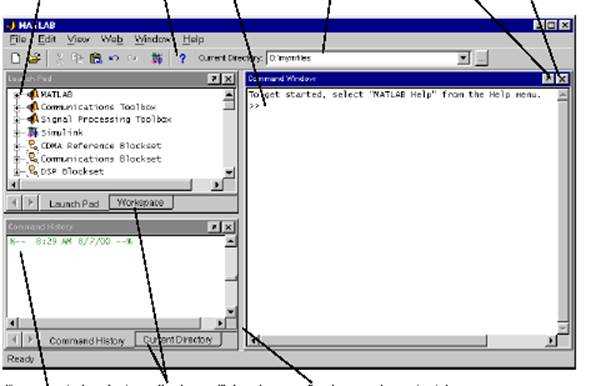
Просмотр и вызов Переход к рабочему Нажатием левой клавиши мыши и перемещением
mirznanii.com



