28.05.202016.12.2018

Матрица прямоугольная пример – Виды матриц. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому и треугольному виду

• by alexxlab
• Комментариев к записи Матрица прямоугольная пример – Виды матриц. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому и треугольному виду нет
• Советы абитуриенту

(35)84.Что такое прямоугольные и квадратные матрицы? Примеры.

Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины столбцов.

aij– элемент матрицы, который находится в i-ой строке и j-м столбце.

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

.

Примеры:

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной

. В примерах это первая матрица и третья.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

↑ назад в содержание ↑

(36)85.Что такое линейные операции над матрицами? Примеры.

Во всех случаях, когда вводятся новые математические объекты, необходимо договариваться о правилах действийнад ними, а также определить – какие объекты считаются равнымимежду собой.

Природа объектов не имеет никакого значения. Это могут быть вещественные или комплексные числа, векторы, матрицы, строки или что-то иное.

К числу стандартных действий относятся линейные операции, а именно: умножение на число и сложение; в данном конкретном случае – умножкние матрицы на число и сложение матриц.

При умножении матрицы на число каждый матричный элемент умножается на это число, а сложение матриц подразумевает попарное сложение элементов, расположенных в эквивалентных позициях.

Терминологическое выражение ” линейная комбинация<” (векторов, матриц, строк, столбцов и так далее) всегда означает одно и тоже: алгебраическая сумма этих векторов (или матриц, строк, столбцов и так далее), предварительно умноженных на числовые коэффициенты.

Матрицы  A = || a_i j ||  и  B = || a_i j ||  считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны:

(1)

для любых допустимых значений индексов  i  и  j.  К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число).  Умножение матрицы на число  При умножении матрицы  A  на число  λ  (слева или справа) каждый ее матричный элемент умножается на это число:

(2)

Сложение матриц  Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц  A = || a_i j ||  и  B = || b_i j ||  является матрица  C = || c_i j

 || , элементы которой равны сумме соответствующих матричных элементов:

(3)

Линейной комбинацией матриц A и B называется выражение вида  , гдеи– числовые коэффициенты.

↑ назад в содержание ↑

studfiles.net

Виды матриц. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому и треугольному виду

Матрица – это особый объект в математике. Изображается в форме прямоугольной или квадратной таблицы, сложенной из определенного числа строк и столбцов. В математике имеется большое разнообразие видов матриц, различающихся по размерам или содержанию. Числа ее строк и столбцов именуются порядками. Эти объекты употребляются в математике для упорядочивания записи систем линейных уравнений и удобного поиска их результатов. Уравнения с использованием матрицы решаются посредством метода Карла Гаусса, Габриэля Крамера, миноров и алгебраических дополнений, а также многими другими способами. Базовым умением при работе с матрицами является приведение к стандартному виду. Однако для начала давайте разберемся, какие виды матриц выделяют математики.

Нулевой тип

Все компоненты этого вида матрицы – нули. Между тем, число ее строк и столбцов абсолютно различно.

Квадратный тип

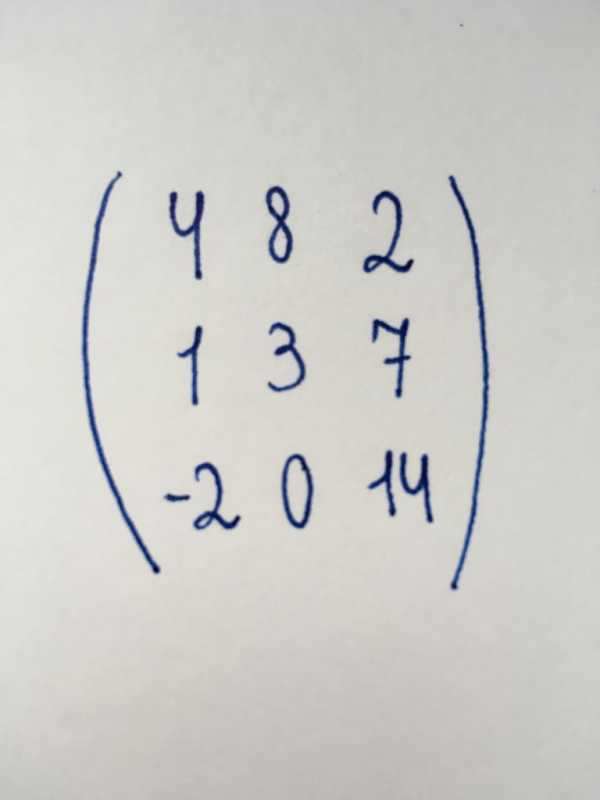
Количество столбцов и строк этого вида матрицы совпадает. Иначе говоря, она представляет собой таблицу формы “квадрат”. Число ее столбцов (или строк) именуются порядком. Частными случаями считается существование матрицы второго порядка (матрица 2×2), четвертого порядка (4×4), десятого (10×10), семнадцатого (17×17) и так далее.

Вектор-стобец

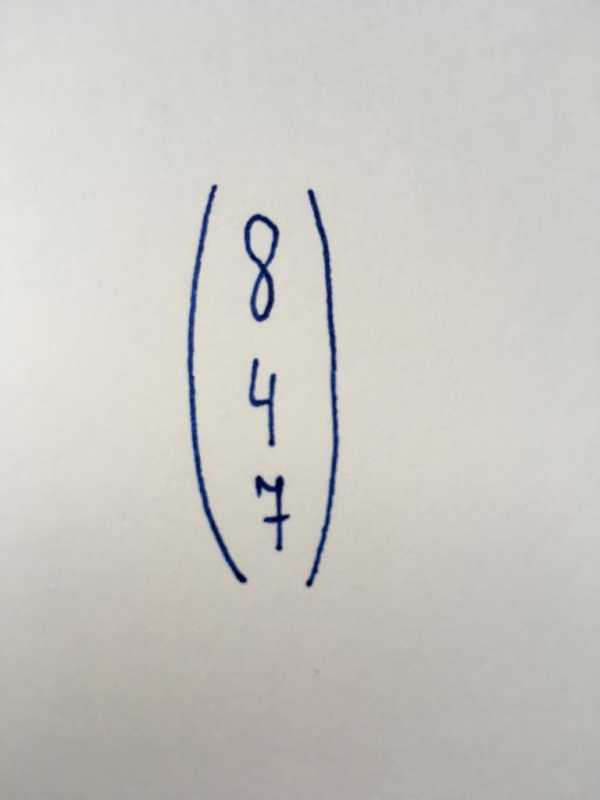
Это один из простейших видов матриц, содержащий только один столбец, который включает в себя три численных значения. Она представляет ряд свободных членов (чисел, независимых от переменных) в системах линейных уравнений.

Вектор-строка

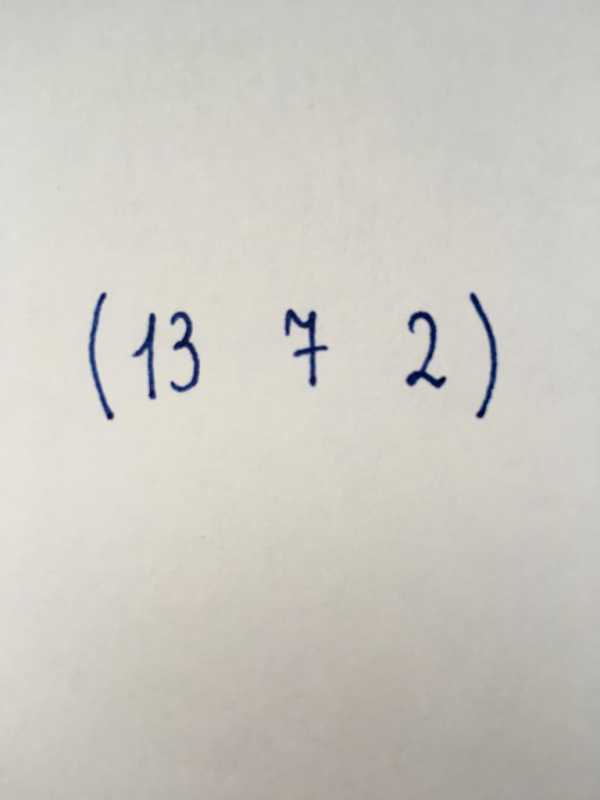
Вид, аналогичный предыдущему. Состоит из трех численных элементов, в свою очередь организованных в одну строку.

Диагональный тип

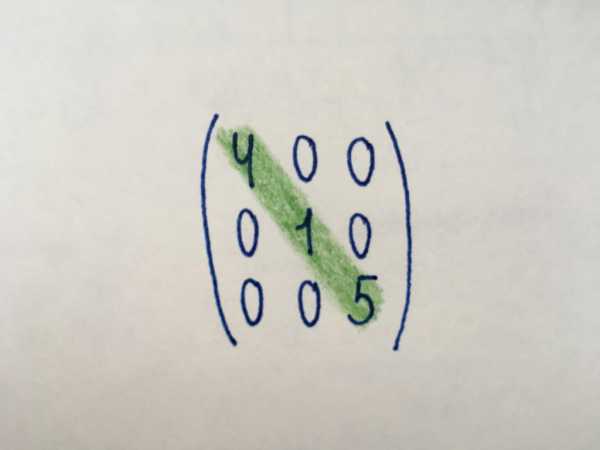
Числовые значения в диагональном виде матрицы принимают только компоненты главной диагонали (выделена зеленым цветом). Основная диагональ начинается с элемента, находящегося в правом верхнем углу, а заканчивается числом в третьем столбце третьей строки. Остальные компоненты равны нулю. Диагональный тип представляет собой только квадратную матрицу какого-либо порядка. Среди матриц диагонального вида можно выделить скалярную. Все ее компоненты принимают одинаковые значения.

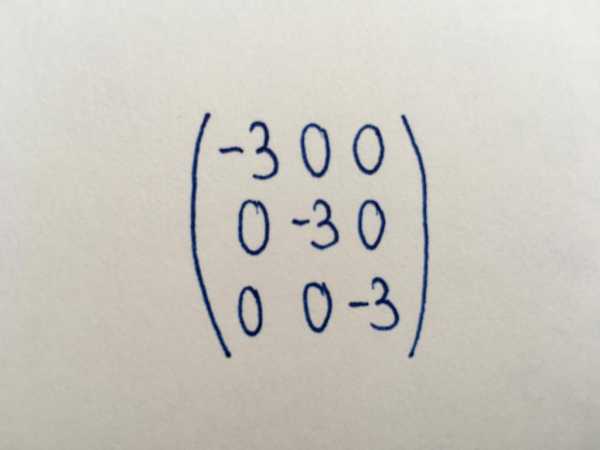
Единичная матрица

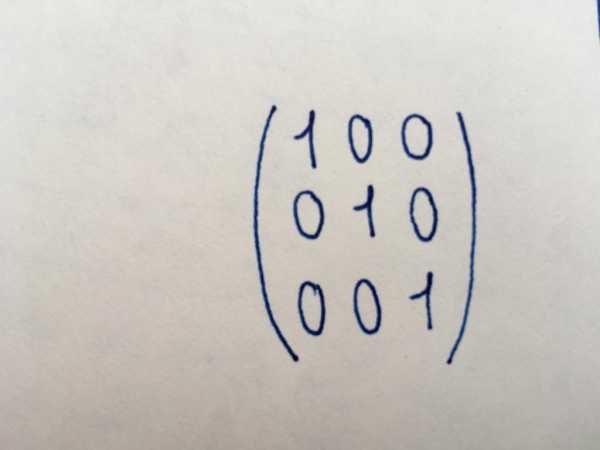
Подвид диагональной матрицы. Все ее числовые значения являются единицами. Используя единичный тип матричных таблиц, выполняют ее базовые преобразования или находят матрицу, обратную исходной.

Канонический тип

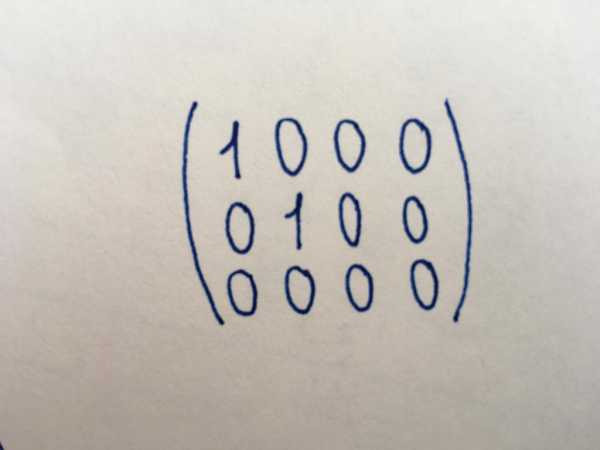
Канонический вид матрицы считается одним из основных; приведение к нему часто необходимо для работы. Число строк и столбцов в канонической матрице различно, она необязательно принадлежит к квадратному типу. Она несколько похожа на единичную матрицу, однако в ее случае не все компоненты основной диагонали принимают значение, равное единице. Главнодиагональных единиц может быть две, четыре (все зависит от длины и ширины матрицы). Или единицы могут не иметься вовсе (тогда она считается нулевой). Остальные компоненты канонического типа, как и элементы диагонального и единичного, равны нулю.

Треугольный тип

Один из важнейших видов матрицы, применяемый при поиске ее детерминанта и при выполнении простейших операций. Треугольный тип происходит от диагонального, поэтому матрица также является квадратной. Треугольный вид матрицы подразделяют на верхнетреугольный и нижнетреугольный.

В верхнетреугольной матрице (рис. 1) только элементы, которые находятся над главной диагональю, принимают значение, равное нулю. Компоненты же самой диагонали и части матрицы, располагающейся под ней, содержат числовые значения.

В нижнетреугольной (рис. 2), наоборот, элементы, располагающиеся в нижней части матрицы, равны нулю.

Ступенчатая матрица

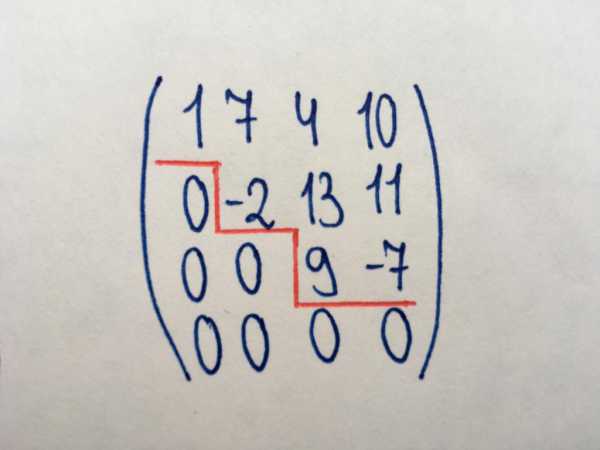
Вид необходим для нахождения ранга матрицы, а также для элементарных действий над ними (наряду с треугольным типом). Ступенчатая матрица названа так, потому что в ней содержатся характерные “ступени” из нулей (как показано на рисунке). В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю. Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.

Таким образом, мы рассмотрели важнейшие типы матриц, необходимые для работы с ними. Теперь разберемся с задачей преобразования матрицы в требуемую форму.

Приведение к треугольному виду

Как же привести матрицу к треугольному виду? Чаще всего в заданиях нужно преобразовать матрицу в треугольный вид, чтобы найти ее детерминант, по-другому называемый определителем. Выполняя данную процедуру, крайне важно “сохранить” главную диагональ матрицы, потому что детерминант треугольной матрицы равен именно произведению компонентов ее главной диагонали. Напомню также альтернативные методы нахождения определителя. Детерминант квадратного типа находится при помощи специальных формул. Например, можно воспользоваться методом треугольника. Для других матриц используют метод разложения по строке, столбцу или их элементам. Также можно применять метод миноров и алгебраических дополнений матрицы.

Подробно разберем процесс приведения матрицы к треугольному виду на примерах некоторых заданий.

Задание 1

Необходимо найти детерминант представленной матрицы, используя метод приведения его к треугольному виду.

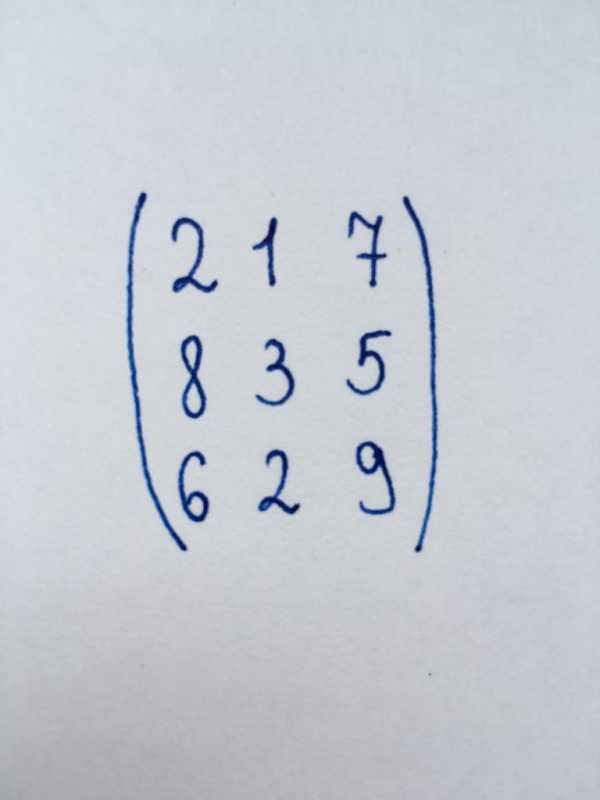
Данная нам матрица представляет собой квадратную матрицу третьего порядка. Следовательно, для ее преобразования в треугольную форму нам понадобится обратить в нуль два компонента первого столбца и один компонент второго.

Чтобы привести ее к треугольному виду, начнем преобразование с левого нижнего угла матрицы – с числа 6. Чтобы обратить его в нуль, умножим первую строку на три и вычтем ее из последней строки.

Важно! Верхняя строка не изменяется, а остается такой же, как и в исходной матрице. Записывать строку, в четыре раза большую исходной, не нужно. Но значения строк, компоненты которых нужно обратить в нуль, постоянно меняются.

Далее займемся следующим значением – элементом второй строки первого столбца, числом 8. Умножим первую строку на четыре и вычтем ее из второй строки. Получим нуль.

Осталось только последнее значение – элемент третьей строки второго столбца. Это число (-1). Чтобы обратить его в нуль, из первой строки вычтем вторую.

Выполним проверку:

detA = 2 x (-1) x 11 = -22.

Значит, ответ к заданию: -22.

Задание 2

Нужно найти детерминант матрицы методом приведения его к треугольному виду.

Представленная матрица принадлежит к квадратному типу и является матрицей четвертого порядка. Значит, необходимо обратить в нуль три компонента первого столбца, два компонента второго столбца и один компонент третьего.

Начнем приведение ее с элемента, находящегося в нижнем углу слева, – с числа 4. Нам нужно обратить данное число в нуль. Удобнее всего сделать это, умножив на четыре верхнюю строку, а затем вычесть ее из четвертой. Запишем итог первого этапа преобразования.

Итак, компонент четвертой строки обращен в нуль. Перейдем к первому элементу третьей строки, к числу 3. Выполняем аналогичную операцию. Умножаем на три первую строку, вычитаем ее из третьей строки и записываем результат.

Далее видим число 2 во второй строке. Повторяем операцию: умножаем верхнюю строку на два и вычитаем ее из второй.

Нам удалось обратить в нуль все компоненты первого столбца данной квадратной матрицы, за исключением числа 1 – элемента главной диагонали, не требующего преобразования. Теперь важно сохранить полученные нули, поэтому будем выполнять преобразования со строками, а не со столбцами. Перейдем ко второму столбцу представленной матрицы.

Снова начнем с нижней части – с элемента второго столбца последней строки. Это число (-7). Однако в данном случае удобнее начать с числа (-1) – элемента второго столбца третьей строки. Чтобы обратить его в нуль, вычтем из третьей строки вторую. Затем умножим вторую строку на семь и вычтем ее из четвертой. Мы получили нуль вместо элемента, расположенного в четвертой строке второго столбца. Теперь перейдем к третьему столбцу.

В данном столбце нам нужно обратить в нуль только одно число – 4. Сделать это несложно: просто прибавляем к последней строке третью и видим необходимый нам нуль.

После всех произведенных преобразований мы привели предложенную матрицу к треугольному виду. Теперь, чтобы найти ее детерминант, нужно только произвести умножение получившихся элементов главной диагонали. Получаем: detA = 1 x (-1) x (-4) x 40 = 160. Следовательно, решением является число 160.

Итак, теперь вопрос приведения матрицы к треугольному виду вас не затруднит.

Приведение к ступенчатому виду

При элементарных операциях над матрицами ступенчатый вид является менее “востребованным”, чем треугольный. Чаще всего он используется для нахождения ранга матрицы (т. е. количества ее ненулевых строк) или для определения линейно зависимых и независимых строк. Однако ступенчатый вид матрицы является более универсальным, так как подходит не только для квадратного типа, но и для всех остальных.

Чтобы привести матрицу к ступенчатому виду, сначала нужно найти ее детерминант. Для этого подойдут вышеназванные методы. Цель нахождения детерминанта такова: выяснить, можно ли преобразовать ее в ступенчатый вид матрицы. Если детерминант больше или меньше нуля, то можно спокойно приступать к заданию. Если же он равен нулю, выполнить приведение матрицы к ступенчатому виду не получится. В таком случае нужно проверить, нет ли ошибок в записи или в преобразованиях матрицы. Если подобных неточностей нет, задание решить невозможно.

Рассмотрим, как привести матрицу к ступенчатому виду на примерах нескольких заданий.

Задание 1. Найти ранг данной матричной таблицы.

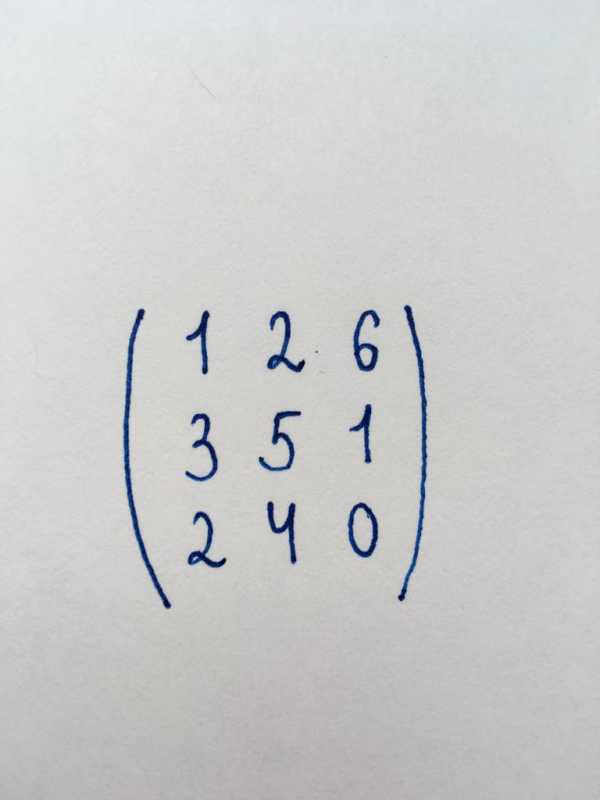
Перед нами квадратная матрица третьего порядка (3×3). Мы знаем, что для нахождения ранга необходимо привести ее к ступенчатому виду. Поэтому сначала нам необходимо найти детерминант матрицы. Воспользуемся методом треугольника: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) – (1 x 1 x 4) – (2 x 3 x 0) – (6 x 5 x 2) = 12.

Детерминант = 12. Он больше нуля, значит, матрицу можно привести к ступенчатому виду. Приступим к ее преобразованиям.

Начнем его с элемента левого столбца третьей строки – числа 2. Умножаем верхнюю строку на два и вычитаем ее из третьей. Благодаря этой операции как нужный нам элемент, так и число 4 – элемент второго столбца третьей строки – обратились в нуль.

Далее обращаем в нуль элемент второй строки первого столбца – число 3. Для этого умножаем верхнюю строку на три и вычитаем ее из второй.

Мы видим, что в результате приведения образовалась треугольная матрица. В нашем случае продолжить преобразование нельзя, так как остальные компоненты не удастся обратить в нуль.

Значит, делаем вывод, что количество строк, содержащих числовые значения, в данной матрице (или ее ранг) – 3. Ответ к заданию: 3.

Задание 2. Определить количество линейно независимых строк данной матрицы.

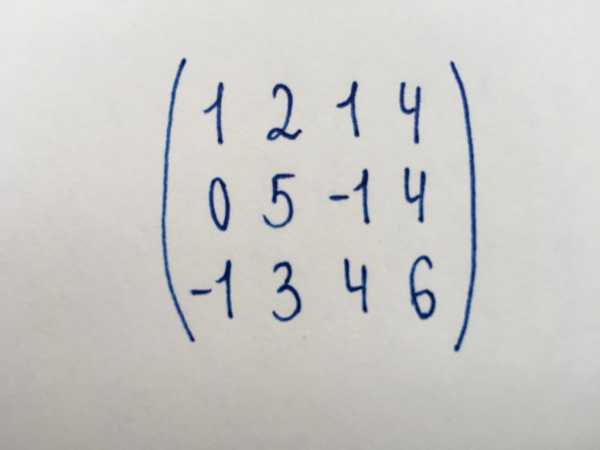
Нам требуется найти такие строки, которые нельзя какими-либо преобразованиями обратить в нуль. Фактически нам нужно найти количество ненулевых строк, или ранг представленной матрицы. Для этого выполним ее упрощение.

Мы видим матрицу, не принадлежащую к квадратному типу. Она имеет размеры 3×4. Начнем приведение также с элемента левого нижнего угла – числа (-1).

Прибавляем первую строку к третьей. Далее вычитаем из нее вторую, чтобы обратить число 5 в нуль.

Дальнейшие ее преобразования невозможны. Значит, делаем вывод, что количество линейно независимых строк в ней и ответ к заданию – 3.

Теперь приведение матрицы к ступенчатому виду не является для вас невыполнимым заданием.

На примерах данных заданий мы разобрали приведение матрицы к треугольному виду и ступенчатому виду. Чтобы обратить в нуль нужные значения матричных таблиц, в отдельных случаях требуется проявить фантазию и правильно преобразовать их столбцы или строки. Успехов вам в математике и в работе с матрицами!

fb.ru

I. Матрицы и определители 2

Лекция 1. Матрицы и определители, их характеристики 2

1.1. Понятие матрицы 4

1.2. Определители второго, третьего, n-го порядка 6

1.3. Свойства определителей 8

1.4. Разложение определителя по элементам строки или столбца 10

1.5. Вычисление определителей n-го порядка (2 метода) 12

1.6. Задания для самопроверки 15

Лекция 2. Алгебра матриц 16

2.1. Основные операции над матрицами и их свойства 17

2.2. Обратная матрица 20

2.3. Решение матричных уравнений 23

2.4. Невырожденные системы n линейных уравнений с n неизвестными 24

2.5. Задания для самопроверки 29

Ответы к примерам для самопроверки 30

I. Матрицы и определители

Лекция 1. Матрицы и определители, их характеристики

Содержание

1. Понятие матрицы.

2. Определители второго, третьего,

n-го порядка.

3. Свойства определителей.

4. Разложение определителя по элементам строки или столбца.

5. Вычисление определителей n-го порядка (2 метода).

6. Задания для самопроверки

Определения

Теоремы и свойства

алгебраическое дополнение элемента квадратной матрицы главная и побочная диагонали матрицы диагональная матрица единичная матрица квадратная матрица матрица минор элемента квадратной матрицы определитель n-го порядка определитель второго порядка определитель третьего порядка транспонированная матрица треугольная матрица

Свойства определителей о величине определителя треугольной матрицы о величине определителя, выраженной через алгебраические дополнения о величине определителя, если ко всем элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k о перестановке любых 2-х строк (столбцов) определителя о сумме произведений элементов некоторой строки (столбца) на соответствующие алгебраические дополнения элементов другой строки (столбца) об общем множителе строки (столбца) определителя об определителе транспонированной матрицы об определителе, в некоторой строке которого каждый элемент равен сумме двух слагаемых об определителе, у которого две строки (2 столбца) пропорциональны об определитель с двумя равными строками (столбцами)

1.1. Понятие матрицы

Звуковое сопровождение лекции

Определение

Матрицей размера 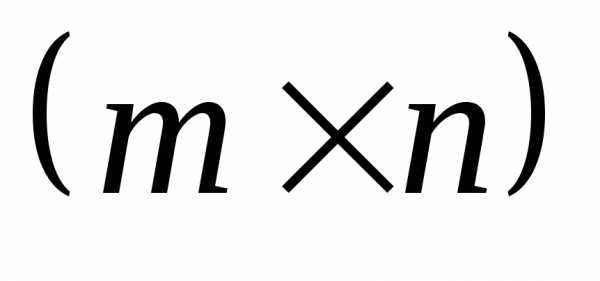называется прямоугольная таблица чисел, где– номер строки,– номер столбца, таких, на пересечении которых расположены числа,

.

Пример

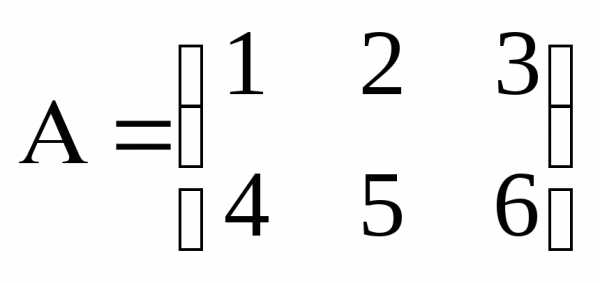–матрица размера .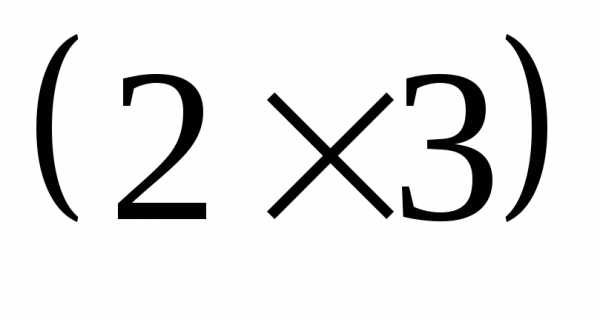

Определение

Если 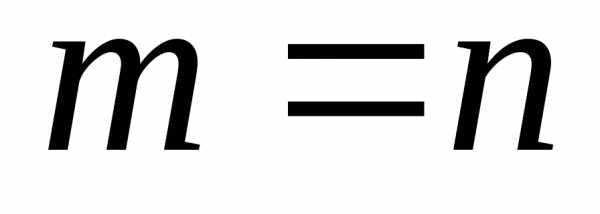, матрица называется

квадратной порядка .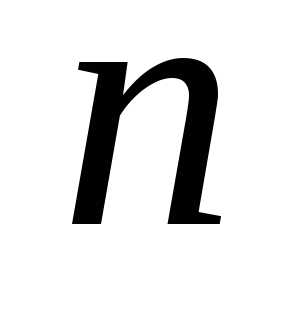

Пример

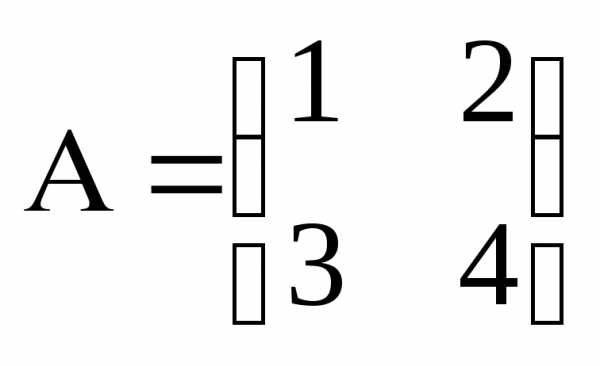–квадратная матрица второго порядка.

Определение

Главная и побочная диагональ квадратной матрицы –

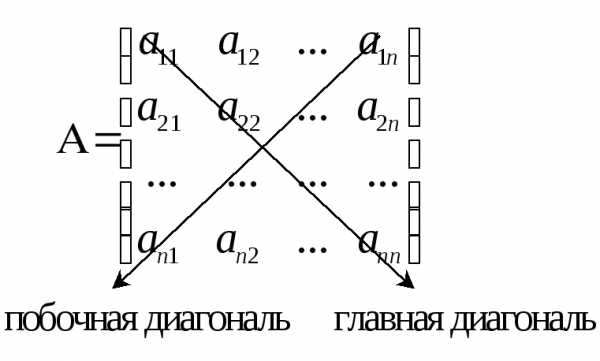
Частные случаи квадратных матриц

а) треугольная матрица – выше или ниже главной диагонали все элементы равны нулю.

Пример

;

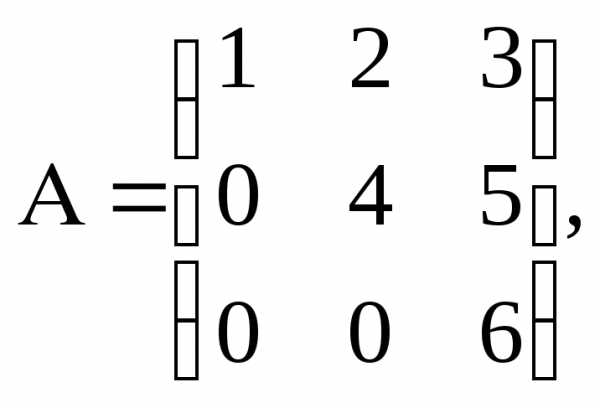
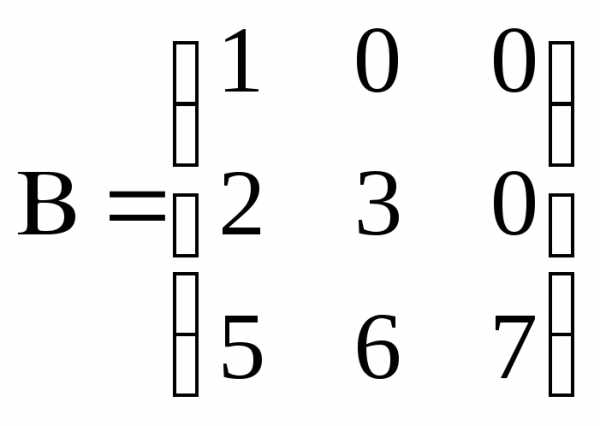б) диагональная матрица – выше и ниже главной диагонали – нули, на главной диагонали произвольные числа.

Пример

;

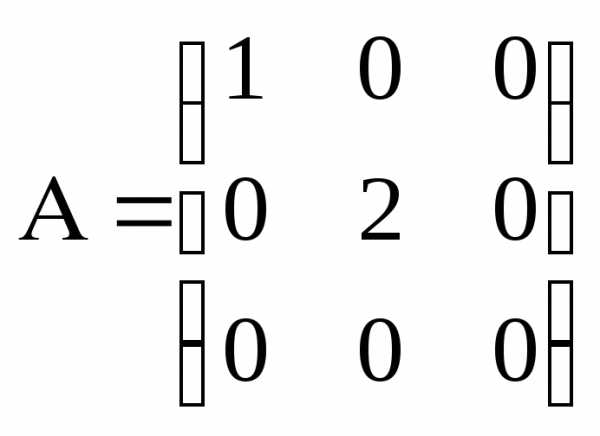в) единичная матрица – диагональная матрица, на главной диагонали которой – единицы.

Пример

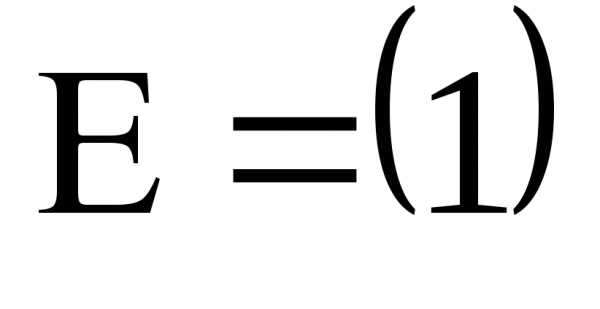–единичная матрица первого порядка.

–единичная матрица второго порядка.

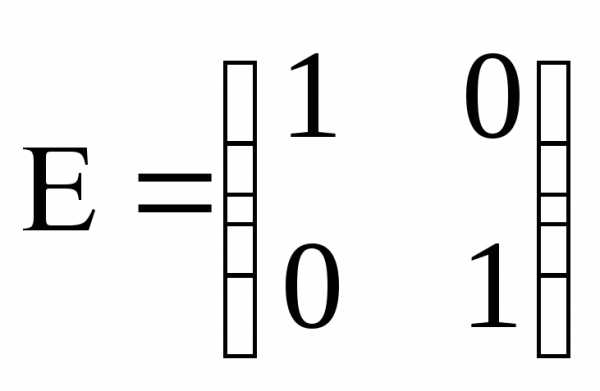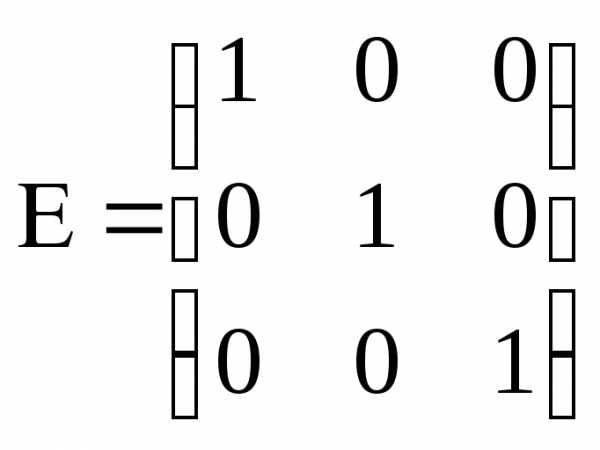–единичная матрица третьего порядка.

Таким образом ,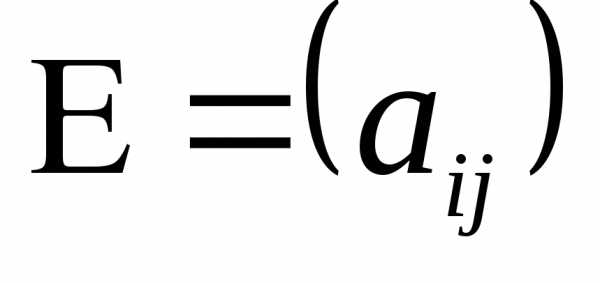

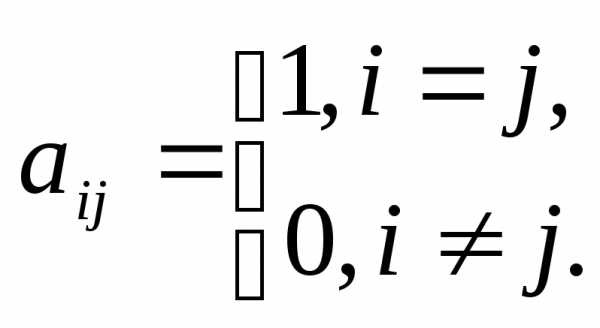
Определение

Транспонированная матрица – матрица , построенная из матрицы, путем замены строк на столбцы и наоборот (строки и столбцы меняются ролями).

Пример

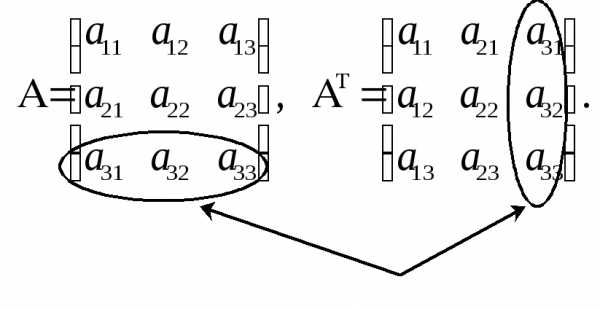
Пример

, .

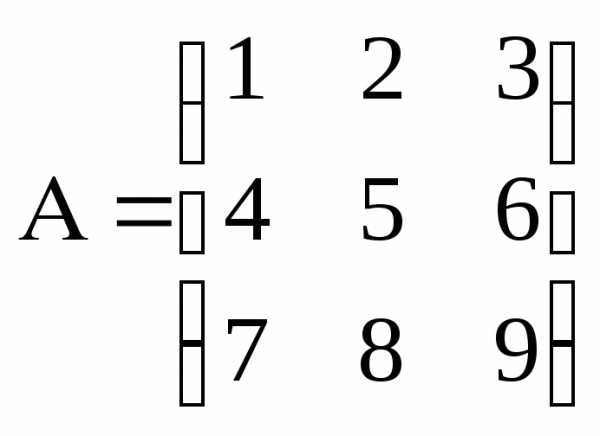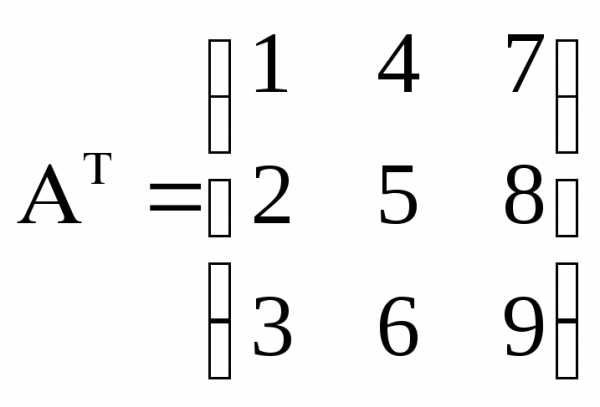studfiles.net

Прямоугольная матрица – Энциклопедия по экономике

Прямоугольная матрица Р моделирует размещение производства или потребления различных видов нефтепродуктов в районах страны. Буквами от а до z обозначают виды нефтепродуктов. Цифровые индексы у букв означают № районов, например, Ь2 означает объем потребления второго вида нефтепродуктов во втором районе и т. д. Каждая строка характеризует объем и номенклатуру нефтепродуктов всех отраслей производства в одном из районов каждый столбец модели характеризует объем и размещение потребления одного из видов нефтепродуктов по всем районам. Число столбцов обычно не равно числу строк.  [c.373]
Структура группирует по существенно важным признакам юридические и экономические отношения организации. Методология этой группировки носит статистический характер, и ее принципы позволяют сделать вывод о том, что бухгалтерский учет может рассматриваться как частный случай экономической статистики. При этом надо помнить, что модель структуры имеет форму прямоугольной матрицы, где по столбцам перечисляются дебетуемые счета, а по строкам — кредитуемые.  [c.166]

Отметим, что четвертая группа уравнений в модели Вальраса является своеобразным прообразом модели В. Леонтьева затраты — выпуск , однако она еще представляет собой прямоугольную матрицу (nxm) элементов, в то время как у В. Леонтьева — квадратную матрицу (пхп) элементов. Кроме того, в модели Леонтьева структурирован валовой выпуск (он подразделяется на промежуточный и конечный продукт), показаны источники производства добавленной стоимости, имеется, раздел баланса с характеристиками использования элементов конечного продукта и раздел перераспределения доходов. Но все же самая существенная идея модели затраты — выпуск уже содержалась в выводах Вальраса.  [c.82]

Нечеткая прямоугольная матрица – это дважды индексированное  [c.33]

Две прямоугольные матрицы С = (с у) и С”= ( “t) размером т п назовем эквивалентными (С С”), если с” у = с + а,- +Ру- / =1, 2,. .., т j — 1, 2,. .., п. Задачи выбора, определяемые эквивалентными матрицами, являются эквивалентными, так как можно доказать, что множества оптимальных назначений двух задач выбора с эквивалентными матрицами совпадают.  [c.203]

Прямоугольная матрица 187 Прямоугольные игры 295 Прямые задачи управления 102 Прямые затраты 236, 295 Прямые инвестиции 121 Прямые налоги 210 Псевдослучайные величины 295 Псевдослучайные числа 295 Пуассоновский поток 270, 295 Пуассоновский случайный процесс 333 Пустое допустимое множество 237 Пустое множество 201 Путь 295  [c.485]

Для прямоугольных матриц определена операция транспонирования. Рассмотрим произвольную прямоугольную матрицу А. Матрица, получающаяся из матрицы А заменой строк столбцами, называется транспонированной по отношению к матрице А и обозначается А А  [c.58]

Крупноформатный электронный бланк — это совокупность объектов, активных в данный момент и обычно представляемых в виде прямоугольной матрицы элементов, похожей на бумажную таблицу или ведомость, используемую в бухгалтерском учете. Каждой клетке этой таблицы на экране соответствует одна запись в памяти. Запись определяет правило нахождения значения, простейший вид которого предусматривает обработку элемента-клетки, например числа или фрагмента текста. Более сложное правило может предусматривать нахождение значения по какой-либо математической формуле в зависимости от значений других элементов с учетом их относительных или абсолютных позиций либо (что гораздо лучше) присвоенных им имен. Правило нахождения значения может предусматривать также проверку некоторого условия и установление значения своего элемента в соответствии с результатом проверки.  [c.101]

Как следует из определения, единичная матрица может быть только квадратной, прямоугольная матрица не может быть диагональной или единичной, так как у нее отсутствует ось симметрии, которой и является главная диагональ.  [c.367]

При транспонировании прямоугольных матриц происходит изменение их размера с mxn на nxm, при транспонировании квадратных матриц размер их не изменяется. Ниже приводятся примеры транспонирования прямоугольной и квадратных матриц  [c.374]

Значения / и J образуют две прямоугольных матрицы J+ и / . На пересечении г-й строки и /-го столбца первой матрицы стоит оценка обоснованности гипотезы сг=>+о/, а на том же месте во второй матрице — оценка обоснованности гипотезы с = о/.  [c.184]

Теорема о ранге матрицы. Нахождение ранга матрицы элементарными преобразованиями. Ранг произведения матриц. Представление прямоугольной матрицы в виде произведения двух матриц полного ранга.  [c.11]

Если N > q, то естественно ожидать, что прямоугольная матрица Л имеет полный ранг по столбцам. Тогда условие d A = 0 возможно только если  [c.17]

Нечеткие последовательности, нечеткие прямоугольные матрицы, нечеткие функции и операции над ними  [c.35]

Нечеткая прямоугольная матрица – это дважды индексированное конечное множество нечетких чисел, причем первый индекс пробегает М строк, а второй – N столбцов. При этом, как и в случае матриц действительных чисел, операции над нечеткими прямоугольными матрицами сводятся к операциям над нечеткими компонентами этих матриц. Например,  [c.35]

Введем в рассмотрение прямоугольные матрицы R T=[R I Rj )…. I Rn ], А = [I I A ,… I An ] и квадратные матрицы А вида  [c.307]

Понятие матрица пришло из математики. Матричный орган, связанный взаимными отношениями, составленными в прямоугольную схему, называется матрицей. В матричной системе имеются главные и поперечные функции.  [c.34]

Коэффициенты обычно располагаются в виде прямоугольной таблицы, которая состоит из определенного количества строк и столбцов в зависимости от разнообразия переменных. Схема такой таблицы, называемой в линейной алгебре матрицей, следующая  [c.233]

Исходя из правил перемножения матриц, можно записать вектор потребностей как результат умножения прямоугольной нормативной матрицы  [c.37]

Таким образом, при использовании электронно-вычислительных машин процесс расчета потребности в нефтепродуктах на выполнение всего объема работ по плану может быть сведен к перемножению прямоугольной нормативной матрицы на вектор объемов работ.  [c.38]

Одним из факторов, влияющих на безотказность работы БИС ПЛМ является исключение возможности восстановления запрограммированной БИС, что обусловлено механизмом разрушения плавкой перемычки из нихрома в цепи запоминающего элемента (ЗЭ). Плавкая перемычка зажата в слоях из двуокиси кремния, сформированной на массивной кремниевой подложке и имеет форму, приведенную на рисунке. Для разрушения перемычки ЗЭ в матрице ПЛМ на нее воздействуют серией прямоугольных электрических импульсов, переводящих выбранный разряд в непроводящее состояние, что соответствует логическим О или 1 . Запрограммированная перемычка в процессе эксплуатации при воздействии на нее электрическими импульсами способна восстановиться. Одной, из причин восстановления перемычки является разброс геометрических параметров элементов ПЗУ при изготовлении.  [c.31]

Первый квадрант МОБ — это прямоугольная таблица межотраслевых материальных связей. Показатели таблицы представляют собой величины прямых межотраслевых потоков продукции и обозначаются как ху, где / и j — соответственно номера производящих и потребляющих отраслей. Таким образом, этот квадрант имеет вид квадратной матрицы л, сумма всех элементов которой равна годовому фонду возмещения затрат средств производства в материальной сфере.  [c.508]

Матрица А размера га х п (т х п матрица) — это прямоугольный массив вещественных чисел 1  [c.23]

Подматрица матрицы Л есть прямоугольный массив, полученный из Л вычеркиванием некоторых строк и столбцов. Минором называется определитель квадратной подматрицы Л. Минором элемента а – называется определитель подматрицы Л, полученной вычеркиванием ее г-й строки и j-ro столбца. Алгебраическим дополнением а -, обозначаемым с -, называется произведение (— 1)г+-7 на минор aij. Матрица С = ( ij) называется матрицей алгебраических дополнений матрицы А. Транспонированная к С матрица называется присоединенной к Л и обозначается А . Имеем  [c.30]

Замечание. Допущение 3° может быть ослаблено и заменено следующим Матрицы Ли( (й 4) прямоугольные, ранг Аи равен числу строк элементы мат-  [c.245]

Это название объясняется следующей возможностью описания игр такого рода. Составим прямоугольную таблицу, в которой строки соответствуют стратегиям первого игрока, столбцы — стратегиям второго, а клетки таблицы, стоящие на пересечении строк и столбцов, соответствуют ситуациям игры. Если поставить в каждую клетку выигрыш первого игрока в соответствующей ситуации, то получим описание игры в виде некоторой матрицы. Эта матрица называется матрицей игры или матрицей выигрышей. П  [c.25]

Сведение норм расхода (или удельных расходов) энергоресурсов, поступающих на предприятия со стороны, в прямоугольную матрицу, оличество строк соответствует количеству видов энергоресурсов, поступающих на предприятие со стороны, а количество и расположение столбцов то же, что и в матрице для энергоресурсов собственного производства (см. п. 2).  [c.198]

В результате обследования рынков формируется прямоугольная матрица X = = ( ..), t=l,…, т j = 1,. .., п, где х . — значение /-и характеристики г -го рынка. Отметим, что здесь не рассматриваются вопросы планирования эксперимента, в частности, какие именно характеристики и как измерять. Можно считать, что в данной матрице отражены все доступные наблюдению характеристики рынков или же только те из них, которые мы считаем наиболее информативными. В этом случае выбор осуществляется на основе показателя информативности каждой из характеристик либо на основе результатов сравнения матриц близости между объектамиD. = (dkl ), k, I = 1,…, т, где, например, dkl = xkj -x , j = 1,…, п.  [c.74]

Возможйые варианты (исходы) игры сводятся в прямоугольную таблицу — платежную матрицу, в которой строки соответствуют различным стратегиям игрока А, столбцы — стратегиям игрока В, qtj называется ценой игры (табл. 8.23).  [c.150]

Как показывает практика, наиболее рациональна такая организация работ, при которой за каждой задачей закреп-ляется один ответственный. В предлагаемой модели принимается строгое разделение ответственности за выполнение каждой задачи за одной и той же задачей не должно быть назначено более одного ответственного ни одна задача не может не иметь ответственного. Условимся в матрице, учитывающей участие штатных категорий в выполнении задач, стоящих перед подразделением, ответственных за задачу обозначать знаком ++ . В общем случае функциональная схема многоцелевого подразделения (табл. 21) представляет собой прямоугольную таблицу размера N+n, где N — число задач, решаемых подразделением, п — число штатных категорий, принимающих участие в решении этих задач. Табл. 21 дает полную картину деятельности подразделения и взаимодействия отдельных штатных категорий в процессе ее. Так, например, рассматривая ыо строку таблицы, устанавливаем, что в решении  [c.218]

МАТРИЦА [matrix] — система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы. Таблица имеет следующий вид  [c.187]

ПРЯМОУГОЛЬНЫЕ ИГРЫ [re tangular games] — парные игры с нулевой суммой, имеющие седловую точку. Называются так, потому что их матрица игры прямоугольная.  [c.295]

В частности, столбцы ортогональной матрицы являются ортонормированны-ми. Прямоугольная (не квадратная) матрица может обладать одним из свойств А А = I или А А = /, но не обоими одновременно. Такая матрица называется полу ортогональной.  [c.26]

Матрицы Лiг( oi 1) прямоугольные, ранг Ац равен чрслу ее строк, элементы матрицы .((ш -1) и псевдообратной матрицы А (ш – >) неотрицательны и, кроме  [c.247]

Сепдовыми точками являются здесь все четыре угловых ситуации. То, что прямоугольное множество (Г) выглядит здесь несвязным, не имеет значения порядок строк и столбцов матрицы может быть произвольно изменен (см. п. 1. 9).  [c.35]

economy-ru.info

Диагональная матрица, формула и примеры

Пример диагональной матрицы

   

Частные случаи диагональных матриц

1. Скалярная матрица – диагональная матрица, у которой все диагональные элементы равны, например

      

2. Единичная матрица – скалярная матрица, у которой все диагональные элементы равны 1:

      

   Подробнее про единичные матрицы читайте по ссылке.

3. Нулевая матрица – скалярная матрица, у которой все диагональные элементы равны 0:

      

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

---