29.03.201913.12.2018

Матрицы определитель математика – Матрицы и определители | Высшая математика | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана

• by alexxlab
• Комментариев к записи Матрицы определитель математика – Матрицы и определители | Высшая математика | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана нет
• Советы абитуриенту

ОПРЕДЕЛИТЕЛЬ | Энциклопедия Кругосвет

Содержание статьи

ОПРЕДЕЛИТЕЛЬ, или детерминант, – в математике запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число («значение» определителя). Очень часто под понятием «определитель» имеют в виду как значение определителя, так и форму его записи. Определители позволяют удобно записывать сложные выражения, возникающие, например, при решении линейных уравнений в аналитической геометрии и в математическом анализе. Открытие определителей приписывают японскому математику С.Кова (1683) и, независимо, Г.Лейбницу (1693). Современная теория восходит к работам Ж.Бине, О.Коши и К.Якоби в начале 19 в.

Простейший определитель состоит из 4 чисел, называемых элементами и расположенных в виде 2-х строк и 2-х столбцов. О таком определителе говорят, что он 2-го порядка. Например, таков определитель

значение которого равно 2ґ5 – 3ґ1 (т.е. 10 – 3 или 7). В общем случае определитель 2-го порядка принято записывать в виде

а его значение равно a₁b₂ – a₂b₁, где a и b – числа или функции.

Определитель 3-го порядка состоит из 9 элементов, расположенных в виде 3-х строк и 3-х столбцов. В общем случае определитель n-го порядка состоит из n² элементов, и обычно его записывают как

Первый индекс каждого элемента указывает номер строки, второй – номер столбца, на пересечении которых стоит этот элемент, поэтому a_ij – элемент i-й строки и j-го столбца. Часто такой определитель записывают в виде |a_ij|.

Один из методов вычисления определителя, почти всегда используемый при вычислении определителей высокого порядка, состоит в разложении по «минорам». Минором, соответствующим любому элементу определителя, называется определитель меньшего на 1 порядка, получаемый из исходного вычеркиванием строки и столбца, на пересечении которых стоит этот элемент. Например, минором, соответствующим элементу

a₂ из определителя

«Алгебраическим дополнением» элемента называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, на пересечении которых стоит элемент, четна, и со знаком минус, если она нечетна. В приведенном выше примере элемент a₂ состоит в 1-м столбце и во 2-й строке; сумма (1 + 2) нечетна, и поэтому алгебраическое дополнение элемента a₂ равно его минору, взятому со знаком минус, т.е.

Значение определителя равно сумме произведений элементов любой строки (или любого столбца) на их алгебраические дополнения. Например, определитель

разложенный по первому столбцу, имеет вид

а его разложение по второй строке, имеет вид

Вычислив каждый минор и умножив его на коэффициент, нетрудно убедиться в том, что оба выражения совпадают.

Значение определителя.

Под значением определителя

принято понимать сумму всех произведений из n элементов, т.е.

В этой формуле суммирование ведется по всем перестановкам j₁, ј, j_n чисел 1, 2, ј, n и перед членом ставится знак плюс, если перестановка четна, и минус, если эта перестановка нечетна. Такая сумма насчитывает ровно n! членов, половина которых берется со знаком плюс, половина – со знаком минус. Каждый член суммы содержит по одному члену из каждого столбца и каждой строки определителя. Можно доказать, что эта сумма совпадает с выражением, получаемым при разложении определителя по минорам.

Свойства определителя.

Среди наиболее важных свойств определителя назовем следующие.

(i) Если все элементы любой строки (или любого столбца) равны нулю, то и значение определителя равно нулю:

(ii) Если элементы двух строк (или двух столбцов) равны или пропорциональны, то значение определителя равно нулю:

(iii) Значение определителя не изменится, если все его строки и столбцы поменять местами, т.е. записать первую строку в виде первого столбца, вторую строку – в виде второго столбца и т.д. (такая операция называется транспонированием). Например,

(iv) Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на произвольный множитель. В следующем примере элементы второй строки умножаются на –2 и прибавляются к элементам первой строки:

(v) Если поменять местами две строки (или два столбца), то определитель изменит знак:

(vi) Если все элементы одной строки (или одного столбца) содержат общий множитель, то этот множитель можно вынести за знак определителя:

Пример. Вычислим значение следующего определителя 4-го порядка:

Прибавим к 1-й строке 4-ю строку:

Вычтем 1-й столбец из 4-го столбца:

Умножим 3-й столбец на 3 и вычтем из 4-го столбца:

Если угодно, то строки и столбцы можно поменять местами:

Разложим определитель по элементам четвертой строки. Три элемента этой строки равны нулю, ненулевой элемент стоит в третьем столбце, а поскольку сумма (3 + 4) нечетна, его алгебраическое дополнение имеет знак минус. В результате получаем:

Минор можно разложить по элементам третьей строки: два ее элемента равны нулю, а отличный от нуля элемент стоит в третьем столбце; сумма (3 + 3) четна, поэтому предыдущее равенство можно продолжить:

Применения.

Решение системы уравнений

можно получить, если первое уравнение умножить на b₂, второе – на b₁, а затем вычесть одно уравнение из другого. Проделав эти операции, мы получим

или, если

то

Такая запись решения с помощью определителей допускает обобщение на случай решения системы n линейных уравнений с n неизвестными; каждый определитель будет n-го порядка. Определителем системы линейных уравнений

будет

Заметим, что если D = 0, то уравнения либо несовместны, либо не являются независимыми. Поэтому предварительное вычисление определителя D позволяет проверить, разрешима ли система линейных уравнений.

Определители в аналитической геометрии.

Общее уравнение конического сечения представимо в виде

Определитель

называется дискриминантом. Если D = 0, то кривая вырождается в пару параллельных или пересекающихся прямых либо в точку (см. также КОНИЧЕСКИЕ СЕЧЕНИЯ).

Другой пример: площадь треугольника A с вершинами в точках (обход – против часовой стрелки) (x₁, y₁), (x₂, y₂

) и (x₃, y₃) определяется выражением

Связь определителей с матрицами.

Матрицей называется запись массива чисел в виде прямоугольной таблицы. Определители связаны с квадратными матрицами; например, определитель матрицы

Если A, B и С – квадратные матрицы и , то |A|Ч|B| = |C|. См. также АЛГЕБРА АБСТРАКТНАЯ.

Якобиан.

Если x = f (u, v), y = g (u, v) – преобразование координат, то определитель

называется якобианом или определителем Якоби этого преобразования. Если J № 0 в некоторой точке, то в ее окрестности уравнения преобразования можно однозначно разрешить относительно u и v, представив их как функции от x и y.

www.krugosvet.ru

Как найти определитель матрицы 2,3 порядка

Чтобы найти определитель матрицы нужно воспользоваться формулами, которые действительны для определителей 2 и 3 порядка.

Формула

Пусть задана матрица второго порядка . Тогда её определитель вычисляется по формуле:

Из произведения элементов, стоящих на главной диагонали , вычитается произведение элементов, расположенных на побочной диагонали . Это правило верно только (!) для определителя 2-го порядка.

Если дана матрица третьего порядка , то вычислить её определитель следует по формуле:

Примеры решений

Пример 1

Пусть задана матрица Вычислить её определитель.

Решение

Как найти определитель матрицы? Обратим внимание на то что матрица квадратная второго порядка, то есть количество столбцов равно количеству строк и они содержат по 2 элемента. Поэтому применим первую формулу. Перемножим элементы, стоящие на главной диагонали и вычтем из них произведение элементов, стоящих на побочной диагонали:

Ответ

Пример 2

Дана матрица . Требуется вычислить определитель.

Решение

Так как в задаче квадратная матрица 3-го порядка, то найти определитель следует по второй формуле. Для простоты решения задачи достаточно подставить вместо переменных, стоящих в формуле значения из матрицы нашей задачи: Стоит отметить когда мы находим произведения элементов на побочной диагонали и подобных её, то перед произведениями ставится знак минус.

Ответ

Пример 3

Рассмотрим матрицу

Решение

Замечаем сразу, что количество строк не равно количеству столбцов, поэтому матрица не является квадратной. Найти определить позволяется только для квадратных матриц, поэтому задача не имеет решения.

Ответ

Невозможно посчитать определитель

xn--24-6kcaa2awqnc8dd.xn--p1ai

Математика Определители Системы Матрицы основные определения

Математика Определители. Системы

Матрицы (основные определения) • Определение. Матрицей размера m n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются • ai j , где i- номер строки, j- номер столбца. • А=. • • Замечание. Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Определитель квадратной матрицы • Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной порядка n. • Каждой квадратной матрице А может быть поставлено в соответствие некоторое число. Такое число называют определителем матрицы и обозначают символом IAI или • det A. При этом порядком определителя называют порядок соответствующей матрицы • Замечание • Пусть n=1. Тогда А=(a 11) и IAI= a 11 , т. е. определитель матрицы первого порядка равен ее единственному элементу.

Определитель 2 -ого порядка . 2) Пусть n=2, тогда IAI= Примеры: 3) 4) 5) Ответы( выбрать правильный вариант): 3) А. -5 В. 10 С. -14 4) А. -5 В. 10 С. 20 5) А. 0 В. 10 С. -4

Определитель 3 -его порядка Правило вычисления определителя третьего порядка можно схематически изобразить так, дописав два первых столбца:

Вычисление определителей 3 -его порядка • • =( 1 1 2 -1 1 1+1 2 1) – ( 1 1 1 + 2 2 (-1))= =(2 -1 +2) – (1+ 1 – 4) =3 – (-2) = 3 +2 = 5 • Пример: вычислить определители: • • • 1) 2) 3)

Ответы • 1) 19 • 2) 19 • 3) 0

Другой способ вычисления определителей 3 -его порядка • Определитель третьего порядка может быть вычислен с помощью определителей второго порядка по теореме о разложении определителя по первой строке:

Пример • Вычислить определитель двумя способами • 1 способ. Используем правило Саррюса, дописав в определителе два первых столбца • = (1· 2· 1+ 1· 3·(-1)+0· 1· 2)– (0· 2·(-1)+1· 3· 2+1· 1· 1)=-8 • 2 способ. Используем разложение определителя по элементам первой строки • = ( 2· 1 – 3· 2) -1 (1· 1+3) +0= -4 -4=-8

Свойства определителей 1) Определитель не изменится при замене строк столбцами (транспонировании). 2) При перестановки двух строк определитель меняет знак. 3) Общий множитель всех элементов строки (столбца) можно выносить за знак определителя. 4) Определитель равен нулю, если соответствующие элементы двух строк (столбцов) пропорциональны ( в частности равны). 5) Определитель равен нулю, если все элементы строки (столбца) равны нулю.

Системы линейных алгебраических уравнений Система m линейных уравнений с n неизвестными . Числа коэффициенты при неизвестных; свободные члены. Если , то система называется однородной, в противном случае – неоднородной. Если m=n, т. е. число уравнений равно числу неизвестных, то система называется квадратной.

Δ Пример системы • Дана система. Выписать ее коэффициенты. • Здесь m=3 n=3 ( система квадратная) ; • а 11= 1 а 12 = 2 а 13 =0 b 1 =-1 а 21 =2 а 22 = 3 а 23 =1 b 2 =3 а 31 =3 а 32 = -1 а 33 =-2 b 3 =8

Решение системы Определение. Совокупность n чисел называется решением системы , если после замены этими числами каждое из уравнений системы превращается в верное равенство. Покажем, что линейная система может: 1) не иметь решений, 2) иметь единственное решение, 3) иметь бесконечное множество решений.

Примеры решения систем и их геометрическая интерпретация 1)Система решений не имеет, ( прямые параллельны) 2) Система имеет единственное решение х=2 , у= -1 ( прямые пересекаются) 3) Система имеет бесконечно много решений: х=t , у=1 -t, где t- любое число. ( одна и та же прямая)

Классификация систем по типу решений • Определение. Система линейных уравнений, не имеющая ни одного решения, называется несовместной. • Система, обладающая хотя бы одним решением, называется совместной. • Если система имеет единственное решение, то она называется совместной определенной. • Если система имеет бесчисленное множество решений, то она называется совместной неопределенной.

Методы решения систем • Существует два основных метода решения систем. • 1. Метод Крамера( метод определителей). Этот метод применим только для решения квадратных систем, у которых матрица коэффициентов при неизвестных невырождена ( ее определитель отличен от нуля). • Такие системы имеют единственное решение. • 2. Метод Гаусса. Этот метод является универсальным и может быть применим к любым системам.

Решение систем линейных уравнений Пусть дана система 3 -х уравнений с тремя неизвестными. Составим из коэффициентов при неизвестных определитель третьего порядка и обозначим его символом Δ, т. е. Δ = – главный определитель системы.

Решение систем линейных уравнений по формулам Крамера Если главный определитель системы Δ≠ 0, тогда система имеет единственное решение , которое может быть найдено по формулам Крамера: Х 1=Δ 1/Δ Х 2=Δ 2/Δ Х 3=Δ 3/Δ , где Δi ( i=1, 2, 3) – определитель, полученный из главного, заменой i столбца столбцом свободных членов, т. е. Δ 1 = Δ 2 = Δ 3 = Замечание: после нахождения решения необходимо сделать проверку.

Алгоритм метода Крамера • 1) Вычисляем главный определитель системы Δ и проверяем, что он отличен от нуля. • 2) Вычисляем Δ 1, Δ 2 , Δ 3. • 3) Вычисляем х 1, х 2 , х 3. • 4) Делаем проверку. • 5) Пишем ответ. • Замечание. Рассмотренный метод можно применять для решения системы двух уравнений с двумя неизвестными. • При этом в пункте 2) находят только Δ 1 и Δ 2

Пример № 1 контрольной работы • Найти точку пересечения прямых и построить прямые , заданные уравнениями • х-3 у+2=0 и 3 х+у-3=0 • Решение. Для нахождения точки пересечения непараллельных прямых следует решить систему двух уравнений с двумя неизвестными х и у

Решение примера № 1 контрольной работы • Для решения системы используем формулы Крамера • х=Δ 1/Δ у=Δ 2/Δ, • где • х = 0, 7 у=0, 9. Проверим полученный результат подстановкой в систему: 0, 7 -3 0, 9=-2 (верно) 3 0, 7+0, 9=3 (верно). • Ответ: х=0, 7 у=0, 9–координаты точки пересечения прямых.

Пример 2 контрольной работы • Решить систему с проверкой

Пример 2 ( продолжение) 1) Вычислим главный определитель системы • • • 1 2 Δ= 2 3 = (1∙ 3 ∙ (-2) + 2 ∙ 1 ∙ 3 + 3 ∙ 2 ∙ 1) 3 1 – ( 3 ∙ 3 +1 ∙ 1+2 ∙ (-2)) = = (-6+6+6) – (27+1 -8)=6 -20=-14 ≠ 0 следовательно , метод Крамера применим, т. е. далее считаем Δ 1 Δ 2 Δ 3

Δ Пример (продолжение) 2)Δ 1 = = -28, Δ 2 = =0, Δ 3 = = 14 3) Подставляем в формулы Крамера Δ, Δ 1 , Δ 2 , Δ 3 Δ = -14 Δ 1 = -28 , Δ 2 = 0, Δ 3 = 14 х1 =(-28)/(-14), х 2 =0/(-14), х 3 =14/(-14) или х1 =2, х 2 =0, х 3 =-1.

Пример 2 (проверка) 4) Проверка: подставляем полученные значения переменных в левую часть исходной системы ( х1 =2, х 2 =0, х 3 =-1) : 5) Ответ: х1 =2, х 2 =0, х 3 =-1.

present5.com

Определитель матрицы | umath.ru

Рассмотрим набор натуральных чисел от до : . Перестановкой этих чисел называется их запись в некотором порядке без повторений. Например, последовательность является перестановкой множества .

Обозначим перестановки этих чисел как . Из комбинаторики известно, что число всех таких различных перестановок равно .

Определение. Говорят, что числа и перестановки образуют инверсию (или беспорядок), если при верно неравенство . Число всех инверсий в перестановке обозначим .

Например, , так как перед числом стоит число , а перед числом стоят числа , большие единицы.

Пусть дана квадратная матрица

   

Определение. Определителем (или детерминантом) квадратной матрицы размера называется число

   

где сумма берётся по всевозможным перестановкам номеров столбцов матрицы .

Определитель матрицы принято обозначать следующим образом:

   

Свойства определителей

1. Определитель единичной матрицы равен единице:

      

2. При транспонировании матрицы её определитель не изменяется:

      

3. При перестановке двух столбцов или строк матрицы знак её определителя меняется на противоположный.
4. Определитель матрицы, содержащей два одинаковых столбца (строки), равен нулю.
5. При вычислении определителя матрицы из столбца (строки) можно выносить общий множитель.

      

6. При добавлении к некоторому столбцу (строке) матрицы линейной комбинации остальных столбцов определитель матрицы не изменяется.

   Линейной комбинацией столбцов называется сумма этих столбцов, умноженных на некоторые коэффициенты.

7. Определитель обратной матрицы (в случае, если она существует) равен

      

8. Определитель произведения матриц размера равен произведению их определителей:

      

umath.ru

Матрицы и определители

Дисциплина: Высшая математика

Тема: Матрицы и определители

Понятие матрицы

При изучении вопросов, связанных с действием над векторами, а также при изучении систем линейных уравнений приходится иметь дело с таблицами из чисел, которые называются матрицами.

Определение . Матрицей называется прямоугольная таблица из чисел, содержащая строк и столбцов .

Числа

и называются порядками матрицы. Если , то матрица называется квадратной. Для обозначения матрицы пользуются либо вертикальными двойными черточками, либо круглыми скобками: или .

Для краткого обозначения матрицы может быть использована и одна буква, например,

. Кроме того, вместо всей таблицы может быть написано: , где ; .

Числа

называются элементами матрицы, – номер строки, – номер столбца.

Для квадратной матрицы вводится понятие главной и побочной диагонали: главная диагональ идет из верхнего левого угла в нижний правый; побочная – из верхнего правого в нижний левый.

Ранг матрицы. Эквивалентные матрицы

Дана прямоугольная матрица:

Выделим в этой матрице k произвольных строк и k произвольных столбцов (k Ј m, k Ј n ).

Определение. Определитель k -го порядка, составленный из элементов матрицы A , расположенных на пересечении выделенных строк и столбцов, называется минором k -го порядка матрицы A . Матрица A имеет C ^k_m *C ^k_n миноров k -го порядка.

Определение. Рассмотрим всевозможные миноры матрицы A , отличные от нуля. Рангом матрицы A называется наибольший порядок отличных от нуля миноров этой матрицы. Если все элементы матрицы равны нулю, то ранг этой матрицы принимают равным нулю.

Определение. Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Ранг матрицы A будем обозначать через r (A) . Если r (A) = r( B) , то матрицы A и B называются эквивалентными .

Полезно иметь ввиду, что ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимаются:

1) замена строк столбцами, а столбцов соответствующими строками;

2) перестановка строк матрицы;

3) вычеркивание строки, все элементы которой равны нулю;

4) умножение какой-либо строки на число, отличное от нуля;

5) прибавление к элементам одной строки соответствующих элементов другой строки.

Действия над матрицами

Определение . Две матрицы называются равными, если они имеют одинаковые порядки и все их соответствующие элементы совпадают .

Определение. Суммой двух матриц () и () одинаковых порядков называется матрица () того же порядка, элементы которой равны

.

На письме это действие может быть записано так:

. Операция сложения обладает, очевидно, обычными свойствами: перестановочным ; сочетательным .

Определение . Произведением матрицы на число называется матрица , элементы которой равны

.

Умножение матрицы на число может быть записано:

или .

Эта операция обладает следующими свойствами: сочетательным относительно числового множителя

; распределительным относительно суммы матриц ; распределительным относительно суммы чисел .

После первых двух действий необходимо отметить, что вычитание матриц производится аналогично сложению, а деление матрицы на число может быть определено как умножение на обратное число.

Определение . Произведением матрицы (), имеющей порядок , на матрицу (), имеющую порядок , называется матрица (), имеющая порядок , элементы которой равны , где

.

Записывается это действие так

. Из сказанного выше следует, что для нахождения элемента , в произведении необходимо попарно перемножить все соответствующие элементы -ой строки матрицы на элементы -го столбца матрицы , а затем все это сложить. Из определения также следует, что для умножения двух матриц необходимо, чтобы число столбцов матрицы было равно числу строк матрицы . Отсюда следует, что одновременно произведение и существует только лишь в том случае, когда число столбцов равно числу строк , а число столбцов равно числу строк . В этом случае и будут квадратными матрицами, но разных порядков. Чтобы оба произведения были одинакового порядка, необходимо, чтобы и были квадратными матрицами одинакового порядка.

Произведение матриц

имеет свойства: сочетательное ; распределительное . Перестановочным свойством в общем случае произведение матриц не обладает. Оно выполняется лишь в некоторых случаях.

mirznanii.com

Определители квадратных матриц

	Главная > Учебные материалы > Математика:  Определители квадратных матриц
	Репетитор: Васильев Алексей Александрович  Предметы: математика, физика, информатика, экономика.        Стоимость: 2000 руб / 90 мин.  Репетитор: Крюков Илья Хассанович  Предметы: математика, экономика, эконометрика, теория вероятностей.        Стоимость: 2000 руб / 90 мин.  Репетитор: Скрипаленко Михаил Михайлович  Предметы: математика (ЕГЭ), английский язык (GMAT, GRE (general), GRE subject test in maths, IELTS, TOEFL, BEC).        Стоимость: 1200 руб / 60 мин.  Репетитор: Матвеева Милада Андреевна  Предметы: русский язык, литература (ЕГЭ, ГИА).        Стоимость: 1200 руб / 60 мин.  Репетитор: Тверской Василий Борисович  Предметы: математика, физика.        Стоимость: 3500 руб / 90 мин.  Репетитор: Поздняков Андрей Александрович  Предметы: английский язык, (ЕГЭ). Подготовка к TOEFL и IELTS.        Стоимость: 2000 руб / 60 мин.  Репетитор: Ершикова Марина Львовна  Предметы: бухгалтерский учет (кроме банковского), налогообложение, аудит.        Стоимость: 1500 руб / 60 мин.
	1.Определители квадратных матриц. 2.Свойства определителей.
	1 2 3 4 5 6 7 8 9
	1.Определители квадратных матриц.    Как известно из раздела матричной алгебры, матрицы получили широкое распрастранение в экономике. Для того, чтобы как-то характеризовать матрицу, а также решать различные задачи с использованием матриц, в математике введено понятие определитель матрицы. Т.е. определитель матрицы – это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать.
	Для матрицы первого порядка определитель равен элементу а11.
	Для матрицы второго порядка определитель равен разности произведений элементов матрицы, рассчитанный по формуле:
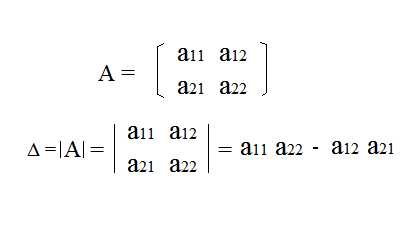	Для матрицы третьего порядка определитель равен числу, рассчитанному по формуле:
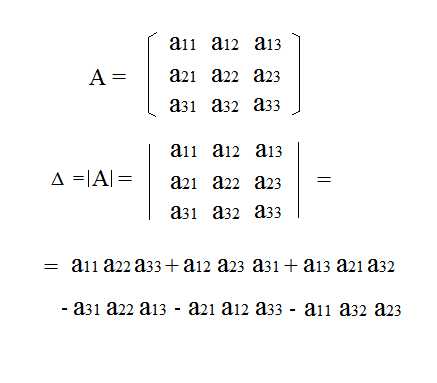	Определители квадратных матриц можно вычислить и другим способом: с помощью разложения элементов матрицы по строке. Для того, чтобы использовать такой способ, предварительно рассчитывают миноры и алгебраические дополнения. Минором Mij элемента аij называется определитель n-1 порядка, а алгебраическое дополнение это произведение Аij = (-1)i+j Mij
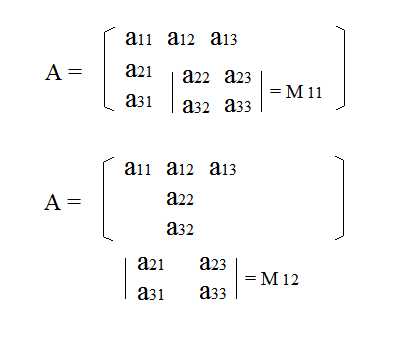	Таким образом, определитель третьего порядка можно разложить по элементам первой строки так:
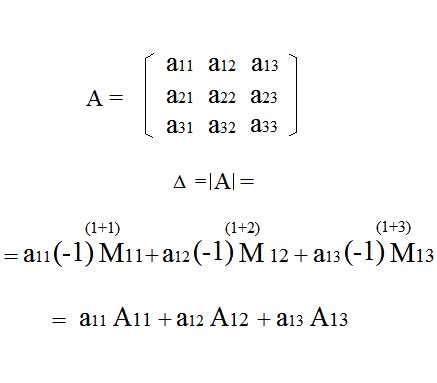	2.Свойства определителей.
	1. При транспонировании определитель не меняется. 2. Если поменять местами любые две строки (столбца) матрицы, то определитель поменяет знак на противоположный. 3. Для любой матрицы, определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. 4. Определитель равен нулю, если матрица содержит две одинаковые строки (столбца). 5. Определитель равен нулю, если все элементы какой-либо строки (столбца) равны нулю. 6. Если суммировать произведения элементов любой строки (столбца) на алгебраические дополнения элементов любой другой строки (столбца), то определитель равен нулю. 7. Общий множитель любой строки (столбца) можно вынести за знак определителя.
	Пример.
	1 2 3 4 5 6 7 8 9

www.mathtask.ru

37. Определитель матрицы | Решение задач по математике и другим предме

Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое Определителем матрицы и вычисляемое по определенному правилу.

Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме , или в свернутой форме . Предыдущая формула получается разложением определителя по первой строке.

Возьмем теперь квадратную матрицу -го порядка

(9.2)

Для записи определителя -го порядка матрицы будем применять обозначения . При матрица состоит из одного элемента и ее определитель равен этому элементу. При получаем определитель .

Минором элемента матрицы называют определитель матрицы -го порядка, получаемого из матрицы вычеркиванием -той строки и -го столбца.

Пример 7. Найти минор матрицы:

.

По определению, минор элемента есть определитель матрицы, получаемой из матрицы вычеркиванием первой строки и второго столбца. Следовательно, .

Алгебраическим дополнением элемента матрицы называется минор , взятый со знаком . Алгебраическое дополнение элемента обозначается , следовательно, .

Пример 8. Найти алгебраическое дополнение элемента матрицы из примера 7.

.

Определителем квадратной матрицы -го порядка называется число:

,

(9.3)

Где ‑ элементы первой строки матрицы (9.2), а их алгебраические дополнения.

Запись по формуле (9.3) называется Разложением определителя по первой строке.

Рассмотрим свойства определителей.

Свойство 1. При транспонировании матрицы ее определитель не меняется.

Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:

Определителем квадратной матрицы -го порядка называется число:

,

(9.4)

Где ‑ элементы первого столбца матрицы (9.2), а их алгебраические дополнения.

Свойство 2. Если поменять местами две строки или два столбца матрицы , то ее определитель изменит знак на противоположный.

Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:

Определитель квадратной матрицы -го порядка (будем в дальнейшем говорить определитель -го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.

, или .

Свойство 3. Определитель, у которого две строки или два столбца одинаковы, равен нулю.

Действительно, поменяем в определителе две одинаковые сроки местами. Тогда, по свойству 2 получим определитель , но с другой стороны, определитель не изменится, т. е. . Отсюда .

Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя умножить на число , то определитель умножится на .

.

Умножим элементы -той строки на . Тогда получим определитель:

.

Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.

Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.

Свойство 5. Определитель, у которого две строки (два столбца) пропорциональны, равен нулю.

Пусть -я строка пропорциональна -ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.

Свойство 6. Если каждый элемент строки (столбца) определителя есть сумма двух слагаемых, то определитель равен сумме двух определителей: у одного из них -той строкой (столбцом)служат первые слагаемые, а у другого – вторые.

Разложив определитель по -той строке получим:

.

Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Прибавив к элементам -той строки определителя соответствующие элементы -ой строки, умноженные на число , получим определитель . Определитель равен сумме двух определителей: первый есть , а второй равен нулю, так как у него -тая и -тая строки пропорциональны.

Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т. е.:

Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.

Рассмотрим вспомогательный определитель , который получается из данного определителя заменой -той строки -той строкой. Определитель равен нулю, так как у него две одинаковые строки. Разложив его по -той строке получим:

.

Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.

Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.

Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т. е. .

< Предыдущая		Следующая >

matica.org.ua

---