Метод крамера и метод гаусса решения систем линейных уравнений – Метод Гаусса решения систем линейных уравнений (рассмотрим на примере системы из трёх уравнений и трёх неизвестных)
- Комментариев к записи Метод крамера и метод гаусса решения систем линейных уравнений – Метод Гаусса решения систем линейных уравнений (рассмотрим на примере системы из трёх уравнений и трёх неизвестных) нет
- Советы абитуриенту
- Решение систем линейных уравнений методами Крамера и Гаусса — КиберПедия
- Тема 3 системы линейных уравнений. Правила крамера. Метод гаусса конспект 3
- Матричный метод решения системы линейных алгебраических уравнений. Формулы Крамера. Метод Гаусса
- Метод Крамера для решения систем линейных уравнений
- Метод Гаусса решения систем линейных уравнений (рассмотрим на примере системы из трёх уравнений и трёх неизвестных)
- 8. Формулы Крамера решения систем линейных алгебраических уравнений.
- 9. Решение системы линейных уравнений методом Крамера
Решение систем линейных уравнений методами Крамера и Гаусса — КиберПедия
Пусть дана система n уравнений с n неизвестными:
Основная матрица А такой системы квадратная. Определитель этой матрицы
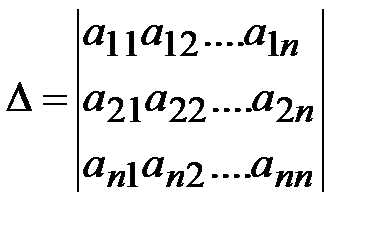
называется определителем системы.
Если определитель системы отличен от нуля, то система называется невырожденной и имеет единственное решение.
В дальнейшем мы будем иметь дело только с такими системами.
Наиболее простым методом для решения таких систем линейных уравнений является метод Крамера.
Формулы Крамера имеют вид:
Более универсальным и эффективным является метод Гаусса, состоящий в последовательном исключении неизвестных.
Решение осуществляется в два этапа: 1) система приводится к треугольному виду, 2) последовательно определяют неизвестные .
Задача 1.
Решить систему уравнений методами Крамера и Гаусса:
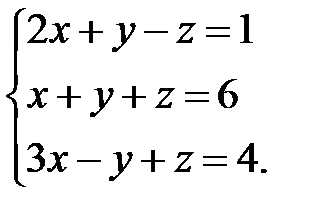
Решение:
а) Метод Крамера.
Найдем определитель системы . Предварительно сложив второй столбец с третьим и разложив определитель по элементам последнего столбца.
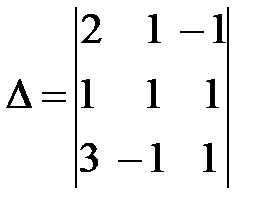 = =2(-1) =-2(-2-3)=10 .
= =2(-1) =-2(-2-3)=10 .
Так как , то система имеет единственное решение.
Найдем определители и , заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов (при вычислении определителя выполним преобразования аналогичные предыдущему.)
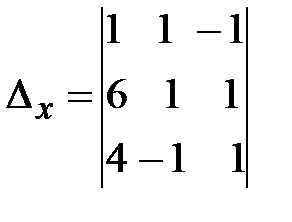 = =2(-1) -2(-1-4)=10.
= =2(-1) -2(-1-4)=10.
При вычислении определителя последнюю строку складываем с первой и вычитаем из второй строки. Разлагаем по элементам последнего столбца.
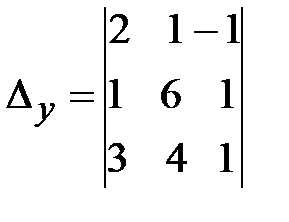 =
= 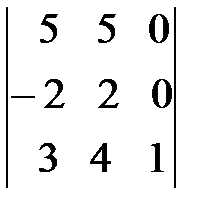 =1(-1) =10+10=20.
=1(-1) =10+10=20.
При вычислении определителя последнюю строку складываем с первой и со второй строки и разлагаем получившийся определитель по элементам второго столбца.
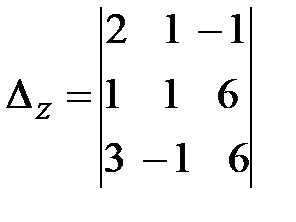 =
= 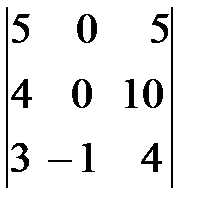 =-1(-1) =50-20=30.
=-1(-1) =50-20=30.
Подставляя найденные значения в формулы Крамера, получим:
Х = у = z =
б) Метод Гаусса.
Составим расширенную матрицу системы:
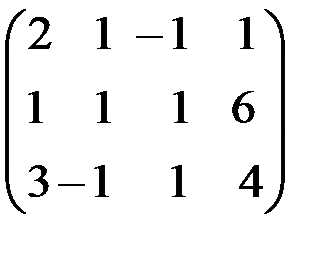
Разрешающим элементом удобно иметь единицу, поэтому переставим второе уравнение на место первого.
Получим нули в первом столбце, умножив первое уравнение последовательно на (-2) и (-3) и складывая со вторым и третьим.
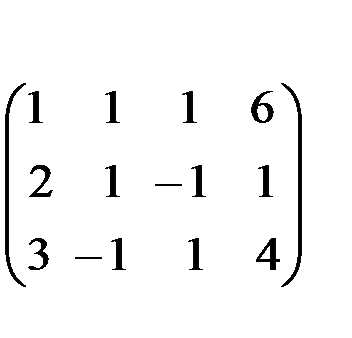 (-2) (-3)
(-2) (-3) 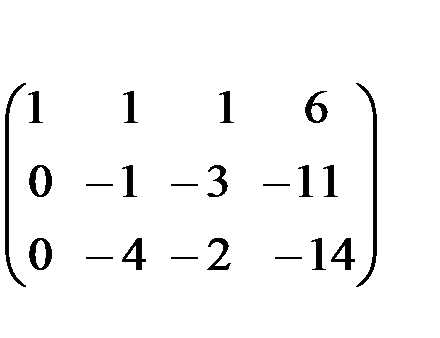
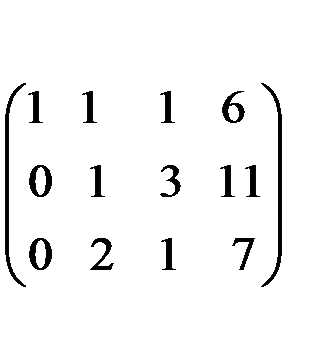
С помощью второго элемента второй строки сделаем нуль во втором столбце третьей строки, для чего умножим вторую строку на (-2) и сложим с третьей.
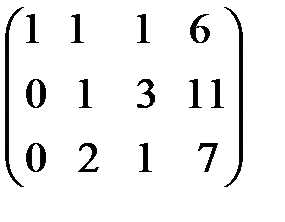 (-2)
(-2) 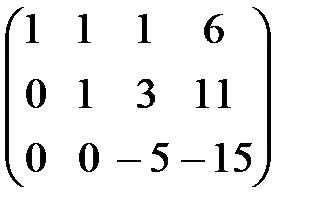
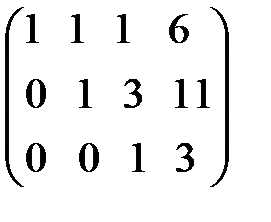 .
.
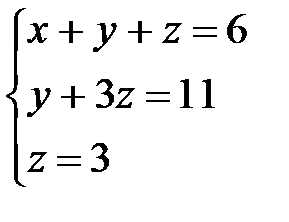
Из последнего уравнения сразу находим значение z=3, подставляя которое во второе уравнение находим у=11-3z=11-9=2. Затем из первого уравнения найдем
х=1, у=2, z=3.
Задача 2. Данную систему уравнений записать в матричной форме и решить ее c помощью обратной матрицы:
x1— 2х2+x3=1,
2x1+3х2 — x3=8
x1 — х2+2х3=- 1
Решение. Обозначим через А матрицу коэффициентов при неизвестных; Х — матрицу-столбец неизвестных Х1, X2, X3; H – матрицу-столбец свободных членов:
1 -2 1 X1 1
А= 2 3 -1 , Х= Х2 H= 8 .
1 -1 2 X3 -1
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: A× Х=Н (l)
Если матрица А — невырожденная (ее определитель отличен от нуля), то она имеет обратную матрицу А-1. Умножив обе части уравнения (1) на А-1 слева получим:
Но (Е — единичная матрица), а ЕХ=Х, Поэтому
(2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
Пусть имеем невырожденную матрицу
а11 а12 а13
А= а21 а22 а23 . Тогда А-1=
а31 а32 а33
где Аij (i=1, 2, 3; j=l, 2, 3) — алгебраическое дополнение элемента аij в определителе матрицы А, которое является произведением (-l)i+
j на минор (определитель) второго порядка, полученный вычерчиванием i-й строки и j-гo столбца в определителе матрицы А.Вычислим определитель и алгебраические дополнения Аij элементов матрицы А.
1 -2 1
= 2 3 -1 =10 0, следовательно, матрица А имеет обратную матрицу А-1
1 -1 2
Тогда
5 3 -1
А-1= = -5 1 3
-5 -1 7
По формуле (2) находим решение данной системы уравнений в матричной форме:
= 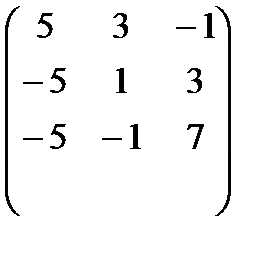 ×
×
Отсюда x1=3, x2 =0, x3=-2
Тема 3 системы линейных уравнений. Правила крамера. Метод гаусса конспект 3
3.1 Правило крамера
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными, которые ждут вас в электротехнике на 2 курсе!
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Теорема
Система nуравнений сnнеизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.
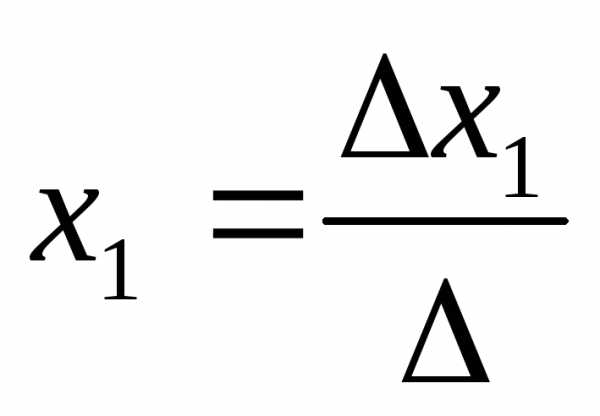
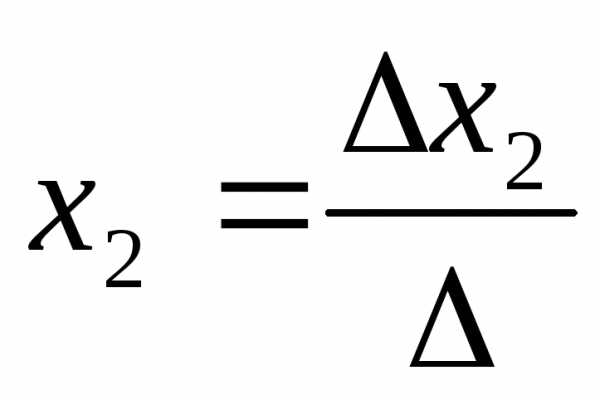 …
…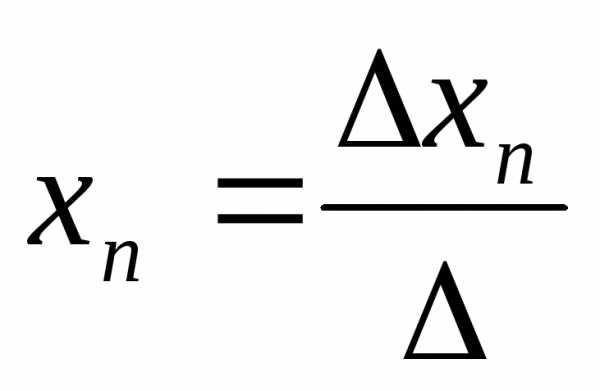

Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называютглавным определителем системы.
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам: ,
Пример 1
Решить систему уравнений: 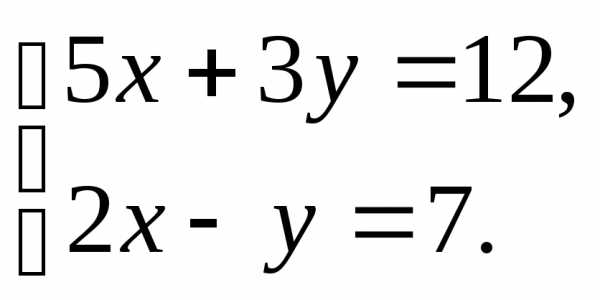
Решение
Составим и вычислим определитель
 :
: – система имеет одно решение, можно
применить теорему Крамера
– система имеет одно решение, можно
применить теорему Крамера
2) Составим и вычислим определитель 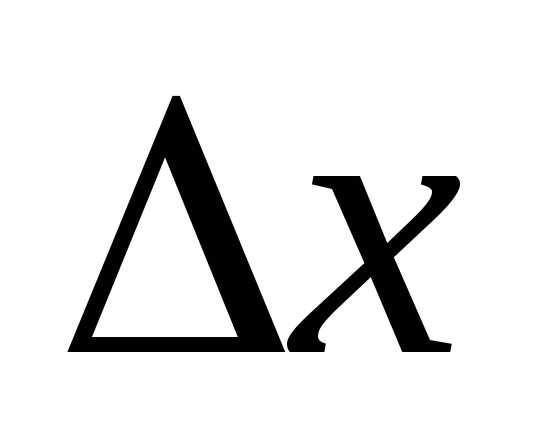 :
: 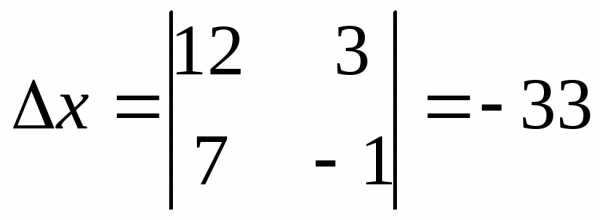
Составим и вычислим определитель
 :
:Найдем значения xиyпо формулам Крамера
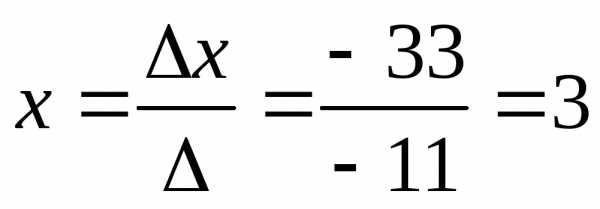
Ответ: (3; -1)
Пример 2
Решить систему линейных уравнений
Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему мы взяли из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
, значит, система имеет единственное решение.
;
;
Ответ: ,
3.2 МЕТОД ГАУССА
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).
Вернемся к простейшей системе и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы:. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строкиматрицыможнопереставлятьместами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
2) Строку матрицы можно умножить (разделить)на любое число,отличное от нуля. Рассмотрим, например, матрицу. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
3) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера:. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2:, ико второй строке прибавляем первую строку умноженную на –2:. Теперь первую строку можно разделить «обратно» на –2:.
Как видите, строка, которую ПРИБАВЛЯЛИ–не изменилась.Всегдаменяется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
На практике так подробно, конечно, не расписывают, а пишут короче: Еще раз: ко второй строкеприбавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: »
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку:»
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку:»
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку:»
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ:рассмотренные манипуляциинельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических»действиях с матрицамичто-то переставлять внутри матриц ни в коем случае нельзя! Вернемся к нашей системе. Она уже почти решена.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований –привести матрицу к ступенчатому виду:. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называетсятрапециевидный видилитреугольный вид.
В результате элементарных преобразований получена эквивалентнаяисходной система уравнений:
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Ответ:
Пример 1
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы:
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число: Почти всегда здесь должна находитьсяединица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
Теперь первая строка у нас останется неизменной до конца решения. Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение,ко второй строке прибавляем первую строку, уже умноженную на –2:
Результат записываем во вторую строку: Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужнок третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). Ик третьей строке прибавляем первую строку, умноженную на –3:
Результат записываем в третью строку:
На практике эти действия обычно выполняются устно и записываются в один шаг:
Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатовпоследователени обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО:Далее нужно получить единицу на следующей «ступеньке»:
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
Для этого к третьей строке прибавляем вторую строку, умноженную на –2:Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат:
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:
Ответ:
ПРАКТИКУМ 3
ЗАДАНИЕ N 1
Систему решают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)2)3)x 4)y
Решение:Решение системы линейных уравнений по правилу Крамера находится по формулами, где. Здесь– главный определитель системы, в котором первый столбец состоит из коэффициентов приx, а второй столбец – из коэффициентов приy. В нашем случаеЕсли, то правило Крамера для решения системы уравнений не применяют.– это определитель, который получается из главного определителя системы путем замены столбца, состоящего из коэффициентов приxна столбец, состоящий из соответствующих свободных членов. Имеем, тогдаАналогично– это определитель, который получается из главного определителя системы путем замены столбца, состоящего из коэффициентов приy, на столбец, состоящий из соответствующих свободных членов. Получим, тогда
ЗАДАНИЕ N 2
Тема: Правило КрамераСистемурешают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)2)3)4)y
Решение:Решение системы линейных уравнений по правилу Крамера находится по формулами, где. Здесь– главный определитель системы, в котором первый столбец состоит из коэффициентов приx, а второй столбец – из коэффициентов приy. В нашем случаеЕсли, то правило Крамера для решения системы уравнений не применяют.– это определитель, который получается из главного определителя системы путем замены столбца, состоящего из коэффициентов приxна столбец, состоящий из соответствующих свободных членов. ИмеемАналогично– это определитель, который получается из главного определителя системы путем замены столбца, состоящего из коэффициентов приy, на столбец, состоящий из соответствующих свободных членов. Получим, тогда
ЗАДАНИЕ N 3Тема: Системы линейных уравненийСистема линейных уравнений
имеет решение …
Решение:Из третьего уравнения системы найдемИз второго уравнения легко получить, чтоЗная значенияyиz, из первого уравнения системы получим Решение данной системы:
ЗАДАНИЕ N 4
Тема: Системы линейных уравненийСистема линейных уравнений
имеет решение …
Решение:Из третьего уравнения системы найдем, чтоИз второго уравнения системы получимЗная значенияyиz, из первого уравнения системы найдем Решение данной системы:
ЗАДАНИЕ N 5
Тема: Системы линейных уравненийСистема линейных уравнений
имеет решение …
Решение:Найдем сумму первого и второго уравнений системы, получим, тогдаНайдемyиз первого или второго уравнений системы, получимИз третьего уравнения имеемРешение данной системы:
ЗАДАНИЕ 6
Тема: Системы линейных уравнений
Решить систему по формулам Крамера.
Решение:
Решим систему по формулам Крамера. , значит, система имеет единственное решение.
Ответ: .
ЗАДАНИЕ 7
Решить систему линейных уравнений методом Гаусса
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху –1, что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по накатанной колее:
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно,, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх: Да тут подарок получился:
Ответ: .
САМОСТОЯТЕЛЬНАЯ РАБОТА 3
ЗАДАНИЕ N 1
Тема: Правило КрамераСистемурешают по правилу Крамера. Вычислите: 1)2)3)4)x
ЗАДАНИЕ N 2
Тема: Правило Крамера Системурешают по правилу Крамера. Вычислите: 1)2)3)x 4)y
ЗАДАНИЕ N 3
Правило КрамераСистемурешают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)2)3)x 4)y
1 | 2 | 3 | 4 | 5 |
– 14 | 14 | – 2 | 2 | 1 |
ЗАДАНИЕ N 4
Правило КрамераСистемурешают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)2)3)4)x
ЗАДАНИЕ N 5Тема: Системы линейных уравненийСистема линейных уравнений
имеет решение …
ЗАДАНИЕ N 6Тема: Системы линейных уравнений Система линейных уравненийимеет решение …
ЗАДАНИЕ N 7
Тема: Системы линейных уравненийСистема линейных уравненийимеет решение …
ЗАДАНИЕ N 8Тема: Системы линейных уравненийСистема линейных уравненийимеет решение …
ЗАДАНИЕ N 9
Тема: Системы линейных уравненийСистема линейных уравненийимеет решение …
ЗАДАНИЕ N 10
Решить систему линейных уравнений методом Гаусса
studfiles.net
Матричный метод решения системы линейных алгебраических уравнений. Формулы Крамера. Метод Гаусса
Рассмотрим систему, составленную из трех линейных алгебраических уравнений с тремя неизвестными.
(6.1.11.)
Решением (2.1)называется система из трех чисел, удовлетворяющая требованию: если в (2.1) вместо и подставить соответственно и , то получим три верных равенства (три тождества).
(6.1.12)
– основная матрица системы (2.1)
(6.1.13)
– расширенная матрица (2.1)
; ; (6.1.14)
система (2.1) может быть записана в матричном виде так:
AX=D (6.1.15)
X – неизвестная матрица-столбец. Введем вспомогательные определители:
Предполагая, что матрица A – невырожденная и умножая (2.5) слева и почленно на A-1, получим
–(6.1.16) матричный способ решения системы.
Используя понятие равенства двух матриц, получим
(6.1.17)
(6.1.18)
(6.1.19)
Элементарными преобразованиями матрицы называются следующие преобразования:
- Перестановка местами произвольных двух строк (столбцов).
- Умножение строки (столбца) на отличное от нуля число.
- Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число.
Пример 6. 1.2. Найти матрицу, обратную матрице . Проверить результат.
Обратную матрицу находим по формуле .
Вычислим определитель матрицы по правилу треугольника:
Определитель не равен нулю, следовательно, обратная матрица существует. Составляем матрицу из алгебраических дополнений ( ) и транспонируем ее.
;
;
;
;
;
;
;
;
;
.
Выполним проверку:
· =
.
·
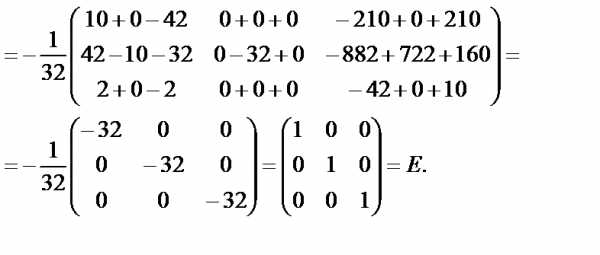
Получим: A-1×A=A×A-1=E. Следовательно, обратная матрица найдена верно.
Ответ: 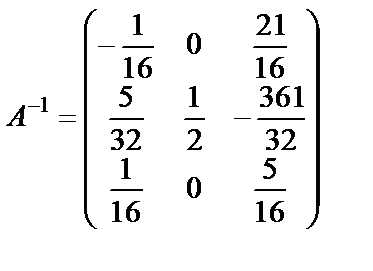 .
.
Пример 6.1.3. Решить систему линейных уравнений по формулам Крамера
.
Решение:
Найдем главный определитель системы
Так как число уравнений и число неизвестных системы между собой равны m=n=3 и определитель отличен от нуля, система имеет единственное решение.
Найдем вспомогательные определители:
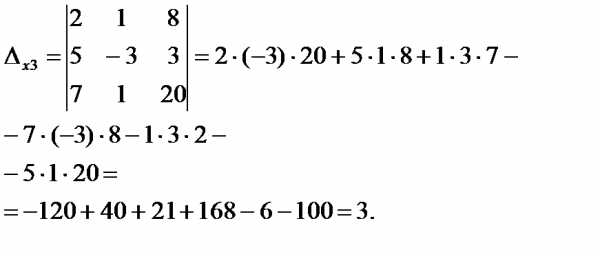
Неизвестные находим по формулам Крамера:
; .
Ответ: .
Пример 6.1.4.. Решить систему линейных уравнений методом Гаусса
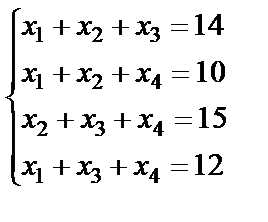 .
.
Решение.
Метод Гаусса – это метод последовательного исключения неизвестных преобразованием данной системы линейных уравнений к эквивалентной. Преобразования уравнений системы заменяются преобразованием строк расширенной матрицы системы до приведения основной матрицы к треугольной или трапециевидной форме. Обнуление элементов выполняется элементарными преобразованиями матрицы(умножение строк на числа, отличные от нуля с последующим сложением).
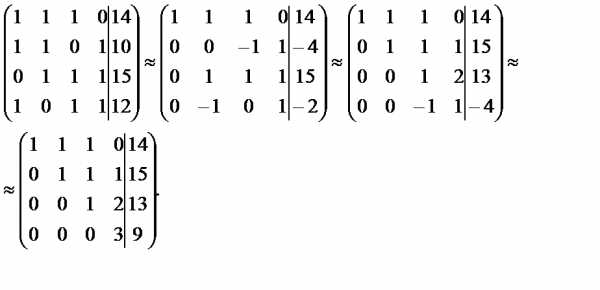
.
Ответ: .
Пример 6.1.5. Применить теорему Кронекера – Капели и найти все решения системы методом Гаусса .
Решение.
Однородная матрица всегда имеет тривиальное решение, в данном случае (0;0;0;0), поэтому нас интересуют другие решения системы.
Применяем метод Гаусса:
.
Так как размерности основной и расширенной матриц системы 3×4 и 3×5 соответственно, ранги этих матриц не могут превышать числа 3. Попробуем посмотреть, есть ли для этих матриц минор третьего порядка, отличный от нуля. Составим его из первых двух и четвертого столбца: , так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали. Следовательно, ранги основной и расширенной матриц равны 3. По теореме Кронекера-Капелли данная система совместна. Так как число уравнений m=3 меньше числа неизвестных n=4, то она имеет бесчисленное множество решений. Закрепленных (базисных) переменных будет 3 (так как r=3), свободных переменных будет (n-r=4-3=1) одна. Минор, который мы составили выше, называется базисным, а переменные, входящие в него, базисными. Следовательно, – базисные переменные, а – свободная, то есть . Выполним обратный ход метода Гаусса:
.
Решением системы будет множество четверок чисел , где .
Например, (0;2;2;0), (0;-1;-1;0), – решения системы.
Ответ: .
Замечание. Обратите внимание, что тривиальное решение тоже задается этим множеством.
Пример 6. 1.6. Даны координаты векторов и в некотором базисе. Показать, что векторы образуют базис и найти координаты вектора в этом базисе.
; ; ; ; .
Решение.
Если векторы образуют базис, то существует разложение вектора в этом базисе , то есть
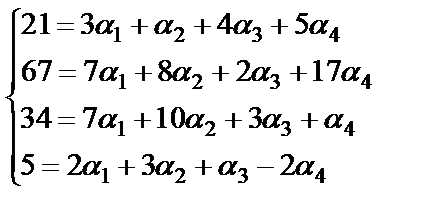 .
.
Отсюда вытекает решение задачи: найти координаты вектора в базисе означает решить систему четырех уравнений с четырьмя неизвестными . Эта система будет иметь единственное решение, если ее основной определитель будет отличен от нуля.
Решаем методом Гаусса:

Так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали , видим, что он отличен от нуля. Следовательно, векторы независимы и образуют базис.
Найдем координаты вектора b в этом базисе
.
Следовательно, или b=(5;0;-1;2) в базисе .
Ответ: .
Похожие статьи:
poznayka.org
Метод Крамера для решения систем линейных уравнений
Теорема Крамера. Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Это решение может быть найдено по формулам
, где – определитель системы
, , …,
Пример. Решить систему уравнений методом Крамера:
D = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.
D2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
D3 = = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x1 = = 1; x2 = = 2; x3 = = 3.
Практическое занятие №4
Наименование занятия: Решение систем линейных уравнений методом Гаусса
Цель занятия:Научиться решать системы линейных уравнений методом Гаусса
Подготовка к занятию:Повторить теоретический материал по теме «Системы линейных уравнений»
Литература:
- Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.
- Дадаян А.А. «Математика», 2004г.
Задание на занятие:
- Решить системы линейных уравнений методом Гаусса
1)
2)
4)
5)
3)
6)
Порядок проведения занятия:
- Получить допуск к работе
- Выполнить задания
- Ответить на контрольные вопросы.
Содержание отчета:
- Наименование, цель занятия, задание;
- Выполненное задание;
- Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
- Какие преобразования систем линейных уравнений являются эквивалентными?
- Опишите алгоритм решения системы линейных уравнений методом Гаусса.
ПРИЛОЖЕНИЕ
Рассмотрим произвольную систему линейных уравнений. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
,
где aij – коэффициенты, а bi – постоянные. Решением системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.
Для этой системы линейных уравнений вида матрица
А = называется матрицей системы, а матрица
А*= называется расширенной матрицей системы
Метод Гаусса
Суть метода заключается в том, что систему уравнений с помощью элементарных преобразований приводят к эквивалентной ей системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называются прямым ходом. Затем из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
Элементарными преобразованиями системявляются:
1) Умножение или деление коэффициентов и свободных членов на одно и то же число
2) Сложение и вычитание уравнений
3) Перестановка уравнений системы местами.
4) Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю
Пример. Решить систему линейных уравнений методом Гаусса
Составим расширенную матрицу системы.
А* = .
Выполним над этой матрицей следующие преобразования:
1) поменяем местами 1 и 2 строки;
2) прибавим к элементам 2 строки 1-ю строку, умноженную на -2;
3) прибавим к элементам 3 строки 1-ю строку, умноженную на -7;
4) прибавим к элементам 3 строки 2-ю строку, умноженную на -3;
А* =
Получили систему с треугольной матрицей. Таким образом, исходная система может быть представлена в виде:
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Практическое занятие №5
Наименование занятия: Операции над векторами
Цель занятия:Научиться выполнять действия с векторами
Подготовка к занятию:Повторить теоретический материал по теме «Векторы. Операции над векторами»
Литература:
- Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.
- Дадаян А.А. «Математика», 2004г.
Задание на занятие:
- Даны векторы и . Построить векторы , .
- Найти координаты векторов , , , если А(2; 3), В(-1; -3), С(-7; 5).
- Даны векторы = (-2; 4) и = (3; 1). Найти: , , , .
- Найти длину вектора , если А(5; 2), В(8; -2).
- Дан треугольник с вершинами А(7; 7), В(4; 3), С(3; 4). Найти его периметр.
- Отрезок АВ задан точками А(2; 3), В(10; 11). Найти координаты точки С, если известно, что .
- Найти длину медианы АМ треугольника с вершинами А(7; -4), В(-1; 8), С(-12; -1).
- Найти скалярное произведение векторов = (5; 7) и = (4; 3).
- Найти угол между векторами = (4; 0) и = (2; -2).
- Найти углы треугольника с вершинами А(6; 7), В(3; 3), С(1; -5).
Порядок проведения занятия:
- Получить допуск к работе
- Выполнить задания
- Ответить на контрольные вопросы.
Содержание отчета:
- Наименование, цель занятия, задание;
- Выполненное задание;
- Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
- Что называется вектором? Длиной вектора?
- Как сложить два вектора?
- Как найти разность двух векторов?
- Как умножить вектор на число?
- Как найти координаты вектора, заданного двумя точками?
- Как найти длину вектора, заданного двумя точками?
- Как найти длину вектора, заданного своими координатами?
- Как вычисляется скалярное произведение векторов, заданных своими координатами?
- Как найти угол между векторами?
ПРИЛОЖЕНИЕ
Векторомназывается направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевойвектор – это вектор, начало и конец которого совпадают.
Длиной (модулем) вектора называется расстояние между началом и концом вектора.
Действия над векторами
1. Суммой двух векторов называется вектор , удовлетворяющий условию: если начало вектора перенести в точку, являющуюся концом вектора , начало вектора совпадет с началом вектора , а конец – с концом вектора (правило треугольника).
2. Произведением вектора на число a называется вектор , удовлетворяющий следующим условиям:
1) ;
2) вектор коллинеарен вектору ;
3) вектор соноправлен с вектором ( ), если a > 0 и противоположно направлен ( ¯ ), если a < 0.
Координаты вектора
Пусть точки А(х1, y1) и B(x2, y2), заданы в прямоугольной декартовой системе координат. Чтобы найти координаты вектора нужно из координат его конца вычесть координаты начала т.е. = (x2 – x1, y2 – y1).
infopedia.su
Метод Гаусса решения систем линейных уравнений (рассмотрим на примере системы из трёх уравнений и трёх неизвестных)
Высшая математика
Семестр
Лекция № 2.
Методы решения систем линейных уравнений.
система линейных уравнений в скалярном виде ( – коэффициенты при переменных и свободные коэффициенты – известные числа, – неизвестные)
или в матричном сокращенном виде:
Мы будем рассматривать частный случай системы линейных уравнений, а именно случай, когда – т.е. число уравнений равно числу неизвестных.В этом случае матрица системы будет квадратной.Еёопределитель называется определителем системы.В зависимости от значения определителя возможны три случая:
=> система алгебраических уравнений имеет единственное решение (совместная и определённая)
система алгебраических уравнений не имеет решений (несовместная)
система алгебраических уравнений имеет бесконечно много решений
(совместная и неопределённая)
Методы решения системы линейных алгебраических уравнений с квадратной матрицей
- Метод обратной матрицы (рассмотрен на прошлой лекции)
– система в матричном виде
формула для поиска решения (в случае )
- Метод Крамера
- Метод Гаусса
Рассмотрим подробно методы Крамера и Гаусса.
Метод Крамера для решения систем линейных алгебраических уравнений
(в случае )
(на примере системы из двух уравнений с двумя неизвестными)
Дано:
– система в скалярном виде .
Требуется решить её методом Крамера
1 шаг – записать систему в матричном виде:
2 шаг: вычислить – определитель системы.
(определитель вычисляется крест на крест)
Если , то на 3 шаг не переходим. В этом случае систему нельзя решить методом Крамера, т.к. она не имеет единственного решения.
Если , то переходим к третьему шагу.
Шаг – вычислить ещё 2 дополнительные характеристики
– определитель матрицы системы, он получается после замены первого столбца матрицы A столбцом свободных коэффициентов B
определитель матрицы системы, он получается после замены второго столбца матрицы A столбцом свободных коэффициентов B
(определители вычисляются крест на крест)
4 шаг – по найденным выше трём характеристикам ищется решение
формулы для поиска решения по методу Крамера
Метод Крамера не подходит для решения систем большой размерности, т.е. носит чисто теоретический характер. Это связано с тем, что вычисление определителей очень длительный процесс и даже современным компьютерам не под силу справиться с этой задачей.
При подсчёте каждого определителя по приведенным выше формулам надо вычислить слагаемых, что нереально уже при умеренных . Например, уже при имеем . Если одно слагаемое вычисляется за секунд, что вполне допустимо для современных машин, то время расчёта составит совершенно фантастическую цифру :
лет.
Пример:
1 шаг:
2 шаг:
=> переходим к 3 шагу
3 шаг:
4 шаг:
(* – как считать определители – см. предыдущую лекцию)
Метод Гаусса решения систем линейных уравнений (рассмотрим на примере системы из трёх уравнений и трёх неизвестных)
В отличие от метода Крамера метод Гаусса подходит для решения систем большой размерности.Приведём сведения для оценки его трудоёмкости.
формула оценки времени расчёта на компьютере системы из n уравнений в минутах при условии, что на одну операцию надо сек.
0,01 мин. – время расчёта для 100 уравнений
11 мин. – время расчёта для 1000 уравнений
7 дней– время расчёта для 10000 уравнений
studopedya.ru
8. Формулы Крамера решения систем линейных алгебраических уравнений.
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
= det (aij)
и n вспомогательных определителей i (i=), которые получаются из определителя заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
xi= i( i = ). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i= i/ .
Если главный определитель системы и все вспомогательные определители i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Пример 2.14. Решить методом Крамера систему уравнений:
x1 + x2 + x3 + x4 = 5,
x1 + 2x2 – x3 + 4x4 = -2,
2x1 – 3x2 – x3 – 5x4 = -2,
3x1 + x2 +2x3 + 11 x4 = 0.
Решение. Главный определитель этой системы
значит, система имеет единственное решение. Вычислим вспомогательные определители i ( i = ), получающиеся из определителя путем замены в нем столбца, состоящего из коэффициентов при xi, столбцом из свободных членов:
Отсюда x1 = 1/ = 1, x2 = 2/ = 2, x3 = 3/ = 3, x4 = 4/ = -1, решение системы – вектор С=(1, 2, 3, -1)T.
9. Метод Гаусса решения систем линейных алгебраических уравнений.
Наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 2.13. Решить систему уравнений методом Гаусса:
x + y – 3z = 2,
3x – 2y + z = – 1,
2x + y – 2z = 0.
Решение. Выпишем расширенную матрицу данной системы
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
~ ;
б) третью строку умножим на (-5) и прибавим к ней вторую:
.
В результате всех этих преобразований данная система приводится к треугольному виду:
x + y – 3z = 2,
-5y + 10z = -7,
– 10z = 13.
Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = – 0,7.
studfiles.net
9. Решение системы линейных уравнений методом Крамера
Метод Крамера:
а11х1 + а12х2 = b1
a21x1+ a22x2 = b2
x1 = (b1a22 – b2a12)/(a11a22-a12a21)=/\x1/ /\
x2 = (a11b2-a21b1)/(a11a22-a12a21)=/\x2/ /\
/\ – главный определитель системы
/\x1, /\x2 –Определители для данных неизвестных
Формулы хj = /\xj//\ – формулы Крамера.
если detA не равен 0, система имеет одно решение
если detA=0 и хотя бы один /\xj не равен 0, решений нет
если detA=0 и /\xj = 0, система имеет множество решений.
10. Решение системы линейных уравнений методом Гаусса
Метод Гаусса основан на элементарных преобразованиях системы:
1) Можно менять уравнение местами
2) К любому уравнению умноженному на число не равное 0, можно прибавить другое уравнение, умноженное на число не равное 0.
Метод Гаусса или метод исключения заключается в том, что под главной диагональю получаем коэффициенты равные нулю. Система уравнений сводится к виду:
а11х1+а12х2+…+amxn=b1
а’22x2+…a’mxn=b2’
……………………..
Cmnxn=b*n
Если Сmn не равно 0, то xn = b*n/Cmn – система имеет 1 решение
Сmn=0, b*n не равно 0, решений нет
Сmn=0, b*n=0 – множество решений
11.Решение произвольных систем линейных m уравнений с n неизвестными
12. Модель Леонтьева
Пусть имеется n-отраслей экономики, одна часть продукции используется на внутренние нужды отрасли, вторая часть предназначена для потребления другими отраслями, третья часть на личные нужды.
xi – общий валовый объем продукции, i – отрасли xij –объем продукции i-отрасли потребляемой j-отраслью. Yi – объем конечного продукта, выпускаемый i-отраслью для общественного потребления.
xi = ∑ xij + yij (1)
Общий или валовый продукт i-отрасли равен суммарному продукту потребляемому j-отраслью + конечный продукт этой отрасли. Уравнение (1) называется уравнением баланса.
Если элементы уравнения имеют стоимостные выражения, то уравнения называются стоимостным межотраслевым балансом.
aij=xij/xj
Модель Леотьева линейная: xi = ∑ aij xj + yi
В матричном виде: X = AX + Y
X = (E-A)-1Y
Матрица А продуктивна если сумма элементов столбцов матрицы не превосходит 1 и хотя бы одна из сумм строго меньше 1.
13.Векторы. Линейные операции над векторами
n-вектором называется упорядоченная совокупность n-действительных чисел, записанных в виде х=(х1,х2,….хn), xi-компоненты вектора
х=у, если равны xi=yi
суммой двух векторов одной размерности n называется вектор z = x + y, zi=xi+yi
Произведением вектора на число называется вектор λх=z, zi=λxi
Свойства операций над векторами:
1) x+y=y+x – сумма коммутативна
2) x+(y+z)=(x+y)+z – ассоциативна
3) α(β · x) = (α·β)·x – α и β действительные числа
4) α(х + y)= αx + αy – дистрибутивность
5) (α + β) х = αх + βх
6) О = (0,0,…0), х+О=х
7) (-х) – противоположный х
х+(-х) = 0
8) 1·х=х
Множество n-мерных векторов с действительными компонентами, удовлетворяющих свойствам называется векторным пространством R.
14.Проекция вектора на ось
Проекцией вектора а на ось L называется число, обозначаемое прL а и равное |a| cos α, где α (0≤ α≤п/2) – угол между положительным направлением оси L и направлением вектора а, т. е. по определению прL а = |a| cos α.
studfiles.net

 :
: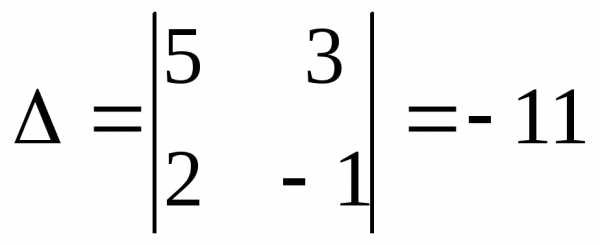 – система имеет одно решение, можно
применить теорему Крамера
– система имеет одно решение, можно
применить теорему Крамера :
:

