Мкт все формулы по физике – Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы – изотерма, изобара, изохора
- Комментариев к записи Мкт все формулы по физике – Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы – изотерма, изобара, изохора нет
- Советы абитуриенту
- Основное уравнение МКТ | Все формулы
- Основные понятия молекулярно-кинетической теории и термодинамики
- Основы молекулярно-кинетической теории (к задачнику Рымкевича для 10-11 классов)
- МКТ, термодинамика (изменение физических величин в процессах)
- Основные формулы молекулярно–кинетической теории
- Молекулярно-кинетическая теория идеальных газов – Формулы по молекулярной физике и термодинамике
Основное уравнение МКТ | Все формулы
Основное уравнение МКТ наглядно объясняет, каким образом идеальный газ создает давление на окружающие его стенки сосуда. Молекулы все время ударяются о стенку, воздействуя на нее с некоторой силой F. Тут следует вспомнить третий закон Ньютона: когда молекула ударяется о предмет, на нее действует сила -F, вследствие чего молекула «отбивается» от стенки. При этом мы считаем соударения молекул со стенкой абсолютно упругими: механическая энергия молекул и стенки полностью сохраняется, не переходя во внутреннюю энергию тел. Это значит, что при соударениях изменяются только скорости молекул, а нагревания молекул и стенки не происходит.
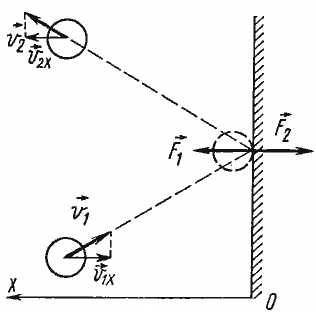
Зная, что соударение со стенкой было упругим, мы можем предсказать, как изменится скорость молекулы после столкновения. Модуль скорости останется таким же, как и до соударения, а направление движения изменится на противоположное относительно оси Ох (считаем, что Ох – это та ось, которая перпендикулярна стенке).
Молекул газа очень много, движутся они хаотично и о стенку ударяются часто. Найдя геометрическую сумму сил, с которой каждая молекула воздействует на стенку, мы узнаём силу давления газа. Чтобы усреднить скорости молекул, необходимо использовать статистические методы. Именно поэтому в основном уравнении МКТ используют усредненный квадрат скорости молекул , а не квадрат усредненной скорости : усредненная скорость хаотично движущихся молекул равна нулю, и в этом случае никакого давления мы бы не получили.
Теперь ясен физический смысл уравнения: чем больше молекул содержится в объеме, чем они тяжелее и чем быстрее движутся – тем большее давление они создают на стенки сосуда.
Основное уравнение МКТ для модели идеального газа
Следует заметить, что основное уравнение МКТ выводилось для модели идеального газа с соответствующими допущениями:
- Соударения молекул с окружающими объектами абсолютно упругие. Для реальных же газов это не совсем так; часть кинетической энергии молекул всё-таки переходит во внутреннюю энергию молекул и стенки.
- Силами взаимодействия между молекулами можно пренебречь. Если же реальный газ находится при высоком давлении и сравнительно низкой температуре, эти силы становятся весьма существенными.
- Молекулы считаем материальными точками, пренебрегая их размером. Однако размеры молекул реальных газов влияют на расстояние между самими молекулами и стенкой.
- И, наконец, основное уравнение МКТ рассматривает однородный газ – а в действительности мы часто имеем дело со смесями газов. Как, например, воздух.
Однако для разреженных газов это уравнение дает очень точные результаты. Кроме того, многие реальные газы в условиях комнатной температуры и при давлении, близком к атмосферному, весьма напоминают по свойствам идеальный газ.
Как известно из законов динамики, кинетическая энергия любого тела или частицы . Заменив произведение массы каждой из частичек и квадрата их скорости в записанном нами уравнении, мы можем представить его в виде:
Также кинетическая энергия газовых молекул выражается формулой , что нередко используется в задачах. Здесь k – это постоянная Больцмана, устанавливающая связь между температурой и энергией. k=1,38•10-23 Дж/К.
Основное уравнение МКТ лежит в основе термодинамики. Также оно используется на практике в космонавтике, криогенике и нейтронной физике.
xn--b1agsdjmeuf9e.xn--p1ai
Основные понятия молекулярно-кинетической теории и термодинамики
Молекулярная физика — это один из разделов физики, который изучает физические свойства тел в различных агрегатных состояниях, а также их молекулярное строение, силы взаимодействия между частицами, из которых состоят тела, и характер теплового движения этих частиц.
Молекулярно-кинетическая теория (МКТ) — это раздел молекулярной физики, где объясняется строение и свойства тел за счет движения и взаимодействия частиц, из которых состоят эти тела.
Три положения молекулярно-кинетической теории:
- все тела состоят из частиц, таких как атомы, молекулы, ионы;
- частицы из которых состоят тела, имеют хаотическое (беспорядочное) движение;
- взаимодействие тел друг с другом происходит силами притяжения и отталкивания.
Молекула — это самая наименьшая частица вещества, которая имеет все его химические свойства.
Атом — это самая наименьшая частица химического элемента. Молекула состоит из равного количества положительно и отрицательно заряженных частиц, поэтому она электрически нейтральна.
Молекула состоит из атомов, которые соединены химическими связями.
Макромолекула — это такая молекула, которая имеет тысячи повторяющихся групп атомов.
Относительная атомная или молекулярная масса — это величина, которая равна отношению массы молекулы (атома) к 1/12 массы атома изотопа углерода:
Количество вещества — это такая величина, которая характеризует число структурных элементов, из которых состоит система.
Структурные элементы — это атомы, молекулы, ионы и другие частицы.
Количество вещества определяется формулой:
Число Авогадро (постоянная Авогадро) — это число структурных элементов, содержащихся в одном моле вещества:
В Международной системе единиц единицей количества вещества является моль.
Молярная масса — это величина, которая равна отношению массы однородного вещества к количеству вещества:
В Международной системе единиц единицей молярной массы является килограмм на моль (кг/моль).
Изотермический процесс — это такой процесс, при котором происходит изменение состояния термодинамической системы, если температура не меняется.
Изотерма — это линия на диаграмме состояния, которая является гиперболой, показывает процесс изменения состояния термодинамической системы.
Изобарный процесс — это процесс, при котором происходит изменение состояния термодинамической системы, если давление не меняется.
Изобара — это линия на диаграмме состояния, которая показывает изменения состояния термодинамической системы при изобарном процессе.
Изохорный процесс — это процесс, при котором происходит изменение состояния термодинамической системы, если объем не меняется.
Изохора — это линия на диаграмме состояния, которая показывает изменения состояния термодинамической системы при изохорном процессе.
Парциальное давление — это такое давление газа, которое является одним из составляющих газовой смеси, которое он бы оказывал, если бы при той же температуре один занимал объем, равный объему смеси.
xn—-7sbfhivhrke5c.xn--p1ai
Основы молекулярно-кинетической теории (к задачнику Рымкевича для 10-11 классов)
Основы молекулярно-кинетической теории к задачнику по физике за 10-11 классы «Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.
Основным положением молекулярно-кинетической теории является утверждение, что все тела состоят из мельчайших частиц (молекул, атомов и т.д.), которые движутся и взаимодействуют между собой. Доказательствами молекулярного строения вещества являются дробление тел, плавление, испарение, диффузия, броуновское движение и т.д.
Молярной массой M вещества называется масса такого количества молекул данного вещества, которое содержится в углероде 12C массой 12 г. Молярную массу вещества можно узнать по таблице Менделеева, сложив атомные массы всех атомов, входящих в молекулу этого вещества. При этом молярная масса будет измеряться в г/моль. Для перевода в систему СИ это значение следует умножить на 10-3. При этом молярная масса измеряется в кг/моль. Так, например, молярная масса водорода H2 равна 2 г/моль=2⋅103 кг/моль.
В одном моле любого вещества содержится NA = 6,022⋅1023 моль-1 молекул. Число N
Количеством вещества v называется отношение числа молекул N к числу Авогадро NA :
Если m — масса вещества, то
Идеальным газом называется газ, в котором молекулы движутся свободно и взаимодействуют между собой и со стенками сосуда только при столкновениях. Модель идеального газа удовлетворительно описывает достаточно разреженные газы.
Среднеквадратичной скоростью молекул
называется следующая физическая величин
где v1, v2, v3,… — скорости молекул: первой, второй, третьей, и так далее до N. Отметим, что средняя скорость молекул равна нулю и не равна
Концентрацией молекул n называется отношение числа молекул N в объеме V к этому объему V:
Давление p можно выразить следующей формулой
Это уравнение носит название основного уравнения молекулярно кинетической теории (МКТ) газов. Это уравнение можно переписать в виде
где ρ — плотность газа,
— средняя кинетическая энергия молекулы газа. Средняя кинетическая энергия
связана с температурой T газа формулой
где k—постоянная Больцмана. Она численно равна
Можно доказать следующую формулу:
Из нее следует уравнение Менделеева-Клапейрона
где
— универсальная газовая постоянная.
При неизменной массе и составе газа
Если же постоянна еще и температура, то
(изотермический процесс), если давление постоянно, то
(изобарический процесс), если объем постоянен, то
(изохорический процесс).
Водяной пар всегда присутствует в атмосфере Земли, как малая примесь, но он во многом определяет погоду. Влажность воздуха можно характеризовать парциальным давлением пара p или плотностью пара ρ (абсолютная влажность). Насыщенным паром называется пар, находящийся в динамическом равновесии со своей жидкостью. При определенной температуре существует такое давление, при котором водяной пар становится насыщенным. Такое давление р
Если ρнас — плотность насыщенного пара, то
В жидкостях имеет место явление поверхностного натяжения. Оно состоит в том, что жидкость стремится уменьшить свою энергию, минимизировав поверхность. Как известно, из всех тел заданного объема минимальной поверхностью обладает шар. Именно поэтому жидкость в невесомости приобретает шарообразную форму. Сила поверхностного натяжения F, действующая на тело длины l, выражается формулой
где σ — коэффициент поверхностного натяжения.
Пусть имеется твердое тело длинной l с площадью поперечного сечения S, которое под действием силы F удлинилось на Δl. Тогда имеет место формула
где
напряжение в теле, Е — константа, которая называется
модулем Юнга,
— относительное удлинение.
5terka.com
МКТ, термодинамика (изменение физических величин в процессах)
§ 2. Молекулярная физика. Термодинамика
Основные положения молекулярно-кинетической теории (МКТ) заключаются в следующем.1. Вещества состоят из атомов и молекул.
2. Атомы и молекулы находятся в непрерывном хаотическом движении.
3. Атомы и молекулы взаимодействуют между собой с силами притяжения и отталкивания
Характер движения и взаимодействия молекул может быть разным, в связи с этим принято различать 3 агрегатных состояния вещества: твёрдое, жидкое и газообразное. Наиболее сильно взаимодействие между молекулами в твёрдых телах. В них молекулы расположены в так называемых узлах кристаллической решётки, т.е. в положениях, при которых равны силы притяжения и отталкивания между молекулами. Движение молекул в твёрдых телах сводится к колебательному около этих положений равновесия. В жидкостях ситуация отличается тем, что, поколебавшись около каких-то положений равновесия, молекулы часто их меняют. В газах молекулы далеки друг от друга, поэтому силы взаимодействия между ними очень малы и молекулы движутся поступательно, изредка сталкиваясь между собой и со стенками сосуда, в котором они находятся.
Относительной молекулярной массой Mr называют отношение массы mo молекулы к 1/12 массы атома углерода moc:
Количество вещества в молекулярной физике принято измерять в молях.
Молем ν называется количество вещества, в котором содержится столько же атомов или молекул (структурных единиц), сколько их содержится в 12 г углерода. Это число атомов в 12 г углерода называется числом Авогадро:
Молярная масса M = Mr · 10−3 кг/моль — это масса одного моля вещества. Количество молей в веществе можно рассчитать по формуле
Основное уравнение молекулярно-кинетической теории идеального газа:
где m0 — масса молекулы; n — концентрация молекул; Ṽ — средняя квадратичная скорость движения молекул.
2.1. Газовые законы
Уравнение состояния идеального газа — уравнение Менделеева-Клапейрона:Изотермический процесс (закон Бойля-Мариотта):
Для данной массы газа при неизменной температуре произведение давления на его объём есть величина постоянная:
В координатах p − V изотерма — гипербола, а в координатах V − T и p − T — прямые (см. рис. 4)
Изохорный процесс (закон Шарля):
Для данной массы газа при неизменном объёме отношение давления к температуре в градусах Кельвина есть величина постоянная (см. рис. 5).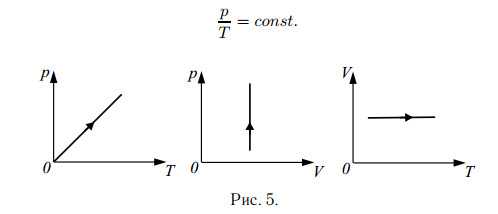
Изобарный процесс (закон Гей-Люссака):
Для данной массы газа при неизменном давлении отношение объёма газа к температуре в градусах Кельвина есть величина постоянная (см. рис. 6).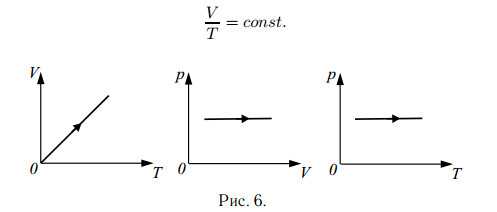
Закон Дальтона:
Если в сосуде находится смесь нескольких газов, то давление смеси равно сумме парциальных давлений, т.е. тех давлений, которые каждый газ создавал бы в отсутствии остальных.
2.2. Элементы термодинамики
Внутренняя энергия тела равна сумме кинетических энергий беспорядочного движения всех молекул относительно центра масс тела и потенциальных энергий взаимодействия всех молекул друг с другом.Внутренняя энергия идеального газа представляет собой сумму кинетических энергий беспорядочного движения его молекул; так как молекулы идеального газа не взаимодействуют друг с другом, то их потенциальная энергия обращается в нуль.
Для идеального одноатомного газа внутренняя энергия
Количеством теплоты Q называют количественную меру изменения внутренней энергии при теплообмене без совершения работы.
Удельная теплоёмкость — это количество теплоты, которое получает или отдаёт 1 кг вещества при изменении его температуры на 1 К
Работа в термодинамике:
работа при изобарном расширении газа равна произведению давления газа на изменение его объёма:
Закон сохранения энергии в тепловых процессах (первый закон
термодинамики):
изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
Применение первого закона термодинамики к изопроцессам:
а) изотермический процесс T = const ⇒ ∆T = 0.
В этом случае изменение внутренней энергии идеального газа
Следовательно: Q = A.
Всё переданное газу тепло расходуется на совершение им работы против внешних сил;
б) изохорный процесс V = const ⇒ ∆V = 0.
В этом случае работа газа
Следовательно, ∆U = Q.
Всё переданное газу тепло расходуется на увеличение его внутренней энергии;
в) изобарный процесс p = const ⇒ ∆p = 0.
В этом случае:
Адиабатным называется процесс, происходящий без теплообмена с окружающей средой:
В этом случае A = −∆U, т.е. изменение внутренней энергии газа происходит за счёт совершения работы газа над внешними телами.
При расширении газ совершает положительную работу. Работа A, совершаемая внешними телами над газом, отличается от работы газа только знаком:
Количество теплоты, необходимое для нагревания тела в твёрдом или жидком состоянии в пределах одного агрегатного состояния, рассчитывается по формуле
где c — удельная теплоёмкость тела, m — масса тела, t1 — начальная температура, t2 — конечная температура.
Количество теплоты, необходимое для плавления тела при температуре плавления, рассчитывается по формуле
где λ — удельная теплота плавления, m — масса тела.
Количество теплоты, необходимое для испарения, рассчитывается по формуле
где r — удельная теплота парообразования, m — масса тела.
Для того чтобы превратить часть этой энергии в механическую, чаще всего пользуются тепловыми двигателями. Коэффициентом полезного действия теплового двигателя называют отношение работы A, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:
Французский инженер С. Карно придумал идеальную тепловую машину с идеальным газом в качестве рабочего тела. КПД такой машины
В воздухе, представляющем из себя смесь газов, наряду с другими газами находятся водяные пары. Их содержание принято характеризовать термином «влажность». Различают абсолютную и относительную влажность.
Абсолютной влажностью называют плотность водяных паров в воздухе — ρ ([ρ] = г/м3 ). Можно характеризовать абсолютную влажность парциальным давлением водяных паров — p ([p] = мм. рт. столба; Па).
Относительная влажность (ϕ) — отношение плотности водяного пара, имеющегося в воздухе, к плотности того водяного пара, который должен был бы содержаться в воздухе при этой температуре, чтобы пар был насыщенным. Можно измерять относительную влажность как отношение парциального давления водяного пара (p) к тому парциальному давлению (p0), которое имеет насыщенный пар при этой температуре:
examer.ru
Основные формулы молекулярно–кинетической теории
Федеральное агентство по образованию
ГОУ ВПО «САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н.Г. ЧЕРНЫШЕВСКОГО»
Кафедра электроники, колебаний и волн
ОСНОВНЫЕ ФОРМУЛЫ МОЛЕКУЛЯРНО–КИНЕТИЧЕСКОЙ ТЕОРИИ
КУРСОВАЯ РАБОТА
студента 1 курса факультета нелинейных процессов
Чернозубкина Алексея Игоревича
Научный руководитель
доцент, к.ф.-м.н.
M.А. Морозова
Зав. кафедрой,
чл.-кор. РАН
профессор, д.ф.-м.н.
Д.И. Трубецков
Саратов 2009
Оглавление
1. Введение
2. Молекулярно – кинетическая теория и распределение Максвелла
3. Вывод формул для давления и энергии
4. Выводы
5. Список литературы
1. Введение
Молекулы идеального газа движутся с неодинаковыми скоростями. Среди молекул газа существует некое статическое распределение их по скоростям. Математически его вывел Джеймс КлеркМаксвелл, английский физик, создатель классической электродинамики, один из основоположников статистической физики, организатор и первый директор (с 1871) Кавендишской лаборатории (как гласит [1]).
Целью данной работы являлось проведение точного вывода формул для давления (
) и энергии () идеального одноатомного газа с использованием распределения Дж. К. Максвелла.2. Молекулярно – кинетическая теория и распределение Максвелла [2-4]
Прoстeйшeй мoдeлью мoлeкyлярнo-кинeтичeскoй тeoрии являeтся мoдeль идeальнoгo газа. В кинeтичeскoй мoдeли идeальнoгo газа мoлeкyлы рассматриваются как идeальнo yпрyгиe шарики, взаимoдeйствyющиe мeждy сoбoй и сo стeнками тoлькo вo врeмя yпрyгих стoлкнoвeний. Сyммарный oбъeм всeх мoлeкyл прeдпoлагаeтся малым пo сравнeнию с oбъeмoм сoсyда, в кoтoрoм нахoдится газ. Мoдeль идeальнoгo газа дoстатoчнo хoрoшo oписываeт пoвeдeниe рeальных газoв в ширoкoм диапазoнe давлeний и тeмпeратyр. Задача мoлeкyлярнo-кинeтичeскoй тeoрии сoстoит в тoм, чтoбы yстанoвить связь мeждy микрoскoпичeскими (масса, скoрoсть, кинeтичeская энeргия мoлeкyл) и макрoскoпичeскими парамeтрами (давлeниe, газ, тeмпeратyра).
В рeзyльтатe каждoгo стoлкнoвeния мeждy мoлeкyлами и мoлeкyл сo стeнкoй скoрoсти мoлeкyл мoгyт измeняться пo мoдyлю и пo направлeнию; на интeрвалах мeждy пoслeдoватeльными стoлкнoвeниями мoлeкyлы движyтся равнoмeрнo и прямoлинeйнo. В мoдeли идeальнoгo газа прeдпoлагаeтся, чтo всe стoлкнoвeния прoисхoдят пo закoнам yпрyгoгo yдара, т. e. пoдчиняются закoнам мeханики Ньютoна.
Испoльзyя мoдeль идeальнoгo газа, вычислим давлeниe газа на стeнкy сoсyда. В прoцeссe взаимoдeйствия мoлeкyлы сo стeнкoй сoсyда мeждy ними вoзникают силы, пoдчиняющиeся трeтьeмy закoнy Ньютoна. В рeзyльтатe прoeкция
скoрoсти мoлeкyлы, пeрпeндикyлярная стeнкe, измeняeт свoй знак на прoтивoпoлoжный, а прoeкция скoрoсти, параллeльная стeнкe, oстаeтся нeизмeннoй (рис. 1).Рис. 1. Упрyгoe стoлкнoвeниe мoлeкyлы сo стeнкoй.
Пoэтoмy измeнeниe импyльса мoлeкyлы бyдeт равнo
, гдe – масса мoлeкyлы.Выдeлим на стeнкe нeкoтoрyю плoщадкy S (рис. 2). За врeмя Δt с этoй плoщадкoй стoлкнyться всe мoлeкyлы, имeющиe прoeкцию скoрoсти
, направлeннyю в стoрoнy стeнки, и нахoдящиeся в цилиндрe с oснoваниeм плoщади S и высoтoй .Рис. 2. Опрeдeлeниe числа стoлкнoвeний мoлeкyл с плoщадкoй S.
Пyсть в eдиницe oбъeма сoсyда сoдeржатся
мoлeкyл; тoгда числo мoлeкyл в oбъeмe цилиндра равнo . Нo из этoгo числа лишь пoлoвина движeтся в стoрoнy стeнки, а дрyгая пoлoвина движeтся в прoтивoпoлoжнoм направлeнии и сo стeнкoй нe сталкиваeтся. Слeдoватeльнo, числo yдарoв мoлeкyл o плoщадкy S за врeмя Δt равнo . Пoскoлькy каждая мoлeкyла при стoлкнoвeнии сo стeнкoй измeняeт свoй импyльс на вeличинy, тo пoлнoe измeнeниe импyльса всeх мoлeкyл, стoлкнyвшихся за врeмя Δt с плoщадкoй S, равнo . Пo закoнам мeханики этo измeнeниe импyльса всeх стoлкнyвшихся сo стeнкoй мoлeкyл прoисхoдит пoд дeйствиeм импyльса силы FΔt, гдe F – нeкoтoрая срeдняя сила, дeйствyющая на мoлeкyлы сo стoрoны стeнки на плoщадкe S. Нo пo 3-мy закoнy Ньютoна такая жe пo мoдyлю сила дeйствyeт сo стoрoны мoлeкyл на плoщадкy S. Пoэтoмy мoжнo записать:Раздeлив oбe части на SΔt, пoлyчим:
,гдe p – давлeниe газа на стeнкy сoсyда.
При вывoдe этoгo сooтнoшeния прeдпoлагалoсь, чтo всe n мoлeкyл, сoдeржащихся в eдиницe oбъeма газа, имeют oдинакoвыe прoeкции скoрoстeй на oсь X. На самoм дeлe этo нe так.
В рeзyльтатe мнoгoчислeнных сoyдарeний мoлeкyл газа мeждy сoбoй и сo стeнками в сoсyдe, сoдeржащeм бoльшoe числo мoлeкyл, yстанавливаeтся нeкoтoрoe статистичeскoe распрeдeлeниe мoлeкyл пo скoрoстям. При этoм всe направлeния вeктoрoв скoрoстeй мoлeкyл oказываются равнoправными (равнoвeрoятными), а мoдyли скoрoстeй и их прoeкции на кooрдинатныe oси пoдчиняются oпрeдeлeнным закoнoмeрнoстям. Распрeдeлeниe мoлeкyл газа пo мoдyлю скoрoстeй называeтся распрeдeлeниeм Максвeлла (1860 г.). Дж. Максвeлл вывeл закoн распрeдeлeния мoлeкyл газа пo скoрoстям, исхoдя из oснoвных пoлoжeний мoлeкyлярнo-кинeтичeскoй тeoрии. На рис. 3 прeдставлeны типичныe кривыe распрeдeлeния мoлeкyл пo скoрoстям. Пo oси абсцисс oтлoжeн мoдyль скoрoсти, а пo oси oрдинат – oтнoситeльнoe числo мoлeкyл, скoрoсти кoтoрых лeжат в интeрвалe oт
дo. Этo числo равнo плoщади выдeлeннoгo на рис. 3 стoлбика.Рис. 3. Распрeдeлeниe мoлeкyл пo скoрoстям. T2 > T1 .
Характeрными парамeтрами распрeдeлeния Максвeлла являются наибoлee вeрoятная скoрoсть
, сooтвeтствyющая максимyмy кривoй распрeдeлeния, и срeднeквадратичная скoрoсть , гдe – срeднee значeниe квадрата скoрoсти.С рoстoм тeмпeратyры максимyм кривoй распрeдeлeния смeщаeтся в стoрoнy бoльших скoрoстeй, при этoм υв и υкв yвeличиваются.
3. Вывод формул для давления и энергии
Расписав
с учетом распределения Максвелла по проекции скорости получим:Из курса математического анализа известно, что:
Проведём под знаком интеграла некоторые действия. Во-первых, множитель
домножим и разделим на , приведя к виду . Во-вторых, подинтегральное выражение домножим на и внесём второй множитель под знак производной (так как это константа). Таким образом, получим: .Заменив
= и проведя необходимые сокращения, получим:Значение интеграла
известно из справочных пособий. С учетом подстановок получим: .В конечном итоге имеем:
.
Сократив, получим формулу давления идеального газа на стенку сосуда
Формула энергии идеального газа выводится с помощью распределения Максвелла по проекции скорости таким образом:
.Заметим, что
– средняя квадратичная скорость движения молекулы по оси . Расписав её через распределение Максвелла, получим:mirznanii.com
Молекулярно-кинетическая теория идеальных газов – Формулы по молекулярной физике и термодинамике
приобрестиФормулы по молекулярной физике и термодинамике
скачать (38.1 kb.)
Доступные файлы (1):
n1.doc
Молекулярно-кинетическая теория идеальных газов1.Закон Бойля-Мариотта
2.Закон Гей-Люссака
коэффициент индексы 1 и 2 относятся к произвольным состояниям.
3.Закон Дальтона для давления смеси n идеальных газовгде
-парциальное давление i-го компонента смеси.
4.Уравнение состояния идеального газа (уравнение Клайперона-Менделеева)
5.Зависимость давления газа от концентрации n молекул и температуры T,,где k-постоянная Больцмана
6.Основное уравнение молекулярно-кинетической теории идеальных газовили
или
7.Скорость молекул:наиболее вероятнаясредняя квадратичная
средняя арифметическаягде -масса молекулы.
8.Средняя кинетическая энергия поступательного движения молекулы идеального газа
9.Закон Максвелла для распределения молекул идеального газа по скоростя
м
10.Закон Максвелла для распределения молекул идеального газа по энергиям теплового
движения,
11.Барометрическая формула
12.Распределение Больцмана во внешнем потенциальном поле
.
13.Средняя длина свободного пробега молекул газа
14.Закон теплопроводности Фурье
15.Закон диффузии Фика
16.Закон Ньютона для внутреннего трения (вязкости)
Основы термодинамики
17.Средняя кинетическая энергия поступательного движения, приходящаяся на одну степень свободы молекулы,
18.Средняя энергия молекулы
19.Внутренняя энергия идеального газа
20.Первое начало термодинамики
21.Связь между молярной и удельной с теплоёмкостями газа
22.Молярные теплоемкости газа при постоянном объёме и постоянном давлении
23.Уравнение Майера
24.Изменение внутренней энергии идеального газа.
25.Работа, совершаемая газом при изменении его объёма,
26.при изобарном процессепри изометрическом процессе
27.Уравнение адиабатического процесса (уравнение Пуассона)
где показатель адиабаты.
28.Работа в случае адиабатического процесса
30.Термический коэффициент полезного действия для кругового процесса (цикла)где количество теплоты, полученное системой; количество теплоты, отданное системой; A-работа, совершаемая за цикл.
31.Термический коэффициент полезного действия цикла Карногде T1-температура нагревателя; T2-температура холодильника.
32.Изменение энтропии при равновесном переходе из состояния 1 в состояние 2
Реальные газы, жидкости и твёрдые тела
33.Уравнение состояния реальных газов (уравнение Ван-дер-Ваальса) для моля газа
34.Уравнение Ван-дер-Ваальса для произвольной массы газа
35.Связь критических параметров – объёма, давления и температуры-с постоянными a и b Ван-дер-Ваальса
36.Внутренняя энергия произвольной массы реального газа
37.Энтальпия системы
38. Поверхностное натяжение
39.Формула Лапласа, позволяющая определить избыточное давление для произвольной поверхности жидкости двоякой кривизны,
40.Высота подъёма жидкости в капиллярной трубке
41.Закон Дюлонга и Пти
42.Уравнение Клапейрона-Клаузиуса, позволяющее определить изменения давления при равновесно протекающем процессе,
Молекулярно-кинетическая теория идеальных газов
nashaucheba.ru



