N формула – Бином Ньютона. Целая положительная степень n суммы. (a + b)n=. Родственные формулы.
- Комментариев к записи N формула – Бином Ньютона. Целая положительная степень n суммы. (a + b)n=. Родственные формулы. нет
- Советы абитуриенту
Формула суммы n первых членов геометрической прогрессии + примеры
Геометрическая прогрессия – это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число.
Геометрическая прогрессия обозначается b1,b2,b3, …, bn, … .
Отношение любого члена геометрической погрешности к её предыдущему члену равно одному и тому же числу, то есть b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+1)/bn = … . Это следует непосредственно из определения арифметической прогрессии. Это число называют знаменателем геометрической прогрессии. Обычно знаменатель геометрической прогрессии обозначают буквой q.
Монотонная и постоянная последовательность
Одним из способов задания геометрической прогрессии является задание её первого члена b1 и знаменателя геометрической погрешности q. Например, b1=4, q=-2. Эти два условия задают геометрическую прогрессию 4, -8, 16, -32, … .
Если q>0 (q не равно 1), то прогрессия является монотонной последовательностью. Например, последовательность, 2, 4,8,16,32, … является монотонно возрастающей последовательностью (b1=2, q=2).
Если в геометрической погрешности знаменатель q=1, то все члены геометрической прогрессии будут равны между собой. В таких случаях говорят, что прогрессия является постоянной последовательностью.
Формула n-ого члена геометрической прогрессии
Для того, чтобы числовая последовательность (bn) являлась геометрической прогрессией необходимо, чтобы каждый её член, начиная со второго, являлся средним геометрическим соседних членов. То есть необходимо выполнение следующего уравнения
(b(n+1))^2 = bn * b(n+2),для любого n>0, где n принадлежит множеству натуральных чисел N.
Формула n-ого члена геометрической прогрессии имеет вид:
bn=b1*q^(n-1),
где n принадлежит множеству натуральных чисел N.
Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии имеет вид:
Sn = (bn*q – b1)/(q-1), где q не равно 1.
Рассмотрим простой пример:
В геометрической прогрессии b1=6, q=3, n=8 найти Sn.
Для нахождения S8 воспользуемся формулой суммы n первых членов геометрической прогрессии.
S8= (6*(3^8 -1))/(3-1) = 19 680.
Нужна помощь в учебе?
Предыдущая тема: Определение геометрической прогрессии: формула n-го члена прогрессии
Следующая тема:   Сумма бесконечной геометрической прогрессии при |q|
Все неприличные комментарии будут удаляться.
www.nado5.ru
Определение геометрической прогрессии: формула n-го члена прогрессии
Геометрическая прогрессия – это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число. Геометрическая прогрессия обозначается b1,b2,b3, …, bn, …
Свойства геометрической прогрессии
Отношение любого члена геометрической погрешности к её предыдущему члену равно одному и тому же числу, то есть b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+1)/bn = … . Это следует непосредственно из определения арифметической прогрессии. Это число называют знаменателем геометрической прогрессии. Обычно знаменатель геометрической прогрессии обозначают буквой q.
Одним из способов задания геометрической прогрессии является задание её первого члена b1 и знаменателя геометрической погрешности q. Например, b1=4, q=-2. Эти два условия задают геометрическую прогрессию 4, -8, 16, -32, … .
Если q>0 (q не равно 1), то прогрессия является монотонной последовательностью. Например, последовательность, 2, 4,8,16,32, … является монотонно возрастающей последовательностью (b1=2, q=2).
Если в геометрической погрешности знаменатель q=1, то все члены геометрической прогрессии будут равны между собой. В таких случаях говорят, что прогрессия является постоянной последовательностью.
Формула n-го члена прогрессии
Для того, чтобы числовая последовательность (bn) являлась геометрической прогрессией необходимо, чтобы каждый её член, начиная со второго, являлся средним геометрическим соседних членов. То есть необходимо выполнение следующего уравнения – (b(n+1))^2 = bn * b(n+2), для любого n>0, где n принадлежит множеству натуральных чисел N.
Формула n-ого члена геометрической прогрессии имеет вид:
bn=b1*q^(n-1), где n принадлежит множеству натуральных чисел N.
Рассмотрим простой пример:
В геометрической прогрессии b1=6, q=3, n=8 найти bn.
Воспользуемся формулой n-ого члена геометрической прогрессии:
b8 = 6*3^7 = 13122.
Нужна помощь в учебе?
Предыдущая тема: Электронный учебник по геометрии: все темы школьной программы
Следующая тема:   Формула суммы n первых членов геометрической прогрессии + примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru
Формула азота в химии
Атомная масса: 14,008.а.е.м.
Электронная и графическая формула азота
Электронная формула: 1s2 2s2 2p3.
Электронно-графическая формула внешнего электронного слоя атома азота:
Азот является одним из самых распространенных элементов на Земле, а также одним из основных биогенных элементов, входит в состав белков и нуклеиновых кислот.
Азот – простое вещество, состоящее из двух атомов азота.
Формула: N2.
Структурная формула азота
Структурная формула:
Молярная масса: 28,016 г/моль.
При нормальных условиях азот – бесцветный газ, не имеет запаха, цвета и вкуса, плохо растворим в воде. В жидком состоянии – бесцветная, подвижная жидкость. При контакте с воздухом жидкий азот поглощает из него кислород. В твердом состоянии (−209,86°C) существует в виде снегоподобной массы или больших белоснежных кристаллов.
Молекула азота очень прочная, поскольку между атомами азота в молекуле N2 образуется тройная связь N≡N. Вследствие этого многие соединения азота имеют положительную энтальпию образования (галогениды, азиды, оксиды), а соединения азота термически неустойчивы и довольно легко разлагают ся при нагревании. Химически азот довольно инертен, поэтому в природе находится главным образом в свободном состоянии.
Азот при обычных условиях реагирует только с литием:
при нагревании может вступить в реакцию с некоторыми другими металлами и неметаллами, также с образованием нитридов:
Наибольшее практическое значение имеет аммиак (нитрид водорода) NH3, который получается при взаимодействии водорода с азотом:
В электрическом разряде азот реагирует с кислородом, образуя оксид азота(II) NO:
Азот также может образовывать комплексные соединения с переходными металлами.
Примеры решения задач
ru.solverbook.com
Формула углеводорода в химии
Углеводороды в органической химии рассматриваются как базовые соединения, все остальные органические соединения можно считать их производными.
Углеводороды образуют гомологические ряды. Члены каждого гомологического ряда характеризуются определенной закономерностью изменения химических и физических свойств, общей формулой и сходной структурой.
Классификация углеводородов
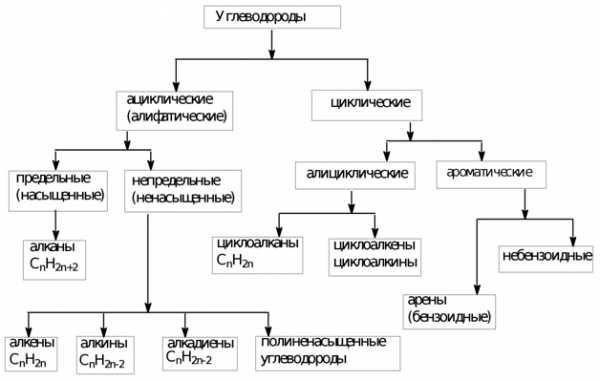
|
Описание |
Формула |
|---|---|
|
Алканы – предельные ациклические углеводороды с одинарными связями С–С. Гомологический ряд метана. Общая формула CnH2n+2 (n 1). Возможна изомерия углеродного скелета, оптическая изомерия. Наиболее характерны реакции замещения, окисления, горения, дегидрирования. |
Метан |
|
Алкены – непредельные ациклические углеводороды, содержащие одну двойную связь С=С. Гомологический ряд этилена. Общая формула CnH2n (n 2). Возможна изомерия углеродного скелета, изомерия положения двойной связи и межклассовая. Наиболее характерны реакции присоединения, горения. |
Этилен |
|
Алкины – непредельные ациклические углеводороды, содержащие одну тройную связь С≡С. Гомологический ряд ацетилена. Общая формула CnH2n–2 (n 2). Возможна изомерия углеродного скелета, изомерия положения тройной связи, межклассовая и пространственная. Наиболее характерны реакции присоединения, горения. |
Ацетилен |
|
Алкадиены
– непредельные ациклические углеводороды, содержащие две двойные связи С=С. Гомологический ряд диеновых углеводородов. Общая формула Cn |
Бутадиен-1,3 |
|
Циклоалканы – предельные карбоциклические углеводороды с одинарными связями С–С. Гомологический ряд полиметиленов. Общая формула CnH2n (n 3). Возможна изомерия углеродного скелета, пространственная, межклассовая. Для циклоалканов с n = 3–4 наиболее характерны реакции присоединения с раскрытием цикла. |
Циклопропан |
|
Арены – непредельные карбоциклические углеводороды с бензольным кольцом. Гомологический ряд бензола. Общая формула CnH2n–6 (n 6). Возможна изомерия углеродного скелета боковых цепей, а также их взаимного положения в бензольном кольце. Наиболее характерны реакции электрофильного замещения. |
Бензол |
Примеры решения задач по теме «формула углеводорода»
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Формула количества вещества в химии
Определение и формула количества вещества
Моль
Масса одного атома 12С равна 12 а.е.м., поэтому число атомов в 12 г изотопа 12С равно:
NA = 12 г / 12 × 1,66057×10-24 г = 1/1,66057×10-24 = 6,0221×10-23.
Таким образом, моль вещества содержит 6,0221×10-23 частиц этого вещества.
Физическую величину NA называют постоянной Авогадро, она имеет размерность [NA] = моль-1. Число 6,0221×10-23 называют числом Авогадро. Таким образом количество вещества будет вычисляться как:
n = N / NA,
где N – число структурных звеньев, а NA — постоянная Авогадро.
Молярная масса (М) – это масса 1 моль вещества. Легко показать, что численные значения молярной массы М и относительной молекулярной массы M r равны, однако первая величина имеет размерность [M] = г/моль, а вторая безразмерна:
M = NA × m (1 молекулы) = NA × Mr × 1 а.е.м. = (NA ×1 а.е.м.) × Mr = × Mr.
Это означает, что если масса некоторой молекулы равна, например, 44 а.е.м., то масса одного моля молекул равна 44 г.
Постоянная Авогадро является коэффициентом пропорциональности, обеспечивающим переход от молекулярных отношений к молярным. Поэтому другая формула для вычисления количество вещества выглядит следующим образом:
n = m / M,
где m – масса вещества (г), а М – его молярная масса (г/моль).
Количество вещества газа можно рассчитать при помощи закона Авогадро: в равных объемах различных газов при одинаковых условиях (температуре и давлении) содержится одинаковое число молекул. Следовательно, при нормальных условиях 1 моль различных газов занимает объем, равный 22,4 л.
n= V /Vm,
где V – объем газа (л), а Vm – молярный объем (л/моль).
Примеры решения задач
ru.solverbook.com



