Нахождение пределов функции – .
Предел функции в точке
Сегодня рассмотрим подборку новых задач на нахождение предела в точке. Начнем с простых примеров на подстановку значения, чаще всего рассматривают в 11 классе школьной программы по математике.
Далее остановимся и проанализируем пределы с неопределенностями, методы раскрытия неопределенностей, применением первой и второй важных границ и их последствий.
Приведенные примеры полностью не охватят всей темы, но на многие вопросы внесут ясность.
Найти предел функции в точке:
Пример 46. Предел функции в точке определяем подстановкой
Так как знаменатель дроби не превращается в ноль то такую задача под силу решить каждому выпускнику школы.
Пример 47. Имеем долю полиномов, кроме того знаменатель не содержит особенности (не равен нулю).
Еще одна задача, фактически за 11 класс.
Пример 48. Методом подстановки определяем предел функции
Из условия следует, что граница функции равна двум, если переменная стремится к бесконечности.
Пример 49.Прямая подстановка x=2 показывает, что граница в точке имеет особенность {0/0}. Это означает, что и числитель и знаменатель скрыто содержат (x-2).
Выполняем разложение полиномов на простые множители, а потом сокращаем дробь на указанный множитель (x-2).
Предел дроби, которая останется, находим методом подстановки.
Пример 50.Предел функции в точке имеет особенность типа {0/0}.
Избавляемся разницы корней методом умножения на сумму корней (сопряженное выражение), полином раскладываем.
Далее, упростив функцию, находим значение предела в единице.
Пример 51.Рассмотрим задачу на сложные пределы.
До сих пор от иррациональности избавлялись методом умножения на сопряженное выражение.
Здесь же, в знаменателе, имеем корень кубический, поэтому нужно использовать формулу разности кубов.
Все остальные преобразования повторяются от условия к условию.
Полином раскладываем на простые множители,
далее сокращаем на множитель, который вносит особенность (0)
и подстановкой x=-3 находим предел функции в точке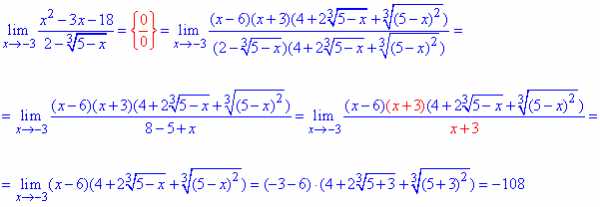
Пример 52.Особенность вида {0/0} раскрываем с помощью первого замечательного предела и его последствий.
Сначала разницу синусов распишем согласно тригонометрической формуле
sin(7x)-sin(3x)=2sin(2x)cos(5x).
Далее числитель и знаменатель дроби дополняем выражениями, которые необходимы для выделения важных пределов.
Переходим к произведению пределов и оцениваем вложение каждого множителя.
Здесь использовали первый замечательный предел:
и следствия из него
где a и b – произвольные числа.
Пример 53.Чтобы раскрыть неопределенность при переменной стремящейся к нулю, используем второй замечательный предел.
Чтобы выделить экспоненту, приводим показатель к 2-му замечательному пределу, а все остальное, что останется в предельном переходе, даст степень експоненты.
Здесь использовали следствие из второго замечатеьного предела:
Вычислить предел функции в точке:
Пример 54. Нужно найти предел функции в точке. Простая подстановка значения показывает, что имеем деление нулей.
Для ее раскрытия разложим на простые множители полиномы и выполним сокращение на множитель, который вносит особенность (х+2).
Однако числитель дальше содержит (x+2), а это значит, что при x=-2 граница равна нулю.
Пример 55.Имеем дробную функцию – в числителе разница корней, в знаменателе – поленом.
Прямая подстановка дает особенность вида {0/0}.
Переменная стремится к минус единице, а это значит, что следует искать и избавляться особенности вида (x+1).
Для этого избавляемся иррациональности умножением на сумму корней, а квадратичную функцию раскладываем на простые множители.
После всех сокращений методом подстановки определяем предел функции в точке
Пример 56.С виду подлимитной функции можно ошибочно заключить, что нужно применить первый предел, но вычисления показали, что все гораздо проще.
Сначала распишем сумму синусов в знаменателе sin(2x)+sin(6x)=2sin(4x)*cos(2x).
Далее расписываем tg(2x), и синус двойного угла sin(4x)=2sin(2x)cos (2x).
Синусы упрощаем и методом подстановки вычисляем предел дроби
Пример 57.Задача на умение использовать вторую замечательный предел:
суть заключается в том, что следует выделить ту часть, которая дает экспоненту.
Остальное, что останется в показателе в предельном переходе даст степень экспоненты.
На этом разбор задач на пределы функций и последовательностей не заканчивается.
В настоящее время подготовлено более 150 готовых ответов к пределам функций, поэтому изучайте и делитесь ссылками на материалы с однокласниками.
yukhym.com
2 Предел функции
2.1 Понятие предела функции
Во многих практических задачах требуется определить скорость изменения функции при изменении аргумента. В этом случае используется понятие производной функции. Это понятие в свою очередь вводится с помощью понятия предела функции. Поясним смысл понятия предела на примере.
Функция 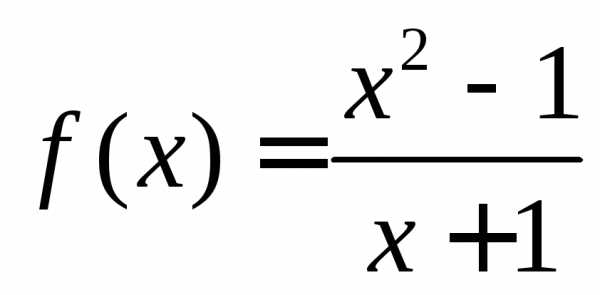 не определена при значении
не определена при значении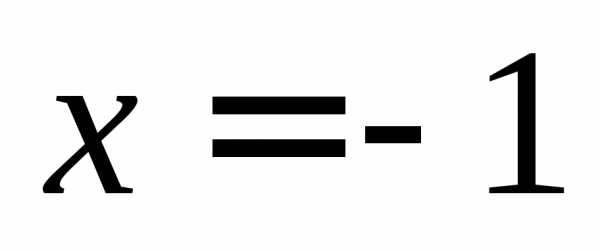 ,
так как при нем знаменатель обращается
в нуль. Таким образом, при
,
так как при нем знаменатель обращается
в нуль. Таким образом, при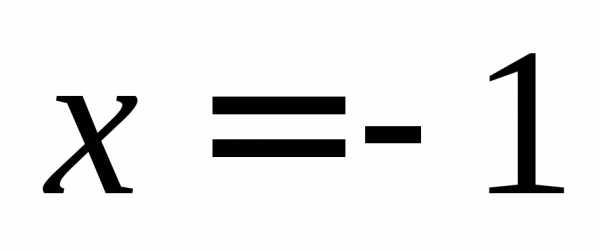 функция имеет разрыв (рисунок 2.1).
функция имеет разрыв (рисунок 2.1).
Рисунок
2.1 – Функция |
Однако
если положить значение функции в точке 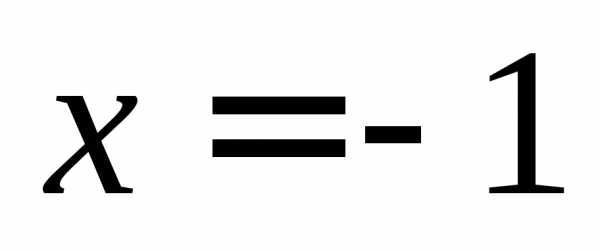 равным,
то получим функцию непрерывную на всей
числовой оси. Математически это
записывается как
равным,
то получим функцию непрерывную на всей
числовой оси. Математически это
записывается как
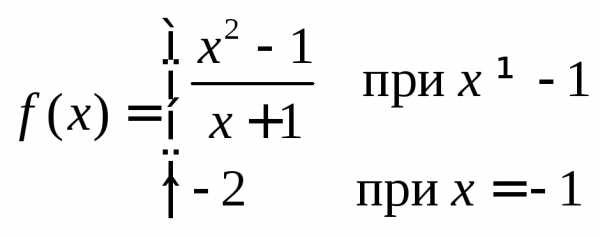
В
общем случае, если 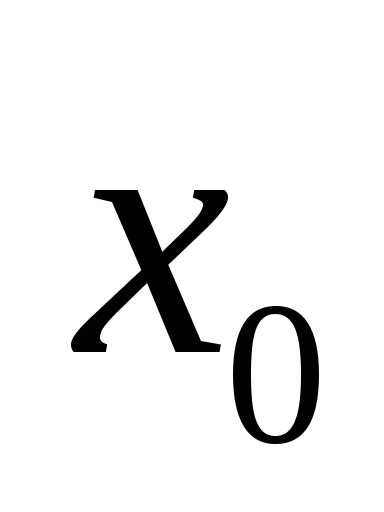 –
точка разрыва функции
–
точка разрыва функции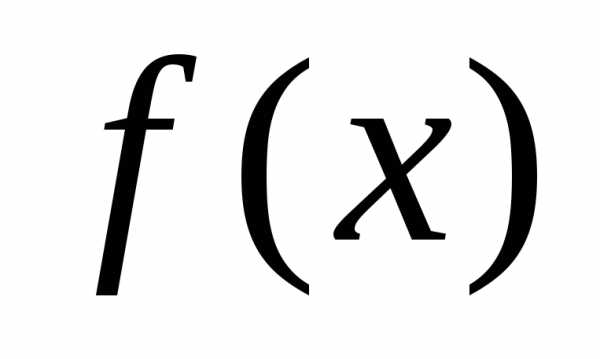 ,
но возможно найти для нее в точке
,
но возможно найти для нее в точке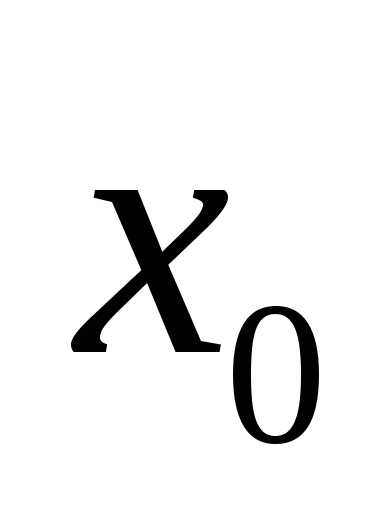 такое значение А, при котором измененная
функция
такое значение А, при котором измененная
функция станет
непрерывной, то это число А называетсяпределом
функции
станет
непрерывной, то это число А называетсяпределом
функции 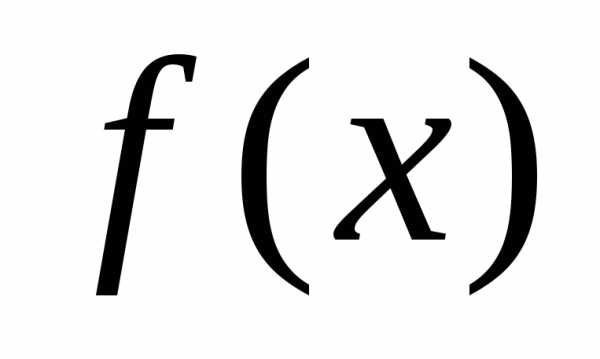
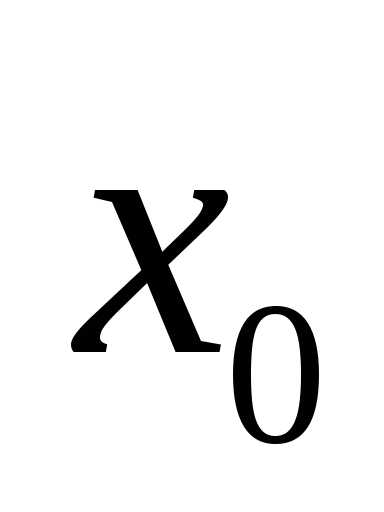 ,
а точка
,
а точка – точкой устранимого разрыва.
– точкой устранимого разрыва.Математически это записывается формулой:
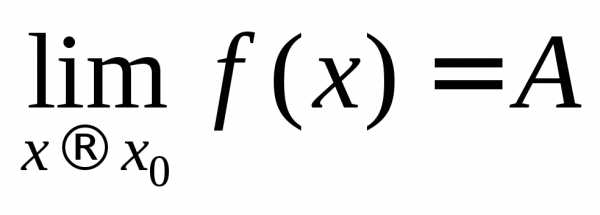
Существование
предела функции 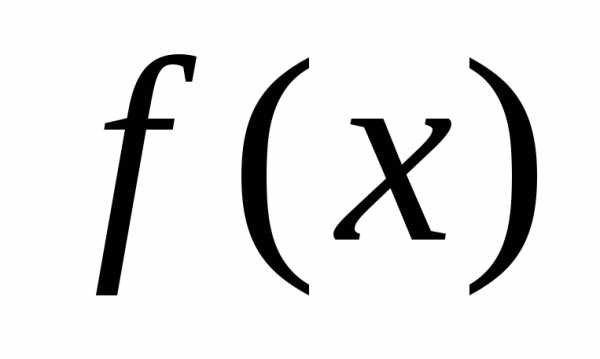 в точке
в точке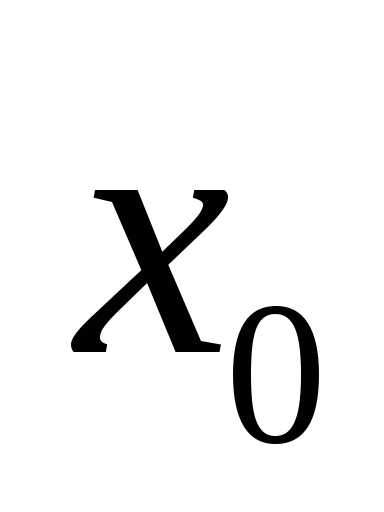 означает, что функция
означает, что функция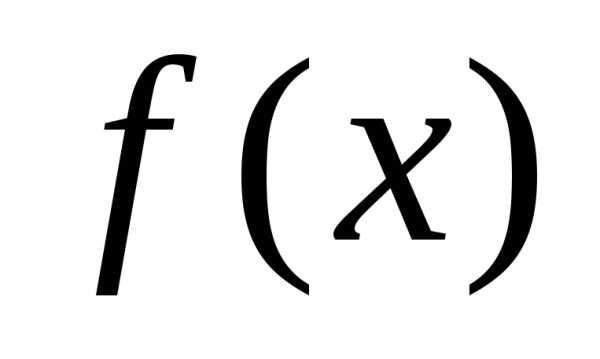 приближенно равна
приближенно равна для всех значений
для всех значений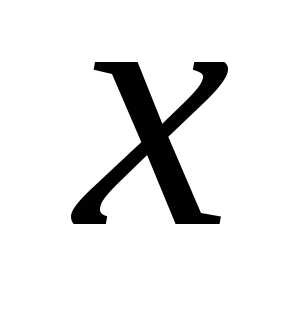 ,
близких к
,
близких к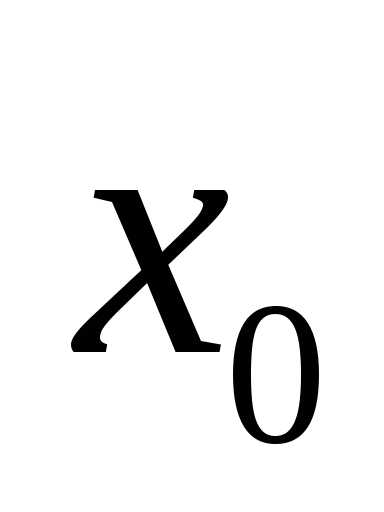 .
.
Определение. Постоянное число А называется пределом функции
 ,
если, задав произвольное как угодно
малое положительное число,
можно найти такое
>0 (зависящее от ),
что для всех x,
лежащих в
– окрестности числа
,
если, задав произвольное как угодно
малое положительное число,
можно найти такое
>0 (зависящее от ),
что для всех x,
лежащих в
– окрестности числа 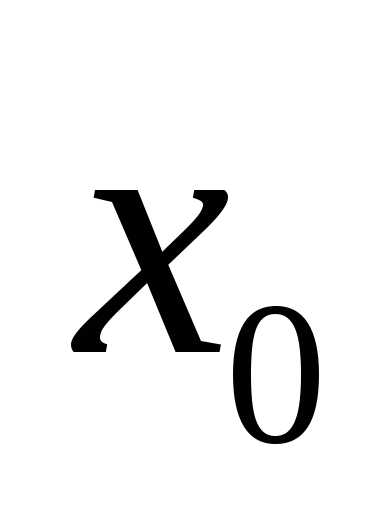 ,
т.е. дляx,
удовлетворяющих неравенству
,
значения функцииf(x) будут лежать в
– окрестности числа А, т.е.
.
,
т.е. дляx,
удовлетворяющих неравенству
,
значения функцииf(x) будут лежать в
– окрестности числа А, т.е.
.Это определение называют определением предела функции по Коши, или “на языке – “.
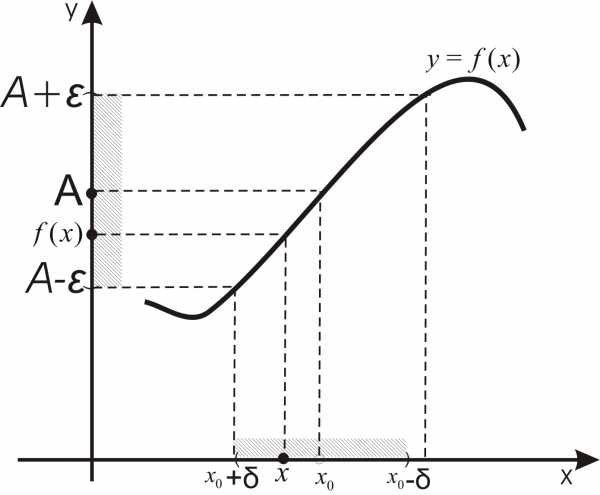
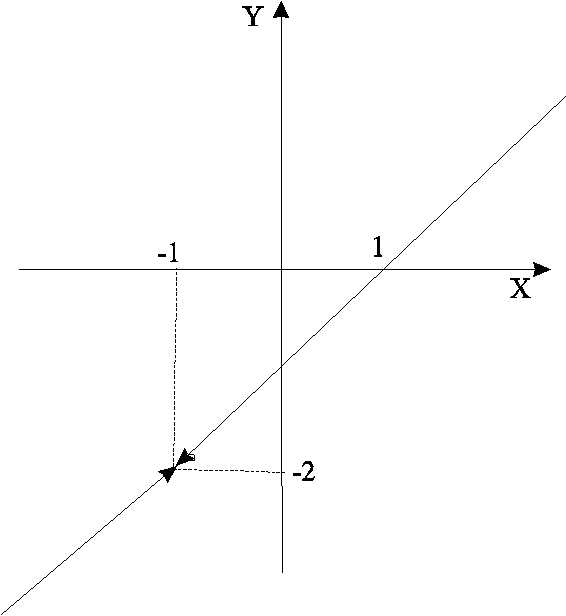
На
рисунке 2.2. проиллюстрировано определение
предела функции 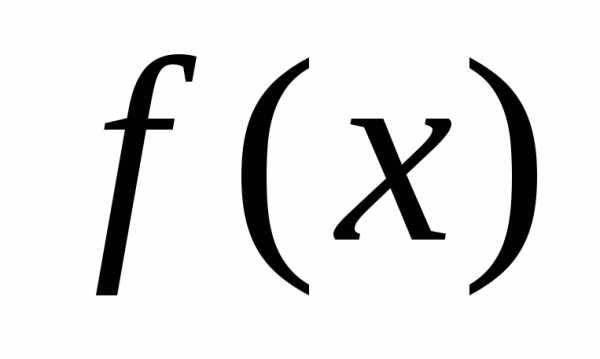 при
при .
Для построения этого рисунка необходимо
выполнить следующие действия:
.
Для построения этого рисунка необходимо
выполнить следующие действия:
построить график функции
иА; и отметить точки
и отметить точки
построить окрестность точки А, выбрав произвольное число
 ;
;по точкам
 ,
, и графику функции построить
и графику функции построить окрестность
точки
окрестность
точки .
Расстояния от точки
.
Расстояния от точки до точек
до точек и
и должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки
должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки ;
;взять произвольную точку
 ,
принадлежащую окрестности точки
,
принадлежащую окрестности точки ,
и по графику функции найти значение
,
и по графику функции найти значение ,
которое должно попасть в построенную
окрестность точкиА.
,
которое должно попасть в построенную
окрестность точкиА.
Рисунок 2.2 – Определение предела функции |
Если  и при этом
и при этом 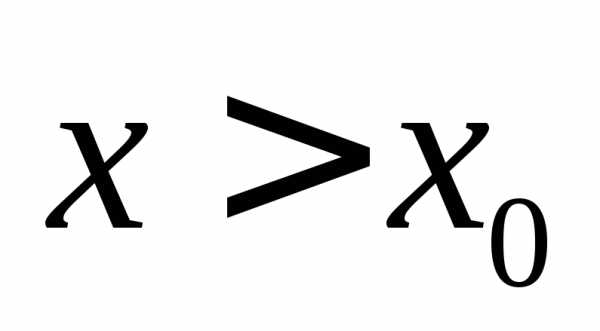 ,
то пишут .
Если, в частности,
,
то пишут .
Если, в частности, 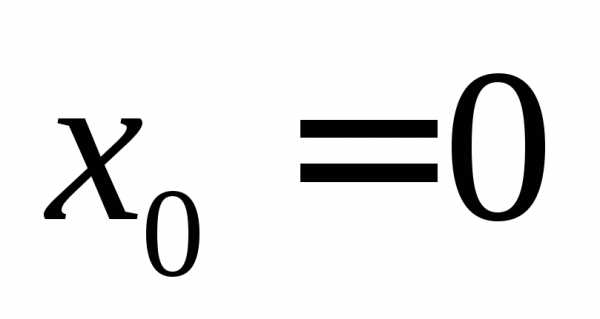 ,
то вместо символа 0+0 пишут +0.
,
то вместо символа 0+0 пишут +0.
Аналогично
если  и при этом
и при этом 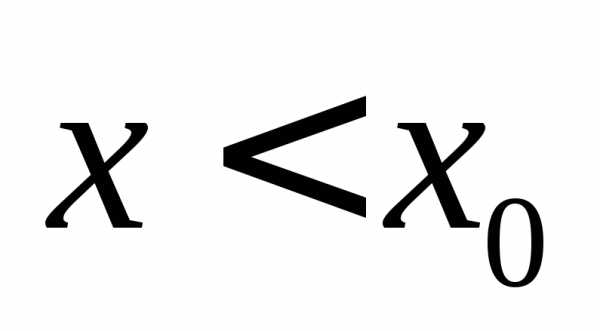 ,
то пишут .
,
то пишут .
Числа 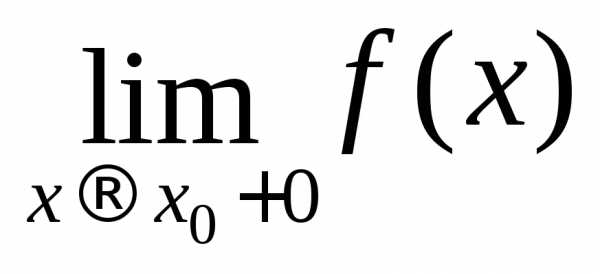 и
и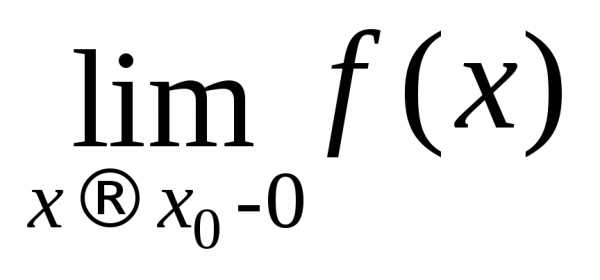 называются соответственнопределом
справа и пределом слева функции f(x) в точке
называются соответственнопределом
справа и пределом слева функции f(x) в точке 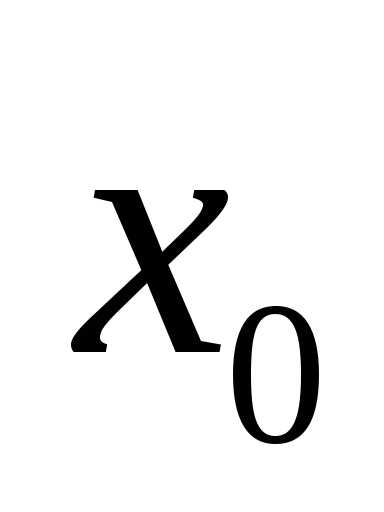 .
.
Для
существования предела функции f(x) при  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 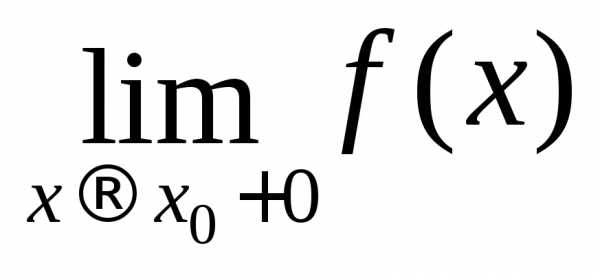 =
=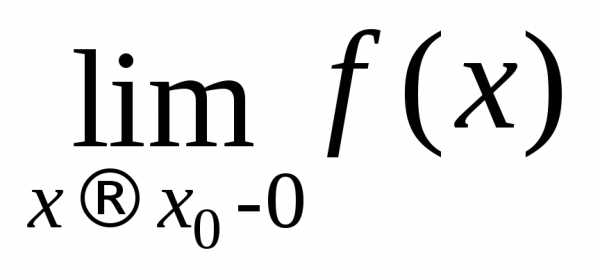 .
.
Определение. Переменная величина (т.е. последовательность или функция), имеющая своим пределом ноль, называется бесконечно малой величиной.
Определение. Переменная величина, имеющая бесконечный предел, называется
2.2 Правила вычисления пределов
При вычислении пределов следует учитывать следующие основные правила:
1. Предел суммы (разности) функций равен сумме (разности) пределов слагаемых:
.
2. Предел произведения функций равен произведению пределов сомножителей:
.
3. Предел отношения двух функций равен отношению пределов этих функций:
.
4. Постоянный множитель можно выносить за знак предела:
.
5. Предел постоянной равен самой постоянной:
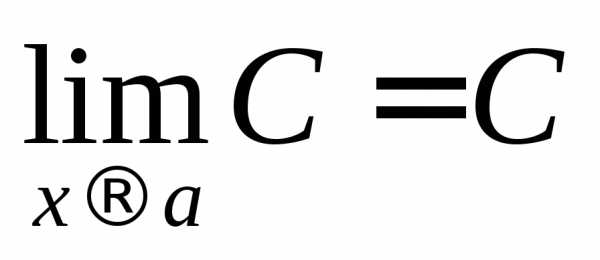 .
.
6. Для непрерывных функций символы предела и функции можно поменять местами:
.
Нахождение
предела функции 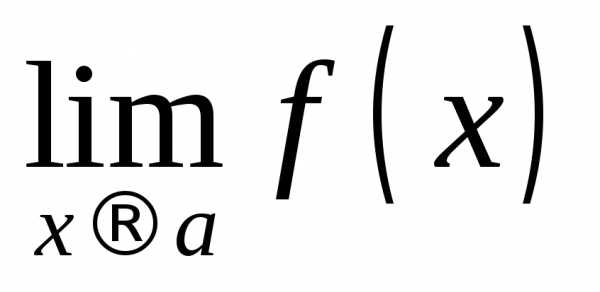 следует начинать с подстановки значения
следует начинать с подстановки значения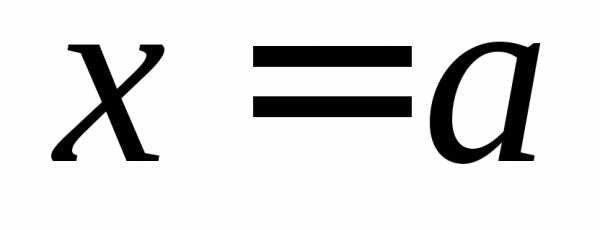
Пример
2.1. Вычислить предел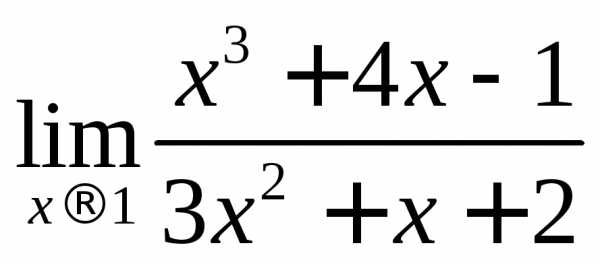 .
.
Решение.
.
Выражения
вида 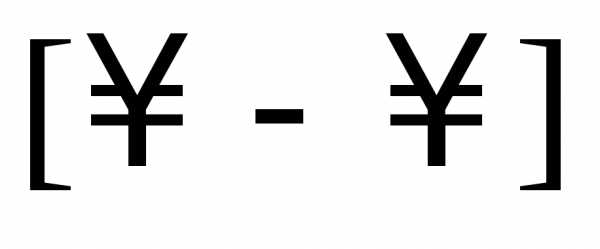 ,
,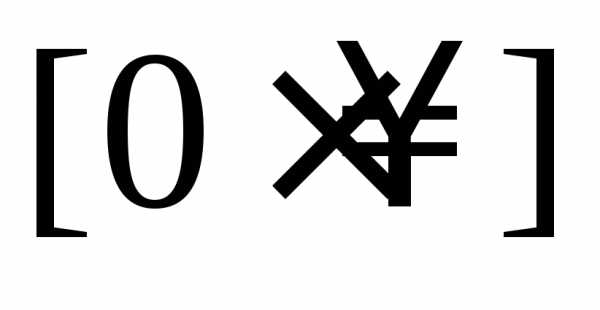 ,
, ,
, ,
, ,
,
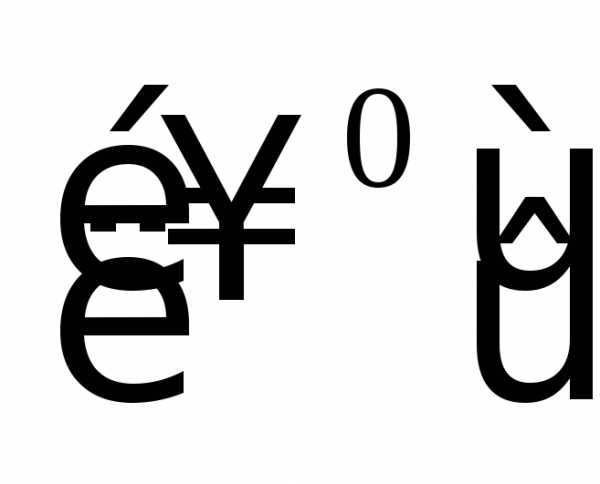 называютсянеопределённостями.
называютсянеопределённостями.
Если
получается неопределенность вида 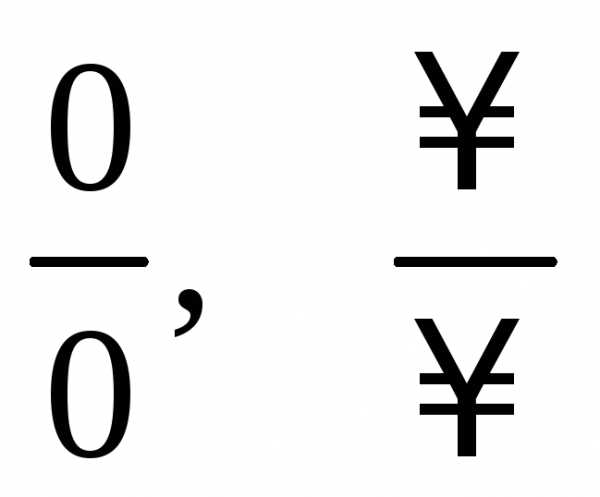 ,
то для нахождения предела нужно
преобразовать функцию так, чтобы раскрыть
эту неопределенность.
,
то для нахождения предела нужно
преобразовать функцию так, чтобы раскрыть
эту неопределенность.
Неопределенность
вида 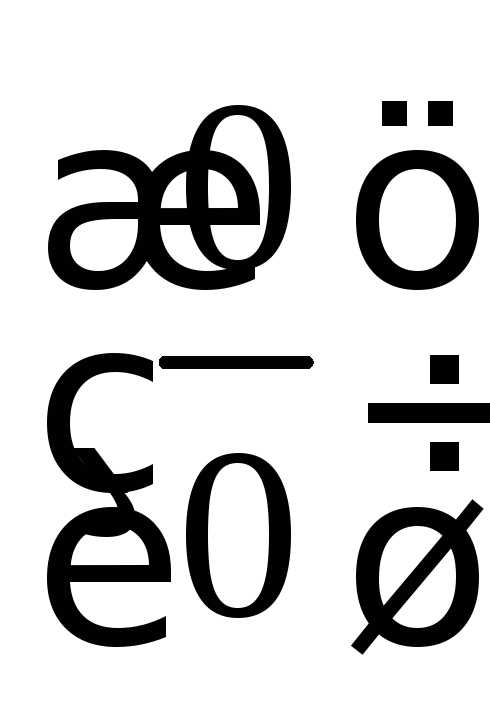 обычно получается, когда задан предел
отношения двух многочленов. В этом
случае, для вычисления предела
рекомендуется разложить многочлены на
множители и сократить на общий множитель.
Этот множитель равен нулю при предельном
значениих.
обычно получается, когда задан предел
отношения двух многочленов. В этом
случае, для вычисления предела
рекомендуется разложить многочлены на
множители и сократить на общий множитель.
Этот множитель равен нулю при предельном
значениих.
Пример
2.2. Вычислить предел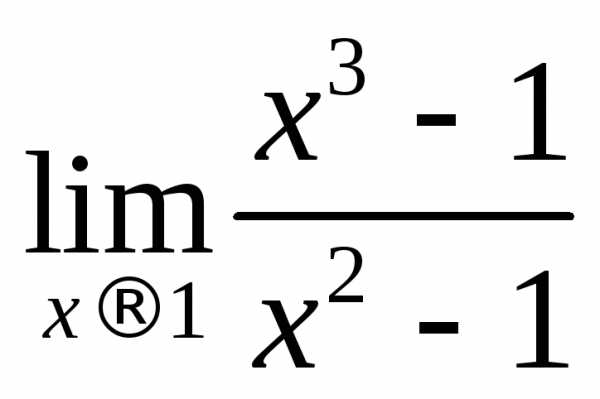 .
.
Решение.
Подставляя 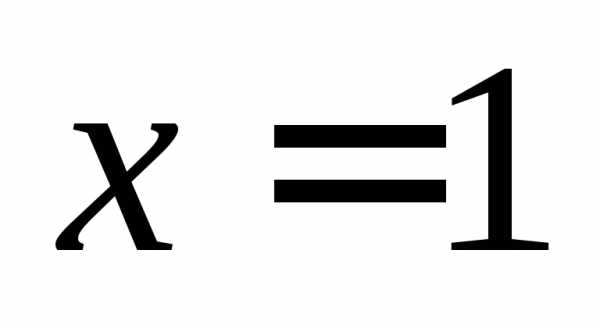 ,
получим неопределенность:
,
получим неопределенность:
.
Разложим числитель и знаменатель на множители:
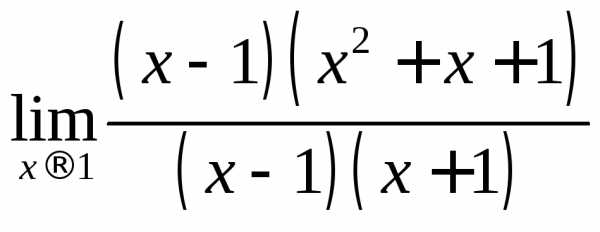 ;
;
Сократим
на общий множитель 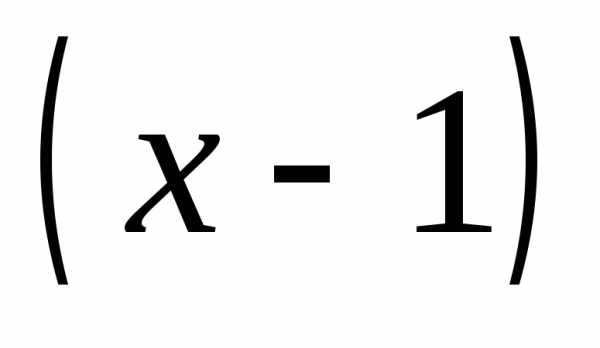 и получим
и получим
.
Неопределенность
вида 
Пример
2.3.Вычислить предел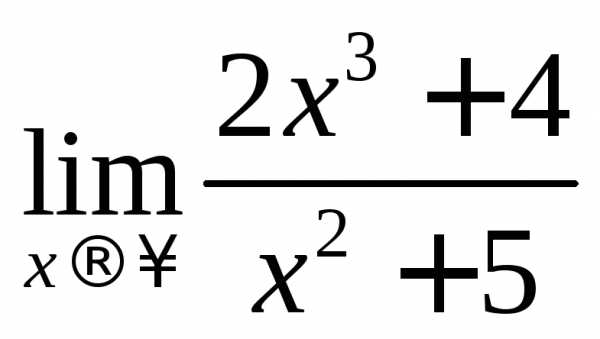 .
.
Решение. При подстановке ∞ получается
неопределенность вида ,
поэтому разделим все члены выражения
наx3.
,
поэтому разделим все члены выражения
наx3.
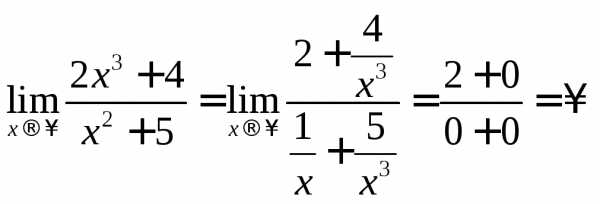 .
.
Здесь
учитывается, что  .
.
При вычислении пределов функции, содержащей корни, рекомендуется умножить и разделить функцию на сопряженное выражение.
Пример
2.4. Вычислить предел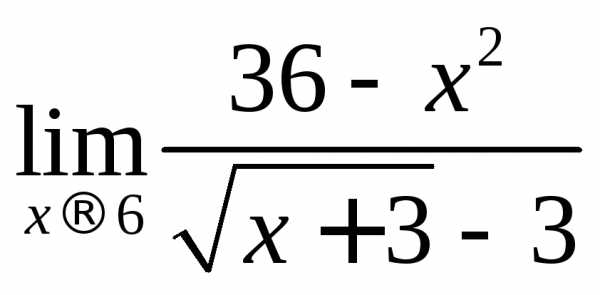
Решение.
При
вычислении пределов для раскрытия
неопределенности вида  или (1)∞часто используются первый
и второй замечательные пределы:
или (1)∞часто используются первый
и второй замечательные пределы:
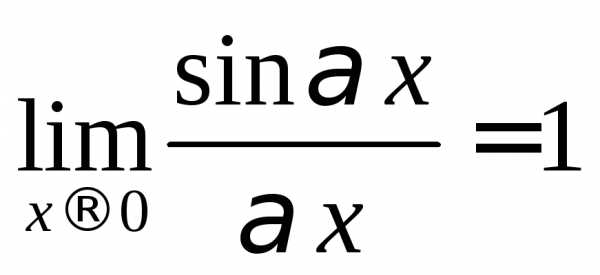
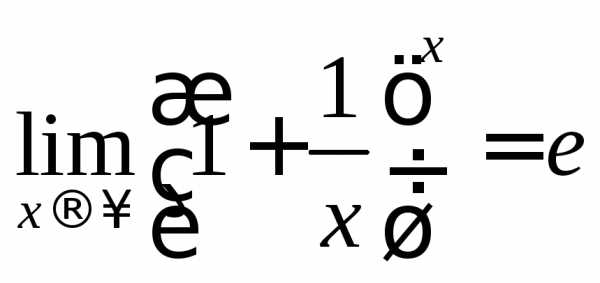 и
и 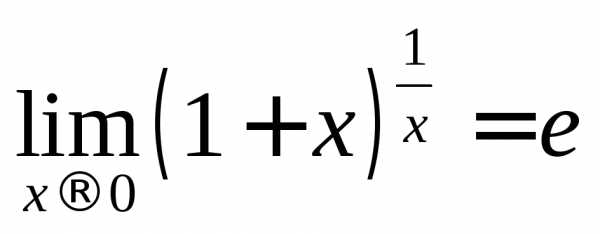
Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины.
Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример.
Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед.
Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 1,5 = 150, а еще через полгода – в 150 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 (1 +1/3) 237 (ден. ед.).
Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
100 (1 +1/10)10 259 (ден. ед.),
100 (1+1/100)100 270 (ден. ед.),
100 (1+1/1000)1000 271 (ден. ед.).
При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что
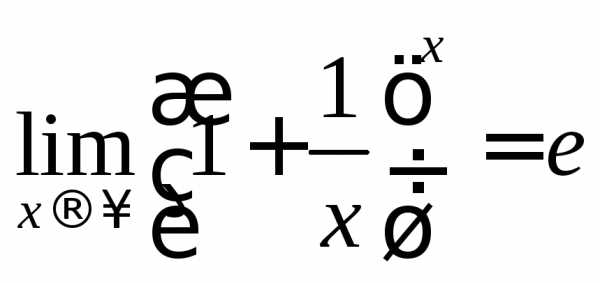
Пример
2.5. Вычислить предел функции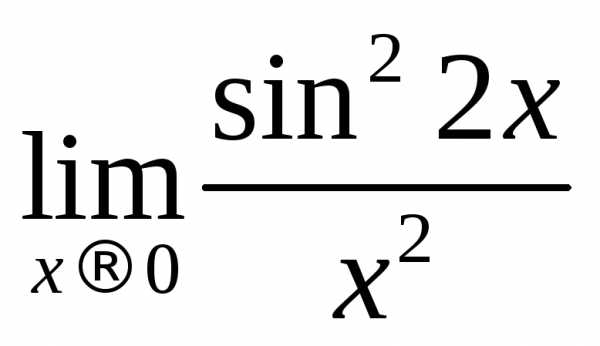
Решение.
Пример
2.6. Вычислить
предел функции 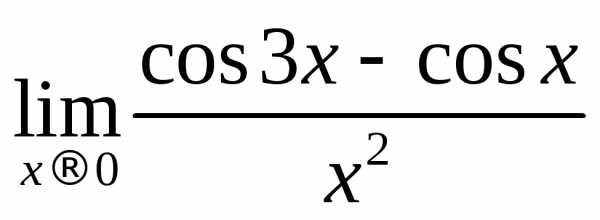 .
.
Решение. Подставляя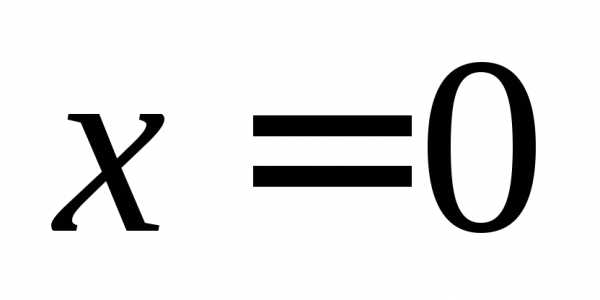 получим неопределенность:
получим неопределенность:
.
Используя тригонометрическую формулу, преобразуем числитель в произведение:
В результате получаем
Здесь
учитывается второй замечательный предел 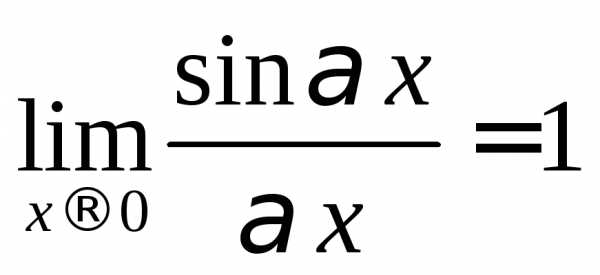 .
.
Пример
2.7. Вычислить предел функции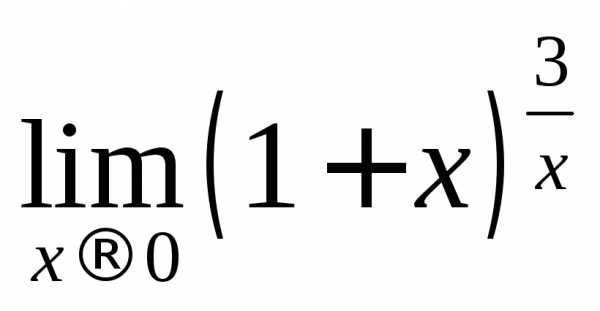
Решение.
.
Для
раскрытия неопределенности вида  или
или можно использовать правило Лопиталя,
которое основано на следующей теореме.
можно использовать правило Лопиталя,
которое основано на следующей теореме.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных
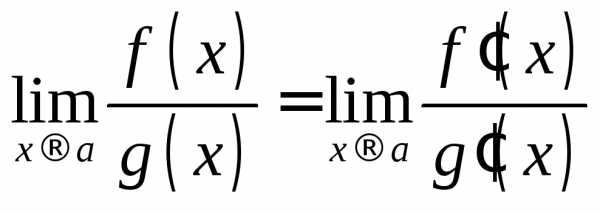
Заметим, что это правило можно применять несколько раз подряд.
Пример
2.8.Найти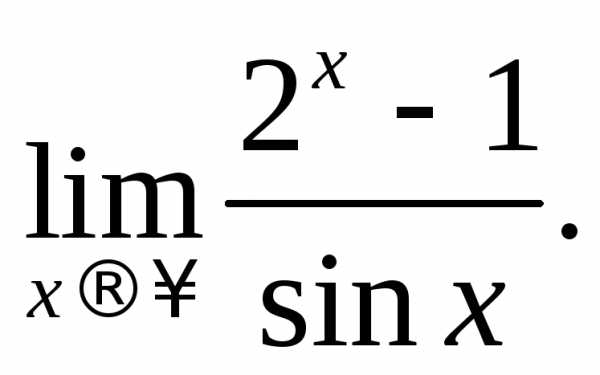
Решение. При подстановке ,
имеем неопределенность вида
,
имеем неопределенность вида .
Применяя правило Лопиталя, получим
.
Применяя правило Лопиталя, получим
studfiles.net
Правила вычисления пределов функции. — МегаЛекции
Понятие о пределе числовой последовательности.
Последовательностью называется совокупность значений функции натурального аргумента n.
Определение 1.1.Число а называется пределом числовой последовательности , если для любого существует такое число N, что при .
В этом случае пишут: . Определение предела последовательности можно записать с использованием логических кванторов ( – квантор общности, читается «для любого» или «для всех»; – квантор существования, читается «существует» или «найдется»):
, если
Последовательность, имеющая предел, называется сходящейся. Для того, чтобы последовательность имела предел, необходимо и достаточно, чтобы она была монотонной и ограниченной. Предел последовательности единственен, если он существует. Если , то последовательность называется бесконечно малой.
J Пример 1.1. Рассмотрим последовательность . С ростом n члены последовательности уменьшаются и становятся сколь угодно мало отличающимися от 0. Докажем, что .
По определению предела , если . Положим . Тогда Это означает, что . J
Если последовательности – бесконечно малые, а – ограниченная последовательность, то последовательности являются бесконечно малыми.
J Пример 1.2. ,т.к. – бесконечно малая, а – ограниченная последовательность. J
Если , то последовательность называется бесконечно большой. Если последовательность бесконечно большая, то она не ограничена.
J Пример 1.3. ,т.к.члены последовательности с ростом n растут и становятся сколь угодно большими при больших n. J
Правила вычисления пределов последовательностей.
1. ; 2. ; 3. ;
4. ; 5. при условии .
J Пример 1.4. Найти пределы : 1) ; 2) ; 3) .
Решение.
1) При числитель и знаменатель стремятся к бесконечности. Преобразуем данную последовательность, разделив все члены дроби на . Используя правила нахождения пределов, найдём: .
2) Разделим все члены дроби на и используем необходимые правила: .
3) Разделим все члены дроби на , получим: . J
Воспользуемся результатами приведённых примеров. Если в условии задачи имеем неопределенность вида , то:
1) если старшие степени n в числителе и знаменателе равны, то ответ равен отношению
коэффициентов при данных степенях
2) если старшая степень n находится в числителе, то ответ будет ;
3) если старшая степень находится в знаменателе, то ответ будет 0.
Если , то последовательности и называются эквивалентными, обозначение: . В решении примеров последовательности можно заменять эквивалентными. Рассмотрим решение примера 1.4 с использованием эквивалентностей:
1) ; 2) ; 3) .
J Пример 1.5.Найти .
Решение.
Рассмотрим числитель . Знаменатель эквивалентен 3n. Таким образом, . J
J Пример 1.6.Найти
Решение.
Перейдем к эквивалентным последовательностям и найдем предел их отношения: . J
J Пример 1.7.Найти
Решение.
Имеем неопределенность вида . Избавимся от иррациональности и рассмотрим неопределенность .
= =
J
И от того, что что-то очень сложно, ты не
пытаешься это сделать? Научиться ходить
вначале тоже было тяжело, но ты позани-
мался, и теперь, глядя на тебя, может пока-
заться, что это все не трудно.
Р. Бах. Иллюзии
☼ Упражнения 1.1.Вычислить пределы:
1) ; 5) ; 9) ;
2) ; 6) ; 10) ;
3) ; 7) ; 11) ;
4) ; 8) ; 12) . ☼
Число е.
Последовательность монотонная и ограниченная. Следовательно, она имеет конечный предел. Этот предел определяет эйлерово число . Число е – иррациональное, е .
J Пример 1.7.Найти пределы: 1) ;2) ;3) .
Решение.
1) .
2) .
3) . J
– Надо же как все просто.
– Как научиться ходить. Потом ты начинаешь
удивляться, что в этом было такого сложного.
Р. Бах. Иллюзии
☼ Упражнения 1.2.Вычислить пределы:
1) ; 2) ; 3) ; 4) ; 5) ;
6) ; 7) ; 8) . ☼
Предел функции.
Пусть функция f( ) определена на некотором промежутке Х и пусть точка или .
Определение 1.2.Число А называется пределом функции ( ) в точке , если такое, что для всех , , удовлетворяющих неравенству , выполняется неравенство .
Записывается так:
J Пример 1.8.Используя определение, докажем, что функция в точке имеет предел, равный единице, т.е.
Возьмем любое . Найдем такое , при котором из неравенства следовало бы неравенство . Преобразуя неравенство, получаем . Отсюда видно, что если взять , то для всех , удовлетворяющих неравенству , выполняется требуемое неравенство . Это и означает, что В частности, если , то . J
☼ Упражнения 1.3.Используя определение, доказать, что:
1) ; 2) ; 3) ; 4) ;
5) ; 6) ; 7) ; 8) . ☼
Правила вычисления пределов функции.
Пусть функции и имеют в точке пределы В и A. Тогда
1. = ;
2. ; 3. (при ).
4. ; 5. = С B;
Правила верны также и в случае, когда является одним из символов или .
J Пример 1.9.Найти .
Решение.
По правилам вычисления предела функции находим
= . J
☼ Упражнения 1.4.Найти пределы:
1) ; 2) ; 3) ; 4) ;
5) ; 6) ; 7) ; 8) . ☼
1.6. Раскрытие неопределенностей вида и .
J Пример 1.10.Найти .
Решение.
Имеем неопределенность вида . Разложим числитель и знаменатель на множители и сократим на общий множитель, который обращает в нуль числитель и знаменатель дроби: = . J
J Пример 1.11.Найти .
Решение.
Имеем неопределенность вида . Так же, как и в случае последовательностей заменим бесконечно большие функции на эквивалентные и найдем предел дроби: . J
J Пример 1.12.Найти .
Решение.
Имеем неопределенность вида . Заменим бесконечно большие функции на эквивалентные и найдем предел дроби: . J
J Пример 1.13.Найти .
Решение.
Имеем неопределенность вида . Заменим бесконечно большие функции на эквивалентные и найдем предел дроби: . J
Сопоставляя результаты решений примеров 1.11 – 1.13 установим правило нахождения пределов с неопределенностью . Если – многочлены степеней m и k соответственно, то
где – отношение коэффициентов при старших степенях многочленов.
J Пример 1.14.Вычислить .
Решение.
Учитывая условие , получаем .J
☼ Упражнения 1.5.Найти пределы:
1) ; 2) ; 3) ; 4) ;
5) ; 6) ; 7) ;
8) ; ☼
1.7. Раскрытие неопределенности вида .
Неопределенность вида при помощи алгебраических преобразованийприводится к неопределенности .
J Пример 1.15.Найти .
Решение.
Имеем неопределенность вида . Умножим и разделим рассматриваемое выражение на сопряженное и заменим знаменатель на эквивалентную величину: = . J
J Пример 1.16.Найти .
Решение.
Имеем неопределенность вида . Для вычисления этого предела используем прием умножения и деления на сопряженное выражение:
= =
= = . J
J Пример 1.17.Найти .
Решение.
Имеем неопределенность вида . Преобразуем данное выражение и
найдем предел дроби:
= = = = . J
☼ Упражнения 1.6.Найти пределы:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ; 7) ; 8) . ☼
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Пределы функций. Нахождение пределов функции в точке и на бесконечности.
Теория пределов позволяет определить характер поведения функции у = f(x) при заданном изменении аргумента.
Пусть функция f(х) определена в некоторой окрестности точки х =х0, за исключением, быть может, самой точки х0.
Число А называется пределом функции f(х) в точке х0, если для любого числа >0 найдется такое положительное число , что для любого х х0, удовлетворяющего неравенству | х – хо | < , выполняется соотношение | f(x) – А | <
То, что функция f(x) в точке х0 имеет предел, равный А, обозначают следующим образом:
Геометрически существование данного предела означает, что каково бы ни было >0, найдется такое число , что для всех х, заключенных между х0 + , и х0 – (кроме, быть может, самой точки хс), график функции у = f(x) лежит в полосе, ограниченной прямыми у = А + и у = А- (рис.1)
Рисунок 1
Таким образом, понятие предела функции дает возможность ответить на вопрос, к чему стремятся значения функции, когда значения аргумента стремятся к х0
Число А называют пределом функции f(x) при х, стремящимся к х0, если разность f(x) – А по абсолютной величине есть величина бесконечно малая.
Понятие бесконечно малой величины.
В природе существует много таких переменных величин, которые в процессе своего изменения неограниченно приближаются к нулю. Таким величинам присвоено специальное название -“бесконечно малые” величины.
Переменная величина хп называется бесконечно малой, если она в процессе изменения становится и затем остается по абсолютной величине меньше любого, наперед заданного, сколько угодно малого положительного числа, т.е. хп < ( – эпсилон). Рассмотрим колебание математического маятника.
Математическим маятником называется материальная точка, подвешенная на тонкой, невесомой, нерастяжимой нити.
Пусть в начальный момент времени маятник отклонен от положения равновесия на угол = 15°. Если маятник отпустить, то он будет совершать колебания. Из-за сопротивления среды амплитуда колебания маятника будет постепенно уменьшаться; поэтому какое бы положительное число ни было задано, угол по абсолютной величине станет и впредь будет оставаться меньше .
Следовательно, угол в данном процессе является бесконечно малой величиной.
Примерами бесконечно малой величины являются: масса тающей в воде льдины, разность уровней однородной жидкости в сообщающихся сосудах и т.д.
Пусть задана числовая последовательность аn, n N. Тогда последовательность Sn = а1+ а2+а3+…+аn = , n N называется числовым рядом и обозначается а1+ а2+а3+…+аn + … или .
Числа а1,а2, … называется членами ряда , соответственно первым, вторым и т.д.; аn называется n – м или общим членом ряда
Ряд аn+1+ аn+2+ аn+3+… = называется n – м остатком ряда
Согласно определению ряды – это особый вид последовательностей, поэтому можно говорить о сходимости и расходимости рядов.
Ряд называется сходящимся, если последовательность его частичных сумм сходится.
Если последовательность частичных сумм ряда расходится, то он называется расходящимся.
Ряд а2+а3+…+аn + … или .называется сходящимся, если существует предел
Этот предел называется суммой ряда а2+а3+…+аn + … или .
Если ряд а2+а3+…+аn + … или сходится и Ы – его сумма, то будем писать
Теорема 1. Если ряд сходится, то и любой его остаток сходится. Если какой–нибудь остаток ряда сходится, то и ряд сходится.
Теорема 2. Если ряды с общими членами аn и bn сходятся и , , то для любых чисел α и β ряд с общим членом сn = αan и βbn сходится и
Пример:
Решение:
Общий член этого ряда имеет вид
сn =
Ряды с общими членами аn = и bn = сходятся и
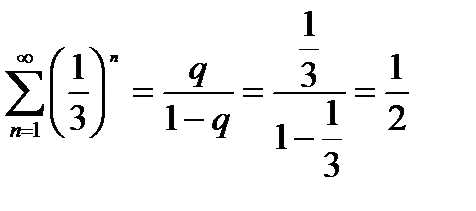 ,
, 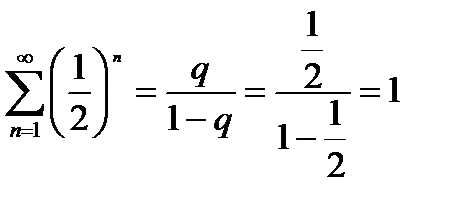
В силу теоремы 2 данный ряд сходится и
Теорема 3. (необходимое условие сходимости ряда)Если ряд с общим членом аn сходится, то аn при n .
Похожие статьи:
poznayka.org

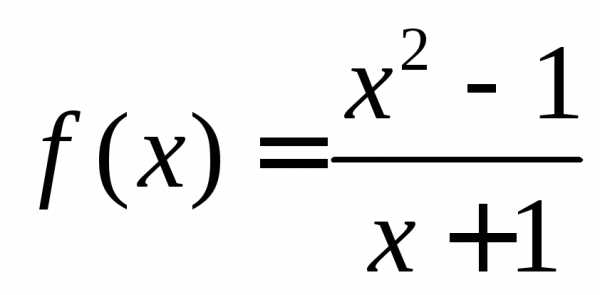
 и отметить точки
и отметить точки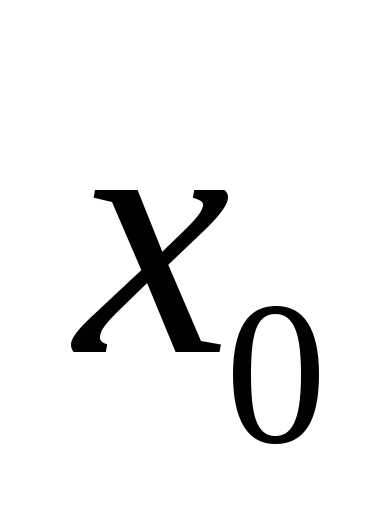
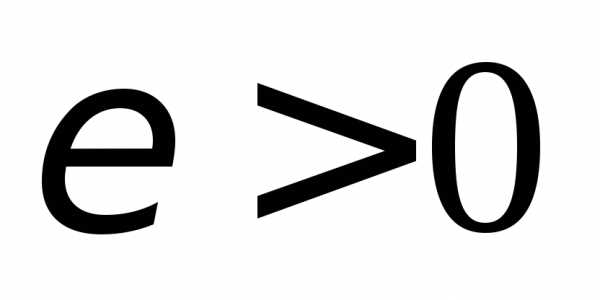 ;
; ,
,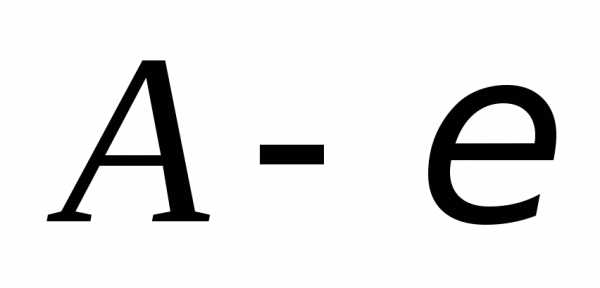 и графику функции построить
и графику функции построить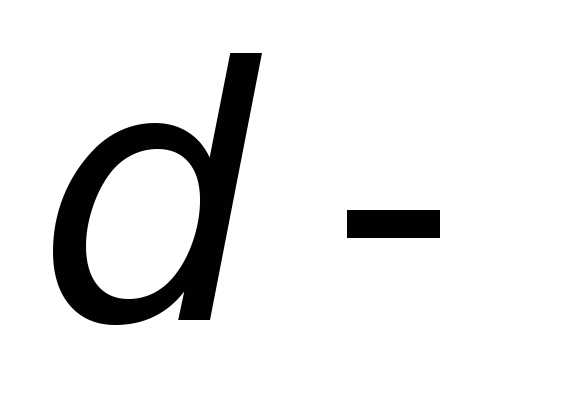 окрестность
точки
окрестность
точки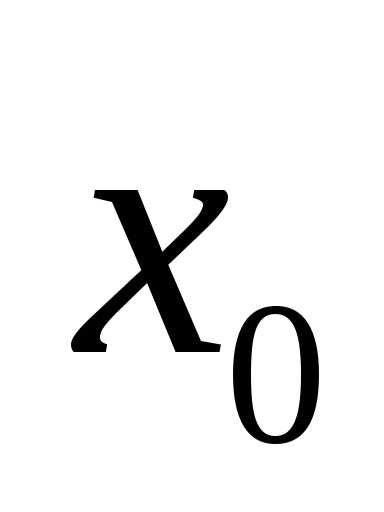 .
Расстояния от точки
.
Расстояния от точки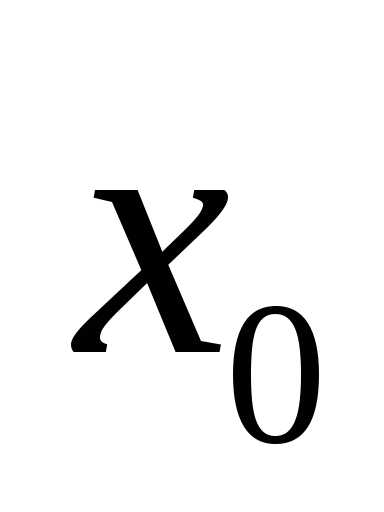 до точек
до точек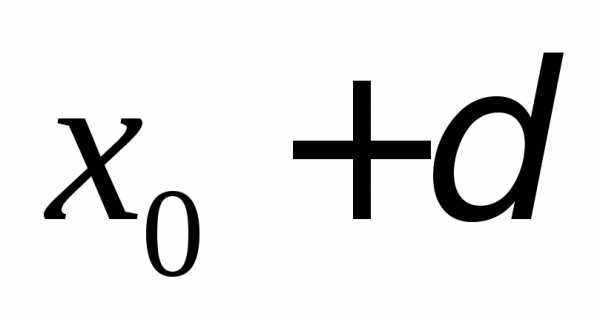 и
и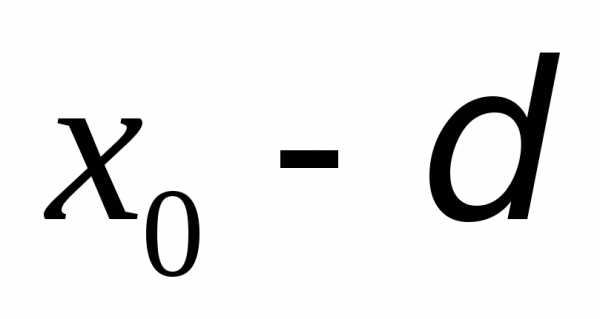 должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки
должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки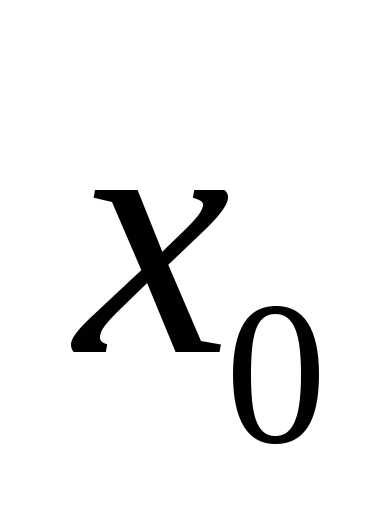 ;
;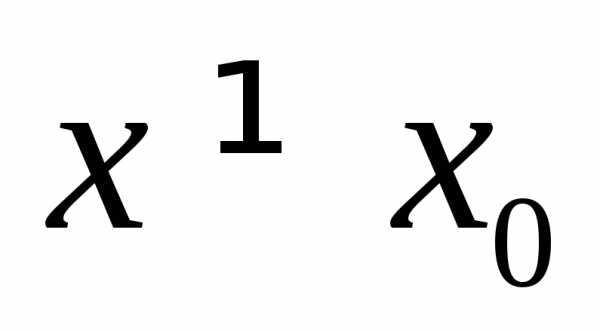 ,
принадлежащую окрестности точки
,
принадлежащую окрестности точки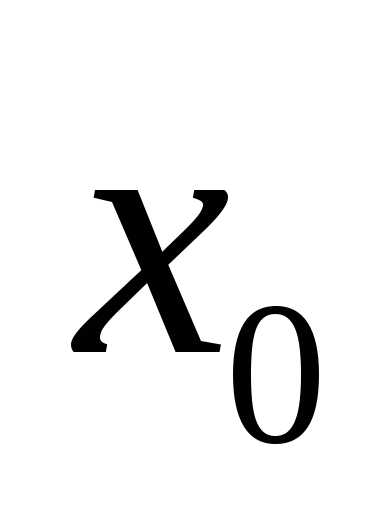 ,
и по графику функции найти значение
,
и по графику функции найти значение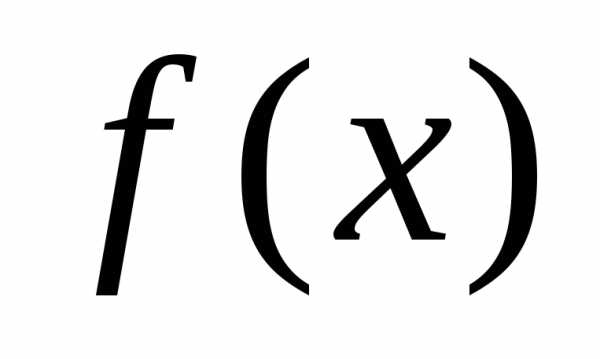 ,
которое должно попасть в построенную
окрестность точкиА.
,
которое должно попасть в построенную
окрестность точкиА.