Неопределенности пределы – , .
Неопределенности пределов Википедия
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
(Здесь 0{\displaystyle 0} — бесконечно малая величина, а ∞{\displaystyle \infty } — бесконечно большая величина)
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов ( 00){\displaystyle \left(~0^{0}\right)}, (1∞){\displaystyle \left(1^{\infty }\right)}, (∞0){\displaystyle \left(\infty ^{0}\right)} пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
- ( 00)=(e0⋅ln0)=(e0⋅(−∞)){\displaystyle \left(~0^{0}\right)=\left(e^{0\cdot ln{0}}\right)=\left(e^{0\cdot (-\infty )}\right)}
- ( 1∞)=(e∞⋅ln1)=(e∞⋅0){\displaystyle \left(~1^{\infty }\right)=\left(e^{\infty \cdot ln{1}}\right)=\left(e^{\infty \cdot 0}\right)}
- ( ∞0)=(e0⋅ln∞)=(e0⋅∞){\displaystyle \left(~\infty ^{0}\right)=\left(e^{0\cdot ln{\infty }}\right)=\left(e^{0\cdot \infty }\right)}
Для раскрытия неопределённостей типа ∞∞{\displaystyle {\frac {\infty }{\infty }}} используется следующий алгоритм:
- Выявление старшей степени переменной;
- Деление на эту переменную как числителя, так и знаменателя.
Для раскрытия неопределённостей типа (00){\displaystyle \left({\frac {0}{0}}\right)} существует следующий алгоритм:
- Разложение на множители числителя и знаменателя;
- Сокращение дроби.
Для раскрытия неопределённостей типа (∞−∞){\displaystyle (\infty -\infty )} иногда удобно применить следующее преобразование:
- Пусть f(x)→x→a∞{\displaystyle f(x){\xrightarrow {x\to a}}\infty } и g(x)→x→a∞{\displaystyle g(x){\xrightarrow {x\to a}}\infty };
- limx→a[f(x)−g(x)]=(∞−∞)=limx→a(11f(x)−11g(x))=limx→a1g(x)−1f(x)1g(x)⋅1f(x)=(00){\displaystyle \lim _{x\to a}[f(x)-g(x)]=(\infty -\infty )=\lim _{x\to a}\left({\frac {1}{\frac {1}{f(x)}}}-{\frac {1}{\frac {1}{g(x)}}}\right)=\lim _{x\to a}{\frac {{\frac {1}{g(x)}}-{\frac {1}{f(x)}}}{{\frac {1}{g(x)}}\cdot {\frac {1}{f(x)}}}}=\left({\frac {0}{0}}\right)}.
Данный вид неопределённостей может раскрываться с использованием асимптотических разложений уменьшаемого и вычитаемого, при этом бесконечно большие члены одного порядка должны уничтожаться.
При раскрытии неопределённостей также применяются замечательные пределы и их следствия.
Пример
limx→aax−xax−a,a>0{\displaystyle \lim _{x\to a}{\frac {a^{x}-x^{a}}{x-a}},a>0} — пример[1] неопределённости вида (00){\displaystyle \left({\frac {0}{0}}\right)}. По правилу Лопиталя limx→aax−xax−a=limx→aaxlna−axa−11=aa(lna−1){\displaystyle \lim _{x\to a}{\frac {a^{x}-x^{a}}{x-a}}=\lim _{x\to a}{\frac {a^{x}\ln a-ax^{a-1}}{1}}=a^{a}(\ln a-1)}. Второй способ — прибавить и отнять в числителе aa{\displaystyle a^{a}} и дважды применить теорему Лагранжа, к функциям ax{\displaystyle a^{x}} и xa{\displaystyle x^{a}} соответственно:
ax−xax−a=ax−aa−(xa−aa)x−a=aclna(x−a)−ada−1(x−a)x−a=aclna−ada−1{\displaystyle {\frac {a^{x}-x^{a}}{x-a}}={\frac {a^{x}-a^{a}-(x^{a}-a^{a})}{x-a}}={\frac {a^{c}\ln a(x-a)-ad^{a-1}(x-a)}{x-a}}=a^{c}\ln a-ad^{a-1}}
здесь c, d лежат между a и x, поэтому они стремятся к a при x стремящемся к a, отсюда получаем тот же предел, что и в первом способе.
Примечания
- ↑ Демидович Б.П. Задача №1358 // Сборник задач и упражнений по математическому анализу. — 7-е изд. — М.: Наука, 1969. — С. 136.
wikiredia.ru
Неопределенности пределов Википедия
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
(Здесь 0{\displaystyle 0} — бесконечно малая величина, а ∞{\displaystyle \infty } — бесконечно большая величина)
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов ( 00){\displaystyle \left(~0^{0}\right)}, (1∞){\displaystyle \left(1^{\infty }\right)}, (∞0){\displaystyle \left(\infty ^{0}\right)} пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
- ( 00)=(e0⋅ln
ru-wiki.ru
Неопределённости пределов Вики
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
(Здесь 0{\displaystyle 0} — бесконечно малая величина, а ∞{\displaystyle \infty } — бесконечно большая величина)
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов ( 00){\displaystyle \left(~0^{0}\right)}, (1∞){\displaystyle \left(1^{\infty }\right)}, (∞0){\displaystyle \left(\infty ^{0}\right)} пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
- ( 00)=(e0⋅ln0)=(e0⋅(−∞)){\displaystyle \left(~0^{0}\right)=\left(e^{0\cdot ln{0}}\right)=\left(e^{0\cdot (-\infty )}\right)}
- ( 1∞)=(e∞⋅ln1)=(e∞⋅0){\displaystyle \left(~1^{\infty }\right)=\left(e^{\infty \cdot ln{1}}\right)=\left(e^{\infty \cdot 0}\right)}
- ( ∞0)=(e0⋅ln∞)=(e0⋅∞){\displaystyle \left(~\infty ^{0}\right)=\left(e^{0\cdot ln{\infty }}\right)=\left(e^{0\cdot \infty }\right)}
Для раскрытия неопределённостей типа ∞∞{\displaystyle {\frac {\infty }{\infty }}} используется следующий алгоритм:
- Выявление старшей степени переменной;
- Деление на эту переменную как числителя, так и знаменателя.
Для раскрытия неопределённостей типа (00){\displaystyle \left({\frac {0}{0}}\right)} существует следующий алгоритм:
- Разложение на множители числителя и знаменателя;
- Сокращение дроби.
Для раскрытия неопределённостей типа (∞−∞){\displaystyle (\infty -\infty )} иногда удобно применить следующее преобразование:
- Пусть f(x)→x→a∞{\displaystyle f(x){\xrightarrow {x\to a}}\infty } и g(x)→x→a∞{\displaystyle g(x){\xrightarrow {x\to a}}\infty };
- limx→a[f(x)−g(x)]=(∞−∞)=limx→a(11f(x)−11g(x))=limx→a1g(x)−1f(x)1g(x)⋅1f(x)=(00){\displaystyle \lim _{x\to a}[f(x)-g(x)]=(\infty -\infty )=\lim _{x\to a}\left({\frac {1}{\frac {1}{f(x)}}}-{\frac {1}{\frac {1}{g(x)}}}\right)=\lim _{x\to a}{\frac {{\frac {1}{g(x)}}-{\frac {1}{f(x)}}}{{\frac {1}{g(x)}}\cdot {\frac {1}{f(x)}}}}=\left({\frac {0}{0}}\right)}.
Данный вид неопределённостей может раскрываться с использованием асимптотических разложений уменьшаемого и вычитаемого, при этом бесконечно большие члены одного порядка должны уничтожаться.
При раскрытии неопределённостей также применяются замечательные пределы и их следствия.
Пример[ | код]
limx→aax−xax−a,a>0{\displaystyle \lim _{x\to a}{\frac {a^{x}-x^{a}}{x-a}},a>0} — пример[1] неопределённости вида (00){\displaystyle \left({\frac {0}{0}}\right)}. По правилу Лопиталя limx→aax−xax−a=limx→aaxlna−axa−11=aa(lna−1){\displaystyle \lim _{x\to a}{\frac {a^{x}-x^{a}}{x-a}}=\lim _{x\to a}{\frac {a^{x}\ln a-ax^{a-1}}{1}}=a^{a}(\ln a-1)}. Второй способ — прибавить и отнять в числителе aa{\displaystyle a^{a}} и дважды применить теорему Лагранжа, к функциям ax{\displaystyle a^{x}} и xa{\displaystyle x^{a}} соответственно:
ax−xax−a=ax−aa−(xa−aa)x−a=aclna(x−a)−ada−1(x−a)x−a=aclna−ada−1{\displaystyle {\frac {a^{x}-x^{a}}{x-a}}={\frac {a^{x}-a^{a}-(x^{a}-a^{a})}{x-a}}={\frac {a^{c}\ln a(x-a)-ad^{a-1}(x-a)}{x-a}}=a^{c}\ln a-ad^{a-1}}
здесь c, d лежат между a и x, поэтому они стремятся к a при x стремящемся к a, отсюда получаем тот же предел, что и в первом способе.
Примечания[ | код]
- ↑ Демидович Б.П. Задача №1358 // Сборник задач и упражнений по математическому анализу. — 7-е изд. — М.: Наука, 1969. — С. 136.
ru.wikibedia.ru
Пределы Неопределенности Пределы с неопределенностью Алгоритм
 Пределы
Пределы
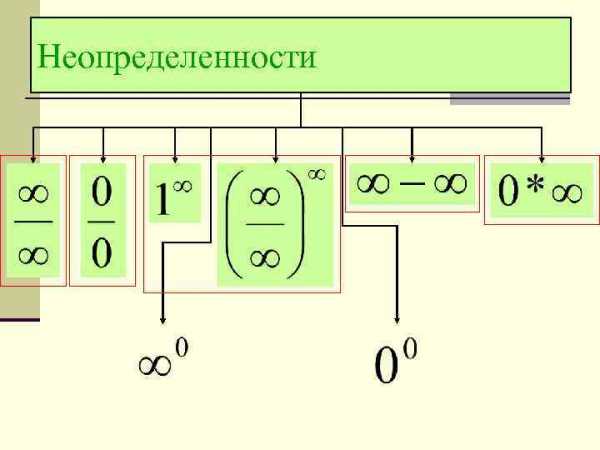 Неопределенности
Неопределенности
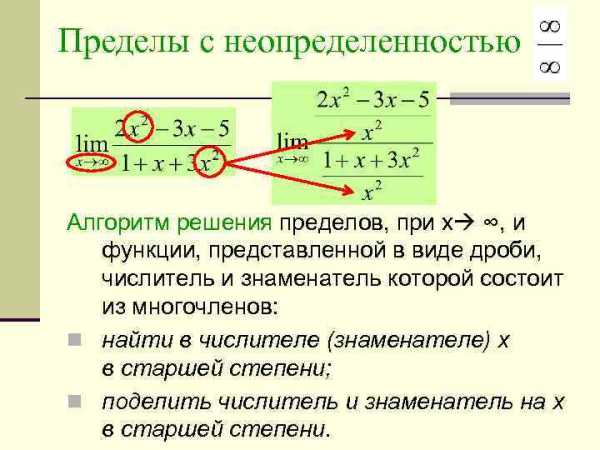 Пределы с неопределенностью Алгоритм решения пределов, при х ∞, и функции, представленной в виде дроби, числитель и знаменатель которой состоит из многочленов: n найти в числителе (знаменателе) х в старшей степени; n поделить числитель и знаменатель на х в старшей степени.
Пределы с неопределенностью Алгоритм решения пределов, при х ∞, и функции, представленной в виде дроби, числитель и знаменатель которой состоит из многочленов: n найти в числителе (знаменателе) х в старшей степени; n поделить числитель и знаменатель на х в старшей степени.
 Пределы с неопределенностью Подставим предел в функцию: Разрешим неопределенность:
Пределы с неопределенностью Подставим предел в функцию: Разрешим неопределенность:
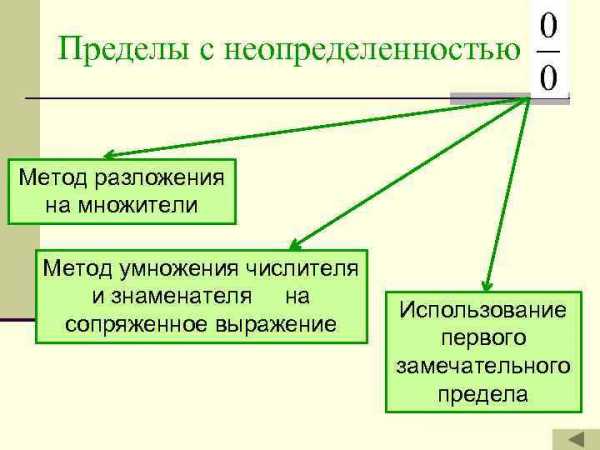 Пределы с неопределенностью Метод разложения на множители Метод умножения числителя и знаменателя на сопряженное выражение Использование первого замечательного предела
Пределы с неопределенностью Метод разложения на множители Метод умножения числителя и знаменателя на сопряженное выражение Использование первого замечательного предела
 Пределы с неопределенностью Метод разложения на множители Алгоритм решения пределов, при х, стремящемуся к конечному числу, и функции, представленной в виде дроби, числитель и знаменатель которой состоит из многочленов: n подставить конечное число, к которому стремится х, в функцию; n раскрывать неопределенность , раскладывая на множители числитель и знаменатель (как правило, решается квадратное уравнение и (или) используются формулы сокращенного умножения).
Пределы с неопределенностью Метод разложения на множители Алгоритм решения пределов, при х, стремящемуся к конечному числу, и функции, представленной в виде дроби, числитель и знаменатель которой состоит из многочленов: n подставить конечное число, к которому стремится х, в функцию; n раскрывать неопределенность , раскладывая на множители числитель и знаменатель (как правило, решается квадратное уравнение и (или) используются формулы сокращенного умножения).
 Пределы с неопределенностью Метод разложения на множители 1. Подставим конечное число, к которому стремиться х в функцию: 2. Разрешим неопределенность: Разложим числитель и знаменатель на множители. 2. 1. В числителе решим квадратное уравнение: 2. 1. 1. Найдем дискриминант
Пределы с неопределенностью Метод разложения на множители 1. Подставим конечное число, к которому стремиться х в функцию: 2. Разрешим неопределенность: Разложим числитель и знаменатель на множители. 2. 1. В числителе решим квадратное уравнение: 2. 1. 1. Найдем дискриминант
 Пределы с неопределенностью Метод разложения на множители 2. 1. 2. Найдем корни: 2. 1. 3. Разложим на множители квадратный трехчлен: 2. 2. Подставим (- 1) в функцию:
Пределы с неопределенностью Метод разложения на множители 2. 1. 2. Найдем корни: 2. 1. 3. Разложим на множители квадратный трехчлен: 2. 2. Подставим (- 1) в функцию:
 Пределы с неопределенностью Умножение на сопряженное выражение Алгоритм решения пределов, при х, стремящемуся к конечному числу, и функции, представленной в виде дроби, числитель и знаменатель которой состоит из многочленов, представляющих разность корней или корень минус любое число: n подставить конечное число, к которому стремится х, в функцию; n помножить числитель и знаменатель на сопряженное выражение; n раскрыть неопределенность, разложив на множители числитель и знаменатель.
Пределы с неопределенностью Умножение на сопряженное выражение Алгоритм решения пределов, при х, стремящемуся к конечному числу, и функции, представленной в виде дроби, числитель и знаменатель которой состоит из многочленов, представляющих разность корней или корень минус любое число: n подставить конечное число, к которому стремится х, в функцию; n помножить числитель и знаменатель на сопряженное выражение; n раскрыть неопределенность, разложив на множители числитель и знаменатель.
 Пределы с неопределенностью Умножение на сопряженное выражение 1. Подставим конечное число, к которому стремиться х в функцию: 2. Разрешим неопределенность: 2. 1. Избавимся от корней в числителе, возведя уменьшаемое и вычитаемое числителя в квадрат. Используем формулу разности квадратов. Помножим разность в числителе на сумму (это и есть сопряженное выражение). Чтобы не изменилась функция, на него же помножим знаменатель.
Пределы с неопределенностью Умножение на сопряженное выражение 1. Подставим конечное число, к которому стремиться х в функцию: 2. Разрешим неопределенность: 2. 1. Избавимся от корней в числителе, возведя уменьшаемое и вычитаемое числителя в квадрат. Используем формулу разности квадратов. Помножим разность в числителе на сумму (это и есть сопряженное выражение). Чтобы не изменилась функция, на него же помножим знаменатель.

 Пределы с неопределенностью Первый замечательный предел или Пример
Пределы с неопределенностью Первый замечательный предел или Пример
 Пределы с неопределенностями Второй замечательный предел или где е = 2, 71828…
Пределы с неопределенностями Второй замечательный предел или где е = 2, 71828…
 Пределы с неопределенностями Второй замечательный предел Пример 1: 1. Возведем в степень 3 х основание, и чтобы не изменился результат, помножим показатель степени на 1/3 х. 2. Знак предела переместим в показатель степени.
Пределы с неопределенностями Второй замечательный предел Пример 1: 1. Возведем в степень 3 х основание, и чтобы не изменился результат, помножим показатель степени на 1/3 х. 2. Знак предела переместим в показатель степени.
 Пределы с неопределенностями Второй замечательный предел Пример 2: 1. Преобразуем полученную неопределенность в
Пределы с неопределенностями Второй замечательный предел Пример 2: 1. Преобразуем полученную неопределенность в
 Пределы с неопределенностями Второй замечательный предел 2. Организуем второй замечательный предел:
Пределы с неопределенностями Второй замечательный предел 2. Организуем второй замечательный предел:
 Пределы с неопределенностями Второй замечательный предел 3. Разрешим неопределенность в показателе степени:
Пределы с неопределенностями Второй замечательный предел 3. Разрешим неопределенность в показателе степени:
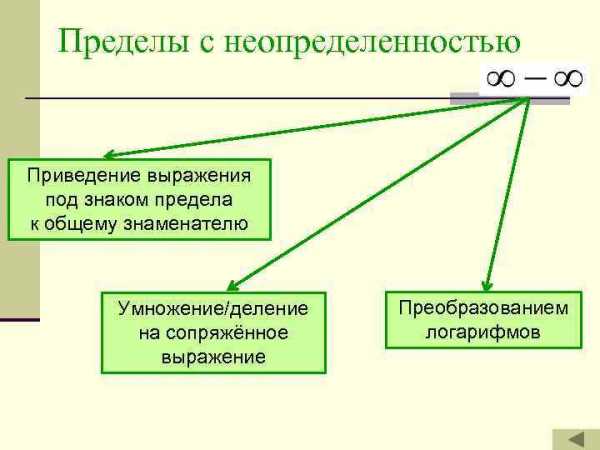 Пределы с неопределенностью Приведение выражения под знаком предела к общему знаменателю Умножение/деление на сопряжённое выражение Преобразованием логарифмов
Пределы с неопределенностью Приведение выражения под знаком предела к общему знаменателю Умножение/деление на сопряжённое выражение Преобразованием логарифмов
 Пределы с неопределенностью Приведение к общему знаменателю 1. Преобразуем неопределенность. Разложим знаменатели на множители: в первом вынесем х за скобку; во втором используем формулу разности кубов 2. Приведем выражение к одному знаменателю.
Пределы с неопределенностью Приведение к общему знаменателю 1. Преобразуем неопределенность. Разложим знаменатели на множители: в первом вынесем х за скобку; во втором используем формулу разности кубов 2. Приведем выражение к одному знаменателю.
 Пределы с неопределенностью Приведение к общему знаменателю 3. Используем формулу квадрата разности и раскладываем числитель на множители.
Пределы с неопределенностью Приведение к общему знаменателю 3. Используем формулу квадрата разности и раскладываем числитель на множители.
 Пределы с неопределенностью Замена переменной в пределе Метод замены переменной используется не только тогда, когда получается неопределенность данного типа. Цель метода – свести решение к первому замечательному пределу.
Пределы с неопределенностью Замена переменной в пределе Метод замены переменной используется не только тогда, когда получается неопределенность данного типа. Цель метода – свести решение к первому замечательному пределу.
 Пределы с неопределенностью Замена переменной в пределе 1. Преобразуем неопределенность.
Пределы с неопределенностью Замена переменной в пределе 1. Преобразуем неопределенность.
 Пределы с неопределенностью Замена переменной в пределе 2. Произведем замену переменной так, чтобы предел стремился не к единице, а к нулю: t=1 – х. Тогда если х 1, то t 1 -1=0. Так как под знаком предела х заменится на t, выразим через t и х в знаменателе: х=1 – t.
Пределы с неопределенностью Замена переменной в пределе 2. Произведем замену переменной так, чтобы предел стремился не к единице, а к нулю: t=1 – х. Тогда если х 1, то t 1 -1=0. Так как под знаком предела х заменится на t, выразим через t и х в знаменателе: х=1 – t.
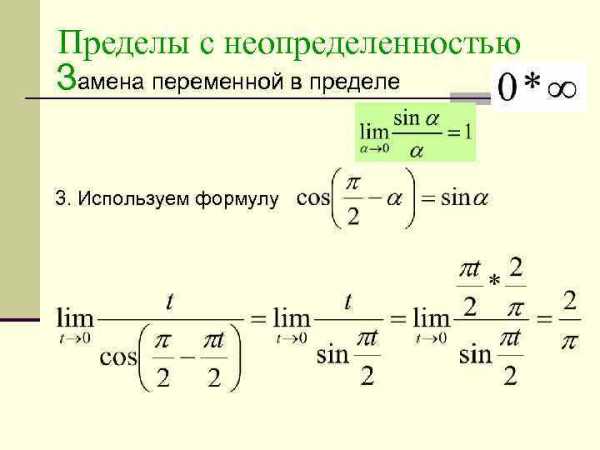 Пределы с неопределенностью Замена переменной в пределе 3. Используем формулу
Пределы с неопределенностью Замена переменной в пределе 3. Используем формулу
present5.com
Неопределенности пределов – это… Что такое Неопределенности пределов?
- Неопределенности пределов
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа
- , , 0 / 0, 00, , ,
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.
Для раскрытия неопределённостей видов 00, , пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
Пример
Wikimedia Foundation. 2010.
- Неопределенное поведение
- Неопознанный подводный объект
Смотреть что такое “Неопределенности пределов” в других словарях:
ПРЕВЫШЕНИЕ ПРЕДЕЛОВ НЕОБХОДИМОЙ ОБОРОНЫ — согласно ч. 3 ст. 37 УК умышленные действия, явно не соответствующие характеру и степени общественной опасности посягательства. Это не означает равенства по интенсивности посягательства и оборонительных действий. Поэтому причинение смерти при… … Энциклопедия юриста
Европейский центральный банк — (European Central Bank) Европейский центральный банк – это крупнейшее международное кредитно банковкое учреждение государств Евросоюза и Зоны Евро Структура и фкункции Европейского Центрального банка, Европейская система центральных банков,… … Энциклопедия инвестора
среднее — 3.3 среднее (mean): Среднее значение для (выбранного) времени усреднения результатов измерений анемометром. Источник: ГОСТ Р ИСО 1 … Словарь-справочник терминов нормативно-технической документации
Дифференциальное исчисление — Исчисление бесконечно малых, включающее так называемое Д. исчисление, а также ему обратное интегральное, принадлежит к числу наиболее плодотворных открытий человеческого ума и составило эпоху в истории точных наук. Ближайшим поводом к изобретению … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Александр II (часть 2, I-VII) — ЧАСТЬ ВТОРАЯ. Император Александр II (1855—1881). I. Война (1855). Высочайший манифест возвестил России о кончине Императора Николая и о воцарении его преемника. В этом первом акте своего царствования молодой Государь принимал пред лицом… … Большая биографическая энциклопедия
группа — 1.3.2 группа : Лампы с одинаковыми электрическими параметрами и характеристиками катода, физическими размерами и методом зажигания. Источник: ГОСТ Р МЭК 61195 99: Лампы люминесцентные двухцокольные. Требования безопасности … Словарь-справочник терминов нормативно-технической документации
Евро — (Euro) Евро это единая европейская валюта Евро: описание монет и банкнот, история создания и развития, место в мировой экономике Содержание >>>>>>>>>> … Энциклопедия инвестора
Суверенитет — (Sovereignty) Суверенитет это независимость государства от других стран Суверенитет России и его проблемы, суверенитет Украины, суверенитет республики Беларусь, суверенитет Казахстана, суверенитет Чечни, Проблемы суверенитета стран Европы,… … Энциклопедия инвестора
Сервитуты — ограничения собственности, сообщающие лицам, в пользу которых они установлены, самостоятельные вещные права пользования (так назыв. права в чужой вещи ) чужим недвижимым имуществом в точно определенном размере. Различают несколько видов этих… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Россия. Русское право: Русское гражданское право — Вступление. Русское гражданское право как в своем историческом развитии, так и современном состоянии в противоположность римскому и новому западноевропейскому характеризуется неопределенностью форм гражданско правовых отношений отдельных и… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
dvc.academic.ru
Неопределенности пределов – это… Что такое Неопределенности пределов?
- Неопределенности пределов
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа
- , , 0 / 0, 00, , ,
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.
Для раскрытия неопределённостей видов 00, , пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
Пример
Wikimedia Foundation. 2010.
- Неопределенное поведение
- Неопознанный подводный объект
Смотреть что такое “Неопределенности пределов” в других словарях:
ПРЕВЫШЕНИЕ ПРЕДЕЛОВ НЕОБХОДИМОЙ ОБОРОНЫ — согласно ч. 3 ст. 37 УК умышленные действия, явно не соответствующие характеру и степени общественной опасности посягательства. Это не означает равенства по интенсивности посягательства и оборонительных действий. Поэтому причинение смерти при… … Энциклопедия юриста
Европейский центральный банк — (European Central Bank) Европейский центральный банк – это крупнейшее международное кредитно банковкое учреждение государств Евросоюза и Зоны Евро Структура и фкункции Европейского Центрального банка, Европейская система центральных банков,… … Энциклопедия инвестора
среднее — 3.3 среднее (mean): Среднее значение для (выбранного) времени усреднения результатов измерений анемометром. Источник: ГОСТ Р ИСО 1 … Словарь-справочник терминов нормативно-технической документации
Дифференциальное исчисление — Исчисление бесконечно малых, включающее так называемое Д. исчисление, а также ему обратное интегральное, принадлежит к числу наиболее плодотворных открытий человеческого ума и составило эпоху в истории точных наук. Ближайшим поводом к изобретению … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Александр II (часть 2, I-VII) — ЧАСТЬ ВТОРАЯ. Император Александр II (1855—1881). I. Война (1855). Высочайший манифест возвестил России о кончине Императора Николая и о воцарении его преемника. В этом первом акте своего царствования молодой Государь принимал пред лицом… … Большая биографическая энциклопедия
группа — 1.3.2 группа : Лампы с одинаковыми электрическими параметрами и характеристиками катода, физическими размерами и методом зажигания. Источник: ГОСТ Р МЭК 61195 99: Лампы люминесцентные двухцокольные. Требования безопасности … Словарь-справочник терминов нормативно-технической документации
Евро — (Euro) Евро это единая европейская валюта Евро: описание монет и банкнот, история создания и развития, место в мировой экономике Содержание >>>>>>>>>> … Энциклопедия инвестора
Суверенитет — (Sovereignty) Суверенитет это независимость государства от других стран Суверенитет России и его проблемы, суверенитет Украины, суверенитет республики Беларусь, суверенитет Казахстана, суверенитет Чечни, Проблемы суверенитета стран Европы,… … Энциклопедия инвестора
Сервитуты — ограничения собственности, сообщающие лицам, в пользу которых они установлены, самостоятельные вещные права пользования (так назыв. права в чужой вещи ) чужим недвижимым имуществом в точно определенном размере. Различают несколько видов этих… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Россия. Русское право: Русское гражданское право — Вступление. Русское гражданское право как в своем историческом развитии, так и современном состоянии в противоположность римскому и новому западноевропейскому характеризуется неопределенностью форм гражданско правовых отношений отдельных и… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
dik.academic.ru



