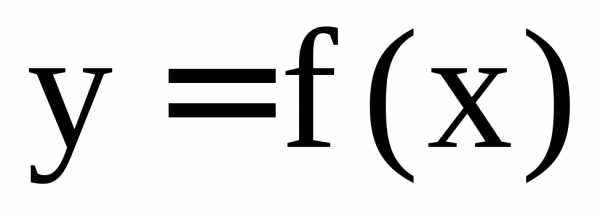Односторонний предел как найти – 45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы
- Комментариев к записи Односторонний предел как найти – 45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы нет
- Советы абитуриенту
2. Табличный способ
На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов, таблица квадратных корней.
Во многих случаях табличное задание функции оказывается удобным. Оно позволяет найти значения функции для значений аргумента, имеющихся в таблице, без всяких вычислений. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае одной величине придают определенные значения, а потом из опыта для каждого из таких значений находят значение (обычно приближенное) второй величины. Таким образом опыт позволяет составить некоторую таблицу значений функции. Существуют методы, позволяющие по такой таблице подбирать формулы, задающие функции (с определенной точностью).
3. Графический способ
Часто функция может быть задана с помощью графика..
3.Предел функции. Односторонние пределы.
Определение
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Левый и правый пределы функции
Определение
Число называется правым пределом функции в точке , если для такое, что для любого и , выполняется неравенство (рис. 1). Правый предел обозначается
Число называется левым пределом функции в точке , если для такое, что для любого и , выполняется неравенство (рис. 2). Левый предел обозначается
Левый и правый пределы функции называются односторонними пределами.
Теорема
Если существуют и , причем , то существует и . Обратное утверждение также верно.
В случае, если , то предел не существует.Задание. Найти односторонние пределы функции при
Решение. Правый предел:
Левый предел:
4.Первый замечательный предел.
Первый замечательный предел:
Определение
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Применение первого замечательного предела на практике
Пример
Задание. Найти предел
Решение. Воспользуемся заменой и первым замечательным пределом.
Ответ.
Пример
Задание. Найти предел
Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.
Ответ.
Следствия из первого замечательного предела
1°
2°
3°
4°
5.Второй замечательный предел.
1
Второй замечательный предел:
здесь е – число Эйлера.
Пример
Задание. Найти предел
Решение. Подставим , получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.
Ответ.
Следствия из второго замечательного предела
1°
2°
3°
4°
5°
6°
6.Непрерывность элементарных функций
Важнейшим свойством всех элементарных функций является их непрерывность в каждой точке определения. Убедимся в этом на примере некоторых элементарных функций.Рациональные функции.— непрерывна во всех точках, поскольку для любого значения аргумента.— непрерывна во всех точках, так как.— непрерывна по теореме о произведении непрерывных функций.Многочлен— непрерывен по теореме о сумме (разности) непрерывных функций.По теореме о частном непрерывных функцийдробно-рациональная функция— непрерывна везде, где.Тригонометрические функции.,— непрерывны всюду. Рассмотрим функцию.Так как, а последнее выражение стремится к нулю при, то и. Неравенствоследует из того что синус угла α (отсчитываемый от направления оси абсцисс) представляет собой величину ординаты точки на единичной окружности, а угол α есть длина дуги этой окружности.Аналогично доказывается непрерывность.По теореме о частном непрерывных функцийтригонометрические функции,— непрерывны всюду, где знаменатель не обращается в ноль.— непрерывна всюду, так как, а непрерывность приочевидна.
studfiles.net
Предел функции. Односторонний предел
Задачи на нахождение предела очень часто можно встретить в таких науках как механика, физика, высшая математика, прикладная математика и т.д. Суть таких задач заключается в отыскании значения функции при движении аргумента до некоторого значения при котором функция может быть и неопределена. Поведение функции в определенной точке и называется ее пределом. Он может принимать как постоянное значение так и быть равным бесконечности ().
ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ
Пусть имеем функцию которая определена в некоторой окрестности точки . Число называется пределом функции при , если для любого малого наперед заданного положительного числа можно найти такое положительное число что для всех удовлетворяющих неравенство
выполняется неравенство
В упрощенной форме определения записывают так
При функция является бесконечно большой, если для любого числа можно найти такое число что для всех , удовлетворяющих неравенство оправдывается неравенство
В краткой форме это определение примет вид
Функция является бесконечно малой при , если выполняется
ОДНОСТОРОННИЕ ГРАНИЦЫ
Запись можно понимать как приближение к точке слева, когда и дело, когда . аким образом, приближение точек до может быть двусторонним. На основе этого введены определения правой и левой границы.
Число есть пределом функции слева (левой границей), если для любого числа существует такое, что при выполняется неравенство
Число является пределом функции справа (правой границей) если для сколь угодно малого значения найдется такое что для всех из промежутка выполняется неравенство
Левая и правая границы называются односторонними границами.
Функция имеет предел в точке тогда и только тогда, когда существуют одновременно границы справа и слева и они равны между собой
Рассмотрим примеры из сборника задач Дубовика В.П., Юрика И.И. “Высшая математика” на нахождение границ.
———————————–
Пример 1. Найти пределы.
1) (4. 331)
2) (4. 333)
3) (4. 337)
4) (4. 342)
5) (4. 348)
6) (4. 357)
Решение.
1) Первые примеры не являются сложными и их решения сводится к подстановки значения аргумента в функцию
2) Как и в предыдущем примере проводим подстановку
3) Выполняем подстановку переменной в предел
4) В такого типа примерах нужно знаменатель разложить по правилу разности квадратов, после этого выполнить подстановку
5) В таких примерах нужно числитель и знаменатель сократить на множитель, который вносит наибольший вклад
6) В подобных примерах ищут наибольший показатель переменной в числителе и знаменателе, а потом проводят анализ. При следовании корни ведут себя следующим образом
С оценки показателей видим что числитель быстрее растет чем знаменатель
следовательно функция бесконечно большая и ее предел бесконечный
На этом вводной урок нахождения пределов функций завершен. Другие примеры вычисления пределов и методику их нахождения Вы найдете в следующих материалах.
———————————–
Посмотреть материалы:
yukhym.com
4. Предел функции. Односторонние пределы.
Рассмотрим функцию f(x), определённую на некотором множестве X, которое имеет предельную точку x0 (которая, в свою очередь, не обязана ему принадлежать). Значение A называется пределом (предельным значением) функции f(x) в точке x0 , если для любого наперёд взятого положительного числа ε найдётся отвечающее ему положительное число такое, что для всех аргументовx, удовлетворяющих условию , выполняется неравенство |f(x)-A|< ε.Определение 2:
Пусть числовая функция f(x) задана на множестве X, в котором отыщется сколь угодно большой элемент, то есть для всякого положительного в нём найдётся элемент, лежащий за границами отрезка[-,]. В этом случае числоA называется пределом функции f(x) на бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное числотакое, что для всех точек, превышающихпо абсолютному значению, справедливо неравенство |f(x)-A|< ε.
Определение 3:
lim f(x)=∞ (при x→a)
Говорят, что предел функции f(x) при x→a.
Если для любого M найдется такое (М), что для всех |x-a|<,f(x)>M.
Определение 4:
lim f(x)=∞ (при x→∞)
Говорят, что предел функции f(x) при x→∞, если для любого M найдется такое N(M), что для всех | x| >M будет выполняться неравенство |f(x)|>M.
Односторонние пределы:
Очевидно, что x стремясь к а остается либо больше а, либо меньше а. В этом случае говорят об односторонних пределах
Определение:
В называется пределом функции f(x) при x→a справа, если x→a остается больше (правосторонний предел):
Аналогично определяется предел слева:
5. Непрерывность функции. Классификации точек разрыва. Теорема о непрерывных на отрезке функциях.
Непрерывность функции:
Определение 1:
Пусть функция f(x) определена в некоторой окрестности U(а) и x<=a и называется непрерывной слева[lim f(x)=f(a) (при x→a)].
Определение 2:
Функция f(x) определенная в некоторой окрестности U(a) и x>=a называется непрерывной справа, если: lim f(x)=f(a) (при x→a).
Определение 1:
Функция называется непрерывной на (a,b) если она непрерывна к каждой точке этого интервала.
Определение 2:
Функция называется непрерывной на интервале (a,b), если она непрерывна в каждой внутренней точки (a,b).
Классификация точек разрыва.
1.
Если f(x0-0)=f(x0+0)=f(x0),
то в точке функция
2. Если f(x0-0)=f(x0+0)¹f(x0), или в точке x0 функция вообще не определена, то при функция имеет устранимый разрыв.
3. Если f(x0-0) и f(x0+0) принимает конечные значения и f(x0+0)¹f(x0 – 0), то в точке функция имеет разрыв первого рода (скачок).
4. Если хотя бы один из односторонних пределов f(x0 -0) или f(x0+0) равен ±¥, то в точке функция имеет разрыв второго рода (бесконечный разрыв).
6. Бесконечно малые функции и их свойства.
Определение:
α(x) является бесконечно малой при x→a или к ∞, если для любого ε>0 существует δ.
Теорема: если функция f(x), где b – конечное число, а α(x) – бесконечно малая при x→a f(x)=b+ α(x), то lim f(x)=b (при x→0).
Представим f(x)=b+ α(x) в следующем виде α(x)=f(x)-b => |f(x)-b|=|α(x)|< ε для всех xU(a, δ). Для всех xU(a, δ), |f(x)-b|< ε, lim f(x)=b (при x→a). Если lim f(x)=b (при x→a, x→∞) то f(x)=b+ α(x), α(x) – бесконечно малая функция.
Свойства:
1) Произведение бесконечно малой функции α(x) при x→a и функции f(x), ограниченной в некоторой δ 1-окрестности точки a, есть функция бесконечно малая.
Доказательство:
Функция f(x)
является ограниченной в некоторой
окрестности точки a
и, следовательно, существует такое число
B > 0,
что |f(x)|<b,
для всех x
удовлетворяющих условию |x-a|<
δ
Выберем из чисел δ 1 и δ 2 наименьшее и обозначим его символом δ. Тогда условие |x-a|< δ
является более сильным, чем условия |x-a|< δ1 и |x-a|< δ 2 и поэтому влечет неравенства |f(x)|<b и |α(x)|< ε/2. Таким образом, для любого произвольно малого числа ε > 0 выполняется неравенство
для всех x из δ-окрестности точки a.
2) Сумма конечного числа бесконечно малой функции есть функция бесконечно малая:
Доказательство. Пусть ε > 0 – произвольно малое число; α(x) и β(x)– бесконечно малые функции при x→a. Тогда существуют такие положительные числа δ1 и δ 2, что условия
|x-a|< δ1 и |x-a|< δ2 влекут за собой соответствующие неравенства |α(x)|< ε/2 и |β(x)|< ε/2. Если δ=min{ δ1, δ2}, то условие |x-a|< δ перекрывает оба условия |x-a|< δ1 и |x-a|< δ2 и, следовательно,
Следствие. Сумма любого конечного числа бесконечно малых функций есть функция бесконечно малая.
3) Если при x→x0 функция α(x) является бесконечно малой величиной, а функция f(x) – ограниченной, то их произведение α(x)·f(x) есть величина бесконечно малая при x→x0.
Доказательство. Так как α(x) бесконечно малая величина, то.С другой стороны, еслиf(x) ограниченная функция, то |f(x)|≤C. Поскольку α(x) может быть меньше любого наперед заданного положительного числа, то α(x)< ε/C.Обозначим γ(x)= α(x)·f(x). Отсюда следует, что,то естьγ(x)= α(x)·f(x) является бесконечно малой величиной, что и требовалось доказать. Это правило тем более справедливо, если перемножаются бесконечно малые величины.
4) Произведение конечного числа бесконечно малой функции есть функция бесконечно малая:
|α(x)| и |β(x)| – бесконечно малые, то |α(x)|· |β(x)| – бесконечно малые.
Следствие: если α(x) – бесконечно малая функция, то α(x)n тоже бесконечно малая.
Определение 1: Б.м. α(x) называется б.м. более высокого порядка малости чем β(x), если lim(α(x)/ β(x))=0 (при x→a, x→∞).
α(x)=0[β(x)] – математическая запись вышеперечисленного.
Определение 2: Б.м. α(x) называется одного порядка малости из функции β(x), если lim(α(x)/ β(x))=a (при x→k, x→∞), где а≠0 и а≠∞.
Определение 3: Б.м. α(x) и β(x) называется эквивалентным б.м. если lim(α(x)/ β(x))=1 (при x→k, x→а).
Определение 4: Если lim(α(x)/[ β(x)]n)=A≠∞≠0, то α(x) б.м. порядка n от β(x).
studfiles.net
Односторонние пределы
Пусть
Х – область определения функции,
которая, быть может, не содержит точку 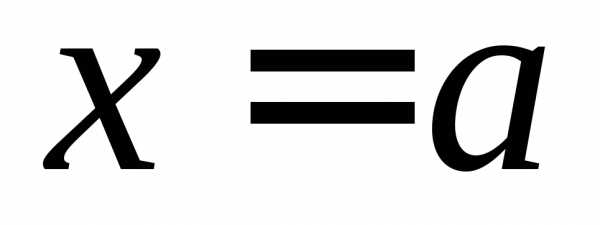 ,
но для любого
,
но для любого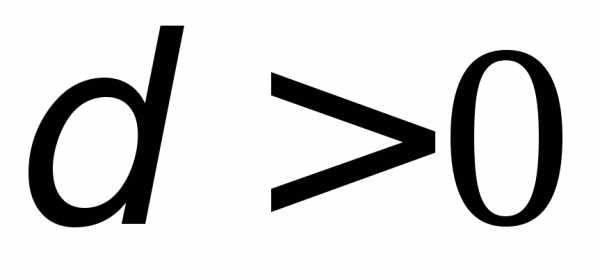 правая полуокрестность точки
правая полуокрестность точки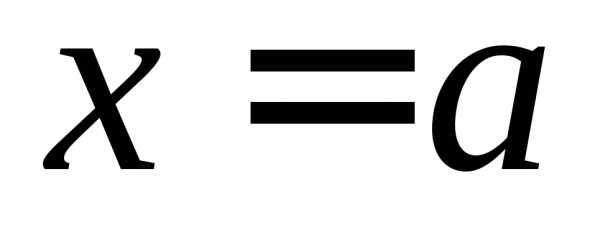 (интервал)
содержит точки множества Х.
(интервал)
содержит точки множества Х.
ОПРЕДЕЛЕНИЕ 7 (правый предел функции в точке 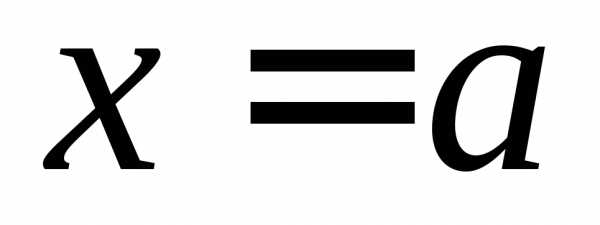 по Гейне). Число
по Гейне). Число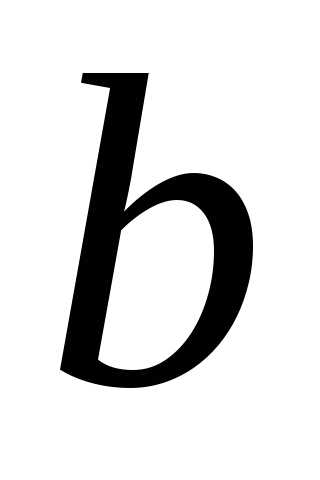 называется правым пределом функции
называется правым пределом функции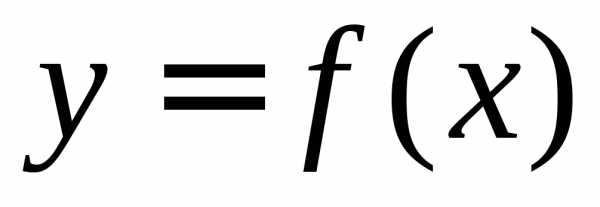 в точке
в точке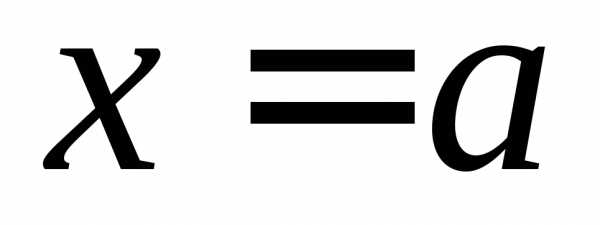 ,
если для любой последовательности
значений ее аргумента
,
если для любой последовательности
значений ее аргумента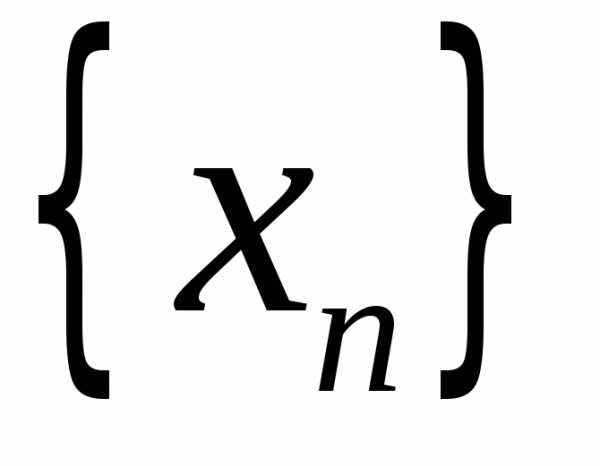 ,
сходящейся к
,
сходящейся к и состоящей их чисел, больших
и состоящей их чисел, больших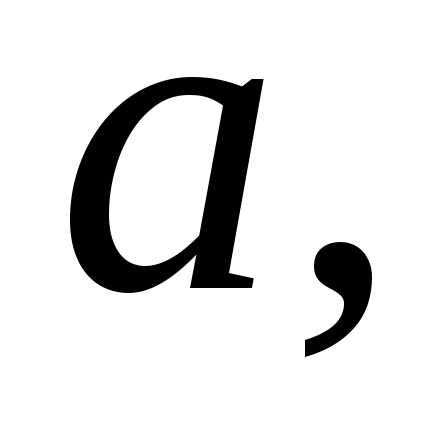 соответствующая последовательность
значений функций
соответствующая последовательность
значений функций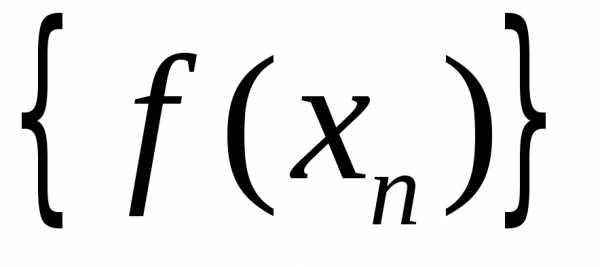 сходится к
сходится к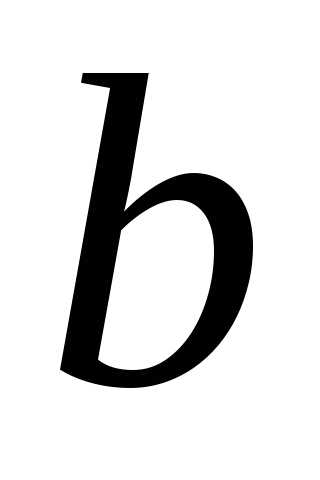 .
Обозначение:
.
Обозначение:
ОПРЕДЕЛЕНИЕ 8 (правый предел функции в точке 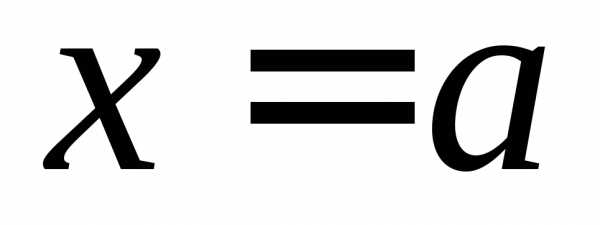 по Коши). Число
по Коши). Число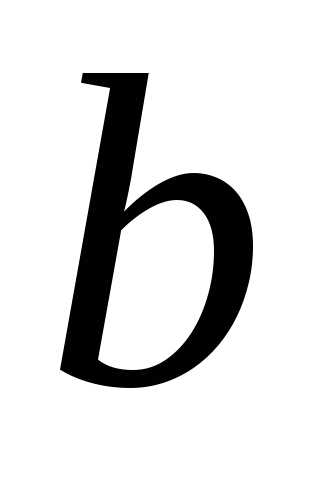 называется правым пределом функции
называется правым пределом функции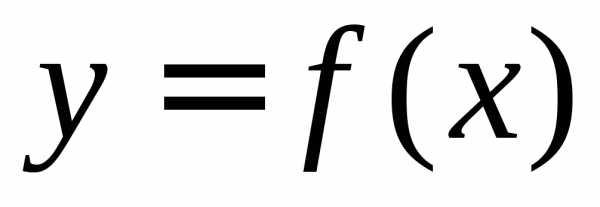 в
точке
в
точке ,
если,
,
если,
Для определения
левого предела будем считать, что любая
левая полуокрестность точки 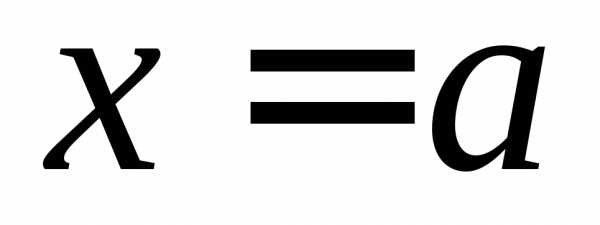 ,
интервал,
содержит точки Х.
,
интервал,
содержит точки Х.
ОПРЕДЕЛЕНИЕ 9 (левый предел функции в точке 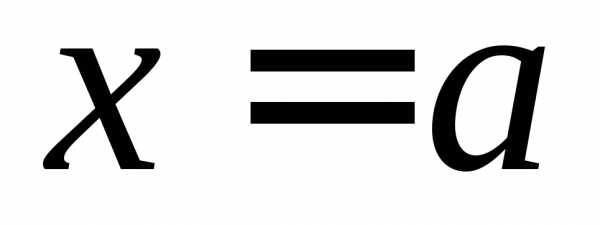 по Гейне). Число
по Гейне). Число называется левым пределом функции
называется левым пределом функции в точке
в точке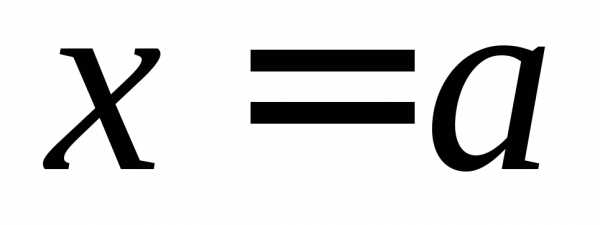 ,
если для любой последовательности
значений ее аргумента
,
если для любой последовательности
значений ее аргумента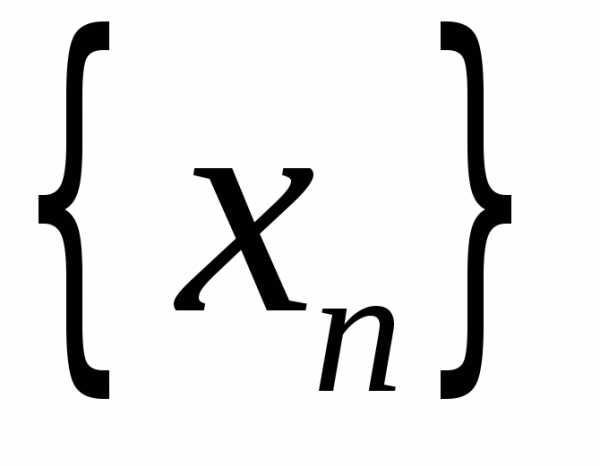 ,
сходящейся к
,
сходящейся к и состоящей их чисел, меньших
и состоящей их чисел, меньших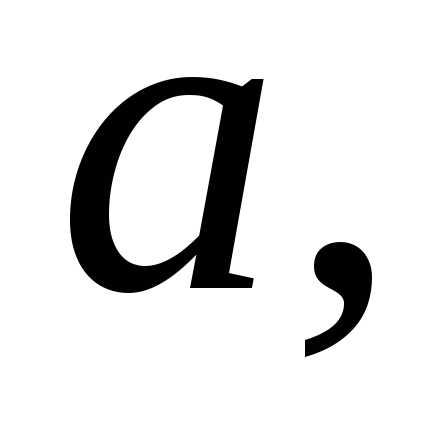 соответствующая последовательность
значений функций
соответствующая последовательность
значений функций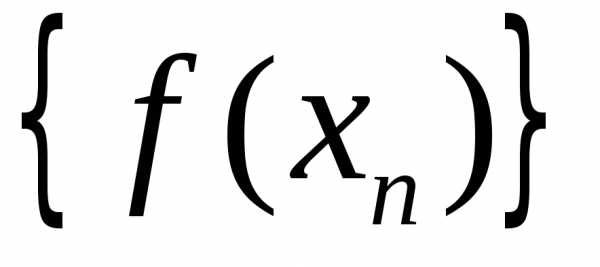 сходится к
сходится к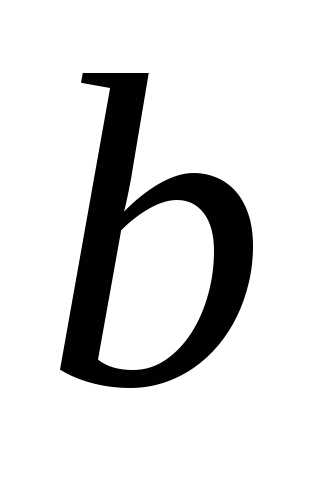 .
Обозначение:
.
Обозначение:
ОПРЕДЕЛЕНИЕ 10 (левый предел функции в точке 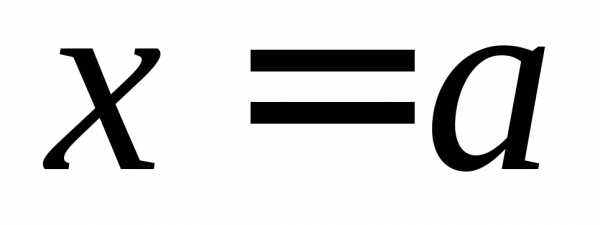 по Коши). Число
по Коши). Число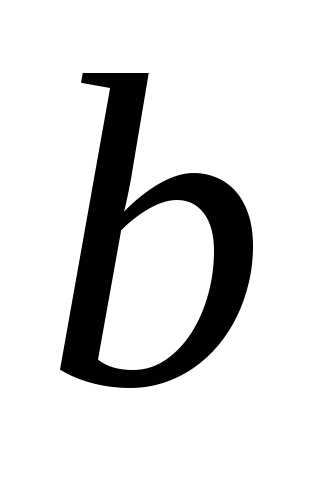 называется левым пределом функции
называется левым пределом функции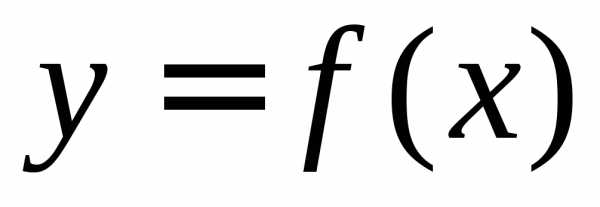 в
точке
в
точке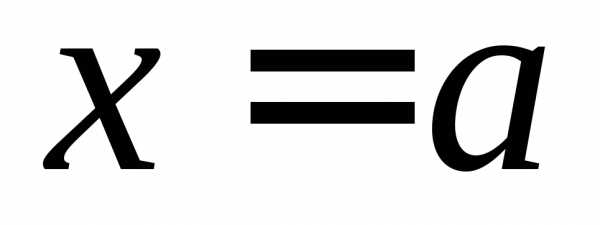 ,
если,
,
если,
ПРИМЕР. Найти односторонние пределы (правый и левый) функции
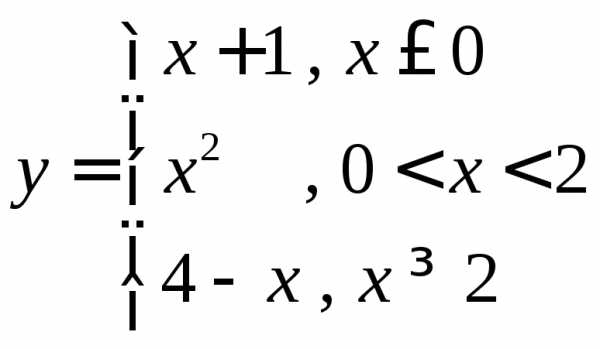
в точках 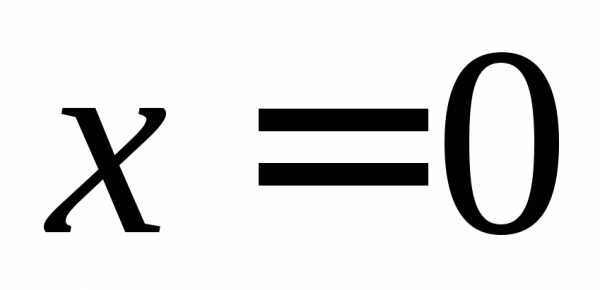 и
и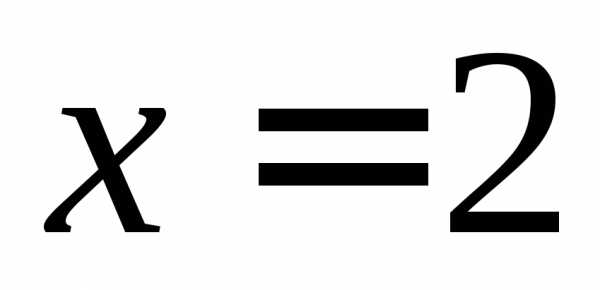 .
.
Так как справа от
0 и близко к нему 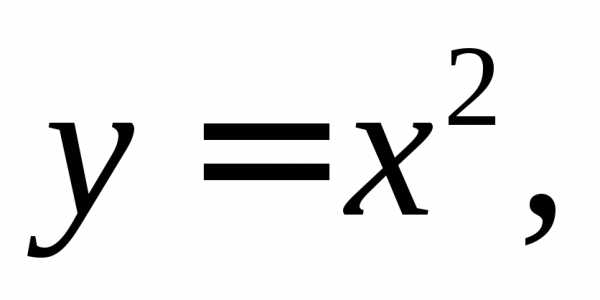 тоОчевидно,
тоОчевидно,
что хорошо видно на графике функции (рис. 5):
y 1 -1 О 2 4 x Рис. 5 |
Существуют
ли |
для того, чтобы функция имела в точке предел , необходимо и достаточно, чтобы в этой точке существовали равные односторонние пределы.
ПРИМЕР.
Найти односторонние пределы функции 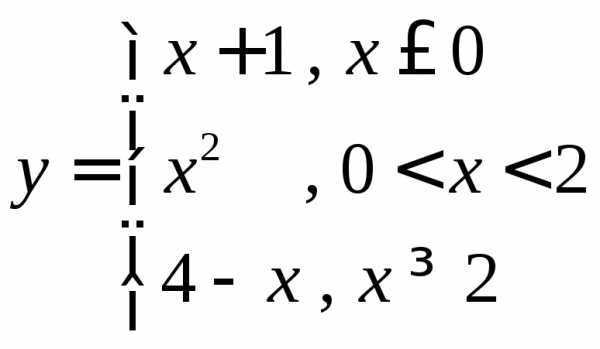 в точке
в точке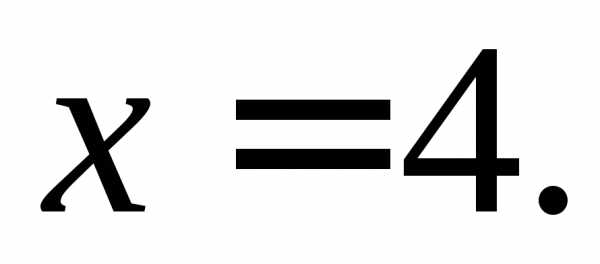
ПРИМЕР.
Найти односторонние пределы функции  в точке
в точке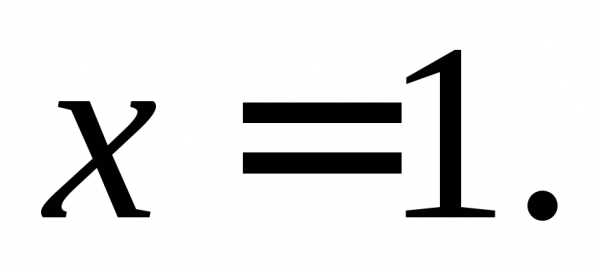
y 1 О 1 2 x Рис. 6 | Предел функции в этой точке существует, так как односторонние пределы равны (рис.6). |
Сравнение бесконечно малых
ОПРЕДЕЛЕНИЕ.
Функция 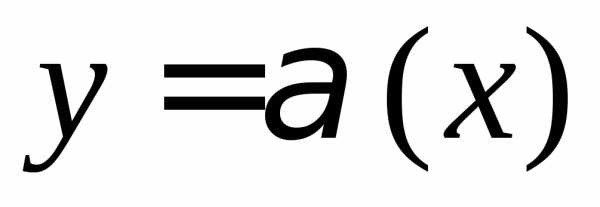 называетсябесконечно
малой (б.м.)
в точке
называетсябесконечно
малой (б.м.)
в точке 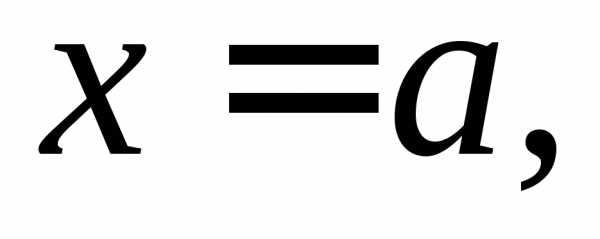 если
если
ПРИМЕРЫ. 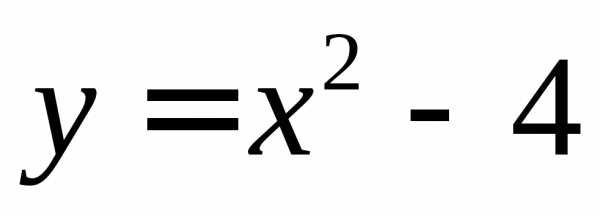 – б.м. в точках
– б.м. в точках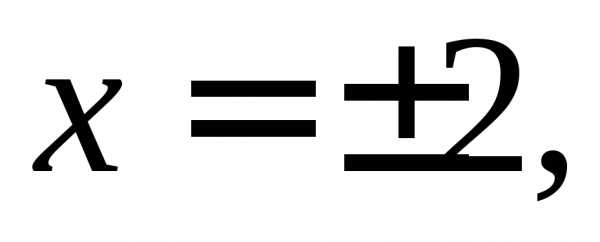
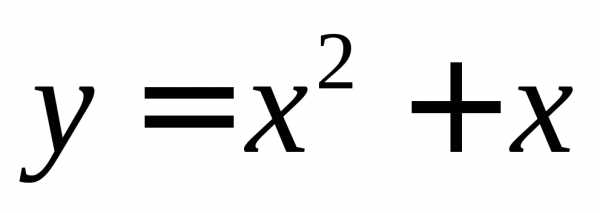 – б.м. в точках
– б.м. в точках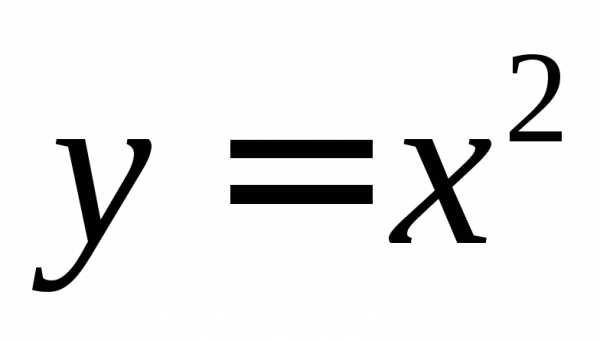 – б.м. в точке
– б.м. в точке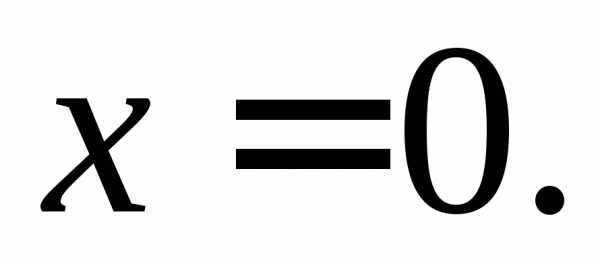
Пусть 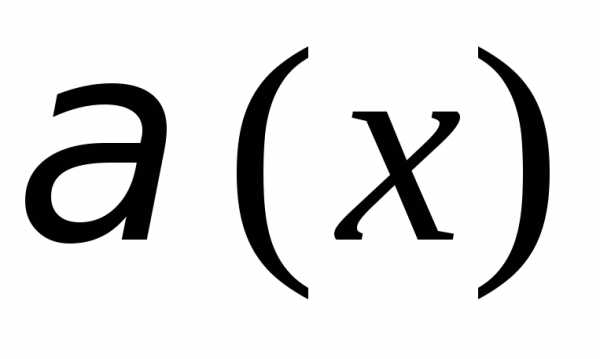 и
и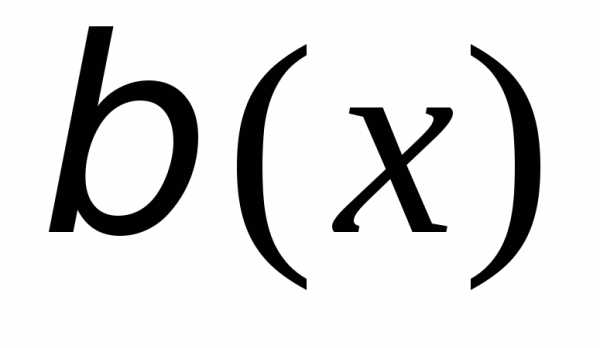 – б.м. в точке
– б.м. в точке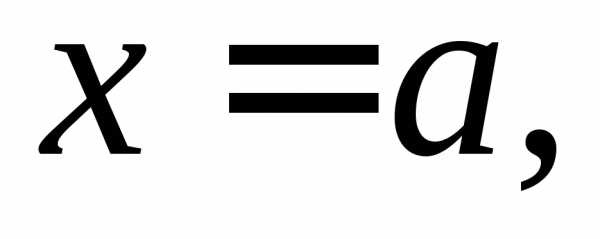 то естьПредел отношения б.м. функций
то естьПредел отношения б.м. функций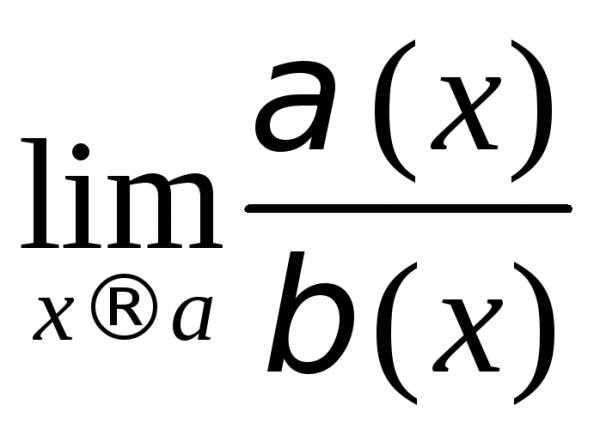 называетсянеопределенностью
вида
называетсянеопределенностью
вида 
ПРИМЕР.
– б.м. в точке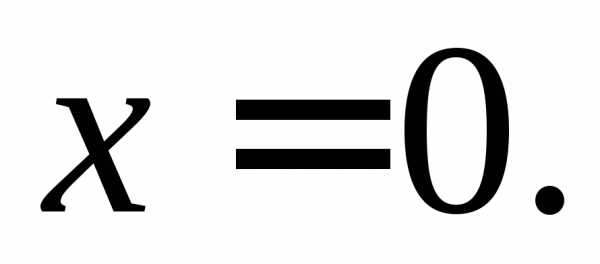

ОПРЕДЕЛЕНИЕ.
1) Б.м. в точке  функция
функция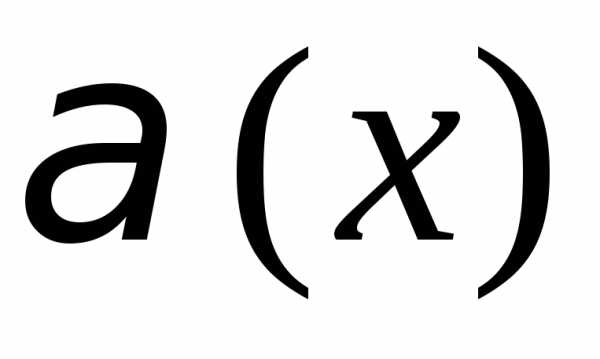 имеетболее
высокий порядок малости,
чем
имеетболее
высокий порядок малости,
чем 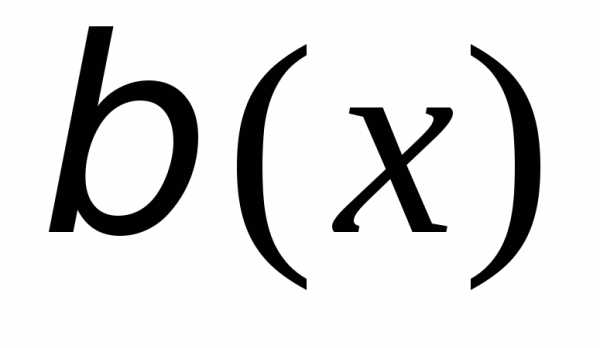 ,
если
,
если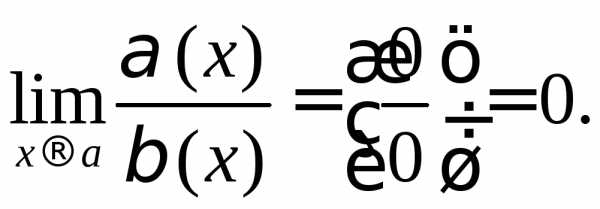
2) Б.м. в точке 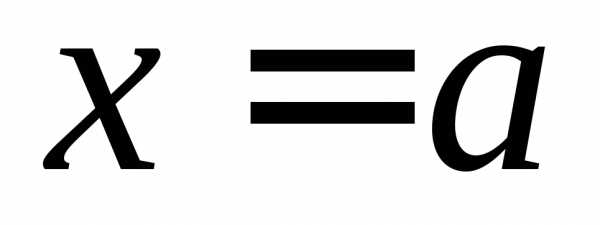 функции
функции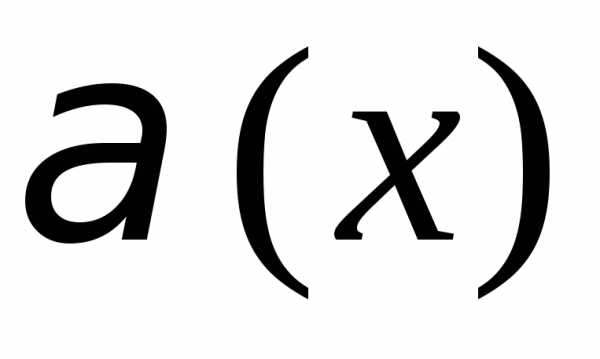 и
и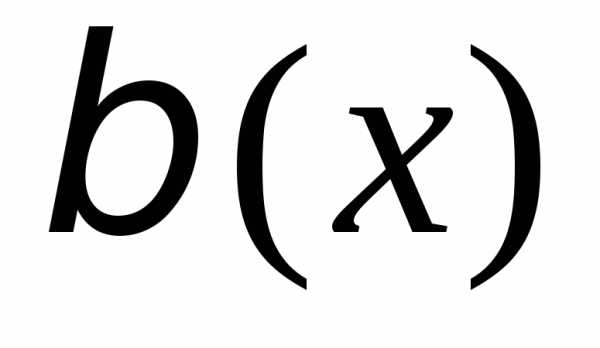 одного порядка
малости,
если
одного порядка
малости,
если
3) Б.м. в точке 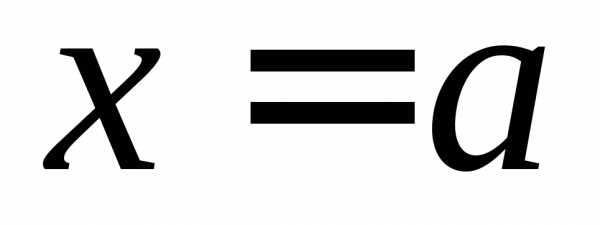 функции эквивалентны, если
функции эквивалентны, если
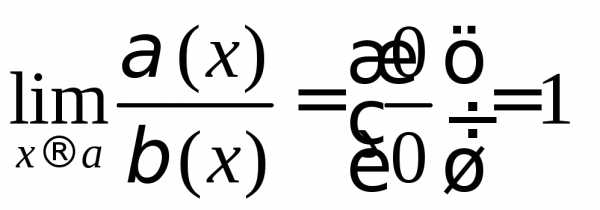 .
.
Эквивалентные б.м. обозначаются так:
ПРИМЕР. 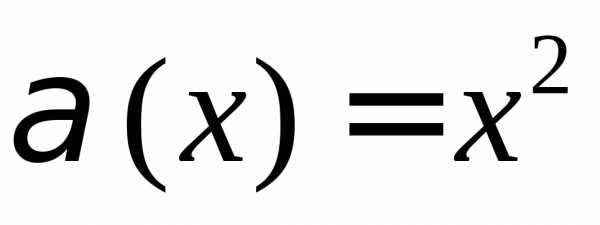 имеет более высокий порядок малости в
точке
имеет более высокий порядок малости в
точке ,
чем
,
чем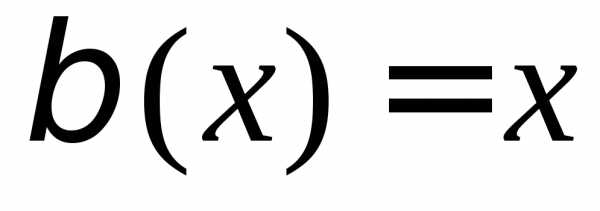 и
и
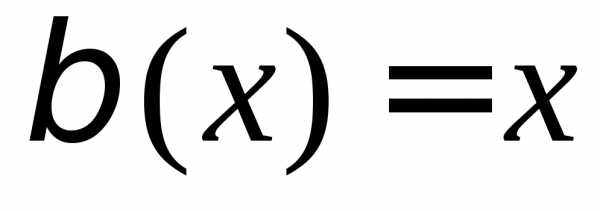 и
одного порядка малости.
и
одного порядка малости.
ПРИМЕР.
Сравнить функции 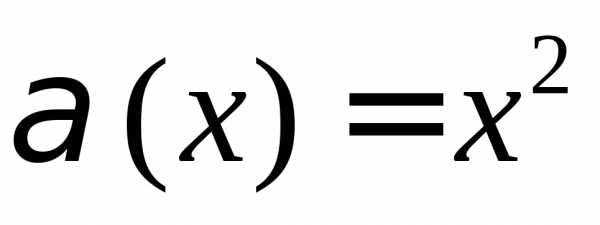 и,
б.м. в точке
и,
б.м. в точке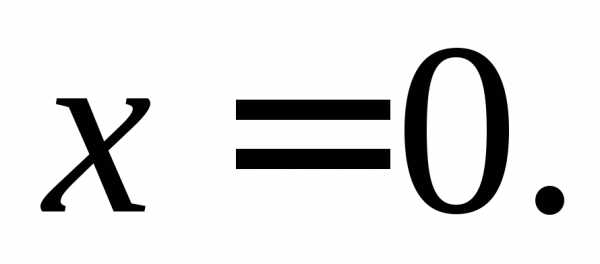
Вычислим предел отношения:
в точке 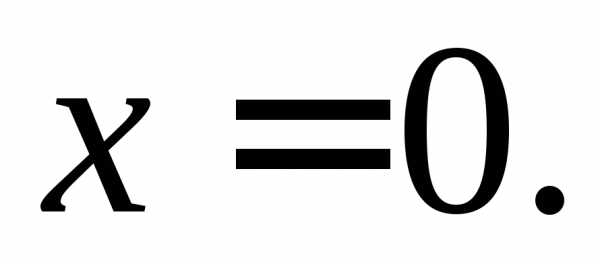
ТЕОРЕМА (принцип замены эквивалентных бесконечно
малых). Пусть
б.м.
функции в точке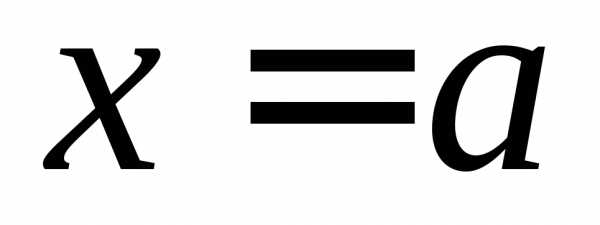 иТогда
иТогда
ДОКАЗАТЕЛЬСТВО. Так как то
Что и требовалось доказать.
studfiles.net
Предел функции в точке Односторонние пределы Предел функции
 Предел функции в точке Односторонние пределы Предел функции при x стремящемся к бесконечности Основные теоремы о пределах Вычисление пределов Первый замечательный предел Второй замечательный предел
Предел функции в точке Односторонние пределы Предел функции при x стремящемся к бесконечности Основные теоремы о пределах Вычисление пределов Первый замечательный предел Второй замечательный предел
 Предел функции в точке Пусть функция y = f(x) определена в некоторой окрестности точки x 0, кроме, быть может самой точки x 0. Число А называют пределом функции в точке x 0 (или при ), если для любого положительного ε найдется такое положительное число δ, что для всех х из δ – окрестности точки x 0 справедливо неравенство:
Предел функции в точке Пусть функция y = f(x) определена в некоторой окрестности точки x 0, кроме, быть может самой точки x 0. Число А называют пределом функции в точке x 0 (или при ), если для любого положительного ε найдется такое положительное число δ, что для всех х из δ – окрестности точки x 0 справедливо неравенство:
 Предел функции в точке ε окрестность точки А y А 0 х0 х δ окрестность точки x 0 Геометрический смысл предела: для всех х из δ – окрестности точки x 0 точки графика функции лежат внутри полосы, шириной 2ε, ограниченной прямыми: у = А + ε , у = А – ε.
Предел функции в точке ε окрестность точки А y А 0 х0 х δ окрестность точки x 0 Геометрический смысл предела: для всех х из δ – окрестности точки x 0 точки графика функции лежат внутри полосы, шириной 2ε, ограниченной прямыми: у = А + ε , у = А – ε.
 Односторонние пределы Пример, когда есть предел слева и когда есть предел справа. В определении предела функции предполагается, что x стремится к x 0 любым способом: оставаясь меньше, чем x 0 (слева от x 0), большим, чем x 0 (справа от x 0), или колеблясь около точки x 0. Бывают случаи, когда способ приближения аргумента x к x 0 существенно влияет на значение предела, поэтому вводят понятия односторонних пределов. Число А 1 называют пределом функции слева в точке x 0, если для любого ε > 0 найдется такое δ >0, что для всех справедливо неравенство: Предел слева записывают так:
Односторонние пределы Пример, когда есть предел слева и когда есть предел справа. В определении предела функции предполагается, что x стремится к x 0 любым способом: оставаясь меньше, чем x 0 (слева от x 0), большим, чем x 0 (справа от x 0), или колеблясь около точки x 0. Бывают случаи, когда способ приближения аргумента x к x 0 существенно влияет на значение предела, поэтому вводят понятия односторонних пределов. Число А 1 называют пределом функции слева в точке x 0, если для любого ε > 0 найдется такое δ >0, что для всех справедливо неравенство: Предел слева записывают так:
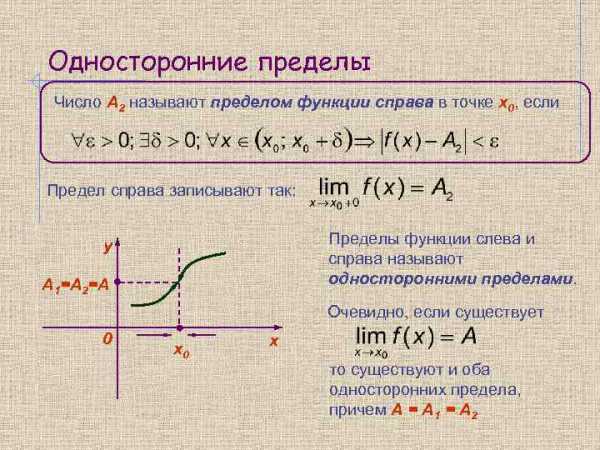 Односторонние пределы Число А 2 называют пределом функции справа в точке x 0, если Предел справа записывают так: Пределы функции слева и справа называют односторонними пределами. y А 2 А 1=А 2=А А 1 0 Очевидно, если существует х0 х то существуют и оба односторонних предела, причем А = А 1 = А 2
Односторонние пределы Число А 2 называют пределом функции справа в точке x 0, если Предел справа записывают так: Пределы функции слева и справа называют односторонними пределами. y А 2 А 1=А 2=А А 1 0 Очевидно, если существует х0 х то существуют и оба односторонних предела, причем А = А 1 = А 2
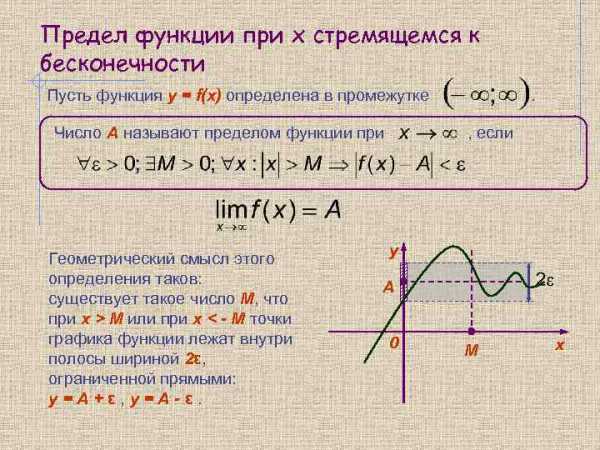 Предел функции при x стремящемся к бесконечности Пусть функция y = f(x) определена в промежутке Число А называют пределом функции при Геометрический смысл этого определения таков: существует такое число М, что при х > M или при x
Предел функции при x стремящемся к бесконечности Пусть функция y = f(x) определена в промежутке Число А называют пределом функции при Геометрический смысл этого определения таков: существует такое число М, что при х > M или при x
 Основные теоремы о пределах Рассмотрим теоремы, которые облегчают нахождение пределов функций. Формулировка теорем, когда или аналогичны, поэтому будем пользоваться обозначением: . Предел суммы (разности) двух функций равен сумме (разности) пределов: Предел произведения двух функций равен произведению пределов: Постоянный множитель можно выносить за знак предела:
Основные теоремы о пределах Рассмотрим теоремы, которые облегчают нахождение пределов функций. Формулировка теорем, когда или аналогичны, поэтому будем пользоваться обозначением: . Предел суммы (разности) двух функций равен сумме (разности) пределов: Предел произведения двух функций равен произведению пределов: Постоянный множитель можно выносить за знак предела:
 Основные теоремы о пределах Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю: Предел степени с натуральным показателем равен той же степени предела: Предел показательно – степенной функции:
Основные теоремы о пределах Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю: Предел степени с натуральным показателем равен той же степени предела: Предел показательно – степенной функции:
 Основные теоремы о пределах Если между соответствующими значениями трех функций выполняются неравенства: при этом: тогда: Если функция f(x) монотонна и ограничена при x x 0, то существует соответственно ее левый предел: или ее правый предел:
Основные теоремы о пределах Если между соответствующими значениями трех функций выполняются неравенства: при этом: тогда: Если функция f(x) монотонна и ограничена при x x 0, то существует соответственно ее левый предел: или ее правый предел:
 Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x 0 в функцию f(x). Если при этом получается конечное число, то предел равен этому числу. Если при подстановки предельного значения x 0 в функцию f(x) получаются выражения вида: то предел будет равен:
Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x 0 в функцию f(x). Если при этом получается конечное число, то предел равен этому числу. Если при подстановки предельного значения x 0 в функцию f(x) получаются выражения вида: то предел будет равен:
 Вычисление пределов Часто при подстановке предельного значения x 0 в функцию f(x) получаются выражения следующих видов: Эти выражения называются неопределенности, а вычисление пределов в этом случае называется раскрытие неопределенности.
Вычисление пределов Часто при подстановке предельного значения x 0 в функцию f(x) получаются выражения следующих видов: Эти выражения называются неопределенности, а вычисление пределов в этом случае называется раскрытие неопределенности.
 Первый замечательный предел Функция не определена при x = 0. Найдем предел этой функции при М С x О В А Обозначим: S 1 – площадь треугольника OMA, S 2 – площадь сектора OMА, S 3 – площадь треугольника OСА, Из рисунка видно, что S 1
Первый замечательный предел Функция не определена при x = 0. Найдем предел этой функции при М С x О В А Обозначим: S 1 – площадь треугольника OMA, S 2 – площадь сектора OMА, S 3 – площадь треугольника OСА, Из рисунка видно, что S 1
 Первый замечательный предел М С x О В А
Первый замечательный предел М С x О В А
 Первый замечательный предел Формула справедлива также при x
Первый замечательный предел Формула справедлива также при x
 Первый замечательный предел
Первый замечательный предел
 Рассмотрим последовательность числовую где a 1=2, a 2=2. 25, a 3=2. 37 … Можно предположить, последовательность возрастающей. что эта будет
Рассмотрим последовательность числовую где a 1=2, a 2=2. 25, a 3=2. 37 … Можно предположить, последовательность возрастающей. что эта будет
 Воспользуемся формулой где m – любое действительное число. В нашем случае:
Воспользуемся формулой где m – любое действительное число. В нашем случае:
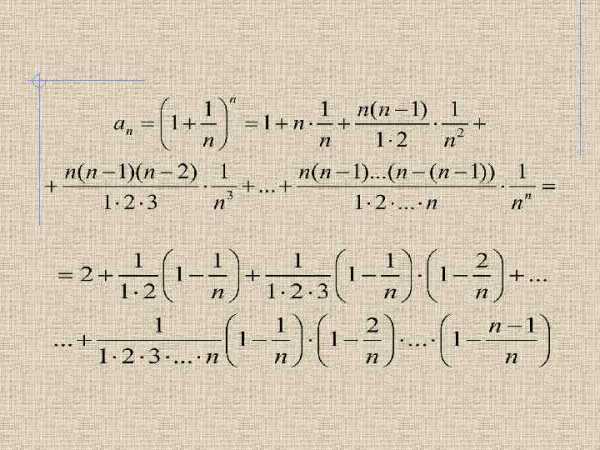
 Видно, что с ростом n увеличивается число положительных слагаемых, которых всего будет n+1, и растет величина каждого слагаемого, т. е. Это значит, что данная последовательность возрастает. Теперь покажем, ограниченной. что она является Поскольку каждая скобка меньше единицы, отбрасываем эти скобки и получаем неравенство:
Видно, что с ростом n увеличивается число положительных слагаемых, которых всего будет n+1, и растет величина каждого слагаемого, т. е. Это значит, что данная последовательность возрастает. Теперь покажем, ограниченной. что она является Поскольку каждая скобка меньше единицы, отбрасываем эти скобки и получаем неравенство:
 Теперь каждую дробь в правой части заменяем большей дробью с двойкой в знаменателе: Получаем:
Теперь каждую дробь в правой части заменяем большей дробью с двойкой в знаменателе: Получаем:
 Сумма есть сумма n-1 членов геометрической прогрессии, где первый член и знаменател ь По формуле суммы членов геометрической прогрессии имеем:
Сумма есть сумма n-1 членов геометрической прогрессии, где первый член и знаменател ь По формуле суммы членов геометрической прогрессии имеем:
 Т. к. Sn-1
Т. к. Sn-1
 Согласно признаку существования предела, монотонная и ограниченная последовательность имеет предел. Числом е или вторым замечательным пределом называется предел числовой последовательности
Согласно признаку существования предела, монотонная и ограниченная последовательность имеет предел. Числом е или вторым замечательным пределом называется предел числовой последовательности
 е – число Эйлера е=2, 718281… Можно показать, что функция при где х пробегает все значения, а не только целые, тоже имеет предел, равный е:
е – число Эйлера е=2, 718281… Можно показать, что функция при где х пробегает все значения, а не только целые, тоже имеет предел, равный е:

 Пусть , тог да
Пусть , тог да
 1 Вычислить
1 Вычислить

 2 Вычислить
2 Вычислить

present5.com
Односторонние пределы
Пусть
Х – область определения функции,
которая, быть может, не содержит точку  ,
но для любого
,
но для любого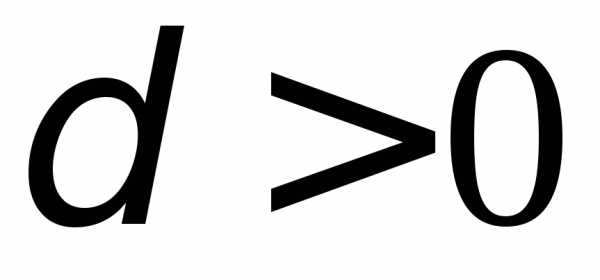 правая полуокрестность точки
правая полуокрестность точки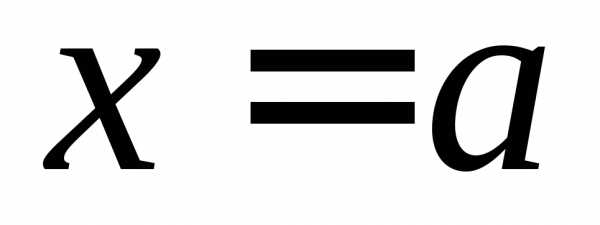 (интервал)
содержит точки множества Х.
(интервал)
содержит точки множества Х.
ОПРЕДЕЛЕНИЕ 7 (правый предел функции в точке  по Гейне). Число
по Гейне). Число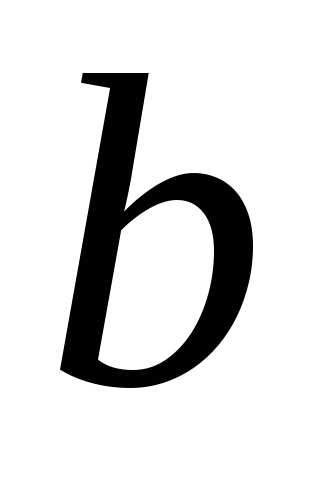 называется правым пределом функции
называется правым пределом функции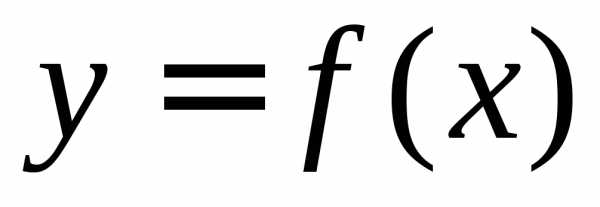 в точке
в точке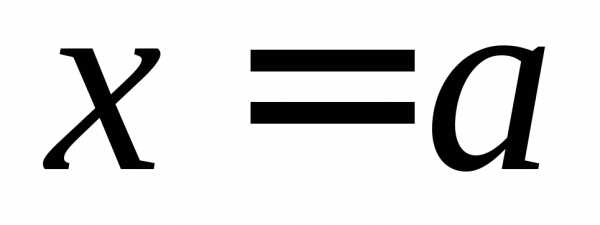 ,
если для любой последовательности
значений ее аргумента
,
если для любой последовательности
значений ее аргумента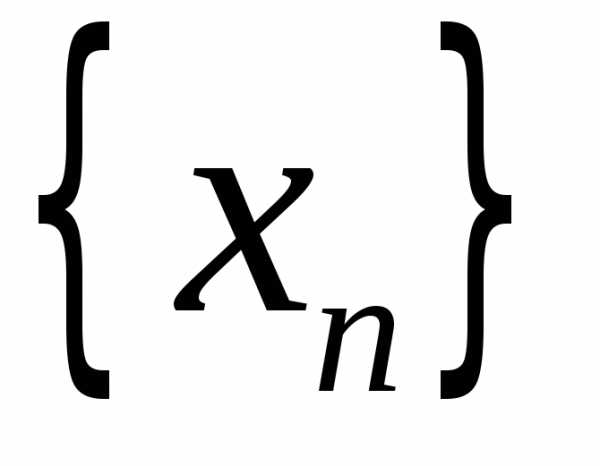 ,
сходящейся к
,
сходящейся к и состоящей их чисел, больших
и состоящей их чисел, больших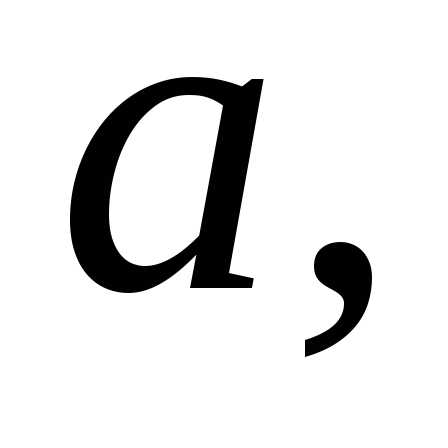 соответствующая последовательность
значений функций
соответствующая последовательность
значений функций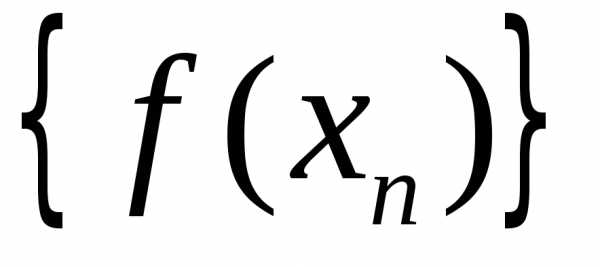 сходится к
сходится к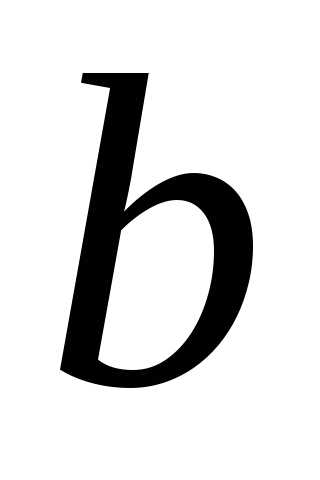 .
Обозначение:
.
Обозначение:
ОПРЕДЕЛЕНИЕ 8 (правый предел функции в точке 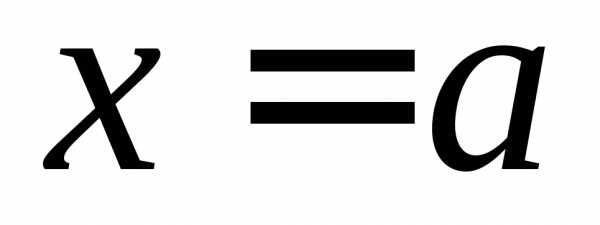 по Коши). Число
по Коши). Число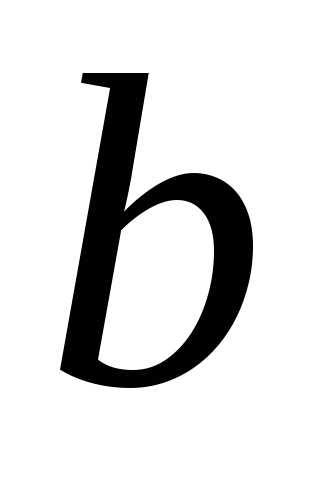 называется правым пределом функциив
точке
называется правым пределом функциив
точке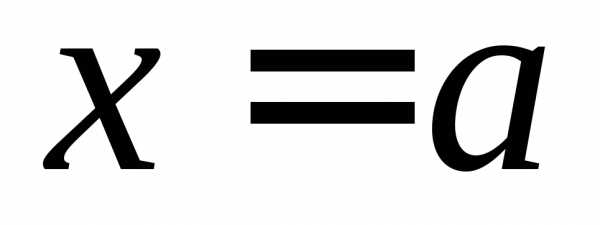 ,
если,
,
если,
Для определения
левого предела будем считать, что любая
левая полуокрестность точки 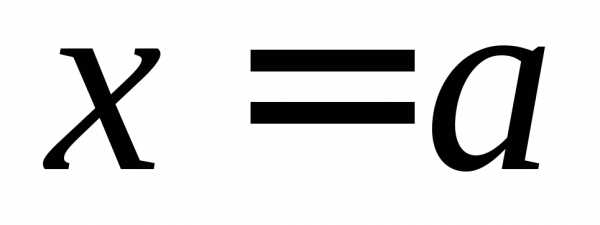 ,
интервал,
содержит точки Х.
,
интервал,
содержит точки Х.
ОПРЕДЕЛЕНИЕ 9 (левый предел функции в точке 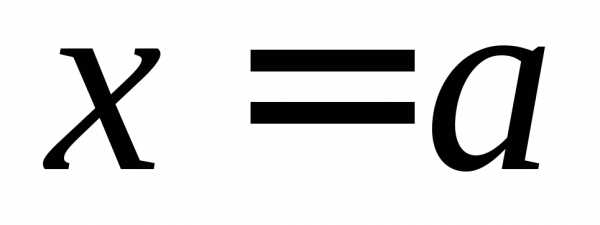 по Гейне). Число
по Гейне). Число называется левым пределом функции
называется левым пределом функции в точке
в точке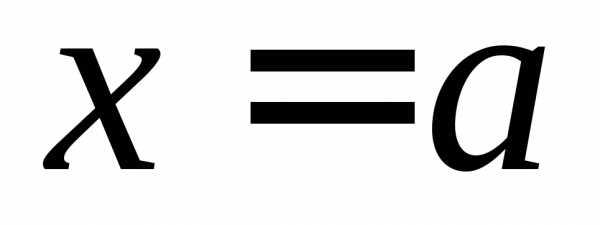 ,
если для любой последовательности
значений ее аргумента
,
если для любой последовательности
значений ее аргумента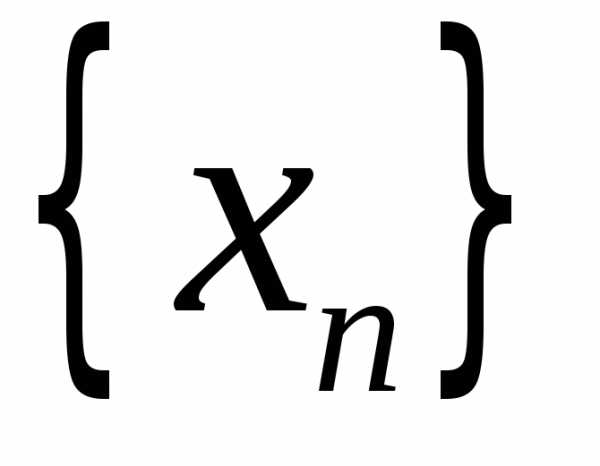 ,
сходящейся к
,
сходящейся к и состоящей их чисел, меньших
и состоящей их чисел, меньших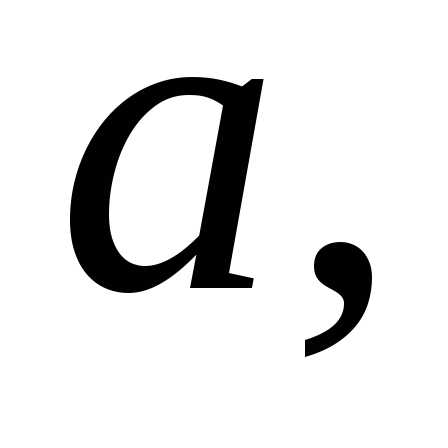 соответствующая последовательность
значений функций
соответствующая последовательность
значений функций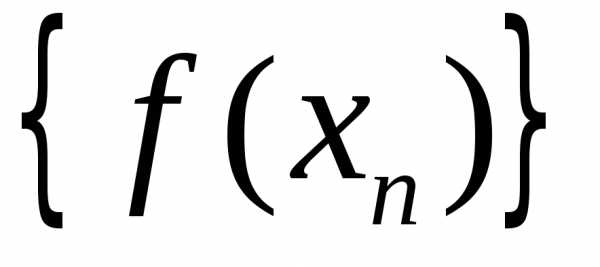 сходится к
сходится к .
Обозначение:
.
Обозначение:
ОПРЕДЕЛЕНИЕ 10 (левый предел функции в точке 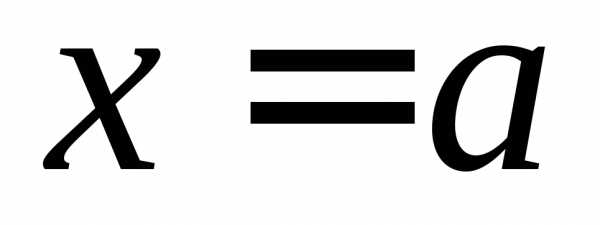 по Коши). Число
по Коши). Число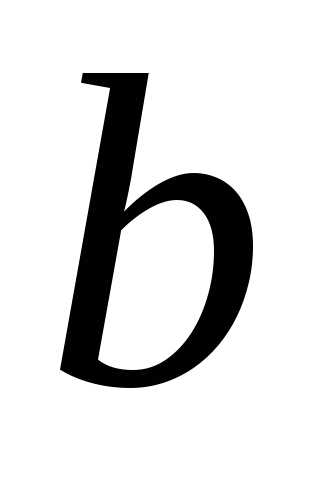 называется левым пределом функции
называется левым пределом функции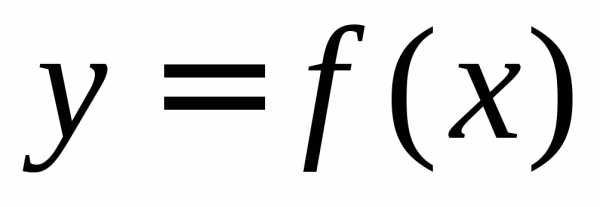 в
точке
в
точке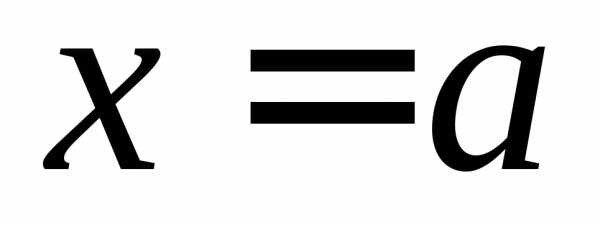 ,
если,
,
если,
ПРИМЕР. Найти односторонние пределы (правый и левый) функции
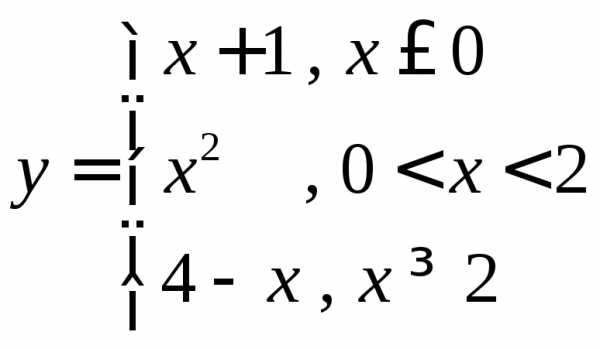
в точках 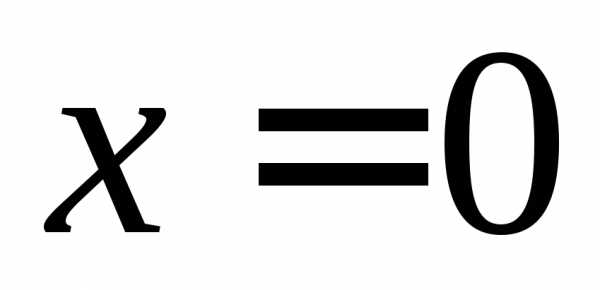 и
и .
.
Так как справа от
0 и близко к нему 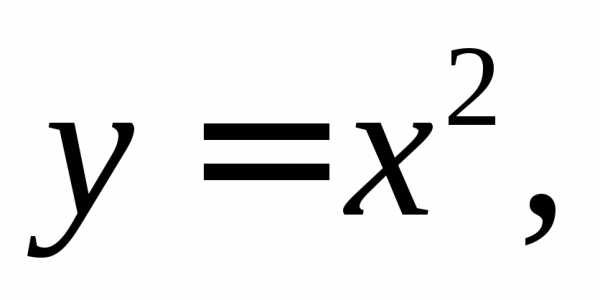 тоОчевидно,
тоОчевидно,
что хорошо видно на графике функции (рис. 5):
y 1 -1 О 2 4 x Рис. 5 |
Существуют
ли |
для того, чтобы функция имела в точке предел , необходимо и достаточно, чтобы в этой точке существовали равные односторонние пределы.
ПРИМЕР.
Найти односторонние пределы функции 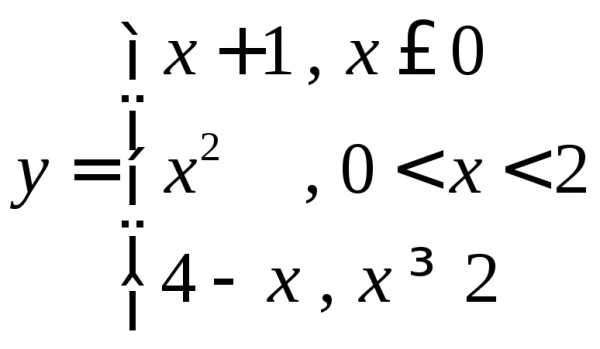 в точке
в точке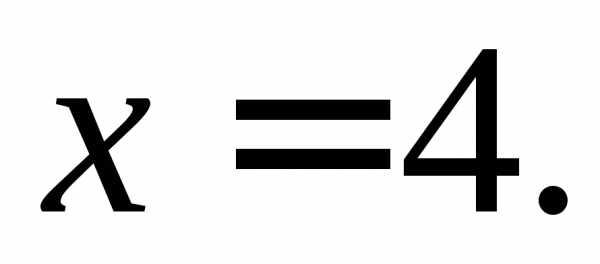
ПРИМЕР.
Найти односторонние пределы функции 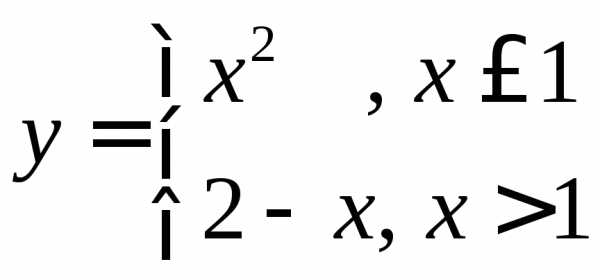 в точке
в точке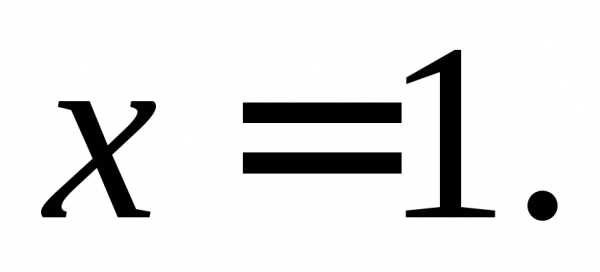
y 1 О 1 2 x Рис. 6 | Предел функции в этой точке существует, так как односторонние пределы равны (рис.6). |
Сравнение бесконечно малых
ОПРЕДЕЛЕНИЕ.
Функция 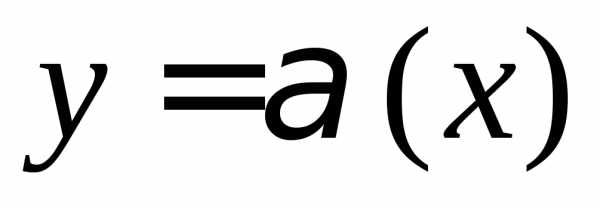 называетсябесконечно
малой (б.м.)
в точке
называетсябесконечно
малой (б.м.)
в точке 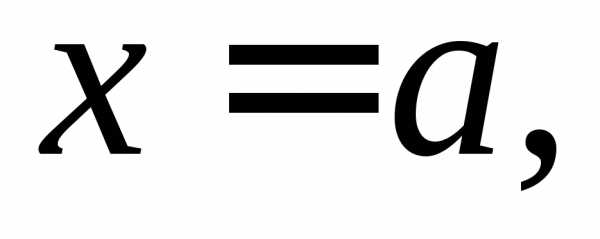 если
если
ПРИМЕРЫ. 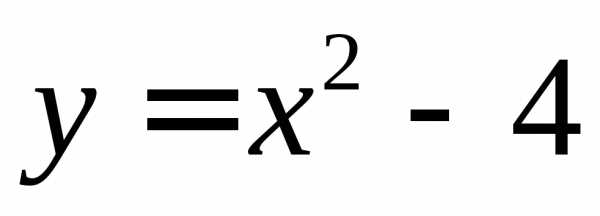 – б.м. в точках
– б.м. в точках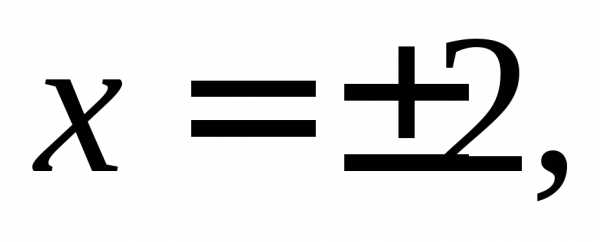
 – б.м. в точках
– б.м. в точках – б.м. в точке
– б.м. в точке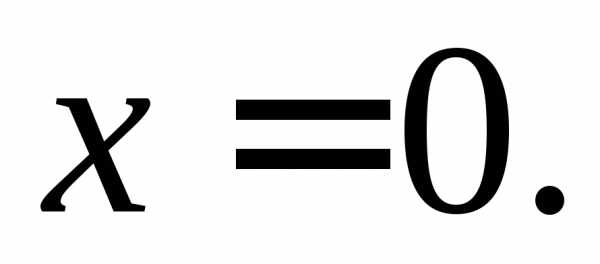
Пусть 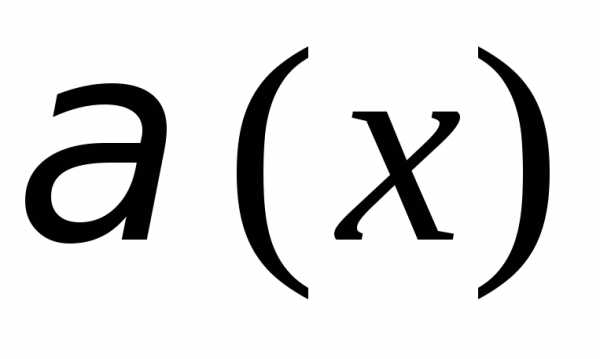 и
и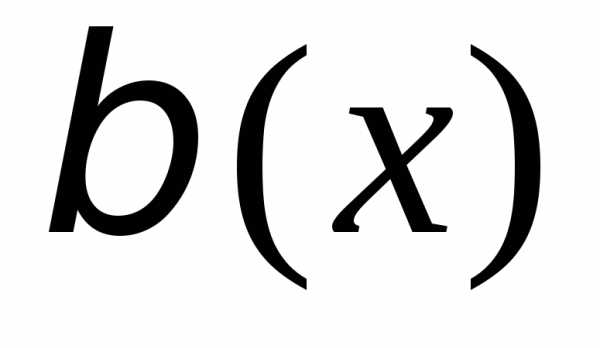 – б.м. в точке
– б.м. в точке то естьПредел отношения б.м. функций
то естьПредел отношения б.м. функций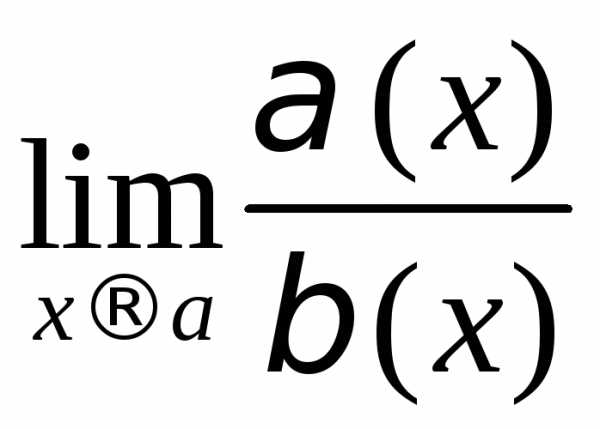 называетсянеопределенностью
вида
называетсянеопределенностью
вида 
ПРИМЕР.
– б.м. в точке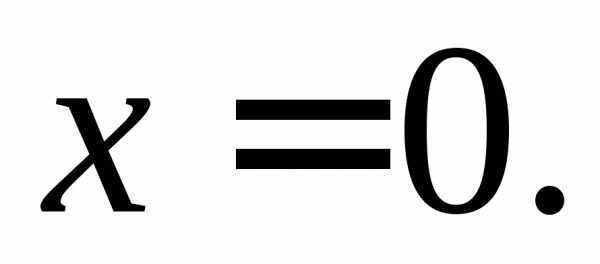
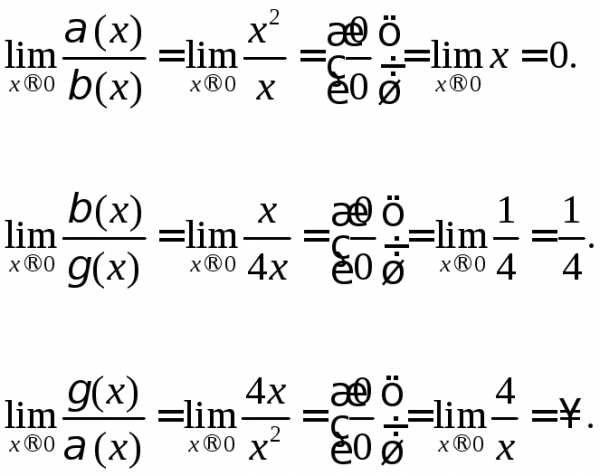
ОПРЕДЕЛЕНИЕ.
1) Б.м. в точке 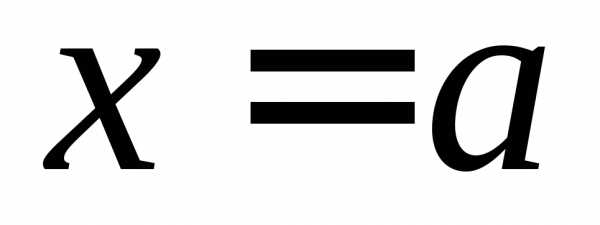 функция
функция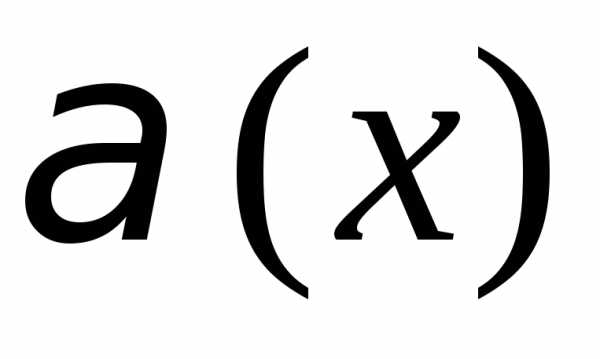 имеетболее
высокий порядок малости,
чем
имеетболее
высокий порядок малости,
чем 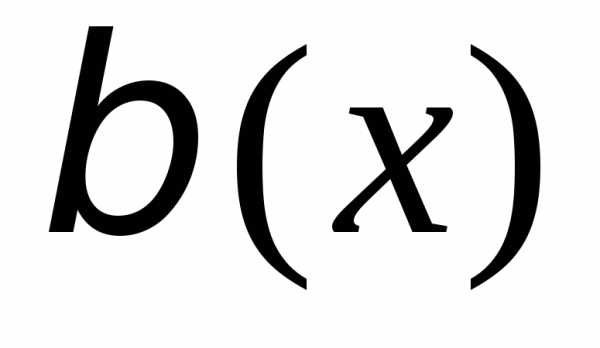 ,
если
,
если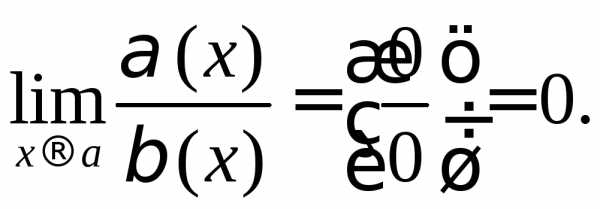
2) Б.м. в точке  функции
функции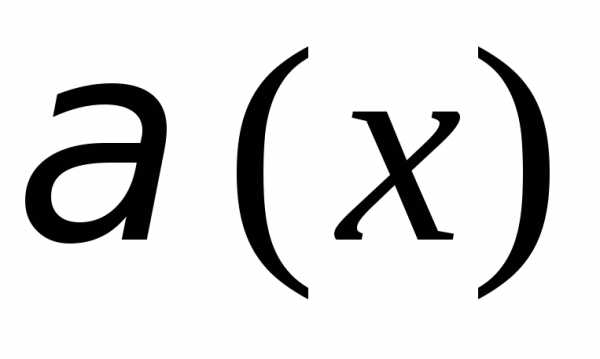 и
и одного порядка
малости,
если
одного порядка
малости,
если
3) Б.м. в точке 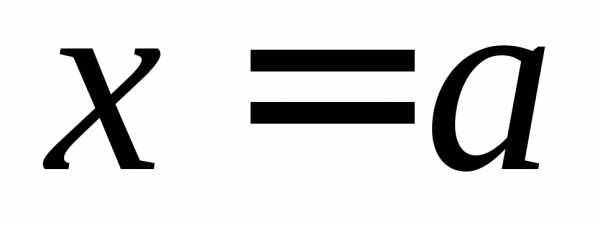 функции эквивалентны, если
функции эквивалентны, если
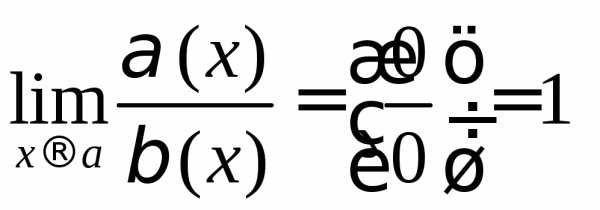 .
.
Эквивалентные б.м. обозначаются так:
ПРИМЕР. 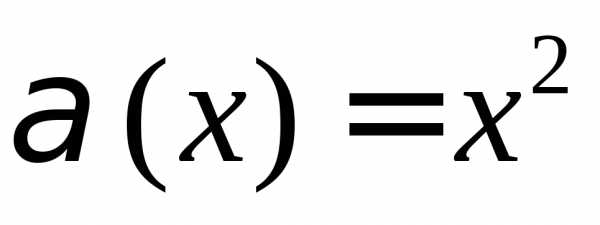 имеет более высокий порядок малости в
точке
имеет более высокий порядок малости в
точке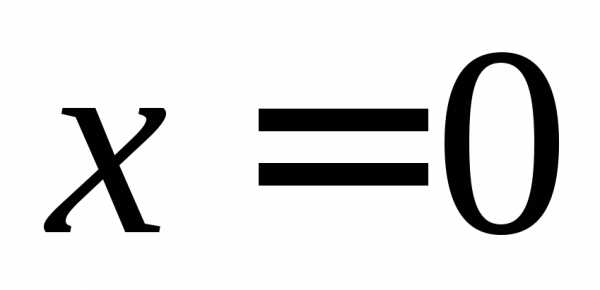 ,
чем
,
чем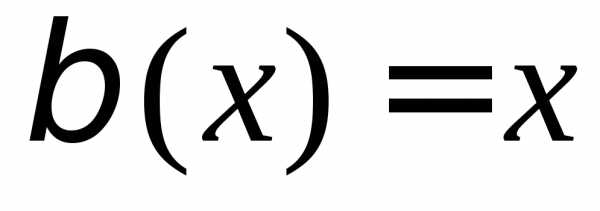 и
и
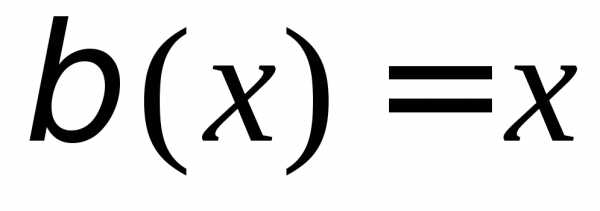 и
одного порядка малости.
и
одного порядка малости.
ПРИМЕР.
Сравнить функции 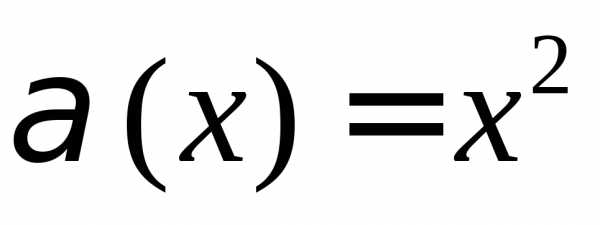 и,
б.м. в точке
и,
б.м. в точке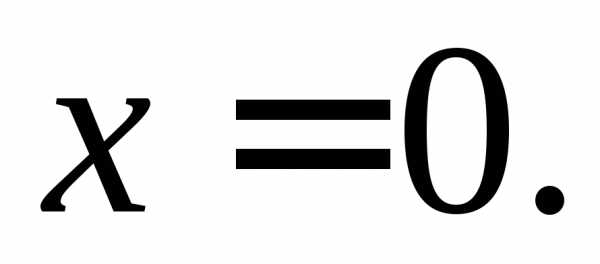
Вычислим предел отношения:
в точке 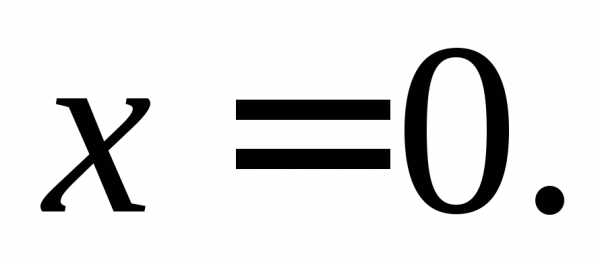
ТЕОРЕМА (принцип замены эквивалентных бесконечно
малых). Пусть
б.м.
функции в точке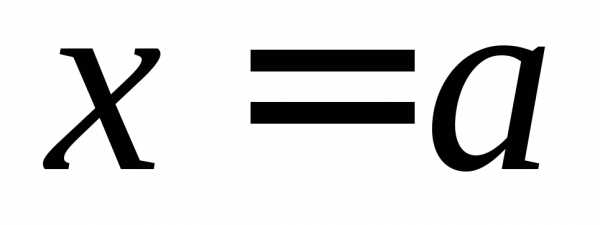 иТогда
иТогда
ДОКАЗАТЕЛЬСТВО. Так как то
Что и требовалось доказать.
studfiles.net
односторонние пределы — ПриМат
Перед тем как рассматривать теорему, давайте вспомним, что такое монотонная функция и нарисуем её график.
Функция называется монотонно возрастающей на отрезке , если
Функция называется монотонно убывающей на отрезке , если
Функция называется строго монотонно убывающей на отрезке , если
Функция называется строго монотонно возрастающей на отрезке , если
Пример графика монотонно возрастающей функции.
На графике видно, что , соответствующие значения функции
Пример графика монотонно убывающей функции.
На графике видно, что , соответствующие значения функции
Формулировка:
Если функция определена и монотонна на отрезке , то в каждой точке эта функция имеет конечные пределы слева и справа, а в точках и правосторонний и левосторонний пределы.
Доказательство:
Пусть, например, функция монотонно возрастает на . Выберем произвольную внутреннюю точку . Тогда ограничена сверху на .
Согласно определению:
а)
б) обозначим .
Если , то .
Итог:
Итак , .
Аналогично доказываем, что функция имеет в точке предел справа причем , .
Следствие. Если функция определена и монотонна на интервале , предел справа и слева, причем если возрастает, то
,
если убывает, то
.
Лимит времени: 0
Информация
Тест по теме Пределы монотонных функций.
Желаем удачи!
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 2
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Математический анализ 0%
Спасибо Вам за прохождение данного теста, надеюсь вы узнали для себя что-нибудь новое!
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Таблица лучших: Предел монотонной функции
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Поделиться ссылкой:
ib.mazurok.com

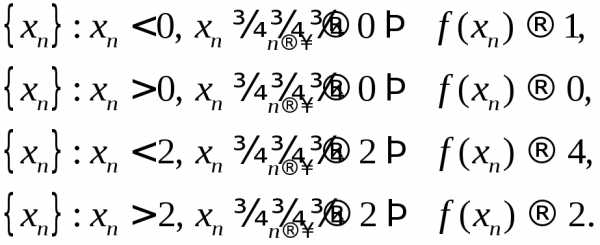
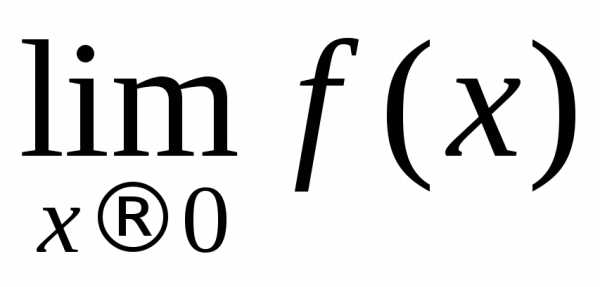 и
и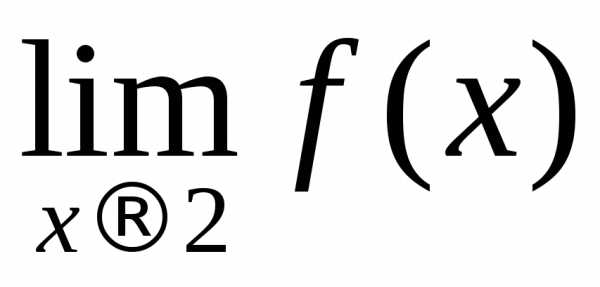 ? Не существуют, так как левый предел
не равен правому пределу в этих точках.
Имеет место утверждение:
? Не существуют, так как левый предел
не равен правому пределу в этих точках.
Имеет место утверждение: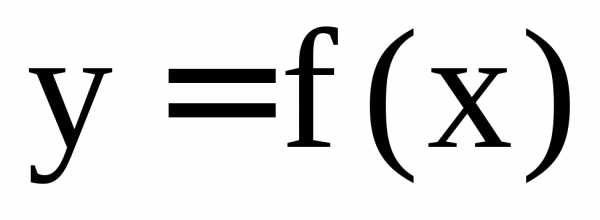
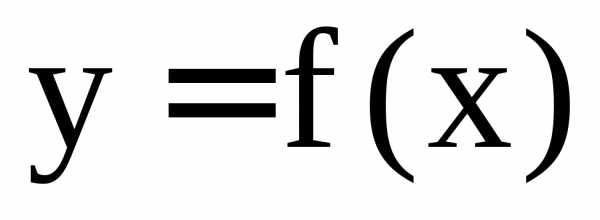
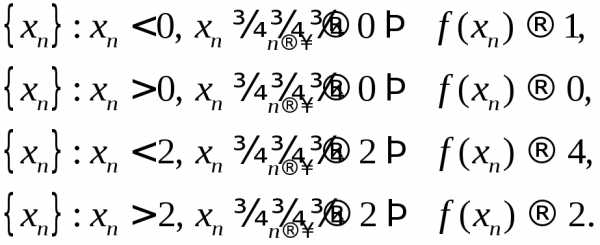
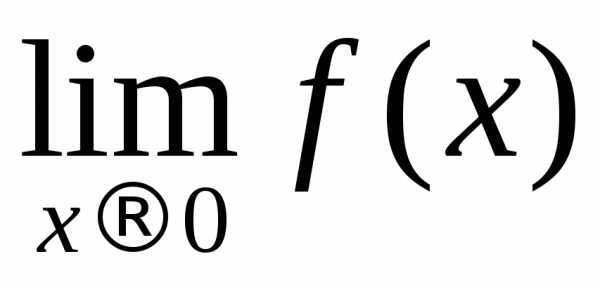 и
и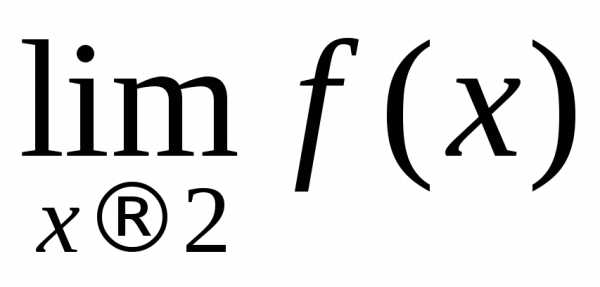 ? Не существуют, так как левый предел
не равен правому пределу в этих точках.
Имеет место утверждение:
? Не существуют, так как левый предел
не равен правому пределу в этих точках.
Имеет место утверждение: