08.01.202027.12.2018

Определение метод гаусса – Метод Гаусса — Википедия

• by alexxlab
• Комментариев к записи Определение метод гаусса – Метод Гаусса — Википедия нет
• Советы абитуриенту

Описание метода Гаусса

Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что с помощью элементарных преобразований исходная система приводится к равносильной ей системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних (по номеру), неизвестных находятся все остальные неизвестные. Дана система (1)

(1)

Начинаем осуществлять прямой ход. Считаем, что коэффициент а₁₁ ≠ 0; если же это не так, меняем местами уравнения.

Первый шаг состоит в том, чтобы исключить неизвестное х₁ из всех уравнений, кроме первого. Для этого ко второму уравнению прибавим первое уравнение, умноженное на число

, к третьему уравнению прибавим первое уравнение, умноженное на число 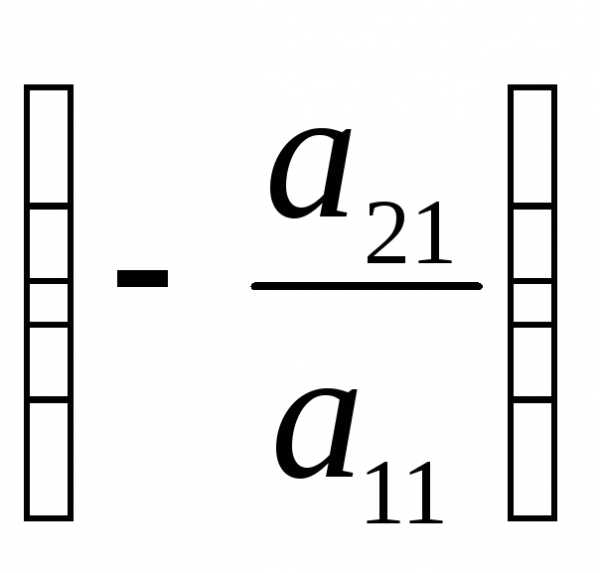, и так далее до последнего уравнения. После первого шага получим систему: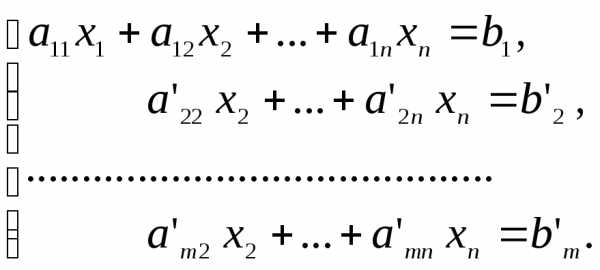

Полученная система равносильна исходной системе.

Вторым шагом исключают неизвестное из всех уравнений, кроме первого и второго. Для этого повторяем все действия первого шага для второго и последующих уравнений, а именно: считаем, что коэффициент 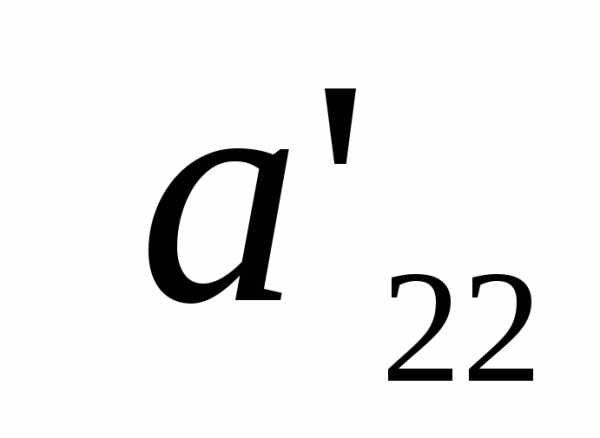 ≠ 0 и так далее. Если в результате преобразований получается нулевое уравнение, то его удаляют, если же получается несовместное уравнение, то решение системы закончено – она несовместна. Процесс исключения неизвестных продолжаем до тех пор, пока это возможно. Обозначим количество уравнений, оставшихся после прямого хода, через

r. Это число равно рангу основной матрицы системы и может быть меньше или равно n. Рассмотрим оба случая.

1) Если r = n, то система после прямого хода принимает вид:

где с₁₁ ≠ 0, с₂₂ ≠ 0, …, с_nn ≠ 0.

Обратным ходом, начиная с последнего уравнения, последовательно найдем значения x_n, (где x_n = 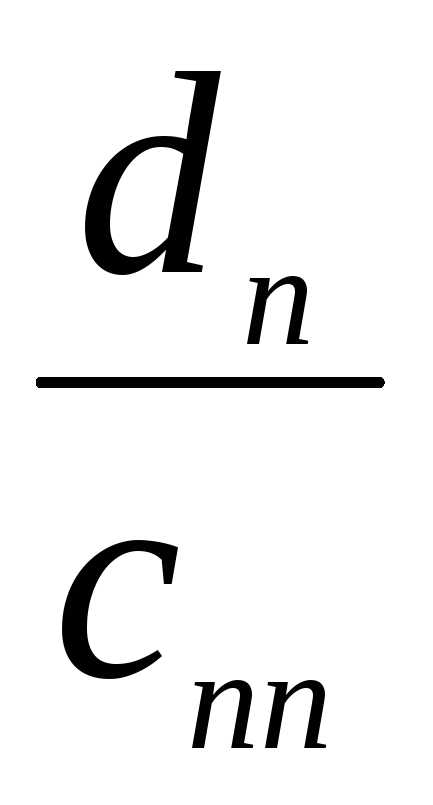), x_n – 1, …, x₁. В этом случае система линейных уравнений имеет единственное решение, то есть является определенной.

2) Если r < n, то система после прямого хода принимает вид:

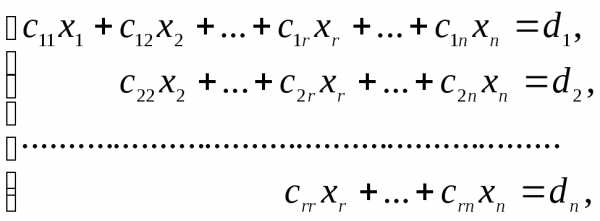
где с₁₁ ≠ 0, с₂₂ ≠ 0, …, с_rr ≠ 0. Неизвестные x₁, x₂, …, x_r, с которых начинаются уравнения, называются главными неизвестными, а остальные x_r + 1, x _r + 2, …, x_n – свободными. В этом случае обратным ходом, начиная с последнего уравнения, выражают главные неизвестные через свободные неизвестные. Получают следующие равенства:

x₁ = k_1,r + 1x_r + 1 + … + k_1,nx_n + t₁

,

x₂ = k_2,r + 1x_r + 1 + … + k_2,nx_n + t₂,

……………………………………..

x_r = k_r,r + 1x_r + 1 + … + k_r,nx_n + t_r.

Определение 6.10. Общим решением системы называется выражение главных неизвестных через свободные.

Если свободным неизвестным придать какие-нибудь числовые значения, то из общего решения получим значения главных неизвестных. Таким образом, получают частное решение системы. Из способа его получения следует, что система имеет более одного решения, то есть является неопределенной.

Пример 6.3. Решить методом Гаусса систему линейных уравнений:

Решение. Преобразования с системой линейных удобнее производить не с самими уравнениями, а с матрицей их коэффициентов. Расширенная матрица этой системы имеет вид: (А|B) = .

Осуществляем прямой ход. Первым шагом исключаем неизвестное х₁ из всех уравнений, кроме первого. Так как а₁₁ = 1 ≠ 0, то переставлять уравнения местами не нужно. Прибавим ко второму уравнению системы первое уравнение, умноженное на (–1), к третьему уравнению – первое, умноженное на (–3). Получим после преобразований следующую матрицу: , в которой элемент а₂₂ = 1. Перестановка местами уравнений (первое уравнение трогать не следует) не поможет, поэтому переходим к следующему неизвестному

х₃ и исключаем его из всех уравнений, кроме первого и второго. Для этого к третьему уравнению прибавим второе, умноженное на (–2) и вычеркнем получившееся нулевое уравнение. После прямого хода получаем следующую систему: 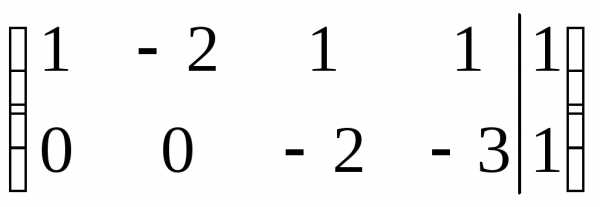. Прямой ход завершен. В этом случае n = 4, r = 2, r < n, и, следовательно, система неопределенная. Главные неизвестные – это те неизвестные, с которых начинаются уравнения, в нашем случае это х₁ и х₃. Неизвестные х₂ и х₄ – свободные.

Обратным ходом надо выразить главные неизвестные через свободные. Для этого в столбцах, содержащих ведущие элементы строк, следует получить нули. Здесь это элемент а₁₃. Прибавим к первому уравнению, умноженному на 2, второе и выпишем получившуюся матрицу коэффициентов:

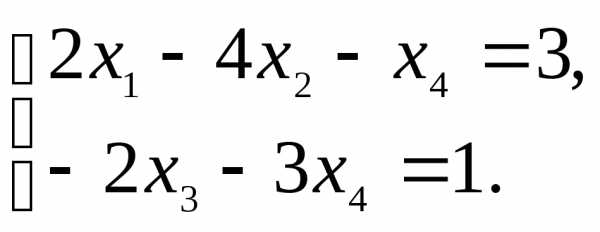, а затем и сами уравнения: Из этих уравнений получаем общее решение: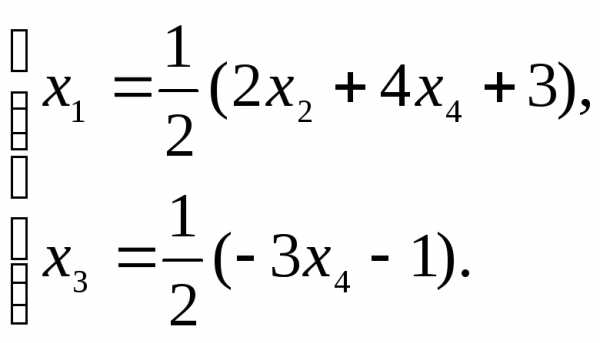

Найдем какое-нибудь частное решение; пусть х₂ = 3, х₄ = 1, тогда из общего решения получим значения х₁ = 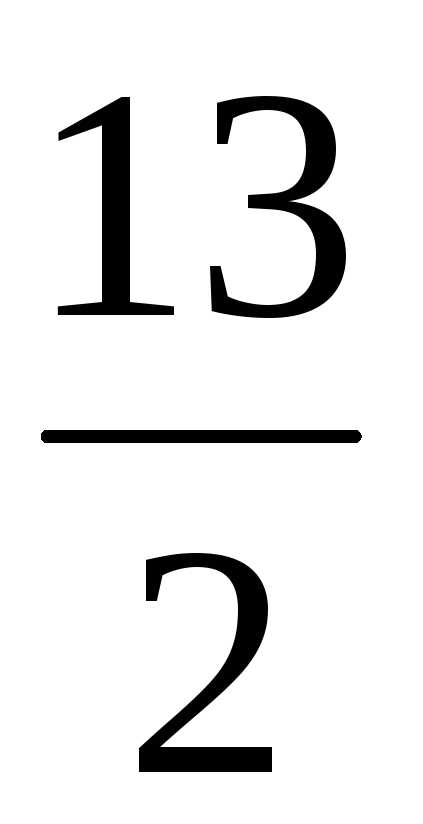, и х₁ = –2. Таким образом, частное решение – вектор а = (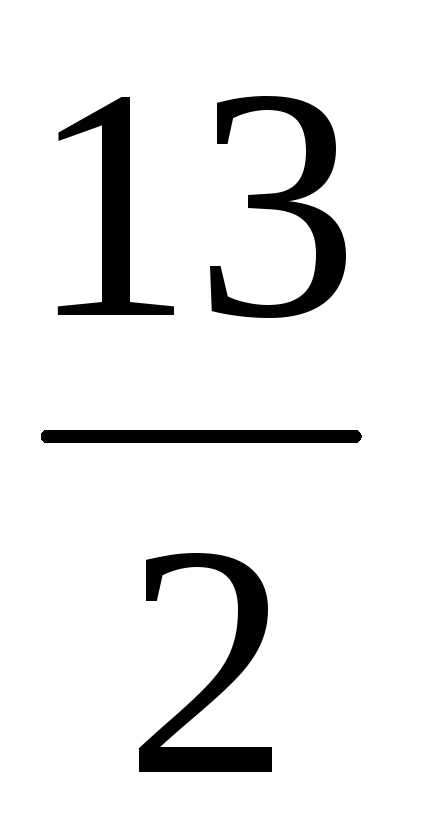, 3, –2, 1).

Ответ: общее решение {(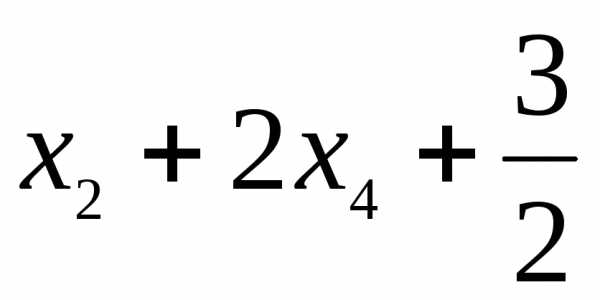, х₂, 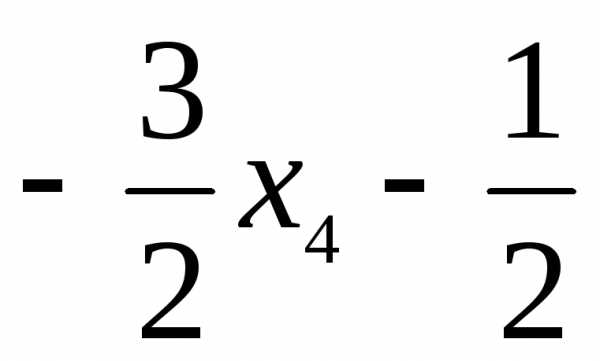, х

4)}, где х₂, х₄  R;

частное решение, если х₂ = 3, х₄ = 1, то (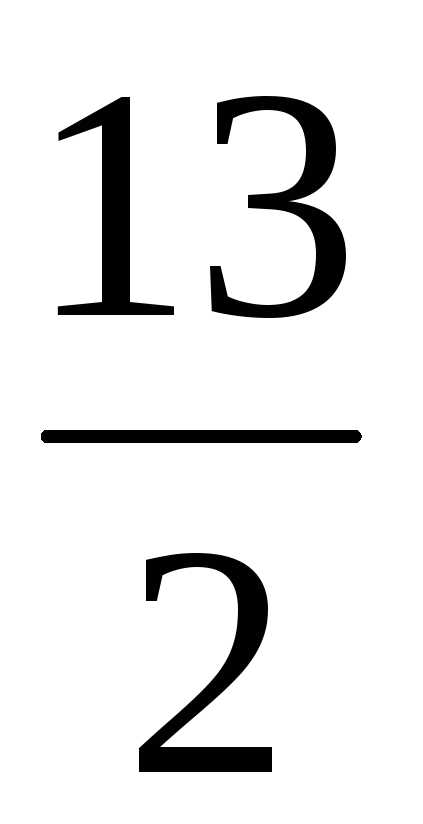, 3, –2, 1).

studfiles.net

Метод Гаусса

Определение и описание метода Гаусса

Метод преобразований Гаусса (также известный как преобразование методом последовательного исключения неизвестных переменных из уравнения или матрицы) для решения систем линейных уравнений представляет собой классический методом решения системы алгебраических уравнений (СЛАУ). Также этот классический метод используют для решения таких задач как получение обратных матриц и определения ранговости матрицы.

Преобразование с помощью метода Гаусса заключается в совершении небольших (элементарных) последовательных изменениях системы линейных алгебраических уравнений, приводящих к исключению переменных из неё сверху вниз с образованием новой треугольной системы уравнений, являющейся равносильной исходной.

Определение 1

Эта часть решения носит название прямого хода решения Гаусса, так как весь процесс осуществляется сверху вниз.

После приведения исходной системы уравнений к треугольной осуществляется нахождение всех переменных системы снизу вверх (то есть первые найденные переменные занимают находятся именно на последних строчках системы или матрицы). Эта часть решения известна также как обратный ход решения методом Гаусса. Заключается его алгоритм в следующем: сначала вычисляется переменные, находящиеся ближе всего к низу системы уравнений или матрицы, затем полученные значения подставляются выше и таким образом находится ещё одна переменная и так далее.

Описание алгоритма метода Гаусса

Последовательность действий для общего решения системы уравнения методом Гаусса заключается в поочередном применении прямого и обратного хода к матрице на основе СЛАУ. Пусть исходная система уравнений имеет следующий вид:

$\begin{cases} a_{11} \cdot x_1 +…+ a_{1n} \cdot x_n = b_1 \\ … \\ a_{m1} \cdot x_1 + a_{mn} \cdot x_n = b_m \end{cases}$

Чтобы решить СЛАУ методом Гаусса, необходимо записать исходную систему уравнений в виде матрицы:

$A = \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & … & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix}$, $b=\begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix}$

Матрица $A$ называется основной матрицей и представляет собой записанные по порядку коэффициенты при переменных, а $b$ называется столбцом её свободных членов. Матрица $A$, записанная через черту со столбцом свободных членов называется расширенной матрицей:

$A = \begin{array}{ccc|c} a_{11} & … & a_{1n} & b_1 \\ \vdots & … & \vdots & …\\ a_{m1} & … & a_{mn} & b_m \end{array}$

Теперь необходимо с помощью элементарных преобразований над системой уравнений (или над матрицей, так как это удобнее) привести её к следующему виду:

$\begin{cases} α_{1j_{1}} \cdot x_{j_{1}} + α_{1j_{2}} \cdot x_{j_{2}}…+ α_{1j_{r}} \cdot x_{j_{r}} +… α_{1j_{n}} \cdot x_{j_{n}} = β_1 \\ α_{2j_{2}} \cdot x_{j_{2}}…+ α_{2j_{r}} \cdot x_{j_{r}} +… α_{2j_{n}} \cdot x_{j_{n}} = β_2 \\ …\\ α_{rj_{r}} \cdot x_{j_{r}} +… α_{rj_{n}} \cdot x_{j_{n}} = β_r \\ 0 = β_(r+1) \\ … \\ 0 = β_m \end{cases}$ (1)

Матрица, полученная из коэффициентов преобразованной системы уравнения (1) называется ступенчатой, вот так обычно выглядят ступенчатые матрицы:

$A = \begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \\ 0 & a_{22} & a_{23} & b_2\\ 0 & 0 & a_{33} & b_3 \end{array}$

Для этих матриц характерен следующий набор свойств:

1. Все её нулевые строки стоят после ненулевых
2. Если некоторая строка матрицы с номером $k$ ненулевая, то в предыдущей строчке этой же матрицы нулей меньше, чем в этой, обладающей номером $k$.

После получения ступенчатой матрицы необходимо подставить полученные переменные в оставшиеся уравнения (начиная с конца) и получить оставшиеся значения переменных.

Основные правила и разрешаемые преобразования при использовании метода Гаусса

При упрощении матрицы или системы уравнений этим методом нужно использовать только элементарные преобразования.

Таким преобразованиями считаются операции, которые возможно применять к матрице или системе уравнений без изменения её смысла:

• перестановка нескольких строк местами,
• прибавление или вычитание из одной строчки матрицы другой строчки из неё же,
• умножение или деление строчки на константу, не равную нулю,
• строчку, состоящую из одних нулей, полученную в процессе вычисления и упрощения системы, нужно удалить,
• Также нужно удалить лишние пропорциональные строчки, выбрав для системы единственную из них с более подходящими и удобными для дальнейших вычислений коэффициентами.

Все элементарные преобразования являются обратимыми.

Разбор трёх основных случаев, возникающих при решении линейных уравнений используя метод простых преобразований Гаусса

Различают три возникающих случая при использовании метода Гаусса для решения систем:

1. Когда система несовместная, то есть у неё нет каких-либо решений
2. У системы уравнений есть решение, причём единственное, а количество ненулевых строк и столбцов в матрице равно между собой.
3. Система имеет некое количество или множество возможных решений, а количество строк в ней меньше чем количество столбцов.

Исход решения с несовместной системой

Для этого варианта при решении матричного уравнения методом Гаусса характерно получение какой-то строчки с невозможностью выполнения равенства. Поэтому при возникновении хотя бы одного неправильного равенства полученная и исходная системы не имеют решений вне зависимости от остальных уравнений, которые они содержат. Пример несовместной матрицы:

$\begin{array}{ccc|c} 2 & -1 & 3 & 0 \\ 1 & 0 & 2 & 0\\ 0 & 0 & 0 & 1 \end{array}$

В последней строчке возникло невыполняемое равенство: $0 \cdot x_{31} + 0 \cdot x_{32} + 0 \cdot x_{33} = 1$.

Система уравнений, у которой есть только одно решение

Данные системы после приведения к ступенчатой матрице и удаления строчек с нулями имеют одинаковое количество строк и столбцов в основной матрице. Вот простейший пример такой системы:

$\begin{cases} x_1 – x_2 = -5 \\ 2 \cdot x_1 + x_2 = -7 \end{cases}$

Запишем её в виде матрицы:

$\begin{array}{cc|c} 1 & -1 & -5 \\ 2 & 1 & -7 \end{array}$

Чтобы привести первую ячейку второй строчки к нулю, домножим верхнюю строку на $-2$ и вычтем её из нижней строчки матрицы, а верхнюю строчку оставим в исходном виде, в итоге имеем следующее:

$\begin{array}{cc|c} 1 & -1 & -5 \\ 0 & 3 & 10 \end{array}$

Этот пример можно записать в виде системы:

$\begin{cases} x_1 – x_2 = -5 \\ 3 \cdot x_2 = 10 \end{cases}$

Из нижнего уравнения выходит следующее значение $x$: $x_2 = 3 \frac{1}{3}$. Подставим это значение в верхнее уравнение: $x_1 – 3 \frac{1}{3}$, получаем $x_1 = 1 \frac{2}{3}$.

Система, обладающая множеством возможных вариантов решений

Для этой системы характерно меньшее количество значащих строк, чем количество столбцов в ней (учитываются строки основной матрицы).

Переменные в такой системе делятся на два вида: базисные и свободные. При преобразовании такой системы содержащиеся в ней основные переменные необходимо оставить в левой области до знака “=”, а остальные переменные перенести в правую часть равенства.

У такой системы есть только некое общее решение.

Разберём следующую систему уравнений:

$\begin{cases} 2y_1 + 3y_2 + x_4 = 1 \\ 5y_3 – 4y_4 = 1 \end{cases}$

Запишем её в виде матрицы:

$\begin{array}{cccc|c} 2 & 3 & 0 & 1 & 1 \\ 0 & 0 & 5 & 4 & 1 \\ \end{array}$

Наша задача найти общее решение системы. Для этой матрицы базисными переменными будут $y_1$ и $y_3$ (для $y_1$ – так как он стоит на первом месте, а в случае $y_3$ – располагается после нулей).

В качестве базисных переменных выбираем именно те, которые первые в строке не равны нулю.

Оставшиеся переменные называются свободными, через них нам необходимо выразить базисные.

Используя так называемый обратный ход, разбираем систему снизу вверх, для этого сначала выражаем $y_3$ из нижней строчки системы:

$5y_3 – 4y_4 = 1$

$5y_3 = 4y_4 + 1$

$y_3 = \frac{4/5}y_4 + \frac{1}{5}$.

Теперь в верхнее уравнение системы $2y_1 + 3y_2 + y_4 = 1$ подставляем выраженное $y_3$: $2y_1 + 3y_2 – (\frac{4}{5}y_4 + \frac{1}{5}) + y_4 = 1$

Выражаем $y_1$ через свободные переменные $y_2$ и $y_4$:

$2y_1 + 3y_2 – \frac{4}{5}y_4 – \frac{1}{5} + y_4 = 1$

$2y_1 = 1 – 3y_2 + \frac{4}{5}y_4 + \frac{1}{5} – y_4$

$2y_1 = -3y_2 – \frac{1}{5}y_4 + \frac{6}{5}$

$y_1 = -1.5x_2 – 0.1y_4 + 0.6$

Решение готово.

Пример 1

Решить слау методом Гаусса. Примеры. Пример решения системы линейных уравнений заданных матрицей 3 на 3 используя метод Гаусса

$\begin{cases} 4x_1 + 2x_2 – x_3 = 1 \\ 5x_1 + 3x_2 – 2x^3 = 2\\ 3x_1 + 2x_2 – 3x_3 = 0 \end{cases}$

Запишем нашу систему в виде расширенной матрицы:

$\begin{array}{ccc|c} 4 & 2 & -1 & 1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$

Теперь для удобства и практичности нужно преобразовать матрицу так, чтобы в верхнем углу крайнего столбца была $1$.

Для этого к 1-ой строчке нужно прибавляем строчку из середины, умноженную на $-1$, а саму среднюю строчку записываем как есть, выходит:

$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$

Далее к средней строчке прибавим верхнюю, умноженную на $5$, а последнюю строчку преобразуем, умножив первую строчку на 3 и сложив с последней, получаем:

$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 0 & -2 & 3 & -3 \\ 0 & -1 & 0 & -3\\ \end{array}$

Домножим верхнюю и последнюю строчки на $-1$, а также поменяем местами последнюю и среднюю строки:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & -2 & 3 & -3\\ \end{array}$

Далее сложим последнюю строчку с удвоенной средней:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 3 & 3\\ \end{array}$

И разделим последнюю строчку на $3$:

$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1\\ \end{array}$

Получаем следующую систему уравнений, равносильную исходной:

$\begin{cases} x_1 + x_2 – x_3 = 1\\ x_2 = 3 \\ x_3 = 1 \end{cases}$

Из верхнего уравнения выражаем $x_1$:

$x1 = 1 + x_3 – x_2 = 1 + 1 – 3 = -1$.

Пример 2

Пример решения системы, заданной с помощью матрицы 4 на 4 методом Гаусса

$\begin{array}{cccc|c} 2 & 5 & 4 & 1 & 20 \\ 1 & 3 & 2 & 1 & 11 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.

В начале меняем местами верхнюю исследующую за ней строчки, чтобы получить в левом верхнем углу $1$:

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 2 & 5 & 4 & 1 & 20 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.

Теперь умножим верхнюю строчку на $-2$ и прибавим ко 2-ой и к 3-ьей. К 4-ой прибавляем 1-ую строку, домноженную на $-3$:

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 4 & 5 & 5 & 18\\ 0 & -1 & 3 & -1 & 4 \\ \end{array}$

Теперь к строке с номером 3 прибавляем строку 2, умноженную на $4$, а к строке 4 прибавляем строку 2, умноженную на $-1$.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 0 & 5 & 1 & 10\\ 0 & 0 & 3 & 0 & 6 \\ \end{array}$

Домножаем строку 2 на $-1$, а строку 4 делим на $3$ и ставим на место строки 3.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 5 & 1 & 10 \\ \end{array}$

Теперь прибавляем к последней строке предпоследнюю, домноженную на $-5$.

$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 1 & 0 \\ \end{array}$

Решаем полученную систему уравнений:

$\begin{cases} m = 0 \\ g = 2\\ y + m = 2\ \ x + 3y + 2g + m = 11\end{cases}$

$y=2$, $x = 0$.

spravochnick.ru

Метод Гаусса Википедия

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы^[1].

История[ | ]

Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах».^[2]

Описание метода[ | ]

Пусть исходная система выглядит следующим образом:

{a11x1+…+a1nxn=b1…am1x1+…+amnxn=bm{\displaystyle \left\{{\begin{array}{lcr}a_{11}x_{1}+\ldots +a_{1n}x_{n}&=&b_{1}\\\ldots &&\\a_{m1}x_{1}+\ldots +a_{mn}x_{n}&=&b_{m}\\\end{array}}\right.}

Её можно записать в матричном виде:

Ax=b,{\displaystyle Ax=b,}

где

A=(a11…a1n…am1…amn),x=(x1⋮xn),b=(b1⋮bm).(1){\displaystyle A=\left({\begin{array}{ccc}a_{11}&\ldots &a_{1n}\\\ldots &&\\a_{m1}&\ldots &a_{mn}\end{array}}\right),\quad x=\left({\begin{array}{c}x_{1}\\\vdots \\x_{n}\end{array}}\right),\quad b=\left({\begin{array}{c}b_{1}\\\vdots \\b_{m}\end{array}}\right).\quad (1)}

ru-wiki.ru

Метод Гаусса — Википедия РУ

Пусть исходная система выглядит следующим образом:

{a11x1+…+a1nxn=b1…am1x1+…+amnxn=bm{\displaystyle \left\{{\begin{array}{lcr}a_{11}x_{1}+\ldots +a_{1n}x_{n}&=&b_{1}\\\ldots &&\\a_{m1}x_{1}+\ldots +a_{mn}x_{n}&=&b_{m}\\\end{array}}\right.} 

Её можно записать в матричном виде:

Ax=b,{\displaystyle Ax=b,} 

где

A=(a11…a1n…am1…amn),x=(x1⋮xn),b=(b1⋮bm).(1){\displaystyle A=\left({\begin{array}{ccc}a_{11}&\ldots &a_{1n}\\\ldots &&\\a_{m1}&\ldots &a_{mn}\end{array}}\right),\quad x=\left({\begin{array}{c}x_{1}\\\vdots \\x_{n}\end{array}}\right),\quad b=\left({\begin{array}{c}b_{1}\\\vdots \\b_{m}\end{array}}\right).\quad (1)} 

Матрица A{\displaystyle A}  называется основной матрицей системы, b{\displaystyle b}  — столбцом свободных членов.

Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):

{α1j1xj1+α1j2xj2+…+α1jrxjr+…+α1jnxjn=β1α2j2xj2+…+α2jrxjr+…+α2jnxjn=β2…αrjrxjr+…+αrjnxjn=βr0=βr+1…0=βm,{\displaystyle \left\{{\begin{array}{rcl}\alpha _{1j_{1}}x_{j_{1}}+\alpha _{1j_{2}}x_{j_{2}}+\ldots +\alpha _{1j_{r}}x_{j_{r}}+\ldots +\alpha _{1j_{n}}x_{j_{n}}&=&\beta _{1}\\\alpha _{2j_{2}}x_{j_{2}}+\ldots +\alpha _{2j_{r}}x_{j_{r}}+\ldots +\alpha _{2j_{n}}x_{j_{n}}&=&\beta _{2}\\&\ldots &\\\alpha _{rj_{r}}x_{j_{r}}+\ldots +\alpha _{rj_{n}}x_{j_{n}}&=&\beta _{r}\\0&=&\beta _{r+1}\\&\ldots &\\0&=&\beta _{m}\end{array}}\right.,} 

где α1j1,…,αrjr≠0.{\displaystyle \alpha _{1j_{1}},\ldots ,\alpha _{rj_{r}}\neq 0.} 

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj1,…,xjr{\displaystyle x_{j_{1}},\ldots ,x_{j_{r}}} ^[3].

Тогда переменные xj1,…,xjr{\displaystyle x_{j_{1}},\ldots ,x_{j_{r}}}  называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число βi≠0{\displaystyle \beta _{i}\neq 0} , где i>r{\displaystyle i>r} , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.

Пусть βi=0{\displaystyle \beta _{i}=0}  для любых i>r{\displaystyle i>r} .

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x{\displaystyle x}  (αiji,i=1,…,r{\displaystyle \alpha _{ij_{i}},\,i=1,\ldots ,r} , где i{\displaystyle i}  — номер строки):

{xj1+α^1j2xj2+…+α^1jrxjr=β^1−α^1jr+1xjr+1−…−α^1jnxjnxj2+…+α^2jrxjr=β^2−α^2jr+1xjr+1−…−α^2jnxjn…xjr=β^r−α^rjr+1xjr+1−…−α^rjnxjn,β^i=βiαiji,α^ijk=αijkαiji(2){\displaystyle \left\{{\begin{array}{rcc}x_{j_{1}}+{\widehat {\alpha }}_{1j_{2}}x_{j_{2}}+\ldots +{\widehat {\alpha }}_{1j_{r}}x_{j_{r}}&=&{\widehat {\beta }}_{1}-{\widehat {\alpha }}_{1j_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{1j_{n}}x_{j_{n}}\\x_{j_{2}}+\ldots +{\widehat {\alpha }}_{2j_{r}}x_{j_{r}}&=&{\widehat {\beta }}_{2}-{\widehat {\alpha }}_{2j_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{2j_{n}}x_{j_{n}}\\&\ldots &\\x_{j_{r}}&=&{\widehat {\beta }}_{r}-{\widehat {\alpha }}_{rj_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{rj_{n}}x_{j_{n}}\\\end{array}}\right.,\qquad {\widehat {\beta }}_{i}={\frac {\beta _{i}}{\alpha _{ij_{i}}}},\quad {\widehat {\alpha }}_{ij_{k}}={\frac {\alpha _{ij_{k}}}{\alpha _{ij_{i}}}}\quad (2)} ,

где i=1,…,r,k=i+1,…,n.{\displaystyle i=1,\ldots ,r,\quad k=i+1,\ldots ,n.} 

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой. 2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.

Критерий совместности

Упомянутое выше условие βi=0{\displaystyle \beta _{i}=0}  для всех i>r{\displaystyle i>r}  может быть сформулировано в качестве необходимого и достаточного условия совместности:

Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).

Теорема Кронекера — Капелли. Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Следствия: Количество главных переменных равно рангу системы и не зависит от её решения. Если ранг совместной системы равен числу переменных данной системы, то она определена.

Алгоритм

Блок схема представлена на рисунке. Данный рисунок адаптированный для написания программы на языке С/С++, где a[0] столбец свободных членов.

  Алгоритм Гаусса для решения СЛАУ

Описание

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

• На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
• На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Метод Гаусса требует O(n3){\displaystyle O(n^{3})}  арифметических операций.

Этот метод опирается на:

Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.

Простейший случай

В простейшем случае алгоритм выглядит так:

{a11⋅x1+a12⋅x2+…+a1n⋅xn=b1(1)a21⋅x1+a22⋅x2+…+a2n⋅xn=b2(2)…am1⋅x1+am2⋅x2+…+amn⋅xn=bm(m){\displaystyle \left\{{\begin{array}{lcc}a_{11}\cdot x_{1}+a_{12}\cdot x_{2}+\ldots +a_{1n}\cdot x_{n}&=b_{1}&(1)\\a_{21}\cdot x_{1}+a_{22}\cdot x_{2}+\ldots +a_{2n}\cdot x_{n}&=b_{2}&(2)\\\ldots &&\\a_{m1}\cdot x_{1}+a_{m2}\cdot x_{2}+\ldots +a_{mn}\cdot x_{n}&=b_{m}&(m)\end{array}}\right.} 

(2)→(2)−(1)⋅(a21a11):a22′⋅x2+a23′⋅x3+…+a2n′⋅xn=b2′(3)→(3)−(1)⋅(a31a11):a32′⋅x2+a33′⋅x3+…+a3n′⋅xn=b3′…(m)→(m)−(1)⋅(am1a11):am2′⋅x2+am3′⋅x3+…+amn′⋅xn=bn′(3)→(3)−(2)⋅(a32′a22′):a33′′⋅x3+…+a3n′′⋅xn=b3′′…(m)→(m)−(m−1)⋅(am,n−1(m−2)am−1,n−1(m−2)):amm(m−1)⋅xm+…+amn(m−1)⋅xn=bm(m−1){\displaystyle {\begin{array}{ccc}(2)\to (2)-(1)\cdot ({\frac {a_{21}}{a_{11}}})&:&a_{22}^{\prime }\cdot x_{2}+a_{23}^{\prime }\cdot x_{3}+\ldots +a_{2n}^{\prime }\cdot x_{n}=b_{2}^{\prime }\\(3)\to (3)-(1)\cdot ({\frac {a_{31}}{a_{11}}})&:&a_{32}^{\prime }\cdot x_{2}+a_{33}^{\prime }\cdot x_{3}+\ldots +a_{3n}^{\prime }\cdot x_{n}=b_{3}^{\prime }\\\ldots &&\\(m)\to (m)-(1)\cdot ({\frac {a_{m1}}{a_{11}}})&:&a_{m2}^{\prime }\cdot x_{2}+a_{m3}^{\prime }\cdot x_{3}+\ldots +a_{mn}^{\prime }\cdot x_{n}=b_{n}^{\prime }\\(3)\to (3)-(2)\cdot ({\frac {a_{32}^{\prime }}{a_{22}^{\prime }}})&:&a_{33}^{\prime \prime }\cdot x_{3}+\ldots +a_{3n}^{\prime \prime }\cdot x_{n}=b_{3}^{\prime \prime }\\\ldots &&\\(m)\to (m)-(m-1)\cdot ({\frac {a_{m,n-1}^{(m-2)}}{a_{m-1,n-1}^{(m-2)}}})&:&a_{mm}^{(m-1)}\cdot x_{m}+\ldots +a_{mn}^{(m-1)}\cdot x_{n}=b_{m}^{(m-1)}\end{array}}} 

• Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.

Пример

Покажем, как методом Гаусса можно решить следующую систему:

{2x+y−z=8−3x−y+2z=−11−2x+y+2z=−3{\displaystyle \left\{{\begin{array}{ccc}2x+y-z&=&8\\-3x-y+2z&=&-11\\-2x+y+2z&=&-3\end{array}}\right.} 

Обнулим коэффициенты при x{\displaystyle x}  во второй и третьей строчках. Для этого прибавим к ним первую строчку, умноженную на 32{\displaystyle \textstyle {\frac {3}{2}}}  и 1{\displaystyle 1} , соответственно:

{2x+y−z=812y+12z=12y+z=5{\displaystyle \left\{{\begin{array}{rcc}2x+y-z&=&8\\{\frac {1}{2}}y+{\frac {1}{2}}z&=&1\\2y+z&=&5\end{array}}\right.} 

Теперь обнулим коэффициент при y{\displaystyle y}  в третьей строке, вычтя из неё вторую строку, умноженную на 4{\displaystyle 4} :

{2x+y−z=812y+12z=1−z=1{\displaystyle \left\{{\begin{array}{rcc}2x+y-z&=&8\\{\frac {1}{2}}y+{\frac {1}{2}}z&=&1\\-z&=&1\\\end{array}}\right.} 

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

z=−1{\displaystyle z=-1}  из третьего;

y=3{\displaystyle y=3}  из второго, подставив полученное z{\displaystyle z} 

x=2{\displaystyle x=2}  из первого, подставив полученные z{\displaystyle z}  и y{\displaystyle y} .

Таким образом исходная система решена.

В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.

http-wikipediya.ru

---