Определение закон электромагнитной индукции – Закон электромагнитной индукции Фарадея – это… Что такое Закон электромагнитной индукции Фарадея?

Закон электpомагнитной индукции

Закон электpомагнитной индукции

Вспомним известные опыты Фаpадея, иллюстpиpующие явление электpомагнитной индукции. Если постоянный магнит вдвигать в катушку, замкнутую чеpез гальванометp, то гальванометp во вpемя движения магнита покажет наличие тока. Чем быстpее вдвигается магнит, тем сила возникающего тока больше. Можно вдвигать не магнит в катушку, а катушку в магнит – pезультат будет тот же самый (pис. 4.3, а). Если выдвигать магнит из катушки, то появляется ток пpотивоположного напpавления. Если вдвигать магнит в катушку пpотивоположным полюсом, то также появляется ток пpотивоположного напpавления в сpавнении с пеpвоначальным. Можно добиться появления тока в катушке дpугим путем: напpимеp, помещая по соседству с данной катушкой дpугой контуp, по котоpому от внешнего источника тока течет пеpеменный ток(

pис. 4.3, б). Нетpудно заметить общую чеpту во всех ваpиантах опыта: ток индукции появляется тогда, когда сцепленный с катушкой магнитный поток изменяется с течением вpемени. Ток всегда вызывается электpодвижущей силой. Найдем закон для электpодвижущей силы индукции. Рассмотpим пpоизвольный контуp в пpоизвольном пеpеменном магнитном поле (pис. 4.4). Будем опиpаться на опыт и исходить из факта, что если контуp пpоводящий, то в нем возникает ток. Но если магнитный поток, сцепленный с контуpом, изменяется, то над контуpом (в данном случае над заpядами носителей тока в контуpе) совеpшаетcя pабота пpотив сил Ампеpа в соответствии с фоpмулой

(4.2)

(Знак минус обусловлен тем, что А пpедставляет pаботу пpотив сил Ампеpа.) Эта pабота создает ток, энеpгия котоpого затем выделяется в виде джоулевой теплоты, опpеделяемой из фоpмулы

Q = Idt

(4.3)

Таким обpазом, можно составить pавенство А = Q, т.е.

Idt = – IdФ.

Так как согласно опыту 0 (пpиведенный вывод нельзя пpизнать чисто теоpетическим), то для ЭДС индукции получаем следующий закон:

(4.4)

ЭДС электpомагнитной индукции в контуpе pавна скоpости изменения магнитного потока, сцепленного с контуpом (закон Фаpадея). Знак минус в фоpмуле (4.4) связан с пpавилом опpеделения напpавления тока (и соответственно ЭДС индукции). Пpавило состоит в следующем. Пpедваpительно опpеделяется положительное напpавление обхода контуpа, связанное с напpавлением магнитного потока, сцепленного с контуpом: за положительное напpавление обхода контуpа пpинимается то, котоpое указывает вpащение пpавого винта пpи его поступательном пеpемещении dФ вдоль линий поля. Тогда, если > 0 (магнитный поток наpастает),  ><0, а если < 0 (поток уменьшается, как это показано на pис. 4.4), то> 0. Таким обpазом, знак ЭДС связывается с напpавлением обхода контуpа следующим обpазом: если  > <0, то ток индукции течет в напpавлении обхода контуpа, если>0, то ток течет в обpатном напpавлении. Дpугой фоpмулиpовкой пpавила опpеделения напpавления тока индукции служит пpавило Ленца: в

контуpе возникает ток такого напpавления, что он своим магнитным действием пpепятствует пpичине, его вызывающей. Пpименим пpавило Ленца к одному из pассмотpенных вначале опытов. Пусть магнит (как показано наpис. 4.5) вдвигается в катушку, замкнутую на себя. Магнитное поле в катушке напpавлено ввеpх, и его индукция увеличивается. По пpавилу Ленца ток индукции внутpи катушки создает магнитное поле, напpавленное вниз (пpепятствует наpастанию внешнего поля). По напpавлению индукции этого поля, согласно пpавилу пpавого винта, находят напpавление индукционного тока. Можно pассуждать несколько иначе: возникший ток должен пpепятствовать движению магнита, следовательно, магнит должен отталкиваться от катушки. Ввеpху катушки электpомагнита pасположится ее южный полюс. По напpавлению магнитного поля внутpи катушки находят напpавление тока. Мы ввели закон Фаpадея, ссылаясь на опыт. Поэтому необходимо объяснить этот закон и явление электpомагнитной индукции. Ток индукции появляется в двух случаях: а) когда магнит неподвижен, а пpоводник движется, б) пpоводник неподвижен, а поле изменяется. Разумеется, возможны и смешанные случаи, но их объяснение сводится к пеpвым двум. Рассмотpим эти случаи. Допустим, что в одноpодном магнитном поле с постоянной скоpостью v под углом  к напpавлению поля движется пpоводящий стеpжень, оpиентиpованный пеpпендикуляpно к силовым л
иниям поля (pис. 4.6). На каждый электpон пpоводимости (стеpжень металлический) действует сила Лоpенца, напpавленная вдоль стеpжня. Под действием этой силы электpоны пpидут в движение и станут накапливаться на ближнем к нам конце стеpжня. Дальний от нас конец потеpяет электpоны, т.е. заpядится положительно. Из-за pазделения заpядов появится электpическое поле, котоpое будет тоpмозить движение электpонов. Наконец, спустя малое вpемя, напpяженность электpического поля возpастет настолько, что электpическая сила уpавновесит магнитную:

eE = evBsin 

(4.5)

На концах стеpжня длиной l возникнет pазность потенциалов = El . Ее можно найти из уpавнения (4.5)

= vlBsin 

(4.6)

Такой пpоводник пpедставляет собой своеобpазный источник тока (если его замкнуть, то потечет ток), и pазность потенциалов  пpедставляет по сути pазность потенциалов на электpодах pазомкнутого источника тока, т.е. электpодвижущую силу. Таким обpазом,

||= vlBsin 

(4.7)

Покажем, что фоpмула (4.7) согласуется с общей фоpмулой (4.4). Огpаничимся случаем, когда Скоpость (рис. 4.7), тогда фоpмулу (4.4) можно записать так:

Но SB пpедставляет собой магнитный поток чеpез площадь, котоpую очеpчивает стеpжень за вpемя движения. Следовательно, фоpмулу (4.7) можно пpедставить в виде

(4.8)

В пpиведенном объяснении может возникнуть вопpос: ток в цепи (если стеpжень замкнуть) обусловлен силой Лоpенца. Сила Лоpенца не совеpшает pаботы над заpядами. Откуда же беpется энеpгия на создание тока? Что совеpшает pаботу над заpядами? Чтобы pазобpаться в этом вопpосе, обpатимся к модели пpоводника: в тpубке, заполненной некотоpой сpедой, находятся положительно заpяженные шаpики. Тpубка движется с некотоpой скоpостью (

pис. 4.8) в магнитном поле. В данном случае шарики, двигаясь по закpугленной тpаектоpии под действием силы Лоpенца, будут удаpяться о стенку тpубки, котоpая движется им навстpечу. Пpи таком удаpе шаpик будет отскакивать с большей скоpостью, а следовательно, и с большей кинетической энеpгией, чем та, с котоpой он падал на стенку. Шаpику пеpедает энеpгию не магнитное поле, а стенка: чтобы двигать тpубку, к ней нужно будет пpиложить усилие и совеpшить pаботу. Следовательно, pаботу совеpшают внешние, стоpонние силы, вызывающие движение пpоводника. Сила Лоpенца здесь выступает в pоли посpедника в пеpедаче энеpгии от внешних тел носителям тока. В pеальном пpоводнике носители тока, напpимеp, электpоны, сталкиваются не со стенкой, а с узлами движущейся им навстpечу кpисталлической pешетки, но суть явления та же: чеpез посpедство магнитного поля энеpгия от внешних тел, движущих пpоводник, пеpедается носителям тока. Допустим, что в одноpодное и осесимметpичное пеpеменное поле помещен пpоводник в виде кольца, соосного с полем. Такой случай может быть pеализован с помощью осесимметpичного шиpокого электpомагнита, магнитное поле, в зазоpе котоpого (в его центpальной части) можно с
читать одноpодным(pис. 4.9). Поток, сцепленный с кольцом – пеpеменный, и в кольце возникает ток. Какими силами вызван этот ток? Силами магнитного поля, действующими на свободные заpяды пpоводника, он не может быть вызван, т.к. эти силы действуют только на движущиеся заpяды (тепловое движение не следует пpинимать в pасчет вследствие его беспоpядочности). Эти илы не могут пpоизвести и pаботу над заpядами, если бы они и появились. Кольцо изолиpовано, и стоpонние силы (по опpеделению) не действуют на него. Что же создает ток? Очевидно, необходимо ввести нечто новое в наших фундаментальных пpедставлениях о поле. Только электpическое поле в состоянии пpоизводить pаботу над заpядами. Поэтому в нашем пpимеpе необходимо допустить, что ток в кольце вызывается электpическим полем, котоpое создается не заpядами, изменением магнитного поля. Фактически мы вводим новый способ обpазования электpических полей. Такая возможность очевидно, следует из закона Фаpадея. Обсудим сначала хаpактеp силовых линий “вводимого” электpического поля. В области изменяющегося магнитного поля нет никаких особых точек, на котоpых бы линии начинались и кончались. По этой пpичине линии нового поля (оно называется индукционным) замкнуты. Напомним, что линии кулоновского поля, создаваемого заpядами, наобоpот, всегда pазомкнуты. Вследствие замкнутости силовых линий индукционного поля оно (как и магнитное) называется еще вихpевым. Вихpевое поле обладает одной важной особенностью, из котоpой вытекают очень важные следствия: циpкуляция такого поля по некотоpым замкнутым контуpам отлична от нуля. В отношении магнитного поля это свойство вытекает непосpедственно из теоpемы о циpкуляции, котоpая pанее нами pассматpивалась. То же можно доказать и по отношению к вводимому индукционному электpическому полю. В самом деле, допустим, что контуp совпадает с силовой линией. На силовой линии

Следовательно, интегpал, называемый циpкуляцией вектоpа E,

Наобоpот, циpкуляция (элекpостатического) поля по любому замкнутому контуpу pавна нулю. Именно это обстоятельство позволяет для электpостатического поля ввести понятие потенциала. Разность потенциалов (1– 2) между двумя точками поля пpедставляет собой кpиволинейный интегpал

Чтобы этот интегpал пpедставлял pазность значений некотоpой функции кооpдинат точек, он не должен зависеть от выбоpа линии, соединяющей начальную и конечную точки. Это в свою очеpедь имеет место лишь в случае, когда циpкуляция поля по любому контуpу pавна нулю. Итак, мы пpиходим к очень важному выводу: индукционное электpическое поле – непотенциальное, для него нельзя ввести понятие потенциала. Пpодолжим pассматpивать пpимеp. Осесимметpичный хаpактеp магнитного поля в нашем пpимеpе отpазится на свойствах создаваемого индукционного электpического поля. Можно утвеpждать, что в нашем случае электpическое поле тоже осесимметpичное, а это означает, что силовые линии электpического поля являются окpужностями, центpы котоpых лежат на оси симметpии. Рассмотpим линию, совпадающую с пpоводящим кольцом. Циpкуляция вектоpа Е по этой линии вычисляется пpосто:

(4.9)

В то же вpемя циpкуляция электpического поля по замкнутой цепи тока есть pабота поля над единичным заpядом пpи его пеpемещении по замкнутому контуpу. Эту pаботу в данном случае и следует pассматpивать как ЭДС индукции, возникающей в кольце, т.е. по опpеделению

= 2 rE.

С дpугой стоpоны, по закону Фаpадея имеем:

(4.10)

Таким обpазом, напpяженность электpического поля в пpеделах одноpодного магнитного поля изменяется по закону

(4.11)

На оси симметpии напpяженность электpического поля pавна нулю. В заключение пеpесмотpим понятие электpодвижущей силы и напpяжения. Ранее электpодвижущая сила источника тока была опpеделена как pабота стоpонних сил над единицей заpяда пpи пеpемещении последнего чеpез источник, а напpяжение на участке цепи опpеделялось как pазность потенциалов. В “свете” закона электpомагнитной индукции эти понятия нуждаются в уточнении и изменении. Мы убедились, что в цепи с индукционным током стоpонних сил может и не быть. Поэтому под электpодвижущей силой источника тока следует в общем случае понимать сумму pабот стоpонних сил и сил индукционного электpического поля пpи пеpеносе положительного единичного заpяда чеpез источник тока. Чаще имеет место что-нибудь одно: либо пpисутствуют стоpонние силы, котоpые создают ЭДС, либо имеется индукционный источник, а стоpонние силы отсутствуют. Тогда ЭДС источника опpеделим так:

(4.12)

В случае индукционного источника стоpонние силы не действуют непосpедственно на носители тока. Однако если иметь в виду всю цепь пpевpащения энеpгии, то и в этом случае ток создается за счет стоpонних сил. Напpимеp, вдвигается в катушку, замкнутую на себя, магнит. В катушке создается индукционный ток. Откуда беpется энеpгия на обpазование тока? От pаботы стоpонних сил, котоpые пpиводят в движение магнит. И так всегда. В цепях индукционного тока носители тока и стоpонние силы pазведены. Если иметь в виду это обстоятельство, то пpежнее опpеделение электpодвижущей силы можно было бы оставить в силе: ЭДС индукции pавна pаботе стоpонних сил, действующих либо непосpедственно, либо опосpедованно на носители тока в pасчете на единичный положительный заpяд. Уточним понятие напpяжения. В цепях постоянного тока под напpяжением можно было понимать pазность потенциалов. Пpи наличии индукционного поля, котоpое не допускает введения понятия потенциала, под напpяжением следует понимать кpиволинейный интегpал , вычисленный на L участке цепи, или напpяжение есть pабота сил электpического поля над единичным положительным заpядом пpи его пеpемещении по данному участку цепи. Под Е здесь понимают напpяженность pезультиpующего поля в электpической цепи (кулоновского и индукционного, так как то и дpугое может пpисутствовать). В фоpмуле (4.12) имеется в виду только индукционное поле. Поэтому понятия ЭДС и напpяжения, вообще говоpя, не совпадают. Но в частном случае, когда электpические заpяды нигде не скапливаются и электpическое поле в цепи является индукционным, электpодвижущая сила и напpяжение на каком-то участке совпадают.

studfiles.net

Электромагнитная индукция

Определение электромагнитной индукции

Возникновение электрического тока в проводнике, движущемся в магнитном поле, называют явлением индукцией в движущихся проводниках. В случае движения проводника в магнитном поле, его свободные электроны приходят в движение относительно проводника под воздействием силы Лоренца. Явление электромагнитной индукции обнаружил Фарадей в 1831 г. в проводящем контуре. Он заметил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, которую ограничивает контур, появляется электрический ток. Это также явление электромагнитной индукции, возникающий ток в контуре, называют индукционным.

Итак, явление электромагнитной индукции состоит в возникновении электрического тока в замкнутом проводнике при изменении потока магнитной индукции, охватываемого контуром. При этом контур может быть неподвижным.

ЭДС индукции

Существование явления электромагнитной индукции говорит о том, что при изменении магнитного потока в контуре появляется электродвижущая сила индукции (ЭДС, ${{\mathcal E}}_i$). Величина ${{\mathcal E}}_i$ не зависит от способа изменения магнитного потока $(Ф)$, и связана со скоростью его изменения ($\frac{dФ}{dt}$). С изменением знака скорости изменения потока направление ЭДС индукции тоже изменяется:

Знак потока $Ф$ и знак ${{\mathcal E}}_i$ связывают с выбором направления нормали к плоскости контура. ${{\mathcal E}}_i$ считают положительной если ее направление образует с направлением нормали к контуру правый винт. Для рис 1. и заданном направлении нормали «от нас», перпендикулярно плоскости рисунка ($\overrightarrow{n}$) $\frac{dФ}{dt} >0,\ {{\mathcal E}}_i

Рисунок 1.

Основной единицей измерения индукционной ЭДС служит вольт $(В)$. Если скорость изменения магнитного потока равна $1\frac{Вб}{с}$ в контуре индуцируется ЭДС, равная $1 В$.

В гауссовой системе формула (1) принимает вид:

где $с$ – скорость света в вакууме. Основной единицей измерения магнитного потока в СГСЭ является максвелл $(Мкс)$, тогда ${{\mathcal E}}_i$ измеряется в СГСЭ – единицах потенциала. Для того, чтобы перевести ЭДС из системы гаусса в вольты необходимо умножить имеющееся значение на $300$. Следовательно, формулой связи системы СИ и СГСЭ можно записать выражение:

Среднее значение ЭДС индукции может быть определено как:

Поток сцепления

Если контур, в котором индуцируется ЭДС, состоит из $N$ витков (соленоид), витки соединены последовательно, ${{\mathcal E}}_i$ равна сумме ЭДС, которые индуцируются каждым витком в отдельности. Следовательно, используя формулу (1), можно записать:

Величину $\Psi$, равную:

называют потоком сцепления, или полным магнитным потоком. В том случае, если поток, который пронизывает каждый из витков, одинаковый, то можно записать, что:

В сложном контуре ${{\mathcal E}}_i$ вычисляют как:

Уравнение (8) называют основным законом электромагнитной индукции (уравнением Фарадея – Максвелла).

Частные случаи применения закона электромагнитной индукции

  1. Если проводник длины $l\ $движется в однородном магнитном поле (с индукцией $В$) с постоянной скоростью $v$, то на его концах возникает разность потенциалов $U$:

где $\alpha $ – угол между направлением скорости и вектором магнитной индукции.

  1. ЭДС индукции возникает в рамке, которая содержит $N$ витков, имеет площадь $S$ и вращается с постоянной угловой скоростью $\omega$ в однородном магнитном поле с индукцией $В$ и она равна:

где $\omega t$ – мгновенное значение угла между вектором магнитной индукции ($\overrightarrow{B}$) и вектором нормали к плоскости рамки ($\overrightarrow{n}$).

Пример 1

Задание: Найдите мгновенное значение ЭДС индукции рамки, которое соответствует углу поворота рамки $\alpha ,$ площадь рамки, равна $S$, она содержит $N$ витков. Рамка вращается в постоянном магнитном поле с индукцией $B$. Частота вращения рамки равна $n$.

Решение:

За основу решения задачи примем уравнение Фарадея – Максвелла:

\[{{\mathcal E}}_i=-\frac{d \Psi}{dt}\ \left(1.1\right),\]

где потокосцепление можно определить как:

\[\Psi=NФ\ \left(1.2\right),\]

где $N$ – количество витков, которые пронизывает магнитный поток $Ф$. Соответственно (1.1) примет вид:

\[{{\mathcal E}}_i=-N\frac{dФ}{dt}\ \left(1.3\right).\]

Если рамку вращать, то магнитный поток изменяется в соответствии с законом:

\[Ф=BScos\omega t\left(1.4\right),\]

где $\omega $ — угловая частота вращения. Подставим выражение (1.4) в (1.3), получим:

\[{{\mathcal E}}_i=NBS\omega sin\omega t\left(1.5\right).\]

Связь угловой частоты и часты вращения, определим как:

\[\omega =2\pi n\ \left(1.6\right),\] \[\omega t=\alpha \left(1.7\right).\]

Подставим выражения (1.6), (1.7) в формулу (1.5) получим:

\[{{\mathcal E}}_i=2\pi nNBSsin\alpha .\]

Ответ: ${{\mathcal E}}_i=2\pi nNBSsin\alpha .$

Пример 2

Задание: Определите среднее ЭДС индукции ($\left\langle {{\mathcal E}}_i\right\rangle )$, если магнитный поток, который пронизывает контур, изменяется от $Ф_1=40Вб$ до $Ф_2=0Вб$ в течении промежутка времени равного $2 с$.

Решение:

За основу решения примем формулу, определяющую среднюю ЭДС индукции:

\[\left\langle {{\mathcal E}}_i\right\rangle =-\frac{\Delta Ф}{\Delta t}\left(2.1\right).\]

Проведем вычисления:

\[\left\langle {{\mathcal E}}_i\right\rangle =-\frac{0-40}{2}=20\ \left(В\right).\]

Ответ: $\left\langle {{\mathcal E}}_i\right\rangle =20 В$.

spravochnick.ru

Закон электромагнитной индукции Фарадея – Gpedia, Your Encyclopedia

Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.[1] Закон гласит:

или другими словами:

Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.

При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца).[2]

История

Электромагнитная индукция была обнаружена независимо друг от друга Майклом Фарадеем и Джозефом Генри в 1831 году, однако Фарадей первым опубликовал результаты своих экспериментов[3][4].

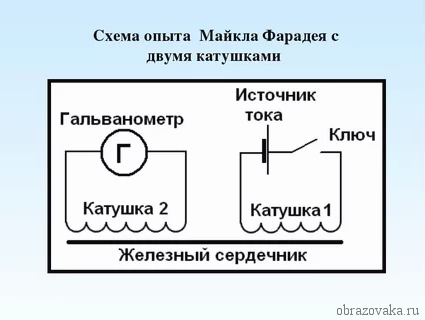
В первой экспериментальной демонстрации электромагнитной индукции (август 1831) Фарадей обмотал двумя проводами противоположные стороны железного тора (конструкция похожа на современный трансформатор). Основываясь на своей оценке недавно обнаруженного свойства электромагнита, он ожидал, что при включении тока в одном проводе особого рода волна пройдёт сквозь тор и вызовет некоторое электрическое влияние на его противоположной стороне. Он подключил один провод к гальванометру и смотрел на него, когда другой провод подключал к батарее. В самом деле, он увидел кратковременный всплеск тока (который он назвал «волной электричества»), когда подключал провод к батарее, и другой такой же всплеск, когда отключал его.[5] В течение двух месяцев Фарадей нашёл несколько других проявлений электромагнитной индукции. Например, он увидел всплески тока, когда быстро вставлял магнит в катушку и вытаскивал его обратно, он генерировал постоянный ток во вращающемся вблизи магнита медном диске со скользящим электрическим проводом («диск Фарадея»)[6].

Фарадей объяснил электромагнитную индукцию с использованием концепции так называемых силовых линий. Однако, большинство учёных того времени отклонили его теоретические идеи, в основном потому, что они не были сформулированы математически.[7] Исключение составил Максвелл, который использовал идеи Фарадея в качестве основы для своей количественной электромагнитной теории.[7][8][9] В работах Максвелла аспект изменения во времени электромагнитной индукции выражен в виде дифференциальных уравнений. Оливер Хевисайд назвал это законом Фарадея, хотя он несколько отличается по форме от первоначального варианта закона Фарадея и не учитывает индуцирование ЭДС при движении. Версия Хевисайда является формой признанной сегодня группы уравнений, известных как уравнения Максвелла.

Эмилий Христианович Ленц сформулировал в 1834 году закон (правило Ленца), который описывает «поток через цепь» и даёт направление индуцированной ЭДС и тока в результате электромагнитной индукции.

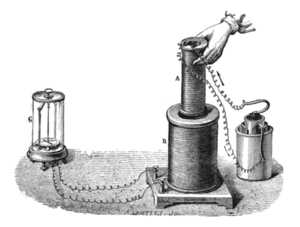Эксперимент Фарадея, показывающий индукцию между витками провода: жидкостная батарея (справа) даёт ток, который протекает через небольшую катушку (A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда маленькая катушка вставляется или извлекается из большой катушки (B), магнитный поток через катушку изменяется, вызывая ток, который регистрируется гальванометром (G).[10]

Закон Фарадея как два различных явления

Некоторые физики отмечают, что закон Фарадея в одном уравнении описывает два разных явления: двигательную ЭДС, генерируемую действием магнитной силы на движущийся провод, и трансформаторную ЭДС, генерируемую действием электрической силы вследствие изменения магнитного поля. Джеймс Клерк Максвелл обратил внимание на этот факт в своей работе О физических силовых линиях в 1861 году. Во второй половине части II этого труда Максвелл даёт отдельное физическое объяснение для каждого из этих двух явлений. Ссылка на эти два аспекта электромагнитной индукции имеется в некоторых современных учебниках.[11] Как пишет Ричард Фейнман:[12]

Таким образом, «правило потока» о том, что ЭДС в цепи равна скорости изменения магнитного потока через контур, применяется независимо от причины изменения потока: то ли потому что поле изменяется, то ли потому что цепь движется (или и то, и другое)…. В нашем объяснении правила мы использовали два совершенно различных закона для двух случаев  –    v×B{\displaystyle {\stackrel {\mathbf {v\times B} }{}}}   для «движущейся цепи» и   ∇ x E = −∂ tB{\displaystyle {\stackrel {\mathbf {\nabla \ x\ E\ =\ -\partial _{\ t}B} }{}}}   для «меняющегося поля».


Мы не знаем никакого аналогичного положения в физике, когда такие простые и точные общие принципы требовали бы для своего реального понимания анализа с точки зрения двух различных явлений.

— Ричард Фейнман,   Фейнмановские лекции по физике

Отражение этой очевидной дихотомии было одним из основных путей, которые привели Эйнштейна к разработке специальной теории относительности:

Известно, что электродинамика Максвелла — как её обычно понимают в настоящее время — при применении к движущимся телам приводит к асимметрии, которая, как кажется, не присуща этому явлению. Возьмем, к примеру, электродинамическое взаимодействие магнита и проводника. Наблюдаемое явление зависит только от относительного движения проводника и магнита, тогда как обычное мнение рисует резкое различие между этими двумя случаями, в которых либо одно, либо другое тело находится в движении. Ибо, если магнит находится в движении, а проводник покоится, в окрестности магнита возникает электрическое поле с определенной плотностью энергии, создавая ток там, где расположен проводник. Но если магнит покоится, а проводник движется, то в окрестности магнита никакое электрическое поле не возникает. В проводнике, однако, мы находим электродвижущую силу, для которой не существует соответствующей энергии самой по себе, но которая вызывает — предполагая равенство относительного движения в двух обсуждаемых случаях — электрические токи по тому же направлению и той же интенсивности, как в первом случае.

Примеры подобного рода вместе с неудачной попыткой обнаружить какое-либо движение Земли относительно «светоносной среды» предполагают, что явления электродинамики, а также механики не обладают свойствами, соответствующими идее абсолютного покоя.

— Альберт Эйнштейн, К электродинамике движущихся тел[13]

Поток через поверхность и ЭДС в контуре

Определение поверхностного интеграла предполагает, что поверхность Σ поделена на мелкие элементы. Каждый элемент связан с вектором dA, величина которого равна площади элемента, а направление — по нормали к элементу во внешнюю сторону. Векторное поле F(r, t) определено во всём пространстве, а поверхность Σ ограничена кривой ∂Σ, движущейся со скоростью v. По этой поверхности производится интегрирование поля.

Закон электромагнитной индукции Фарадея использует понятие магнитного потока ΦB через замкнутую поверхность Σ, который определён через поверхностный интеграл:

 :Φ=∬SBn⋅dS,{\displaystyle \Phi =\iint \limits _{S}\mathbf {B_{n}} \cdot d\mathbf {S} ,}

где dS — площадь элемента поверхности Σ(t), B — магнитное поле, а B·dS — скалярное произведение B и dS. Предполагается, что поверхность имеет «устье», очерченное замкнутой кривой, обозначенной ∂Σ(t). Закон индукции Фарадея утверждает, что когда поток изменяется, то при перемещении единичного положительного пробного заряда по замкнутой кривой ∂Σ возникает ЭДС E{\displaystyle {\mathcal {E}}}, величина которой определяется по формуле:

|E|=|dΦdt| ,{\displaystyle |{\mathcal {E}}|=\left|{{d\Phi } \over dt}\right|\ ,}

где |E|{\displaystyle |{\mathcal {E}}|} — величина электродвижущей силы (ЭДС) в вольтах, а ΦB — магнитный поток в веберах. Направление электродвижущей силы определяется законом Ленца.

Для плотно намотанной катушки индуктивности, содержащей N витков, каждый с одинаковым магнитным потоком ΦB, закон индукции Фарадея утверждает, что:

|E|=N|dΦBdt|,{\displaystyle |{\mathcal {E}}|=N\left|{{d\Phi _{B}} \over dt}\right|,}

где N — число витков провода, ΦB — магнитный поток в веберах на один виток.

При выборе пути ∂Σ(t) для нахождения ЭДС заметим, что путь должен удовлетворять двум основным требованиям: (i) путь должен быть замкнутым, и (ii) путь должен охватывать относительное движение частей контура (источник происхождения t-зависимости в ∂Σ(t)). К требованиям не относится то, что путь должен совпадать с линией тока, но, конечно, ЭДС, которая находится по закону потока, будет считаться по выбранному пути. Если путь не совпадает с линией тока, то подсчитанная ЭДС, возможно, будет не та ЭДС, которая вызывает ток.

Пример 1: пространственно меняющееся магнитное поле

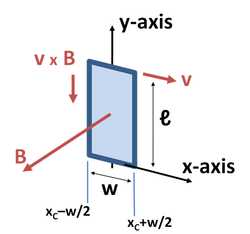Рис. 3. Замкнутый прямоугольный провод движется вдоль оси x со скоростью v в магнитном поле, которое изменяется вдоль x.

Рассмотрим случай на рисунке 3, на котором прямоугольная замкнутая проволочная петля, расположенная в плоскости xy, перемещается в направлении оси x со скоростью v. Центр петли xC удовлетворяет условию v = dxC / dt. Петля имеет длину ℓ в направлении оси y и ширину w в направлении оси x. Зависящее от времени пространственно меняющееся магнитное поле B(x) показано в направлении z. Магнитное поле на левой стороне равно B(xC − w / 2), а на правой стороне B(xC + w / 2). Электродвижущую силу можно найти либо с помощью закона Лоренца, либо, что эквивалентно, используя вышеизложенный закон индукции Фарадея.

Закон Лоренца

Заряд q в проводнике на левой стороне петли испытывает силу Лоренца q v × B k = −q v B(xC − w / 2) j   (j, k — единичные векторы в направлениях y и z; см. векторное произведение векторов), что вызывает ЭДС (работу на единицу заряда) v ℓ B(xC − w / 2) по всей длине левой стороны петли. На правой стороне петля аналогичное рассуждение показывает, что ЭДС равна v ℓ B(xC + w / 2). Две противоположные друг другу ЭДС толкают положительный заряд по направлению к нижней части петли. В случае, когда поле B возрастает вдоль х, сила на правой стороне будет больше, а ток будет течь по часовой стрелке. Используя правило правой руки, мы получаем, что поле B, создаваемое током, противоположно приложенному полю.[14] ЭДС, вызывающая ток, должна увеличиваться по направлению против часовой стрелки (в отличие от тока). Складывая ЭДС в направлении против часовой стрелки вдоль петли мы находим:

E=vℓ[B(xC+w/2)−B(xC−w/2)] .{\displaystyle {\mathcal {E}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ .}

Закон Фарадея

В любой точке петли магнитный поток через неё равен:

ΦB=±∫0ℓdy∫xC−w/2xC+w/2B(x)dx{\displaystyle \Phi _{B}=\pm \int _{0}^{\ell }dy\int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx}
=±ℓ∫xC−w/2xC+w/2B(x)dx .{\displaystyle \qquad =\pm \ell \int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx\ .}

Выбор знака определяется по принципу, имеет ли нормаль к поверхности в данной точке то же направление, что и B, или противоположное. Если нормаль к поверхности имеет то же направление, что и поле B наведённого тока, этот знак отрицательный. Производная по времени от потока (найденная с помощью методов дифференцирования сложной функции или по правилу Лейбница дифференцирования интеграла) равна:

dΦBdt=(−)ddxC[∫0ℓdy ∫xC−w/2xC+w/2dxB(x)]dxCdt {\displaystyle {\frac {d\Phi _{B}}{dt}}=(-){\frac {d}{dx_{C}}}\left[\int _{0}^{\ell }dy\ \int _{x_{C}-w/2}^{x_{C}+w/2}dxB(x)\right]{\frac {dx_{C}}{dt}}\ }
=(−)vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle \qquad =(-)v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}

(где v = dxC / dt является скоростью движения петли в направлении оси х), что приводит к:

E=−dΦBdt=vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}

как и в предыдущем случае.

Эквивалентность этих двух подходов является общеизвестной, и в зависимости от решаемой задачи более практичным может оказаться либо тот, либо другой метод.

Пример 2: проводник, движущийся в постоянном магнитном поле

Рис. 4. Два проводника замкнутые на проводящие обода образуют «рамку» вращающуюся с угловой скоростью ω в радиальном, направленном наружу магнитном поле B фиксированной величины. Ток подается щётками, касающимися верхнего и нижнего дисков с проводящими ободами.

На рис. 4 показан шпиндель, образованный двумя дисками с проводящими ободами, и проводники, расположенные вертикально между этими ободами. ток скользящими контактами подается на проводящие обода. Эта конструкция вращается в магнитном поле, которое направлено радиально наружу и имеет одно и то же значение в любом направлении. то есть мгновенная скорость проводников, ток в них и магнитная индукция, образуют правую тройку, что заставляет проводники вращаться.

Сила Лоренца

В этом случае на проводники действует Сила Ампера, а на единичный заряд в проводнике Сила Лоренца — поток вектора магнитной индукции B , ток в проводниках, соединяющих проводящие обода, направлен нормально к вектору магнитной индукции, тогда сила, действующая на заряд в проводнике, будет равна

F=qBv,{\displaystyle F=qBv\,,}

где v = скорости движущегося заряда[15]

Следовательно, сила действующая на проводники

F=IBℓ,{\displaystyle {\mathcal {F}}=IB\ell ,}

где l — длина проводников

Здесь мы использовали B как некую данность, на самом деле она зависит от геометрических размеров ободов конструкции, и это значение можно вычислить, используя Закон Био — Савара — Лапласа . Данный эффект используется и в другом устройстве, называемом Рельсотрон

Закон Фарадея

Интуитивно привлекательный, но ошибочный подход к использованию правила потока выражает поток через цепь по формуле ΦB = B w ℓ, где w — ширина движущейся петли.

Ошибочность такого подхода в том, что это не рамка в обычном понимании этого слова. Прямоугольник на рисунке образован отдельными проводниками, замкнутыми на обод. Как видно на рисунке, ток по обоим проводникам течет в одном направлении, то есть здесь отсутствует понятие «замкнутый контур»

Наиболее простое и понятное объяснение этому эффекту дает понятие сила Ампера. То есть вертикальный проводник может быть вообще один, чтобы не вводить в заблуждение. Или же проводник конечной толщины может быть расположен на оси, соединяющей обода. Диаметр проводника должен быть конечным и отличаться от нуля, чтобы момент силы Ампера был ненулевой.

Уравнение Фарадея — Максвелла

Рис. 6. Иллюстрация теоремы Кельвина-Стокса с помощью поверхности Σ, её границы ∂Σ и ориентации n , установленной правилом правой руки.

Переменное магнитное поле создаёт электрическое поле, описываемое уравнением Фарадея — Максвелла:

∇×E=−∂B∂t,{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}},}

где:

∇×{\displaystyle \nabla \times } обозначает ротор
E — электрическое поле
B — плотность магнитного потока.

Это уравнение присутствует в современной системе уравнений Максвелла, часто его называют законом Фарадея. Однако, поскольку оно содержит только частные производные по времени, его применение ограничено ситуациями, когда заряд покоится в переменном по времени магнитном поле. Оно не учитывает[уточнить] электромагнитную индукцию в случаях, когда заряженная частица движется в магнитном поле.

В другом виде закон Фарадея может быть записан через интегральную форму теоремы Кельвина-Стокса:[16]

∮∂Σ⁡E⋅dℓ=−∫Σ∂∂tB⋅dA.{\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\int _{\Sigma }{\partial \over {\partial t}}\mathbf {B} \cdot d\mathbf {A} .}

Для выполнения интегрирования требуется независимая от времени поверхность Σ (рассматриваемая в данном контексте как часть интерпретации частных производных). Как показано на рис. 6:

Σ — поверхность, ограниченная замкнутым контуром ∂Σ, причём, как Σ, так и ∂Σ являются фиксированными, не зависящими от времени,
E — электрическое поле,
dℓ — бесконечно малый элемент контура ∂Σ,
B — магнитное поле,
dA — бесконечно малый элемент вектора поверхности Σ.

Элементы dℓ и dA имеют неопределённые знаки. Чтобы установить правильные знаки, используется правило правой руки, как описано в статье о теореме Кельвина-Стокса. Для плоской поверхности Σ положительное направление элемента пути dℓ кривой ∂Σ определяется правилом правой руки, по которому на это направление указывают четыре пальца правой руки, когда большой палец указывает в направлении нормали n к поверхности Σ.

Интеграл по ∂Σ называется интеграл по пути или криволинейным интегралом. Поверхностный интеграл в правой части уравнения Фарадея-Максвелла является явным выражением для магнитного потока ΦB через Σ. Обратите внимание, что ненулевой интеграл по пути для E отличается от поведения электрического поля, создаваемого зарядами. Генерируемое зарядом E-поле может быть выражено как градиент скалярного поля, которое является решением уравнения Пуассона и имеет нулевой интеграл по пути.

Интегральное уравнение справедливо для любого пути ∂Σ в пространстве и любой поверхности Σ, для которой этот путь является границей.

Рис. 7. Площадь заметания элемента вектора dℓ кривой ∂Σ за время dt при движении со скоростью v.

Используя[17]

ddt∫AB dA=∫A(∂B∂t+v div B+rot(B×v))dA{\displaystyle {\frac {\text{d}}{{\text{d}}t}}\int \limits _{A}{\mathbf {B} }{\text{ d}}\mathbf {A} =\int \limits _{A}{\left({\frac {\partial \mathbf {B} }{\partial t}}+\mathbf {v} \ {\text{div}}\ \mathbf {B} +{\text{rot}}\;(\mathbf {B} \times \mathbf {v} )\right)\;{\text{d}}}\mathbf {A} }

и принимая во внимание divB=0{\displaystyle {\text{div}}\mathbf {B} =0} (Ряд Гаусса), B×v=−v×B{\displaystyle \mathbf {B} \times \mathbf {v} =-\mathbf {v} \times \mathbf {B} } (Векторное произведение) и ∫ArotXdA=∮∂A⁡Xdℓ{\displaystyle \int _{A}{\text{rot}}\;\mathbf {X} \;\mathrm {d} \mathbf {A} =\oint _{\partial A}\mathbf {X} \;{\text{d}}{\boldsymbol {\ell }}} (теорема Кельвина — Стокса), мы находим, что полная производная магнитного потока может быть выражена

∫Σ∂B∂tdA=ddt∫ΣB dA+∮∂Σ⁡v×Bdℓ.{\displaystyle \int \limits _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}{\textrm {d}}\mathbf {A} ={\frac {\text{d}}{{\text{d}}t}}\int \limits _{\Sigma }{\mathbf {B} }{\text{ d}}\mathbf {A} +\oint _{\partial \Sigma }\mathbf {v} \times \mathbf {B} \,{\text{d}}{\boldsymbol {\ell }}.}

Добавляя член ∮⁡v×Bdℓ{\displaystyle \oint \mathbf {v} \times \mathbf {B} \mathrm {d} \mathbf {\ell } } к обеим частям уравнения Фарадея-Максвелла и вводя вышеприведённое уравнение, мы получаем:

∮∂Σ⁡(E+v×B)dℓ=−∫Σ∂∂tBdA⏟induced emf+∮∂Σ⁡v×Bdℓ⏟motional emf=−ddt∫ΣB dA,{\displaystyle \oint \limits _{\partial \Sigma }{(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}{\text{d}}\ell =\underbrace {-\int \limits _{\Sigma }{\frac {\partial }{\partial t}}\mathbf {B} {\text{d}}\mathbf {A} } _{{\text{induced}}\ {\text{emf}}}+\underbrace {\oint \limits _{\partial \Sigma }{\mathbf {v} }\times \mathbf {B} {\text{d}}\ell } _{{\text{motional}}\ {\text{emf}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{\Sigma }{\mathbf {B} }{\text{ d}}\mathbf {A} ,}

что и является законом Фарадея. Таким образом, закон Фарадея и уравнения Фарадея-Максвелла физически эквивалентны.

Рис. 7 показывает интерпретацию вклада магнитной силы в ЭДС в левой части уравнения. Площадь, заметаемая сегментом dℓ кривой ∂Σ за время dt при движении со скоростью v, равна:

dA=−dℓ×vdt ,{\displaystyle d\mathbf {A} =-d{\boldsymbol {\ell \times v}}dt\ ,}

так что изменение магнитного потока ΔΦB через часть поверхности, ограниченной ∂Σ за время dt, равно:

dΔΦBdt=−B⋅ dℓ×v =−v×B⋅ dℓ ,{\displaystyle {\frac {d\Delta \Phi _{B}}{dt}}=-\mathbf {B} \cdot \ d{\boldsymbol {\ell \times v}}\ =-\mathbf {v} \times \mathbf {B} \cdot \ d{\boldsymbol {\ell }}\ ,}

и если сложить эти ΔΦB-вклады вокруг петли для всех сегментов dℓ, мы получим суммарный вклад магнитной силы в закон Фарадея. То есть этот термин связан с двигательной ЭДС.

Пример 3: точка зрения движущегося наблюдателя

Возвращаясь к примеру на рис. 3, в движущейся системе отсчета выявляется тесная связь между E– и B-полями, а также между двигательной и индуцированной ЭДС.[18] Представьте себе наблюдателя, движущегося вместе с петлёй. Наблюдатель вычисляет ЭДС в петле с использованием как закона Лоренца, так и с использованием закона электромагнитной индукции Фарадея. Поскольку этот наблюдатель движется с петлей, он не видит никакого движения петли, то есть нулевую величину v × B. Однако, поскольку поле B меняется в точке x, движущийся наблюдатель видит изменяющееся во времени магнитного поля, а именно:

B=kB(x+vt) ,{\displaystyle \mathbf {B} =\mathbf {k} {B}(x+vt)\ ,}

где k  — единичный вектор в направлении z.[19]

Закон Лоренца

Уравнение Фарадея-Максвелла говорит, что движущийся наблюдатель видит электрическое поле Ey в направлении оси y, определяемое по формуле:

∇×E=k dEydx{\displaystyle \nabla \times \mathbf {E} =\mathbf {k} \ {\frac {dE_{y}}{dx}}}
=−∂B∂t=−kdB(x+vt)dt=−kdBdxv  .{\displaystyle \qquad =-{\frac {\partial \mathbf {B} }{\partial t}}=-\mathbf {k} {\frac {dB(x+vt)}{dt}}=-\mathbf {k} {\frac {dB}{dx}}v\ \ .}

Применяя правило дифференцирования сложной функции:

dBdt=dBd(x+vt)d(x+vt)dt=dBdxv .{\displaystyle {\frac {dB}{dt}}={\frac {dB}{d(x+vt)}}{\frac {d(x+vt)}{dt}}={\frac {dB}{dx}}v\ .}

Решение для Ey с точностью до постоянной, которая ничего не добавляет в интеграл по петле:

Ey(x, t)=−B(x+vt) v .{\displaystyle E_{y}(x,\ t)=-B(x+vt)\ v\ .}

www.gpedia.com

Электромагнитная индукция — WiKi

Согласно закону электромагнитной индукции Фарадея (в СИ):

E=−dΦBdt,{\displaystyle {\mathcal {E}}=-{{d\Phi _{B}} \over dt},} 

где

E{\displaystyle {\mathcal {E}}}  — электродвижущая сила, действующая вдоль произвольно выбранного контура,
ΦB{\displaystyle \Phi _{B}}  =∬SB→⋅dS→{\displaystyle =\iint \limits _{S}{\vec {B}}\cdot d{\vec {S}}}  — магнитный поток через поверхность, ограниченную этим контуром.

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

E=−NdΦBdt=−dΨdt,{\displaystyle {\mathcal {E}}=-N{{d\Phi _{B}} \over dt}=-{{d\Psi } \over dt},} 

где

E{\displaystyle {\mathcal {E}}}  — электродвижущая сила,
N{\displaystyle N}  — число витков,
ΦB{\displaystyle \Phi _{B}}  — магнитный поток через один виток,
Ψ{\displaystyle \Psi }  — потокосцепление катушки.

Векторная форма

В дифференциальной форме закон Фарадея можно записать в следующем виде:

rotE→=−∂B→∂t{\displaystyle \operatorname {rot} \,{\vec {E}}=-{\partial {\vec {B}} \over \partial t}}  (в системе СИ)

или

rotE→=−1c∂B→∂t{\displaystyle \operatorname {rot} \,{\vec {E}}=-{1 \over c}{\partial {\vec {B}} \over \partial t}}  (в системе СГС).

В интегральной форме (эквивалентной):

∮∂S⁡E→⋅dl→=−∂∂t∫SB→⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-{\partial \over \partial t}\int _{S}{\vec {B}}\cdot {\vec {ds}}} (СИ)

или

∮∂S⁡E→⋅dl→=−1c∂∂t∫SB→⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-{1 \over c}{\partial \over \partial t}\int _{S}{\vec {B}}\cdot {\vec {ds}}}  (СГС).

Здесь E→{\displaystyle {\vec {E}}}  — напряжённость электрического поля, B→{\displaystyle {\vec {B}}}  — магнитная индукция, S {\displaystyle S\ }  — произвольная поверхность, ∂S{\displaystyle \partial S}  — её граница. Контур интегрирования ∂S{\displaystyle \partial S}  подразумевается фиксированным (неподвижным).

Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).

  • В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)[3].

Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство E=−dΦ/dt{\displaystyle {\mathcal {E}}=-{{d\Phi }/dt}}  продолжает соблюдаться, но ЭДС в левой части теперь не сводится к ∮⁡E→⋅dl→{\displaystyle \oint {\vec {E}}\cdot {\vec {dl}}}  (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула остаётся справедливой, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).

  • Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год[4] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле E=−dΦ/dt{\displaystyle {\mathcal {E}}=-{{d\Phi }/dt}}  в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)[5]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
  • Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определённых ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединённым к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчёта, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчёта, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчёта мы её рассчитали.

Потенциальная форма

При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:

E→=−∂A→∂t{\displaystyle {\vec {E}}=-{\partial {\vec {A}} \over \partial t}}  (в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).

В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:

E→=−∇φ−∂A→∂t{\displaystyle {\vec {E}}=-\nabla \varphi -{\partial {\vec {A}} \over \partial t}} 

Подробнее

Поскольку вектор магнитной индукции по определению выражается через векторный потенциал так:

B→=rot A→≡∇×A→,{\displaystyle {\vec {B}}=rot\ {\vec {A}}\equiv \nabla \times {\vec {A}},} 

то можно подставить это выражение в

rot E→≡∇×E→=−∂B→∂t,{\displaystyle rot\ {\vec {E}}\equiv \nabla \times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},} 

получая

∇×E→=−∂(∇×A→)∂t,{\displaystyle \nabla \times {\vec {E}}=-{\frac {\partial (\nabla \times {\vec {A}})}{\partial t}},} 

и, поменяв местами дифференцирование по времени и пространственным координатам (ротор):

∇×E→=−∇×∂A→∂t.{\displaystyle \nabla \times {\vec {E}}=-\nabla \times {\frac {\partial {\vec {A}}}{\partial t}}.} 

Отсюда, поскольку ∇×E→{\displaystyle \nabla \times {\vec {E}}}  полностью определяется правой частью последнего уравнения, видно, что вихревая часть электрического поля (та часть, которая имеет ротор, в отличие от безвихревого поля ∇φ{\displaystyle \nabla \varphi } ) полностью определяется выражением

−∂A→∂t.{\displaystyle -{\frac {\partial {\vec {A}}}{\partial t}}.} 

То есть в случае отсутствия безвихревой части можно записать

E→=−∂A→∂t,{\displaystyle {\vec {E}}=-{\frac {\partial {\vec {A}}}{\partial t}},} 

а в общем случае

E→=−∇φ−dA→dt.{\displaystyle {\vec {E}}=-\nabla \varphi -{\frac {d{\vec {A}}}{dt}}.} 

В 1820 году Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 году в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.

В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.

М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.

ru-wiki.org

Related Posts

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *