Первый закон ньютона закон инерции – Инерция. Первый закон Ньютона — урок. Физика, 9 класс.
- Комментариев к записи Первый закон ньютона закон инерции – Инерция. Первый закон Ньютона — урок. Физика, 9 класс. нет
- Советы абитуриенту
Инерция. Первый закон Ньютона — урок. Физика, 9 класс.
Инерция — это явление сохранения скорости движения тела при отсутствии внешних воздействий.
Обрати внимание!
Согласно закону инерции, тела (материальные точки) находятся в покое или движутся прямолинейно и равномерно (т.е. сохраняют свою скорость неизменной), если на них не действуют другие тела.
На протяжении многих веков в науке господствовала точка зрения древнегреческого учёного Аристотеля и его последователей: при отсутствии внешнего воздействия тело может только покоиться, а для того чтобы тело двигалось с постоянной скоростью, нужно, чтобы на него непрерывно действовало другое тело.
Первым отверг такие представления Галилео Галилей. Он предположил, что в результате взаимодействий любого тела с другими телами происходят изменения скорости его движения. При отсутствии действия других тел скорость тела не изменяется ни по модулю, ни по направлению.
Таким образом, Галилей пришёл к выводу о том, что при отсутствии внешних воздействий тело может не только покоиться, но и двигаться прямолинейно и равномерно. А сила, которую приходится прикладывать к телу для поддержания его движения, необходима только для того, чтобы уравновесить другие приложенные к телу силы, например, силу трения.
Обрати внимание!
После прекращения воздействий тело движется равномерно и прямолинейно по касательной к первоначальной траектории движения.
На основе вывода Галилея английский учёный Исаак Ньютон сформулировал закон инерции.В изложении Ньютона закон инерции читается так:
Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Всякое тело находится в покое или движется равномерно и прямолинейно, если на него не действуют другие тела или их действия компенсируют друг друга.
Закон инерции называют первым законом Ньютона или первым законом механики.
www.yaklass.ru
Первый закон Ньютона: инерция
Физика > Первый закон Ньютона: инерция
Первый закон Ньютона и инерция. Изучите основы механики Ньютона, момент инерции движения в физике, формулировка и формула первого закона, инерциальная система.
Первый закон движения Ньютона концентрируется на инерции. Тело в состоянии покоя будет оставаться стабильным, а смещающийся объект продолжит движение.
Задача обучения
- Разобраться в Первом законе движения.
Основные пункты
- Три закона физики Ньютона составляют основу механики.
- Первый закон гласит: тело в состоянии покоя останется стабильным, пока на него не повлияет внешняя сила, также и движущееся тело останется в движении, пока не почувствует внешнее воздействие.
- Чистая внешняя сила – сумма всех факторов, влияющих на объект.
- Наличие воздействующих сил не означает присутствие чистой внешней силы. Одинаковые по величине силы, но действующие в противоположных направлениях, могут отменить друг друга.
- Трение – сила между перемещающимся телом и поверхностью. Это внешняя сила, влияющая на замедление.
- Инерция – тенденция тела в движении продолжать двигаться. Зависит от массы, поэтому чем тяжелее тело, тем сложнее изменить направление движения.
Термины
- Инертность – свойство объекта, которое вступает в сопротивление с любой трансформацией текущего положения (эквивалентно массе).
- Равномерное движение – перемещение с неизменной скоростью.
- Трение – сила, сопротивляющаяся относительному движению.
История
Исаак Ньютон интересовался перемещением объектов в различных условиях. В 1687 году он описал три знаменитых закона движения, применимых для характеристики физических объектов и систем. Они составляют основу механики и описывают связь сил, воздействующих на тело, и вызванные этим движения. Три закона гласят:
– Если объект не испытывает никакого силового влияния, то скорость останется стабильной. Если объект пребывает в покое, то скорость равняется нулю.
– Ускорение параллельно и прямо пропорционально чистой силе, влияющей на объект, и находится в направлении чистой силы и обратно пропорционально массе.
– Если первый объект влияет силой на второй, то тот одновременно влияет на первый. То есть их силы одинаковы по величине и противоположны по направлению.
Первый закон движения
Итак, тело пребывает в движении или покое, пока на него не воздействует внешняя сила. То есть, движущееся тело сохранит свою скорость, если на него ничего не влияет. Это именуют равномерным движением.
Примеры
Давайте разберем Первый закон Ньютона в конкретной системе отсчета. Представьте, что вы едете на коньках в инерциальной системе. Если оттолкнетесь от одного борта, то по Первому закону Ньютона должны прибыть ко второму. Но этого не случится. Не забывайте, что движение продолжается, если на него не влияет внешняя сила. В нашем мире этой силой чаще всего выступает трение. В данном случае – трение между коньками и льдом.
А как насчет ремней безопасности? В случае автомобильной аварии, они должны защитить нас. Допустим, машина едет со скоростью 60 миль/ч. Если резко затормозить, то машина ощущает внешнюю силу и замедляется. Но на водителя это не действует, поэтому он продолжит перемещаться на прежней скорости. Ремень создает противовес и тормозит человека.
Иллюстрация Первого закона Ньютона
Инертность
Иногда этот закон именуют законом инерции или инерциальной системой отсчета. Она выступает свойством тела фиксироваться в состоянии покоя или смещения (с постоянной скоростью). У некоторых инерция больше, потому что эквивалентна массе. Поэтому сложнее изменить направление валуна, чем шарика для гольфа.
v-kosmose.com
| ||||||||||||||||||||||||||||||||
Рис. 1 Преобразование Галилея | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Рис. 2 Галилео Галилей (1564–1642) и Исаак Ньютон (1642–1727) | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Рис. 3 Нахождение вектора равнодействующей силы | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Рис. 5 Иллюстрация третьего закона Ньютона | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
www.nscience.ru
Первый закон Ньютона – закон инерции. Инерциальная система отсчета.
1. За первый закон движения Ньютон принял закон инерции, высказанный в частной форме еще Галилеем. Согласно этому закону тело, не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называется свободным.
Свободных тел не существует. Поэтому они являются физическими абстракциями. Однако можно поставить тело в такие условия, когда внешние воздействия на него по возможности устранены или практически компенсируют друг друга. Представив, что эти воздействия беспредельно уменьшаются, мы и приходим в пределе к представлению о свободном теле и свободном движении.
2. Закон инерции не может быть справедлив во всех системах отсчета. Классическая механика постулирует, что существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчета. Таким образом, содержание закона инерции сводится к утверждению, что существует по крайней мере одна инерциальная система отсчета.
3. Земная система отсчета не может быть точно инерциальной, так как Земля испытывает два вращательных движения: вокруг собственной оси и вокруг Солнца. Однако эти движения происходят относительно медленно и для множества движений можно считать, что земная система отсчета инерциальна. Нужны специальные опыты, чтобы вскрыть ее инерциальность.
Гелиоцентрическая система отсчета, оси в которой направлены на почти неподвижные удаленные звезды, еще лучше удовлетворяет требованию инерциальности. В этой системе можно изучать движение тел, малых по сравнению с размерами Галактики.
4. То есть, если существует класс движений, который мы желаем изучать, то всегда можно построить систему отсчета, которая будет инерциальной для данного класса движений.
6 Масса. Импульс. Второй закон Ньютона. Сила.
1. Всякое тело оказывает сопротивление при попытках привести его в движение или изменить модуль или направление его скорости. Это свойство называется инертностью. У разных тел оно проявляется в разной степени. Мера инертности называется массой.
Для сравнения масс можно применить закон сохранения импульса, который будет сформулирован позднее. Из этого закона можно найти отношение масс. Для перехода от отношения масс к массам как таковым, необходимо выбрать эталон массы.
2. За эталон выбрана масса международного эталона килограмма, хранящегося в Международном бюро мер и весов (расположено в г. Севр близ Парижа) и представляющего собой цилиндр диаметром и высотой 39.17 мм из платино-иридиевого сплава (90 % платины, 10 % иридия). Первоначально килограмм определялся как масса одного кубического дециметра (литра) чистой воды при температуре 4 °C и стандартном атмосферном давлении на уровне моря.
3. Для формулировки второго закона Ньютона введем понятие импульса. Импульсом или количеством движения МТ называется вектор, равный произведению массы точки на ее скорость:
.
Импульсом или количеством движения системы материальных точек назовем сумму импульсов отдельных материальных точек:
Эти формулы годятся для медленных движений ( ). В случае скоростей, близких к скорости света, формула для импульса МТ должна быть изменена.
4. Для формулировки второго закона Ньютона надо ввести понятие силы. Силой в механике считают всякую причину, изменяющую импульс тела. Это качественное определение.
Количественное определение: в инерциальной системе отсчета производная импульса МТ по времени представляется уравнением:
Отсюда, второй закон Ньютона: в инерциальной системе отсчета производная импульса МТ по времени равна действующей на нее силе. Для медленных движений и постоянной массе эту формулу можно представить в виде:
Здесь однозначно определяется свойствами рассматриваемой МТ и окружающих ее тел, а также положениями и скоростями этих тел относительно МТ. Величина называется слой, действующей на рассматриваемую МТ. В частных случаях сила может определяться только положением или только одной ее скоростью, но не может явно зависеть от ускорения этой точки. Из закона следует, что сила – вектор, и сложение сил подчиняется правилу параллелограмма.
Это уравнение не есть способ определения силы. Силы должны определятся как-нибудь по-другому. Например, с помощью динамометра. Подробности в учебнике.
3. Рассмотрим соотношение между первым и вторым законами Ньютона. Если положить , то получится . Отсюда следует, что , т.е. импульс, а с ним и скорость свободно движущейся МТ постоянны. Таким образом, формально первый закон Ньютона следует из второго. Однако формула, определяющая второй закон Ньютона, имеет смысл только в инерциальных системах отсчета, а для введения таких систем требуется отдельный, первый закон Ньютона.
4. Второй закон Ньютона позволяет ввести единицу силы. В системе СИ такая единица называется ньютон (Н). Один ньютон = эта сила, которая массе в 1 кг сообщает ускорение в 1 м/с2.Есть другая система, очень любимая физиками, СГС (сантиметр (см), грамм (г), секунда (с)). В этой системе единица силы называется дина (дин).
7 Третий закон Ньютона. Формулирование задачи движения материальных точек. Начальные условия.
Рассмотрим замкнутую систему, состоящую из двух взаимодействующих МТ. В этом случае справедлив закон сохранения импульса
Дифференцируя это уравнение по времени и использовав второй закон Ньютона, получим:
.
Где и — силы, с которыми рассматриваемые МТ действуют друг на друга. Привлечем опытный факт, согласно которому силы и направлены вдоль прямой, соединяющей взаимодействующие точки. Тогда мы приходим к третьему закону Ньютона:
Силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.
2. Аналогично, можно сформулировать третий закон Ньютона, если МТ много. Для этого рассматриваются отдельно силы взаимодействия отдельных точек друг с другом. Пусть — сила, с которой i-я точка действует на k-ю, — сила, с которой k-я точка действует на i-ю. Третий закон утверждает, что обе эти силы направлены вдоль прямой, соединяющей взаимодействующие точки, причем .
3. Векторное уравнение движения МТ можно записать в координатной форме:
То есть получили три дифференциальных уравнения. Для их решения необходимо задать либо две векторные, либо шесть числовых постоянных. Обычно берут значения радиус-вектора и скорости в момент времени . Их называют начальными условиями.
Пример. Движение в поле силы тяжести.
Галилеем было установлено, что все тела в пустоте вблизи Земли падают с одинаковым ускорением. Сила тяжести выражается формулой , и уравнение движения переходит в
.
Простым дифференцированием можно убедиться, что это уравнение имеет общее решение:
при произвольных значениях постоянных векторов и . Эти два вектора должны быть заданы при .
4. Для системы из материальных точек необходимо задать начальный радиус-вектор и начальная скорость, т.е. всего векторов или чисел, определяющих начальные значения координат и скоростей материальных точек системы.
Силы в механике. Гравитационные силы. Закон всемирного тяготения. Принцип суперпозиции. Факты, подтверждающие закон всемирного тяготения. Сила упругости. Закон Гука. Сила трения. Сухое трение. Трение покоя. Трение скольжения.
1. Взаимодействие тел может происходить либо при непосредственном соприкосновении, либо на расстоянии. В первом случае взаимодействующие тела тянут или толкают друг друга. Возникающие при этом силы обычно вызываются деформациями тел. Если деформации малы, то от них можно отвлечься, учтя их влияние введением сил натяжения и давления.
2. Помимо сил, действующих при соприкосновении тел, в природе существуют силы, которые действуют на расстоянии, без участия промежуточной среды. К таким силам относятся гравитационные силы и силы взаимодействия наэлектризованных и намагниченных тел.
3. Согласно основным представлениям механики Ньютона силы, действующие на всякое тело в какой-либо момент времени, зависят от положения и скоростей остальных тел в тот же самый момент времени. Такое представление приводит к бесконечно большой скорости передачи взаимодействий. Опытные же факты привели к заключению, что скорость передачи взаимодействий ограничена скоростью света в вакууме. Отсюда сразу следует, что третий закон Ньютона не выполняется для взаимодействий на расстоянии. Физики нашли выход из этого. Они введи понятие поля. Тело возбуждают в окружающем пространстве силовое поле, которое в месте нахождения тела проявляется в виде действующих на него сил. И обратно. Взаимодействия прикосновением являются частными случаями полевого взаимодействия — через молекулярные поля.
4. Сила упругости.
Силами упругости называются силы, возникающие при деформации тел, то есть при изменении их формы и размеров. При этом изменяются расстояния между молекулами внутри тела, и электромагнитные силы пытаются вернуть молекулы обратно. Если после прекращения действия силы, вызвавшей деформацию, тело принимает первоначальную форму и размеры, то деформация называется упругой.
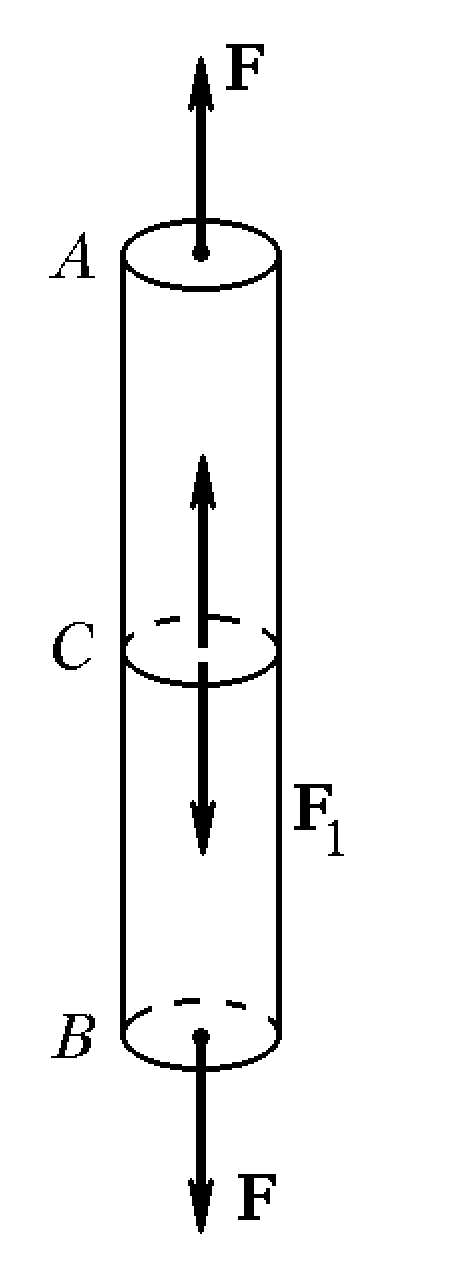
Простейшими деформациями являются деформации растяжения и сжатия. Они описываются законом Гука при малых упругих деформациях.
На рисунке рассмотрен случай растяжения. Сила, вызывающая растяжения стержня обозначена . Равная ей по величине и противоположно направленная возвращающая сила выражается через экспериментальный закон Гука:
.
Здесь – размер, на который увеличилась длина стержня, а называется коэффициентом жесткости стержня. Знак минус указывает на то, что сила направлена в сторону, обратную изменения длины стержня. Если разделить силу на площадь сечения стержня , а удлинение на первоначальную длину стержня , то закон Гука преобразуется к виду:
.
Здесь называется модулем Юнга и зависит только от вещества стержня. Для конкретного стержня величина выражается из формулы
.
Аналогично представляется другая деформация — сдвига. Ее мы рассматривать не будем. Все малые деформации сводятся к деформациям растяжения и сдвига.
5. Гравитационная сила. Сила тяжести.
Исаак Ньютон воспользовался тремя законами астронома Иоганна Кеплера и вывел закон всемирного тяготения, выражающийся формулой:
.
Здесь и — массы взаимодействующих материальных точек, — расстояние между точками, — сила взаимодействия, — гравитационная постоянная. Сила направлена по прямой, соединяющей МТ и является силой притяжения. В настоящее время этот закон обобщен в общей теории относительности. Как объясняется эта формула изнутри, пока не известно. За последние несколько лет выяснилось, что возможно существует темная материя, в которой предполагается гравитационная сила отталкивания.
Вблизи планеты, в том числе вблизи Земли ( ), эта формула преобразуется к виду:
,
где называется ускорением свободного падения. Эта сила обычно называется силой тяжести.
Силы трения.
Силы трения действует на поверхности между движущимися телами. Различают сухое трение между твердыми телами и внутреннее трение между отдельными слоями одной и той же жидкости.
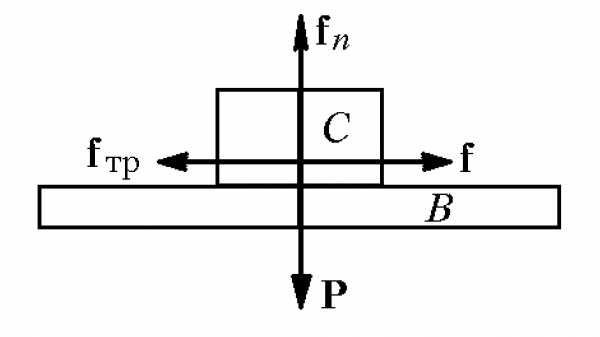 Сейчас рассмотрим сухое трение, которое в свою очередь подразделяется на трение скольжения и трение качение. Ограничимся трением скольжения, которое представлено на рисунке. Тело расположено поверх тела . Рассмотрим силы, действующие на тело . — вес тела, — сила реакции опоры, — сила, толкающая тело вправо, — сила трения скольжения.
Сейчас рассмотрим сухое трение, которое в свою очередь подразделяется на трение скольжения и трение качение. Ограничимся трением скольжения, которое представлено на рисунке. Тело расположено поверх тела . Рассмотрим силы, действующие на тело . — вес тела, — сила реакции опоры, — сила, толкающая тело вправо, — сила трения скольжения.
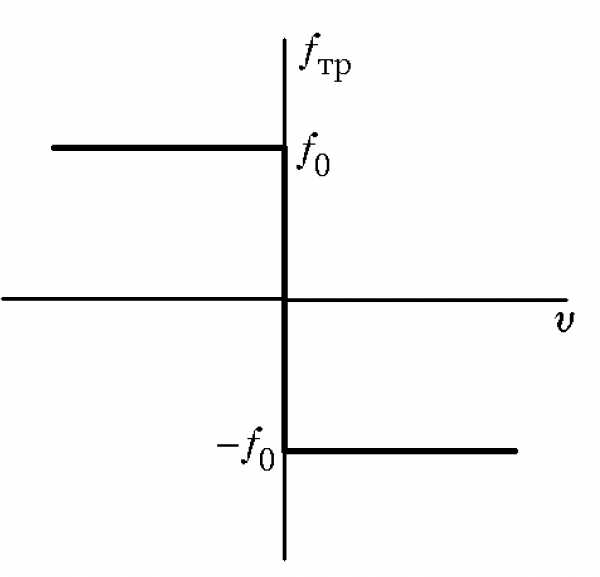
В состоянии покоя вес и реакция опоры уравновешены. Если приложить силу , то при небольших ее величинах тело будет неподвижно, то есть сила трения равна по величине этой силе. Такая сила трения называется силой трения покоя. Но она не может быть больше некоторой опытной величины . Для этой величины установлено, что , где — коэффициент трения. Определяется материалами тел. Приближенная зависимость силы трения от скорости движения верхнего тела относительно нижнего представлено на рисунке.
Сила внутреннего трения будет рассмотрена в другом месте.
infopedia.su
§4. Закон инерции (первый закон Ньютона).
Ньютон дал следующую формулировку закона инерции [6, с.232]: “Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние”.
Историю закона инерции следует начать с Галилея, так как до него понятия движения тел по инерции не было. Аристотель, например, утверждал, что для поддержания движения свободного тела к нему необходимо постоянно прикладывать силу. Галилей в своей работе “Диалоги о двух важнейших системах мира, птолемеевой и коперниковой” утверждал [6, с.161]: “Когда тело движется по горизонтальной плоскости, не встречая никакого сопротивления, то… движение его является равномерным и продолжалось бы бесконечно, если бы плоскость простиралась в пространстве без конца”.
Позже Р. Декарт сформулировал закон инерции в виде двух законов природы [7, с.368-369]: “Первый закон природы: всякая вещь пребывает в том состоянии, в каком она находится, пока ее что-либо не изменит”.
“Второй закон природы: всякое движущееся тело стремится продолжать свое движение по прямой”.
И еще [7, с.200]: “…каждая частица материи в отдельности продолжает находиться в одном и том же состоянии до тех пор, пока столкновение с другими частицами не вынуждает ее изменить это состояние…раз уже она начала двигаться, то будет продолжать это движение постоянно с равной силой до тех пор, пока другие ее не остановят или не замедлят ее движение”.
Приведенные формулировки закона инерции, данные Декартом, по своей сути почти ничем не отличаются от формулировки И.Ньютона, за исключением второго закона природы, который можно отнести к каждому моменту движения тела при наличии действующих на него сил. Целесообразность такой формулировки закона инерции –будет показана ниже.
В одной из современных формулировок закон инерции выглядит так [8, с.70]: “Если на материальную точку не действуют силы, то она сохраняет состояние покоя или равномерного и прямолинейного движения”.
Данная формулировка закона инерции очень похожа на формулировку И.Ньютона, но с одной только разницей: у Ньютона речь идет о теле, а здесь – о материальной точке. И это, на первый взгляд, не существенное различие, на самом деле является принципиальным.
Во-первых, понятие материальной точки является условным, поскольку в природе таких материальных объектов нет. Поэтому создателям механики и в голову не могло прийти сравнивать реальные тела с математической точкой, то есть с фикцией. Другое дело, что движение тел во многих случаях можно было описать как движение одной его точки, за которую принимался центр масс тела. Однако, некритическое отношение к этому вопросу привело в дальнейшем уже к принципиальному убеждению, что законы механики относятся только к материальной точке или к системе материальных точек, а не к реальным телам. Хотя ясно, что точка остается точкой, если ее даже и назвать материальной. И этим самым развитию механики был поставлен труднопреодолимый барьер. Ниже этот вопрос будет обсуждаться подробнее.
Во-вторых, отнесение закона инерции к движению только материальной точки приводит к тому, что сам этот закон также становится фикцией, так как движутся все-таки реальные тела, состоящие из атомов, а в атомах имеются ядра и электроны, которые вращаются вокруг своих осей, а электроны еще и вокруг ядер, причем в целом довольно хаотично. И если средневековые ученые могли еще думать, что все частицы любого тела могут двигаться с одинаковыми скоростями, поскольку они не знали, что все тела состоят из атомов, то современные ученые должны этот факт учитывать.
Таким образом, к закону движения по инерции может быть два варианта отношения: или считать его условным, фиктивным, или учесть реальность и относить его к реальным телам, а не к точкам. При этом необходимо учесть и тот факт, что движения материальных объектов без силового воздействия на них в природе практически не существует.
Такая постановка вопроса приводит к необходимости осмысления новой сущности закона инерции и изменения его формулировки. В §4 первой главы мы уже говорили о необходимости представить этот закон в дифференциальной форме, то есть считать его справедливым, для любого момента движения материальных объектов, независимо от характера этого движения. Сейчас мы сделаем некоторые уточнения для предложенной там формулировки. Это связано, во-первых, с тем, что любое материальное тело представляет собой совокупность частиц, которые в одно и то же время могут иметь разные скорости и ускорения, как, например, во вращательном движении. И, во-вторых, необходимо иметь в виду, что силовое воздействие на тело и его частицы обусловлено подводом энергии
Тогда закон инерции можно сформулировать следующим образом:
– Инерция – это стремление тела, как единого целого сохранить состояние покоя или скорость (энергию) своего движения в любой момент этого движения как при действии на него сил, так и при отсутствии такого воздействия; при прекращении силового воздействия тело будет двигаться в соответствии с имеющейся у него на данный момент скоростью в любой выбранной системе отсчета.
Можно дать и другую формулировку закона инерции:
– В любой момент своего движения материальный объект стремится двигаться с имеющейся у него на данный момент скоростью (энергией) независимо от выбранной системы отсчета, и только внешние воздействия препятствуют такому движению.
Ярким подтверждением справедливости дифференциальной трактовки закона инерции является движение тел по окружности, не связанных жестко с центром вращения, как, например, при движении планет вокруг Солнца (в главе III будет показано, что движение планет вокруг Солнца можно считать вращательным движением). В популярной литературе это движение часто объясняется так: за счет притяжения Солнца планеты падают на него, но наличие у них скорости в касательном направлении смещает планету в сторону, в результате чего и получается движение по окружности (приближенно). С точки же зрения закона инерции круговой характер движения планет следует объяснять таким образом: в любой момент своего движения планета стремится двигаться по направлению имеющейся у нее на данный момент скорости, но под действием притяжения Солнца в каждый момент движения происходит изменение этой скорости (при круговом вращательном движении меняется только направление скорости), в результате чего траектория движения искривляется и становится окружностью при постоянной действующей силе. Здесь следует подчеркнуть, что основное движение планет это движение по инерции, а сила притяжения со стороны Солнца только искривляет траекторию этого движения.
Таким образом, если бы не было инерции у тел, то их движение всегда происходило бы только по направлению действующих на них сил.
Трактовка закона инерции в дифференциальной форме ставит также вопрос и о причинах его существования, то есть о его физической сущности. То, что тела при отсутствии на них силового воздействия должны двигаться с постоянной скоростью, нам понятно, так как при наличии сил появляется ускорение. Но движение по инерции пусть и мгновенное при постоянном силовом воздействии требует осмысления. Здесь, очевидно, следует сравнивать кинетические энергии, связанные с инерционным движением и силовым воздействием. Поскольку любое тело при движении имеет какую-то скорость, то оно имеет и определенную кинетическую энергию. Силовое воздействие тоже связано с затратами энергии. Из опыта нам известно, что чем больше будет сила, приложенная к движущемуся телу, тем сильнее изменится характер его движения. Это значит, что чем больше будет подведенная к телу энергия по сравнению с энергией его движения, тем больше будет ее влияние на характер движения тела. Поэтому можно утверждать, что инерция движущегося тела определяется его кинетической энергией. Именно соотношение кинетической энергии тела и энергии силового воздействия определяет закон движения тела.
Найдем затраты энергии на искривление траектории при вращательном движении тел. К телу, движущемуся по окружности (рис.1), подводится энергия в радиальном направлении, в результате чего изменяется направление его скорости, но не ее величина. Можно ли в этом случае сказать, что происходит изменение кинетической энергии тела? Если иметь в виду только ее величину, то нет. Если же учитывать направленность кинетической энергии, то да. Этот пример является еще одним подтверждением направленности кинетической энергии, ее векторной сущности при движении тел и их взаимодействии, потому что для изменения направления движения необходимо приложить силу, то есть подвести добавочную энергию в определенном направлении. Величина радиальной (центростремительной) силы определяется величиной изменения кинетической энергии тела , отнесенной к величине его радиального перемещения при угле поворота . Изменение кинетической энергии тела будет равно подведенной к нему энергии :
, (1)
где m – масса тела, – изменение окружной скорости тела при угле поворота от начального положения.
В соответствии с рис.1,б имеем:
, (2)
где V – окружная скорость тела.
Центростремительная сила определяется отношением при , где в соответствии с рис.1,а будет равно:
(3)
Тогда:
(4)
Затраты кинетической энергии определим, представив выражение (1) с учетом выражения (2) в виде:
(5)
Последовательно увеличивая значение угла в 2, 3,…n раз, придем к формуле:
, (6)
где за один полный оборот число шагов n будет равно:
(7)
В соответствии с формулой (6) затраты кинетической энергии при вращательном движении графически представлены на рис.2. Поскольку энергия все время потребляется, то максимальное значение энергии , соответствующее половине оборота, следует удвоить, чтобы найти затраты энергии за полный оборот.
Тогда, имея в виду, что для половины оборота , получим:
(8)
Таким образом, чтобы заставить тело двигаться по окружности, к нему надо подвести энергию в 8 раз большую, чем его собственная энергия движения.
Интересно также отметить следующий результат, вытекающий из полученного нами соотношения. Поскольку затраты энергии можно определить через работу центростремительной силы:
, (9)
где S – перемещение точки приложения силы, соответствующее направлению ее действия.
Используя выражения (8) и (4), получим:
(10)
Отсюда следует, что перемещение S представляет собой два диаметра окружности радиуса r, а работа центростремительной силы будет определяться кратчайшим расстоянием между наиболее удаленными точками окружности при движении тела сперва в одну (удаление), а затем другую (приближение) стороны от его начального положения.
Таким образом, инерцию тела можно определить как его стремление сохранить свою кинетическую энергию при внешнем воздействии. Характер движения тела будет зависеть от соотношения его собственной кинетической энергии и энергии, к нему подведенной. При этом характер движения будет зависеть не только от величины подведенной энергии, но и от направления ее подведения.
Если к телу не подводится никакой энергии, то его энергия не изменяется и оно движется с постоянной по величине и направлению скоростью. Однако, здесь следует иметь в виду, что так можно говорить, если рассматривать тело как единое целое. Если же иметь в виду и частички, из которых состоит тело (электроны и ядра), то для них такое утверждение будет неверно, так как они движутся с переменными скоростями и ускорениями. Очевидно, о постоянстве скорости можно говорить только для центра масс тела. А в целом о теле можно сказать только, что оно движется с постоянной энергией, так как энергия его частичек тоже не меняется. При таком определении инерции не исключается возможность и вращательного движения тела по инерции с постоянной угловой скоростью, или даже сочетание его прямолинейного движения с постоянной скоростью и вращения вокруг центра масс с постоянной угловой скоростью.
Что касается затрат энергии на вращение частичек тела, то противоположно расположенные частички взаимно воздействуют друг на друга (без внешнего воздействия), в связи с чем затрат энергии не происходит.
В свете всего сказанного выше закон инерции Ньютона можно считать интегральным законом, справедливым для конечных промежутков времени. Этот закон можно обобщить и на случай вращательного движения, сформулировав его следующим образом:
– Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного прямолинейного или равномерного вращательного движения пока в результате взаимодействий не изменится его кинетическая энергия.
Таким образом, мы расширили существующее понятие интегрального закона инерции, обобщив его и на равномерное вращательное движение и связав его с постоянством кинетической энергии тела. Причем сделали мы это в классической традиции, связав его с постоянством скорости движения тел. Скорость движения будет постоянной как при отсутствии действия на тело каких-либо сил, так и при действии на него уравновешенной системы сил. Это обстоятельство учитывается в ряде современных формулировок закона инерции. Приведем наиболее развернутую характеристику закона инерции, данную в физической энциклопедии [9, с.144]: “Инертность (инерция) (от лат. iners, род. падеж inertis – бездеятельный) в механике – свойство материальных тел, проявляющееся в том, что тело сохраняет неизменным состояние своего движения или покоя по отношению к т. н. Инерциальной системе отсчета, когда внешние воздействия на тело (силы) отсутствуют или взаимно уравновешиваются. Если же на тело действует неуравновешенная система сил, то свойство инертности сказывается в том, что изменение состояния покоя или движения тела, то есть изменение скоростей его точек, происходит постепенно, а не мгновенно; при этом движение изменяется тем медленнее, чем больше инертность тела. Мерой инертности тела является его масса”.
Не будем подробно анализировать эту формулировку, обратим внимание только на утверждение о соответствии закону инерции движения тела под действием уравновешенной системы сил. Такое утверждение вызывает сомнения. Действительно, можно ли назвать движением по инерции движение автомобиля с работающим двигателем, хотя он и движется с постоянной скоростью? Ведь при таком движении происходят затраты энергии, внешней по отношению к автомобилю. Это обстоятельство заставляет задуматься при рассмотрении закона инерции с энергетических позиций. Сомнительно, чтобы движение по инерции было связано с затратами внешней энергии. Рассмотрим с этой точки зрения еще несколько примеров. Вернемся снова к движению планет по их орбитам. Предположим для упрощения, что орбиты будут круговыми. Тогда на планеты силы тяготения будут действовать только в радиальном направлении, в касательном же направлении никаких сил не будет и, значит, не будет затрат энергии. В этом случае возникает желание назвать движение в касательном направлении движением по инерции. Но тогда получается, что движение одного и того же тела (планеты) будет одновременно и по инерции в касательном направлении, при котором величина скорости будет постоянной и не инерционным в радиальном направлении, так как при этом будет изменяться направление скорости и будет затрачиваться внешняя энергия (энергия Солнца). Очевидно, что два указанных направления должны быть взаимно перпендикулярными, так как только тогда взаимодействия в этих направлениях не будут влиять друг на друга.
Рассмотрим теперь движение автомобиля с отключенным двигателем, то есть движение накатом, когда на машину действует только сила сопротивления. Машина при этом тормозится, а скорость ее уменьшается. Движение машины в этом случае происходит за счет ее собственной кинетической энергии без использования внешней энергии. Возникает вопрос: можно ли такое движение назвать движением по инерции? Если исходить из классической формулировки закона инерции, то нет. Если же попытаться понять сущность такого движения, то кроме собственной инерции у тела ничего нет, что заставляло бы его двигаться. Значит, именно инерция тела, связанная с его запасом кинетической энергии, заставляет тело продолжать движение до тех пор, пока не будет исчерпан весь ее запас. Если же это так, то такое движение тоже следует считать движением по инерции.
В связи со всем изложенным закон инерции в интегральной форме можно сформулировать следующим образом:
– Если в каком-либо направлении движение тела происходит без затрат внешней энергии или за счет собственной кинетической энергии, такое движение будет движением по инерции.
Под данное определение будут подходить прямолинейное и вращательное движения, совместное вращательное и прямолинейное движения без затрат внешней энергии и при торможении, вращение планет вокруг Солнца и т. п.
Автор выносит на обсуждение такое понимание сущности закона инерции.
И, наконец, следует подчеркнуть важное следствие, имеющее место при использовании закона инерции в дифференциальной форме: в случае реальности сил инерции все системы отсчета – инерциальные и неинерциальные – можно считать равноправными, так как в любой из них будут выполняться все законы механики.
energy-source.ru



