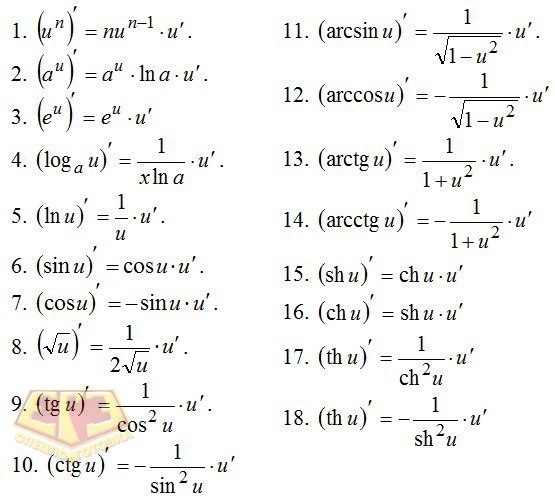
Po формула – Все главные формулы по математике – Математика – Теория, тесты, формулы и задачи
- Комментариев к записи Po формула – Все главные формулы по математике – Математика – Теория, тесты, формулы и задачи нет
- Советы абитуриенту
Все главные формулы по математике – Математика – Теория, тесты, формулы и задачи
Оглавление:
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Игрек вершины параболы:
Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:
Для корня четной степени имеется следующее свойство:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника
:Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h – высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула – через две диагонали, вторая – через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника
через две диагонали и угол между ними:Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Геометрия в пространстве (стереометрия)
К оглавлению…
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: “трёхмерная Теорема Пифагора”):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Координаты
К оглавлению…
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости – первые две формулы, для трехмерной системы координат – все три формулы):
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Расширенная PDF версия документа “Все главные формулы по школьной математике”:
К оглавлению…
educon.by
Основные формулы по геометрии – Математика – Теория, тесты, формулы и задачи
Знание формул по геометрии является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по геометрии, которые надежно хранятся в памяти ученика – это основной инструмент, которым он должен оперировать при решении геометрических задач. На этой странице сайта представлены основные формулы по школьной геометрии.
Изучать основные формулы по школьной геометрии онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (адрес электронной почты и ссылки в социальных сетях здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
educon.by
Формула давления | Все формулы
Давление столба жидкости (гидростатическое давление) равно плотности этой жидкости, умноженной на высоту столба жидкости и ускорение свободного падения.
Здесь – давление, – плотность жидкости, – ускорение свободного падения ( м/с), – высота столба жидкости (глубина, на которой находится сдавливаемое тело).
Единица измерения давления – Па (паскаль).
Это векторная величина. В каждой точке жидкости давление одинаково во всех направлениях. Чаще всего в задачах требуется найти давление столба воды. Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:
Где – сила тяжести, действующая на жидкость (её вес), – площадь поверхности, на которую оказывается давление.
Примеры решения задач по теме «Давление»
ПРИМЕР 1
| Задание | Высота воды в аквариуме 1 м. Найти давление на дно аквариума. |
| Решение | Напоминаем, плотность воды кг/м, а м/с. Таким образом: (Па) |
| Ответ | Давление воды составляет 9800 Паскаль |
xn--b1agsdjmeuf9e.xn--p1ai
Формула работы
– работа (может обозначаться как ), – сила, – перемещение.
Единица измерения работы — Дж (джоуль).
Указанная формула применима к телу, движущемуся прямолинейно и постоянном значении воздействующей на него силы. Если между вектором силы и прямой, описывающей траекторию тела есть угол, то формула принимает вид:
Кроме того, понятие работы можно определить как изменение энергии тела:
Именно такое применение этого понятия чаще всего встречается в задачах.
Примеры решения задач по теме «Механическая работа»
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Формула ЭДС
Здесь – ЭДС, – работа сторонних сил, – величина заряда.
Единица измерения напряжения – В (вольт).
ЭДС – скалярная величина. В замкнутом контуре ЭДС равна работе сил по перемещению аналогичного заряда по всему контуру. При этом ток в контуре и внутри источника тока будут течь в противоположных направлениях. Внешняя работа, которая создаёт ЭДС, должна быть не электрического происхождения (сила Лоренца, электромагнитная индукция, центробежная сила, сила, возникающая в ходе химических реакций). Эта работа нужна для преодоления сил отталкивания носителей тока внутри источника.
Если в цепи идёт ток, то ЭДС равна сумме падений напряжений во всей цепи.
Примеры решения задач по теме «Электродвижущая сила»
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Формула средней скорости | Все формулы
Средняя скорость тела – это отношение пути ко времени прохождения этого пути. Скорость движения при этом не обязана быть постоянной.
Здесь – средняя скорость, – весь путь, пройденный телом, – время прохождения пути.
Единица измерения скорости – м/с (метр в секунду).
Средняя скорость – скалярная величина. Если тело двигалось с разными скоростями равные промежутки времени, то средняя скорость равна среднему арифметическому всех скоростей, в противном случае
Где – отрезок пути, – время прохождения этого отрезка.
Примеры решения задач по теме «Средняя скорость»
ПРИМЕР 1
| Задание | Тело прошло 5 м за 12 секунд, затем 7 м за 3 секунды. Найти среднюю скорость тела. |
| Решение | Решение очевидно ( и – путь и время прохождение этого пути для определённых отрезков): |
| Ответ | Средняя скорость тела равна метров в секунду. |
xn--b1agsdjmeuf9e.xn--p1ai
Формулы по экономике
Формулы спроса и эластичности
В первую очередь необходимо рассмотреть формулы по экономике, которые касаются спроса и предложения. Уравнение функции спроса можно представить в виде следующей формулы:
y= к*x+b
Сама функция спроса выглядит следующим образом:
QD= к*P+b
Функция предложения:
Qs= к*P+b
Если рассмотреть показатели эластичности, то можно выделить формулы по экономике, определяющие эластичность спроса по цене:
EDP= Δ QD (%) : Δ P (%)
EDP= (Q2 –Q1)/(Q2 + Q1) : (P2 –P1)/(P2 + P1)
Вторая формула представляет собой расчет средней точки, здесь значение P1 – цена продукции до изменения, P2 – цена продукции после изменения, Q1 – спрос до изменения цены, Q2 –спрос после изменения цены.
Формула коэффициента эластичности спроса в общем виде:
EDI= (Q2 –Q1)/ Q1 : (Р2 –Р1)/ Р1
Формулы макроэкономики
Формулы по экономике включают в себя формулы по микроэкономике (спрос и предложение, издержки фирмы и др.), а также формулы по макроэкономике. Важной формулой по макро экономике является формула расчета необходимого в обращении количества денег:
КД = ∑ ЦТ – К + СП – ВП / СО
КД — количество денег в обращении,
ЦТ — сумма цен на товары;
К — товары, продаваемые в кредит;
СП — срочные платежи;
ВП — взаимно погашаемые платежи по бартерным сделкам;
СО — годовая скорость оборота денежной единицы.
Для того чтобы определить денежную массу в обращении необходимо воспользоваться следующей формулой:
М = Р * Q / V
Здесь M — денежная масса, которая находится в обращении;
V — скорость обращения денег;
Р — средние цены на продукцию;
Q — количество выпущенной продукции в постоянных ценах.
Уравнение обмена может быть представлено следующим равенством:
M*V = P*Q
Это уравнение отражает, равенство совокупных расходов в денежном выражении и стоимости всех товаров и услуг, которые выпущены в государстве.
Другие формулы макроэкономики
Рассмотрим еще несколько формул по экономике, среди которых важное место занимает формула вычисления реального дохода:
РД = НД / ИПЦ * 100 %
Здесь РД – реальный доход,
НД – номинальный доход,
ИПЦ – показатель индекса потребительских цен.
Формула для вычисления индекса потребительских цен представлена следующим выражением:
ИПЦ = СТТГ / СТБГ
СТТГ – стоимость потребительской корзины в текущем году,
СТБГ – в базовом году.
В соответствии с показателем индексов цен можно определить темп инфляции по соответствующей формуле:
ТИ =(ИПЦ1 – ИПЦ0) / ИПЦ0 * 100 %
В соответствии с темпами инфляции можно выделить несколько видов:
1. Ползучая инфляция с ростом цен до 5 % годовых,
2. Умеренная инфляция до 10 % годовых,
3. Галопирующая инфляция с ростом цен 20-200% годовых,
4. Гиперинфляция с катастрофическим ростом цен более 200 % в год.
Формулы для расчета процентов
Экономические расчеты часто требуют расчета процентов. Формулы по экономике включают расчет, как сложного, так и простого процента. Формула расчета простого процента представлена следующим образом:
С = Р * (1 + in/360)
Здесь P — сумма долга, включая проценты;
С — общая сумма кредита;
n – количество дней;
i — годовой процент в долях.
Формула для вычисления сложного процента выглядит так:
С = Р (1 + in/360)k
K – количество лет.
Формула для расчёта сложного процента, который вычисляется за несколько лет:
С = Р (1+i)k
Формула безработицы, занятости и ВНП
Формулы по экономике также помогают рассчитать уровень безработицы:
УБ = Число безработных/ЧРС * 100%
Здесь ЧРС – численность рабочей силы.
Формула для вычисления уровня занятости выглядит следующим образом:
УЗ = Число занятых / ЧРС * 100 %
Формула для вычисления валового национального продукта вычисляется так:
ВНП = % + ЗП + Тр + КНал – ЧС + Р + Ам + ДС
Здесь Тр – корпорации,
Кнал – косвенные налоги,
ЧС – чистые субсидии,
Р – рента,
Ам – сумма амортизации,
ДС – доходы от собственности.
Формула расчёта ВНП в соответствии с расходами:
ВНП = ЛПР + ГЗ + ВЧВИ – ЧИ
Расчет выручки, прибыли и издержек
Формулы по экономике при расчете выручки и прибыли:
TR = P*Q
Прибыль = TR — TC
Формула для вычисления средних общих издержек выглядит так:
АС = AFC + AVC или
АС = TC / Q
Для того чтобы рассчитать общие издержки необходимо применить следующую формулу:
ТС = TFC + TVC
Формула для вычисления средних постоянных издержек:
AFC = TFC / Q
При расчете средних переменных издержек можно воспользоваться следующей формулой:
AVC = TVC / Q
Примеры решения задач
ru.solverbook.com
