Понятно и просто математика – 40+ сайтов по математике | Семейное Образование — Все о внешкольном образовании в России и в мире: хоумскулинг, анскулинг, альтернативные школы, индивидуальный учебный план, заочная и очно-заочная форма обучения в школе.

Содержание

Доступная математика

Математика, изучение которой начинается даже не со школьной скамьи, а еще с детского сада, представляет собой науку, предметом изучения которой являются структуры, отношения и порядки. Исторически получилось так, что ее основой стали операции подсчета, а так же описания и измерения форм тех объектов, что существуют в реальности.

Ученые утверждают, что сама по себе математика представляет ни что иное, как совокупность неких истин, существующих совершенно объективно, и именно этим она особенно интересна. Можно с полным на то правом утверждать, что в определенном смысле она представляет собой универсальный язык описания самых различных предметов и явлений, поскольку дает для этого наиболее действенные, плодотворные и удобные способы.

Как утверждают опытные методисты, математику необходимо начинать изучать с осмысления той роли, которую она играет в современном обществе. Именно эта наука (а точнее – ее методология) положена в основы всей современной вычислительной техники, а также имеет огромное прикладное значение. Именно появление в последние десятилетия электронно-вычислительных машин, имеющих по-настоящему высокую степень быстродействия, сделало

математику существенно более значимой, чем она была ранее.

В изучении математики (как, впрочем, и любой другой науки) успехов можно достичь тогда и только тогда, когда для этого используется правильный подход. Один из его основных принципов состоит в том, что необходимый для освоения материал не нужно чрезмерно усложнять. Если не «перегружать» процесс освоения премудростей математики, то постичь их можно быстрее и проще.

Порой на школьных уроках ученикам не удается понять некоторые моменты того математического материала, который преподают учителя. В таких случаях, придя домой, необходимо попробовать разобраться в них самостоятельно. Важно запомнить, что

математика относится к тем наукам, изучать которые необходимо, не допуская никаких пробелов в знаниях. Дело в том, что в ее курсе чрезвычайно сильна взаимосвязь между всеми темами, что и обеспечивает настоящую целостность.

Одна из главных задач преподавателей математики состоит в том, чтобы найти действительно доступный и понятный ученикам материал. Сделать это зачастую бывает совсем не просто, да и объяснение некоторых понятий представляет определенную сложность.

Необходимо особо отметить, что в постижении премудростей математики огромную роль играет самостоятельное изучение. Практика показывает, что наиболее прочно и основательно усваиваются именно те знания, которые были получены самостоятельно. Поэтому при изучении этой весьма непростой науки необходимо как можно больше заниматься ею самостоятельно, тем более что то время, которое отданное ей в школе, существенно ограничено.

В принципе, весь процесс обучения является довольно длительным и весьма сложным. Одним из эффективных способов, позволяющих существенно увеличить его качество и интенсивность, является широкое применение современной электронно-вычислительной техники. Это позволяет постигать основы

доступной математики с использованием действительно занимательного материала, возможности подсказки, проверки ответов и т.п.

Описанная понятным и доступным языком математика позволяет лучше и быстрее усвоить тот материал, который связан с операциями подсчета, а также многими другими действиями, характерными для этой науки. Значительную помощь при этом оказывают доступные примеры.

Давно замечено, что изучение математики чрезвычайно сильно развивает логическое мышление, так что она нужна абсолютно всем.

simple-math.ru

Простое восприятие математики. Как учить математику просто?

Математика это точная наука, которая воспринимается разными людьми по-разному. Успехи в изучении математики достигаются тогда, когда к процессу изучения подходят правильно. Не стоит чрезмерно усложнять то, что необходимо учить. Правильный подход к процессу обучения помогает добиться реальных успехов. Есть предметы, которые ученики могут учить сами по себе, в зависимости от личных способностей и без особых сложностей, но математика не является таким предметом. В процессе изучения математики очень важна роль преподавателя. Если преподаватель правильно объясняет основы математики и позволяет понять элементарные вещи, учить математику будет гораздо проще.

В том случае, если вы не можете понимать что-то на уроках математики в школе, желательно все же разобраться во всем самостоятельно. В изучении математики нельзя допускать никаких пробелов, так как в таком случае нельзя будет говорить о качестве математики. Все темы тесно между собой связаны и, чтобы понять все как одно целое необходимо тщательно изучать каждую частицу, в данном случае каждую тему. Учить математику проще с помощью тематических блогов в сети. Если вам сложно понять некоторые темы ищите материал, который доступно и понятно разъясняет примеры рациональных чисел, иррациональных чисел и т.д. Очень важно всегда учить теорию с примерами, что позволяет не только запоминать некий материал, но также пользоваться им во благо.

Как учить математику просто? Найти понятный и доступный материал. Не все преподаватели могут доступно объяснить некоторые понятия, так как важно не только наличие знаний, но и умение передавать другим эти знания. Самостоятельное обучение занимает ответственное место в процессе образования, так как большинство знаний полученные именно путем самостоятельно изучения предмета. Чем больше вы будете работать индивидуально, тем лучше, так как время для изучения в школе ограничено и недостаточно для получения углубленных знаний.

Есть люди, которые понимают математику, и вы можете стать таким же, если изменить свое мышление и смотреть на математику иначе. Это не просто цифры, это настоящая магия. Математику можно по-настоящему любить, если ее понять. Обязательно учите математику и по другим материалам кроме школьного учебника. Это позволит взглянуть на математику другими глазами и понять ее, что очень важно. Математика развивает мышление и логику, а значит, нужна всем, что говорит о необходимости ее изучения.

Полезные книги при изучении математики:

  • «Ключ к пониманию математики», М.Б. Волович
  • «Математическая смекалка. Занимательные задачи, игры, фокусы, парадоксы», Е.И. Игнатьев
  • «Занимательная алгебра», Я.И. Перельман
  • «Задачник по математике. Ненаглядное пособие», Г.Б. Остер
  • «Элементарная алгебра», С.И. Туманов (очень старая, но полезная книга, особенно для тех, кто пытается познать алгебру самостоятельно).

Можете выбрать любую другую книгу доступную и понятную для вас, которая позволит познавать математику эффективно.


Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru

40+ сайтов по математике | Семейное Образование — Все о внешкольном образовании в России и в мире: хоумскулинг, анскулинг, альтернативные школы, индивидуальный учебный план, заочная и очно-заочная форма обучения в школе.

Основная идея – сделать ребёнка максимально самостоятельным, но при этом всё же контролируемым. Данные ресурсы больше подойдут для средних классов, хотя и для малышей тоже есть, что подобрать. Все сайты бесплатные или с бесплатной версией.

И так, программа №1 — это XtraMath. Это всего одна единственная программа, без которой у нас не обходится ни одного дня с математикой.

Суть этой программы — наработать скорость в простейших вычислениях: +,-,/,*. Для этого вы регистрируете вашего ребенка и себя, как родителя. Ребенок самостоятельно выполняет задания, а потом на почту родителям приходит подробнейший отчет об успехах. Отчёт можно смотреть и онлайн. Сайт на английском, но всё предельно понятно и просто. Можно выбирать разный режим — скорость, с которой будут подаваться примеры. Мы сначала прошли обычный, а сейчас делаем тоже самое, но быстрее. После прохождения блока ребенку выдается сертификат, который вы можете себе распечатать.

Алгоритм построения занятий

Далее, хочу рассказать об основном алгоритме, по которому строятся наши занятия дома. Здесь основной перечень сайтов, который подходит для ежедневных тренировок, связанных с освоением школьной программы по базовым темам. Мы не пользуемся ни учебниками, ни тетрадями, распечатками и пр., в равной степени, как и калькулятором.

  1. Новую тему мы смотрим, используя канал MathTutor на сайте Интерурок. Альтернативным вариантом (или дополнительным) подходит Академия Хана  — с украинским или русским переводом. В русской версии роликов больше.
  2. Далее мы нарешиваем примеры для закрепления услышанного, используя тренажер на сайте Rastu. На этом же сайте найдёте и краткую информацию по теме (например формула или принцип расчета). Если пример сделан неправильно, то сверху над ним появится подсказка. Ребёнок занимается самостоятельно, так как на любом этапе видно сколько примеров решено и сколько сделано ошибок. По этому результату всегда понятно: или мы переходим к следующей подтеме, или стоит ещё порешать эту.
  3. Когда уже есть понимание темы, и она закреплена на тренажере, мы используем сайт ozenoknet. Этот сайт подходит именно для закрепления материала, а не для нарешивания в связи с тем, что примеров по каждому разделу не так много. Но зато там есть другие интересности: за выполненные задания ребёнок получает виртуальную коллекцию «призов» и «кубков». Они будут отражаться на его страничке в соответствующих разделах. Кроме этого здесь есть электронный журнал, где отражены все данные отдельно по каждой теме и присвоен уровень: «хорошо», «отлично» и «неплохо».
  4. Ну и напоследок самое приятное — это компьютерные игры на сайтах jmathpage.com и mathplayground.com. Игр необыкновенное множество и все они математические!

Перечень дополнительных ресурсов

1. Математические тренажёры
  • www.mathgames.com/skills — это супер тренажёр, но требует минимальные знания английского. Мой сын от него в восторге! На личной страничке отображается вся статистика о проделанной работе: время затраченное на каждое задание, начало и конец занятий, результаты по каждой теме. Очень удобно использовать, так как выдаёт списки заданий либо по классу (наша программа немного не совпадает) либо по темам.
  • www.ck12.org — ещё один тренажёр на английском. Отдельно для младшей школы, геометрия, алгебра, вычисления и пр.
  • www.buzzmath.com — тренажёр на английском с очень интересной подачей заданий! Уверена вашим деткам он понравится!! На сайте указано, что задания рассчитаны на 6-9-й классы, но на мой взгляд, можно смело решать с 5-го. Сайт платный. Но если заходить как «визитор», то можно заниматься бесплатно. Единственный минус — ваши результаты сохраняться не будут.
  • eu.ixl.com — это отличный сайт, тоже на английском. Этот сайт требует платной регистрации, но если не регистрироваться, то вы ежедневно можете проходить на нём ограниченное число заданий.
  • www.splashmath.com — очень интересный тренажёр с мультяшной анимацией для 1-5 классов на английском языке. Уверена, что с ним математику полюбит любой ребёнок! Сайт платный, но есть и открытая версия, которая позволяет без оплаты решать по 20 вопросов ежедневно. Кроме этого, после каждого занятия вашего чада, с сайта на ваш электронный адрес будет приходить подробный отчёт о проделанной работе: с чем дитё отлично справилось, а по каким темам есть трудности.
  • www.adaptedmind.com — очень весёленький тренажёр с «чудищами», участвующими в решении задачек. Сайт на английском языке для 1-6 классов.
  • www.khanacademy.org/math — тренажёры от Академии Хана. На английском языке. Для того чтобы здесь заниматься, необходимо пройти небольшой тест, который определит, над какими темами стоит работать.
  • www.tenmarks.com — тренажёр на английском языке с предварительным тестированием.
  • www.yaklas.com.ua — отличный сайт, но только с 7-го класса.
    Можно выбрать как украинский язык, так и русский. Есть много разных предметов, кроме математики. Каждая тема делится на теоретическую часть и практическую. Бесплатно можно делать только несколько заданий.
  • bitclass.ru/math — сайт на русском языке. Похож, в общем, на предыдущий, но охватывает темы начиная с 5-го.
  • school-assistant.ru/?class=matematika — сайт на русском языке. Сначала идёт теория, а после — несколько задач на закрепление материала.
  • www.knewton.com/learn — тренажёр на английском, интересная система, построенная на анализе индивидуальной успеваемости: в зависимости от допущенных ошибок — отсылает к тому или иному видео с теорией. К сожалению, большинство заданий рассчитаны на 7-й класс и старше.
  • www.uchportal.ru/load/29-1-2 — тренажеры на русском языке (предварительно скачать по указанным ссылкам)
  • www.kokch.kts.ru/math/index.html — тесты на русском языке
2. Генераторы случайных примеров
  • egeurok.ru — на русском языке. Сначала формируете список заданий, потом ребёнок решает, а после нажимаете ответы и сверяете с ответами вашего чада. Можно распечатывать, а можно и не печатать — кому как удобно.
  • www.math-aids.com — аналогичный вариант на английском языке.
  • www.mathinenglish.com/menuWorksheets.php — примеры на сайте с английским языком.
  • www.math-drills.com/ — отличный сайт на английском.
  • www.worksheetworks.com/math.html — примеры формируете сами исходя из установленных вами ограничений.
  • www.bymath.net — сайт на русском языке. Много теории. По каждой теме есть задания.
3. Математические игры онлайн

На русском языке:

На английском языке:

4. Занимательная математика

Сайты на русском языке.

  • www.problems.ru — сайт для продвинутых математиков — разобранные решения олимпиад и пр.
  • domzadanie.ru — много интересных задачек.
  • nazva.net/rubric/all — отличная копилка для тех, кто любит думать.
5. Программы помощники
  • loviotvet.ru — помогает решать примеры и уравнения с отображением этапов решения, производит наглядно вычисления «в столбик». Сайт на русском языке.
  • www.nigma.ru/index.php?t=math — поможет с уравнениями. Сайт на русском языке.
  • math-prosto.ru — охватывает всего несколько тем как онлайн-решатель, но зато довольно доступно подаётся теория. Сайт на русском языке.
  • www.mathway.com — проверит правильность составления уравнений. Англоязычный ресурс, но всё очень просто и понятно.
  • znanija.com/predmet/matematika — русскоязычный сайт, на котором вы можете задать любой интересующий вас вопрос и получить ответ онлайн от помощника. Есть возможность и для других предметов.
6. Списки полезных ссылок (на английском языке)

Надеюсь, что ваши ежедневные занятия математикой теперь будут ещё увлекательнее!

Источник

semeynoe.com

Как понять математику? или Математика для чайников

Разобраться в математике, порой, действительно становится непросто. Кто-то упустил её ещё в школе, кто-то давным-давно позабыл то, что понимал когда-то, и в университете становится крайне сложно справляться с заданиями по высшей математике. «Горы» формул, интегралы, вычисление производной и прочие «прелести» программы повергают нас в ужас. Разбираясь в этом, зачастую можно почувствовать себя полным «чайником».

Во многих случаях работает метод «списать у соседа». Но здесь есть 2 «но»: 1. одногруппники и одноклассники, зачастую, сами не знают, как решить задания, поэтому списывать оказывается не у кого; 2. это не поможет вам на экзамене и контрольной, ведь там у вас будет свой личный билет с заданиями, которые предстоит решать.

Что же делать?

Самый первый совет, если вы учитесь в университете, посещайте лекции и записывайте. Даже если вы ничего не поймёте на самой лекции, записанные темы и формулы дадут вам шанс разобраться дома, или, как минимум, предъявить конспект на экзамене лектору. Поверьте, наличие конспекта значительно повышает ваши шансы сдать экзамен, даже если знаете вы предельно мало.

В случае, если дома, глядя в учебник по математике и тетрадь, вы также чувствуете, себя «чайником», самым правильным решением будет обратиться к репетитору, лучше – к онлайн-репетитору. Т.к. во-первых, это дешевле, во-вторых, вам смогут объяснить темы и как решать отдельные задания практически в любое время суток, а это очень удобно. Опытных онлайн-репетиторов по вышмату, теории вероятностей и математической статистике вы найдёте здесь. Если нужна помощь по школьному курсу математики, то советуем перейти сразу сюда.

Но самый важный совет, который точно поможет вам в сложной ситуацией с математикой – освойте минимум! Если вы на экзамене не сможете дать правильный ответ на вопрос «Чему равна сумма квадратов катетов прямоугольного треугольника» (а она равна квадрату гипотенузы), то скорее всего, дальше вас даже «тянуть» не станут. Поэтому важно запомнить основные правила, алгоритмы и формулы, которые преподаватели спрашивают на экзамене, либо дают на контрольных. Освоить необходимый минимум вам также легко поможет хороший репетитор по математике, либо, в случае студентов, высшей математике.

Из основного, давайте вспомним правила раскрытия скобок:

…+ (-a+b+c-d) = -a+b+c-d –  Если перед скобками стоит знак плюс, то мы можем просто опустить скобку и оставить каждое значение с тем же знаком, с которым оно стоит.

…- (-a+b+c-d) =  a-b-c+d– Если перед скобками стоит знак минус, то опуская скобки, мы меняем знак каждого значения (был «минус», значит после раскрытия скобки на его месте будет «плюс», и наоборот).

Даже если вы вдруг перепутаете это в письменном экзаменационном задании, а экзаменатор укажет вам на ошибку, вы можете быстро озвучить правило и сказать, что вы просто переволновались и неправильно написали. Это гораздо лучше, чем промолчать, опустив глаза, когда у вас спрашивают «Где здесь допущена ошибка?».

Такое же правило действительно и для умножения.

a(b-c) =ab-ac– Перед «а» нет минуса, а значит знаки сохраняются.

-a(b-c)= ab+ac– Перед «a» есть знак минуса, а значит при раскрытии скобок мы должны поменять знак.

В целом, важно помнить, что ДВА МИНУСА ДАЮТ ПЛЮС, а ТРИ МИНУСА – ДАЮТ МИНУС. Главное не запутаться в этом при решении задач по высшей или даже школьной математике.

Далее рассмотрим приведение подобных слогаемых.

Сталкиваясь с подобными примерами важно помнить, что вы можете вычитать и складывать только те значения, у которых одинаковые переменные и степени. Т.е. от 5ax можно вычесть 9 ax, но нельзя просто вычесть 9ax2 (т.к. у х другая степень), либо нельзя прибавить 9yz, т.к здесь участвуют другие переменные.

Кстати, о степенях. Очень многие напрасно их пугаются, ведь на деле это обычное умножение числа на самого себя.

Как решать дроби?

На самом деле, с ними тоже довольно просто разобраться. Важно запомнить простое правило, что складывать и вычитать дроби можно только с одинаковым знаменателем.

Правило приведения дробей к общему знаменателю:

Например:

Очень важно помнить, что СНАЧАЛА делаем УМНОЖЕНИЕ или ДЕЛЕНИЕ, а ПОТОМ – ВЫЧИТАНИЕ и СЛОЖЕНИЕ. Т.е. в нашем примере будет крайне грубой ошибкой умножить 5 на 8 и сразу прибавить 7. Правильно сначала умножить 5 на 8, затем умножить 7 на 6. И только потом сложить полученные результаты!

Умножаются все дроби по принципу: числитель умножаем на числитель, знаменатель умножаем на знаменатель.

Например:

Как решать задачи на проценты можно посмотреть здесь.

Конечно, весь необходимый минимум в одной статье охватить сложно, поэтому лучше взять хотя бы пару уроков с репетитором, особенно перед тестами и контрольными. Освоение базового материала, безусловно, поможет постепенно освоить математику, успешно написать контрольные и сдать экзамены.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Математический анализ – Математика – Смотреть онлайн видео уроки для начинающих бесплатно!

В категории Математический анализ собраны бесплатные онлайн видео уроки по этой теме. Математический анализ – это совокупность разделов математики, которые занимаются изучением функций и их обобщений методами дифференциального и интегрального исчисления. Сюда относятся: функциональный анализ, включая теорию интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, теория рядов и многомерных интегралов, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, векторный анализ, а также вариационное исчисление. Изучение математического анализа по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Математический анализ Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по математическому анализу приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения!

Всего материалов: 12
Показано материалов: 1-10

Что такое производная функции

Хотите узнать, что такое производная функции в математике? Ты конечно много раз слышал о производной и даже, наверное, брал эту самую производную в школе, совершенно не понимая смысла своих действий. В этом видео я не буду учить тебя формулам, а объясню смысл производной на пальцах так, чтобы даже круглому чайнику было понятно. Но сначала тебе лучше посмотреть мое предыдущее видео, где я так же доступно рассказываю о функции. В этом видеоуроке мы просто, понятно и наглядных жизненных примерах…

Введение в анализ. Мощность множеств

Онлайн урок «Введение в анализ. Мощность множеств» посвящен вопросу о таком понятии как мощность множеств. Этот вопрос касается количественной характеристики множеств. Если множество конечно, то можно говорить о количестве его элементов. Но как быть с бесконечными множествами? Ведь в этом случае не будет понятия больше или меньше. Для решения этой задачи вводится такое понятие как мощность. Мощность – это инструмент количественного сравнения бесконечных множеств. В этом занятии дается…

Предел функции в точке – определение, примеры

В этом онлайн уроке рассказывается о таком понятии как предел функции в точке – определение, примеры. Большинство элементов исследования функций опираются на базовое понятие предела функции. Здесь будет рассмотрен предел функции в точке на простом примере, после чего будет дано строгое определение предела функции в точке с подробной иллюстрацией на графике для лучшего усвоения материала. На данном занятии также рассматриваются другие примеры, и сформулировано строгое определение односторонних…

Сходимость степенных рядов – пример как найти область сходимости, исследование

В этом видео уроке рассказывается о таком понятии как сходимость степенных рядов, пример как найти область сходимости, исследование. Степенной ряд – это частный случай функционального ряда, когда его членами являются степенные функции аргумента x. Область сходимости представляет собой все значения переменной x, при которых соответствующие числовые ряды сходятся. Для исследования можно использовать признак Даламбера и с помощью него показать, что степенной ряд сходится или расходится, и при…

Что такое первообразная

В этом видео я расскажу тебе про первообразную, которая является близкой родственницей производной. На самом деле ты про нее и так уже почти все знаешь, если посмотрел мои предыдущие видео, и нам осталось только расставить точки над i. Первообразная – это «родительская» функция для производной. Найти первообразную – это значит ответить на вопрос: а чей ребенок? Если известна дочка, то мы должны найти маму. Раньше мы наоборот искали дочку по заданной маме. Сейчас мы делаем обратный переход – от…

Геометрический смысл производной

В этом видео я расскажу про геометрический смысл производной. Ты узнаешь, что геометрический смысл производной состоит в том, что производная и угол наклона касательной – это почти одно и то же. Я говорю «почти» потому что производная равна тангенсу угла наклона касательной. Можно считать, что производная и наклон касательной – они тесно связаны. Если угол наклона большой, то и производная большая, а функция в этой точке резко возрастает. Если угол наклона маленький, то и производная маленькая…

Что такое функция в математике

Хотите узнать, что такое функция в математике? В этом видеоуроке мы просто и понятно, с использованием графических иллюстраций и на наглядных жизненных примерах расскажем, что такое функция, что такое ее аргумент, какие бывают функции (возрастающие, убывающие, смешанные), как можно задать функцию (с помощью графика, таблицы, формулы). Вы увидите, что зависимость, которая показывает, как одна величина связана с другой величиной, называется функцией. Любая функция – это связь между величинами…

Предел функции на бесконечности – определение, примеры

Урок «Предел функции на бесконечности – определение, примеры» посвящен вопросу о том, что такое пределы на бесконечности. Большинство элементарных функций определено для сколь угодно большого значения аргумента. В этом случае важно знать поведение функции на бесконечности. Один из элементов исследования такого поведения является нахождение предела функции на бесконечности. Хотя бесконечность не является числом, и ей не соответствует ни одна точка на числовой прямой, определение предела на…

Свойства пределов числовой последовательности

Видео «Свойства пределов числовой последовательности» посвящено вопросу о том, какие свойства имеются у такого математического объекта как предел последовательности. Часть из них носит теоретический характер и помогает лучше понять, что такое предел числовой последовательности. Другие свойства используются на практике и служат для обоснования методов вычисления пределов. В этом онлайн уроке вы ознакомитесь с некоторыми новыми терминами, например, что такое сходящиеся и ограниченные…

Предел числовой последовательности, определение, примеры, решение

В этом видео уроке рассказывается о том, что такое предел числовой последовательности, определение, примеры, решение. В математическом анализе числовые последовательности используются как инструмент для определения и исследования различных математических объектов. Последовательность – это упорядоченное бесконечное множество, элементы которого занумерованы натуральными числами. Для того чтобы определить куда стремиться та или иная числовая последовательность используют такое понятие как предел…

Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.

videourokionline.ru

Zero To Hero

У меня непростые отношения с матанализом: с одной стороны он демонстрирует всю красоту и мощь математики, а с другой — агонию математического образования.

Математический анализ связывает различные темы в элегантной, но довольно сложной для ума манере. Ближайшая аналогия, которая приходит мне на ум, — Дарвиновская теория эволюции: стоит ее понять, и весь мир видится с позиции выживания. Вы понимаете, почему лекарства привели к резистентным микробам (выживает наиболее приспособленный). Вы понимаете, почему сахар и жир сладкие на вкус (вкус стимулирует потребление высококалорийных продуктов в условиях дефицита резервов организма). И все эти моменты складываются в единую, логическую картину.

Матанализ таким же образом проливает свет на всю систему математики. Не кажется ли вам, что все эти формулы как-то связаны?

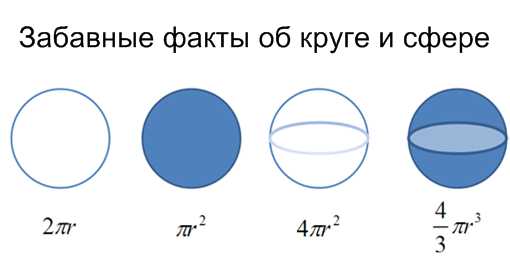
Так и есть. Но большинство из нас изучают эти формулы независимо друг от друга. Математический анализ позволяет начать с «длина окружности = 2 * π * r» и вывести остальные формулы для вычисления площади круга, сферы и даже объема шара — древним грекам очень бы пригодился подобный подход.

К сожалению, матанализ олицетворяет собой все трудности в изучении математики. Большинство уроков объясняются на натянутых, неправдоподобных примерах, заумных доказательствах и банальном заучивании, которое напрочь убивает интуицию.

Так действительно не должно происходить.

Математика, искусство и идеи

Кое-что я понял еще со школы: математика — не самая сложная часть математики; самое тяжелое — мотивация к ее освоению. Особенно, умение не терять энтузиазм, несмотря на:

  • Преподавателей, больше сконцентрированных на штамповке публикаций и своей карьере, чем на преподавании
  • Небеспочвенные опасения, что математика — это сложно, скучно, непопулярно или «не ваш предмет»
  • Учебники и учебные планы, больше нацеленные на получение прибыли и хорошую статистику по тестированиям знаний, чем на пояснение сущности предмета.

‘Плач математика’ [pdf] — отличное эссе на эту тему, которое вызвало бурный резонанс среди многих прочитавших его:

«…если бы мне пришлось создавать механизм с единственной целью разрушить природное любопытство ребенка и его любовь к моделированию, вряд ли бы у меня получилось лучше, чем это уже реализовано — у меня бы просто не хватило фантазии, чтобы тягаться с такими бесчувственными, унылыми идеями, которые воплощены в современных методах изучения математики».

Представьте изучение изобразительного искусства так: Детки, никакого рисования в детском садике. Вместо этого, давайте-ка изучим химию лакокрасочных изделий, физику света и анатомию глаза. После 12 лет изучения этих аспектов, если дети (точнее уже подростки) всё еще не возненавидят искусство, они смогут начать рисовать самостоятельно. В конечном итоге, они теперь владеют полноценным фундаментом для того, чтобы начать уважать искусство. Верно?

Также и с поэзией. Представьте изучение этой цитаты (формулы):

«Но главное: будь верен сам себе; Тогда, как вслед за днем бывает ночь, Ты не изменишь и другим.» —Вильям Шекспир, Гамлет

Это элегантный способ сказать «будь собой» (и если это означает непочтительно писать о математике, пусть будет так). Но если бы мы рассматривали поэзию на уроке математики, вместо поиска смысла мы бы занялись подсчётом количества слогов, анализировали пятистопный ямб, разметкой существительных, глаголов и прилагательных.

Математика и поэзия — это как разные способы пояснить, охарактеризовать одно и то же. Формулы — это средства к достижению цели, способ выражения математической истины.

Мы забыли, что математика оперирует идеями, это не машинальное маниппулирование формулами, которые выражают эти идеи.

Ну это всё понятно, так в чем же твоя великая мысль?

Вот, что я не буду делать: я не буду пересказывать уже написанные учебники. Если вам нужны ответы здесь и сейчас, есть масса вебсайтов, видеоуроков и 20-минуток в помощь.

Вместо этого давайте освоим основные положения матанализа. Уравнений недостаточно — я хочу моментов озарения, чтобы вы действительно видели их смысл и понимали язык математики.

Формальный математический язык — это просто способ коммуникации. Графики, информативные анимированные модели и разговор простым языком могут дать больше знаний, чем целая страница заумных доказательств.

Но матанализ — это сложно!

Я думаю, что любой человек сможет понять основные положения матанализа. Нам не обязательно быть поэтами, чтобы наслаждаться произведениями Шекспира.

Вам будет гораздо проще, если вы знаете алгебру и интересуетесь математикой. Не так давно, чтение и письмо были работой специально обученных писцов. А сегодня это может сделать любой 10-летний ребенок. Почему?

Потому что мы этого ожидаем. Ожидания играют огромную роль в развитии возможностей. Так что ожидайте, что матанализ — это просто еще один предмет. Некоторые люди доходят до мельчайших подробностей (писатели/математики). Но остальные из нас могут просто восторгаться происходящим и попытаться его понять. Я бы хотел, чтобы каждый освоил основные понятия матанализа и сказал «Вот это да!».

Так о чем же матанализ?

Некоторые определяют матанализ как «область математики, которая изучает пределы, дифференцирование, интегрирование функций с одной или более переменных». Это определение верно, но оно совсем не полезно для новичков.

Вот мой ход: Матанализ делает с алгеброй то, что алгебра сделала с арифметикой.

  • Арифметика — это манипуляция числами (сложение, умножение и т.д.).
  • Алгебра находит связи между числами: a2 + b2 = c2 — очень известная связь, описывающая соотношение сторон в прямоугольном треугольнике. Алгебра находит целые наборы чисел — если вы знаете a и b, вы можете вычислить и c.
  • Матанализ находит связи между уравнениями: вы можете видеть, как одно уравнение (длина окружности = 2 * π * r) связано с другим (площадь круга = π * r2).

Используя матанализ, мы можем спросить самые разные вопросы:

  • Как уравнение растет и сокращается? Наращивается со временем?
  • Когда оно достигнет самой высокой/низкой точки?
  • Как мы используем переменные, которые постоянно меняются? (Тепло, движение, популяции, …).
  • И многое, многое другое!

Алгебра и матанализ решают задачи вместе: матанализ находит новые уравнения, а алгебра их решает. Как эволюция, матанализ расширяет ваше понимание того, как работает матушка-природа.

Пример, пожалуйста

Представим, что мы знаем уравнение длины окружности (2 * π * r), и нам нужно найти площадь. С чего начнем?

Представьте, что заполненный диск круга — это как набор матрешек.

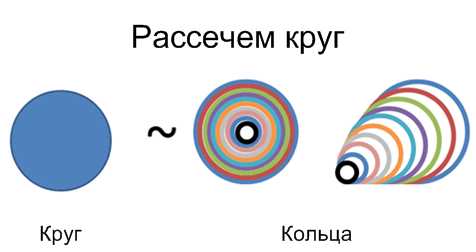
Тут есть два способа нарисовать этот диск:

  • Нарисовать окружность и закрасить ее
  • Нарисовать набор колец толстым маркером

Количество «пространства» (площадь) должно быть одинаковым в обоих случаях, верно? И сколько пространства занимает кольцо?

Самое большое кольцо имеет радиус «r», и длина окружности кольца вычисляется как 2 * π * r. По мере того, как кольца уменьшаются, окружность также становится меньше, но всё равно сохраняется соотношение 2 * π * текущий радиус. Последнее кольцо больше похоже на булавочную головку, и длину окружности уже не вычислишь.

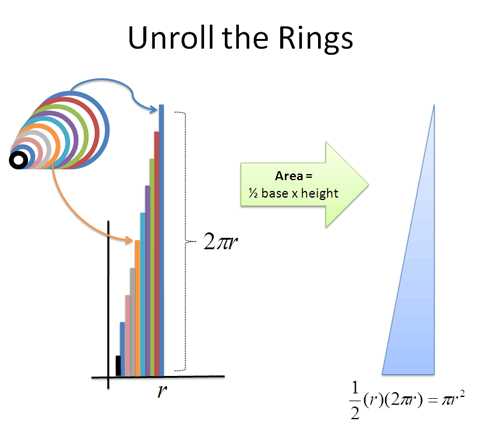
А теперь начинается самое интересное. Давайте раскрутим эти кольца и выровняем их. Что произойдет?

  • У нас получится набор линий, который составит зубчатый треугольник. Но если взять более тонкие кольца, то треугольник становится уже менее зубчатым (об этом мы еще поговорим в других статьях).
  • С одной стороны будет самое маленькое кольцо (0), а с другой — самое большое (2* π * r)
  • Кольца имеют радиусы от 0 до «r». Для каждого возможного радиуса из этого диапазона (от 0 до r), мы просто помещаем раскрученное кольцо на свое место.
  • Общая площадь «кольцевого треугольника» = 1/2 основания * высоту = 1/2 * r *(2 * π * r) = π * r2, а это и есть формула поиска площади круга!

Ух ты! Общая площадь колец = площадь треугольника = площадь круга!

(Изображение из Википедии)

Это был простой пример, но вы уловили основную идею? Мы взяли диск, разделили его, и сложили части вместе немного другим путем. Матанализ показал, что диск и кольцо тесно связаны друг с другом: диск — это действительно набор колец. Это очень популярная тема в матанализе: Большие предметы состоят из более мелких предметов. И иногда именно с этими мелкими предметами работается проще и понятнее.

Немного о примерах

Множество примеров в матанализе основано на физике. Это, конечно, замечательно, но бывает сложно их воспринимать: честно, далеко не всегда удается держать в голове разные физические формулы вроде формулы скорости объекта.

Я предпочитаю начать с простых визуальных примеров, потому что именно так и работает наш мозг. Кольцо/круг, которое мы исследовали — вы бы могли смоделировать то же самое из нескольких отрезков трубок разного диаметра: разделить их, выровнять и уложить в грубый треугольник, чтобы убедиться, что математика действительно работает. С простой физической формулой такое вряд ли удастся провернуть.

Немного о математической строгости (для фанатиков этой науки)

Я чувствую, как математики-педанты жгут свои клавиатуры. Поэтому я вставлю всего несколько слов о «строгости». Знаете ли вы, что мы не учим матанализ способами, которыми его открыл Ньютон или Лейбниц? Они использовали интуитивные идеи «флюксии» и «бесконечно малых величин», которые были заменены пределами, потому что «Конечно, это работает на практике. Но работает ли это в теории?».

Мы создали сложные механические модели, чтобы «точно» доказать матанализ, но мы утратили интуитивное восприятие предмета в процессе таких доказательств.

Мы смотрим на сладость сахара с точки зрения химии мозга, вместо того, чтобы пояснять это языком науки «В сахаре много энергии. Ешьте его».

Я не хочу (и не могу) преподавать матанализ студентам или обучать ученых. Но будет ли плохо, если каждый сможет понимать матанализ на том «неточном» уровне, на котором его понимал Ньютон? Чтобы это также изменило мир для вас, как когда-то изменило для него?

Преждевременная концентрация на точности рассредоточивает учеников и делает математику сложной для изучения. Вот хороший пример: число е технически определено пределом, но открыто оно было именно с помощью интуитивной догадки о росте. Натуральный логарифм может выглядеть как интеграл, или время, которому нужно расти. Какие объяснения лучше помогут новичкам?

Давайте немного порисуем от руки, а в химию погрузимся уже по ходу дела. Приятных вычислений.

(P.S: Один любезный читатель создал анимированное слайд-шоу powerpoint, которое помогает презентовать эту идею более наглядно (лучше посмотреть ее в PowerPoint, там будут видны анимации). Спасибо!)

Перевод статьи «A Gentle Introduction To Learning Calculus»

zero2hero.org

Школьная математика, онлайн-учебник: 1 класс и старше – бесплатно

Вопросы и комментарии

22 августа, 2018 – 10:43

Иштван

14 июня, 2018 – 17:30

Абу

14 июня, 2018 – 17:28

Абу

 Ответить  

13 июня, 2018 – 03:06

Абу

19 апреля, 2018 – 17:57

VzlomT13

 Ответить  

19 апреля, 2018 – 17:56

VzlomT13

15 апреля, 2018 – 17:53

людмила

 Ответить  

14 апреля, 2018 – 13:24

Жасур

 Ответить  

9 октября, 2017 – 20:26

Даниэль

10 января, 2017 – 18:50

Евгений

 Ответить  

9 декабря, 2016 – 19:58

Гость

 Ответить  

24 ноября, 2016 – 03:06

Никита

17 ноября, 2016 – 12:21

tihiro

16 ноября, 2016 – 10:29

оксана

 Ответить  

30 сентября, 2016 – 23:54

Гость

13 сентября, 2016 – 13:43

А Мир

 Ответить  

14 апреля, 2016 – 17:57

Ваня

7 февраля, 2016 – 23:15

инесса

 Ответить  

29 октября, 2015 – 11:29

Елена

21 июля, 2015 – 00:27

Victor

21 июля, 2015 – 15:43

Леонид Некин

21 июля, 2015 – 20:01

Victor

27 июня, 2015 – 11:02

Сафия

5 февраля, 2015 – 07:12

таня короткова…

 Ответить  

27 января, 2015 – 13:45

Дмитрий

 Ответить  

23 ноября, 2014 – 15:59

мари)

 Ответить  

9 ноября, 2014 – 10:41

Елена

 Ответить  

30 октября, 2014 – 12:48

йогу тимати

29 апреля, 2014 – 00:04

ggg

 Ответить  

8 декабря, 2013 – 23:46

Саша

17 ноября, 2013 – 14:01

лера

15 октября, 2013 – 16:58

Orla Colgan

 Ответить  

22 марта, 2013 – 23:03

Akella

6 февраля, 2013 – 15:31

zonenblumen

Страницы: 1  2   >  >>

nekin.info

Related Posts

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *