Правило лопиталя калькулятор онлайн – Калькулятор решения пределов – 14 Июля 2013 – Примеры решений задач
- Комментариев к записи Правило лопиталя калькулятор онлайн – Калькулятор решения пределов – 14 Июля 2013 – Примеры решений задач нет
- Советы абитуриенту
Правило Лопиталя · Калькулятор Онлайн
Введите функцию и точку для предела, которому надо применить правило Лопиталя
Вычислим предел функции с помощью правила Лопиталя. Вы введёте функцию, для которой требуется вычислить предел и точку в которой предел должен сходиться.
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число – “Пи”, которое примерно равно 3.14
- sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- – умножение
- 3/x
- – деление
- x^3
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
www.kontrolnaya-rabota.ru
Нахождение предела функции в точке по правилу Лопиталя
Калькулятор ниже находит предел функции по правилу Лопиталя (через производные числителя и знаменателя). Описание правила смотри ниже.
Допустимые операции: + – / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Точка в которой необходимо посчитать предел
Точность вычисленияЗнаков после запятой: 2
Правило Лопиталя
Предел функции в точке
Сохранить share extension
Правило Лопиталя
Если выполняются следующие условия:
- пределы функций f(x) и g(x) равны между собой и равны нулю или бесконечности:
или ; - функции g(x) и f(x) дифференцируемы в проколотой окрестности a;
- производная функции g(x) не равна нулю в проколотой окрестности a
- и существует предел отношения производной f(x) к производной g(x):
Тогда существует предел отношения функций f(x) и g(x):
,
И он равен пределу отношения производной функции f(x) к производной функции g(x):
В формуле допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:
+ — сложение
– — вычитание
* — умножение
/ — деление
^ — возведение в степень
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) – кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
planetcalc.ru
Вычислить предел (лимит) онлайн
Выберите переменную: x y z n k m и предел Ввести самому + Бесконечность – Бесконечность 0
| x | y | π | e | 1 | 2 | 3 | ÷ | триг. функции | |||
| a2 | ab | ab | exp | 4 | 5 | 6 | × | стереть |
|||
| ( | ) | |a| | ln | 7 | 8 | 9 | – | ↑ | ↓ | ||
| √ | 3√ | C | loga | 0 | . | ↵ | + | ← | → | ||
| TRIG: | sin | cos | tan | cot | csc | sec | назад | |||
| INVERSE: | arcsin | arccos | arctan | acot | acsc | asec | стереть |
|||
| HYPERB: | sinh | cosh | tanh | coth | x | π | ↑ | ↓ | ||
| OTHER: | ‘ | , | y | = | < | > | ← | → | ||
Вычисление пределов функций онлайн
Предел функции
Решение пределов функции онлайн. Найти предельное значение функции либо функциональной последовательности в точке, вычислить предельное значение функции на бесконечности. определить сходимость числового ряда и многое другое можно выполнить благодаря нашему онлайн сервису – вычислить предел функции онлайн. Мы позволяем находить лимиты функций онлайн быстро и безошибочно. Вы сами вводите переменную функции и предел, к которому она стремится, анаш сервис проводит все вычисления за вас, выдавая точный и простой ответ. Причем для нахождения предела онлайн вы можете вводить как числовые ряды, так и аналитические функции, содержащие константы в буквенном выражении. В этом случае найденный предел функции будет содержать эти константы как постоянные аргументы в выражении. Нашим сервисом решаются любые сложные задачи по нахождению
Одним из основных понятий математического анализа является лимит функции и предел последовательности в точке и на бесконечности, важно уметь правильно решать пределы. С нашим сервисом это не составит никакого труда. Производится решение пределов онлайн в течение нескольких секунд, ответ точный и полный. Изучение математического анализа начинается с предельного перехода, пределы используются практически во всех разделах высшей математики, поэтому полезно иметь под рукой сервер для решения лимитов онлайн, каковым является matematikam.ru.
Похожие сервисы:
Calculate limit online
matematikam.ru
Решение предела функции · Калькулятор Онлайн
Введите функцию и точку, для которых надо вычислить предел
Сайт предоставляет ПОДРОБНОЕ решение по нахождению предела функции.Займемся вычислением (решением) пределов функций в точке. Дана функция
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число – “Пи”, которое примерно равно 3.14
- sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- – умножение
- 3/x
- – деление
- x^3
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
www.kontrolnaya-rabota.ru
Предел функции по правилу Лопиталя
Калькулятор вам найдет предел функции по правилу Лопиталя ( напомним что это некий способ нахождения предела функции, раскрывающий такие неопределенности как 0/0 и бесконечность ∞/∞ ). Кому интересно больше узнать о методике данного способа, то вы это можете сделать на данной странице:
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
hostciti.net
Правило Лопиталя: теория и примеры решений
Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).
Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю
(),
то предел отношения этих функций равен пределу отношения их производных
().
Правило Лопиталя для случая предела двух бесконечно больших величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности
(),
то предел отношения этих функций равен пределу отношения их производных
().
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).
Замечания.
1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x = a.
2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе – производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
.
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.
Пример 6. Вычислить
.Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.
Пример 7. Вычислить
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида – ∞/∞, а затем неопределённость вида 0/0.
Пример 8. Вычислить
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.
Применить правило Лопиталя самостоятельно, а затем посмотреть решение
Пример 11. Вычислить
.
Решение. Получаем
(здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как
а затем применили правила Лопиталя).
Пример 12. Вычислить
.
Решение. Получаем
В этом примере использовано тригонометрическое тождество .
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
.
Итак,
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
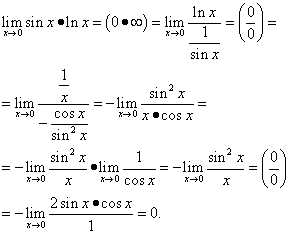 .
.
Итак,
Пример 15. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
Итак,
.
Это случаи, когда вычисление предела разности функций приводит к неопределённости “бесконечность минус бесконечность”: .
Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:
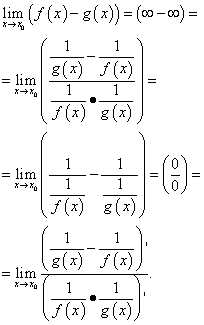
В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т.д.
Пример 16. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Пример 17. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Весь блок “Производная”
function-x.ru
Вычислить пределы используя правило Лопиталя
Чтобы вычислить пределы, используя правило Лопиталя, вспомним его сущность:
Если при непосредственной подстановке вместо х значения, к которому он стремится, получают неопределенность вида бесконечность на бесконечность или ноль на ноль, то их можно раскрыть с помощью вычисления вместо функций числителя и знаменателя их производных.
Пример 1.
Найдем .
Решение.
Подставим вместо х значение, к которому он стремится (то есть ):
В этом случае мы можем воспользоваться правилом Лопиталя и избавиться от этой неопределенности:
Ответ. .
Применив правило Лопиталя, можно опять получить неопределенность этих двух видов (, ). Тогда это правило можно применять еще сколько угодно раз.
Пример 2.
Найдем .
Решение.
Подставим значение х:
Избавимся от полученной неопределенности, вычислив предел от частного производных числителя и знаменателя:
Получили снова неопределенность . Можем применить правило Лопиталя еще раз:
Обратим внимание, что когда применяете правило Лопиталя не один раз, то нужно каждый раз проверять раскрылась ли неопределенность. В противном случае получится неправильный результат.
ru.solverbook.com



