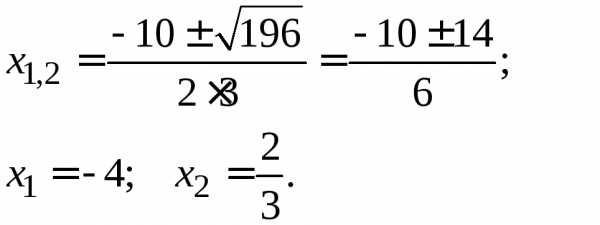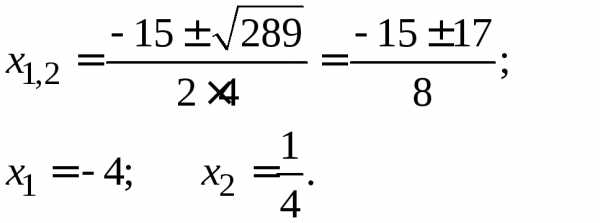Предел 1 бесконечность – 7.Правила лопиталя для раскрытия неопределённостей вида 0/0 и бесконечность/бесконечность. Раскрытие неопределённостей вида 0*бесконечность, бесконечность-бесконечность, 1бесконечность, 00
- Комментариев к записи Предел 1 бесконечность – 7.Правила лопиталя для раскрытия неопределённостей вида 0/0 и бесконечность/бесконечность. Раскрытие неопределённостей вида 0*бесконечность, бесконечность-бесконечность, 1бесконечность, 00 нет
- Советы абитуриенту
- один в степени бесконечность | Математика
- 1 в степени бесконечность | Научные парадоксы Wiki
- Число в степени бесконечность | Математика
- Устранение неопределённости «единица в степени бесконечность» — Мегаобучалка
- 1 в степени бесконечность — Энциклопедия научных парадоксов
- Предел функции одной переменной
- 7.Правила лопиталя для раскрытия неопределённостей вида 0/0 и бесконечность/бесконечность. Раскрытие неопределённостей вида 0*бесконечность, бесконечность-бесконечность, 1бесконечность, 00
один в степени бесконечность | Математика
Рассмотрим, как раскрывается неопределенность один в степени бесконечность в другой форме записи 2 замечательного предела. В этом случае фактически имеем неопределенность один в степени один на ноль.
Второй замечательный предел иначе можно записать так:
а если α=f(x), при условии f(x)→0, при x→0, имеем:
Рассмотрим на примерах, как раскрыть неопределенность один в степени бесконечность в этом случае.
Найти пределы:
Получили неопределенность один в степени один на ноль. Поскольку
Чтобы воспользоваться модификацией второго замечательного предела и раскрыть неопределенность один в степени бесконечность, рассуждаем так:
(не забываем о требовании f(x)→0, при x→0).
Чтобы избавиться от неопределенности ноль на ноль в показателе степени, в числителе выносим за скобки общий множитель x и сокращаем дробь на x:
Будьте внимательны! Если в примере нет неопределенности, предел вычисляем непосредственно:
Неопределенность вида ноль на ноль в показателе степени — первый замечательный предел:
www.matematika.uznateshe.ru
1 в степени бесконечность | Научные парадоксы Wiki
| ||
|
$ 1^\infty $ — это один из примеров математической неопределённости.
Парадокс заключается в том, что любая степень единицы равна самой единице: $ 1^a=1 $. Следовательно, и $ 1^\infty=1 $. Таким образом, это не должно быть неопределённостью. Дополнить парадокс автора филосовской фразой можно так, “ква! хрю!кря!”, это и есть та самая определенность …
и даже то, что некоторые трактуют это тем, что неизвестно-чистая единица или с хвостом, все равно в многозначной степени 1 есть 1: 1,00000000000000000000000000000000000005654600000654046540000^461654365313516546541354 есть единица. Алсо, многие считают, что парадокс – нифига не парадокс, а фигня какая-то
Так почему же это является неопределённостью? Править
По правилу Лопиталя (правило Лопиталя применяется для неопределенностей вида ноль/ноль, бесконечность/бесконечность. А здесь надо логарифимировать предел и переходить к произведению в степени.) $ \lim_{x\to \infty}{1^x}=\lim_{x\to \infty}{x \cdot 1^{x-1}} $. Но поскольку $ x=\infty $ (по условию), то одним из множителей второго предела является $ \infty $, что уже говорит о том, что вычислить этот предел невозможно. Таким образом, $ 1^\infty $ является неопределённостью, и это доказано.
ru.scienceparadoxes.wikia.com
Число в степени бесконечность | Математика
Если при нахождении предела получаем число в степени бесконечность, то для отличных от нуля и единицы значений такое выражение не является неопределенностью и вычисляется непосредственно.Поскольку показательная функция
при а>1 возрастает, то для таких а
При 0<а<1 показательная функция убывает, поэтому в этом случае ее значение на бесконечности стремится к нулю :
Соответственно, применение второго замечательного предела здесь не требуется. Используем следующее свойство пределов:
при условии, что эти пределы существуют.
Рассмотрим примеры, в которых нужно найти число в степени бесконечность.
Найти пределы функций:
1)
Получили неопределенность бесконечность на бесконечность в степени бесконечность.
Найдем пределы основания и показателя степени. (Как находить предел бесконечность на бесконечность, уже рассматривали ранее. Делим и числитель, и знаменатель на старшую степень икса, в данном случае — на x.)
Таким образом, приходим к выводу, что
2) Вычислить предел функции:
Рассуждаем аналогично. При нахождении предела основания степени делим многочлены в числителе и знаменателе на старшую степень икса, то есть на x²:
www.matematika.uznateshe.ru
Устранение неопределённости «единица в степени бесконечность» — Мегаобучалка
Данную неопределённость «обслуживает» второй замечательный предел, и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёттолько об определённости и никакой другой
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы, которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-ой замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
Используем формулу
Чтобы не таскать за собой букву «е» и не мельчить, показатель удобнее вычислить отдельно:
В данном случае:
Таким образом:
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.
В результате:
Готово.
Обещанный подарок с разностью логарифмов и неопределённостью :
Пример 19
Вычислить предел
Сначала полное решение, потом комменты:
(1)-(2) На первых двух шагах используем формулы . У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы, преобразуем неопределённость к виду .
(6) Используем формулу .
(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: . Минус перед дробью вносим в знаменатель:
(8) Без комментариев =)
Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде и заменой свести решение к случаю .
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости . Данную неопределённость далеко не всегда можно свести к неопределённости и воспользоваться 2-ым замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции. На пример: .
Отвлечёмся от показателя и вычислим предел основания:
В пределе получена единица, значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны. На уроке Замечательные пределы. Примеры решениймы без проблем свели данный пример к неопределённости и получили ответ.
Аналогичных пределов можно придумать очень много:
и т.д.
Дроби данных примеров объединяет вышеуказанная особенность: . В других случаях при неопределённости 2-ой замечательный предел не применим.
Пример 21
Найти пределы
Как ни старайся, а неопределённость не удастся преобразовать в неопределённость
Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты: .
Таким образом, 2-ой замечательный предел и, тем более формулу,
! Примечание: не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменательоснования разделить на «икс» в старшей степени (невзирая на показатель):
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может не быть вообще:
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Пример 2
Старшая степень числителя: 2; старшая степень знаменателя: 3.
Разделим числитель и знаменатель на :
Пример 4
Разделим числитель и знаменатель на :
Примечание: самым последним действием умножили числитель и знаменатель на , чтобы избавиться от иррациональности в знаменателе.
Пример 6
Разделим числитель и знаменатель на :
Пример 8
Разделим числитель и знаменатель на :
Примечание: слагаемое стремиться к нулю медленнее, чем , поэтому является «главным» нулём знаменателя.
Пример 10
Пример 12
Умножим и разделим на сопряженное выражение:
Пример 13
Умножим и разделим на сопряженное выражение:
Разделим числитель и знаменатель на :
Пример 15
Проведём замену:
Если , то .
Пример 17
Проведём замену:
Если , то .
Далее используем формулу приведения , тригонометрическую формулу и первый замечательный предел:
Пример 20
Используем формулу
Пример 22
Примечание: бесконечно малая функция стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую роль:
megaobuchalka.ru
1 в степени бесконечность — Энциклопедия научных парадоксов
Материал из Энциклопедия научных парадоксов
| ||
|
1∞{\displaystyle 1^{\infty }} — это один из примеров математической неопределённости.
Парадокс заключается в том, что любая степень единицы равна самой единице: 1a=1{\displaystyle 1^{a}=1}. Следственно, и 1∞=1{\displaystyle 1^{\infty }=1}. Таким образом, это не должно быть неопределённостью.
Так почему же это является неопределённостью?[править]
1∞{\displaystyle 1^{\infty }} — это неформальная запись предела lim(x;y)→(1;+∞)xy{\displaystyle \lim _{(x;y)\to (1;+\infty )}{x^{y}}}. Если сначала устремить x{\displaystyle x} к 1{\displaystyle 1}, а потом уже y{\displaystyle y} к +∞{\displaystyle +\infty }, то получится действительно 1{\displaystyle 1}. Но если сначала устремить y{\displaystyle y} к +∞{\displaystyle +\infty }, а потом x{\displaystyle x} к 1{\displaystyle 1} сверху, то получится +∞{\displaystyle +\infty }. А если сначала устремить y{\displaystyle y} к +∞{\displaystyle +\infty }, а потом x{\displaystyle x} к 1{\displaystyle 1} снизу, то получится 0{\displaystyle 0}. Сам же предел lim(x;y)→(1;+∞)xy{\displaystyle \lim _{(x;y)\to (1;+\infty )}{x^{y}}} может принимать любые значения от 0{\displaystyle 0} до +∞{\displaystyle +\infty }, например, limx→+∞(1+1/x)x=e=2,71…{\displaystyle \lim _{x\to +\infty }{(1+1/x)^{x}}=e=2,71…}
paradox.pifia.ru
Предел функции одной переменной
§. Предел функции
Квантор всеобщности:  – любой, каждый, всякий.
– любой, каждый, всякий.
Квантор существования:  – существует, найдется.
– существует, найдется.
Конечный предел функции в точке
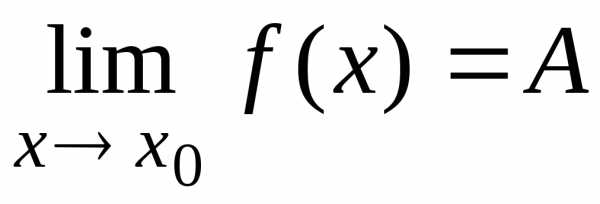

Конечный предел функции на бесконечности
2.
или

1. Теоремы о пределах.
Пусть существуют
конечные пределы 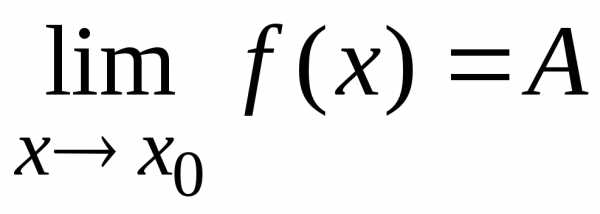 и
и 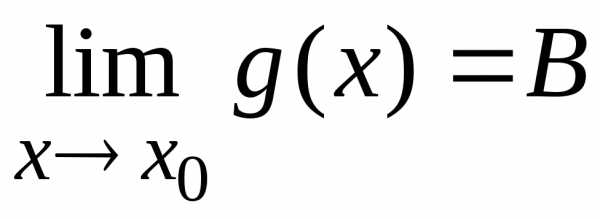 .
Тогда справедливы следующие утверждения:
.
Тогда справедливы следующие утверждения:
;
;
 ,
если
,
если  .
.
2. Бесконечно малые и бесконечно большие функции.
Бесконечно малой
функцией при  называется
функция
называется
функция  ,
предел которой равен нулю при
,
предел которой равен нулю при :
: .
.
Если значения
функции f(x) неограниченно возрастают по абсолютной
величине при  ,
то такую функцию называют бесконечно большой при
,
то такую функцию называют бесконечно большой при  .Предел этой
функции обозначают знаком бесконечности
.Предел этой
функции обозначают знаком бесконечности  :.
:.
Теорема о связи бесконечно малых и бесконечно больших функций.
Если 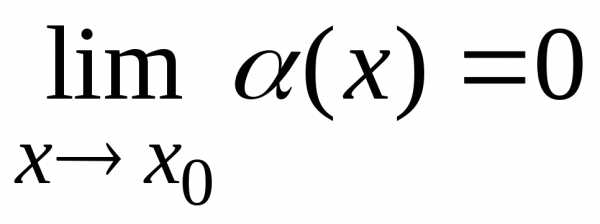 ,
то
,
то .
.
Если 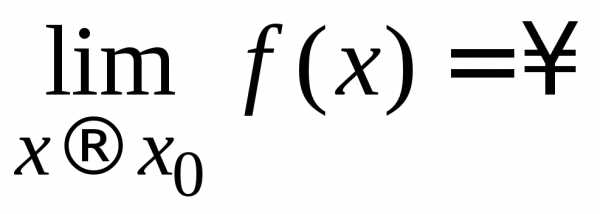 ,
то
,
то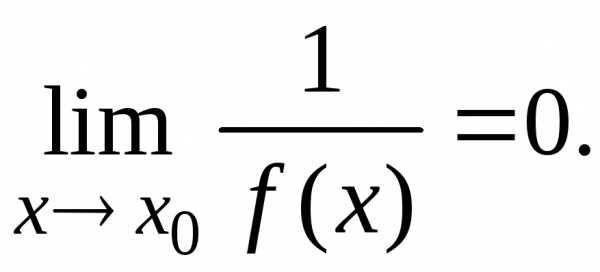
Задача. Вычислить пределы
функции 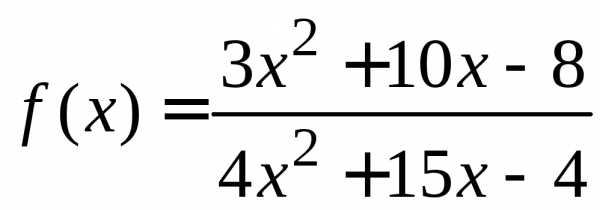 при
при
Решение. В задаче следует найти предел частного. С этой целью необходимо вычислить пределы числителя и знаменателя дроби, подставив в них предельное значение аргумента.
а) .
Здесь применима теорема о пределе частного.
б)  .
.
При подстановке 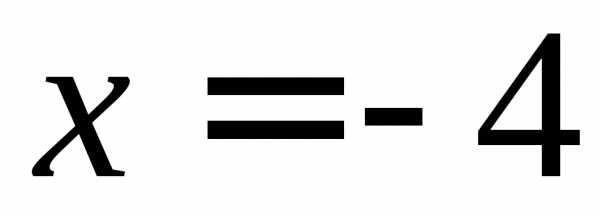 в числитель и знаменатель дроби
убеждаемся, что их значения равны нулю,
поэтому теорема о пределе частного
здесь не применима. В данном случае
говорят, что имеется неопределенность
вида
в числитель и знаменатель дроби
убеждаемся, что их значения равны нулю,
поэтому теорема о пределе частного
здесь не применима. В данном случае
говорят, что имеется неопределенность
вида .
.
Неопределенность
вида  при
при может быть раскрыта сокращением дроби
на множитель вида (х–х0), который
обращает числитель и знаменатель дроби
в нуль, в данном случае на (х+4).
Поэтому, следует разложить на множители
числитель и знаменатель дроби (п.2 и
п.3 прил.1).
может быть раскрыта сокращением дроби
на множитель вида (х–х0), который
обращает числитель и знаменатель дроби
в нуль, в данном случае на (х+4).
Поэтому, следует разложить на множители
числитель и знаменатель дроби (п.2 и
п.3 прил.1).
3х2+10х – 8 = 0; | 4х2+15х– 4 = 0; |
D = | D = |
|
|
3х2+10х–8 = 3(х+4)(х–2/3) = | 4х2+15х – 4 = 4(х+4)(х–1/4 ) = |
= (х+4)(3х–2). | = (х+4)(4х–1). |
Таким образом,
в)
Здесь применима теорема о пределе частного, так как существуют конечные пределы числителя и знаменателя, и предел знаменателя не равен нулю.
г)
Здесь использована теорема о связи бесконечно малой и бесконечно большой функций.
д) 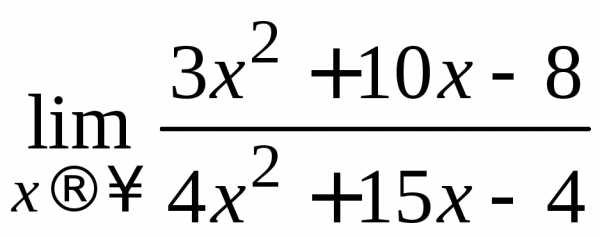 .
.
Пределы числителя
и знаменателя дроби равны  .
В этом случае говорят, что имеется
неопределенность вида «бесконечность
на бесконечность». Теорема о пределе
частного здесь не применима.
.
В этом случае говорят, что имеется
неопределенность вида «бесконечность
на бесконечность». Теорема о пределе
частного здесь не применима.
Чтобы раскрыть
неопределенность вида  при,
каждый член числителя и знаменателя
дроби делят наx в наивысшей степени (в нашем примере
на х2),
отчего величина дроби не изменится, но
исчезнет неопределенность.
при,
каждый член числителя и знаменателя
дроби делят наx в наивысшей степени (в нашем примере
на х2),
отчего величина дроби не изменится, но
исчезнет неопределенность.
так
как 
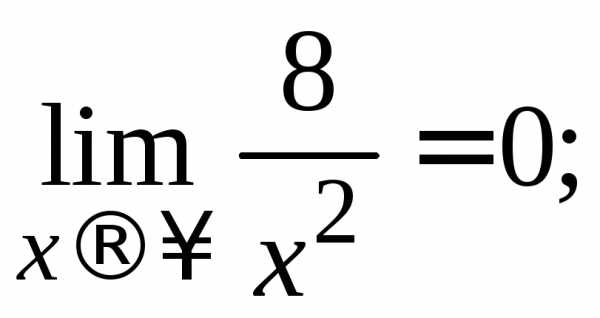
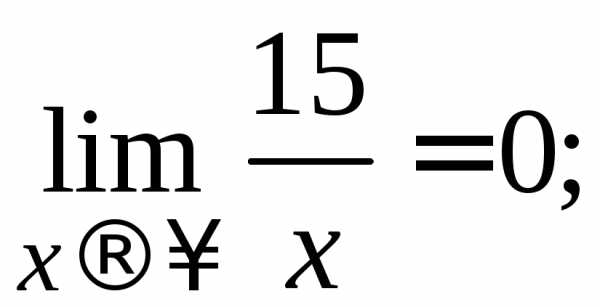
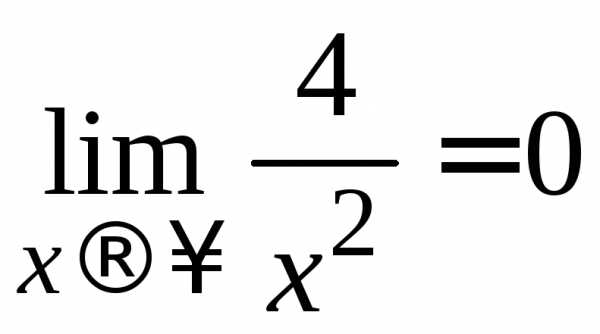
(по теореме о связи бесконечно большой и бесконечно малой функций).
Замечание. Полезно запомнить, что при предел отношения многочленов c одинаковыми наивысшими степенями равен отношению коэффициентов при этих степенях.
В нашем примере,
коэффициенты при наивысшей степени х2 многочленов
равны 3 и 4, поэтому и предел дроби равен  .
.
Ответы.
Замечательные пределы,
эквивалентные бесконечно малые функции
1. Замечательные пределы:
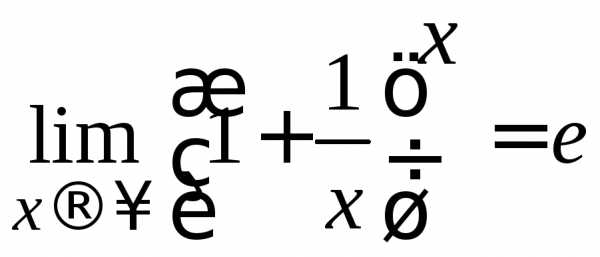 ,
,
или в другой
форме: 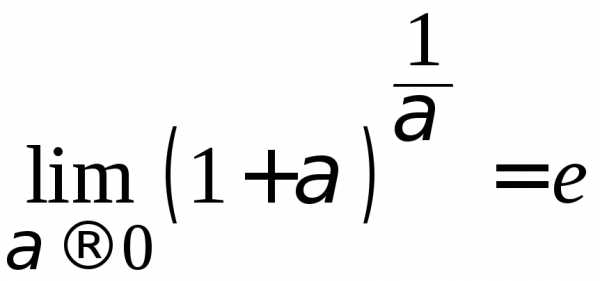 ,
,
где – иррациональное число.
Второй замечательный
предел используется для раскрытия
неопределенности вида  .
.
2.
Две бесконечно малые функции  (x) и
(x) и 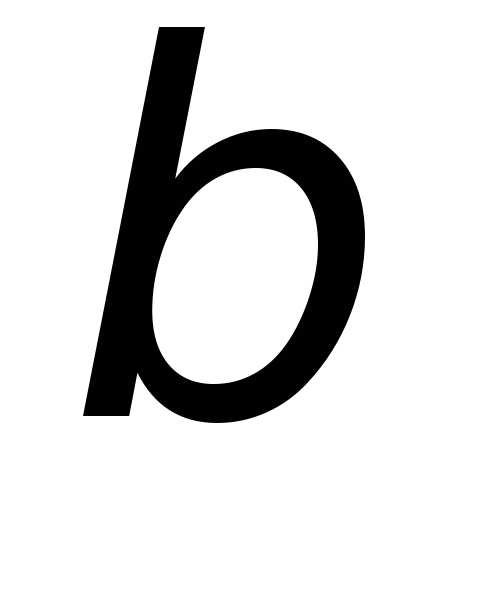 (x) называются эквивалентными
при
(x) называются эквивалентными
при  ,
если
,
если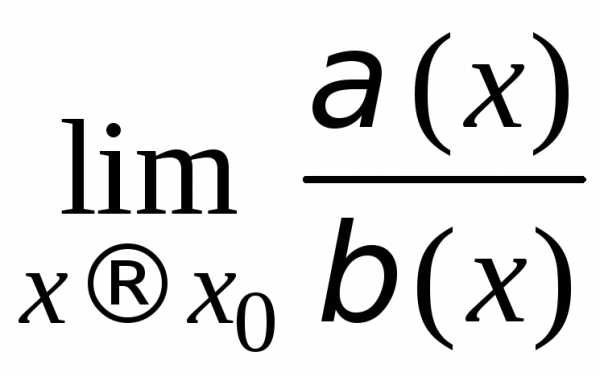 = 1. В этом случае пишут(x)
~(x) при
= 1. В этом случае пишут(x)
~(x) при  .
.
Предел отношения двух бесконечно малых функции не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой функцией.
Наиболее часто используют эквивалентность следующих бесконечно малых функций при :
Задача. Вычислить пределы: а)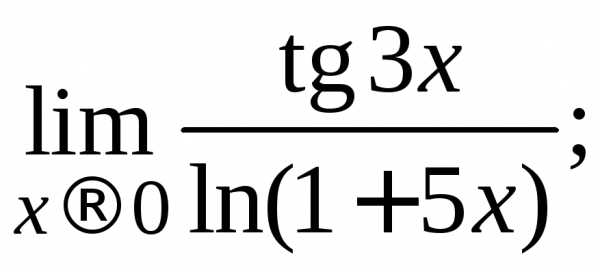 б)
б) 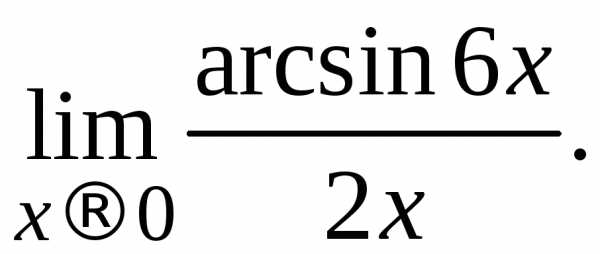
Решение.
В рассматриваемых
задачах неопределенность вида  была раскрыта после замены бесконечно
малых функций на эквивалентныеим
и сокращения полученных дробей на
бесконечно малую функцию х.
была раскрыта после замены бесконечно
малых функций на эквивалентныеим
и сокращения полученных дробей на
бесконечно малую функцию х.
Ответ. 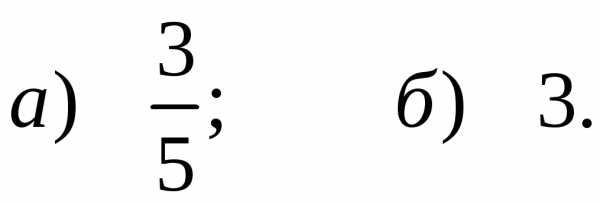
Задача. Вычислить предел 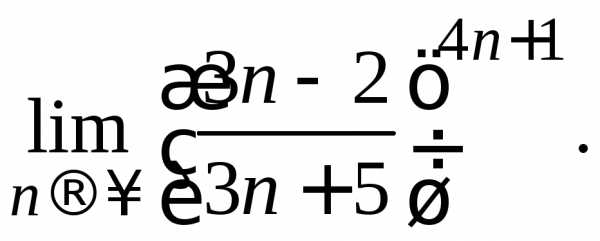
Решение.
Очевидно, что
Далее воспользуемся вторым замечательным пределом:
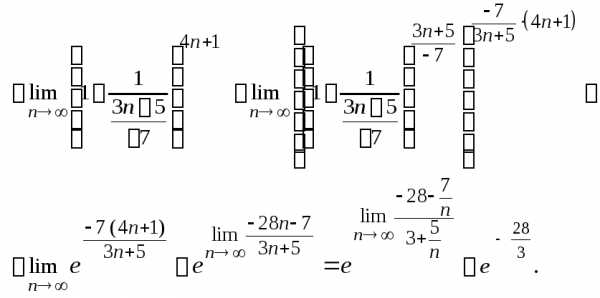
Ответ. 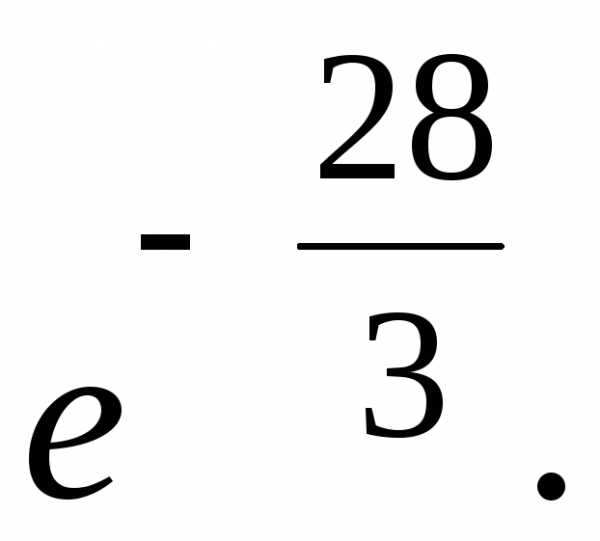
studfiles.net
7.Правила лопиталя для раскрытия неопределённостей вида 0/0 и бесконечность/бесконечность. Раскрытие неопределённостей вида 0*бесконечность, бесконечность-бесконечность, 1бесконечность, 00
Правило Лопиталя-пусть функция f(x) и g(x) имеют производные в окрестности точки хо тогда: 1)если lim f(x)= lim g(x)=бесконечность, то limf(x)/g(x)=(бесконечность/бесконечность)= lim f’(x)/g’(x), при условии что последний предел существует. 2)если lim f(x)=lim g(x)=0, то lim f(x)/g(x)= (0/0)= lim f’(x)/g’(x), при условии что последний существует.
Следовательно если мы имеем неопределённости бесконечность/бесконечность, 0/0, воспользоваться правилом Лопиталя означает найти производные числителя и знаменателя, а затем вычислить новый предел.
Пример lim sin4x/x=(0/0)=lim(sin4x)’/x= lim4cos4x/1=4*cos0=4*1=4
4)бесконечность-бесконечность . Пусть f стремиться к бесконечности, g стремиться к бесконечности, тогда f-g=1/(1/f)- 1/(1/g)=(1/g)-(1/f)/(1/f)*(1/g)=(0/0)
5)1бесконечность,00, бесконечность0. Данные неопределённости также сводятся к неопределённостям бесконечность/бесконечность или 0/0 . для этого можно воспользоваться формулой fg=einfg=eglnf, f>0. Так, если f стремиться к 1, g стремиться к бесконечности, то получаем неопределённость 0*бесконечность (так как ln1=0), после чего можно получить бесконечность/бесконечность или 0/0
8.Дифференциал функции.Связь дифференциала и производной.Использование дифференциала в приближенных вычислениях.
Функция f(x) называется дифференцируемой в точке х0, если ее приращение в этой точке можно представить в виде дельта y=f(x0+дельтаx)-f(x0)=A*дельтаx+a(дельтаx)
Для того чтобы функция f(x) была дифференцируемой в точке х0, необходимо и достаточно, чтобы в точке х0 существовала произвлдная f’(x)=A.
F(x0+дельтаx)-f(х0)=f’(x0)*дельтаx+a(дельтах)
Функция f’(x0)*дельтаx есть главная линейная часть приращения функции f(x) в точке х0.Эту главную линейную часть приращения функции f(x) и называется дифференциалом функции f(x) в точке х0 и обозначают df(x0)=f’(x0)*дельтаХ, в частности для f(x)=x имеем df=dx=1*дельтаХ=дельтаХ, следовательно df(x0)=f’(x0)dx
Для дифференциалов функций f и g справедливы формулы, подобные формулам для производных функций:
1)d(f+g)=df+dg
2)d(f*g)=g*df+f*dg
3)d(f/g)=(gdf-fdg)/g2
Данные формулы будут широко применяться при вычислении интегралов функций. С помощью дифференциала можно также приближенно вычислить значения функции f для ч, близких к x0, Так как отбросив бесконечно малую функцию в формуле 2, получаем: f(x0+дельтаХ)=f(x0)+f’(x0)дельтаХ
9.Исследование на монотонность функции одной переменной. Точки экстремума. Необходимые и достаточные условия существования экстремума.
Пусть задана функция y=f(x) на множестве Х и х0-внутренняя точка множества Х.
Обозначим через U(x0) окрестность точки х0.В точке х0 функция f(x) имеет локальный максимум, если существует такая окрестность U(x0) точки х0, что для всех х из этой окрестности выполнено условие f(x)<=f(x0).
Точки локальных максимума и минимума называются точки локальных экстремумов, а значения функции в них-локальными экстремумами функции.Пусть функция f(x) определена на отрезке[a,b] и имеет локальный экстремум на каком0то из концов этого отрезка.Тогда такой экстремум называется локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для точки а и левой для точки b полуокрестностью.
Критическими точками , т.е. точки подозрительные на экстремум функции на интервале [a,b] , являются точки,в которых производная существует и равна 0 либо она не существует или равна бесконечности.
Первое достаточное условие экстремума-пусть непрерывная функция диффиринцируема в некоторой проколотой окрестности U(x0) точки х0, тогда: 1)если f’(x)>0 при х<x0, х принадлежит U(х0) и f’(x)<0 при х>x0, x принадлежит U(x0), то в точке х0-локальный максимум
2)если f’(x)<0 при x<x0 х принадлежит U(x0) и f’(x)>0при x>x0 x принадлежит U(x0), то в точке х0 локальный минимум.
Функция называется n раз непрерывно-дифференцируемой на некотором промежутке, если на этом промежутке она имеет непрерывные производные до порядка n включительно (n=0,1,2,….)
Второе достаточное условие экстремума- пусть функция f(x) дважды непрерывно-дифференцируема. Если х0-стационарная точка (f’(x0)=0) в которой f’’(x0)>0, то в точке х0 функция имеет локальный минимум. Если же f’’(x0)< 0 то в точке х0 функция имеет локальный максимум.
studfiles.net

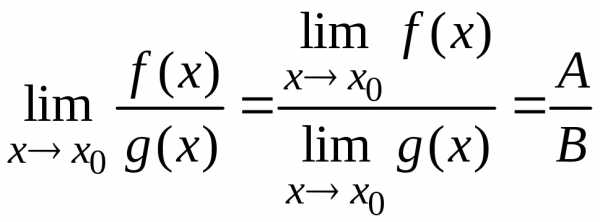 ,
если
,
если 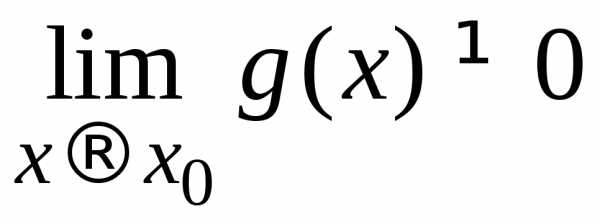 .
.